Physical Background, Computations and Practical Issues of the Magnetohydrodynamic Pressure Drop in a Fusion Liquid Metal Blanket
Abstract
:1. Introduction
- -
- Mechanical stresses in the structural walls are above the materials limit;
- -
- High pumping power that diminishes the overall blanket efficiency;
- -
- Unavailability of high capacity LM pumps.
2. Examples of LM Breeding Blankets and Their Pressure Drop
3. Mathematical Formulation of the Problem
3.1. Governing Equations of LM MHD Flows
3.2. Boundary Conditions
3.3. Dimensionless Form of of Governing Equations and Basic Dimensionless Numbers
4. Special Classes of MHD Flows in a LM Blanket
4.1. Fully Developed MHD Flows
4.2. Quasi-Two-Dimensional Turbulent MHD Flows
4.3. MHD Flows with Buoyancy Effects
5. Origins of the MHD Pressure Drop in a Blanket
6. 2D and 3D MHD Pressure Drop
7. MHD Pressure Drop in Electrically Coupled Blanket Components
8. Approaches to Calculation of the MHD Pressure Drop in a Blanket
- R1 is associated with the poloidal flow in the “cold” feeding duct;
- R2—radial flow from the cold duct to a module;
- R3—flow in the expansion at the entry to a module;
- R4—poloidal (upward) flow in the front duct facing the plasma;
- R5—flow in the U-turn at the top of the module;
- R6—poloidal (downward) flow in the return duct;
- R7—flow in the contraction at the exit from the module;
- R8—radial flow from the exit of a module to the collecting “hot” duct;
- R9—poloidal flow in the “hot” collecting duct.
8.1. Exact Analytical Solutions
8.2. Asymptotic Solutions
8.2.1. Rectangular Duct with Non-Conducting Walls in a Transverse Magnetic Field
8.2.2. Rectangular Duct with Non-Conducting Walls in an Inclined Magnetic Field
8.2.3. Rectangular Duct with Non-Conducting Hartmann Walls and Ideally Conducting Side Walls in a Transverse Magnetic Field
8.2.4. Rectangular Duct with Ideally Conducting Side and Hartmann Walls in a Transverse Magnetic Field
8.2.5. Rectangular Duct with Thin Electrically Conducting Walls in a Transverse Magnetic Field
8.2.6. Circular Pipe with Thin Electrically Conducting Walls in a Transverse Magnetic Field
8.3. Asymptotic Numerical Techniques. Core Flow Approximation
8.4. Full Numerical Computations
8.5. Experiments
9. Examples of 3D Numerical Computations of the MHD Pressure Drop
9.1. MHD Flow Computations for a PbLi Blanket Prototype at Ha ~ 104
9.2. Computations and Analysis of MHD Pressure Drop in the Inlet and Outlet Manifolds of the DCLL Blanket
10. Practical Approaches to Mitigate the MHD Pressure Drop
10.1. Electrical Insulation
10.1.1. Flow Channel Inserts
10.1.2. Electroinsulating Coatings
10.2. Slotted Channel Geometry
10.3. Poloidal, Toroidal and Radial Flows
10.4. Geometrical Discontinuities
11. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdou, M.; Morley, N.B.; Smolentsev, S.; Ying, A.; Malang, S.; Rowcliffe, A.; Ulrickson, M. Blanket/first wall challenges and required R&D on the pathway to DEMO. Fusion Eng. Des. 2015, 100, 2–43. [Google Scholar]
- Smolentsev, S.; Moreau, R.; Bühler, L.; Mistrangelo, C. MHD thermofluid issues of liquid-metal blankets: Phenomena and advances. Fusion Eng. Des. 2010, 85, 1196–1205. [Google Scholar] [CrossRef]
- Smith, D.L.; Baker, C.C.; Sze, D.K.; Morgan, G.D.; Abdou, M.A.; Piet, S.J.; Schultz, K.R.; Moir, R.W.; Gordon, J.D. Overview of the blanket comparison and selection study. Fusion Technol. 1985, 8, 10–113. [Google Scholar] [CrossRef]
- Shercliff, J.A. A Textbook of Magnetohydrodynamics; Pergamon Press: Oxford, UK, 1965. [Google Scholar]
- Roberts, P.H. An Introduction to Magnetohydrodynamics; Longmans, Green and Co.: Harlow, UK, 1967. [Google Scholar]
- Vatazhin, A.; Lyubimov, G.; Regirer, S. Magnetohydrodynamic Flows in Ducts; Nauka: Moscow, Russia, 1970. (In Russian) [Google Scholar]
- Branover, H. Magnetohydrodynamic Flows in Ducts; Halsted Press: New York, NY, USA, 1978. [Google Scholar]
- Glukhih, V.A.; Tananaev, A.V.; Kirillov, I.R. Magnetohydrodynamics in Power Engineering; Energoatomizdat: Moscow, Russia, 1987. (In Russian) [Google Scholar]
- Moreau, R. Magnetohydrodynamics; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 1990. [Google Scholar]
- Müller, U.; Bühler, L. Magnetofluiddynamics in Channels and Containers; Springer: Berlin, Germany, 2001. [Google Scholar]
- Davidson, P.A. An Introduction to Magnetohydrodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Molokov, S.; Moreau, R.; Moffatt, H.K. (Eds.) Magnetohydrodynamics. Historical Evolution and Trends; Springer: Berlin, Germany, 2007. [Google Scholar]
- Lielausis, O. Liquid-Metal Magnetohydrodynamics. At. Energy Rev. 1975, 13, 527–581. [Google Scholar]
- Malang, S.; Leroy, P.; Casini, G.; Mattas, R.; Strebkov, Y. Crucial issues on liquid metal blanket design. Fusion Eng. Des. 1991, 16, 95–109. [Google Scholar] [CrossRef]
- Kirillov, I.R.; Reed, C.B.; Barleon, L.; Miyazaki, K. Present understanding of MHD and heat transfer phenomena for liquid metal blankets. Fusion Eng. Des. 1995, 27, 553–569. [Google Scholar] [CrossRef] [Green Version]
- Morley, N.; Smolentsev, S.; Barleon, L.; Kirillov, I.; Takahashi, M. Liquid magnetohydrodynamics—Recent progress and future directions for fusion. Fusion Eng. Des. 2000, 51–52, 701–713. [Google Scholar] [CrossRef] [Green Version]
- Morley, N.B.; Malang, S.; Kirillov, I. Thermofluid magnetohydrodynamic issues for liquid breeders. Fusion Sci. Tech. 2005, 47, 488–501. [Google Scholar] [CrossRef]
- Mistrangelo, C.; Bühler, L.; Smolentsev, S.; Klüber, V.; Maione, I.; Aubert, J. MHD flow in liquid metal blankets: Major design issues, MHD guidelines and numerical analysis. Fusion Eng. Des. 2020. Submitted. [Google Scholar]
- Reimann, J.; Barleon, L.; Bühler, L.; Lenhart, L.; Malang, S.; Molokov, S.; Platnieks, I.; Stieglitz, R. Magnetohydrodynamic investigations of a self-cooled Pb-17Li blanket with poloidal-radial-toroidal ducts. Fusion Eng. Des. 1995, 27, 593–606. [Google Scholar]
- Smolentsev, S.; Wong, C.; Malang, S.; Dagher, M.; Abdou, M. MHD considerations for the DCLL inboard blanket and access ducts. Fusion Eng. Des. 2010, 85, 1007–1011. [Google Scholar] [CrossRef]
- Smolentsev, S.; Rhodes, T.; Pulugundla, G.; Courtessole, C.; Abdou, M.; Malang, S.; Tillack, M.; Kessel, C. MHD thermohydraulics analysis and supporting R&D for DCLL blanket in the FNSF. Fusion Eng. Des. 2018, 135, 314–323. [Google Scholar]
- Urgorri, F.R.; Smolentsev, S.; Fernández-Berceruelo, I.; Rapisarda, D.; Palermo, I.; Ibarra, A. Magnetohydrodynamic and thermal analysis of PbLi flows in poloidal channels with flow channel insert for the EU-DCLL blanket. Nucl. Fusion 2018, 58, 106001. [Google Scholar] [CrossRef]
- Bühler, L.; Mistrangelo, C. Theoretical studies of MHD flows in support to HCLL design. Fusion Eng. Des. 2016, 109–111, 1609–1613. [Google Scholar] [CrossRef]
- Bühler, L.; Mistrangelo, C.; Brinkmann, H.-J.; Koehly, C. Pressure distribution in MHD flows in an experimental test-section for a HCLL blanket. Fusion Eng. Des. 2018, 127, 168–172. [Google Scholar] [CrossRef]
- Bühler, L.; Mistrangelo, C. MHD flow and heat transfer in model geometries for WCLL blankets. Fusion Eng. Des. 2017, 122, 919–923. [Google Scholar] [CrossRef]
- Tassone, A.; Caruso, G.; Del Nevo, A. Influence of PbLi hydraulic path and integration layout on MHD pressure losses. Fusion Eng. Des. 2020, 155, 111517. [Google Scholar] [CrossRef]
- Rampal, G.; Li Puma, A.; Poitevin, Y.; Rigal, E.; Szczepanski, J.; Boudot, C. HCLL TBM for ITER-design studies. Fusion Eng. Des. 2005, 75–79, 917–922. [Google Scholar] [CrossRef]
- Del Nevo, A.; Arena, P.; Caruso, G.; Chiovaro, P.; Di Maio, P.A.; Eboli, M.; Edemetti, F.; Forgione, N.; Forte, R.; Froio, A.; et al. Recent progress in developing a feasible and integrated conceptual design of the WCLL BB in EUROfusion project. Fusion Eng. Des. 2019, 146, 1805–1809. [Google Scholar] [CrossRef] [Green Version]
- Aubert, J.; Aiello, G.; Arena, P.; Barret, T.; Boccaccini, L. Status of the EU DEMO HCLL breeding blanket design development. Fusion Eng. Des. 2018, 136, 1428–1432. [Google Scholar] [CrossRef]
- Smolentsev, S.; Morley, N.B.; Abdou, M.; Malang, S. Dual-Coolant Lead-Lithium (DCLL) blanket status and R&D needs. Fusion Eng. Des. 2015, 100, 44–54. [Google Scholar]
- Aubert, J.; Aiello, G.; Jonqures, N.; Li Puma, A.; Morin, A.; Rampal, G. Development of the water cooled lithium lead blanket for DEMO. Fusion Eng. Des. 2014, 89, 1386–1391. [Google Scholar] [CrossRef]
- Tassone, A.; Caruso, G.; Del Nevo, A.; Di Piazza, I. CFD simulation of the magnetohydrodynamic flow inside the WCLL breeding blanket module. Fusion Eng. Des. 2017, 124, 705–707. [Google Scholar] [CrossRef]
- Tassone, A.; Siriano, S.; Caruso, G.; Utili, M. MHD pressure drop estimate for the WCLL in-magnet PbLi loop. Fusion Eng. Des. 2020, 160, 111830. [Google Scholar] [CrossRef]
- Smolentsev, S.; Cuevas, S.; Beltrán, A. Induced electric current-based formulation in computations of low magnetic Reynolds number magnetohydrodynamic flows. J. Comput. Phys. 2010, 229, 1558–1572. [Google Scholar] [CrossRef]
- Schuller, F.C. Disruptions in tokamaks. Plasma Phys. Control. Fusion 1995, 37, A135–A162. [Google Scholar] [CrossRef]
- Blanchard, J.; Martin, C. Thermal and electromagnetic transients in liquid metal surfaces of the FNSF. Fusion Sci. Tech. 2019, 75, 918–929. [Google Scholar] [CrossRef]
- Kawczynski, C.; Smolentsev, S.; Abdou, M. Characterization of the lid-driven cavity magnetohydrodynamic flow at finite magnetic Reynolds numbers using far-field magnetic boundary conditions. Phys. Fluids 2018, 30, 067103. [Google Scholar] [CrossRef]
- Krawczyk, A.; Tegopoulos, J.A. Numerical Modelling of Eddy Currents; Clarendon Press: Oxford, UK, 1993. [Google Scholar]
- Smolentsev, S. MHD duct flows under hydrodynamic “slip” condition. Theor. Comput. Fluid Dyn. 2009, 23, 557–570. [Google Scholar] [CrossRef] [Green Version]
- Walker, J.S. Magnetohydrodynamic flows in rectangular ducts with thin conducting walls. J. Mécanique 1981, 20, 79–112. [Google Scholar]
- Shercliff, J.A. The flow of conducting fluids in circular pipes under transverse magnetic fields. J. Fluid Mech. 1956, 1, 644–666. [Google Scholar] [CrossRef]
- Hunt, J.C.R. Magnetohydrodynamic flow in rectangular ducts. J. Fluid Mech. 1965, 21, 577–590. [Google Scholar] [CrossRef]
- Shercliff, J.A. Steady motion of conducting fluids in pipes under transverse magnetic fields. Proc. Camb. Phil. Soc. 1953, 49, 136–144. [Google Scholar] [CrossRef]
- Smolentsev, S.; Vetcha, N.; Abdou, M. Effect of a magnetic field on stability and transitions in liquid breeder flows in a blanket. Fusion Eng. Des. 2013, 88, 607–610. [Google Scholar] [CrossRef]
- Zikanov, O.; Krasnov, D.; Boeck, T.; Thess, A.; Rossi, M. Laminar-turbulent transition in magnetohydrodynamic duct, pipe, and channel flows. Appl. Mech. Rev. 2014, 66, 030802. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary Layer Theory, 8th ed.; Springer: Berlin, Germany, 2004. [Google Scholar]
- Pothérat, A. Quasi two-dimensional perturbations in duct flows with a transverse magnetic field. Phys. Fluids 2007, 19, 074104. [Google Scholar] [CrossRef]
- Sommeria, J.; Moreau, R. Why, how and when MHD turbulence becomes two-dimensional. J. Fluid Mech. 1982, 118, 507–518. [Google Scholar] [CrossRef]
- Smolentsev, S. Averaged model in MHD duct flow calculations. Magnetohydrodynamics 1997, 33, 42–47. [Google Scholar]
- Smolentsev, S.; Moreau, R. One-equation model for quasi-two-dimensional turbulent magnetohydrodynamic flows. Phys. Fluids 2007, 19, 078101. [Google Scholar] [CrossRef]
- Messadek, K.; Moreau, R. An experimental investigation of MHD quasi-two-dimensional turbulent shear flows. J. Fluid Mech. 2002, 456, 137–159. [Google Scholar] [CrossRef]
- Pothérat, A. Three-dimensionality in quasi-two dimensional flows: Recirculations and barrel effects. EPL 2012, 98, 64003. [Google Scholar] [CrossRef] [Green Version]
- Pothérat, A.; Sommeria, J.; Moreau, R. Numerical simulations of an effective 2d model for MHD flows. J. Fluid Mech. 2005, 534, 115–143. [Google Scholar] [CrossRef]
- Smolentsev, S.; Vetcha, N.; Moreau, R. Study of instabilities and transitions for a family of quasi-two-dimensional magnetohydrodynamic flows based on a parametric model. Phys. Fluids 2012, 24, 024101. [Google Scholar] [CrossRef]
- Vetcha, N.; Smolentsev, S.; Abdou, M.; Moreau, R. Study of instabilities and quasi-two-dimensional turbulence in volumetrically heated MHD flows in a vertical rectangular duct. Phys. Fluids 2013, 25, 024102. [Google Scholar] [CrossRef] [Green Version]
- Hamid, A.H.A.; Hussam, W.K.; Sheard, G.J. Combining an obstacle and electrically driven vortices to enhance heat transfer in a quasi-two-dimensional MHD duct flow. J. Fluid Mech. 2016, 792, 364–396. [Google Scholar] [CrossRef]
- Cassells, O.G.W.; Hussam, W.K.; Sheard, G.J. Heat transfer enhancement using rectangular vortex promoters in confined quasi-two-dimensional magnetohydrodynamic flows. Int. J. Heat Mass Transf. 2016, 93, 186–199. [Google Scholar] [CrossRef]
- Zhang, X.; Zikanov, O. Convection instability in a downward flow in a vertical duct with strong transverse magnetic field. Phys. Fluids 2018, 30, 117101. [Google Scholar] [CrossRef] [Green Version]
- Zikanov, O.; Belyaev, I.; Listratov, Y.; Frick, P.; Razuvanov, N.; Sviridov, V. Mixed Convection in Pipe and Duct Flows with Strong Magnetic Fields. Appl. Mech. Rev. 2021, 73, 010801. [Google Scholar] [CrossRef]
- Smolentsev, S.; Morley, N.; Abdou, M. Code development for analysis of MHD pressure drop reduction in a liquid metal blanket using insulation technique based on a fully developed flow model. Fusion Eng. Des. 2005, 73, 83–93. [Google Scholar] [CrossRef]
- Hartmann, J. Hg-Dynamics, I. Theory of the laminar flow of an electrically conductive liquid in a homogeneous magnetic field. Det. Kgl. Dan. Vidensk. Selskkab Mat. Fys. Med. 1937, 15, 1–28. [Google Scholar]
- Rhodes, T.; Smolentsev, S.; Abdou, M. Magnetohydrodynamic pressure drop and flow balancing of liquid metal flow in a prototypic fusion blanket manifold. Phys. Fluids 2018, 30, 057101. [Google Scholar] [CrossRef]
- Norajitra, P.; Bühler, L.; Buenaventura, A.; Diegele, E.; Fisher, U.; Gordeev, S. Conceptual Design of the Dual-Coolant Blanket within the Framework of the EU Power Plant Conceptual Study (TW2-TPR-PPCS12); Final Report FZKA 6780; Forschungszentrum Karlsruhe GmbH: Karlsruhe, Germany, 2003. [Google Scholar]
- Dem’yanenko, V.N.; Karasev, B.G.; Kolesnichenko, A.F.; Lavrent’ev, I.V.; Lielausis, O.A.; Murav’ev, E.V.; Tananaev, A.V. Liquid metal in the magnetic field of a Tokamak reactor. Magnetohydrodynamics 1988, 24, 95–114. [Google Scholar]
- Grinberg, G.K.; Kaudze, M.Z.; Lielausis, O.A. Local MHD resistance on a liquid sodium circuit with a superconducting magnet. Magnetohydrodynamics 1985, 21, 99–103. [Google Scholar]
- Tananaev, A.V.; Aitov, T.N.; Chudov, A.V.; Shmatenko, V.A. Linear approximation application limits in MHD-flow theory for strong magnetic fields. Experimental results. In Liquid Metal Magnetohydrodynamics; Lielpetris, J., Moreau, R., Eds.; Kluwer: Alphen aan den Rijn, The Netherlands, 1989; pp. 37–43. [Google Scholar]
- Chen, L.; Smolentsev, S.; Ni, M.-J. Toward full simulations for a liquid metal blanket: MHD flow computations for a PbLi blanket prototype at Ha∼ 104. Nucl. Fusion 2020, 60, 076003. [Google Scholar] [CrossRef]
- Madarame, H.; Taghavi, K.; Tillack, M.S. The influence of leakage currents on the MHD pressure drop. Fusion Technol. 1985, 8, 264–269. [Google Scholar] [CrossRef]
- Stieglitz, R.; Molokov, S. Experimental study of magnetohydrodynamic flows in electrically coupled bends. J. Fluid Mech. 1997, 343, 1–28. [Google Scholar] [CrossRef]
- McCarthy, K.A.; Abdou, M.A. Analysis of liquid metal MHD flow in multiple adjacent ducts using an iterative method to solve the core flow equations. Fusion Eng. Des. 1991, 13, 363–380. [Google Scholar] [CrossRef]
- Molokov, S. Fully developed liquid-metal flow in multiple rectangular ducts in a strong uniform magnetic field. Eur. J. Mech. B Fluids 1993, 12, 769–787. [Google Scholar]
- Mistrangelo, C.; Bühler, L. Electric flow coupling in the HCLL blanket concept. Fusion Eng. Des. 2008, 83, 1232–1237. [Google Scholar] [CrossRef]
- Gold, R.R. Magnetohydrodynamic pipe flow. Part 1. J. Fluid Mech. 1962, 13, 505–512. [Google Scholar] [CrossRef]
- Tao, Z.; Ni, M.-J. Analytical solutions for MHD flow at a rectangular duct with unsymmetrical walls of arbitrary conductivity. Sci. China Phys. Mech. Astron. 2015, 58, 1–18. [Google Scholar] [CrossRef]
- Shercliff, J.A. The Theory of Electromagnetic Flow-Measurement; Cambridge University Press: Cambridge, UK, 1962. [Google Scholar]
- Alty, C.J.N. Magnetohydrodynamic duct flow in a uniform transverse magnetic field of arbitrary orientation. J. Fluid Mech. 1971, 48, 429–461. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Stuartson, K.J. Magnetohydrodynamic flows in rectangular ducts II. J. Fluid Mech. 1965, 23, 563–581. [Google Scholar] [CrossRef]
- Tillack, M.S. MHD Flow in Rectangular Ducts. Design Equations for Pressure Drop and Flow Quantity; UCLA-FNT-35; University of California: Los Angeles, CA, USA, 1990. [Google Scholar]
- Kulikovskii, A.G. Slow steady flows of a conducting fluid at large Hartmann numbers. Fluid Dyn. 1968, 3, 1–5. [Google Scholar] [CrossRef]
- Chang, C.; Lundgren, S. Duct flow in magnetohydrodynamics. Z. Angew. Math. Phys. 1961, 12, 100–114. [Google Scholar] [CrossRef]
- Shercliff, J.A. Magnetohydrodynamic pipe flow. Part II. High Hartmann number. J. Fluid Mech. 1962, 13, 513–518. [Google Scholar] [CrossRef]
- Bühler, L. Magnetohydrodynamic flows in arbitrary geometries in strong nonuniform magnetic fields—A numerical code for the design of fusion reactor blankets. Fusion Tech. 1995, 27, 3–24. [Google Scholar] [CrossRef]
- McCarthy, K. Analysis of Liquid Metal MHD Flow Using a Core Flow Approximation with Applications to Calculating the Pressure Drop in Basic Geometric Elements of Fusion Reactor Blankets. Ph.D. Thesis, California University, Los Angeles, CA, USA, 1989. [Google Scholar]
- Molokov, S.; Bühler, L. Liquid metal flow in a U-bend in a strong uniform magnetic field. J. Fluid Mech. 1994, 267, 325–352. [Google Scholar] [CrossRef]
- Hua, T.Q.; Picologlou, B.F. Magnetohydrodynamic flow in a manifold and multiple rectangular coolant ducts of self-cooled blankets. Fusion Tech. 1991, 19, 102–112. [Google Scholar] [CrossRef]
- McCarthy, K.A.; Ying, A.Y.; Morley, N.B.; Abdou, M.A. Comparison of the core flow approximation and full solution approach for MHD flow in non-symmetric and multiple ducts. Fusion Eng. Des. 1991, 17, 209–213. [Google Scholar] [CrossRef]
- Hua, T.Q.; Walker, J.S. MHD considerations for poloidal-toroidal coolant ducts of self-cooled blankets. Fusion Tech. 1991, 19, 951–960. [Google Scholar] [CrossRef]
- Butsenieks, I.E.; Vitolin’sh, G.A.; Gel’fgat, Y.M.; Dorofeev, V.S.; Shcherbinin, E.V. Magnetohydrodynamic flow in a square tube with walls of different electrical conductivity in an oblique transverse magnetic field. Magnetohydrodynamics 1971, 3, 53–60. [Google Scholar]
- Sterl, A. Numerical simulation of liquid-metal MHD flows in rectangular ducts. J. Fluid Mech. 1990, 216, 161–191. [Google Scholar] [CrossRef]
- Morley, N.B.; Ni, M.-J.; Munipalli, R.; Huang, P.; Abdou, M.A. MHD simulations of liquid metal flow through a toroidally oriented manifold. Fusion Eng. Des. 2008, 83, 1335–1339. [Google Scholar]
- Ni, M.-J.; Munipalli, R.; Morley, N.B.; Huang, P.; Abdou, M.A. A current density conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. Part I: On a rectangular collocated grid system. J. Comp. Phys. 2007, 227, 174–204. [Google Scholar] [CrossRef]
- Smolentsev, S.; Badia, S.; Bhattacharyay, R.; Bühler, L.; Chen, L.; Huang, Q.; Jin, H.-G.; Krasnov, D.; Lee, D.-W.; Mas de les Valls, E.; et al. An approach to verification and validation of MHD codes for fusion applications. Fusion Eng. Des. 2015, 100, 65–72. [Google Scholar] [CrossRef] [Green Version]
- Smolentsev, S.; Morley, N.; Abdou, M.; Munipalli, R.; Moreau, R. Current approaches to modelling MHD flows in the Dual Coolant Lead Lithium blanket. Magnetohydrodynamics 2006, 42, 225–236. [Google Scholar]
- Chen, L.; Xu, S.J.; Li, M.J.; Ni, M.J.; Zhang, N.M. Study on the impacts of pressure equalization slots on MHD flow and safety of FCI in DCLL blanket. Fusion Eng. Des. 2018, 122, 204–210. [Google Scholar] [CrossRef]
- Krasnov, D.; Zikanov, O.; Boeck, T. Numerical study of magnetohydrodynamic duct flow at high Reynolds and Hartmann numbers. J. Fluid Mech. 2012, 704, 421–446. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, H. Large eddy simulation of magnetohydrodynamic turbulent duct flows. Phys. Fluids 2008, 20, 015102. [Google Scholar] [CrossRef]
- Patel, A.; Pulugundla, G.; Smolentsev, S.; Abdou, M.; Bhattacharyay, R. Validation of numerical solvers for liquid metal flow in a complex geometry in the presence of a strong magnetic field. Theor. Comput. Fluid Dyn. 2017, 32, 165–178. [Google Scholar] [CrossRef]
- Smolentsev, S.; Rhodes, T.; Yan, Y.; Tassone, A.; Mistrangelo, C.; Bühler, L.; Urgorri, F.R. Code-to-code comparison for a PbLi mixed-convection MHD flow. Fusion Sci. Tech. 2020, 76, 653–669. [Google Scholar] [CrossRef]
- Smolentsev, S.; Abdou, M.; Morley, N.B.; Sawan, M.; Malang, S.; Wong, C. Numerical analysis of MHD flow and heat transfer in a poloidal channel of the DCLL blanket with a SiCf/SiC flow channel insert. Fusion Eng. Des. 2006, 81, 549–553. [Google Scholar] [CrossRef]
- Smolentsev, S.; Morley, N.; Abdou, M. MHD and thermal issues of the SiCf/SiC flow channel insert. Fusion Sci. Tech. 2006, 50, 107–119. [Google Scholar] [CrossRef]
- Smolentsev, S.; Malang, S. Double-layer flow channel insert for electric and thermal insulation in the dual-coolant lead-lithium blanket. Fusion Sci. Tech. 2009, 6, 201–205. [Google Scholar] [CrossRef]
- Smolentsev, S.; Xu, Z.; Pan, C.; Abdou, M. Numerical and experimental studies of MHD flow in a rectangular duct with a non-conducting flow insert. Magnetohydrodynamics 2010, 46, 99–111. [Google Scholar]
- Zhang, X.; Xu, Z.; Pan, C. Numerical analysis of MHD duct flow with a flow channel insert. Fusion Eng. Des. 2010, 85, 2090–2094. [Google Scholar] [CrossRef]
- Smolentsev, S.; Courtessole, C.; Abdou, M.; Sharafat, S.; Sahu, S.; Sketchley, T. Numerical modeling of first experiments on PbLi MHD flows in a rectangular duct with foam-based SiC flow channel insert. Fusion Eng. Des. 2016, 108, 7–20. [Google Scholar] [CrossRef] [Green Version]
- Soto, C.; Smolentsev, S.; Garsia-Rosales, C. Mitigation of MHD phenomena in DCLL blankets by flow channel inserts based on a SiC-sandwich material concept. Fusion Eng. Des. 2020, 151, 111381. [Google Scholar] [CrossRef]
- Di Giulio, D.; Suarez, D.; Batet, L.; Mas de les Valls, E.; Savoldi, L. Analysis of flow channel insert deformations influence on the liquid metal flow in DCLL blanket channels. Fusion Eng. Des. 2020, 157, 111639. [Google Scholar] [CrossRef]
- Sutevski, D.; Smolentsev, S.; Morley, N.; Abdou, M. 3D numerical study of MHD flow in a rectangular duct with a flow channel insert. Fusion Sci. Tech. 2011, 60, 513–517. [Google Scholar] [CrossRef]
- Ni, M.J.; Xu, S.J.; Wang, Z.H.; Zhang, N.M. Direct simulation of three-dimensional MHD flows in liquid metal blanket with flow channel insert. Fusion Sci. Technol. 2011, 60, 292–297. [Google Scholar] [CrossRef]
- Xu, S.J.; Zhang, N.M.; Ni, M.J. Influence of flow channel insert with pressure equalization opening on MHD flows in a rectangular duct. Fusion Eng. Des. 2013, 88, 271–275. [Google Scholar] [CrossRef]
- Sutevski, D.; Smolentsev, S.; Abdou, M. 3D Numerical study of pressure equalization in MHD flow in a rectangular duct with insulating flow channel insert. Fusion Eng. Des. 2014, 89, 1370–1374. [Google Scholar] [CrossRef]
- Chen, L.; Li, M.; Ni, M.; Zhang, N. MHD effects and heat transfer analysis in magneto-thermo-fluid-structure coupled field in DCLL blanket. Int. Com. Heat Mass Trans. 2017, 84, 110–120. [Google Scholar] [CrossRef]
- Mistrangelo, C. Three-Dimensional MHD Flow in Sudden Expansions; Wissenschaftliche BerichteFZKA 7201; Forschungszentrum Karlsruhe: Karlsruhe, Germany, 2006. [Google Scholar]
- Mistrangelo, C.; Buhler, L. Liquid metal magnetohydrodynamic flows in manifolds of dual coolant lead lithium blankets. Fusion Eng. Des. 2014, 89, 1319–1323. [Google Scholar] [CrossRef]
- Kim, C.N. Liquid metal magnetohydrodynamic flows in an electrically conducting rectangular duct with sudden expansion. Comput. Fluids 2014, 89, 232–241. [Google Scholar] [CrossRef]
- Kim, C.N. A liquid metal magnetohydrodynamic duct flow with sudden contraction in a direction perpendicular to a magnetic field. Comput. Fluids 2015, 108, 156–167. [Google Scholar] [CrossRef]
- Feng, J.; He, Q.; Chen, H.; Ye, M. Numerical investigation of magnetohydrodynamic flow through sudden expansion pipes in liquid metal blankets. Fusion Eng. Des. 2016, 109–111, 1360–1364. [Google Scholar] [CrossRef]
- Kumamaru, H. Numerical analyses on liquid-metal magnetohydrodynamic flow in sudden channel expansion. J. Nucl. Sci. Technol. 2017, 54, 242–252. [Google Scholar] [CrossRef]
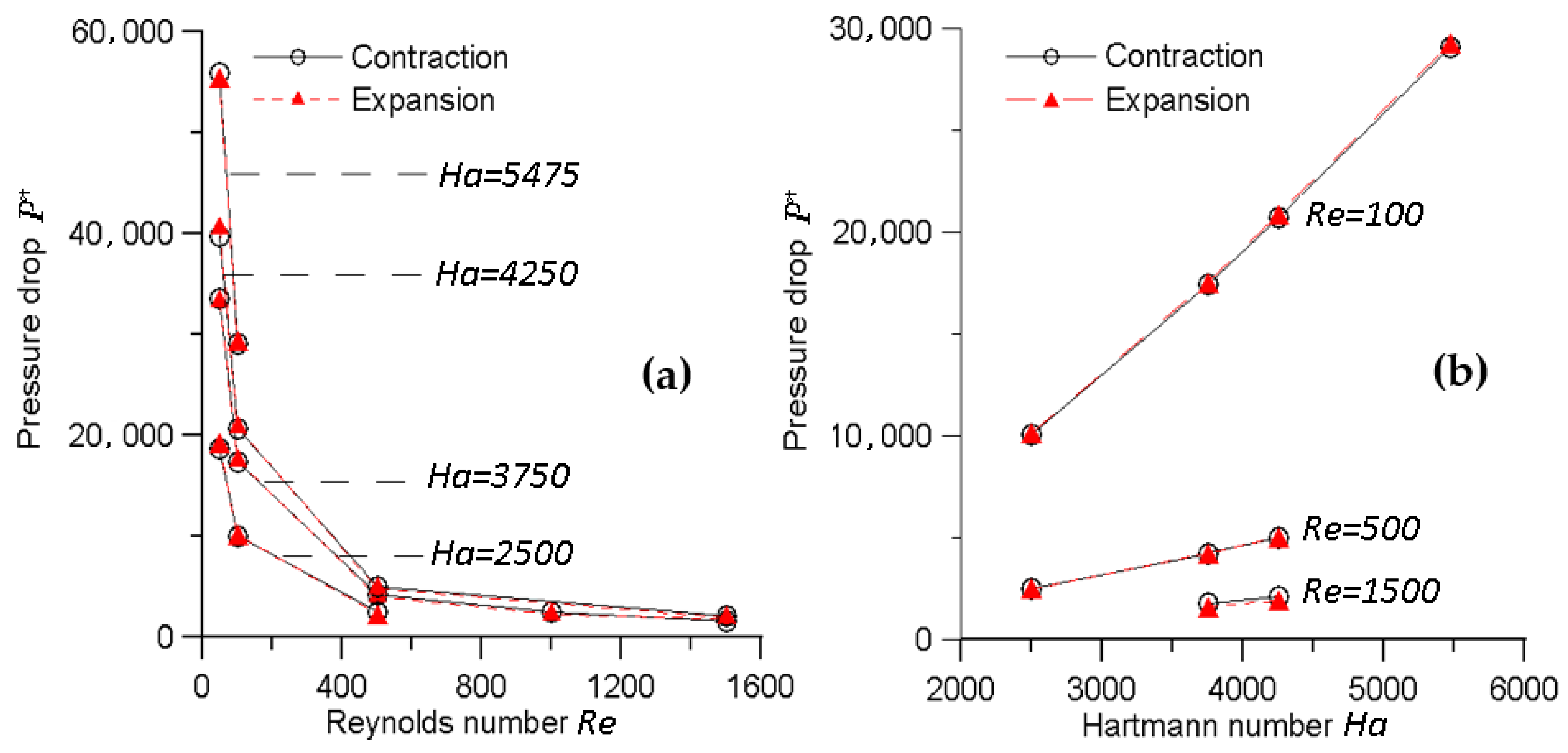
- Kumamaru, H. Numerical analyses on liquid-metal magnetohydrodynamic flow in sudden channel contraction. J. Nucl. Sci. Technol. 2017, 54, 1300–1309. [Google Scholar] [CrossRef]
- Rhodes, T.J.; Smolentsev, S.; Abdou, M. Effect of the length of the poloidal ducts on flow balancing in a liquid metal blanket. Fusion Eng. Des. 2018, 136, 847–851. [Google Scholar] [CrossRef]
- Chen, L.; Li, M.; Ni, M.; Zhang, N. MHD Effects in the U-bend of DCLL Blanket. Procedia Eng. 2015, 126, 461–465. [Google Scholar] [CrossRef] [Green Version]
- He, Q.; Feng, J.; Chen, H. Numerical analysis and optimization of 3D magnetohydrodynamic flows in rectangular U-bend. Fusion Eng. Des. 2016, 109–111, 1313–1317. [Google Scholar] [CrossRef]
- Kumamaru, H.; Takagaki, N. Numerical analyses on liquid-metal magnetohydrodynamic flow in 180°-turn channel. IJMEA 2019, 7, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Mao, J.; Wang, H.; Jin, M. Numerical simulation of MHD flows in a coupled U-turn rectangular duct with different wall conductance ratios. Fusion Eng. Des. 2019, 149, 111334. [Google Scholar] [CrossRef]
- Reed, C.B.; Picologlou, B.F.; Hua, T.Q.; Walker, J.S. ALEX Results—a Comparison of Measurements from a Round and a Rectangular Duct with 3-D Code Predictions. In Proceedings of the Symposium on Fusion Engineering, Monterey, CA, USA, 12–16 October 1987. [Google Scholar]
- Votyakov, E.V.; Zienicke, E.A. Numerical study of liquid metal flow in a rectangular duct under the influence of a heterogenous magnetic field. Fluid Dyn. Mater. Process. 2007, 3, 97–114. [Google Scholar]
- Moreau, R.; Smolentsev, S.; Cuevas, S. Flow in an insulated rectangular duct at the entry of a magnet. Magnetohydrodynamics 2009, 45, 3–15. [Google Scholar] [CrossRef]
- Moreau, R.; Smolentsev, S.; Cuevas, S. MHD flow in an insulating rectangular duct under a non-uniform magnetic field. PMC Phys. B 2010, 3, 3. [Google Scholar] [CrossRef] [Green Version]
- Zhou, T.; Chen, H.; Yang, Z. Effect of fringing magnetic field on magnetohydrodynamic flow in rectangular duct. Fusion Eng. Des. 2011, 86, 2352–2357. [Google Scholar] [CrossRef]
- Albets-Chico, X.; Votyakov, E.V.; Radhakrishnan, H.; Kassinos, S. Effects of the consistency of the fringing magnetic field on direct numerical simulations of liquid–metal flow. Fusion Eng. Des. 2011, 86, 5–14. [Google Scholar] [CrossRef]
- Albets-Chico, X.; Radhakrishnan, H.; Kassinos, S.; Knaepen, B. Numerical simulation of a liquid-metal flow in a poorly conducting pipe subjected to a strong fringing magnetic field. Phys. Fluids 2011, 23, 047101. [Google Scholar] [CrossRef]
- Li, F.-C.; Sutevski, D.; Smolentsev, S.; Abdou, M. Experimental and numerical studies of pressure drop in molten PbLi flows in a circular duct under non-uniform transverse magnetic field. Fusion Eng. Des. 2013, 88, 3060–3071. [Google Scholar] [CrossRef]
- Pulugundla, G.; Smolentsev, S.; Rhodes, T.; Kawczynski, C.; Abdou, M. Numerical investigation of the effect of the wall conductance ratio on MHD flow in a pipe under a transverse non-uniform magnetic field. Fusion Sci. Technol. 2015, 68, 684–689. [Google Scholar] [CrossRef]
- Li, Y.; Zikanov, O. Laminar pipe flow at the entrance into transverse magnetic field. Fusion Eng. Des. 2013, 88, 195–201. [Google Scholar] [CrossRef]
- Klüber, V.; Mistrangelo, C.; Büher, L. Numerical simulation of 3D magnetohydrodynamic liquid metal flow in a spatially varying solenoidal magnetic field. Fusion Eng. Des. 2020, 156, 111659. [Google Scholar] [CrossRef]
- Miyazaki, K.; Konishi, K.; Inoue, S. MHD pressure drop of liquid metal flow in circular duct under variable transverse magnetic field. J. Nucl. Sci. Technol. 1991, 28, 159–161. [Google Scholar] [CrossRef]
- Hartmann, J.; Lazarus, F. Hg-Dynamics II. Experimental investigations of the flow of mercury in a homogenious magnetic field. Det. Kgl. Dan. Vidensk. Selskkab Mat-Fys. Med. 1937, 15, 1–45. [Google Scholar]
- Miyazaki, K.; Kotake, S.; Yamaoka, N.; Inoue, S.; Fujii-E, Y. MHD pressure drop of NaK flow in stainless steel pipe. Nucl. Technol. Fusion 1983, 4, 447–452. [Google Scholar] [CrossRef]
- Miyazaki, K.; Inoue, S.; Yamaoka, N.; Horiba, T.; Yokomizo, K. Magneto-hydro-dynamic pressure drop of lithium flow in rectangular ducts. Fusion Tech. 1986, 10, 830–836. [Google Scholar] [CrossRef]
- Wu, Y.; FDS TEAM. Conceptual design and testing strategy of a dual functional lithium lead test blanket module for ITER and EAST. Nucl. Fus. 2007, 47, 1–7. [Google Scholar] [CrossRef]
- Abdou, M.A.; Ying, A.; Morley, N.; Gulec, K.; Smolentsev, S.; Kotschenreuther, M.; Malang, S.; Zinkle, S.; Rognlien, T.; Fogarty, P.; et al. On the exploration of innovative concepts for fusion chamber technology. Fusion Eng. Des. 2001, 54, 181–247. [Google Scholar] [CrossRef]
- Rhodes, T.; Smolentsev, S. Pressure drop in a prototypical 3D magnetohydrodynamic flow across contraction of a fusion blanket manifold. J. Nucl. Sci. Technol. 2021. Submitted. [Google Scholar] [CrossRef]
- Hunt, J.; Leibovich, S. Magnetohydrodynamic flow in channels of variable cross-section with strong transverse magnetic fields. J. Fluid Mech. 1967, 28, 241–260. [Google Scholar] [CrossRef]
- Malang, S.; Tillack, M.; Wong, C.P.C.; Morley, N.; Smolentsev, S. Development of the lead-ithium (DCLL) blanket concept. Fusion Sci. Technol. 2011, 60, 249–256. [Google Scholar] [CrossRef]
- Katoh, Y.; Snead, L.L.; Henager, C.H.; Nozawa, T.; Hinoki, T.; Iveković, A.; Novak, S.; Gonzalez de Vicente, S.M. Current status and recent research achievements in SiC/SiC composites. J. Nucl. Mater. 2014, 455, 387–397. [Google Scholar] [CrossRef] [Green Version]
- Raffray, A.R.; Jones, R.; Aiello, G.; Billone, M.; Giancarli, L.; Golfier, H.; Hasegawa, A.; Katoh, Y.; Kohyama, A.; Nishio, S.; et al. Design and material issues for high performance SiCf/SiC-based fusion power cores. Fusion Eng. Des. 2001, 55, 55–95. [Google Scholar] [CrossRef]
- Sharafat, S.; Aoyama, A.; Morley, N.; Smolentsev, S.; Katoh, Y.; Williams, B.; Ghoniem, N. Development status of a SiC-foam based flow channel insert for a U.S.-ITER DCLL TBM. Fusion Sci. Technol. 2009, 56, 883–891. [Google Scholar] [CrossRef]
- John, H.; Malang, S.; Sebening, H. (Eds.) DEMO-Relevant Test Blankets for NET/ITER. Part 1: Self-Cooled Liquid Metal Breeder Blanket; KfK4908; Kernforschugszentrum Karlsruhe: Karlsruhe, Germany, 1991. [Google Scholar]
- Katoh, Y.; Snead, L.L.; Henager, C.H.; Hasegawa, A.; Kohyama, A.; Riccardi, B.; Hegeman, J.B.J. Current status and critical issues for development of SiC composites for fusion applications. J. Nucl. Mater. 2007, 367, 659–671. [Google Scholar] [CrossRef]
- Barleon, L.; Casal, V.; Mack, K.-J.; Kreuzinger, H.; Sterl, A.; Thomauske, K. Experimental and Theoretical Work on MHD at the Kernforschungszentrum Karlsruhe—The MEKKA-Program. In Liquid Metal Magnetohydrodynamics; Lielpeteris, J., Moreau, R., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1989; pp. 55–61. [Google Scholar]
- Bühler, L.; Mistrangelo, C. Liquid metal MHD flows near non-insulated gaps between flow channel inserts in DCLL blankets. IEEE Trans. Plasma Sci. 2014, 42, 510–515. [Google Scholar] [CrossRef]
- Kim, C.N. Magnetohydrodynamic flows entering the region of a flow channel insert in a duct. Fusion Eng. Des. 2014, 89, 56–68. [Google Scholar] [CrossRef]
- Bühler, L.; Mistrangelo, C. Pressure drop and velocity changes in MHD pipe flows due to a local interruption of the insulation. Fusion Eng. Des. 2018, 127, 185–191. [Google Scholar] [CrossRef]
- Bühler, L.; Brinkmann, H.-J.; Koehly, C. Experimental study of liquid metal magnetohydrodynamic flows near gaps between flow channel inserts. Fusion Eng. Des. 2019, 146, 1399–1402. [Google Scholar] [CrossRef]
- Bühler, L. Additional magnetohydrodynamic pressure drop at junction of flow channel inserts. In Proceedings of the 17th SOFT Conference, Rome, Italy, 14–18 September 1992; pp. 1301–1305. [Google Scholar]
- Malang, S.; Borgstedt, H.U.; Farum, E.H.; Natesan, K.; Vitkovski, I.V. Development of insulating coatings for liquid metal blankets. Fusion Eng. Des. 1995, 27, 570–586. [Google Scholar] [CrossRef]
- Bühler, L. The influence of small cracks in insulating coatings on flow structure and pressure drop in MHD channel flows. Fusion Eng. Des. 1995, 27, 650–658. [Google Scholar] [CrossRef]
- Ying, A.; Gaizer, A. The effects of imperfect insulating coatings on MHD and heat transfer in rectangular ducts. Fusion Eng. Des. 1995, 27, 634–641. [Google Scholar] [CrossRef]
- Evtushenko, I.A.; Kirillov, I.R.; Reed, C.B. MHD-flow in slotted channels with conducting walls. Fusion Eng. Des. 1995, 27, 627–633. [Google Scholar] [CrossRef]
- Smolentsev, S.; Spagnuolo, G.A.; Serikov, A.; Rasmussen, J.J.; Nielsen, A.H.; Naulin, V.; Marian, J.; Coleman, M.; Malerba, L. On the role of integrated computer modelling in fusion technology. Fusion Eng. Des. 2020, 157, 111671. [Google Scholar] [CrossRef] [Green Version]

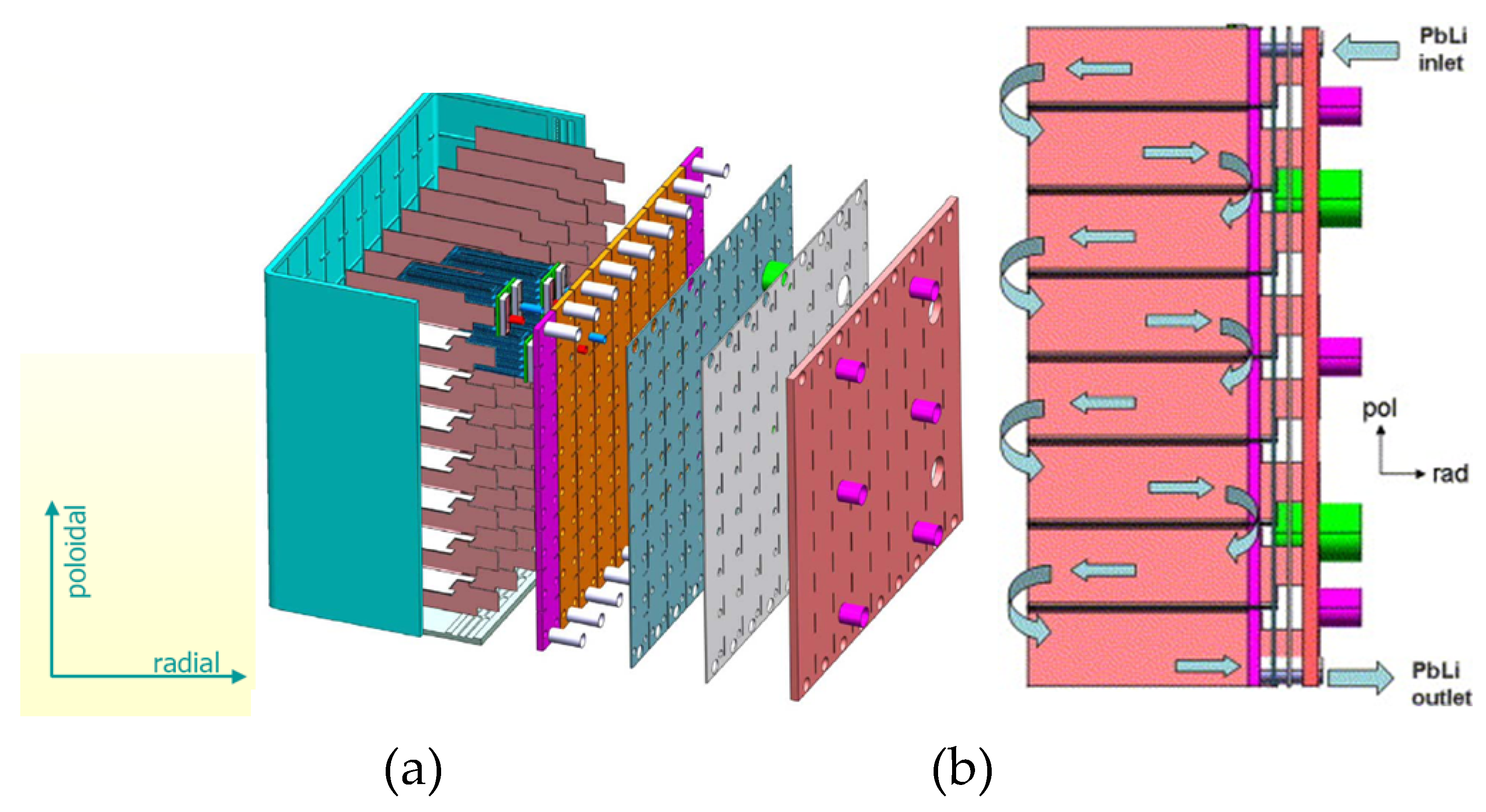

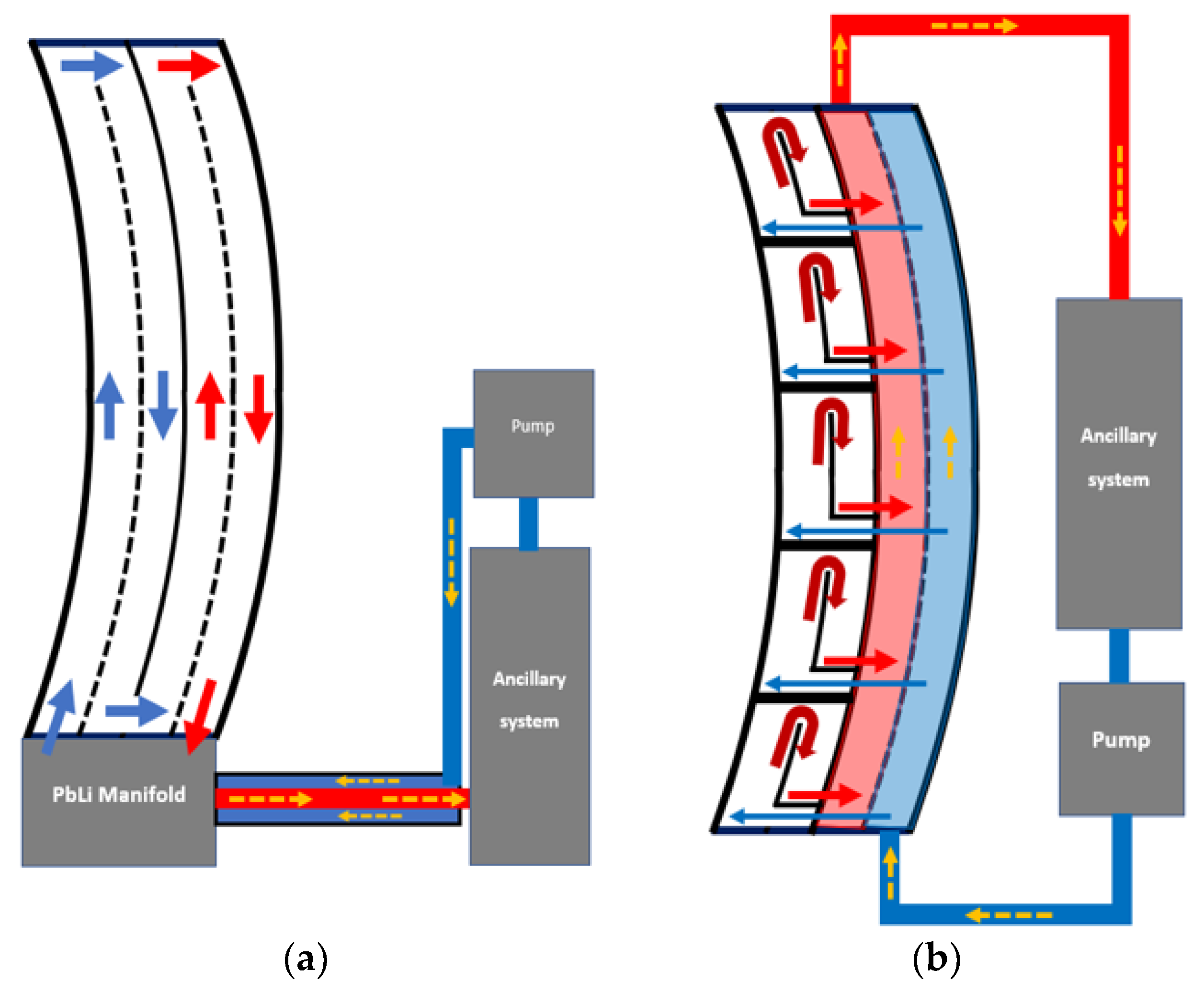
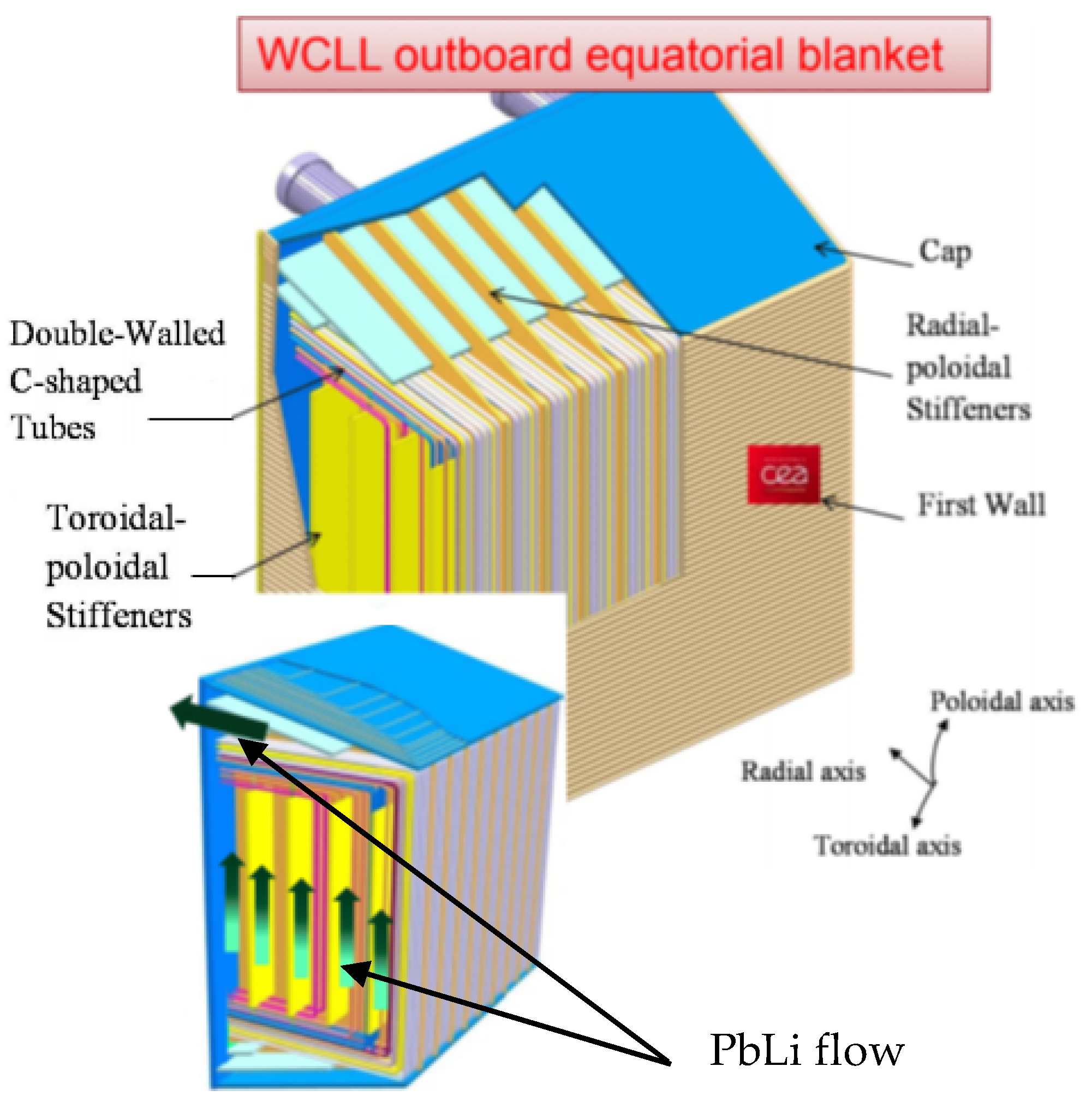

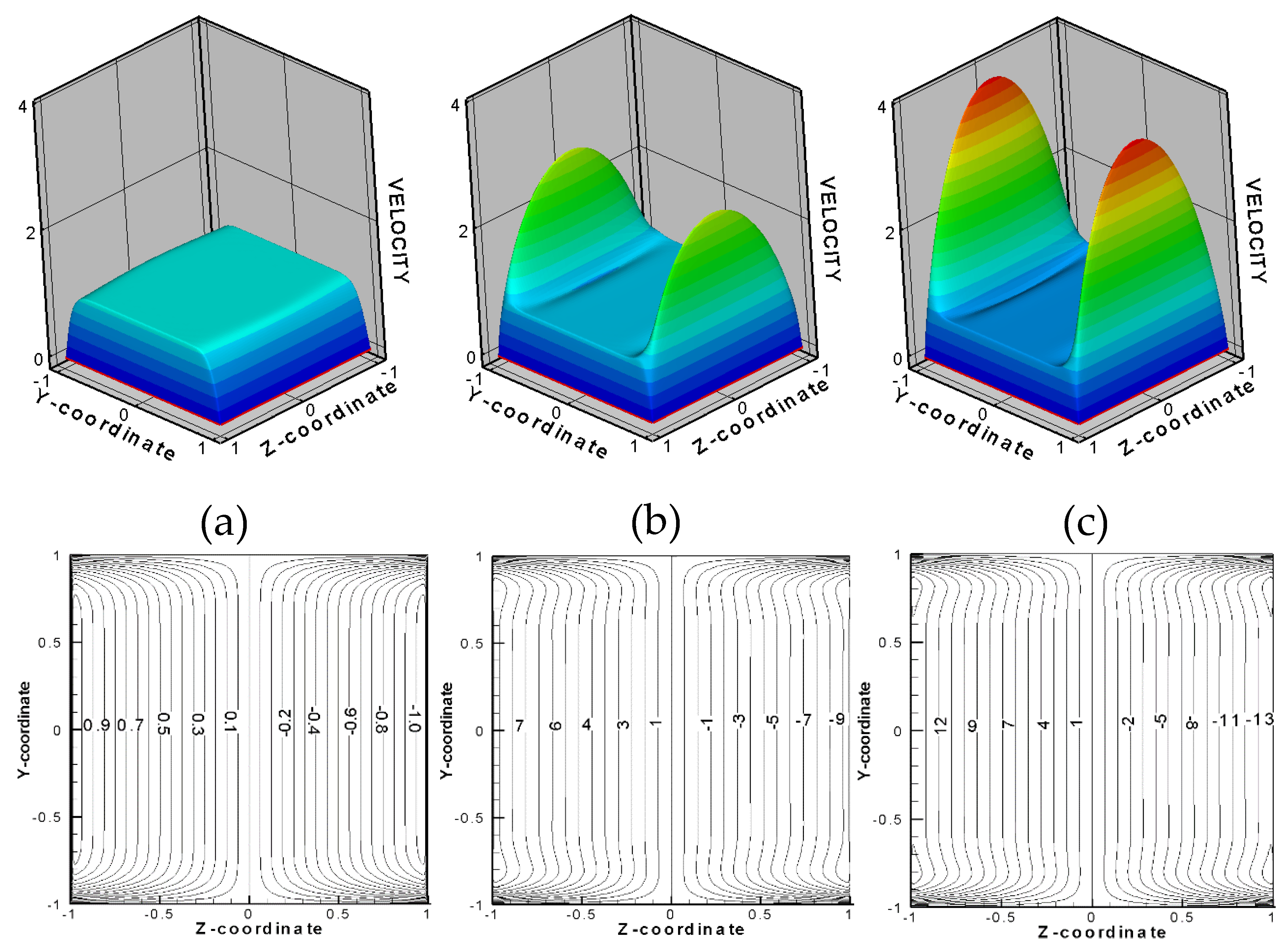
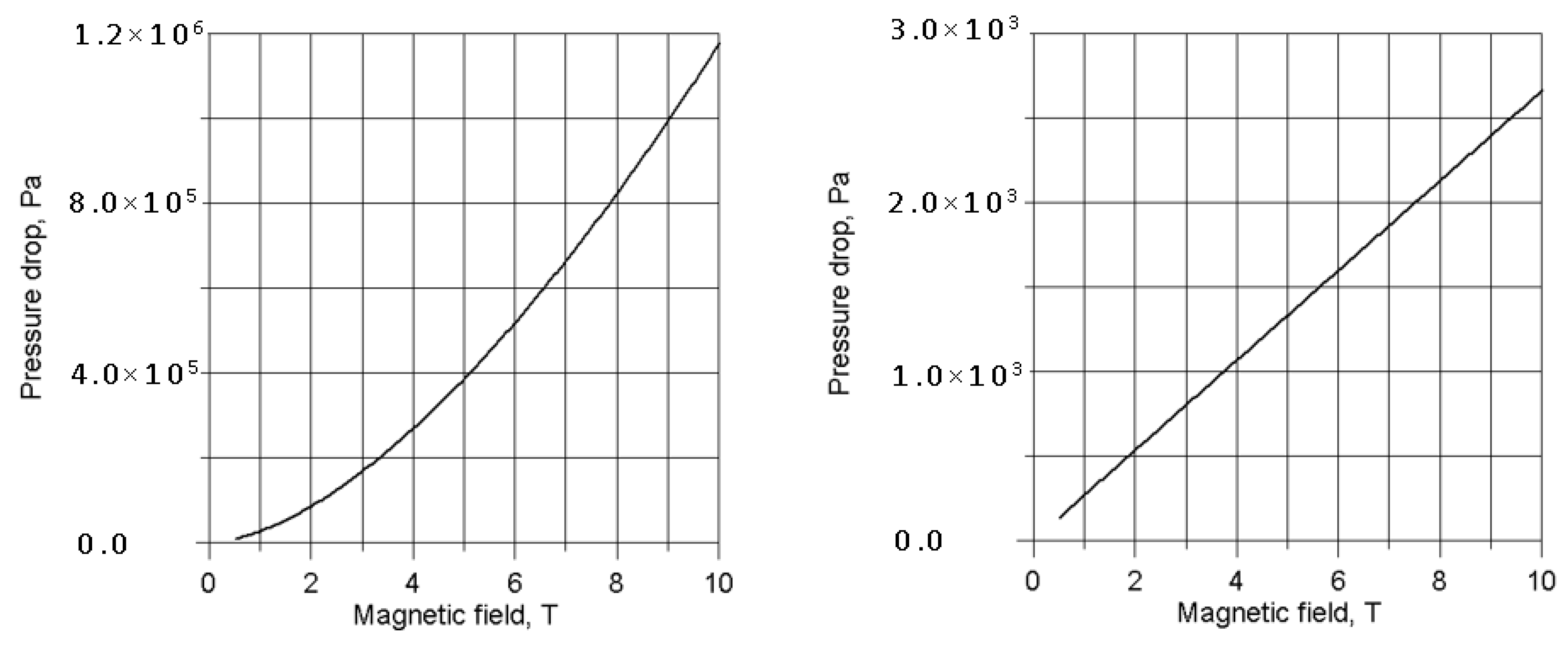

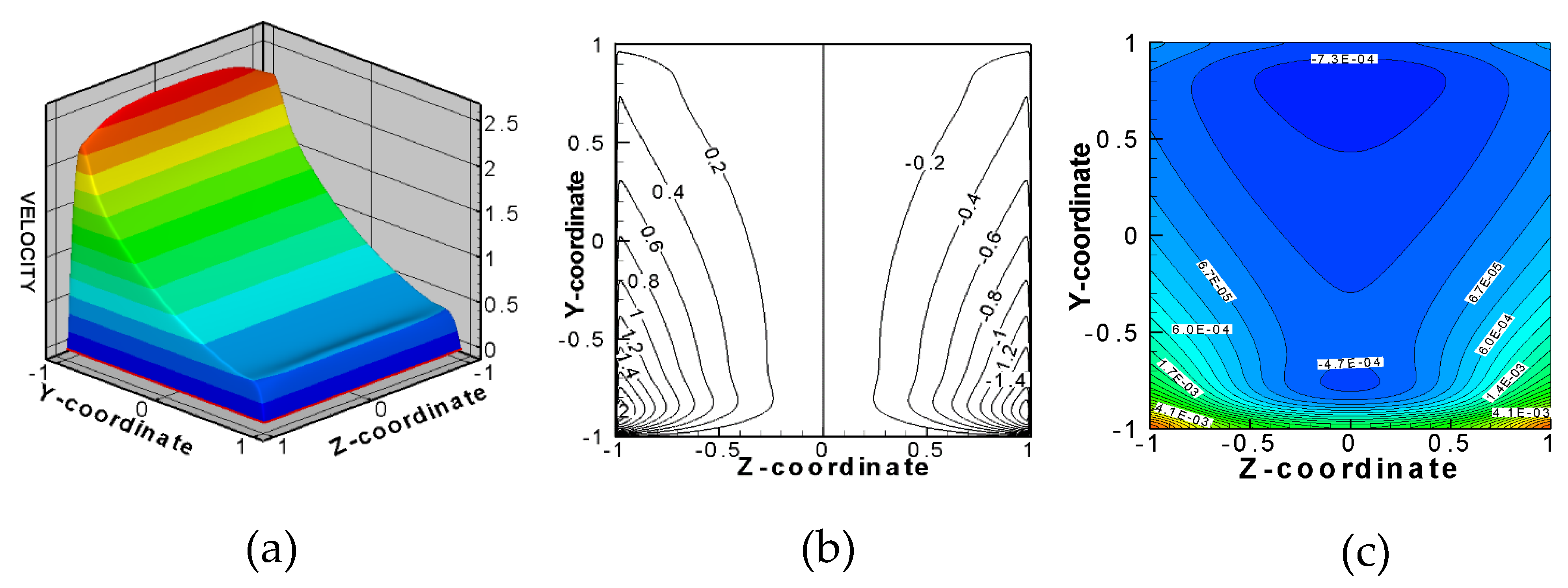


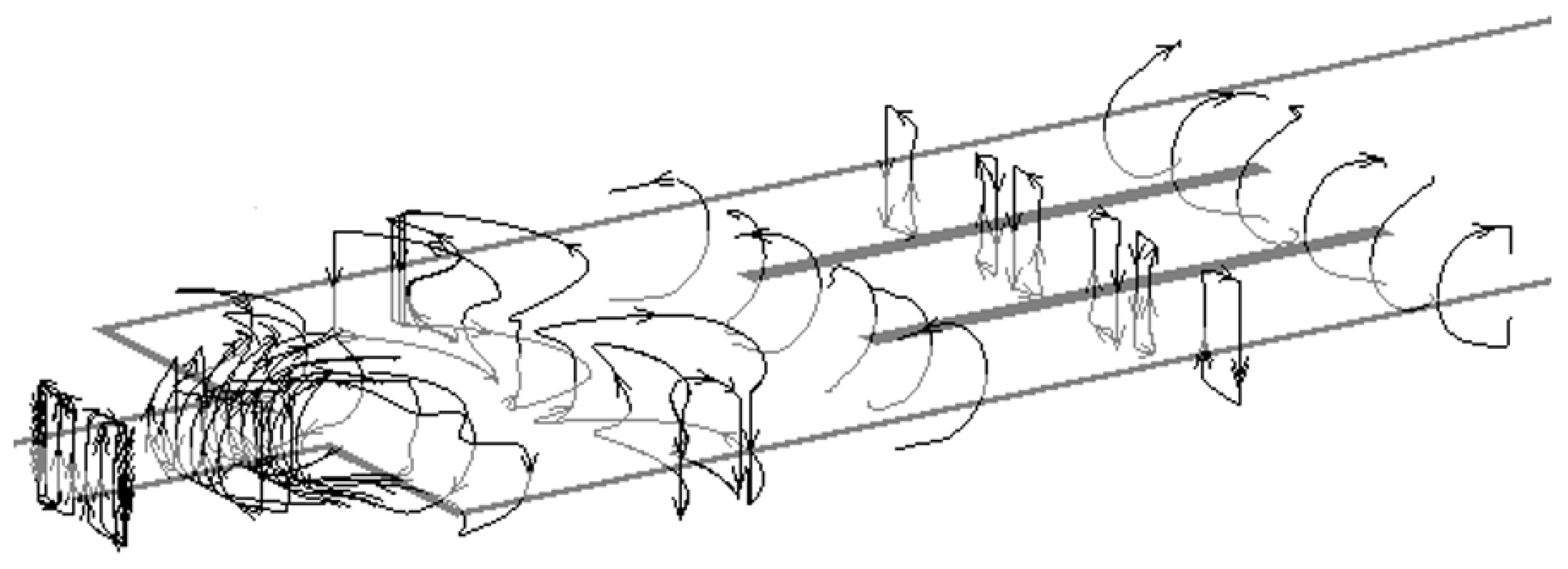


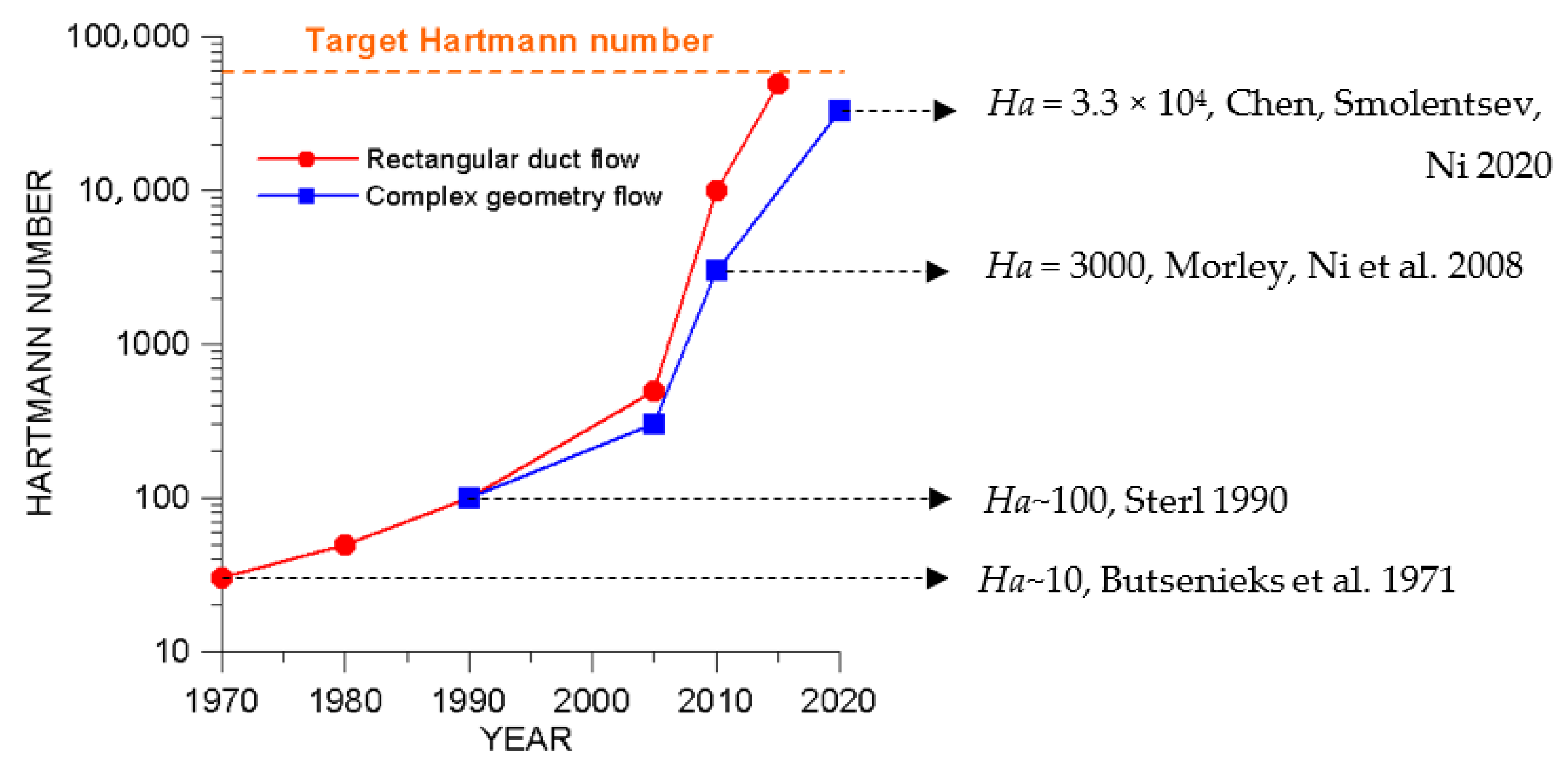



| Parameter | Li/V Self-Cooled, DEMO IB [3] | HCLL, ITER TBM OB [27] | DCLL, FNSF IB/OB [21] | WCLL, DEMO OB [18] |
|---|---|---|---|---|
| Ha | 4.5 × 104 | 1.1 × 104 | 3.7 × 104/1.5 × 104 | 9.8 × 103 |
| Re | 3.2 × 104 | 670 | 7.5 × 104/1.7 × 105 | 120 |
| Gr | 6.0 × 108 | 1.0 × 109 | 6.6 × 1011/1.0 × 1012 | 5.4 × 1011 |
| N | 6.0 × 104 | 1.8 × 105 | 1.8 × 104/1.3 × 103 | 8.0 × 105 |
| , T | 10 | 4 | 10/5.5 | 4 |
| , m/s | 0.5 | 0.001 | 0.087/0.203 | 0.0002 |
| L, m | 0.05 | 0.07 | 0.152/0.109 | 0.117 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smolentsev, S. Physical Background, Computations and Practical Issues of the Magnetohydrodynamic Pressure Drop in a Fusion Liquid Metal Blanket. Fluids 2021, 6, 110. https://doi.org/10.3390/fluids6030110
Smolentsev S. Physical Background, Computations and Practical Issues of the Magnetohydrodynamic Pressure Drop in a Fusion Liquid Metal Blanket. Fluids. 2021; 6(3):110. https://doi.org/10.3390/fluids6030110
Chicago/Turabian StyleSmolentsev, Sergey. 2021. "Physical Background, Computations and Practical Issues of the Magnetohydrodynamic Pressure Drop in a Fusion Liquid Metal Blanket" Fluids 6, no. 3: 110. https://doi.org/10.3390/fluids6030110
APA StyleSmolentsev, S. (2021). Physical Background, Computations and Practical Issues of the Magnetohydrodynamic Pressure Drop in a Fusion Liquid Metal Blanket. Fluids, 6(3), 110. https://doi.org/10.3390/fluids6030110






