On Solving the Nonlinear Falkner–Skan Boundary-Value Problem: A Review
Abstract
:1. Introduction
2. Materials and Methods
2.1. Analytical Treatments
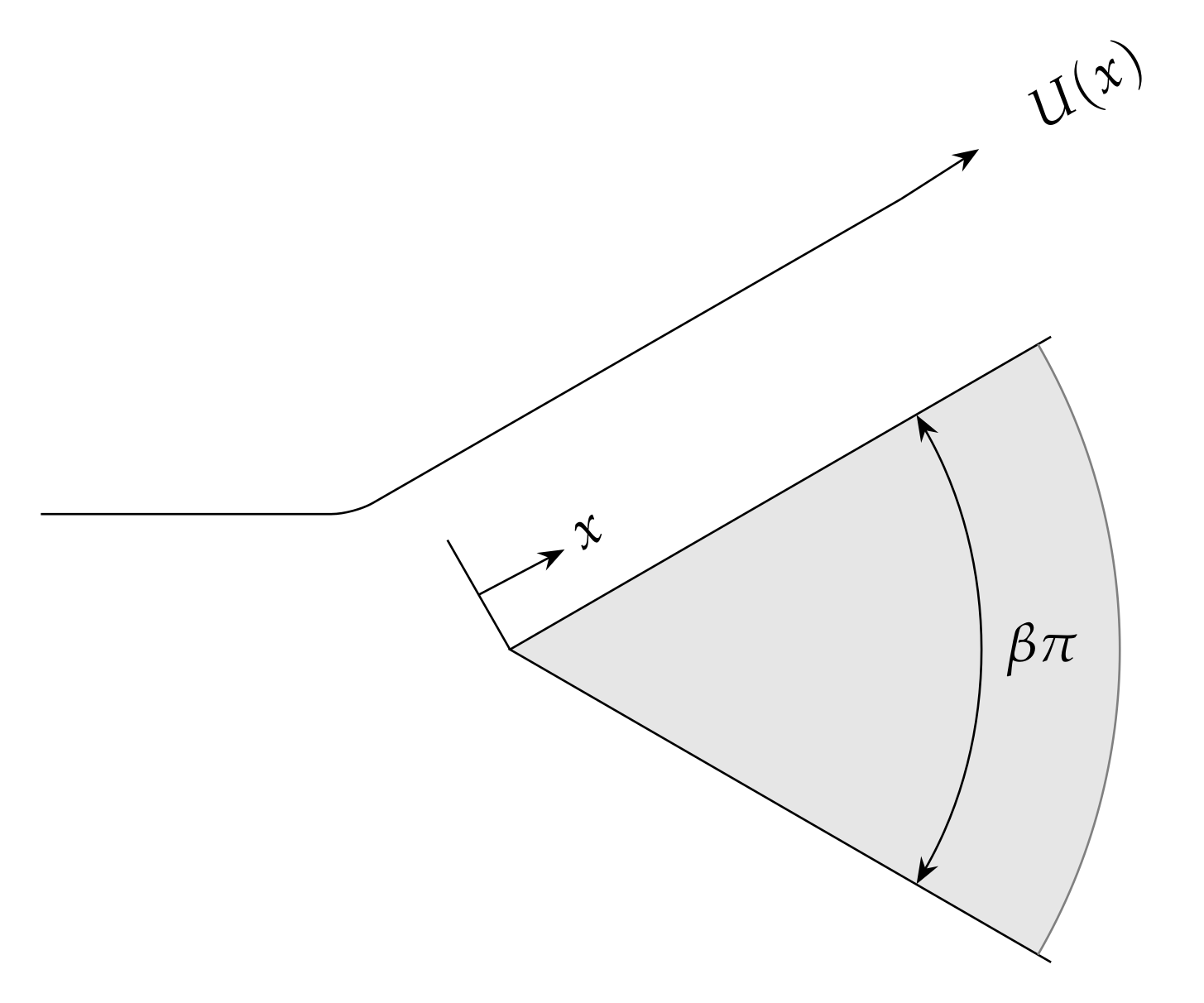
2.1.1. The Pohlhausen Flow
2.1.2. The Blasius Flow
2.1.3. The Crocco–Wang Transformation
2.1.4. Other More General Analytical Approaches
2.2. Numerical Treatments
2.2.1. Shooting
- Cebeci and Keller [45] also employ the idea of parallel shooting to obtain the solution. This approach involves dividing the domain into several subintervals and applying shooting in each subinterval. The motivation for this approach comes from the desire to avoid any instabilities that may be caused while marching the solution using an initial-value method. The authors report successfully obtaining three significant digits in two iterations when shooting was carried out over three subintervals.
- Asaithambi [47] uses the classical, fourth-order Runge-Kutta method to march the solution from to and the secant method to iteratively obtain improved values for . Two initial approximations for were needed.
- Salama [48] uses a single-step method of order 5 to march the solution from to , coupled with a third-order rootfinding method called the Halley’s method [49] to compute and the secant method to compute . It is also important to note that the solutions of (5) and (6) are obtained for values as large as 40.
- In another work, Asaithambi [22] uses recursive evaluation of Taylor coefficients to march the solution from to and the secant method to iteratively obtain improved values for . Two initial approximations for were needed, and higher orders of accuracy, as high as 7, were achieved with ease. Moreover, this work explores (5) and (6) for values as large as 40 as well and compares the results obtained previously by Salama [48].
- Zhang and Chen [50] used the Runge-Kutta (4,5) formula to march the solution from to , and the Newton’s method to improve the guess for , and hence required only one initial guess to get started.
- Sher and Yakhot [51] shoot from the end corresponding to instead of from . They choose an arbitrary value for as , a value close to 1 for as and estimate as using a simple analysis of the asymptotic behavior of the solution.
2.2.2. Finite Differences
- Asaithambi [52] truncates the infinite domain at , uses the transformation as done previously, and sets , to transform the problem (5) and (6) on the physical domain to the systemon the computational domain , subject to the conditionsIn order to discretize (32)–(35), the interval is subdivided into N subintervals for at with . Letting and denote the approximations to and respectively, Equation (32) is discretized asand Equation (33) is discretized asNewton’s method is used for the iterative solution of the nonlinear system (37), Equation (36) is used to update the values of , and (39) is used to update . The solution of the nonlinear system by Newton’s method involves the repeated solution of a linear system with a tridiagonal coefficient matrix. In related work, Asaithambi [53] uses the transformation to map the physical domain to the computational domain and discretizes the transformed equations and boundary conditions using second-order finite differences. This approach does not truncate the physical domain but still requires the iterative solution of a nonlinear system that involves the solution of a tridiagonal linear system during each iteration.
- Salama and Mansour [54] develop an unconditionally stable, fourth order finite difference method that involves only four grid points and apply it to the nonlinear Falkner–Skan problem (5) and (6). Their development uses the method of undetermined coefficients involving the unknown function values at points to derive the discretization for the third derivative by setting the local truncation errors of orders 0, 1, 2, and 3 to zero. The details of the derivation are too technical to be included here and the reader is referred to the original publication [54]. In related work, Salama and Mansour [55] develop a finite difference method of order 6 for solving steady and unsteady two-dimensional laminar boundary-layer equations. This method is also unconditionally stable. The authors illustrate the effectiveness of this method by solving the unsteady separated stagnation point flow, the Falkner–Skan equation and Blasius equation.
- Duque-Daza et al. [56] express (24) asand use subintervals with and for . With , , and denoting , , , and respectively, the authors use the fourth-order difference formulasfor the first and second derivatives of f and the third-order formulafor the third derivative. Plugging (41)–(43) into (40) yields a nonlinear system of algebraic equations in the unknowns . The boundary conditionsare discretized usingThen the Equation (40) itself is evaluated at to obtain , which is discretized asFinally, the condition is used to solve for . For this purpose, the second-order derivative is discretized asand the secant method is used to obtain updated values of from one iteration to the next. In the same article [56], the authors also report the use of a higher order compact finite difference method to solve (5) and (6).
2.2.3. Collocation Methods
- Parand et al. [57] consider (5) subject to the boundary conditionsin which is different from the corresponding condition in (6). The authors use rational Legendre functions as their basis functions, and the correspondingly transformed Gauss-Legendre points as the collocation points. It is important to emphasize here that their approach does not require the problem to be transformed to a suitable form on a finite domain.The rational Legendre functions are defined byin which are the well-known Legendre polynomials. While form a family of polynomials orthogonal on the interval with respect to the weight function , form a family of rational functions that are orthogonal on with respect to the weight functionMoreover, in (52) and (53), L is a constant known as the map parameter. While setting is most common, guidelines for the choice of value for L are given for rational Chebyshev functions in [58] that apply also to the Legendre family. The rational Legendre functions satisfy the relationfor . By setting with , the boundary conditions for are translated to corresponding conditions on . In particular, as now becomes as . Now, a solution of the formis sought by settingat for , where are the zeros of the Legendre polynomial of degree (also known as the Gauss-Legendre nodes). Along with the conditions and , (56) leads to a system of nonlinear algebraic equations in the expansion coefficients in (55).
- Kajani et al. [59] truncate the infinite domain to for a “large enough” L and use what they call shifted Chebyshev polynomials to solve (5) and (6). The shifted Chebyshev polynomials are defined byin which are the well-known Chebyshev polynomials. While the Chebyshev polynomials are orthogonal on with respect to the weight function , the shifted Chebyshev polynomials are orthogonal on the interval with respect to the weight function . The authors seek a solution of the formThey use (58) to obtainin which the coefficients and may be easily expressed in terms of the coefficients by evaluating the integrals needed to go from to and . The solution to (5) and (6) is obtained by settingat , for , where the collocation points are the zeros of , and settingcorresponding to the boundary condition as . Note that the boundary conditions at are automatically satisfied through the definitions of and as given in (59).
2.2.4. Other Methods
- Using a truncated domain at and imposing the asymptotic condition as , Asaithambi [60] solves (5) and (6) by formulating the problem in weak Galerkin form and with piecewise linear functions as basis functions and provides a finite-element solution. For this purpose, Asaithambi [60] rewrites (5) and (6) in the formin which the primes denote differentiation with respect to the variable , , and is the truncated boundary which needs to be determined as part of the solution. Note that the semi-infinite domain is now mapped to the finite domain . Subdividing the interval into N subintervals at with and , the basis functions defined byThus, the method uses both finite-elements and finite-differences to obtain a nonlinear system of algebraic equations which is solved using Newton’s method. However, this system has to be iteratively solved to adjust the value of so that the asymptotic condition is satisfied. Asaithambi [60] handles this by using the secant method y settingand solving for . The superscript here denotes the approximation to the different quantities during the iteration. The approximation is obtained from and using
- Recently, Hajimohammadi et al. [61] have developed a numerical learning approach to solving the Falkner–Skan problem (5) and (6). They cite several works from the literature that have used machine learning methods for the purpose of handling nonlinear models in the continuous domain, and demonstrate that a combination of numerical methods and machine learning methods could deal with nonlinearities much more easily and produce accurate solutions. In their work on the Falkner–Skan problem, they employ a combination of collocation using Rational Gegenbauer (RG) functions and the Least Squares (LS) Support Vector Machines (SM) and present results of their RG_LS_SVM method that compare well with results obtained previously by other researchers. The details of their method are too many to cover in this review and the reader is referred to the original publication [61].
3. Results
4. Discussion
Funding
Data Availability Statement
Conflicts of Interest
References
- Falkner, V.; Skan, S.W. LXXXV. Solutions of the boundary-layer equations. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1931, 12, 865–896. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin, Germany, 2016. [Google Scholar]
- Blasius, H. Grenzschicluen in Flüssigkeiten mit kleiner Reibung. Z. Angew. Maihemalik Phys. 1908, 56, 1–37. [Google Scholar]
- Hiemenz, K. Die Grenzschicht an einem in den gleichformigen Flussigkeitsstrom eingetauchten geraden Kreiszylinder. Dinglers Polytech. J. 1911, 326, 321–324. [Google Scholar]
- Magyari, E.; Keller, B. Exact solutions for self-similar boundary-layer flows induced by permeable stretching walls. Eur. J. Mech. B Fluids 2000, 19, 109–122. [Google Scholar] [CrossRef]
- Weyl, H. On the differential equations of the simplest boundary-layer problems. Ann. Math. 1942, 42, 381–407. [Google Scholar] [CrossRef]
- Coppel, W.A. On a differential equation of boundary-layer theory. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1960, 253, 101–136. [Google Scholar]
- Tam, K.K. A note on the existence of a solution of the Falkner–Skan equation. Can. Math. Bull. 1970, 13, 125–127. [Google Scholar] [CrossRef]
- Craven, A.; Peletier, L. On the uniqueness of solutions of the Falkner–Skan equation. Mathematika 1972, 19, 129–133. [Google Scholar] [CrossRef]
- Stewartson, K. Further solutions of the Falkner–Skan equation. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1954; Volume 50, pp. 454–465. [Google Scholar]
- Hastings, S. Reversed flow solutions of the Falkner–Skan equation. SIAM J. Appl. Math. 1972, 22, 329–334. [Google Scholar] [CrossRef]
- Craven, A.; Peletier, L. Reverse flow solutions of the Falkner–Skan equation for λ> 1. Mathematika 1972, 19, 135–138. [Google Scholar] [CrossRef]
- Lighthill, M.; Rosenhead, L. Laminar Boundary Layers; Clarendon Press: Oxford, UK, 1963. [Google Scholar]
- Hartman, P. On the existence of similar solutions of some boundary layer problems. SIAM J. Math. Anal. 1972, 3, 120–147. [Google Scholar] [CrossRef]
- Veldman, A.; Van de Vooren, A. On a generalized Falkner–Skan equation. J. Math. Anal. Appl. 1980, 75, 102–111. [Google Scholar] [CrossRef] [Green Version]
- Oskam, B.; Veldman, A. Branching of the Falkner–Skan solutions for λ< 0. J. Eng. Math. 1982, 16, 295–308. [Google Scholar]
- Botta, E.F.F.; Hut, F.; Veldman, A.E.P. The role of periodic solutions in the Falkner–Skan problem for λ> 0. J. Eng. Math. 1986, 20, 81–93. [Google Scholar] [CrossRef] [Green Version]
- Rajagopal, K.R.; Gupta, A.; Na, T.Y. A note on the Falkner–Skan flows of a non-Newtonian fluid. Int. J. Non-Linear Mech. 1983, 18, 313–320. [Google Scholar] [CrossRef] [Green Version]
- Massoudi, M.; Ramezan, M. Effect of injection or suction on the Falkner–Skan flows of second grade fluids. Int. J. Non-Linear Mech. 1989, 24, 221–227. [Google Scholar] [CrossRef]
- Padé, O. On the solution of Falkner–Skan equations. J. Math. Anal. Appl. 2003, 285, 264–274. [Google Scholar] [CrossRef] [Green Version]
- Pohlhausen, K. Zur näherungsweisen integration der differentialgleichung der iaminaren grenzschicht. ZAMM J. Appl. Math. Mech./Z. Angew. Math. Mech. 1921, 1, 252–290. [Google Scholar] [CrossRef] [Green Version]
- Asaithambi, A. Solution of the Falkner–Skan equation by recursive evaluation of Taylor coefficients. J. Comput. Appl. Math. 2005, 176, 203–214. [Google Scholar] [CrossRef] [Green Version]
- Boyd, J.P. The Blasius function: Computations before computers, the value of tricks, undergraduate projects, and open research problems. SIAM Rev. 2008, 50, 791–804. [Google Scholar] [CrossRef]
- Yun, B.I. New Approximate Analytical Solutions of the Falkner–Skan Equation. J. Appl. Math. 2012, 2012, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, F.; Al-Barakati, W.H. An approximate analytic solution of the Blasius problem. Commun. Non-Linear Sci. Numer. Simul. 2009, 14, 1021–1024. [Google Scholar] [CrossRef]
- Bougoffa, L.; Wazwaz, A.M. New approximate solutions of the Blasius equation. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 1590–1599. [Google Scholar] [CrossRef]
- Belden, E.R.; Dickman, Z.A.; Weinstein, S.J.; Archibee, A.D.; Burroughs, E.; Barlow, N.S. Asymptotic approximant for the Falkner–Skan boundary layer equation. Q. J. Mech. Appl. Math. 2020, 73, 36–50. [Google Scholar] [CrossRef]
- Crocco, L. Sullo strato limite laminare nei gas lungo una lamina plana. Rend. Math. Appl. Ser. 1941, 5, 138–152. [Google Scholar]
- Wang, L. A new algorithm for solving classical Blasius equation. Appl. Math. Comput. 2004, 157, 1–9. [Google Scholar] [CrossRef]
- Brighi, B.; Fruchard, A.; Sari, T. On the Blasius problem. Adv. Differ. Equ. 2008, 13, 509–600. [Google Scholar]
- Varin, V.P. A solution of the Blasius problem. Comput. Math. Math. Phys. 2014, 54, 1025–1036. [Google Scholar] [CrossRef]
- Homann, F. Der Einfluss grosser Zähigkeit bei der Strömung um den Zylinder und um die Kugel. ZAMM J. Appl. Math. Mech./Z. Angew. Math. Mech. 1936, 16, 153–164. [Google Scholar] [CrossRef]
- Shin, J.Y. A singular nonlinear differential equation arising in the Homann flow. J. Math. Anal. Appl. 1997, 212, 443–451. [Google Scholar] [CrossRef] [Green Version]
- Alizadeh, E.; Farhadi, M.; Sedighi, K.; Ebrahimi-Kebria, H.; Ghafourian, A. Solution of the Falkner–Skan equation for wedge by Adomian Decomposition Method. Commun. Non-Linear Sci. Numer. Simul. 2009, 14, 724–733. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Hayat, T. Solution of the MHD Falkner–Skan flow by homotopy analysis method. Commun. Non-Linear Sci. Numer. Simul. 2009, 14, 3591–3598. [Google Scholar] [CrossRef]
- Marinca, V.; Ene, R.D.; Marinca, B. Analytic approximate solution for Falkner–Skan equation. Sci. World J. 2014, 2014, 1–22. [Google Scholar] [CrossRef]
- Marinca, V.; Herişanu, N. The optimal homotopy asymptotic method for solving Blasius equation. Appl. Math. Comput. 2014, 231, 134–139. [Google Scholar] [CrossRef]
- Madaki, A.; Abdulhameed, M.; Ali, M.; Roslan, R. Solution of the Falkner–Skan wedge flow by a revised optimal homotopy asymptotic method. SpringerPlus 2016, 5, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Ariel, P.D. Homotopy perturbation method and the stagnation point flow. Appl. Appl. Math. 2010, 1, 154–166. [Google Scholar]
- Bararnia, H.; Ghasemi, E.; Soleimani, S.; Ghotbi, A.R.; Ganji, D.D. Solution of the Falkner–Skan wedge flow by HPM–Pade’method. Adv. Eng. Softw. 2012, 43, 44–52. [Google Scholar] [CrossRef]
- Motsa, S.; Sibanda, P. An efficient numerical method for solving Falkner–Skan boundary layer flows. Int. J. Numer. Methods Fluids 2012, 69, 499–508. [Google Scholar] [CrossRef]
- Fang, T.; Zhang, J. An exact analytical solution of the Falkner–Skan equation with mass transfer and wall stretching. Int. J. Non-Linear Mech. 2008, 43, 1000–1006. [Google Scholar] [CrossRef]
- Hartree, D.R. On an equation occurring in Falkner and Skan’s approximate treatment of the equations of the boundary layer. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1937; Volume 33, pp. 223–239. [Google Scholar]
- Smith, A. Improved Solutions of the Falkner and Skan Boundary-Layer Equation; Institute of Aeronautical Sciences Fund Paper FF-115; Institute of the Aeronautical Sciences: Reston, VA, USA, 1954. [Google Scholar]
- Cebeci, T.; Keller, H.B. Shooting and parallel shooting methods for solving the Falkner–Skan boundary-layer equation. J. Comput. Phys. 1971, 7, 289–300. [Google Scholar] [CrossRef]
- Na, T.Y. Computational Methods in Engineering Boundary Value Problems; Academic Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Asaithambi, N. A numerical method for the solution of the Falkner–Skan equation. Appl. Math. Comput. 1997, 81, 259–264. [Google Scholar] [CrossRef]
- Salama, A. Higher-order method for solving free boundary-value problems. Numer. Heat Transf. Part B Fundam. 2004, 45, 385–394. [Google Scholar] [CrossRef]
- Scavo, T.; Thoo, J. On the geometry of Halley’s method. Am. Math. Mon. 1995, 102, 417–426. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, B. An iterative method for solving the Falkner–Skan equation. Appl. Math. Comput. 2009, 210, 215–222. [Google Scholar] [CrossRef]
- Sher, I.; Yakhot, A. New approach to solution of the Falkner–Skan equation. AIAA J. 2001, 39, 965–967. [Google Scholar] [CrossRef]
- Asaithambi, A. A finite-difference method for the Falkner–Skan equation. Appl. Math. Comput. 1998, 92, 135–141. [Google Scholar] [CrossRef]
- Asaithambi, A. A second-order finite-difference method for the Falkner–Skan equation. Appl. Math. Comput. 2004, 156, 779–786. [Google Scholar] [CrossRef]
- Salama, A.; Mansour, A. Fourth-order finite-difference method for third-order boundary-value problems. Numer. Heat Transf. Part B 2005, 47, 383–401. [Google Scholar] [CrossRef]
- Salama, A.; Mansour, A. Finite-difference method of order six for the two-dimensional steady and unsteady boundary-layer equations. Int. J. Mod. Phys. C 2005, 16, 757–780. [Google Scholar] [CrossRef]
- Duque-Daza, C.; Lockerby, D.; Galeano, C. Numerical solution of the Falkner–Skan equation using third-order and high-order-compact finite difference schemes. J. Braz. Soc. Mech. Sci. Eng. 2011, 33, 381–392. [Google Scholar] [CrossRef] [Green Version]
- Parand, K.; Pakniat, N.; Delafkar, Z. Numerical solution of the Falkner–Skan equation with stretching boundary by collocation method. Int. J. Non-Linear Sci. 2011, 11, 275–283. [Google Scholar]
- Boyd, J.P. The optimization of convergence for Chebyshev polynomial methods in an unbounded domain. J. Comput. Phys. 1982, 45, 43–79. [Google Scholar] [CrossRef]
- Kajani, M.T.; Maleki, M.; Allame, M. A numerical solution of Falkner–Skan equation via a shifted Chebyshev collocation method. AIP Conf. Proc. 2014, 1629, 381–386. [Google Scholar]
- Asaithambi, A. Numerical solution of the Falkner–Skan equation using piecewise linear functions. Appl. Math. Comput. 2004, 159, 267–273. [Google Scholar] [CrossRef]
- Hajimohammadi, Z.; Baharifard, F.; Parand, K. A new numerical learning approach to solve general Falkner–Skan model. Eng. Comput. 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Kuo, B.L. Application of the differential transformation method to the solutions of Falkner–Skan wedge flow. Acta Mech. 2003, 164, 161–174. [Google Scholar] [CrossRef]
- Dehghan, M.; Tatari, M.; Azizi, A. The solution of the Falkner–Skan equation arising in the modelling of boundary-layer problems via variational iteration method. Int. J. Numer. Methods Heat Fluid Flow 2011, 21, 136–149. [Google Scholar] [CrossRef]
- Fazio, R. The iterative transformation method. Int. J. Non-Linear Mech. 2019, 116, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, K. A note on the solution of general Falkner–Skan problem by two novel semi-analytical techniques. Propuls. Power Res. 2015, 4, 212–220. [Google Scholar]
| Name of Flow | |||
|---|---|---|---|
| Pohlhausen [21] | 0 | 1 | 1.154701 |
| Blasius [3] | 0 | 0.332058 | |
| Homann [32] | 2 | 1 | 1.311938 |
| Hiemenz [4] | 1 | 1 | 1.232589 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asaithambi, A. On Solving the Nonlinear Falkner–Skan Boundary-Value Problem: A Review. Fluids 2021, 6, 153. https://doi.org/10.3390/fluids6040153
Asaithambi A. On Solving the Nonlinear Falkner–Skan Boundary-Value Problem: A Review. Fluids. 2021; 6(4):153. https://doi.org/10.3390/fluids6040153
Chicago/Turabian StyleAsaithambi, Asai. 2021. "On Solving the Nonlinear Falkner–Skan Boundary-Value Problem: A Review" Fluids 6, no. 4: 153. https://doi.org/10.3390/fluids6040153
APA StyleAsaithambi, A. (2021). On Solving the Nonlinear Falkner–Skan Boundary-Value Problem: A Review. Fluids, 6(4), 153. https://doi.org/10.3390/fluids6040153






