Teaching and Learning Floating and Sinking: Didactic Transformation in a Density-Based Approach

Abstract

This essay synthesizes more than a decade of research, most of which has been published, on the teaching and learning of floating and sinking (FS) phenomena. The research is comprised of the iterative design, development, implementation and evaluation of a Teaching-Learning sequence (TLS) for the teaching and learning of density within FS phenomena. It was initiated within the frame of the European Community supported “Materials Science” project. Due to the many, different aspects of the project, each publication has focused on a particular part of the study (e.g., effectiveness and the iteration process). The didactic transformation for the teaching of FS phenomena is presented and discussed here. In doing so, it is essential to mention: (a) the students’ ideas as the main cause of the scientific knowledge transformation, (b) the scientific/reference knowledge, and (c) the knowledge to be taught and its limitations. Thus, we intend to describe and justify the didactic transformation process and briefly synthesize the published (from previous papers) and unpublished results to show its effectiveness.

1. Introduction

School children are familiar with floating and sinking (FS) [1], which is a main topic in the teaching of fluids in science education [2,3], especially at the primary and lower-secondary levels (10- to 15-year-olds). Although the topic is very common, and children have many everyday life experiences in FS phenomena, their interpretation is challenging, not only because of the difficulty of the scientific concepts and the respective explanatory models that are involved (e.g., density, buoyancy), but also because of these everyday experiences that students have and their subsequent ideas [4].

Research on FS has been extensive in the last few decades, both regarding students’ ideas [5] and, consequently, about ways to effectively teach this topic [6]. Concurrently, Teaching-learning sequences (TLSs), i.e., medium-level curriculum unit packages, that include well-researched teaching-learning activities empirically adapted to student reasoning [7,8], are increasingly present in science education research, because they provide the opportunity to integrate teaching and learning theories and approaches, students’ ideas about science concepts and explanations of natural phenomena, as well as the historical development of scientific concepts [7,8,9,10].

One of the most critical issues in the design and development of a TLS is the didactic transformation of the content, i.e., transforming the scientific knowledge into appropriate knowledge to be taught [7,11,12]. The choice of content and how it is transformed in order for it to be easily understood and readily adopted by students is crucial in the entire process of TLS development. Although this often takes place, none or very little of it is usually conveyed. In other words, even though the didactic transformation process is an essential aspect in every teaching effort, and especially in the design and development of a TLS, researchers rarely describe the process in an explicit and detailed manner, possibly due to space restrictions [8,13]. Thus, colleagues who wish to further investigate any such didactic proposal’s effectiveness do not have all the necessary information to repeat its implementation.

To describe the didactic transformation process of certain content, in our case, FS phenomena, it is important to mention, among other things: (a) students’ ideas about the phenomenon and the concepts related to it, as the main reason for the scientific knowledge transformation, (b) the scientific/reference knowledge, and (c) the knowledge to be taught, in its new form, following scientific knowledge transformation, including its limitations.

Students’ alternative ideas have played a decisive role in the planning of teaching in science education in the last few decades [6]. Consequently, students’ ideas about FS phenomena, and the difficulties they face in adapting interpretations to be consistent with the scientific ones, need to be taken into account in every teaching effort that is developed within the frame of the prevalent constructivist approach [14]. Moreover, the study of the historical development of scientific knowledge concerning FS interpretations could contribute to the didactic transformation process by revealing the difficulties scientists had come up against in understanding and interpreting those phenomena throughout the centuries [14,15,16].

The TLS entitled “Density of materials in floating and sinking phenomena: Experimental procedures and modelling”, which was initiated in the framework of the European Community supported “Materials Science” project (FP6, SAS6-CT-2006-042942), has been described elsewhere [17,18,19,20,21,22]. However, because there were many different aspects of content to be taught, i.e., declarative (density and floating sinking), procedural (control of variables strategy), and epistemological knowledge (nature and role of models), the focus of the previous published papers has been other than describing and justifying the didactic transformation, which we hope to do here.

In this paper, we briefly describe elements of our developmental research that have already been published, focusing, however, on the didactic transformation of content, as this has not yet been thoroughly presented or discussed and which we consider to be of paramount importance. Therefore, our aim is to describe the didactic transformation of the content of the TLS concerning FS phenomena, to underline the factors which influenced the process of its development, and to present the limitations of the transformation. Specifically, we justify the reasons why we chose the density-based explanatory model for FS phenomena, rather than the buoyancy-based (see Section 3), as well as providing arguments for the didactic transformation of the concept of density, which is still an open issue for an effective approach to FS learning. Furthermore, selected essential aspects of the revised version of the TLS, which was adapted from an initial study, are also described [19]. Moreover, a short presentation of both our published (from previous papers) [20,21], and unpublished results in FS [22], on the implementation of the revised TLS in a real-class environment is given. In this sense, we consider that this work is an original sample of a developmental research description in the framework of Design-Based Research approach in science education [8,23,24].

2. Alternative Ideas and Difficulties in Explaining FS Phenomena

Students seem to perceive FS phenomena visually. That is to say that they decide whether an object is in a floating or sinking state based on the object’s position relative to the surface of the liquid [1]. For instance, the majority of students in Joung’s study [1] answered that an object was floating in the water when at least a part of it was above the surface, most of whom chose the case where the object touches the surface of the liquid and fewer chose the case where the object was half-submerged. Also, the majority of students considered that an object had sunk in the water, in the cases where it was below the surface, i.e., (a) at the bottom, or (b) in the middle (between the bottom and the surface of the liquid), with a decreasing frequency of occurrence, respectively. In the same research, students considered an object just below the liquid surface either to be floating or to have sunk. Few students recognized that when the object was between the surface of the liquid and the bottom, then it is in a state between floating and sinking, and therefore, was suspended and remaining at rest in the liquid at the same location [1,25].

In addition, it seems that students explain and describe the phenomena in relation to perception-based macroscopic natural properties, such as weight, length, and volume [5,26,27,28]. In other words, students formulate their estimation concerning the floating of solid objects in a liquid by taking into account: (a) the heaviness/size of the objects, (b) the existence of hollows, (c) the existence of holes, (d) the interface/edge, orientation, shape and/or texture of the floating object, (e) the dimensions of the tanks in which floating takes place, (f) the amount and/or depth of the liquid, and (g) the liquid stickiness [29]. Needless to say, one of the most prevalent alternative ideas that students hold is that of case (a), that is, students most often claim that an object floats because it is small and/or light, and it sinks because it is big and/or heavy [26,30].

Consequently, when interpreting FS phenomena, students tend to focus on the properties of the objects or the liquids. Additionally, they seem to merely use causal linear reasoning, referring only to an object’s or a liquid’s property, instead of causal relational reasoning, which involves comparing object and liquid densities in their interpretations [31]. However, this is not the only obstacle in students using the specific causal relational reasoning to explain FS phenomena. Researchers who have studied students’ conceptions of density [26,32,33] have found that they had difficulty in understanding this abstract concept. Firstly, students find it hard to understand the ratio of two quantities [34], such as that of mass per volume, particularly when those quantities are changing simultaneously [35]. Secondly, the concept of density is a property that is not directly perceived through the senses but can only be understood through mental reasoning and/or calculations [33,36]. Thirdly, students’ difficulty in understanding density is rooted precisely in an already developed conceptual framework about matter and material kind [37], which is composed of perception-based physical quantities where the raw scientific notions of weight, volume and density coexist undifferentiated [33]. Consequently, these students consider density to be proportional to the size of an object or the object’s quantity of matter.

To fully understand the reasons why an object floats or sinks, one needs to comprehend that the concept of water pressure is an intensive property, while the concept of buoyancy is a force, and not, as is usually the case with students, a property of an object, within the framework of Newtonian mechanics [4,5]. However, students very often confuse the FS states with the explanatory model; that is, they equate buoyancy, a construct/force in an explanatory model, with the state of floating. They also seem to think that buoyancy is a property of an object opposed to the interaction between an object and its surrounding fluid, as they are unable to understand buoyancy as a force, i.e., the interaction between two entities. Furthermore, many students have the misconception that the buoyancy of an object is inversely proportional to its density, while others are not sure about the direction of buoyancy [4].

In sum, students confront severe difficulties in interpreting FS phenomena in the framework of both density-based and buoyancy-based explanatory models. The reasons for this difficulty, however, are not the same in both cases. In the former, the difficulty is mainly due to the non-differentiation of the concepts of weight, mass, and density, in contrast to the latter case, where it is mainly due to the students’ inability to understand the concept of force as the interaction between two entities.

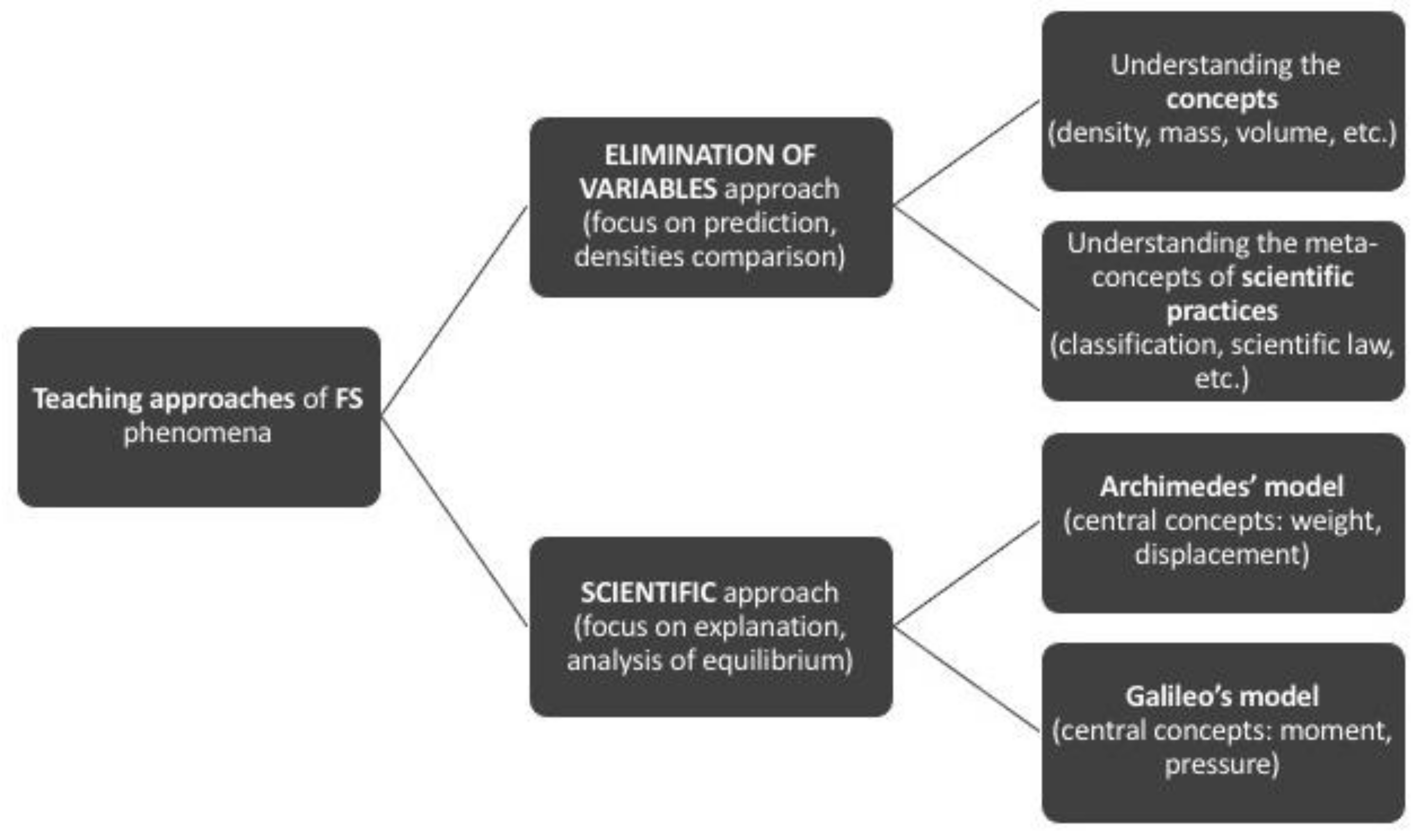
3. Floating and Sinking Teaching Approaches

The way educators approach the teaching of FS phenomena can be put into two broad categories, according to the central concept of the explanation of the phenomena (Figure 1). In the first category are those cases that provide density-based explanations, e.g., [29], following the so-called elimination of variables approach. This approach focuses on highlighting the variables that affect the FS phenomena in order to derive a prediction rule that will determine “which” body will float. In the second category are those cases that provide buoyancy-based explanations, e.g., [38], following the so-called scientific approach, that is, an interpretation using an equilibrium mechanism in order to explain “how” an object floats [15]. Several researchers provide both explanations concurrently [4,32].

The scientific approach is rooted in Archimedes’ and Galileo’s explanatory models [15,39]. In brief, Archimedes explained the floating of a solid in an infinite container, using only the concept of weight as a quality/property of objects [40] and comparing the weight of the solid to the weight of the fluid that was displaced by the immersed portion of the solid. He proposed that the weight of the fluid displaced would be equal to the weight of the solid. However, Archimedes’ model was effective only for FS phenomena in infinite containers [40]. On the other hand, Galileo overcame Archimedes’ inadequacy by explaining floating of a solid in a finite container. Galileo’s model comprised important discriminations of new-defined concepts [15,40], such as the distinction of floating and surface tension phenomena [41] and the differentiation of the concepts of weight and specific weight in a qualitative manner [15]. Both models derive their floatation laws from an analysis of the conditions that result in equilibrium. However, Galileo’s model consists of more delicate and abstract concepts and, subsequently, can explain a larger range of phenomena [15,39]. On the other hand, the elimination of variables approach is rooted in Inhelder and Piaget’s work [42]. These researchers were the first to record children’s explanations on the floating phenomenon, focusing mainly on the ability of children to (a) classify a set of objects according to whether they float or sink in the water, and (b) explain the criterion by which the classification was made [15]. Moreover, they were interested in testing children’s ability to eliminate inconsistencies in their initial explanations, such as using the weight of objects in order to interpret FS phenomena, and at the same time, to formulate the predictive floating law; that is, objects float if their density is less than that of water, where density is defined as the ratio of weight to volume. Thus, contrary to the scientific approach, which focuses on the construction of an interpretive model that will explain “how” a body floats, the elimination of variables approach focuses on the construction of a predictive model for FS phenomena, with the latter being less complicated, and subsequently, an easier process for students [15].

Usually, the density-based approach is adopted by primary schools and junior high schools [6,15], while senior high schools and colleges/universities adopt the buoyancy-based approach [15] or a combination of both [4]. When one develops a curriculum for this topic, the chosen approach, whether density- or buoyancy-based, would also involve selecting different steps, practices and concepts in the teaching and learning process. Therefore, in the case of the elimination of variables approach being chosen, there would need to be an intermediate goal of the learning process, which would involve differentiating weight, volume, and density as this approach requires a clear understanding of these the concepts (Figure 1). Another intermediate goal would be explaining FS phenomena by using a partially correct explanatory model, that is, that an object’s density as a property of materials determines its sinking or floating.

A correct explanatory model within the frame of the elimination of variables approach would be to use the concept of density in causal relational reasoning, that is, comparing the densities of an object and a liquid in order to come to a decision about the FS situation [31]. Contrastingly, in those curricula where FS is taught through an analysis of the equilibrium approach, it is not needed for students to discover or to be introduced to any intermediate/precursor concepts [29]. For example, sinking and floating can be explained as a result of the balance between gravity and buoyancy. In that case, the forces of buoyancy and gravity are the required concepts for the final learning goal. However, both buoyancy and gravity are scientific—rather than intermediate/precursor—concepts, which makes their understanding more difficult. Although the latter explanatory model is more potent than the first one, because it is capable of explaining more cases of natural phenomena, e.g., motion involved in FS phenomena, concurrently, it is more complex, and hence, more difficult to understand, especially for younger students [4]. This is one of the reasons why primary and junior high schools adopt the density-based approach, in other words, the elimination of variables approach. In this case, teachers are faced with the difficult choice of introducing density using one of the following three ways: (a) the mathematical ratio of mass per volume, (b) the particle theory of matter, or (c) a visual representation that emphasizes the qualitative aspect of density [15]. However, the first case, i.e., a mathematical introduction of density, has been proven to be ineffective, due to the fact that students find it hard to differentiate between the concepts of mass, volume and density, or understand that density is an intensive quantity [15,34]. In addition, the second case, i.e., using the particle theory of matter, would most probably create misconceptions or reinforce students’ prior ideas, such as the non-differentiation of density and denseness [43]. It has been shown that introducing density through this approach is rather abstract, which makes it very difficult for 9- to 12-year-old students to comprehend [44]. It would, thus, appear that the last case is the most appropriate because, in contrast to the first two, the use of a visual representation also provides opportunities for differentiating the focal concepts [26].

In the last few decades, teaching approaches have been developed in the framework of inquiry, emphasizing both the content of science and scientific practices [29,45,46]. As can be seen in Figure 1, there is a need for the emphasis to be on the understanding of the meta-concepts of scientific practices, e.g., the process of developing evidence-based conclusions through an experimental procedure, which, from an early stage, had been the focus of the elimination of variables approach. By this comment, we do not claim that inquiry-based teaching is not suitable or feasible to be implemented in the scientific approach of the analysis of equilibrium for FS phenomena. Rather, in order for the results of the eliminating of variables, experimental procedures to be understood and adopted by students, they need to be aware of the reasoning behind the scientific practices involved [15,46]. We claim that the TLS described in the next section is an example of effective density-based implementation, concurrently aiming at declarative knowledge (FS and density), procedural knowledge (control of variables strategy), and epistemological knowledge (nature of models) [18].

4. Description of the TLS: Emphasis on the Content of FS and Its Didactic Transformation

4.1. The Design Principles of the TLS

A case example of the elimination of variables approach for teaching and learning FS phenomena is presented with the five-unit TLS entitled “Density of materials in floating and sinking phenomena: Experimental procedures and modelling”. The design principles of the TLS have been discussed in detail in former publications, e.g., [19]. For the sake of clarity, a brief reference to the six design principles of the TLS is made here, focusing on those regarding FS didactic transformation and relevant activities. More specifically, the design principles of the TLS were as follows [19]:

1.

The didactic transformation of content [11] concerning FS phenomena, that is, firstly, the decision to adopt a density-based approach to negotiate FS phenomena, and, secondly, the decision to introduce the concept of density in a qualitative way. Both decisions were driven by the difficulties that primary school students confront when prompted to negotiate FS phenomena.

2.

The participatory design and developmental character [47] of the TLS includes teachers, together with researchers, in its designing, developing and evaluating processes. Teachers discussed the nature of the TLS activities with the researchers, how they understood the activities, the possible difficulties that students might face, and consequently the possible changes and/or specific teaching methods that would be suggested. Thus, the research was adapted to the particular needs of the school and the students.

3.

The TLS’s iterative process [8], which provided the opportunity to both researchers and teachers to evaluate together the initial implementation of the TLS and to propose improvement modifications [19]. Thus, the iterative evolution of the TLS contributed to the final version of the TLS and its didactic transformation.

4.

The technological problem scenario, to provide a supportive context for learning [48]. The scenario was based on salvaging the Sea Diamond shipwreck. Discussion is initiated with an everyday problem (in our case, technological), which poses questions. These are answered through scientific knowledge that is eventually applied to solve the initial real-life problem. The combination of technological and scientific knowledge in teaching promotes active learning, improves students’ performance and attitudes towards science, enhances positive interaction between teachers and students, and provides students with opportunities to participate in authentic exploratory processes, which are usually carried out by scientists [49,50].

5.

The Inquiry-Based Science Education (IBSE) approach, by emphasizing the need to use scientific practices: (a) as a means of teaching and learning, e.g., investigating the variables that possibly influence the FS phenomena in groups, and (b) as an educational end, whose aim is to understand specific aspects of scientific practices [46,51,52]. Within this framework, learning is perceived as active and student-centered, due to pupils’ increased interest and autonomy [53], and the intention is for them to gain ample practice in scientific reading and writing [54].

6.

The use of digital tools, such as a simulation that was developed from scratch for the TLS [17]. Looking at existing educational software on FS phenomena, the proposals were inappropriate for our task, mainly because it was difficult to implement the inquiry-based activities and also because they tended to have a mathematical approach to the introduction of the concept of density. Therefore, a specially designed software package that followed the design principles of the TLS was designed from scratch. Furthermore, a simulated website on a local network was designed and developed for students to investigate information about materials, with the aim of becoming accustomed to scientific reading and writing skills.

4.2. The Didactic Transformation of the TLS

FS phenomena are not included in the Greek primary school curriculum. However, the concept of density is introduced in fifth grade (10–11-year-olds) as a property of materials, with a limited number of examples, including one task that negotiates the sinking of a real ship. Although the curriculum proposes a guided discovery approach for negotiating phenomena and concepts, and one of the aims explicitly referred to is for students to understand the scientific method, the majority of teachers implement traditional deductive teaching-learning practices, followed by experimental demonstrations, whereas group work is sporadic [19].

As mentioned, the TLS was developed within the “Materials Science” project and is proposed as part of a broader curriculum for primary and lower-secondary level students (10- to 15-year-olds). The general objective of this broader curriculum is to restructure students’ conceptual framework as regards the concepts of matter and material kind [33], including fluids. The elimination of variables rather than an analysis of equilibrium explanatory model for FS phenomena was adopted for reasons to do both with students’ difficulties and the project’s characteristics. Students’ difficulty in understanding and effectively implementing an equilibrium mechanism, such as the buoyancy-based model to explain FS phenomena, has already been documented [4,15] and is analytically discussed in Section 3.

Furthermore, the emphasis of the project, which, on the one hand, is on the properties of materials properties, and the other, on inquiry-based teaching and learning, appears to be more compatible with the elimination of variables approach, that is, the density-based approach for teaching FS phenomena [15] (see Section 3). By highlighting the variables of these phenomena in order to derive a prediction rule that will determine “which” body will float, instead of negotiating the forces that are acting on an object when it is immersed in a liquid, we believe is easier for students in this age range to understand, and thus more conducive to the teaching/learning process.

It was decided to introduce the concept of density through the visual “dots-in-a-box” representation (Figure 2) as a property of materials [26]. As students would have already investigated the variables that affect the FS phenomenon, this visual representation shows several variables in only the one diagram. Obviously, the “dots-in-a-box” representation depicts the weight of the object by the number of dots, and the cube represents its volume or size, while its kind of material is now assigned to the conjunction of the weight and volume and not to any realistic representation of its external appearance. This enables students to easily make comparisons of the densities of the different materials in order to predict and explain FS phenomena, and if possible, to grasp the “heavy for its size” intermediate/precursor concept of density. In this way, the usual introduction of density using the mathematical ratio mass to volume, which has been shown to be difficult for students of these ages to grasp such relationships, has been bypassed [34].

With a view to preventing or eliminating any misconceptions, such as “all hollow objects float” or “objects with air always float”, as reported in the study by Yin et al. [29], we also thought it best to first introduce students to homogenous objects in the variable of solids. In the TLS, density is introduced within the context of floating or sinking of various everyday objects. First, students are introduced to homogeneous and then to composite objects, such as an iron cube and a ship, respectively, using causal relational reasoning, in other words, by comparing the density of the object and liquid, one is able to interpret and/or predict the FS of each object [31].

In sum, the didactic transformation of the TLS consists of two core choices (a) selecting the density-based approach to teach FS, and (b) qualitatively introducing the concept of density through the “dots-in-a-box” representation. Reference is made here to the other two subsidiary but significant aspects of the didactic transformation: (a) integrating scientific and technological knowledge into a context-based approach (fourth design principle), and (b) incorporating guided discovery experimentation into the explicit teaching of procedural and epistemological knowledge within an inquiry-based approach (fifth design principle). The teaching/learning environment for the experimentation activities was initially structured, which was gradually decreased with the aim of enabling students to become more autonomously involved [19,53].

More specifically, FS phenomena are introduced in the fourth design principle through a technological-problem scenario based on salvaging the Sea Diamond shipwreck [19]. The scenario, which runs throughout the entire TLS, has a dual role, on the one hand, it forms the familiarization phase, and on the other, it involves the following scheme: “technological problem”, “scientific investigation”, and “return to the problem” with the aim of increasing students’ curiosity and motivation leading to the solution of the problem [49,50]. In contrast to the traditional approach, which proposes only the scientific investigation of the phenomena and the related concepts, our context-based approach through the technological-problem scenario increases students’ interest and succeeds in involving them in the entire teaching/learning process [48].

The content of the TLS within the fifth design principle, which is the IBSE approach, includes elements of the inquiry method, i.e., aspects of the control of variables method as well as the nature and role of the models [18,19]. In other words, students are explicitly taught that to test if a variable influences a phenomenon, e.g., FS, then only this variable should differ, and all the other independent variables should be controlled [55]. In addition, students are explicitly taught aspects of nature and the role of scientific models, for instance, that models are not an exact representation of reality and that they are used to describe, predict, or explain a phenomenon [19,56]. Our hypothesis that procedural and epistemological knowledge would positively affect the understanding/interpretation of FS phenomena has been confirmed [18]. Thus, our claim that inquiry as a teaching goal constitutes part of the TLS’s didactic transformation has been reinforced.

Summing up, the didactic transformation of the TLS described in this paper is based on (1) the elimination of variables approach to teaching FS phenomena, and (2) the qualitative introduction of the concept of density using the “dots-in-a-box” visual representation [26]. The explanatory model proposed for students to use in order to predict and explain FS phenomena for both solid and composite objects is based on the “dots-in-a-box” representation, in conjunction with the causal relational FS rule, which is, if an object’s density is smaller than the liquid’s density, then the object will float, and if an object’s density is greater than the liquid’s density, then the object will sink. We maintain that it is easier for young students (primary and junior high school) to grasp a qualitative representation of density, as a property of materials, rather than the scientific knowledge of the specific content, which is traditionally presented as a mathematical ratio of mass per volume, or even weight per volume [26,27]. Understanding the concept of density as “heavy for its size”, thus perceiving density to be related simultaneously to both weight and volume, was an implicit teaching goal of the TLS. In this sense, we claim that by using the “dots-in-a-box” visual representation in their explanations for FS phenomena, as a property of materials and not of objects, students can differentiate the concepts of density and weight and consequently come closer to an intensive perception of the concept of density.

Every didactic transformation of content in science education is characterized by limitations related to (a) the kind of explanation of the focal phenomena and/or (b) the range of the phenomena explained when the model that is related to the transformed content is being used [12]. Therefore, the explanatory model of FS presented here (visual representation of density in conjunction with causal relational FS rule) has some limitations in comparison to other more abstract explanatory models (e.g., the analysis of equilibrium model for the explanation of FS and/or mathematical ratio for the representation of density). These are:

1.

Only static FS phenomena can be interpreted: It was decided not to study buoyant force as an alternative explanatory model of FS phenomena because we considered the analysis of equilibrium approach between buoyant and gravity forces, which is implied in the buoyant force model (see Section 3) is particularly difficult for primary school and some junior high school students. Additionally, the concept of displaced liquid, which is not necessary for the density-based model, was omitted as it might distract students from the expected learning outcomes of the TLS. This means that several aspects of FS phenomena regarding objects in fluids that are not at rest but in motion cannot be explained. For instance, the motion of an object that is initially sunk in the water and then is released when the density of the object is smaller than that of the water can only be explained if an analysis of equilibrium model is used.

2.

Only a qualitative estimation of material density can be determined: We are aware that the qualitative “dots-in-a-box” representation does not accurately match the actual value of material density. It provides an approximate estimation of density that also enables an approximate estimation of the inequality of the relationships between the densities (larger-smaller). For example, the relationship between the density of oil and rubber, of course, is not equal to the ratio of one to two (1:2) (Figure 2); the diagram depicts only that the density of rubber is larger than that of oil. However, when it is necessary to determine the density of a composite object consisting of two materials of different densities, the only information the qualitative “dots-in-a-box” representation can give us is that the density of the composite object ranges between the densities of these two materials. In contrast, if we use the mathematical ratio of the concept of density, then we can precisely calculate the average density of the composite object. Another limitation of the qualitative introduction of density as a property of materials is that it cannot predict nor explain changes in density (especially of gases) under temperature and pressure fluctuations. Such changes could be explained microscopically, at an older age though, using the particle model of matter.

4.3. The FS Content of the TLS

The teaching and expected learning trajectory of the TLS implementation, along with a brief description and the activities in the five units, are presented here. The sequence of the activities is a fundamental element of the teaching design and implementation. In order to focus on the content that is directly relevant to FS phenomena, we do not include here any content to do with the control of variables strategy and models, which has, however, been described in previous publications [18,19]. The description follows the scheme of “main aim, content, and activities that students participated in” (

Table 1. Main aim, content and activities concerning FS in the five units of the TLS.

Unit	Main Aim	Content	Activities
1st	Familiarization phase through technological problem.	Technological problem of lifting shipwreck. Distinction of variables that possibly influence FS. Difference between solid and hollow objects.	Groups and classroom discussion. POE activities. Demonstration of experiments.
2nd	Test variables that influence FS.	FS of solid objects influenced both by the material of object and liquid. FS not influenced by other variables, e.g., weight of object.	Groups and classroom discussion. POE activities with gradual increase in openness.
3rd	Introduction of “dots-in-a-box” representation of density. Use of causal relational FS rule for solid objects in water.	“Dots-in-a-box” representation describes “heavier-lighter” relationship between different materials. Compare “dots-in-a-box” representations for solid objects and water to decide objects’ FS in water.	Groups and classroom discussion.
4th	Generalization of causal relational FS rule. “Dots-in-a-box” renamed “density”.	Density of a two-material composite object lies between the densities of these two materials. Compare composite object’s and liquid’s densities to decide object’s FS in a liquid.	Groups and classroom discussion. POE activities.
5th	Lifting shipwreck.	Implementing generalized causal relational FS rule within the technological framework.	Groups and classroom discussion.

). Students worked: (a) in groups of three to complete structured worksheets on both the real and simulated experiments that followed the POE (Predict–Observe–Explain) teaching strategy [57], and/or (b) in a whole class arrangement, following formative assessment activities [4].

In the first unit, our main aim was to provide students with a familiarization phase of FS through the technological problem of salvaging the shipwreck. Students participated in: (a) an introductory discussion about the variables that might influence floating and sinking, resulting in five independent variables: weight, material, and shape of the object, width of the container, type of liquid; and (b) a thorough discussion about the concept of a solid and homogeneous object, in contrast to a hollow object, in order to focus on solid objects. The teacher demonstrated an experiment in the POE approach to check if the first of the five independent variables, i.e., the weight of an object, influences the object’s FS situation.

In the second unit, our main aim was for the students to understand that the FS of a solid and homogeneous object is influenced by the material of the object and the type of liquid. The POE activities that students participated in were characterized by the gradual decrease of scaffolding or the gradual increase of openness. In these activities, students were prompted to test the other four variables that might influence the FS of solid and homogeneous objects; we note here that the teacher has demonstrated the variable weight in the previous unit.

In the third unit, the main aim was the introduction of the “dots-in-a-box” representation of density and the use of this representation to predict and explain FS of solid and homogeneous objects, in conjunction with the causal relational FS rule, i.e., if an object’s “dots-in-a-box” representation is smaller than the water’s, then the object will float in water, and if an object’s “dots-in-a-box” representation is greater, then it will sink in the water. Students: (a) searched and gathered information about the properties of several natural and artificial materials, such as glycerin and polyurethane, and the ways they can be used, (b) negotiated with cubes of the same volume but different material and were assigned with a task prompting them to express the “heavier-lighter” material relationship (Figure 3), and (c) completed a task in a simulated environment, using a balance in order to put cubes of the same volume but different materials in the order of heavier to lighter. The sequence of densities of the materials in Figure 2 resulted from this sequence of tasks.

In the 4th unit, the main aim was to generalize the causal relational FS rule to explain FS in any liquid and for both solid and composite objects. First, students participated in real and simulated experiments of several homogeneous objects in glycerin instead of water, emphasizing once again the role of the type of liquid in the explanatory model of FS phenomena (Figure 4a). In addition, understanding that the density of a two-material composite object lies between the densities of these two materials was crucial, so students participated in real experiments of composite objects in water, emphasizing the role of the average density of an object in predicting and/or interpreting its FS. In this unit, the phrase “dots-in-a-box” was replaced with “density” to refer to the property of materials.

In the 5th unit, the main aim was to find the best solution for lifting the shipwreck, if possible, by implementing the generalized causal relational FS rule. The students had the opportunity to work in groups both in real and in a simulated environment (Figure 4b) so as to investigate the FS of the Sea Diamond shipwreck, studying the effect of excess water in the hold of the ship and discuss how it could be salvaged.

5. Selected Results

Here, a short description of the research method, and selected results on the learning of FS, of the implementation of the revised TLS are presented to show its effectiveness and its didactic transformation.

5.1. Method

The TLS described in this essay was developed, implemented and evaluated twice in an iterative evolution manner [19]. The initial and the revised versions were implemented on twelve and forty-one 5th graders, respectively, in a real-classroom educational context [20,21,22].

Data were collected using several sources (questionnaires, interviews, researchers’ notes, etc.). For the sake of brevity, we focus on six Tasks of the questionnaire (see Appendix A) in order to evaluate the impact of the TLS implementation on students’ FS explanations. The students answered the same questionnaire before, immediately after the TLS intervention, and seven months later (Pre, Post, and Delayed Post, respectively). More specifically, Tasks 1 and 2 were answered all three times, whereas Tasks 3–6 were answered in the Post and Delayed Post Tests. These tasks were not included in the Pre-questionnaire, either because students did not know the ‘dots-in-a-box’ representation before the intervention (Tasks 3 and 4) or because the questions were too complex to be attempted before the intervention (Tasks 5 and 6). While the results for Tasks 1–4 have been published in previous papers [20,21], the findings for Tasks 5 and 6 are presented here for the first time.

5.2. Results

The analysis results of students’ responses for the six Tasks (Means and Standard Deviations) are presented in

Table 2. Means and Standard Deviations of the students’ responses in the six Tasks (n = 41).

	Pre		Post		Delayed Post
	M	SD	M	SD	M	SD
Task 1	1.10	0.664	1.78	0.936	1.68	0.879
Task 2	0.78	0.613	1.39	0.862	1.37	0.859
Task 3	-	-	0.63	0.488	0.56	0.502
Task 4	-	-	0.73	0.449	0.54	0.505
Task 5	-	-	0.44	0.502	0.44	0.502
Task 6	-	-	0.51	0.506	0.46	0.505

.

Tasks 1 and 2 examined students’ explanations about FS phenomena, whereas the ‘dots-in-a-box’ visual representation was not given. In both Tasks, the weight or the size of the object is the characteristic that could mislead students’ responses to the alternative idea that “an object sinks because it is heavy” or “because it is big”. The responses were classified thus: 0 for no or irrelevant answers, 1 for reference to the object’s weight, 2 for reference to the material the object consists of, and 3 for reference to the causal relational FS rule, i.e., comparing the densities of the object and the liquid to predict and/or explain the object’s FS. The study findings showed that there was a statistically significant improvement after the TLS intervention for both Tasks 1 and 2 (z = 3.446, p < 0.001 and z = 3.801, p < 0.001, respectively), which was retained seven months later. More specifically, for Task 1, the mean was 1.10 for the Pre-Test, which went up to a high 1.78 in the Post-Test, and which was maintained with a slight decrease seven months later in the Delayed Post-Test (1.68). The results were similar for Task 2, where the mean in the Pre-Test was only 0.78, which rose to 1.39 immediately after the TLS intervention in the Post-Test and was maintained almost at the same level (1.37) in the Delayed Post-Test.

Tasks 3 and 4 examined students’ explanations about FS in a simulated environment, while the “dots-in-a-box” representation was also given. Students’ responses were classified as 0 for causal linear reasoning, i.e., focusing only on one characteristic of the objects, and 1 for causal relational reasoning, i.e., a comparison of the densities of the object and the liquid. The results showed that most of the students were able to use the “dots-in-a-box” representation to successfully apply causal relational reasoning in their responses, immediately after the intervention and seven months later (Table 2). More specifically, for Tasks 3 and 4, the means for the Post-Test were 0.63 and 0.73, respectively, which decreased slightly in the Delayed Post-Test to 0.56 and 0.54, respectively. In addition, it appears that most of the students who were able to apply causal relational reasoning in Task 4 could also understand differences in float levels in relation to material density [20], a topic that had not been covered in the intervention.

The last two Tasks 5 and 6 examined whether students could effectively determine the position of an object, in relation to the surface of a liquid, in order to establish its density. In Task 5, in order for students to correctly decide the relationship between the densities of the two objects by applying the causal relational FS rule, they would have to disregard the size of the two objects, which could have been misleading. Students that did not, even qualitatively, differentiate between weight and density would intuitively think that the bigger object had a greater density. Students’ responses were classified as 1 for using the causal relational FS rule and 0 in all other cases. The results in Table 2 show that a large number of students were able to successfully answer Task 5, with a mean of 0.44 in both the Post- and delayed Post-Tests, thus indicating that they, at least, qualitatively differentiated between weight and density. For Task 6, in order to successfully apply the causal relational FS rule and come to the conclusion that the density of the object is equal to the density of the liquid, students had first to recognize that the object was in a state between floating and sinking, and therefore suspended, which meant that it remained in the liquid at the same location at rest. Responses were classified as 1 for recognizing that the object was suspended and for successfully applying the causal relational FS rule, and 0 in all other cases. The results in Table 2 show that a large number of students were able to successfully answer this question, with means of 0.51 and 0.46 for the Post- and Delayed Post-Tests, respectively. This finding indicates that the students were able to apply the causal relational FS rule in a new situation, that of the suspension of an object in a liquid, which had not been covered in the TLS intervention.

6. Discussion and Conclusions

In this paper, we describe and examine certain elements in the teaching of floating and sinking, with focus on the didactic transformation of content, which was part of a long-term developmental study. The didactic transformation process is an essential aspect in each teaching effort and especially in the design and development of a TLS.

In our research on the teaching of floating/sinking (FS) phenomena to 5th grade Primary school students, we adopted the elimination of variables approach (density-based) rather than an analysis of equilibrium explanatory model (buoyancy-based). The reasons for this decision were: (1) students find it difficult to understand and effectively implement the buoyancy-based model to explain FS, in contrast to density which is an easier concept to comprehend; (2) The emphasis of our developmental study project was on materials and their properties; and (3) Inquiry-based teaching and learning is more compatible with the elimination of variables approach, for the teaching of FS phenomena, as well as being more in line with the current Greek school curriculum.

The concept of density was introduced to students qualitatively through a visual representation called “dots-in-a-box”. The qualitative method was chosen over (a) the mathematical ratio of mass per volume and (b) the particle theory of matter. The reasons for this choice are as follows: (1) the visual representation makes it easier for students to grasp this scientific concept, whereas the mathematical introduction of density has several times been shown to be ineffective, at least with primary and junior high school students [34]; (2) misconceptions would most likely arise with the particle theory of matter; and (3) introducing density with a visual representation also provides students with opportunities for differentiating the concepts involved in the interpretations of FS phenomena, e.g., density, weight and volume.

The study findings strongly suggest that our TLS and the didactic transformation of content that was developed had a significant level of success in the teaching/learning of FS to young students, which seems to have been maintained seven months later. Most of the students adopted explanations that were compatible with scientific ones and were able to overcome their prior alternative ideas, such as “heavy objects sink and light objects float”. In addition, when given the “dots-in-a-box” visual representation of density, the students successfully implemented the causal relational FS rule, i.e., comparing the densities of the objects and liquid to predict and/or explain the FS state of objects. Finally, several students were able to implement the density-based model, which they had been taught, to explain situations that had not been covered in the TLS intervention, such as successfully predicting the floating level of objects made of different materials and applying the causal relational FS rule for objects suspended in a liquid. Both cases are considered difficult for students in this age range (10–15 y-o) to comprehend and explain [1].

We consider that this work is an original sample of a developmental research description, in the sense of the Design-Based Research approach in science education [8,23,24], and consequently an example of effective good teaching practice, that can help teachers to elaborate on their teaching and inspire innovative treatment of the topic of floating and sinking in science curricula for primary school physics. The teaching and learning intervention for floating/sinking phenomena, which is in itself a difficult conceptual science topic, to this young target population, was successful, we strongly believe, due to the contribution of the didactic transformation of content.