Squeeze Flow of Stress Power Law Fluids
Abstract
:1. Introduction
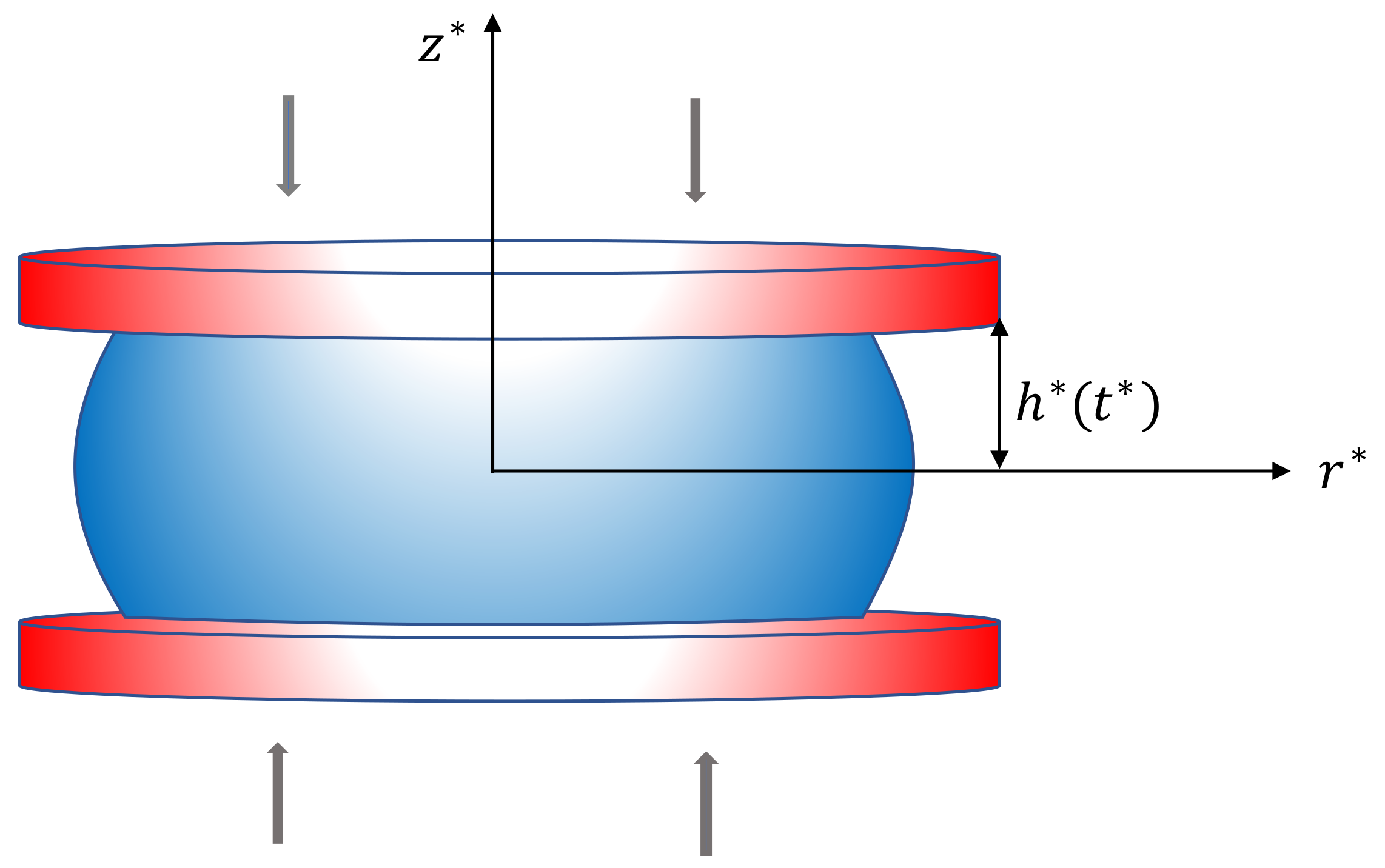
2. Squeeze Flow
3. Zero-Order Approximation
3.1. The Case
3.2. The Case
4. First-Order Approximation
4.1. The Case
4.2. The Case
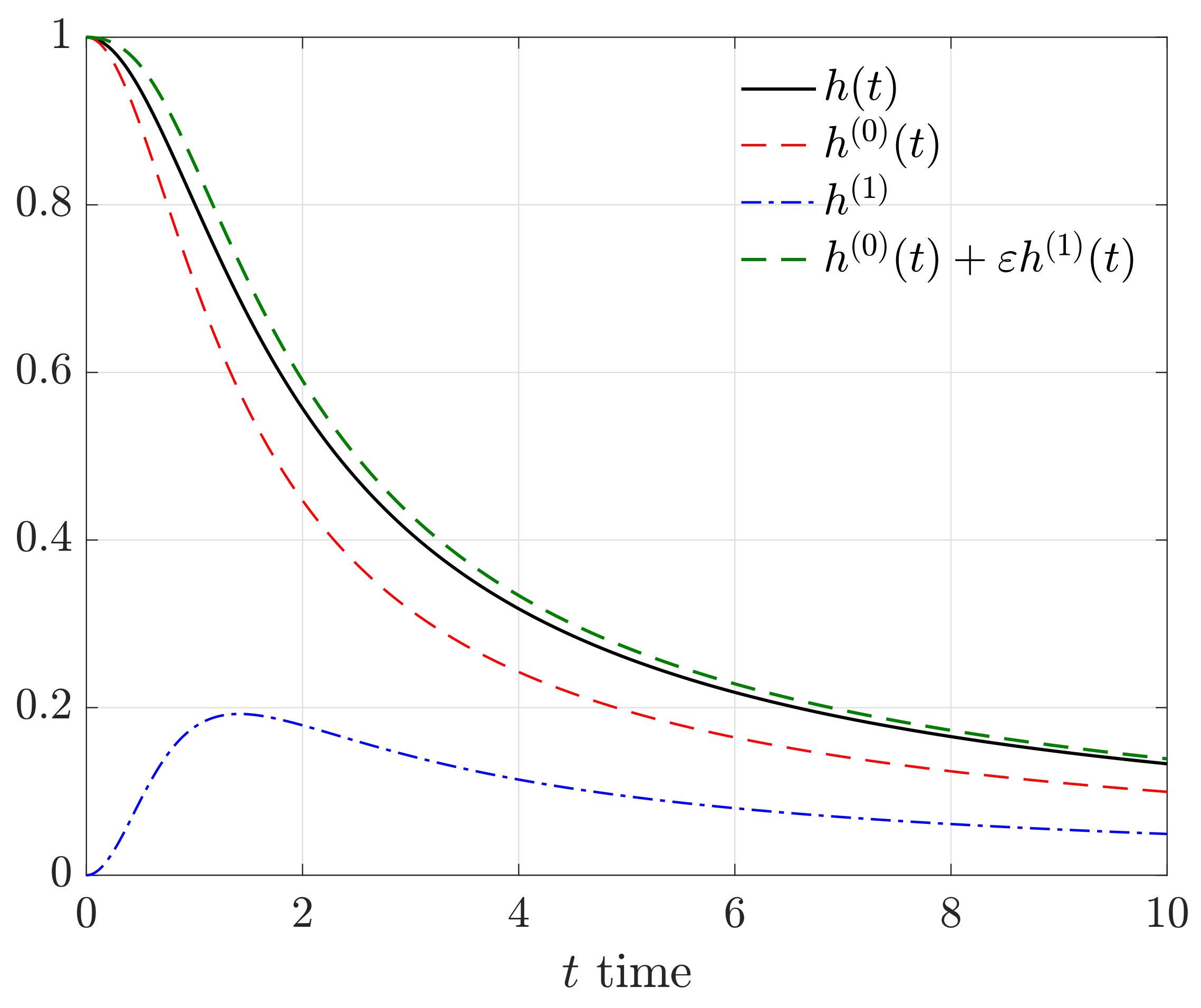
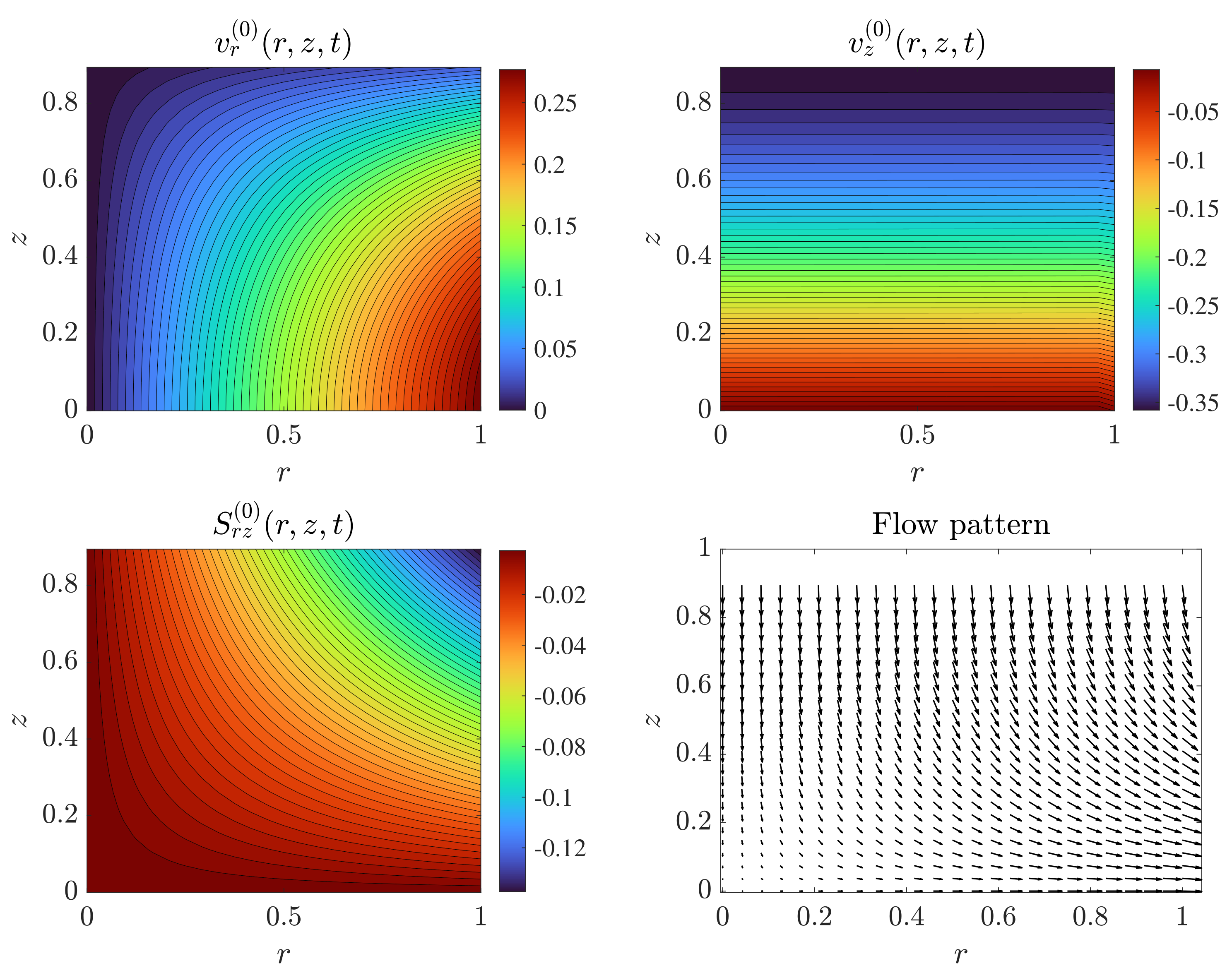
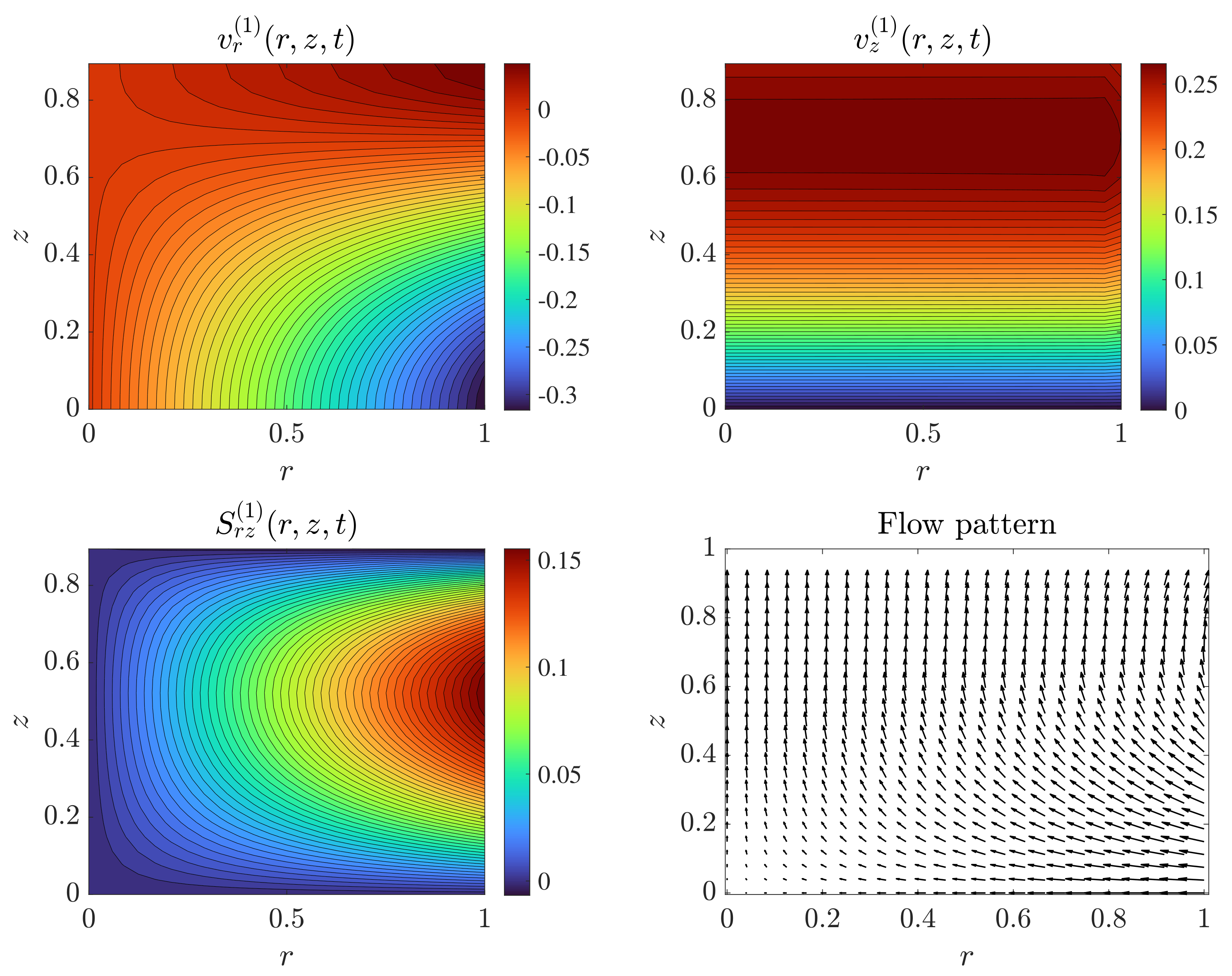
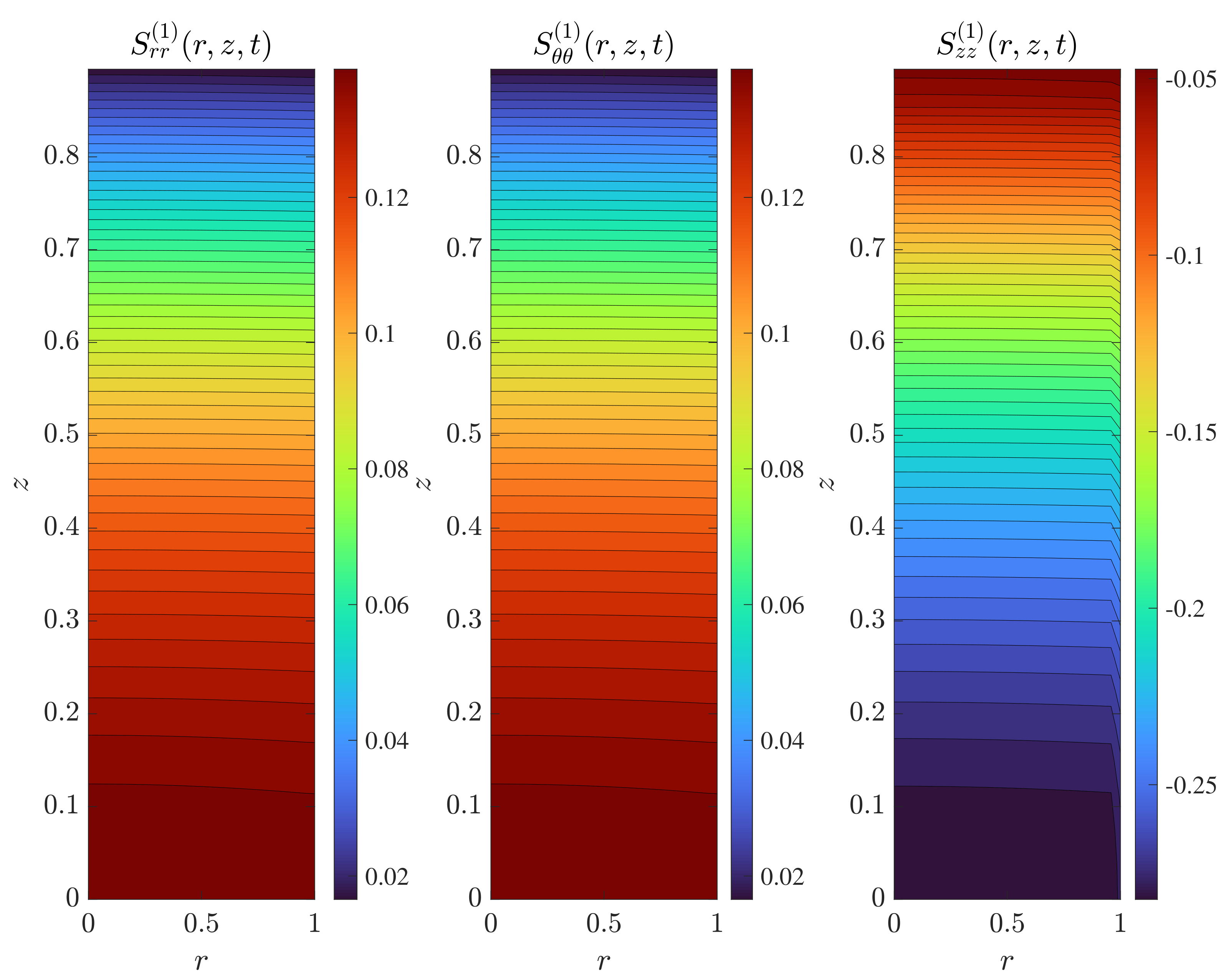
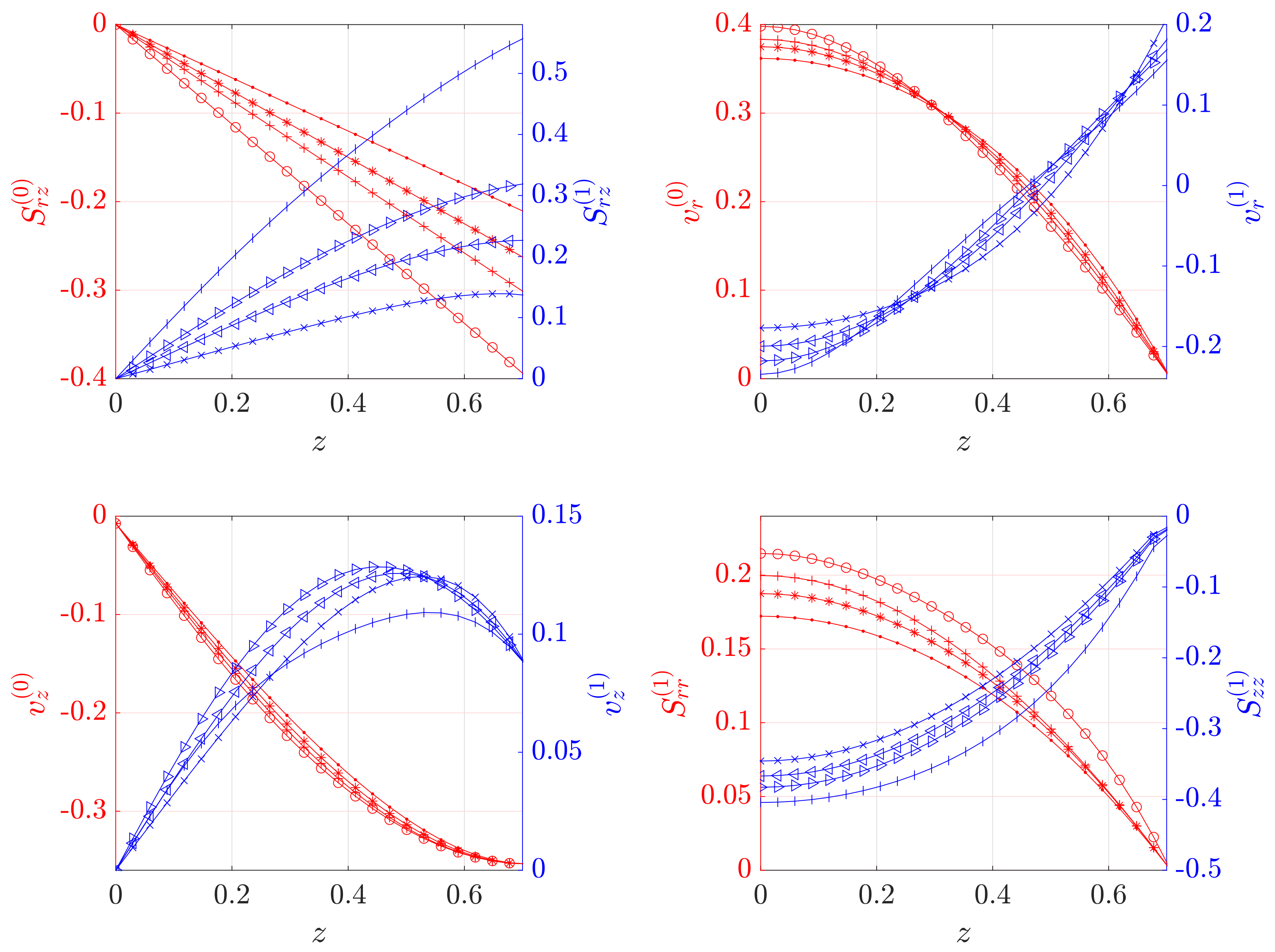
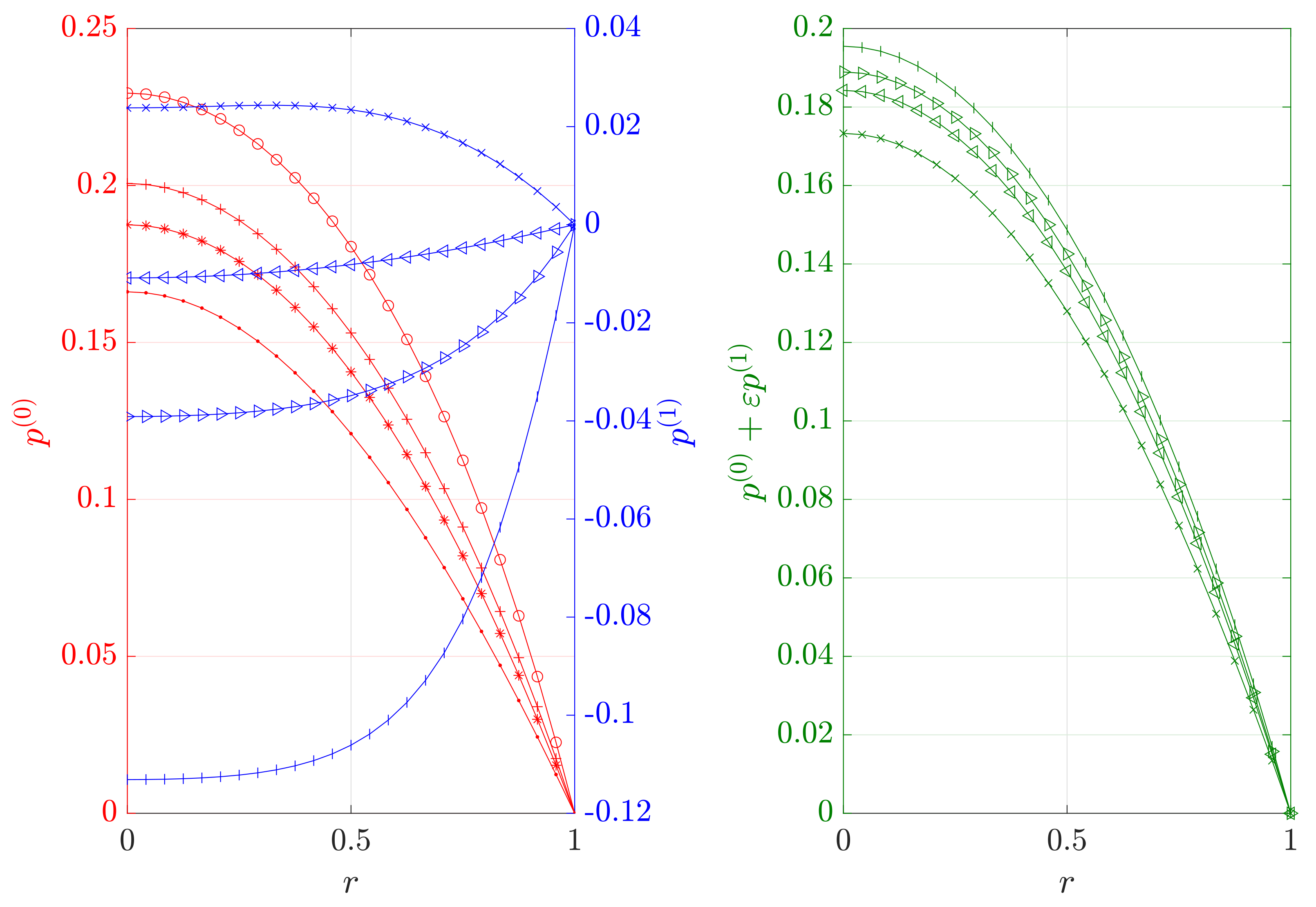
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Málek, J.; Průša, V.; Rajagopal, K.R. Generalizations of the Navier–Stokes fluid from a new perspective. Int. J. Eng. Sci. 2010, 48, 1907–1924. [Google Scholar] [CrossRef]
- Noll, A. A new mathematical theory of simple materials. Arch. Ration. Mech. Anal. 1972, 48, 1–50. [Google Scholar] [CrossRef]
- Anand, M.; Rajagopal, K.; Rajagopal, K.R. A model incorporating some of the mechanical and biomechanical factors underlying clot formation and dissolution in flowing blood. J. Theor. Med. 2003, 5, 183–218. [Google Scholar] [CrossRef] [Green Version]
- Anand, M.; Rajagopal, K.; Rajagopal, K.R. A model for the formation and lysis of blood clots. Pathophysiol. Homeost. Thromb. 2005, 34, 109–120. [Google Scholar] [CrossRef] [PubMed]
- Lawson, J.; Rajagopal, K. Regulation of hemostatic system function by biochemical and mechanical factors. In Modeling of Biological Materials; Mollica, F., Preziosi, L., Rajagopal, K.R., Eds.; Birkhauser: Boston, MA, USA, 2007; pp. 179–210. [Google Scholar]
- Vezirov, T.A.; Gerloff, S.; Klapp, S.H.L. Manipulating shear-induced non-equilibrium transition in colloidal films by feedback control. Soft Matter 2015, 11, 406–413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fusi, L.; Farina, A. Flow of a class of fluids defined via implicit constitutive equation down an inclined plane: Analysis of the quasi-steady regime. Eur. J. Mech. B Fluids 2017, 61, 200–208. [Google Scholar] [CrossRef]
- Fusi, L.; Farina, A.; Saccomandi, G.; Rajagopal, K.R. Lubrication approximation of flows of a special class of non-Newtonian fluids defined by rate type constitutive equations. App. Math. Model. 2018, 60, 508–525. [Google Scholar] [CrossRef]
- Narayan, S.P.A.; Rajagopal, K.R. Unsteady flows of a class of novel generalizations of the Navier–Stokes fluid. Appl. Math. Comput. 2013, 219, 9935–9946. [Google Scholar]
- Perlácova, T.; Průša, V. Tensorial implicit constitutive relations in mechanics of incompressible non-Newtonian fluids. J. Non-Newton. Fluid Mech. 2015, 216, 13–21. [Google Scholar] [CrossRef]
- Le Roux, C.; Rajagopal, K.R. Shear flows of a new class of power law fluids. Appl. Math. 2013, 58, 153–177. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, S.; Karra, S. Flow of “stress power law” fluids between parallel rotating discs with distinct axes. Int. J. Nonlin. Mech. 2015, 74, 73–83. [Google Scholar] [CrossRef]
- Rajagopal, K.R. Remarks on the notion of pressure. Int. J. Nonlin. Mech. 2015, 71, 165–172. [Google Scholar] [CrossRef]
- Engmann, J.; Servais, C.; Burbidge, A.S. Squeeze flow theory and applications to rheometry: A review. J. Non-Newton. Fluid Mech. 2005, 132, 1–27. [Google Scholar] [CrossRef]
- Fusi, L.; Farina, A.; Rosso, F. Planar squeeze flow of a bingham fluid. J. Non-Newton. Fluid Mech. 2015, 225, 1–9. [Google Scholar] [CrossRef]
- Fusi, L.; Farina, A.; Rosso, F. Squeeze flow of a Bingham-type fluid with elastic core. Int. J. Nonlin. Mech. 2016, 78, 59–65. [Google Scholar] [CrossRef]
- Muravleva, L. Axisymmetric squeeze flow of a viscoplastic Bingham medium. J. Non-Newton. Fluid Mech. 2017, 249, 97–120. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fusi, L.; Ballotti, A. Squeeze Flow of Stress Power Law Fluids. Fluids 2021, 6, 194. https://doi.org/10.3390/fluids6060194
Fusi L, Ballotti A. Squeeze Flow of Stress Power Law Fluids. Fluids. 2021; 6(6):194. https://doi.org/10.3390/fluids6060194
Chicago/Turabian StyleFusi, Lorenzo, and Andrea Ballotti. 2021. "Squeeze Flow of Stress Power Law Fluids" Fluids 6, no. 6: 194. https://doi.org/10.3390/fluids6060194
APA StyleFusi, L., & Ballotti, A. (2021). Squeeze Flow of Stress Power Law Fluids. Fluids, 6(6), 194. https://doi.org/10.3390/fluids6060194








