Assessing IDDES-Based Wall-Modeled Large-Eddy Simulation (WMLES) for Separated Flows with Heat Transfer
Abstract
:1. Introduction
2. Methodology
2.1. IDDES-Based WMLES
2.2. Governing Equations
2.3. Errors in Wall Modeling
2.4. Flow Solver
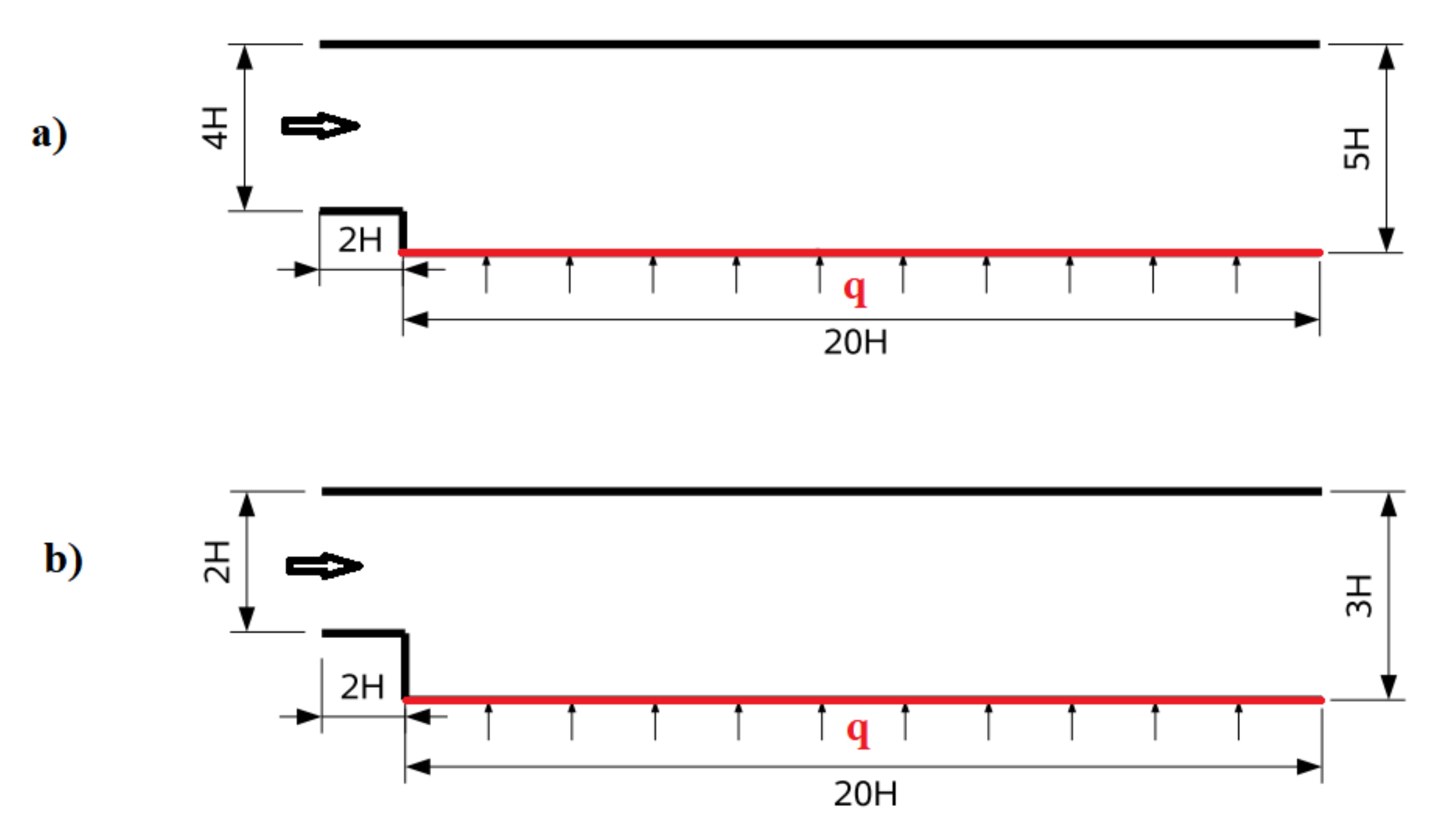
2.5. Flow Configuration
3. Results and Discussion
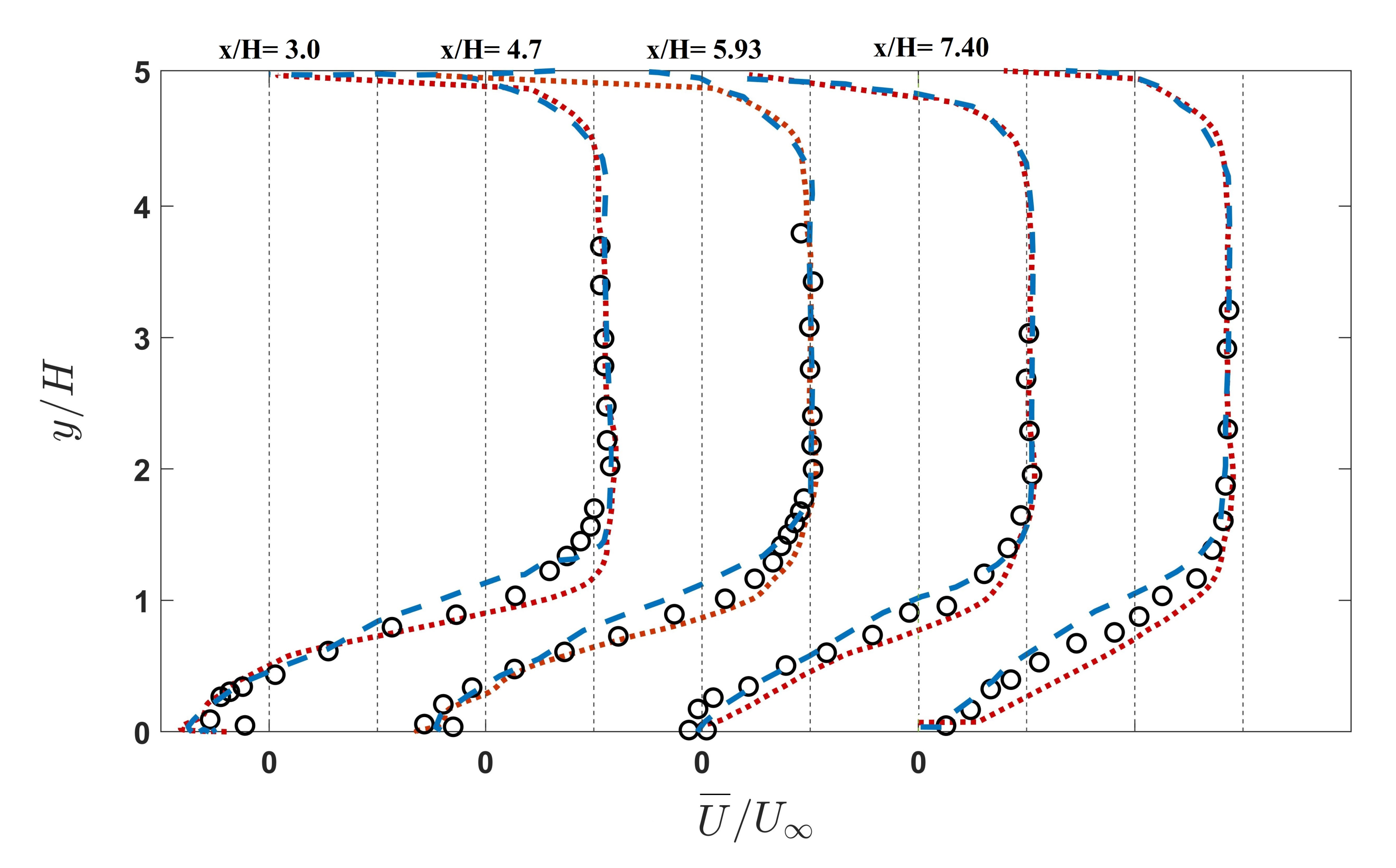
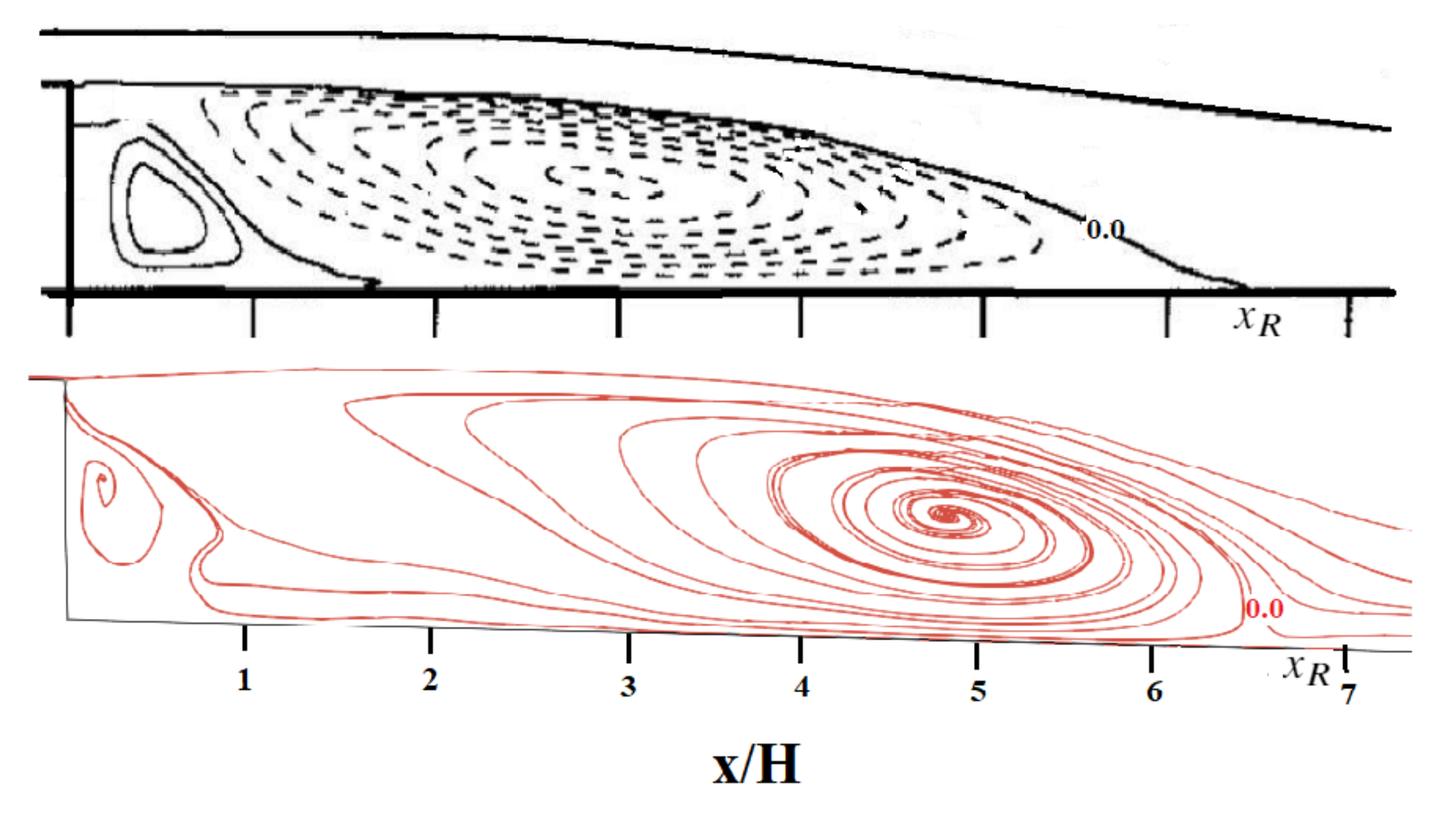
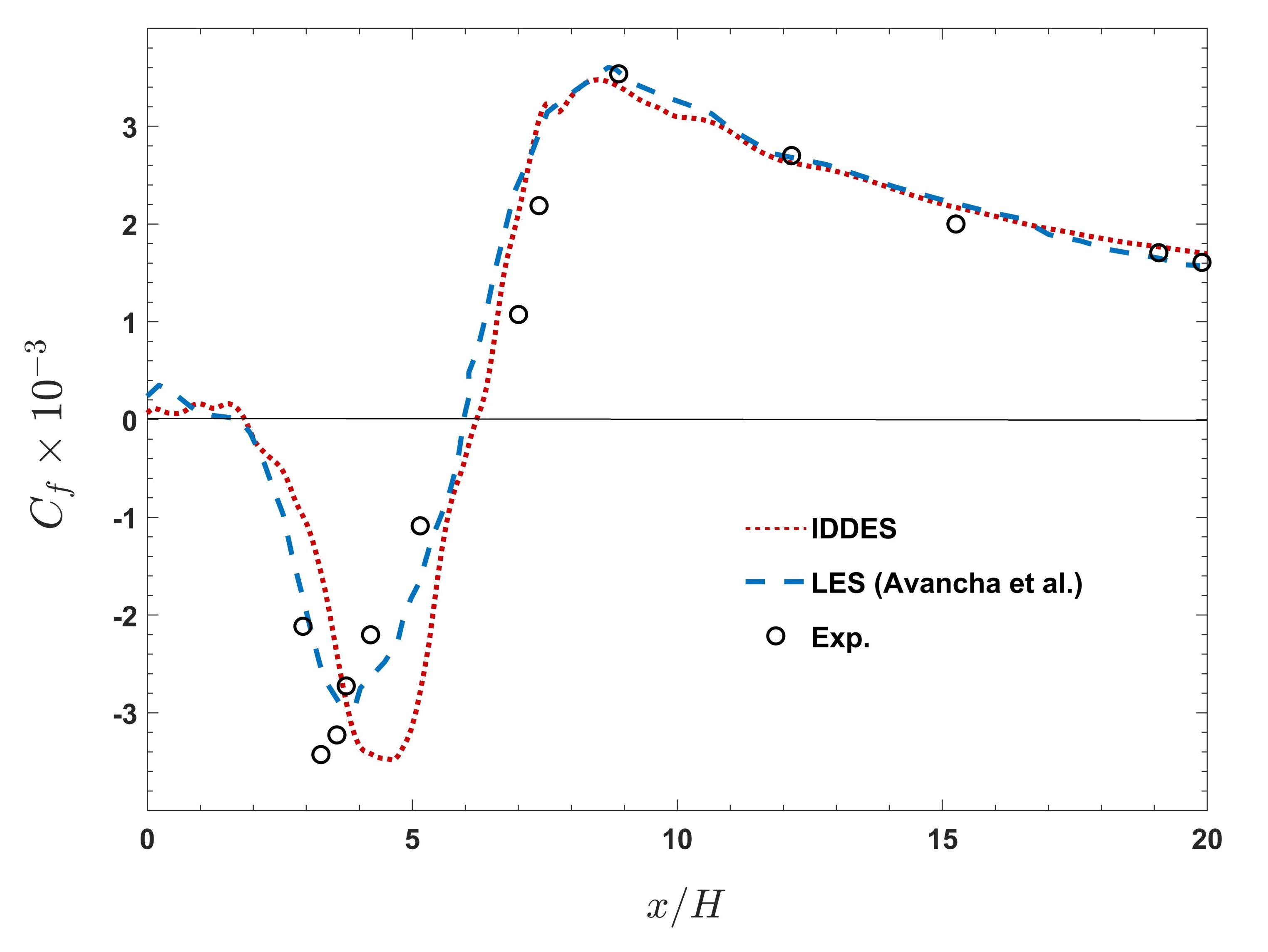
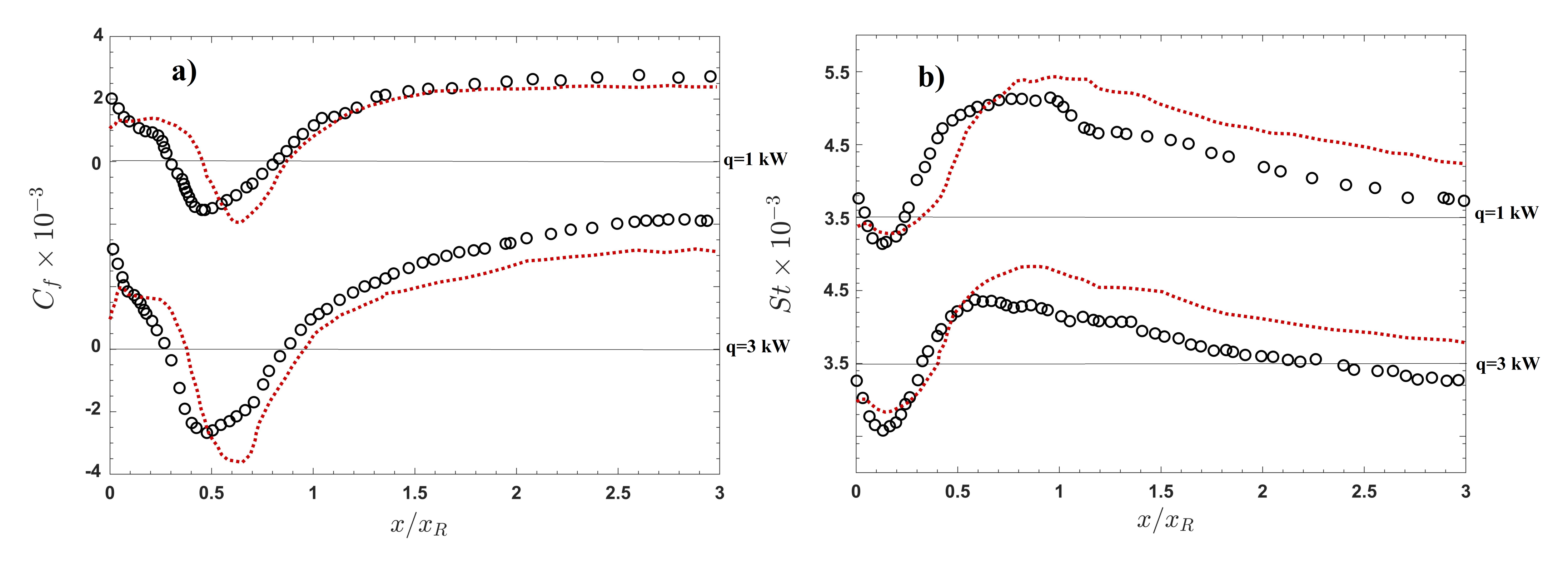
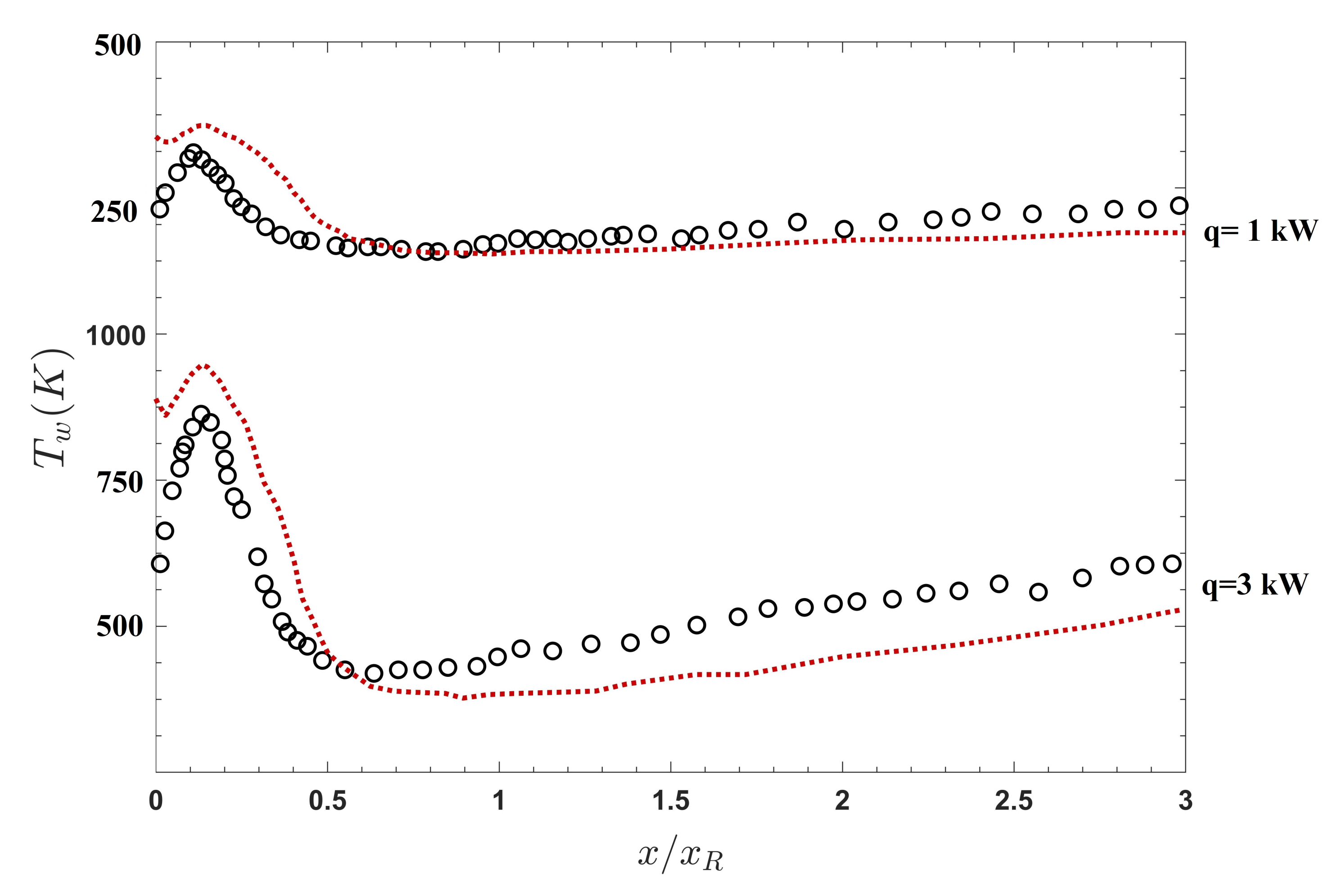
3.1. First Configuration
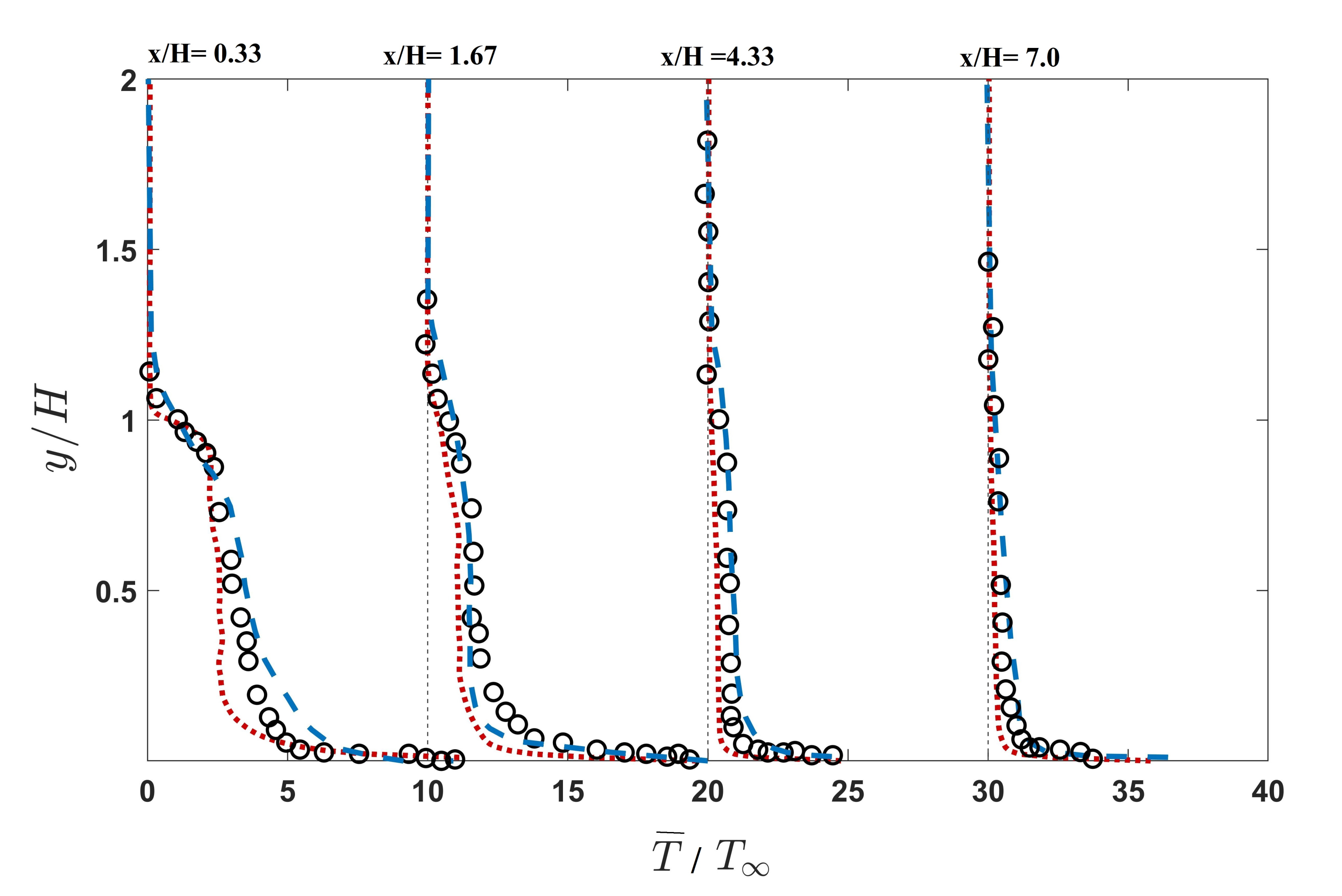
3.2. Second Configuration
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, X.; Zafar, S.; Wang, J.X.; Xiao, H. Predictive large-eddy-simulation wall modeling via physics-informed neural networks. Phys. Rev. Fluids 2019, 4. [Google Scholar] [CrossRef]
- Larsson, J.; Kawai, S.; Bodart, J.; Bermejo-Moreno, I. Large eddy simulation with modeled wall-stress: Recent progress and future directions. Mech. Eng. Rev. 2016, 3, 15-00418. [Google Scholar] [CrossRef] [Green Version]
- Soshi, K.; Johan, L. Wall modeling in large-eddy simulation: Predicting accurate skin friction at very high Reynolds number. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar] [CrossRef]
- Lozano-Durán, A.; Bae, H.J. Self-critical machine-learning wall-modeled LES for external aerodynamics. arXiv 2020, arXiv:2012.10005. [Google Scholar]
- Park, G.I.; Moin, P. Space-time characteristics of wall-pressure and wall shear-stress fluctuations in wall-modeled large eddy simulation. Phys. Rev. Fluids 2016, 1, 024404. [Google Scholar] [CrossRef] [PubMed]
- Nikitin, N.V.; Nicoud, F.; Wasistho, B.; Squires, K.D.; Spalart, P.R. An approach to wall modeling in large-eddy simulations. Phys. Fluids 2000, 12, 1629–1632. [Google Scholar] [CrossRef]
- Piomelli, U.; Balaras, E.; Pasinato, H.; Squires, K.D.; Spalart, P.R. The inner–outer layer interface in large-eddy simulations with wall-layer models. Int. J. Heat Fluid Flow 2003, 24, 538–550. [Google Scholar] [CrossRef] [Green Version]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Shur, M.; Spalart, P.; Strelets, M.; Travin, A. Synthetic Turbulence Generators for RANS-LES Interfaces in Zonal Simulations of Aerodynamic and Aeroacoustic Problems. Flow Turbul. Combust. 2014, 93, 63–92. [Google Scholar] [CrossRef]
- Mockett, C.; Fuchs, M.; Thiele, F. Progress in DES for wall-modelled LES of complex internal flows. Comput. Fluids 2012, 65, 44–55. [Google Scholar] [CrossRef]
- Gieseking, D.A.; Choi, J.I.; Edwards, J.R.; Hassan, H.A. Compressible-Flow Simulations Using a New Large-Eddy Simulation/Reynolds-Averaged Navier-Stokes Model. AIAA J. 2011, 49, 2194–2209. [Google Scholar] [CrossRef]
- Peterson, D.M.; Candler, G.V. Simulations of Mixing for Normal and Low-Angled Injection into a Supersonic Crossflow. AIAA J. 2011, 49, 2792–2804. [Google Scholar] [CrossRef]
- Saini, R.; Karimi, N.; Duan, L.; Sadiki, A.; Mehdizadeh, A. Effects of Near Wall Modeling in the Improved-Delayed-Detached-Eddy-Simulation (IDDES) Methodology. Entropy 2018, 20, 771. [Google Scholar] [CrossRef] [Green Version]
- Guseva, E.; Garbaruk, A.; Strelets, M. Assessment of Delayed DES and Improved Delayed DES Combined with a Shear-Layer-Adapted Subgrid Length-Scale in Separated Flows. Flow Turbul. Combust. 2017, 98. [Google Scholar] [CrossRef]
- Xu, H.H.A.; Yang, X.I.A.; Milani, P.M. Assessing Wall-Modeled Large-Eddy Simulation for Low-Speed Flows with Heat Transfer. AIAA J. 2021, 59, 2060–2069. [Google Scholar] [CrossRef]
- Jakirlić, S.; Kniesner, B. Near-Wall RANS Modelling in LES of Heat Transfer in Backward-Facing Step Flows Under Conditions of Constant and Variable Fluid Properties. In American Society of Mechanical Engineers, Fluids Engineering Division; FEDSM: Montreal, QC, Canada, 2010; Volume 1, pp. 2489–2502. [Google Scholar] [CrossRef]
- Spalart, P.R.; Jou, W.-H.; Strelets, M.; Allmaras, S.R. Comments on the Feasibility of LES for Wings, and on a Hybrid RANS/LES Approach. In Proceedings of the First AFOSR International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997. [Google Scholar]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A New Version of Detached-eddy Simulation, Resistant to Ambiguous Grid Densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Hirsch, C. Numerical Computation of Internal and External Flows, 2nd ed.; Elsevier: Amsterdam, The Nederlands, 2007. [Google Scholar] [CrossRef]
- Gritskevich, M.S.; Garbaruk, A.V.; Menter, F.R. Development of DDES and IDDES formulations to the k-ω shear stress transport model. Flow Turbul. Combust. 2011, 5, 23–42. [Google Scholar] [CrossRef]
- Zangeneh, R. A New Framework for Modeling Shock-Turbulence Interactions. SAE Int. J. Aerospace 2020. [Google Scholar] [CrossRef]
- Ducros, F.; Ferrand, V.; Nicoud, F.; Weber, C.; Darracq, D.; Gacherieu, C.; Poinsot, T. Large-Eddy Simulation of the Shock/Turbulence Interaction. J. Comput. Phys. 1999, 152, 517–549. [Google Scholar] [CrossRef]
- Zangeneh, R. Development of a New Algorithm for Modeling Viscous Transonic Flow on Unstructured Grids at High Reynolds-Numbers. J. Fluids Eng. 2020. [Google Scholar] [CrossRef]
- Zangeneh, R. Evaluation of reattaching Shear-layer in Compressible Turbulent Flows; A Large-Eddy Simulation Approach. In Fluid Engineering Division; ASME: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Zangeneh, R. Numerical Analysis of Transonic Flow around Cones. Open J. Fluid Dyn. 2020, 10, 279–290. [Google Scholar] [CrossRef]
- Zangeneh, R. Development of a deep-learning model to improve large eddy simulations of turbulent flows. In Proceedings of the 5th Thermal and Fluids Engineering Conference (TFEC), New Orleans, LA, USA, 5–8 April 2020. [Google Scholar] [CrossRef]
- Zangeneh, R. Parametric Study of Separation and Reattachment in Transonic Airfoil Flows. AIAA J. 2021, 18, 1–10. [Google Scholar] [CrossRef]
- Zangeneh, R. Wall-modeled Large-eddy Simulation of Hypersonic Turbulent Boundary-layers. In AIAA Scitech 2021 Forum; American Institute of Aeronautics and Astronautics: New Reston, VA, USA, 2021. [Google Scholar]
- Vogel, J.; Eaton, J. Combined Heat Transfer and Fluid Dynamic Measurements Downstream of a Backward-Facing Step. J. Heat Transf. Trans. ASME 1985, 107, 922–929. [Google Scholar] [CrossRef]
- Klein, M.; Sadiki, A. A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations. J. Comput. Phys. 2003, 166, 652–665. [Google Scholar] [CrossRef]
- Akselvoll, K.; Moin, P. Large-eddy simulation of turbulent confined coannular jets. J. Fluid Mech. 1996, 315, 387–411. [Google Scholar] [CrossRef]
- Keating, A.; Piomelli, U.; Bremhorst, K.; Nešić, S. Large-eddy simulation of heat transfer downstream of a backward-facing step. J. Turbul. 2004, 5, 20. [Google Scholar] [CrossRef] [Green Version]
- Kasagi, N.; Matsunaga, A. Three-dimensional particle-tracking velocimetry measurement of turbulence statistics and energy budget in a backward-facing step flow. Int. J. Heat Fluid Flow 1995, 16, 477–485. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 2000, 285, 69–94. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zangeneh, R. Assessing IDDES-Based Wall-Modeled Large-Eddy Simulation (WMLES) for Separated Flows with Heat Transfer. Fluids 2021, 6, 246. https://doi.org/10.3390/fluids6070246
Zangeneh R. Assessing IDDES-Based Wall-Modeled Large-Eddy Simulation (WMLES) for Separated Flows with Heat Transfer. Fluids. 2021; 6(7):246. https://doi.org/10.3390/fluids6070246
Chicago/Turabian StyleZangeneh, Rozie. 2021. "Assessing IDDES-Based Wall-Modeled Large-Eddy Simulation (WMLES) for Separated Flows with Heat Transfer" Fluids 6, no. 7: 246. https://doi.org/10.3390/fluids6070246
APA StyleZangeneh, R. (2021). Assessing IDDES-Based Wall-Modeled Large-Eddy Simulation (WMLES) for Separated Flows with Heat Transfer. Fluids, 6(7), 246. https://doi.org/10.3390/fluids6070246





