Aerodynamic Characteristics of a Single Airfoil for Vertical Axis Wind Turbine Blades and Performance Prediction of Wind Turbines

Abstract

The design of wind turbines requires a deep insight into their complex aerodynamics, such as dynamic stall of a single airfoil and flow vortices. The calculation of the aerodynamic forces on the wind turbine blade at different angles of attack (AOAs) is a fundamental task in the design of the blades. The accurate and efficient calculation of aerodynamic forces (lift and drag) and the prediction of stall of an airfoil are challenging tasks. Computational fluid dynamics (CFD) is able to provide a better understanding of complex flows induced by the rotation of wind turbine blades. A numerical simulation is carried out to determine the aerodynamic characteristics of a single airfoil in a wide range of conditions. Reynolds-averaged Navier–Stokes (RANS) equations and large-eddy simulation (LES) results of flow over a single NACA0012 airfoil are presented in a wide range of AOAs from low lift through stall. Due to the symmetrical nature of airfoils, and also to reduce computational cost, the RANS simulation is performed in the 2D domain. However, the 3D domain is used for the LES calculations with periodical boundary conditions in the spanwise direction. The results obtained are verified and validated against experimental and computational data from previous works. The comparisons of LES and RANS results demonstrate that the RANS model considerably overpredicts the lift and drag of the airfoil at post-stall AOAs because the RANS model is not able to reproduce vorticity diffusion and the formation of the vortex. LES calculations offer good agreement with the experimental measurements.

1. Introduction

Wind turbine efficiency remains a critical component of the overall economic justification for a potential wind farm. Therefore, it is required that prediction methodologies are capable of addressing the performance of wind turbine installations within a specific local environment and operating in a wide range of conditions.

A flow diagram of the model of a wind turbine is given in Figure 1. The flow conditions which are encountered in VAWT aerodynamics are defined. The flow conditions determine a large part of the design criteria of new or existing airfoils and are used in making a sufficiently accurate simulation program. During the development and testing of airfoils, the initial airfoil is used as a reference. The optimization routine is used to modify the blade shape and to calculate the characteristics of the new shape. The simulation methods and the final simulation are applied to predict wind turbine performance. The VAWT simulation program calculates the performance of a VAWT using 2D airfoil data or 3D blade data. The optimization routine is usually not able to predict all flow phenomena, resulting in limited accuracy, and the angular range is limited until the airfoil is stalled. The results of the simulation and the airfoil characteristics are distilled into a general design of the airfoil.

The airfoils of HAWTs and VAWTs normally experience conditions that are different from aerospace applications due to smaller chord length and lower wind speed, resulting in significantly lower Reynolds numbers. They also operate with an unusually wide range of AOAs (from $0^{\circ }$ to ${90}^{\circ }$ for HAWTs and from $0^{\circ }$ to ${360}^{\circ }$ for VAWTs), including both unstalled and stalled conditions.

At high Reynolds numbers, boundary layers are turbulent, and for small AOAs, the flow is attached until the separation at the rear of the blade, with small drag and high lift. Under increasing AOAs, the flow stays attached with a corresponding increase in lift and drag, until stall is reached where the flow separation moves upstream, which results in a decrease in lift and a dramatic increase in drag.

Using the Langley low-turbulence pressure tunnel, tests on the NACA0012 airfoil at AOAs from $0^{\circ }$ to ${180}^{\circ }$ were conducted in [1]. The airfoil used in the investigation had a chord length of 0.1524 m and spanned the entire 0.914 m of the wind tunnel. Expressions from [2] were used to correct the results for the effects of the solid blockage. At a Reynolds number of $\mathrm{Re}=1.8\times {10}^6$, they found the maximum coefficient of lift to occur at an AOA of ${14}^{\circ }$ and have a value of 1.33. A less abrupt peak in the coefficient of lift was seen to occur at an AOA of approximately ${45}^{\circ }$. Similar peaks in the coefficient of lift were observed at ${170}^{\circ }$ and ${145}^{\circ }$, having magnitudes of 0.77 and 1.07, respectively. At zero degrees of AOA, the coefficient of drag was observed to be 0.007, while at ${180}^{\circ }$, it was 0.014. At ${90}^{\circ }$, a value of 2.08 was recorded for the coefficient of drag which is similar to that obtained for a flat plate of infinite aspect ratio. At a lower Reynolds number of $\mathrm{Re}=5\times {10}^5$, the maximum coefficient of lift occurred earlier at an AOA of ${10}^{\circ }$ and with a lower value of about 1. Between ${20}^{\circ }$ and ${125}^{\circ }$, the coefficient of lift was largely unaffected by the decrease in the Reynolds number, but beyond ${125}^{\circ }$, the magnitude was seen to be lower. Overall, this reduction in Reynolds number saw a decrease in the coefficient of drag, except for a range of AOA from ${10}^{\circ }$ to ${20}^{\circ }$, where the coefficient of drag increased from the value measured at a Reynolds number of $\mathrm{Re}=1.8\times {10}^6$.

The variant of the airfoil location at an angle of attack of ${90}^{\circ }$ has a small difference from the flow around a flat plate normal to airstream. Experimental data from [3] show that the value of drag coefficient for a plate with a thickness of 0.2 of its length is 2.8 at $\mathrm{Re}=4\times {10}^4$.

The most well-documented and widely adopted data for high incidence wind turbine applications are probably those of [4]. They conducted experimental tests on the NACA0009, NACA0012, NACA0015, and NACA0012H airfoils over a range of AOAs from $0^{\circ }$ to ${180}^{\circ }$ using a wind tunnel. They used airfoils with a chord length of 0.1524 m for tests conducted at Reynolds numbers of $\mathrm{Re}=3.6\times {10}^5$, $5\times {10}^5$, and $7\times {10}^5$ and an NACA0012 airfoil with a chord length of 0.381 m for tests conducted at a Reynolds number of $\mathrm{Re}=8.6\times {10}^5$, $1.36\times {10}^6$, and $1.76\times {10}^6$. They observed significant hysteresis features in the coefficient of lift measurements of the NACA0012 airfoil at AOAs from $8^{\circ }$ to ${18}^{\circ }$. These features were also seen for the NACA0015 and NACA0012H airfoils but not for the NACA0009 airfoil. A comparison of the coefficient of tangential force curve for each airfoil, calculated from their measurements of the coefficients of lift and drag, suggests that the NACA0015 and NACA0012H airfoils offer better performance on a lift-driven VAWT when compared with the other airfoils used in the experiment. For all airfoils, it was found that beyond an AOA of ${25}^{\circ }$, neither Reynolds number nor geometry had much effect on the coefficient of lift. Similarly for the coefficient of drag, beyond an AOA of ${20}^{\circ }$, Reynolds number and geometry have little effect.

In addition, experimental findings to produce predictions of the aerodynamic characteristics of the NACA0018, NACA0021, and NACA0025 airfoils for a range of Reynolds numbers from ${10}^4$ to ${10}^7$ were used in [4]. Some hysteresis phenomena are observed at the onset of the airfoil stall depending on the initial condition if it is a fully stalled configuration (higher AOAs) or a fully attached condition (lower AOAs). Comprehensive experimental studies on the NACA0012 airfoil were performed in [5,6]. However, their works did not cover Reynolds numbers below $\mathrm{Re}=1.44\times {10}^6$.

Four appropriate airfoils were chosen for testing in [7]. They conducted both experimental tests and CFD simulations on four different airfoils: the symmetric NACA0012 and the asymmetric SG6043, SD7062, and DU06-W-200. Measurements of the aerodynamic characteristics of these airfoils were taken at Reynolds numbers of $\mathrm{Re}=6.5\times {10}^4$, $9\times {10}^4$, and $1.5\times {10}^5$. When comparing their experimental observations with CFD predictions for the NACA0012 airfoil, they saw good agreement up to an AOA of ${10}^{\circ }$. Between ${10}^{\circ }$ and ${14}^{\circ }$, however, CFD did not predict a surface separation bubble, which was observed experimentally. They noted no significant difference in this phenomenon over the different Reynolds numbers. When comparing observations with [8], some differences between findings were noted. Immediately after stall occurred, it was observed that the coefficient of lift dropped to almost zero [8]. However, a much smaller drop in the coefficient of lift to 0.6 was observed in [7]. They did not observe the peak in the coefficient of lift at an AOA of ${45}^{\circ }$ to the same extent as [8], where this peak exceeded the first pre-stall peak. In addition, while [7] observed a discontinuity in the coefficient of lift at ${54}^{\circ }$, study [8] did not. It might be an effect of the test section configuration used in the experiments (closed or open test sections) as discussed in [7].

There was one significant difference in the coefficient of drag, and this was the discontinuity observed in [7] at around ${55}^{\circ }$, which was not observed in [8]. Following this discontinuity, up until the corresponding AOA past ${90}^{\circ }$ of ${125}^{\circ }$, the magnitude of the coefficient of drag was seen to be around 40% lower than observed in [8]. Conclusions related to the asymmetric airfoils that were tested suggested that the benefits of using cambered airfoils (which have a delayed onset of stall) are partly negated by a reduction in performance which occurs when the airfoil operates at an AOA between ${180}^{\circ }$ and ${360}^{\circ }$.

The choice of turbulence models influences the computational results and the required computation resources. The RANS technique with different turbulence models is widely used in aerodynamic modelling with fair accuracy and efficiency. Among the various turbulence models, the shear stress (SST) model is the one combining the k–$\omega$ and k–$\epsilon$ models based on the zonal blending functions. To simulate complex vortex flows with a positive pressure gradient and flow separation, the SST turbulence model is used in computational practice. LES is a computationally expensive approach compared to RANS. However, LES provides a way to reproduce the formation and propagation of complex eddy structures, and the influences of smaller and more homogenous eddies are taken into account by an SGS model. However, LES is compatible with a wider range of turbulent flows than the RANS model, as it retains the unsteady large-scale coherent structures.

At high AOAs, flow separation is known to occur, so a suitable turbulence model must be chosen. It was found that the SST model produces the best results of all steady state models following an evaluation of different turbulence models [9].

Using particle imaging velocimetry, experimental measurements of the development of flow over the leading edge of the NACA0015 airfoil were presented in [10]. It was recorded that vorticity shed from the leading edge of the airfoil. The results of experiments were used to validate further CFD simulations. The simulations compared different turbulence models (Spalart–Allmaras, k–$\epsilon$) in unsteady RANS and LES and detached eddy simulation (DES) approaches. They found that the Spalart–Allmaras model underestimated the generation and shedding of vorticity at the leading edge, and the k–$\epsilon$ model did not predict the shed vortices accurately. The LES approach allowed the vortex shedding to be reproduced, but the area covered by these predicted vortices was larger than what was observed experimentally. The DES model gave results which best agreed with the experimental data.

The flow around the airfoil at a high AOA is unsteady and 3D separated with a nonlinear lift variation. Several important issues for the accurate simulation of high AOA flow fields, such as turbulence modelling and domain dimensionality, were pointed out in [11]. Many previous studies of aerodynamic characteristics of wind turbine blades based on URANS were not able to provide reliable results at high AOAs, when flow separation occurs and flow is characterized by large-scale eddies. On the other hand, DES or LES, although recognized as more advanced and powerful turbulence simulation techniques, are not often used in the latest CFD studies of VAWTs. Two-dimensional CFD simulation capabilities are limited and not able to reproduce flow quantities in the spanwise direction of the wind turbine blade. It was found that 2D Navier–Stokes solvers overpredict the lift and drag of the stalled airfoil, even when AOA was only slightly above the stall angle [12]. To overcome the limitations of 2D models, full 3D models based on numerical solutions of full Navier–Stokes equations are used. In this case, the 2D model is extended in the spanwise direction for a considerable length in order to achieve a realistic reproduction of 3D-separated vortices. The spanwise length is not fully modelled in such a 3D simulation, so it is referred to as a 2.5D CFD simulation hereinafter in order to differentiate it from the conventional 2D and 3D simulations. The 2.5D LES simulations provide the flow field around a single static airfoil, and it was found that the 2D model is not adequate for predicting unsteady flow structures with large-scale separations around airfoils at relatively high AOAs, which was performed in [13]. Simulations of a single airfoil beyond stall using the DES approach, which is essentially a hybrid model of RANS and LES, were presented in [14]. The results of the 2.5 DES model are clearly superior to those of the 2.5D URANS models.

An LES with different spanwise extents and different numerical resolutions to simulate a flow past an airfoil at a Reynolds number of $2.1\times {10}^6$ and AOA of 13.3° was conducted in [15]. It was found that there was a great improvement in the results compared with the experimental data when the width of the computational domain and the numerical resolution were increased. LES gives improvements of separation predictions and the best agreement with experimental results in comparison with the URANS model when using it to simulate high AOA flow [16].

CFD simulations on a static NACA0018 airfoil at a Reynolds number of $\mathrm{Re}=3\times {10}^5$ over a range of AOAs from $0^{\circ }$ to ${180}^{\circ }$ were performed in [16]. The feasibility and accuracy of three different CFD approaches (2D URANS, 2.5D URANS, and 2.5D LES) are investigated, and the aerodynamic characterization of a straight-bladed VAWT is found. The capability of the 2.5D LES model and its ability to accurately predict high AOA flows are assessed. To perform LES simulations with the 2.5D model, periodic boundary conditions are applied to the spanwise direction. URANS calculations were based on the SST turbulence model, and LES calculations were based on the Smagorinsky–Lilly SGS model. The airfoil used had a chord length of 0.2 m. They used a circular domain with a radius of 30 chord lengths and a structured O-mesh and placed 280 cells along the airfoil and 120 cells across the domain. A fine mesh was used, yplus values of less than one were ensured, and the growth rate was limited to 1.08. Among the three methods, 2.5D LES yielded the best agreement with the experimental data reported in [17]. The 2.5 LES calculations provide a more realistic 3D vortex diffusion in separated flows and a more accurate prediction of aerodynamic coefficients at AOAs corresponding to static or dynamic stall conditions [16].

The design parameters of the blades also have crucial effects on the effectiveness. The angle of attack is the most critical design parameter for turbine blades, and therefore its influence on the efficiency needs to be studied by means of investigating the flow over these airfoils. The effect of the angle of attack and Reynolds number has been intensively studied for many different profiles of turbine blades [18]. The lift coefficient and the drag coefficient, which characterize the lift force and the drag force acting on the airfoil, are examined in [19] for various angles of attack at different Reynolds numbers. The aerodynamic performance of both permeable wing and airfoil is presented in [20] in terms of lift, drag, lift to drag ratio, and moment coefficients by varying permeability values and permeable sections. A comparison of different turbulence models is provided in [21]. Under dynamic pitching motions, the opening of the dynamic lift and drag coefficient hysteresis curve is effectively enlarged [22].

The coefficients of lift and drag predicted in [16] with 2.5 LES were close to those observed experimentally in [17] for all AOAs except ${15}^{\circ }$, which was due to the dynamic characteristic of the experiment. It was found, however, that the 2D and 2.5D URANS simulations significantly overpredicted the lift in the stall region and also the drag from ${45}^{\circ }$ to ${135}^{\circ }$ [16]. In general, 2.5D LES showed good agreement with experimental results at relatively low TSRs, but only fair agreement at high TSRs.

Several RANS and LES runs in near-stall and stall conditions were carried out in [23]. The stall condition is found to have an extraneous sound source at low frequencies. It is characterized by two specific tones whose frequencies could correspond to the shear-layer instability followed by a von Karman vortex shedding, observed in [24] in their DNS study at a low Reynolds number. A new vented airfoil design offers a slight increase in tangential force coefficient at an AOA greater than 90 degrees, thus marginally increasing torque at low TSRs [25]. Simulations of flowfield around different airfoils are performed in [26,27].

In general, the static stall angles of symmetric VAWT airfoils range from ${10}^{\circ }$ to ${15}^{\circ }$ [4]. The stall of the airfoil always takes place when the TSR is less than 4. Such a TSR is common in small VAWTs. In particular, at a very low TSRs that often occur in the starting process, the maximum AOA is far beyond the stall angle. Therefore, good reproduction of high AOA flow is inevitable in assessing VAWT performance. Performance of a VAWT is dependent on the airfoil’s aerodynamic characteristics over a full range of AOAs from $0^{\circ }$ to ${180}^{\circ }$. The performance of various types of wind turbines is analysed in [28,29].

Although many experimental and computational studies have been performed over the last few years, the information about drag and lift coefficients has not been explored to quantify the performance of wind turbines and to improve their self-starting capabilities. The accurate and efficient calculation of aerodynamic forces (lift and drag) and the prediction of stall of an airfoil at realistic operating conditions are still challenging tasks. This study focuses on the analysis of the aerodynamic forces on the wind turbine blade at different angles of attack and Reynolds numbers. A numerical simulation is performed to determine the aerodynamic characteristics of a single airfoil in a wide range of conditions. A careful inspection of aerodynamic details revealed that the RANS model delays the occasion of dynamic stall and overpredicts the aerodynamic characteristics of the airfoil. RANS calculations are not able to accurately reproduce the experimentally observed trends in the variation of power coefficient. The application of the RANS approach leads to an overestimation of the VAWT power coefficient. To predict the aerodynamic characteristics of VAWTs and their self-starting capabilities at low rotation speeds, more reliable CFD tools and vortex-resolving approaches to the turbulence simulation are applied. The results computed with the RANS and LES techniques are verified and validated against experimental and computational data from previous works.

2. Physics of Wind Turbine

If the airfoil is set at an AOA in an air stream (Figure 2), it generates a lift force, $F_L$, normal to the free stream and a drag force, $F_D$, in the direction of the free stream. These lift and drag forces can then be resolved to obtain the tangential force, $F_T$, and the axial force, $F_N$, as shown in Figure 2. The tangential force has the instantaneous responsibility of the torque and the power outputs from the wind turbine.

Dimensionless force coefficients provide a convenient way to compare the aerodynamic characteristics of different airfoils, regardless of their size, and are given by

$$\begin{array}{c}\hfill C_L=\frac{2F_L}{\rho U^{2}A},C_D=\frac{2F_D}{\rho U^{2}A},\end{array}$$

where $F_L$ and $F_D$ are lift and drag forces, U is the apparent flow velocity as seen by the airfoil, and $\rho$ is the air density. The apparent flow velocity is a result of the airfoil having motion relative to the flow. An airfoil varies by way of length in the spanwise direction (span, S) and length in the flow-wise direction (chord, C). The reference area of the airfoil is then given by $A=CS$.

The torque coefficient and the power coefficient are

$$\begin{array}{c}\hfill C_T=\frac{2T}{\rho U^{2}AR},C_P=\frac{2P}{\rho U^{3}A},\end{array}$$

where U is the incoming velocity of the wind, P is the mechanical power produced by the wind turbine, T is the mechanical torque on the axis of a wind turbine, and A is the projected area of a wind turbine.

HAWTs use airfoil profiles as the cross sections of their rotor blades. As the wind passes over the airfoil, it produces lift and drag. Taking the rotation of the rotor into account, the airfoil experiences the apparent fluid velocity. The component of lift that acts in the direction of the plane of rotation causes the rotor to rotate and this is opposed by the component of drag that acts in the opposite direction. The components of lift and drag acting at a normal to the plane of rotation (in the direction parallel to the wind) induce stress in the blades and hub.

In the case of lift-driven VAWTs, it is more convenient to resolve the force on the airfoil into components with relation to the airfoil itself, which is the axial component that is tangential to the rotation of the VAWT and normal component. Since the blade of a VAWT is fixed in the radial direction, the axial component of the force drives the rotation of the turbine. The AOA that a blade sees at any moment in time, $\alpha$, is dependent on the angular position of the blade, $\theta$, the tangential velocity of the blade, $\omega R$, and the wind speed, U, and is given by

$$\begin{array}{c}\hfill \alpha ={tan}^{-1}\frac{sin\theta }{cos\theta +\lambda }.\end{array}$$

TSR is one of the most important parameters used to non-dimensionalize the performance of wind turbines when comparing different rotor configurations. TSR is the ratio of the rotational speed of the turbine’s outer tip to the wind speed. It is given by

$$\begin{array}{c}\hfill \lambda =\frac{\omega R}{U},\end{array}$$

where $\omega$ is the angular velocity of the wind turbine rotor, R is the radius, and U is the wind speed. Designing a VAWT with straight blades requires plotting the power coefficient against TSR as a function of rotor solidity [30]. Due to an extremely small power output, there is no practical interest for the operating range of TSRs below 2. Operation above TSRs of 10 means working beyond stall conditions especially for high solidities, where efficiency and power rapidly decrease. The recommended interval of TSRs is between 2 and 10 [31] and strongly depends on solidity of the rotor [30].

Unlike the airfoil blades in an aircraft, VAWT blades frequently experience high AOA beyond the stall angle, especially when they operate at $\lambda <4$. The flow velocity seen by each blade is the vectorial addition of the rotating speed and the incoming wind speed. The velocity component is found from the relation

$$\begin{array}{c}\hfill v_r=U{\left(1+2\lambda sin\theta +{\lambda }^2\right)}^{1/2}.\end{array}$$

The instantaneous torque on a single airfoil of a straight blade VAWT is expressed as follows:

$$\begin{array}{c}\hfill Q=\frac{1}{2}\rho W^{2}A{C}_{T}r,\end{array}$$

where $C_T$ is the tangential force coefficient. The torque coefficient is defined as $C_Q=2Q/\left(\rho W^{2}A{C}_{T}r\right)$, where Q is the average torque. The power coefficient is $C_P=C_Q\lambda$.

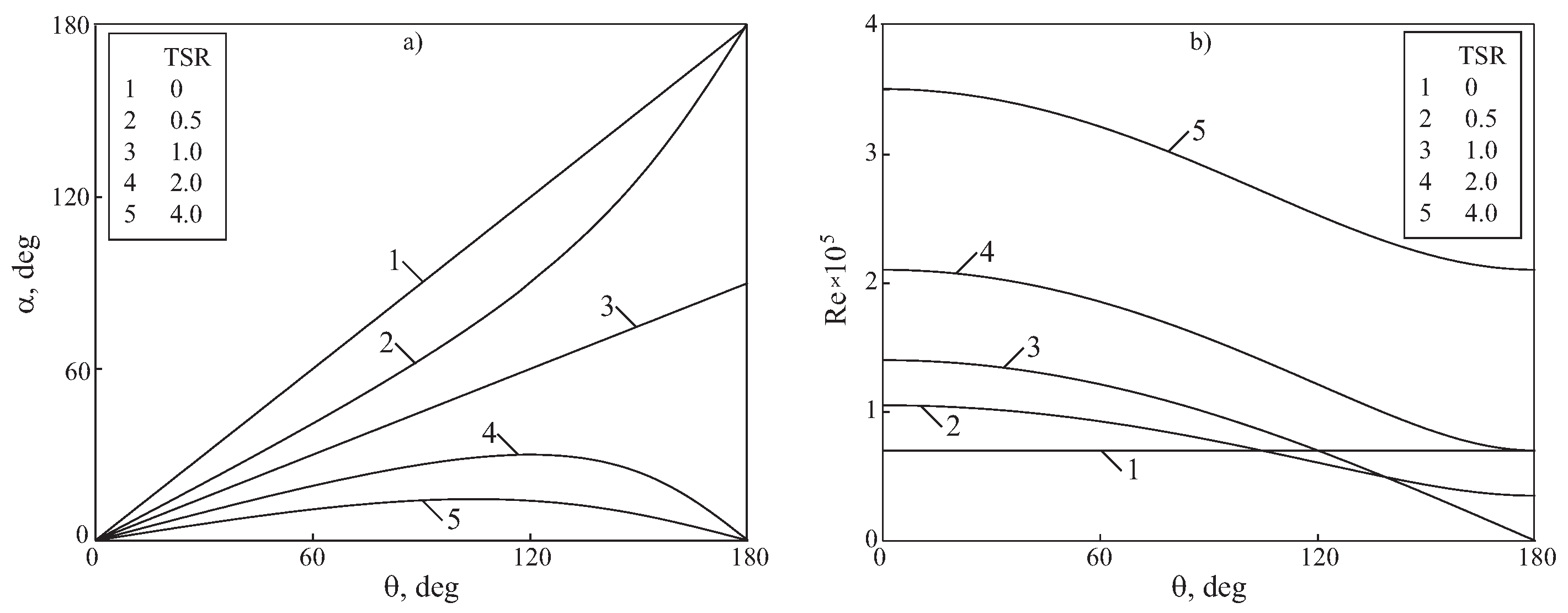
Knowing this allows for an analysis of the Reynolds number and AOA experienced by the airfoil during a full revolution of a VAWT at varying TSRs. Figure 3a shows that at a TSR of zero (this is when the wind turbine is stationary), an airfoil experiences an AOA anywhere from $0^{\circ }$ to ${180}^{\circ }$. This happens until the VAWT reaches a TSR of 1. Beyond $\lambda =1$, the airfoil never experiences an AOA greater than ${90}^{\circ }$, and as the VAWT reaches high TSRs, the range of AOAs experienced decreases further. The peak performance of lift-driven VAWTs occurs at high TSRs ($4<\lambda <8$). This point is explained by observing the peak in the tangential force coefficient of an airfoil, which occurs at low AOAs that are continually experienced at high TSRs. Figure 3b also shows the Reynolds numbers experienced by an airfoil used on a small VAWT in wind speeds of 5 m/s and a cord length of $C=0.2$ m, which is a typical cut-in wind speed for small VAWTs. Up to a TSR of 1, the Reynolds number of the flow is no higher than around $\mathrm{Re}=1.5\times {10}^5$. At peak performance, at TSRs greater than 4, the Reynolds number reaches $\mathrm{Re}=5\times {10}^5$.

3. Numerical Simulation

The airfoil flow at a high AOA is three dimensional, highly separated, and unsteady with a nonlinear lift variation. In the downwind zone (${180}^{\circ }<\theta <{360}^{\circ }$), the airfoil located in the shedding wake from the upwind zone sees a disturbed flow that makes the determination of AOA more difficult. Therefore, good reproduction of high AOA flow is inevitable in assessing VAWT performance. In-house CFD code is used to carry out a numerical simulation and to determine the aerodynamic characteristics of the airfoil. In this study, the URANS approach with the SST model and the LES approach with the WALE model were examined and compared.

The calculations are based on an in-house compressible CFD solver with low-Mach preconditioning (the resulting Mach number is less than 0.3). This solver has been designed for a wide range of aerodynamic applications. To predict aerodynamic characteristics at high AOAs, when a static or dynamic stall can occur and the flow is accomplished by separation and vortex formation, unsteady CFD calculations are performed.

Unlike the airfoil blades in an aircraft, VAWT blades experience high AOAs beyond the stall angle when they operate at a low TSR ($\lambda <4$).

Figure 4 shows the geometric scheme and boundary conditions in the CFD model of a single NACA0012 airfoil. In 3D calculations, the domain is extruded some thickness in the spanwise direction depending on AOA. The inlet boundary is a semicircular boundary with radius $R=15C$ and centre located at the tip of the airfoil when the AOA is zero degrees. The inlet boundary is located far away from the airfoil to avoid wave reflection. To specify non-zero AOA, velocity components on the inlet boundary are calculated at the given AOA. The length of the domain is the distance from the airfoil tip to the outlet and $L=30C$.

Free stream velocity corresponding to the Reynolds number and degree of turbulence (about 5%) is specified on the inlet boundary. Top and bottom boundaries are treated as free-slip walls. No-slip and no-penetration boundary conditions are applied to the airfoil. Non-reflecting boundary conditions are used on the outlet boundary. Periodic boundary conditions are used in the spanwise direction.

Due to the symmetrical nature of airfoils, and also to reduce computational expense, the RANS investigation is performed in the 2D domain. However, the 3D domain is used for LES calculations with periodical boundary conditions in the spanwise direction. An adequate mesh resolution is important to obtain an accurate solution and to ensure that the large eddies in the flow are resolved. Near-wall units (dimensionless distance from the wall relating to the first mesh point) are used to check the mesh resolution for a particular mesh.

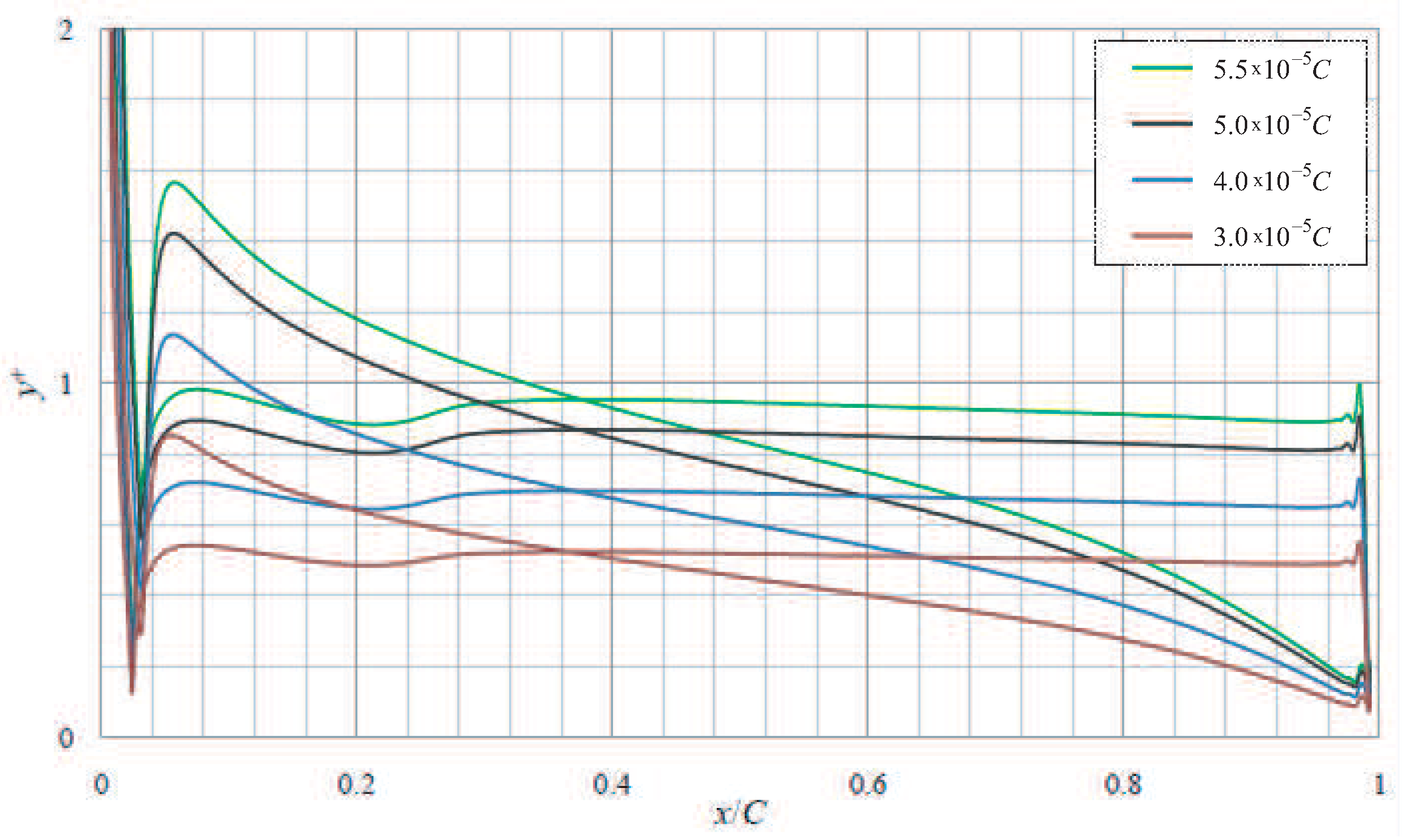
The SST model is considered a promising approach for simulating flow with great adverse pressure gradients and separation. However, the application of the SST model imposes some requirements on mesh quality in the near-wall region. The mesh quality in the near-wall region is described with a non-dimensional coordinate, yplus, and the SST model requires yplus coordinate values of less than 2 (the appropriate value of yplus coordinate is found with the semiempirical correlation for laminar or turbulent boundary layer on a flat plate). To accurately resolve the boundary layer, about 15 mesh nodes are located. Near-wall mesh resolution is adopted for the highest Reynolds number used in the CFD calculations ($\mathrm{Re}=3.6\times {10}^5$).

LES usually needs streamwise and spanwise mesh resolutions based on wall units $x^{+}<50$ and $z^{+}<20$, respectively. The mesh is designed to give $y^{+}<1$ and to locate about five points in the region where $y^{+}<5$.

A first layer thickness is about $5\times {10}^{-5}C$ in the RANS and LES calculations. A growth rate in the inflation layer equals 1.2. For these conditions, about 26 nodes in normal directions are required to cover the boundary layer region if the first layer thickness is $1.5\times {10}^{-5}C$. In CFD calculations, the yplus coordinate is uniformly distributed along the airfoil except for the small area near the stagnation point, where yplus is about 1 in the RANS and yplus is about 0.25 in the LES. Distributions of the yplus coordinate along the airfoil are presented in Figure 5.

Both O- and C-mesh topologies can minimize the skewness of a near-wall mesh, avoid high aspect ratios of cells in the far wake, and converge fast under a high-order discretization scheme.

A hybrid mesh is used in this study. The mesh contains a structured layer emanating from the surface of the airfoil that contains sufficient points to model the flow as it interacts with the no-slip wall of the airfoil, and a tetrahedral unstructured mesh fills the rest of the domain. The sizing controls used include inflation emanating from the airfoil surface, edge sizing along the airfoil surface in the flow-wise direction, edge sizing in the spanwise direction, global growth rate, maximum face size, body of influence radius, and body of influence sizing.

A mesh convergence study to find the optimum mesh parameters has been carried out on the standard NACA0012 airfoil at an AOA of ${10}^{\circ }$ and a Reynolds number of $\mathrm{Re}=3.6\times {10}^5$. These optimum parameters are given in

Table 1. Mesh parameters.

Inflation layer	First layer thickness	$1.50\times {10}^{-5}\mathit{C}$
	Number of layers	26
	Growth rate	1.2
Aerofoil edge sizing	Flow-wise	$1.25\times {10}^{-3}C$
	Spanwise	1
Body of influence	Radius 1	$4C$
	Sizing 1	$5\times {10}^{-2}C$
	Growth rate	1.12
	Radius 2	$2C$
	Sizing 2	$2\times {10}^{-2}C$
	Growth rate	1.12
Global parameters	Max face size	$0.6C$
	Growth rate	1.12
Statistics	Number of nodes	175,000
	Number of cells	380,000

.

In order to resolve the laminar sublayer directly, the first mesh spacing on the airfoil was determined to make yplus values less than 1. Mesh-stretching was limited to less than 1.12 in both streamwise and crossflow directions to ensure numerical stability.

The 3D model differs from the 2D model in the sense that it extends the model in a spanwise direction for a certain length. A pair of translational periodic conditions was enforced in the spanwise direction. To perform 3D calculations, the mesh containing 280 cells along the airfoil wall, 120 cells in the normal direction to the wall, and 40 cells in the spanwise direction is generated. The number of cells was determined through a mesh refinement study.

In the 3D model, the airfoil was extruded in a spanwise direction in order to reproduce 3D turbulence structures. Too small a spanwise width makes the flow become virtually 2D rather than 3D. At low AOAs, a relatively short spanwise width ($S=0.074C$) is sufficient to obtain results comparable with wind tunnel data, whereas in high AOA flow, a much longer width is needed to capture the larger 3D turbulence vortex separation and shedding structures. The spanwise width of $2C$ was selected in the 3D simulations, and the mesh contains 20 layers in the spanwise direction as recommended in [16]. Since periodic boundaries were enforced at the two ends of the domain in the spanwise direction, the actual spanwise variation in averaged physical quantities is almost negligible.

Figure 6 shows the final mesh for the standard airfoil, and the remainder of this section details the method and results of the mesh convergence that led to these parameter values.

A layer of inflation has been used to create a structured layer emanating from the airfoil surface and presented in Figure 7.

The segregated approach was selected to solve the discretized continuity and momentum equations, and a second-order implicit formula was used for the temporal discretization. The SIMPLEC scheme was used to solve the pressure–velocity coupling. In the SST model, the second-order upwind finite-difference scheme and the third-order MUSCL finite-difference scheme are applied for pressure and other variables. The LES numerical method is more sensitive to the choice of discretization scheme. In this case, the bounded central difference scheme is used for spatial discretization and to provide the second-order accurate numerical solution in space and time. The steady state solution predicted with the SST model was used to specify the initial condition for LES simulations.

The most crucial numerical parameter for unsteady CFD calculations is time step size. The non-dimensional time step $\tau =\Delta tU/C$ equals 0.01 (this value corresponds to the physical time step of $\Delta t=0.0001$ s) to keep $\mathrm{CFL}<0.5$. This time step was applied in the simulations of the single airfoil in [12], where the flow was found to be statistically steady after 1.2 s, and airfoil surface pressure was acquired in the following 2.4 s, which was equal to 260 flow-through times according to the free stream velocity and airfoil chord length.

4. Verification of the Model

The benchmark NACA0012 airfoil is a symmetrical airfoil with a thickness-to-chord ratio of 12 per cent. It was chosen for testing because it is one of few airfoils for which wind tunnel data for the entire range of AOAs are available from [4].

The size of the computational domain and the mesh resolution have an effect on the results of the simulations, so domain dependence and mesh convergence studies are carried out in order to achieve reliable results. Verification studies are performed at a Reynolds number of $3.6\times {10}^5$ (the largest Reynolds number used in this study) and AOA of ${10}^{\circ }$. The results obtained are validated against those which have been produced in previous experimental works and CFD predictions [1,4,32,33,34]. Validation of the CFD results is performed at three different Reynolds numbers ($3.6\times {10}^5$, $1.5\times {10}^5$, and $6.5\times {10}^4$) and in a wide range of AOAs from $0^{\circ }$ to ${180}^{\circ }$.

Five computational domains were created to simulate the flow over airfoil having different radius-to-chord ratios. Different radius-to-chord ratios were obtained by extending the domain before and behind the airfoil in such a way that the airfoil was located at the centre of the flow stream. A domain dependence study has been performed to ensure the domain is large enough not to have any bearing on the simulation results. Figure 8 shows that using a small domain with $R<10C$ results in a much higher lift and drag being observed, but once a domain with $R>15C$ is used, there is a little change in the results.

Figure 9 shows how the predicted values of lift and drag converge as the first layer thickness is reduced. For reference, the experimental values for the NACA0012 as measured in [4] at $\mathrm{Re}=3.6\times {10}^5$ are displayed.

The spacing of nodes along the surface of the airfoil affects the accuracy of the CFD predictions. Figure 10 shows how the predicted values of lift and drag converge as the sizing in the flow-wise direction is reduced. Figure 11, on the other hand, shows how the edge sizing in the spanwise direction has little effect on the prediction.

Circular bodies of influence have been used to refine the mesh in the region around the airfoil as shown in Figure 12. The radius and element sizing applied to these bodies of influence both have an effect on the accuracy of the CFD predictions.

Figure 13 shows how the predicted values of lift and drag converge as the radius of the body of influence increases. These graphs are for simulations with an element sizing of $3\times {10}^{-2}C$.

Further investigation proved that it was advantageous to use two bodies of influence. Figure 14 shows how reducing the sizing in the second body of influence with radius $R=2C$ affects the predictions of the simulation. These graphs actually show that convergence has not been achieved and that the sizing of the second, smaller body of influence needs to be reduced further. However, reducing the sizing further would produce a mesh that contains over one million elements in the case of a standard airfoil and close to two million elements in the case of a vented airfoil. This is not convenient because a large number of simulations must be run for different AOAs, different Reynolds numbers, and different geometries. For this reason, a minimum sizing of $2\times {10}^{-2}C$ has been decided upon for the second body of influence.

The maximum face size of the elements of the mesh has an impact on the CFD predictions, and Figure 15 shows how the predicted values of lift and drag converge as the maximum face size is reduced.

5. Results and Discussion

The predictions of the aerodynamic characteristics of the NACA0012 made by CFD are compared to those measured in previous works. In addition to RANS, LES calculations were also performed and compared with RANS predictions in order to better understand the capability of LES.

5.1. Angle of Attack

Simulations have been performed for a range of AOAs from $0^{\circ }$ to ${180}^{\circ }$ in steps no greater than ${10}^{\circ }$ at $\mathrm{Re}=1.5\times {10}^5$ and $\mathrm{Re}=3.6\times {10}^5$.

Figure 16 and Figure 17 show the results of the mean lift and drag coefficients for the studied NACA0012 airfoil obtained with RANS and LES, as well as the wind tunnel test results. Both the computational and experimental Reynolds numbers were equal to $3.6\times {10}^5$. The stall starts at ${12}^{\circ }$ and ends at ${16}^{\circ }$. The flow separation is observed at the trailing edge of the airfoil and shifts towards its leading edge when AOA increases. At the same time, the lift force remains almost constant.

Figure 16 presents a comparison of the computational results with RANS and LES with experimental data from [1,4]. There is a good agreement between experimental and computational results, excluding the range of AOSs between ${35}^{\circ }$ and ${45}^{\circ }$ and the range of AOSs between ${125}^{\circ }$ and ${135}^{\circ }$, where RANS results are different from LES data and experimental measurements.

Figure 17 shows that overall, there is a good similarity between the experimental measurements of [1,4] and the CFD predictions. At $\alpha ={30}^{\circ }$, there is excellent agreement between all observations and the CFD predictions, but then at $\alpha ={40}^{\circ }$, the CFD predicts sharp peaks in lift which were not observed experimentally (similar behaviour is observed in Figure 16 for drag coefficient). The wind tunnel results show a hysteresis loop caused by a deep stall. As stated in [4], this may have been induced by the slow rolling of the airfoil section in the wind tunnel experiments. In CFD simulations, the airfoil is fixed at various AOAs, and no hysteresis loop could be observed.

On closer inspection, Figure 18 shows excellent agreement with the experimental data in the prediction of lift from $\alpha =0^{\circ }$ up until a stall occurs at $\alpha ={12}^{\circ }$. In the range ${12}^{\circ }<\alpha <{20}^{\circ }$, there is a variation in all the data that have been compared, but the CFD model consistently predicts a higher value of lift than all the previous observations. Figure 18 also shows a good agreement for drag. However, the sharp rise that is observed experimentally between $12<\alpha <{16}^{\circ }$ is not predicted by the CFD model.

However, similar peaks were observed in [34] at $\mathrm{Re}=1.5\times {10}^5$ as shown in Figure 19 and Figure 20. Beyond $\alpha ={40}^{\circ }$ up until $\alpha ={130}^{\circ }$, the CFD model then underpredicts both lift and drag. LES calculations are able to represent the experimental results with great accuracy. At the same time, the peaks were predicted by the RANS calculations in [34], similar to those highlighted by the current RANS calculations. The considerably improved results achieved with LES imply that the poor accuracy of the RANS method is mainly due to its inherent limitation in vortex modelling.

For $\mathrm{Re}=1.5\times {10}^5$, in the stall region, CFD seems to overpredict lift compared to both experimental findings [4] and CFD predictions [34]. A peak in lift and drag similar to that predicted in [34] is observed, but the peaks predicted by CFD are both larger and seem to occur earlier. Again, CFD underpredicts drag compared to [4] for the remainder of AOAs.

A relatively good agreement is seen between the sets of data in the pre-stall regime. They give almost identical lift coefficient peak values, although the data from [4] show a slightly earlier stall. After the stall, the lift from the RANS calculations falls to a value of around 0.7, maintaining and gradually increasing that value with increasing AOA to ${56}^{\circ }$. The experimental lift curve shows a quite different post-stall characteristic in which the lift drops to almost zero before sharply rising to the second peak. It is not clear what physical flow mechanism could result in such a dramatic lift loss and recovery in the immediate post-stall zone, and it is unfortunate that this feature was not discussed by [4] in their original work.

At low (pre-stall) AOAs, both RANS computations using the SST turbulence model and LES agree with the experimental results well. However, at high (post-stall) AOAs, RANS results underpredict drag, and lift substantially deviates from the experimental results at ${40}^{\circ }$ and ${130}^{\circ }$. The RANS model provides accurate results for attached boundary layer flows but fails to simulate the large-scale turbulence in separated flows. Therefore, the RANS model is not suitable for resolving flow if the AOA is greater than ${15}^{\circ }$, which often occurs when VAWTs operate in a $\lambda <4$. Compared with the RANS model, the LES shows an excellent agreement with the wind tunnel results from $0^{\circ }$ to ${140}^{\circ }$.

5.2. Effect of Reynolds Number

The effect that the Reynolds number has on the aerodynamic characteristics of the NACA0012 airfoil is investigated. Three different Reynolds numbers are used ($\mathrm{Re}=3.6\times {10}^5$, $\mathrm{Re}=1.5\times {10}^5$, and $\mathrm{Re}=6.5\times {10}^4$). The inlet velocity is adjusted to produce each Reynolds number simulation.

Figure 21 and Figure 22 show that at most AOAs, the lift and drag is not dependent upon the Reynolds number. However, there are certain AOAs where the values of lift and drag are Reynolds number dependent. Specifically, these are in the range of AOA from $8^{\circ }$ to ${30}^{\circ }$ and can be seen in greater detail in Figure 23. As the Reynolds number is reduced, so too is the lift. In addition, as the Reynolds number is reduced, the drag increases. Stall occurs earlier as the Reynolds number is reduced. All these findings are in agreement with previous studies reported in [1,5,7,8].

Figure 24 shows how the coefficient of tangential force (the force tangential to the rotation of the VAWT that provides the torque) varies with the Reynolds number. Obviously, as this force is derived from components of the lift and drag forces, for the majority of AOAs, tangential force is not dependent on the Reynolds number, but in the region where stall occurs, a big variation between different Reynolds numbers can be seen.

The mean static pressure on the surface, characterized by the pressure coefficient, provides a more quantitative assessment of the accuracy of the various simulations.

To observe how the flow varies for these AOAs that show a dependency upon the Reynolds number, it is useful to analyse pressure variations both on the airfoil surface (Figure 25, Figure 26 and Figure 27) and in the domain, along with streamline plots (Figure 28, Figure 29 and Figure 30) which show the path a particle with zero mass would take through the domain. RANS results corresponding to AOAs of ${10}^{\circ }$ and ${12}^{\circ }$ show attached flow with very close loading. The flat pressure distribution on the suction side of the airfoil at an AOA of ${216}^{\circ }$ is a sign of the airfoil stall. However, pressure values are slightly higher than the experimental measurement.

Looking at what happens for an AOA of ${10}^{\circ }$, at $\mathrm{Re}=3.6\times {10}^5$, Figure 28 shows there is no flow separation occurring. At the lower Reynolds number of $\mathrm{Re}=1.5\times {10}^5$, separation has just started to occur on the upper surface of the trailing edge but is barely visible on the streamline graph. At $\mathrm{Re}=6.5\times {10}^4$, the trailing edge separation is slightly larger. In addition, the streamline pattern shows separation has just started to occur on the upper surface of the leading edge which can also be identified by the discontinuity of the coefficient of pressure plot along the airfoil surface in Figure 25, Figure 26 and Figure 27.

For an AOA of $\alpha ={12}^{\circ }$, the streamline pattern shows that separation on the upper surface of the trailing edge has just started to occur at $\mathrm{Re}=3.6\times {10}^5$, while at $\mathrm{Re}=1.5\times {10}^5$, separation at the upper trailing edge has become more visible. The plot of pressure coefficient along the airfoil surface shows that separation at the leading edge has just started to occur, too. At $\mathrm{Re}=6.5\times {10}^4$, the trailing edge separation has extended all the way along the upper surface to meet the leading edge separation.

For an AOA of $\alpha ={16}^{\circ }$, the streamline plot at $\mathrm{Re}=3.6\times {10}^5$ now resembles that of $\alpha ={12}^{\circ }$ at $\mathrm{Re}=1.5\times {10}^5$, with the trailing edge separation extending along the upper surface. However, there is still no sign of any leading edge separation. At $\mathrm{Re}=1.5\times {10}^5$ and $\mathrm{Re}=6.5\times {10}^4$, transient features have started to occur, and it would seem as though the vortices are being shed from the upper surface of the airfoil. The monitor plots of lift and drag show clear periodic oscillations.

The results obtained show that the lift curves in pre-stall are not significantly affected by the Reynolds number. The maximum lift coefficient is observed at an AOA of ${12}^{\circ }$ for all Reynolds numbers used in the calculations. However, the maximal values of lift coefficient increase with the Reynolds number. These maximal values are 0.802, 0.925, and 1.210 for the three Reynolds numbers used in the calculations. This maximum lift is comparable to the value of 0.853 measured in [4] at the Reynolds number of $1.6\times {10}^5$.

The flow separates over the entire airfoil surface if the AOA further increases. The lift decreases to 0.64 before is grows up to 1.45 at an AOA of ${45}^{\circ }$. Then, a lift drop occurs at an AOA of ${54}^{\circ }$, which is followed by further lift reduction to zero at an AOA of ${90}^{\circ }$. The lift drop corresponds to a sudden flow restructuring on the suction side of the airfoil. The pressure distribution on the suction side of the airfoil remains constant over the entire airfoil surface. However, the pressure coefficient undergoes rapid changes in the range of an AOA between ${50}^{\circ }$ and ${60}^{\circ }$.

These trends are reversed as the AOA passes ${90}^{\circ }$ and the airfoil is travelling backwards.

In terms of drag, the usual pre-stall trend is followed as the AOA increases. Drag coefficients decrease slightly with an increasing Reynolds number. Drag then increases sharply at the stall point, corresponding to the observed reduction in lift, and continues to increase rapidly to a peak at approximately ${48}^{\circ }$. Further AOA increase results in a rapid fall in drag. The maximum value of drag coefficient is sensitive to the Reynolds number. However, minimum values of drag are similar for the three tests. Then, the drag increases and reaches a second maximum at an AOA of ${90}^{\circ }$, and the trend is reversed if the AOA if higher than ${90}^{\circ }$.

6. Performance Prediction

A double-multiple streamtube (DMS) model is used to evaluate the power of VAWTs. To apply this model in practice, the aerodynamic characteristics of static airfoil in a wide range of AOAs (from $0^{\circ }$ to ${360}^{\circ }$ for a non-symmetric airfoil and from $0^{\circ }$ to ${180}^{\circ }$ for a symmetric airfoil) are required. The tangential force generated by the blade is dependent on lift and drag, both of which are functions of the angle of attack. At each TSR point, the blade loads, angle of attack, induced local velocities, and torque transmitted to the rotor are determined.

The effect that the airfoil’s aerodynamic characteristics has on the performance of the wind turbine is analysed. The model used is simple, in that it does not take into account wake effects or unsteady occurrences that occur in the flow. The following predictions have been made for a theoretical three-bladed VAWT with radius of 1 m and chord length of 0.2 m. RANS and LES results are used to estimate the performance of the wind turbine.

The coefficient of power as a function of TSR is presented in Figure 31. Figure 32 shows in more detail the variation in the coefficient of power at low TSRs smaller than 1. The averaged trust coefficient for the standard airfoil is 0.0157. Figure 33 shows the dependence of the average starting torque on the wind speed (the height is equal to 2 m). In these figures, solid lines correspond to RANS calculations, and dashed lines correspond to LES calculations. RANS calculations lead to an overestimation of the coefficient of power and average starting torque compared to LES predictions.

The blade aerodynamics loads and induced velocities are calculated for a range of TSR by holding wind velocity constant and varying rotor angular velocity, and by holding rotor angular velocity and varying wind velocity. The differences in power coefficients are due to different Reynolds numbers experienced by a blade during its revolution around the rotor axis. This is because different combinations of freestream wind and rotor angular velocity are used to arrive at the same TSR.

7. Conclusions

RANS and LES of flow over an airfoil were performed in a wide range of AOAs. Their capabilities to predict the aerodynamic forces were evaluated through a comparison with the wind tunnel results and computational data obtained by other researchers with particular attention to high AOA flow beyond stall. Validation with experimental data for the aerodynamic characteristics of the single NACA0012 airfoil has shown reasonable agreement, although some notable differences were observed.

A single static airfoil was simulated with LES. The results computed with LES were compared with those obtained from wind tunnel measurements and RANS simulations. The comparison of CFD results with experimental observations demonstrated that RANS calculations significantly overpredict the lift and drag coefficients of airfoil at AOAs corresponding to post-stall conditions. The main reason is that 2D simulations are not able to reproduce vorticity diffusion and the formation of large-scale eddy structures. RANS simulations tend to overestimate the power coefficients, although they can approximately replicate the variation trend of experimental power coefficients. The RANS model cannot offer an acceptable estimation of the output power of the VAWT because high AOAs are common to airfoil blades in an operating VAWT. In contrast, LES provided a much better agreement with the experimental results and a more realistic description of the aerodynamic details. The RANS simulations remained almost 2D in such highly separated flows, whereas the 3D LES could capture the essential pattern of the 3D flow.

The considerably improved results achieved by LES imply that the poor accuracy of the RANS method is mainly due to its inherent limitation in vortex modelling. The comparison of RANS results with LES predictions and experimental measurements shows that the RANS model leads to a delay of dynamic stall. In addition, RANS calculations overpredict the tangential force in the upwind zones. LES is a promising and effective CFD tool for investigating the aerodynamic characteristics of VAWTs and their self-starting capabilities at low rotation speeds. However, the LES calculations performed were not able to capture the formation of tip vortex and flow divergence in the spanwise direction. This effect may be one of the reasons for the overprediction of the power coefficient in CFD calculations based on the 2D RANS approach.