On the Use of Probability-Based Methods for Estimating the Aerodynamic Boundary-Layer Thickness
Abstract
:1. Introduction
2. Construction of 2D Slices
3. Methods for Determining the Proper Boundary-Layer Thickness
3.1. Method Based on Bernoulli’s Equation
3.2. Probability-Based Methods
4. Numerical Experiments
4.1. Adequate Thickness of Boundary Layer
4.2. Comparison of the Boundary-Layer Thicknesses
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| the free stream velocity | |
| the free stream Mach number | |
| the angle of attack | |
| X, Y, Z | the global Cartesian coordinates |
| x, y, z | the local orthogonal coordinates |
| U, V, W | the velocity components in the local coordinates |
| a threshold parameter for determining the boundary-layer thickness based on the stagnation enthalpy | |
| , , | the probability-based boundary-layer thicknesses for compressble 3D flows |
| , , | parameters in the formulas for , , |
| 2D | two-dimensional |
| 3D | three-dimensional |
| LTT | laminar-turbulent transition |
| TS | Tollmien-Schlichting |
| CF | crossflow |
References
- Weyburne, D. A mathematical description of the fluid boundary layer. Appl. Math. Comput. 2006, 175, 1675–1684, Erratum in 2008, 197, 466. [Google Scholar] [CrossRef]
- Weyburne, D. New thickness and shape parameters for the boundary layer velocity profile. Exp. Therm. Fluid Sci. 2014, 54, 22–28. [Google Scholar] [CrossRef]
- Boiko, A.V.; Demyanko, K.V.; Nechepurenko, Y.M. On computing the location of laminar-turbulent transition in compressible boundary layers. Russ. J. Num. Anal. Math. Model. 2017, 32, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Boiko, A.V.; Demyanko, K.V.; Kirilovskiy, S.V.; Nechepurenko, Y.M.; Poplavskaya, T.V. Modeling of transonic transitional three-dimensional flows for aerodynamic applications. AIAA J. 2021. [Google Scholar] [CrossRef]
- Boiko, A.V.; Kirilovskiy, S.V.; Maslov, A.A.; Poplavskaya, T.V. Engineering modeling of the laminar-turbulent transition: Achievements and problems (Review). J. Appl. Mech. Tech. Phys. 2015, 56, 761–776. [Google Scholar] [CrossRef]
- Cebeci, T.; Chen, H.H.; Arnal, D.; Huango, T.T. Three-dimensional linear stability approach to transition on wings and bodies of revolution at incidence. AIAA J. 1991, 29, 2077–2085. [Google Scholar] [CrossRef]
- Krimmelbein, N.; Krumbein, A. Automatic transition prediction for three-dimensional configurations with focus on industrial application. J. Aircraft 2011, 48, 1878–1887. [Google Scholar] [CrossRef]
- Krumbein, A. eN transition prediction for 3D wing configurations using database methods and a local, linear stability code. Aero. Sci. Tech. 2008, 12, 592–598. [Google Scholar] [CrossRef] [Green Version]
- Mack, L.M. Stability of three-dimensional boundary layers on swept wing at transonic speeds. In Symposium Transsonicum III; Zierep, J., Oertel, H., Jr., Eds.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 209–223. [Google Scholar]
- Nayfeh, A.H. Stability of three-dimensional boundary layers. AIAA J. 1980, 18, 406–416. [Google Scholar] [CrossRef] [Green Version]
- Perraud, J.; Arnal, D.; Casalis, G.; Archambaud, J.P.; Donelli, R. Automatic transition predictions using simplified methods. AIAA J. 2009, 47, 2676–2684. [Google Scholar] [CrossRef] [Green Version]
- Gaponenko, V.R.; Ivanov, A.V.; Kachanov, Y.S. Experimental study of a swept-wing boundary-layer stability with respect to unsteady disturbances. Thermophys. Aeromech. 1995, 2, 287–312. [Google Scholar]
- Hirschel, E.H. Basics of Aerothermodynamics; Springer: Berlin/Heidelberg, Germany, 2005; pp. 201–202. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory, 9th ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Ivanov, A.V.; Mischenko, D.A.; Boiko, A.V. Method of the description of the laminar-turbulent transition position on a swept wing in the flow with an enhanced level of free-stream turbulence. J. Appl. Mech. Tech. Phys. 2020, 61, 250–255. [Google Scholar] [CrossRef]
- Kirilovskiy, S.V.; Boiko, A.V.; Demyanko, K.V.; Nechepurenko, Y.M.; Poplavskaya, T.V. Simulation of the laminar-turbulent transition in the boundary layer of the swept wing in the subsonic flow at angles of attack. AIP Conf. Proc. 2020, 2288, 1–6. [Google Scholar]
- Kreplin, H.P.; Vollmers, H.; Meier, H.U. Measurements of the wall shear stress on an inclined prolate spheroid. Z. Flugwiss. Weltraumforsch. 1982, 6, 248–252. [Google Scholar]
- Kreplin, H.P. Three-dimensional boundary layer and flow field data of an inclined prolate spheroid. In AGARD-AR-303: Selection of Experimental Test Cases for the Validation of CFD Codes; AGARD: Neuilly, France, 1994; Volume II, pp. C2.1–C2.12. [Google Scholar]
- Meier, H.U. Experimental investigation of the boundary layer transition and separation on a body of revolution. Z. Flugwiss. Weltraumforsch. 1980, 4, 65–71. [Google Scholar]
- Massey, B.S.; Clayton, B.R. Laminar boundary layers and their separation from curved surfaces. J. Basic Eng. 1965, 87, 483–493. [Google Scholar] [CrossRef]
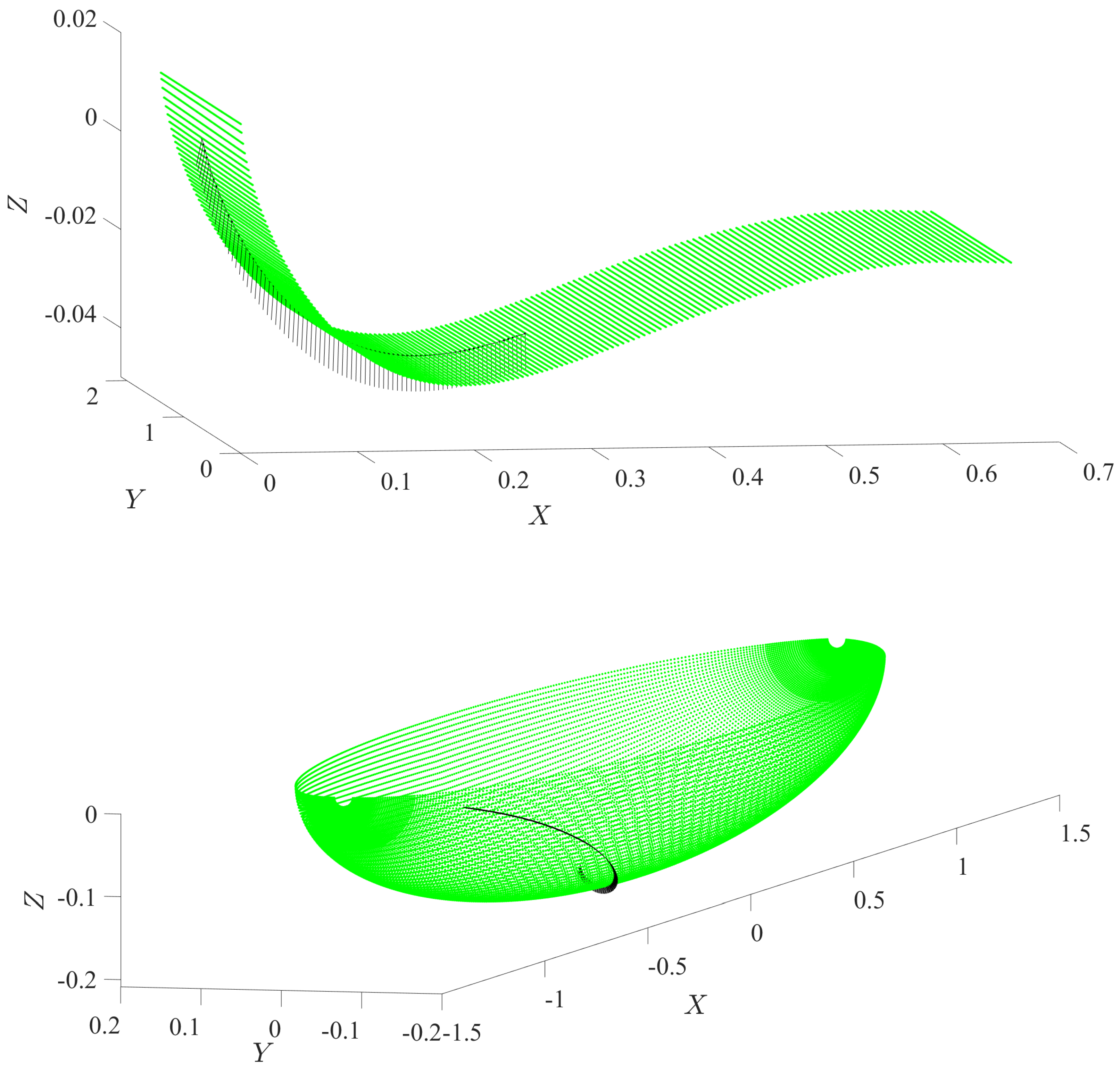
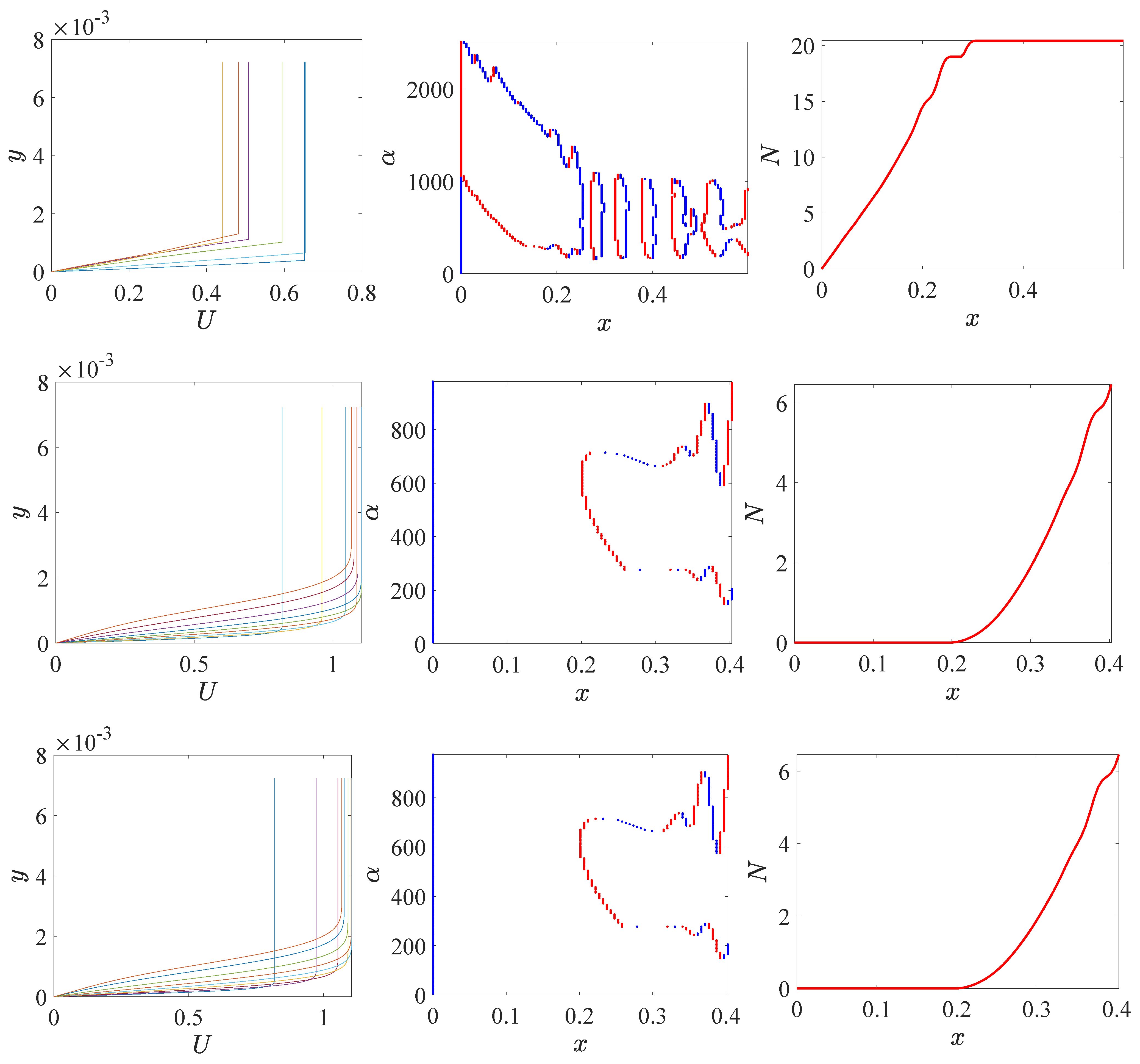

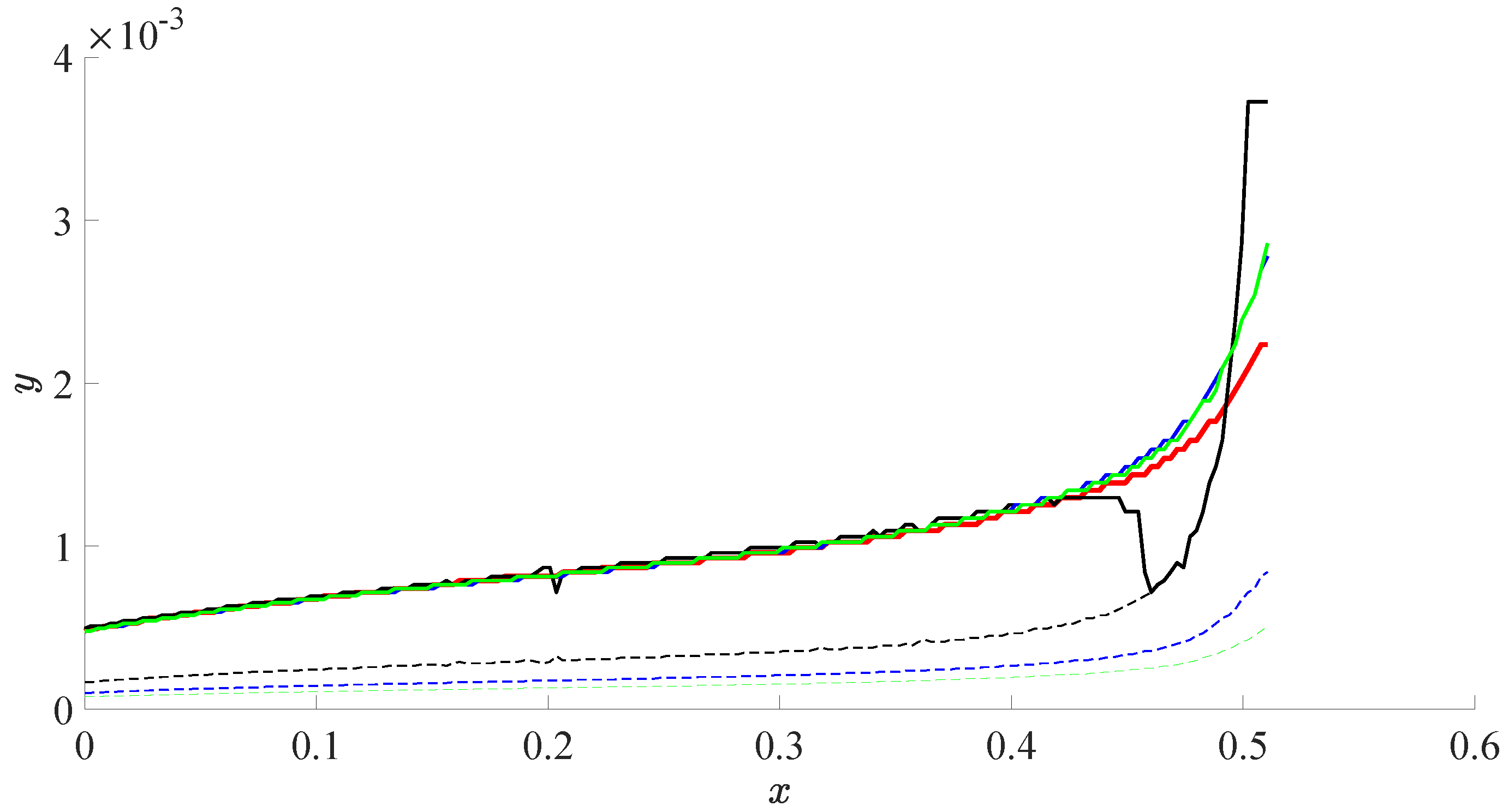
| Parameters (the Slice Position) | p | |||
|---|---|---|---|---|
| Swept wing | , (lower) | 3.73–4.98 | 4.83–6.30 | |
| , (upper) | 3.80–5.06 | 4.84–6.30 | ||
| , (lower) | 3.62–6.14 | 4.70–7.67 | ||
| , (lower) | 3.83–9.74 | 4.94–11.9 | ||
| , (upper) | 3.79–8.82 | 4.86–10.7 | ||
| , (upper) | 3.78–7.15 | 4.80–8.75 | ||
| Prolate spheroid | , (lower) | 3.73–6.96 | 3.79–6.59 | |
| , (middle) | 3.73–6.61 | 4.07–6.77 | ||
| , (upper) | 4.01–5.23 | 5.10–6.51 | ||
| , (middle) | 5.09–6.27 | 6.44–7.82 | ||
| , (lower) | 3.04–6.53 | 4.02–8.11 | ||
| , (middle) | 3.00–6.43 | 3.99–8.03 | ||
| , (upper) | 4.06–4.92 | 5.15–6.30 | ||
| , (middle) | 4.09–5.86 | 5.32–7.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boiko, A.V.; Demyanko, K.V.; Nechepurenko, Y.M.; Zasko, G.V. On the Use of Probability-Based Methods for Estimating the Aerodynamic Boundary-Layer Thickness. Fluids 2021, 6, 267. https://doi.org/10.3390/fluids6080267
Boiko AV, Demyanko KV, Nechepurenko YM, Zasko GV. On the Use of Probability-Based Methods for Estimating the Aerodynamic Boundary-Layer Thickness. Fluids. 2021; 6(8):267. https://doi.org/10.3390/fluids6080267
Chicago/Turabian StyleBoiko, Andrey V., Kirill V. Demyanko, Yuri M. Nechepurenko, and Grigory V. Zasko. 2021. "On the Use of Probability-Based Methods for Estimating the Aerodynamic Boundary-Layer Thickness" Fluids 6, no. 8: 267. https://doi.org/10.3390/fluids6080267
APA StyleBoiko, A. V., Demyanko, K. V., Nechepurenko, Y. M., & Zasko, G. V. (2021). On the Use of Probability-Based Methods for Estimating the Aerodynamic Boundary-Layer Thickness. Fluids, 6(8), 267. https://doi.org/10.3390/fluids6080267






