Neural Network-Based Model Reduction of Hydrodynamics Forces on an Airfoil
Abstract
:1. Introduction
2. Computational Methodology
2.1. Governing Equations
2.2. Discretization Scheme
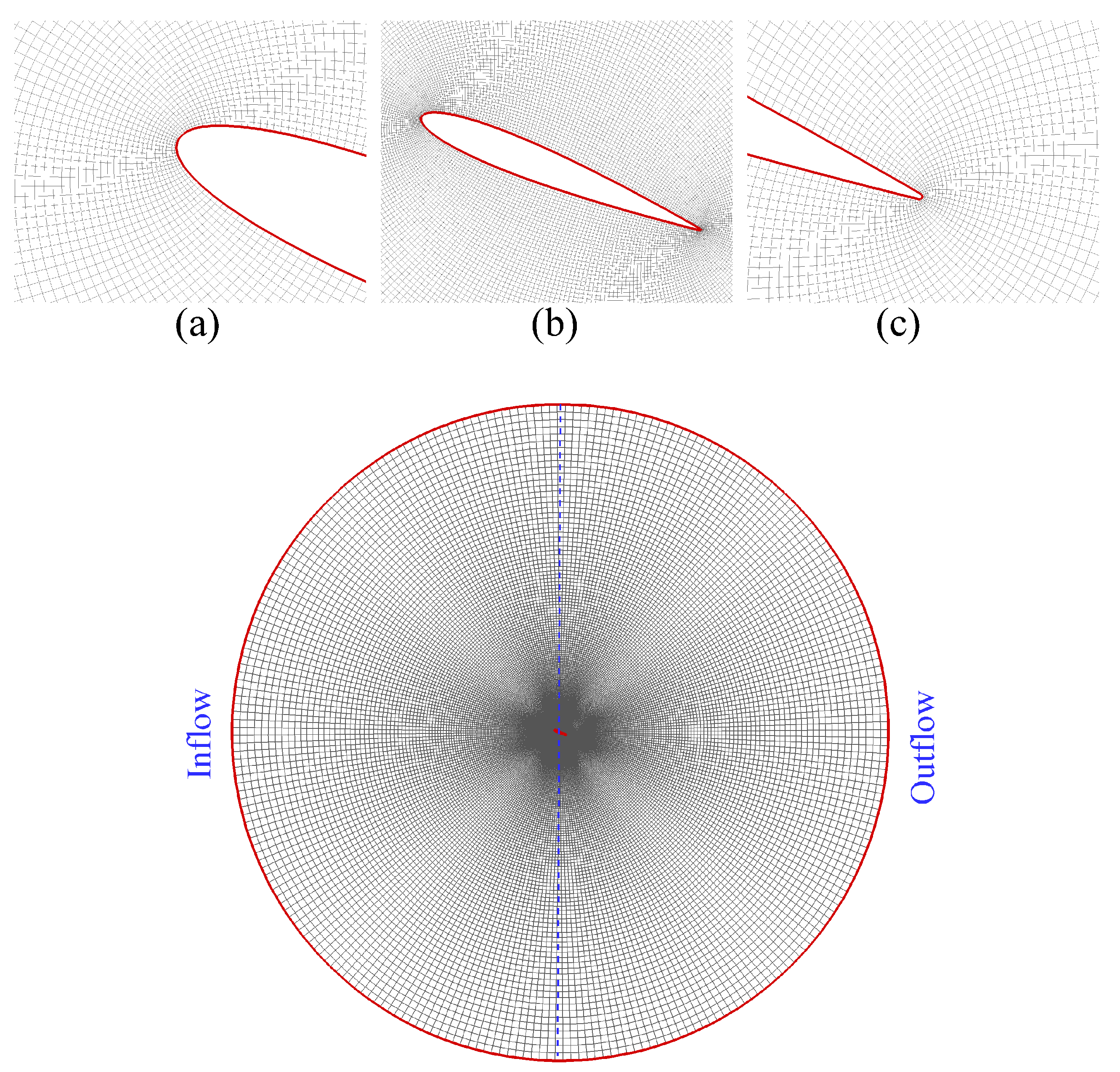
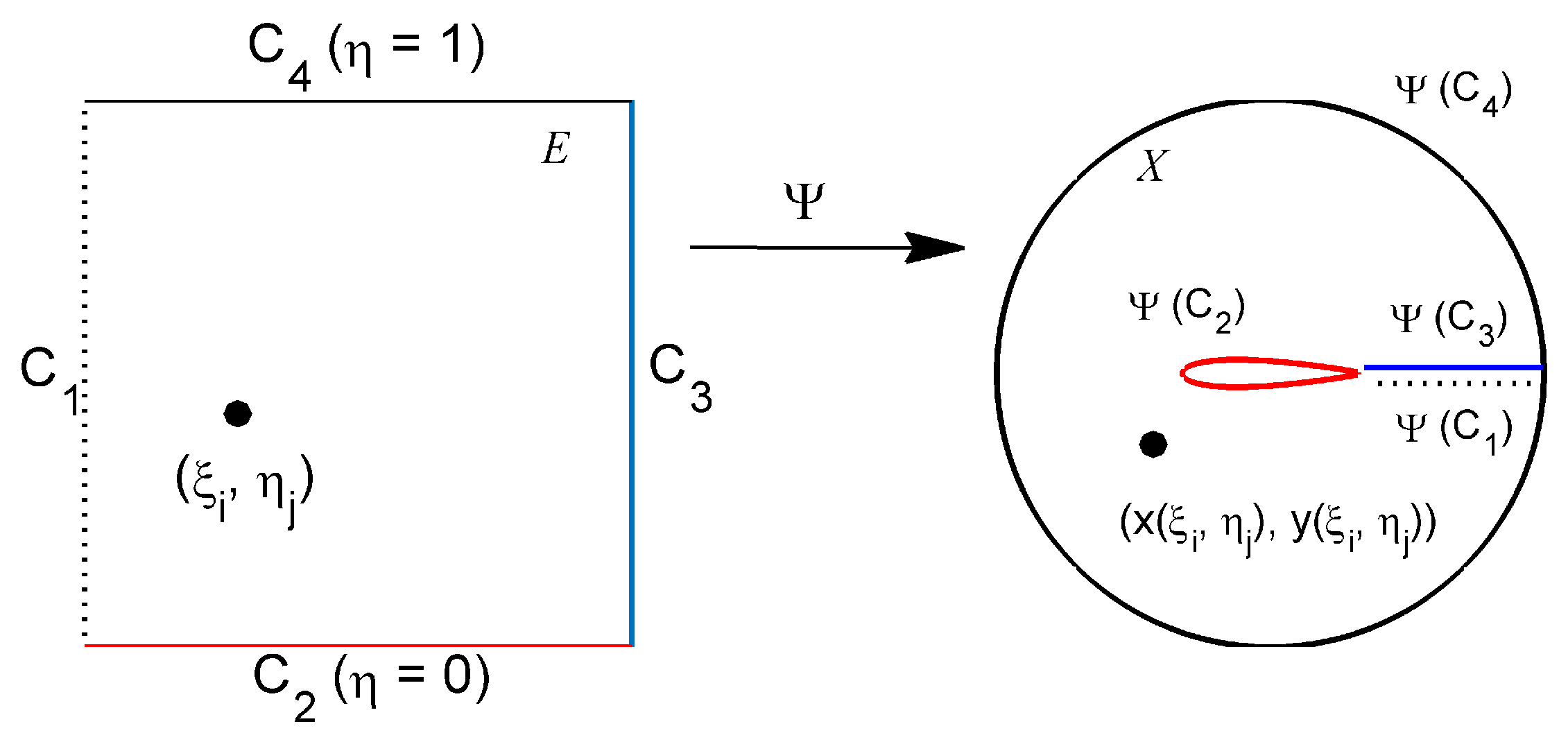
2.3. Grid Generation
3. Validation & Verification
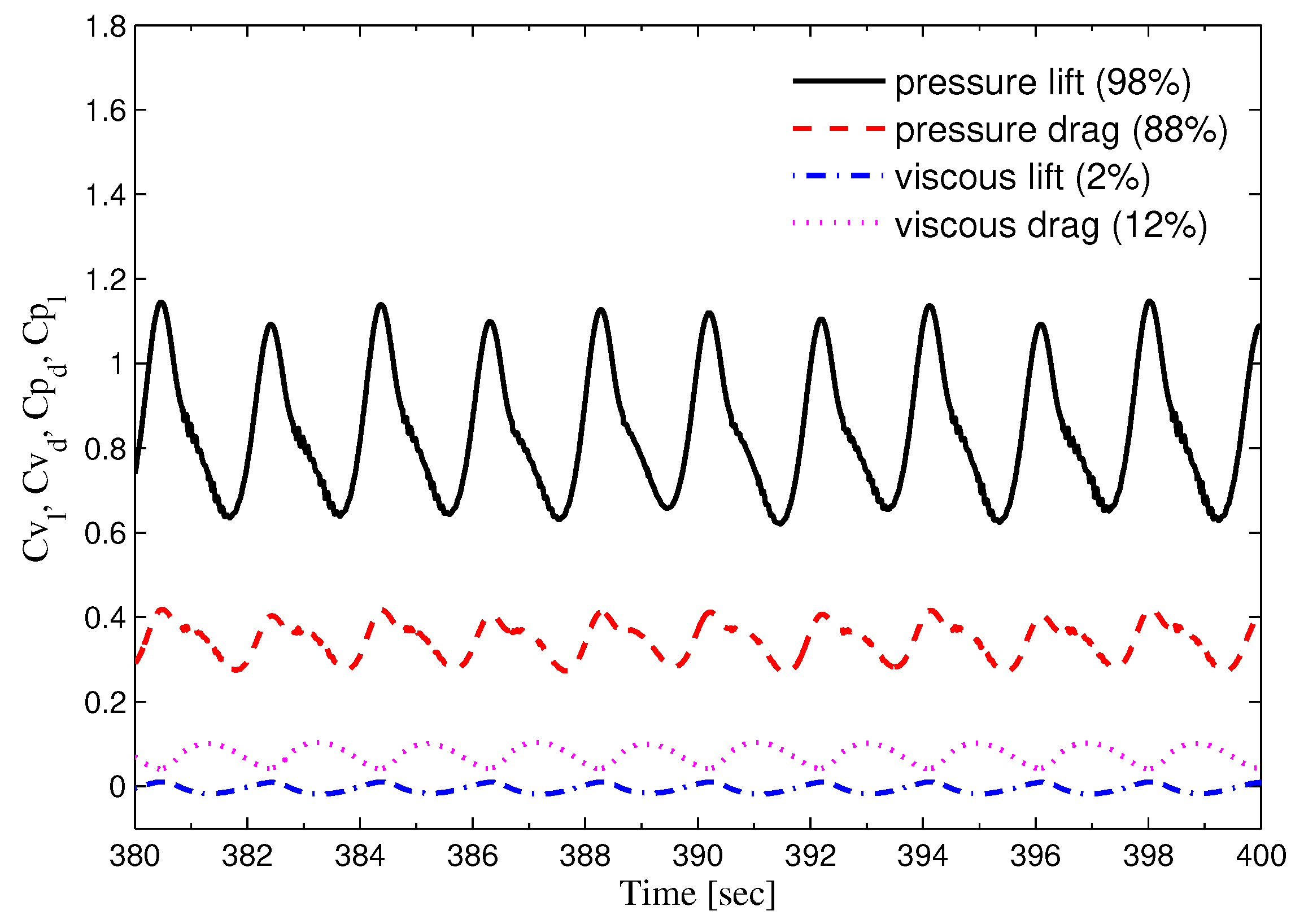
3.1. Hydrodynamic Forces
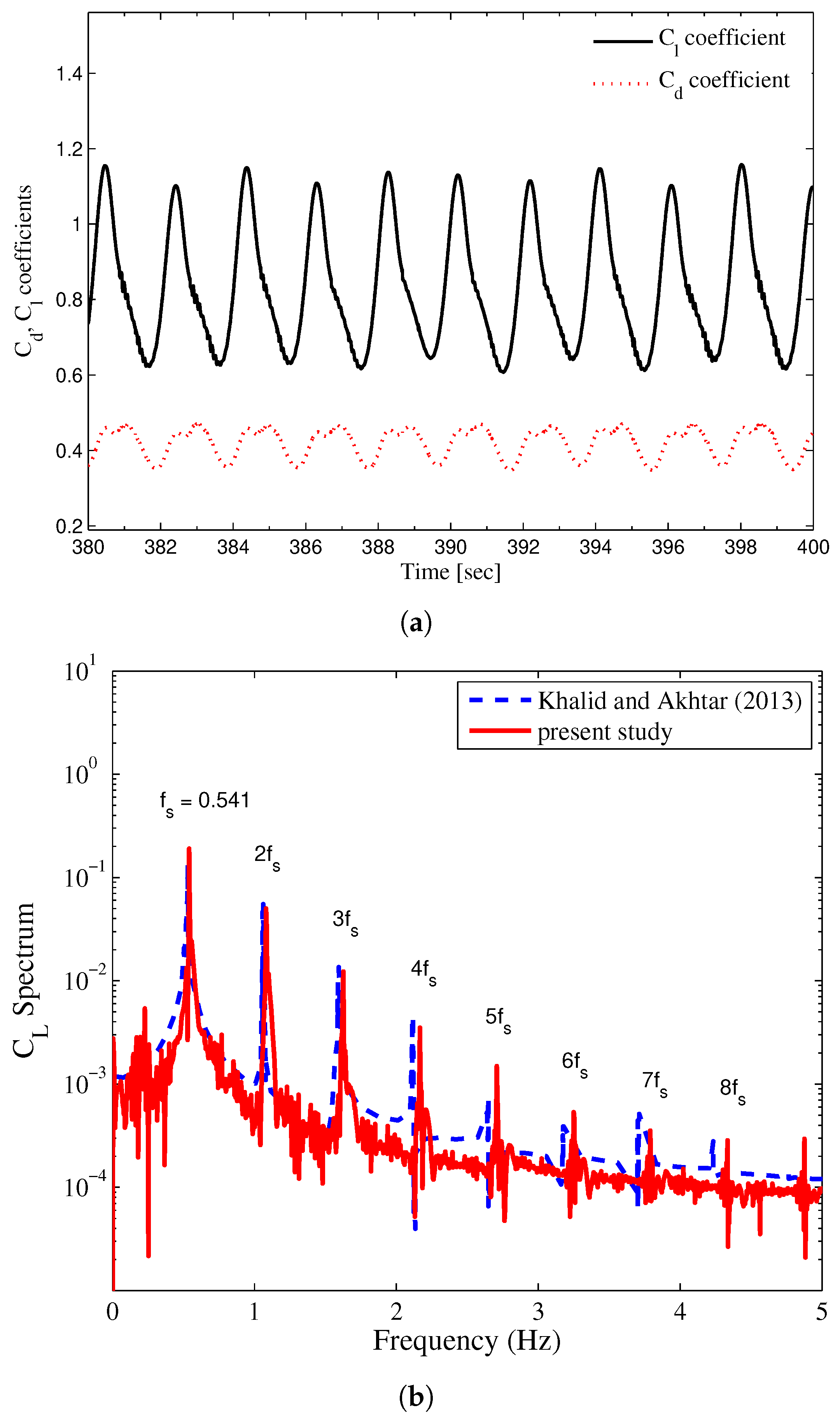
3.2. Validation of the Numerical Simulation
4. Parallel Implementation
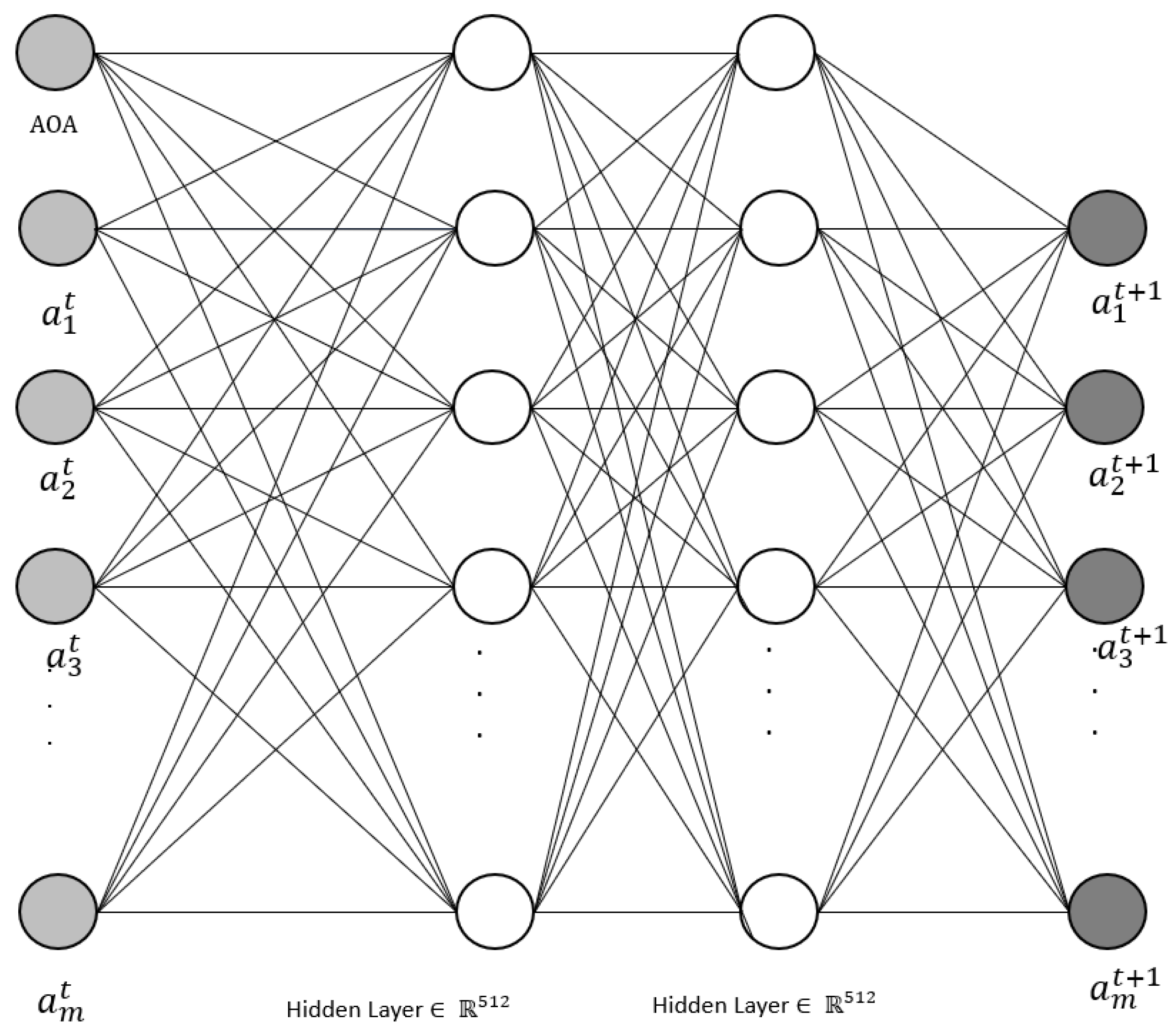
5. Artificial Neural Network
6. Proper Orthogonal Decomposition (POD)
7. Results & Discussion
7.1. Hydrodynamics Forces and Wake
7.2. PMD Analysis
7.3. Lift and Drag Models
7.4. ANN-Based ROM Using PMD
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gault, D.E. An Experimental Investigation of Regions of Separated Laminar Flow; Number 3505; National Advisory Committee for Aeronautics: Moffett Field, CA, USA, 1955. [Google Scholar]
- Tani, I. Low-speed flows involving bubble separations. Prog. Aerosp. Sci. 1964, 5, 70–103. [Google Scholar] [CrossRef]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The Proper Orthogonal Decomposition in the Analysis of Turbulent Flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Bakewell, H.P.; Lumley, J.L. Viscous Sublayer and Adjacent Wall Region in Turbulent Pipe Flow. Phys. Fluids 1967, 10, 1880–1889. [Google Scholar] [CrossRef]
- Mezić, I. Spectral Properties of Dynamical Systems, Model Reduction and Decompositions. Nonlinear Dyn. 2005, 41, 309–325. [Google Scholar] [CrossRef]
- Rowley, C.W.; Mezic, I.; Bagheri, S.; Schlatter, P.; Henningson, D.S. Spectral analysis of nonlinear flows. J. Fluid Mech. 2009, 641, 115–127. [Google Scholar] [CrossRef] [Green Version]
- Kutz, J.N.; Brunton, S.L.; Brunton, B.W.; Proctor, J.L. Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems; SIAM: Philadelphia, PA, USA, 2016. [Google Scholar]
- Hemati, M.; Deem, E.; Williams, M.; Rowley, C.W.; Cattafesta, L.N. Improving separation control with noise-robust variants of dynamic mode decomposition. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 1103. [Google Scholar]
- Dawson, S.T.; Hemati, M.S.; Williams, M.O.; Rowley, C.W. Characterizing and correcting for the effect of sensor noise in the dynamic mode decomposition. Exp. Fluids 2016, 57, 42. [Google Scholar] [CrossRef] [Green Version]
- Towne, A.; Schmidt, O.T.; Colonius, T. Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 2018, 847, 821–867. [Google Scholar] [CrossRef] [Green Version]
- Sieber, M.; Paschereit, C.O.; Oberleithner, K. Spectral proper orthogonal decomposition. J. Fluid Mech. 2016, 792, 798–828. [Google Scholar] [CrossRef] [Green Version]
- Agostini, L. Exploration and prediction of fluid dynamical systems using auto-encoder technology. Phys. Fluids 2020, 32, 67103. [Google Scholar] [CrossRef]
- Taira, K.; Brunton, S.L.; Dawson, S.T.; Rowley, C.W.; Colonius, T.; McKeon, B.J.; Schmidt, O.T.; Gordeyev, S.; Theofilis, V.; Ukeiley, L.S. Modal analysis of fluid flows: An overview. AIAA J. 2017, 55, 4013–4041. [Google Scholar] [CrossRef] [Green Version]
- Taira, K.; Hemati, M.S.; Brunton, S.L.; Sun, Y.; Duraisamy, K.; Bagheri, S.; Dawson, S.T.; Yeh, C.A. Modal analysis of fluid flows: Applications and outlook. AIAA J. 2020, 58, 998–1022. [Google Scholar] [CrossRef]
- Akhtar, I.; Nayfeh, A.H.; Ribbens, C.J. On the stability and extension of reduced-order Galerkin models in incompressible flows. Theor. Comput. Fluid Dyn. 2009, 23, 213–237. [Google Scholar] [CrossRef]
- Imtiaz, H.; Akhtar, I. Closure modeling of low dimensional models using LES analogy. In Proceedings of the 2014 11th International Bhurban Conference on Applied Sciences & Technology (IBCAST), Islamabad, Pakistan, 14–18 January 2014; pp. 243–250. [Google Scholar]
- Wang, Z.; Akhtar, I.; Borggaard, J.; Iliescu, T. Proper orthogonal decomposition closure models for turbulent flows: A numerical comparison. Comput. Methods Appl. Mech. Eng. 2012, 237, 10–26. [Google Scholar] [CrossRef] [Green Version]
- Imtiaz, H.; Akhtar, I. Closure modeling in reduced-order model of Burgers’ equation for control applications. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 231, 642–656. [Google Scholar] [CrossRef]
- Imtiaz, H.; Akhtar, I. Nonlinear closure modeling in reduced order models for turbulent flows: A dynamical system approach. Nonlinear Dyn. 2020, 99, 479–494. [Google Scholar] [CrossRef]
- Lucia, D.J.; Beran, P.S.; Silva, W.A. Reduced-order modeling: New approaches for computational physics. Prog. Aerosp. Sci. 2004, 40, 51–117. [Google Scholar] [CrossRef] [Green Version]
- Rowley, C.W.; Dawson, S.T. Model Reduction for Flow Analysis and Control. Annu. Rev. Fluid Mech. 2017, 49, 387–417. [Google Scholar] [CrossRef] [Green Version]
- Champion, K.; Lusch, B.; Kutz, J.N.; Brunton, S.L. Data-driven discovery of coordinates and governing equations. Proc. Natl. Acad. Sci. USA 2019, 116, 22445–22451. [Google Scholar] [CrossRef] [Green Version]
- Lusch, B.; Kutz, J.N.; Brunton, S.L. Deep learning for universal linear embeddings of nonlinear dynamics. Nat. Commun. 2018, 9, 1–10. [Google Scholar]
- Akhtar, I.; Marzouk, O.A.; Nayfeh, A.H. A van der Pol–Duffing oscillator model of hydrodynamic forces on canonical structures. J. Comput. Nonlinear Dyn. 2009, 4, 041006. [Google Scholar] [CrossRef]
- Hajj, M.R.; Mehmood, A.; Akhtar, I. Single-degree-of-freedom model of displacement in vortex-induced vibrations. Nonlinear Dyn. 2021, 103, 1305–1320. [Google Scholar] [CrossRef]
- Schlegel, M.; Noack, B.R. On long-term boundedness of Galerkin models. J. Fluid Mech. 2015, 765, 325–352. [Google Scholar] [CrossRef] [Green Version]
- Östh, J.; Noack, B.R.; Krajnović, S.; Barros, D.; Borée, J. On the need for a nonlinear subscale turbulence term in POD models as exemplified for a high-Reynolds-number flow over an Ahmed body. J. Fluid Mech. 2014, 747, 518–544. [Google Scholar] [CrossRef] [Green Version]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear model reduction via discrete empirical interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Sabetghadam, F.; Jafarpour, A. α regularization of the POD-Galerkin dynamical systems of the Kuramoto–Sivashinsky equation. Appl. Math. Comput. 2012, 218, 6012–6026. [Google Scholar] [CrossRef]
- Xiao, D.; Fang, F.; Buchan, A.G.; Pain, C.C.; Navon, I.M.; Du, J.; Hu, G. Non-linear model reduction for the Navier–Stokes equations using residual DEIM method. J. Comput. Phys. 2014, 263, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Wentland, C.R.; Duraisamy, K.; Merkle, C. Model reduction for multi-scale transport problems using structure-preserving least-squares projections with variable transformation. arXiv 2020, arXiv:2011.02072. [Google Scholar]
- Grimberg, S.; Farhat, C.; Youkilis, N. On the stability of projection-based model order reduction for convection-dominated laminar and turbulent flows. J. Comput. Phys. 2020, 419, 109681. [Google Scholar] [CrossRef]
- Lee, K.; Carlberg, K.T. Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders. J. Comput. Phys. 2020, 404, 108973. [Google Scholar] [CrossRef] [Green Version]
- Peherstorfer, B. Model reduction for transport-dominated problems via online adaptive bases and adaptive sampling. SIAM J. Sci. Comput. 2020, 42, A2803–A2836. [Google Scholar] [CrossRef]
- Xiao, D.; Fang, F.; Pain, C.; Hu, G. Non-intrusive reduced-order modelling of the Navier–Stokes equations based on RBF interpolation. Int. J. Numer. Methods Fluids 2015, 79, 580–595. [Google Scholar] [CrossRef]
- Bui-Thanh, T.; Damodaran, M.; Willcox, K. Aerodynamic data reconstruction and inverse design using proper orthogonal decomposition. AIAA J. 2004, 42, 1505–1516. [Google Scholar] [CrossRef] [Green Version]
- Audouze, C.; De Vuyst, F.; Nair, P. Reduced-order modeling of parameterized PDEs using time–space-parameter principal component analysis. Int. J. Numer. Methods Eng. 2009, 80, 1025–1057. [Google Scholar] [CrossRef]
- Ly, H.V.; Tran, H.T. Modeling and control of physical processes using proper orthogonal decomposition. Math. Comput. Model. 2001, 33, 223–236. [Google Scholar] [CrossRef] [Green Version]
- Swischuk, R.; Mainini, L.; Peherstorfer, B.; Willcox, K. Projection-based model reduction: Formulations for physics-based machine learning. Comput. Fluids 2019, 179, 704–717. [Google Scholar] [CrossRef]
- San, O.; Maulik, R. Neural network closures for nonlinear model order reduction. Adv. Comput. Math. 2018, 44, 1717–1750. [Google Scholar] [CrossRef] [Green Version]
- San, O.; Maulik, R.; Ahmed, M. An artificial neural network framework for reduced order modeling of transient flows. Commun. Nonlinear Sci. Numer. Simul. 2019, 77, 271–287. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Xiao, D.; Fang, F.; Govindan, R.; Pain, C.C.; Guo, Y. Model identification of reduced order fluid dynamics systems using deep learning. Int. J. Numer. Methods Fluids 2018, 86, 255–268. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, S.E.; San, O.; Rasheed, A.; Iliescu, T. A long short-term memory embedding for hybrid uplifted reduced order models. Phys. D Nonlinear Phenom. 2020, 409, 132471. [Google Scholar] [CrossRef] [Green Version]
- Murata, T.; Fukami, K.; Fukagata, K. Nonlinear mode decomposition with convolutional neural networks for fluid dynamics. J. Fluid Mech. 2020, 882. [Google Scholar] [CrossRef] [Green Version]
- Fukami, K.; Fukagata, K.; Taira, K. Super-resolution reconstruction of turbulent flows with machine learning. J. Fluid Mech. 2019, 870, 106–120. [Google Scholar] [CrossRef] [Green Version]
- Fukami, K.; Fukagata, K.; Taira, K. Machine-learning-based spatio-temporal super resolution reconstruction of turbulent flows. J. Fluid Mech. 2021, 909. [Google Scholar] [CrossRef]
- Hasegawa, K.; Fukami, K.; Murata, T.; Fukagata, K. CNN-LSTM based reduced order modeling of two-dimensional unsteady flows around a circular cylinder at different Reynolds numbers. Fluid Dyn. Res. 2020, 52, 065501. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Karniadakis, G.E. Hidden physics models: Machine learning of nonlinear partial differential equations. J. Comput. Phys. 2018, 357, 125–141. [Google Scholar] [CrossRef] [Green Version]
- San, O.; Iliescu, T. Proper orthogonal decomposition closure models for fluid flows: Burgers equation. arXiv 2013, arXiv:1308.3276. [Google Scholar]
- Noack, B.R.; Papas, P.; Monkewitz, P.A. The need for a pressure-term representation in empirical Galerkin models of incompressible shear flows. J. Fluid Mech. 2005, 523, 339. [Google Scholar] [CrossRef] [Green Version]
- Imtiaz, H.; Akhtar, I. On lift and drag decomposition coefficients in a model reduction framework using pressure-mode decomposition (PMD) analysis. J. Fluids Struct. 2017, 75, 174–192. [Google Scholar] [CrossRef]
- Platzer, M.F.; Jones, K.D.; Young, J.; Lai, J.C. Flapping wing aerodynamics: Progress and challenges. AIAA J. 2008, 46, 2136–2149. [Google Scholar] [CrossRef]
- Ryskin, G.; Leal, L. Orthogonal mapping. J. Comput. Phys. 1983, 50, 71–100. [Google Scholar] [CrossRef]
- Leonard, B.P. A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Methods Appl. Mech. Eng. 1979, 19, 59–98. [Google Scholar] [CrossRef]
- Zang, Y. On the Development of Tools for the Simulation of Geophysical Flows. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1994. [Google Scholar]
- Thompson, J.F.; Thames, F.C.; Mastin, C.W. Automatic numerical generation of body-fitted curvilinear coordinate system for field containing any number of arbitrary two-dimensional bodies. J. Comput. Phys. 1974, 15, 299–319. [Google Scholar] [CrossRef]
- Arina, R. Orthogonal grids with adaptive control. Numer. Grid Gener. Comput. Fluid Dyn. 1986, 113–124. Available online: https://iris.polito.it/handle/11583/1416918?mode=simple.6163#.YTBUud8RWUl (accessed on 5 April 2021).
- Albert, M.R. Orthogonal curvilinear coordinate generation for internal flows. Numer. Grid Gener. Comput. Fluid Mech. 1988, 88, 425–433. [Google Scholar]
- Eça, L. 2D orthogonal grid generation with boundary point distribution control. J. Comput. Phys. 1996, 125, 440–453. [Google Scholar] [CrossRef]
- Hong, H.; Jian-ren, F.; Ke-fa, C. A numerical method for orthogonal grid generation by Laplace system. J. Zhejiang Univ. Sci. A 2000, 1, 125–128. [Google Scholar]
- Liu, Y.; Bai, K.; Wang, X.; Liu, M.Q. Two-Dimensional Orthogonal Grid Generation. In Advanced Materials Research; Trans Tech Publications Ltd.: Freienbach, Switzerland, 2012; Volume 468, pp. 2668–2671. [Google Scholar]
- Ohmi, K.; Coutanceau, M.; Loc, T.P.; Dulieu, A. Vortex formation around an oscillating and translating airfoil at large incidences. J. Fluid Mech. 1990, 211, 37–60. [Google Scholar] [CrossRef]
- Kurtulus, D.F. On the unsteady behavior of the flow around NACA 0012 airfoil with steady external conditions at Re = 1000. Int. J. Micro Air Veh. 2015, 7, 301–326. [Google Scholar] [CrossRef]
- Liu, Y.; Li, K.; Zhang, J.; Wang, H.; Liu, L. Numerical bifurcation analysis of static stall of airfoil and dynamic stall under unsteady perturbation. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3427–3434. [Google Scholar] [CrossRef]
- Khalid, M.; Akhtar, I. Characteristics of flow past a symmetric airfoil at low Reynolds number: A nonlinear perspective. In Proceedings of the ASME 2012 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; pp. 167–175. [Google Scholar]
- Suzuki, T.; Ji, H.; Yamamoto, F. Unsteady PTV velocity field past an airfoil solved with DNS: Part 1. Algorithm of hybrid simulation and hybrid velocity field at Re = 1000. Exp. Fluids 2009, 47, 957. [Google Scholar] [CrossRef]
- HOARAU, Y.; BRAZA, M.; Ventikos, Y.; Faghani, D.; Tzabiras, G. Organized modes and the three-dimensional transition to turbulence in the incompressible flow around a NACA0012 wing. J. Fluid Mech. 2003, 496, 63–72. [Google Scholar] [CrossRef] [Green Version]
- Mittal, S.; Tezduyar, T.E. Massively parallel finite element computation of incompressible flows involving fluid-body interactions. Comput. Methods Appl. Mech. Eng. 1994, 112, 253–282. [Google Scholar] [CrossRef]
- Akhtar, I. Parallel Simulations, Reduced-Order Modeling, and Feedback Control of Vortex Shedding Using Fluidic Actuators. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2008. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: tensorflow.org (accessed on 5 April 2021).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Jin, H.; Song, Q.; Hu, X. Auto-Keras: An Efficient Neural Architecture Search System. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1946–1956. [Google Scholar]
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Sirovich, L. Chaotic dynamics of coherent structures. Phys. D Nonlinear Phenom. 1989, 37, 126–145. [Google Scholar] [CrossRef]
- Sirovich, L.; Kirby, M. Low-dimensional procedure for the characterization of human faces. JOSA A 1987, 4, 519–524. [Google Scholar] [CrossRef]



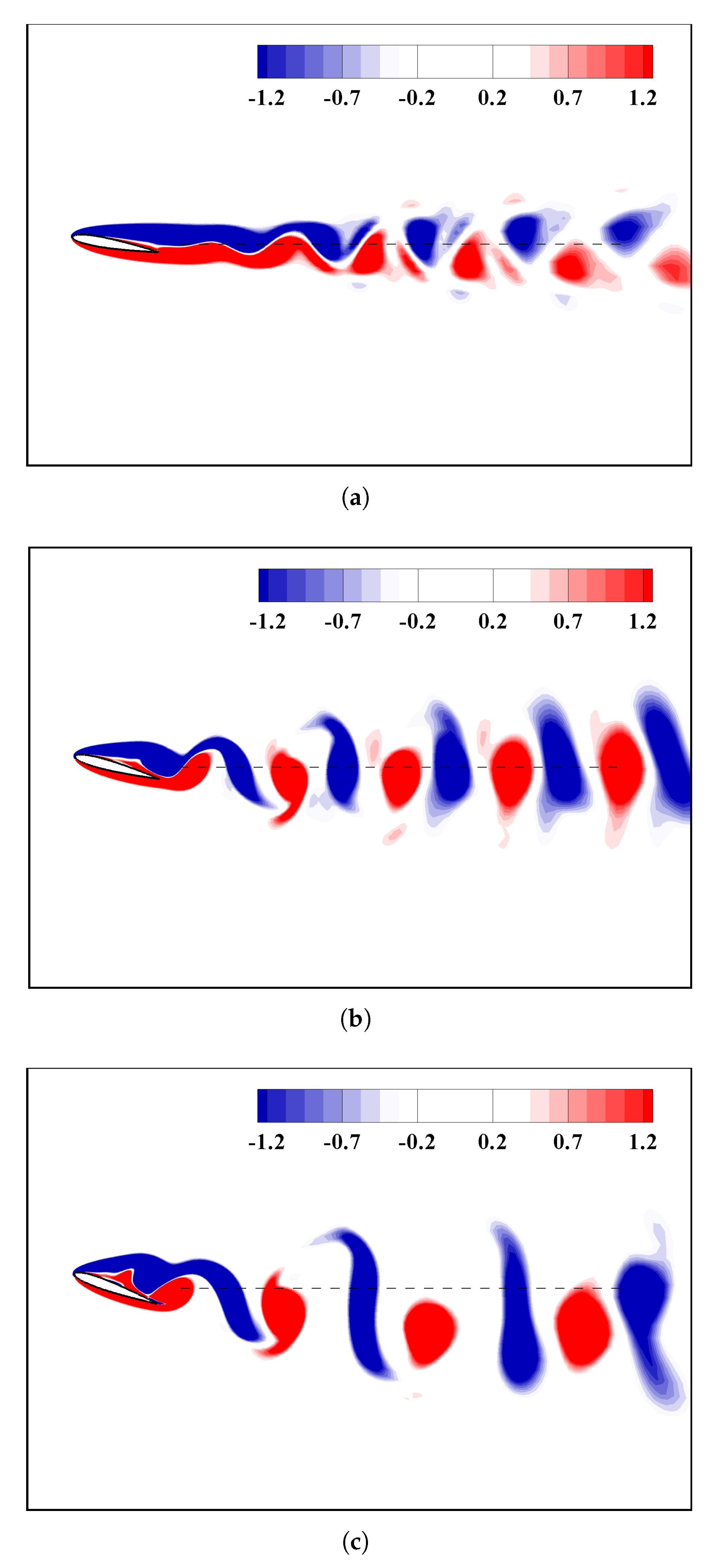

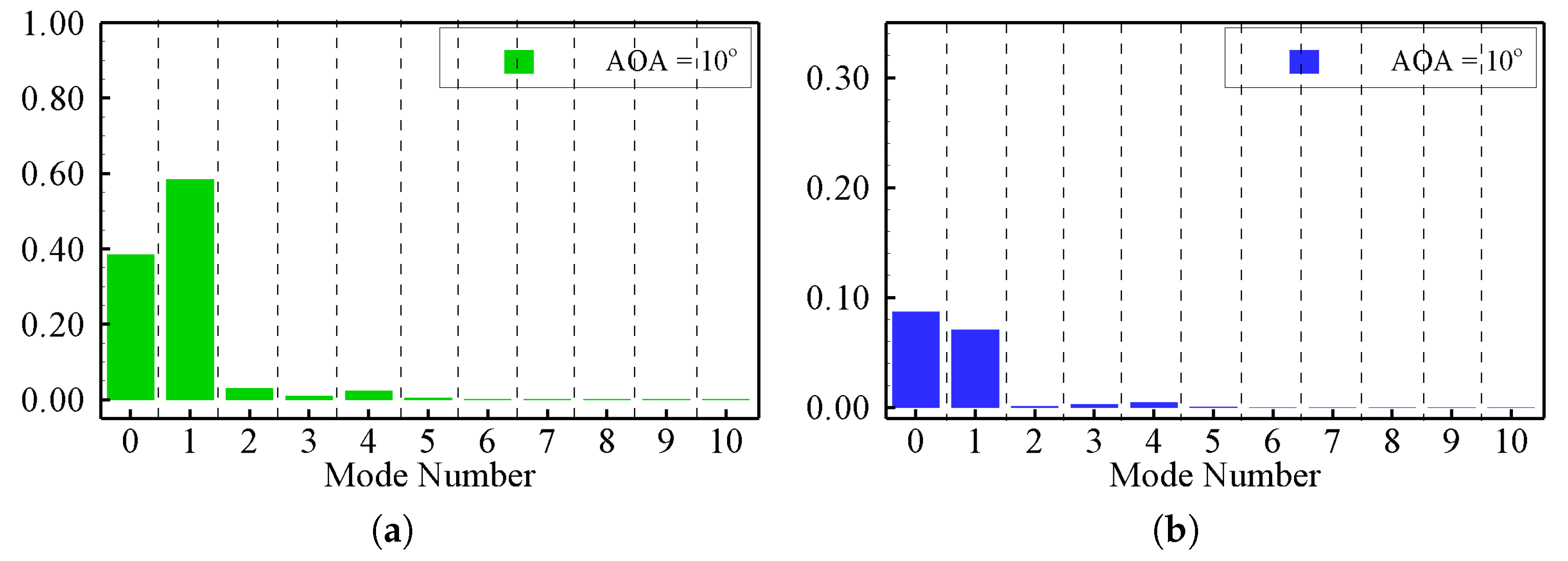
 ), along with dissection into (
), along with dissection into (  ) and (
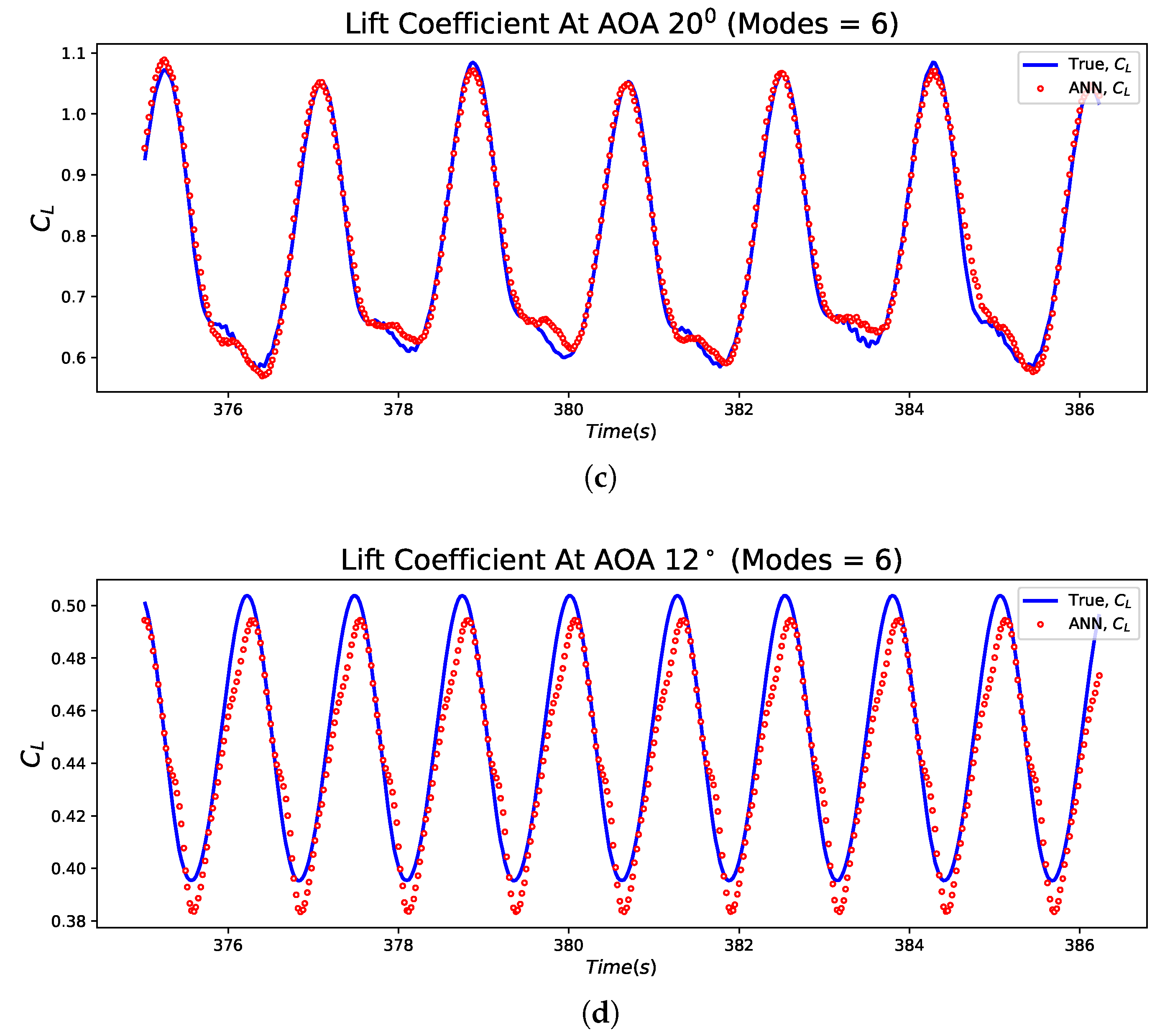
) and (  ): AOA = 10°, 15°, and 20°, top to bottom.
): AOA = 10°, 15°, and 20°, top to bottom.
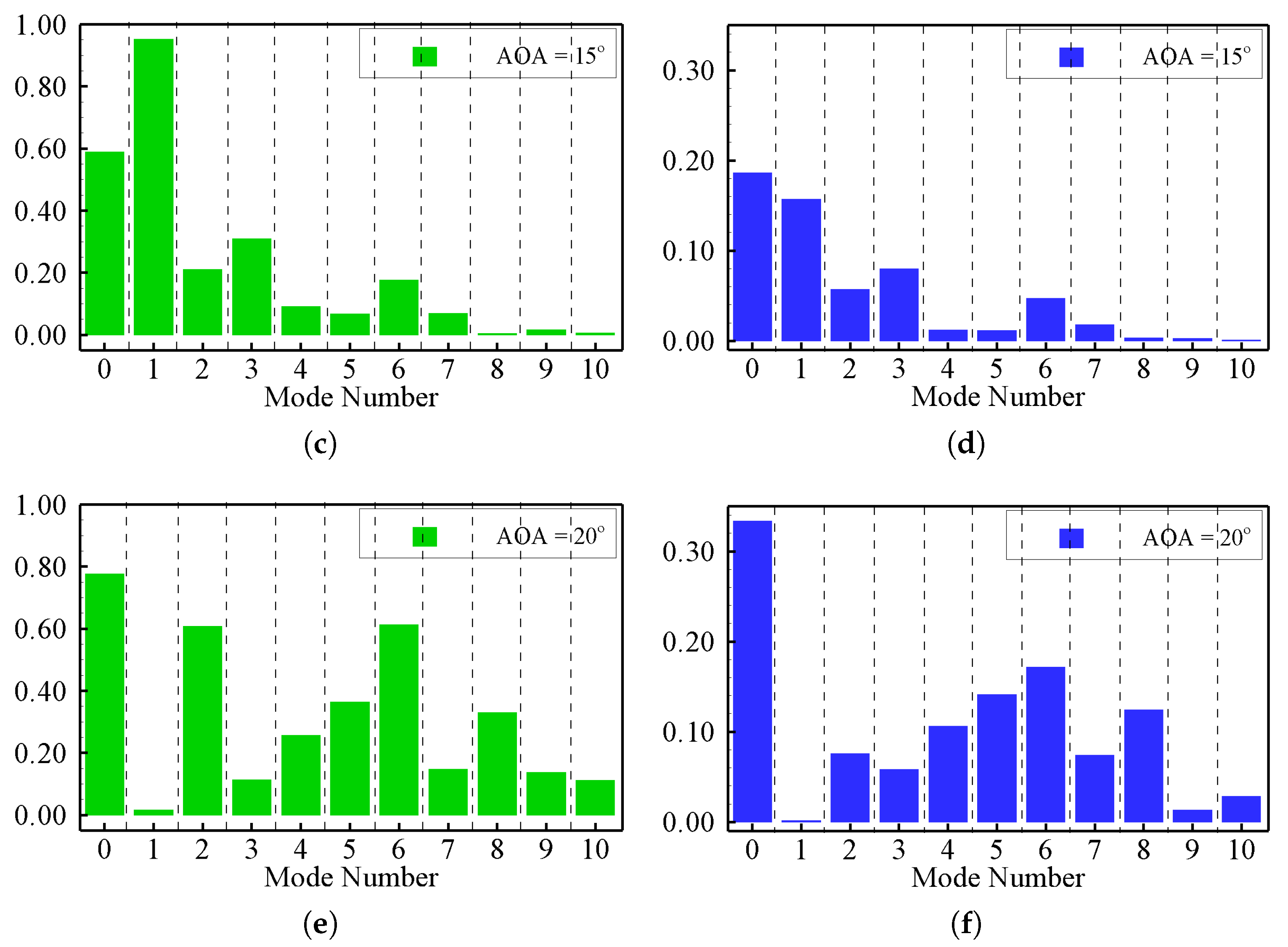
 ), along with dissection into (
), along with dissection into (  ) and (
) and (  ): AOA = 10°, 15°, and 20°, top to bottom.
): AOA = 10°, 15°, and 20°, top to bottom.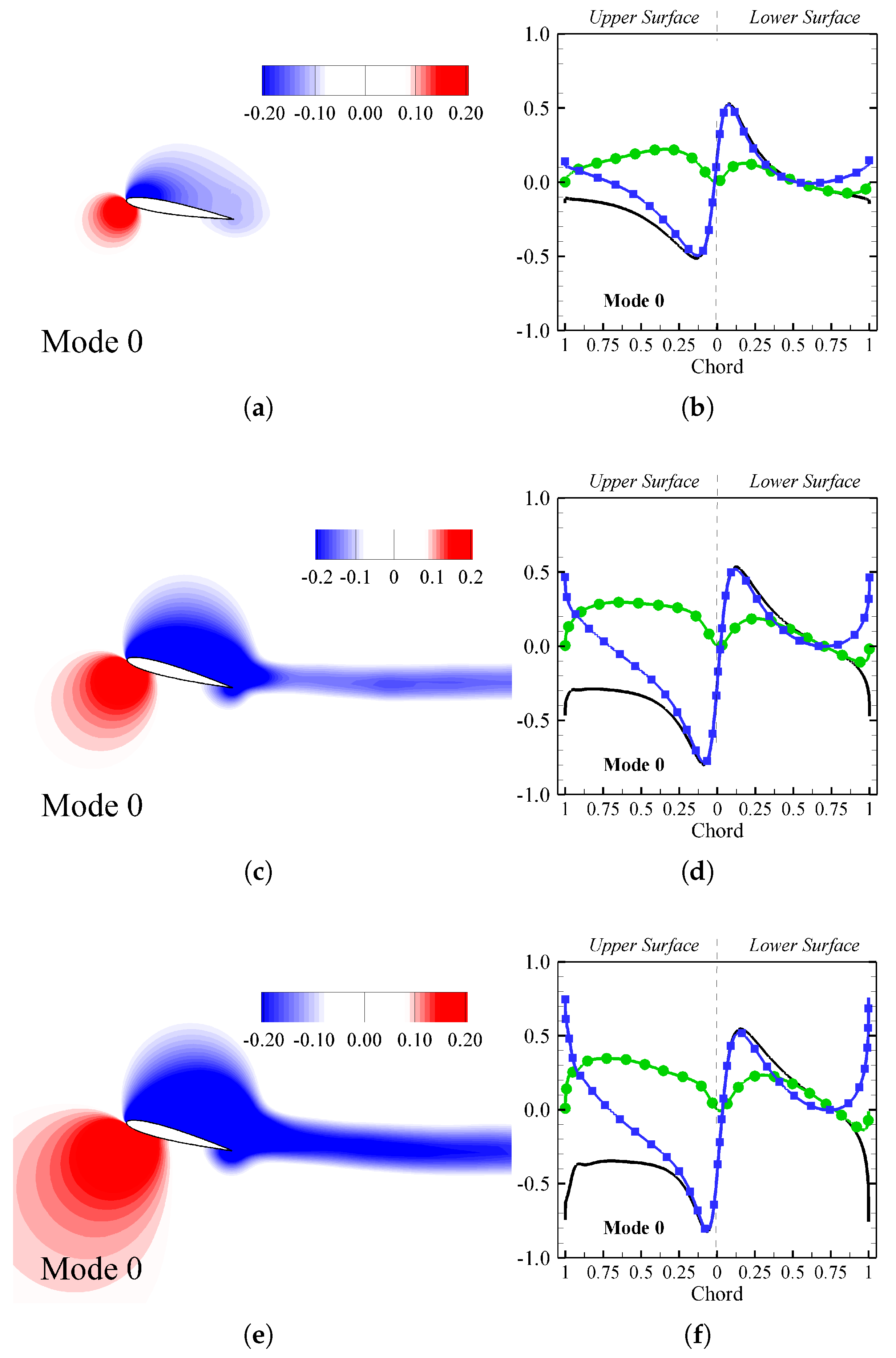
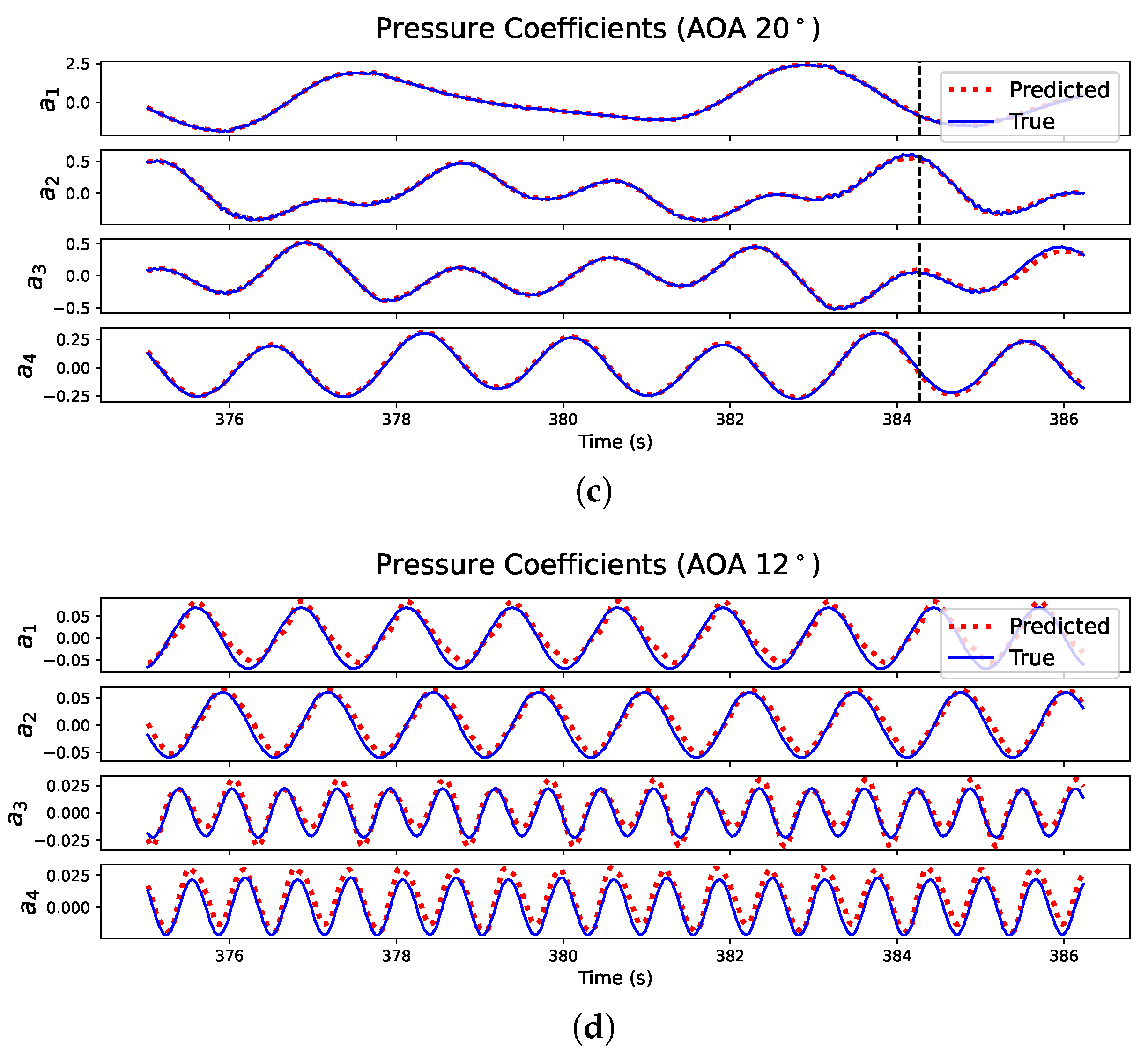
 ), along with dissection into (
), along with dissection into (  ) and (
) and (  ): (
): (  AOA = 10°), (
AOA = 10°), (  AOA = 15°), and (
AOA = 15°), and (  AOA = 20°).
AOA = 20°).
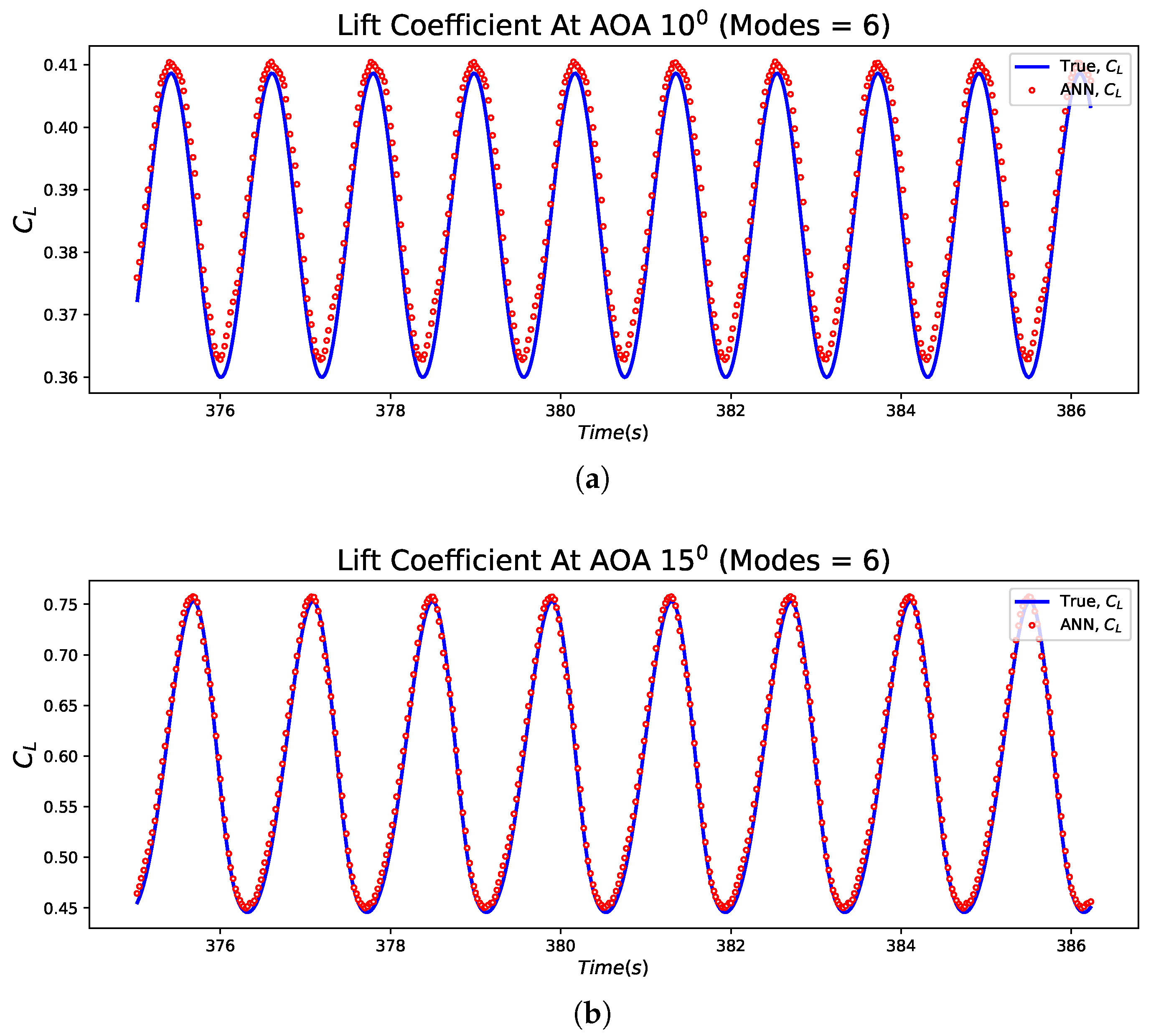
 ), along with dissection into (
), along with dissection into (  ) and (
) and (  ): (
): (  AOA = 10°), (
AOA = 10°), (  AOA = 15°), and (
AOA = 15°), and (  AOA = 20°).
AOA = 20°).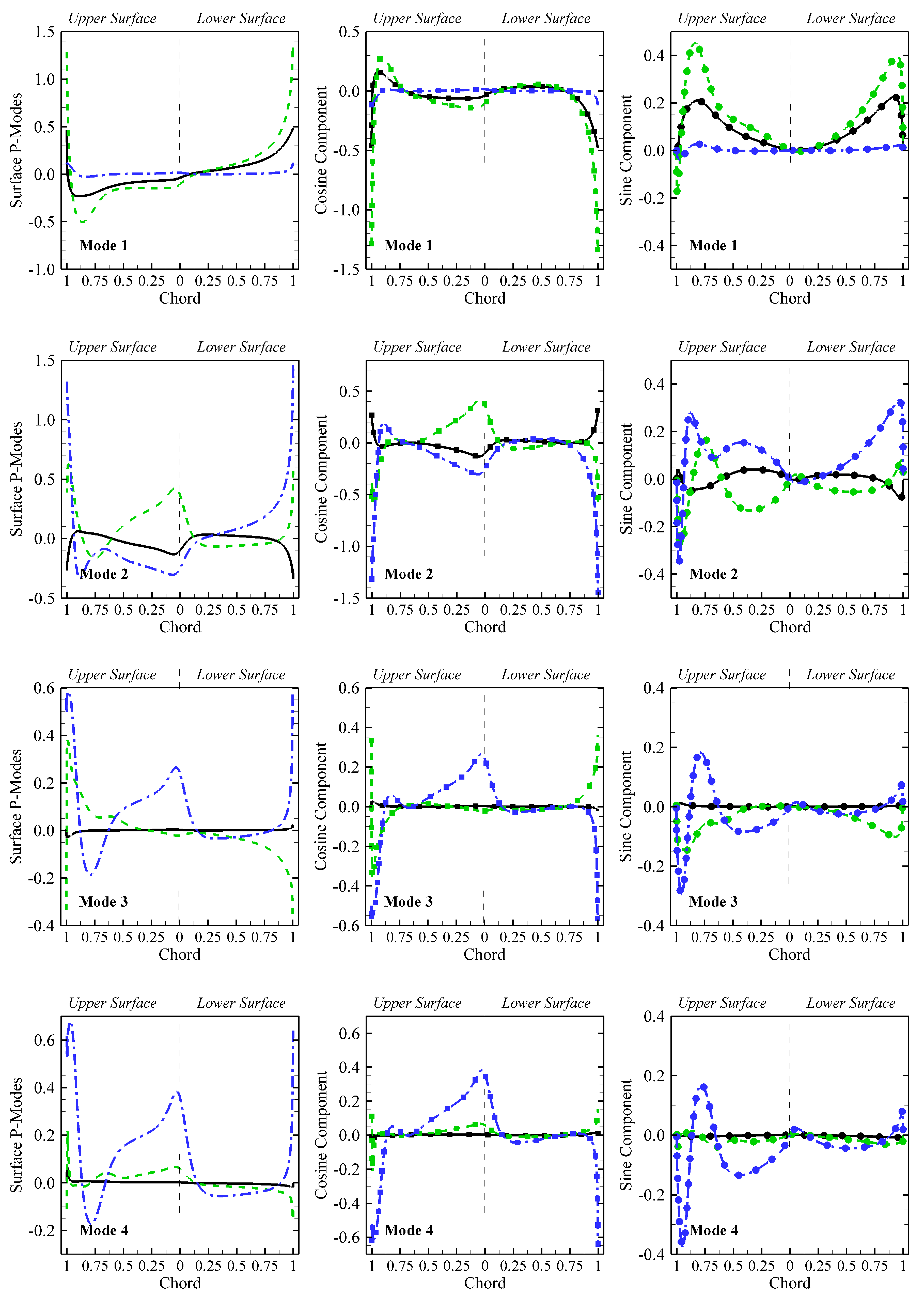

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farooq, H.; Saeed, A.; Akhtar, I.; Bangash, Z. Neural Network-Based Model Reduction of Hydrodynamics Forces on an Airfoil. Fluids 2021, 6, 332. https://doi.org/10.3390/fluids6090332
Farooq H, Saeed A, Akhtar I, Bangash Z. Neural Network-Based Model Reduction of Hydrodynamics Forces on an Airfoil. Fluids. 2021; 6(9):332. https://doi.org/10.3390/fluids6090332
Chicago/Turabian StyleFarooq, Hamayun, Ahmad Saeed, Imran Akhtar, and Zafar Bangash. 2021. "Neural Network-Based Model Reduction of Hydrodynamics Forces on an Airfoil" Fluids 6, no. 9: 332. https://doi.org/10.3390/fluids6090332
APA StyleFarooq, H., Saeed, A., Akhtar, I., & Bangash, Z. (2021). Neural Network-Based Model Reduction of Hydrodynamics Forces on an Airfoil. Fluids, 6(9), 332. https://doi.org/10.3390/fluids6090332





