Stable Schooling Formations Emerge from the Combined Effect of the Active Control and Passive Self-Organization

Abstract

This work presents a numerical study of the collective motion of two freely-swimming swimmers by a hybrid method of the deep reinforcement learning method (DRL) and the immersed boundary-lattice Boltzmann method (IB-LBM). An active control policy is developed by training a fish-like swimmer to swim at an average speed of 0.4 $L/T$ and an average orientation angle of 0${}^{\circ }$. After training, the swimmer is able to restore the desired swimming speed and orientation from moderate external perturbation. Then the control policy is adopted by two identical swimmers in the collective swimming. Stable side-by-side, in-line and staggered formations are achieved according to the initial positions. The stable side-by-side swimming area of the follower is concentrated to a small area left or right to the leader with an average distance of 1.35 L. The stable in-line area is concentrated to a small area about 0.25 L behind the leader. A detailed analysis shows that both the active control and passive self-organization play an important role in the emergence of the stable schooling formations, while the active control works for maintaining the speed and orientation in case the swimmers collide or depart from each other and the passive self-organization works for emerging a stable schooling configuration. The result supports the Lighthill conjecture and also highlights the importance of the active control.

1. Introduction

Collective motion, or schooling, is ubiquitous in fish swimming for reasons such as reproduction [1], avoidance of predators [2], and search for prey [3,4]. Apart from the social relations, the roles of hydrodynamics in schooling have long been the interest of many researchers [5,6,7,8,9,10,11].

As the simplest model of schooling, the collective motion of two fishes has been extensively studied in experiments and numerical simulations. Different hypotheses exist on how hydrodynamics influence the formation of schooling. One important hypothesis is the so-called Lighthill conjecture [6], which conjectures that the interaction forces between the fish and the water push and pull the swimmers into a specific stable formation, such as the atoms in a crystal lattice. To test this hypothesis, a variety of research has been devoted to the emergence of collective locomotion of a two-body self-propelled system. Ramananarivo et al. [12] experimentally studied two synchronized flapping wings in in-line swimming in rotational orbits. The up-and-down flapping motion is prescribed, but the motion in the direction transverse to the flapping is a result of the wing-fluid interaction. Multiple stable arrangements can emerge from the flow-mediated coupling alone and the forward speed of the in-line wings is faster than a single wing. Zhu et al. [13], Dai et al. [14], Park and Sung [15] numerically investigated the self-propelled swimming of foil pairs in different initial arrangements. Several stable configurations are spontaneously formed and self-sustained purely by the fluid-body interactions, including in-line, side-by-side, and staggered formations. The propulsive velocity of the school is also enhanced. In order to maintain specific configurations and avoid the utilization of active control, the swimmers in the above studies are not allowed to yaw or move laterally. Therefore, those studies only probed the 1-DoF (degree of freedom) stability of the arrangements. Recently, Kurt et al. [16] measured the 2-DoF stability of schooling arrangements and found that many of the 1-DoF stable formations are unstable once the lateral movement is allowed. In fact, only the side-by-side arrangement is stable in 2-DoF cases. In addition, Novati et al. [17] and Bergmann and Iollo [18] studied the 3-DoF swimming of self-propelled swimmers arranged in different configurations and found that the swimmers would end up in collision or divergence if they were allowed to yaw.

The above studies mainly focus on the emergence of a 1-DoF or 2-DoF collective motion in a self-propelled system, but the 3-DoF stability of two free swimmers is not yet studied. We note that this is due to the difficulties of maintaining fixed 3-DoF formations in the absence of active control. The main purpose of this work is to numerically realize the stable 3-DoF schooling by introducing active control and reveal the hydrodynamic mechanism underlying the emergence of the schooling formation. Specifically, the deep reinforcement learning (DRL) method is adopted to develop the control strategy. This method is adopted by a variety of works to study the free swimming problems, including path following [19,20], collective motion [17,21,22], point-to-point navigation [23,24,25,26,27,28,29], rheotaxis and position holding in a Kármán vortex street [30]. Effective navigating strategies are developed from the learning. In this work, a control policy is developed by training a fish to swim in a specific speed and orientation with DRL. After training, the fish can restore the desired swimming speed and orientation from moderate external perturbation. Then the control policy is adopted by two identical swimmers in collective swimming. The core idea is that the swimmers tend to maintain a given formation if they always try to maintain the same swimming speed and orientation, thus the adjustment of the formation is due to passive self-organization.

This research advances our understanding of the Lighthill conjecture in the emergence of schooling formation. For the first time, we achieve different stable 3-DoF schooling by introducing appropriate active control in the numerical simulation. We discover that stable side-by-side and in-line configurations arise in the 3-DoF free swimming of fish pairs. Moreover, we reveal that both active control and passive self-organization play an important role in the emergence of stable schooling formations.

The rest of the paper is organized as follows. Numerical models, IB–LBM and multi-agent DRL are simply introduced in Section 2. The results of the simulation are discussed in Section 3. The conclusions are provided in Section 4.

2. Methodology

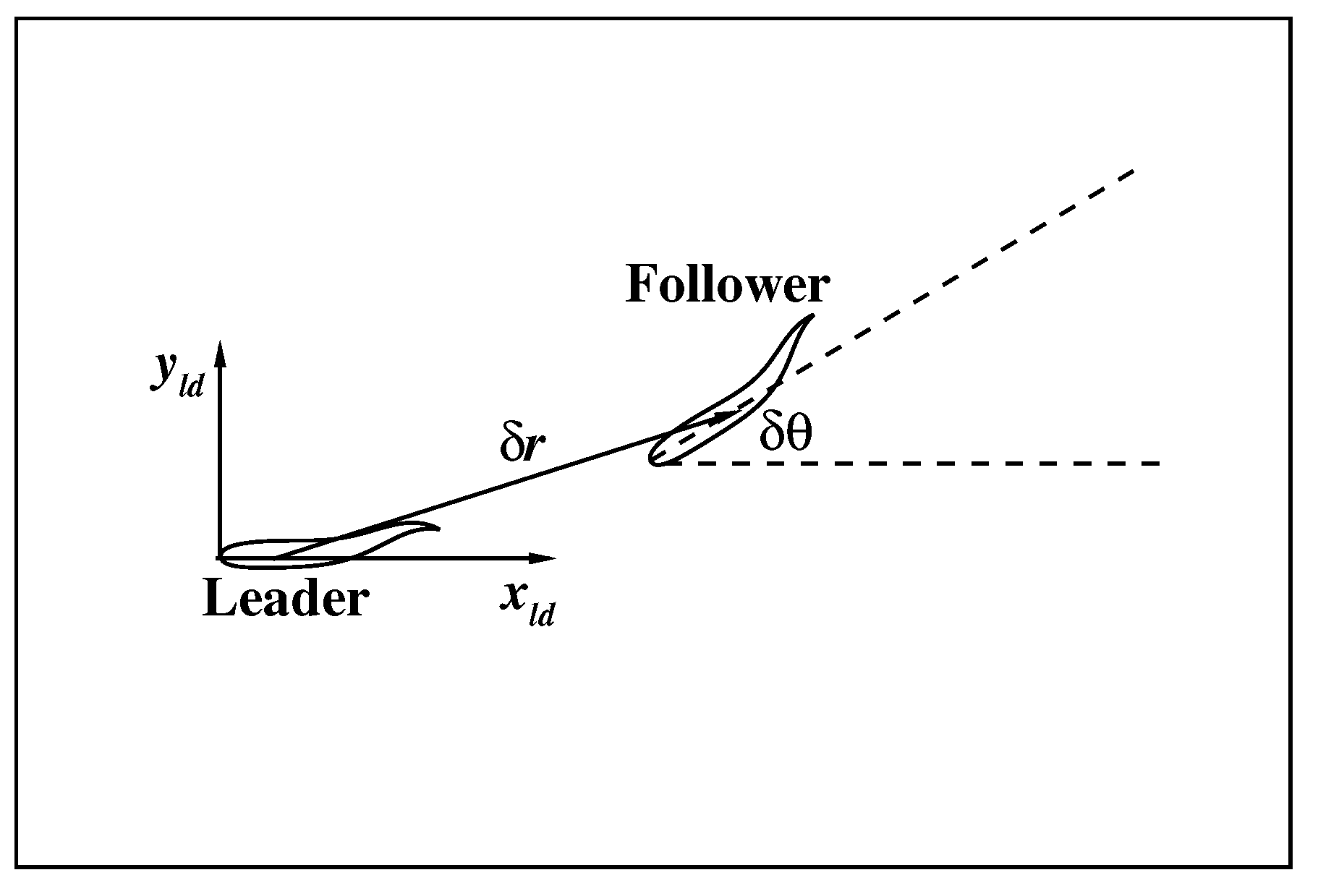
2.1. Kinematic Model of the Fish

Here, it is assumed the shapes of the fishes in schooling are identical, which are the same as in Reference [30]. The half-thickness of the body is mathematically approximated by

$$\frac{d}{L}=0.2610\sqrt{\frac{l}{L}}-0.3112\left(\frac{l}{L}\right)+0.1371{\left(\frac{l}{L}\right)}^2-0.0791{\left(\frac{l}{L}\right)}^3-0.0078{\left(\frac{l}{L}\right)}^4,$$

(1)

where l is the arc length along the mid-line of the body, and L is the body length, which is a constant during swimming [31].

The motion of the fish body includes three parts: the body undulation in the local coordinate system (represented by the mid-line lateral displacement $h_l$ in $x_l$–$y_l$ system), the translation of the mass center ($\mathit{r}$), and the body rotation around the mass center (represented by the orientation angle $\theta$). The undulatory motion can be taken as the superposition of different waves propagating from head to tail. Usually the waveform is sinusoidal-based, the draw of which is that the undulating parameters cannot be smoothly changed online. Therefore, a polynomial-based undulation is adopted to allow smooth change of the waveform. In order to implement the DRL in an easy way as explained later, the kinematics of the newest generated waves can be changed every half cycle. In the n-th half cycle, the mid-line lateral displacement is determined by

$$\begin{array}{ccc}& & h_l(l,t)={\int }_0^{l}sin\left({\theta }_l\right)dl,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}& & {\theta }_l(l,t)=\frac{l}{L}h\left[\frac{{\lambda }_n}{T_n}(t-t_{0n})-\frac{l}{L}\right],\hfill \end{array}$$

(3)

where ${\theta }_l$ is the deflection angle of the mid-line with respect to axis $x_l$, as shown in Figure 1, ${\lambda }_n$ is the wavelength, $T_n$ is the period, t is the time, $t_{0n}=0$ for $n=1$ and ${\sum }_1^{n-1}{T}_n$ for $n>1$, and h is the waveform function described by

$$h\left(\zeta \right)=c_0+c_1\zeta +c_2{\zeta }^2+c_3{\zeta }^3+c_4{\zeta }^4+c_5{\zeta }^5,$$

(4)

where $c_{0–5}$ can be determined by $h\left(0\right)={\left({\theta }_{lmax}\right)}_{n-1}$, $h({\lambda }_n/2)={\left({\theta }_{lmax}\right)}_n$, $h^{\prime }\left(0\right)=h^{\prime }({\lambda }_n/2)=0$, $h^{″}\left(0\right)=-h\left(0\right){(2\pi /{\lambda }_{n-1})}^2$, and $h^{″}({\lambda }_n/2)=-h({\lambda }_n/2){(2\pi /{\lambda }_n)}^2$. ${\left({\theta }_{lmax}\right)}_n$ is the maximum deflection angle at the tail tip of the n-th half wave.

Figure 1. A schematic illustration of the motion of the fish.

The translational and rotational motion of the fish is determined by the FSI in the global coordinate system according to Newton’s laws of motion. The FSI equations are solved by an explicit FSI coupling method as in References [30,32].

2.2. Immersed Boundary-Lattice Boltzmann Method

The lattice Boltzmann method (LBM) is a numerical method used to simulate the fluid dynamics. Instead of solving the Navier–Stokes equations, the LBM solves the discrete lattice Boltzmann equation, which governs the kinematics of the mesoscopic particles,

$$f_i(\mathit{r}+{\mathit{c}}_i\Delta t,t+\Delta t)-f_i(\mathit{r},t)={\Omega }_i(\mathit{r},t)+\Delta t{G}_i(\mathit{r},t),i=0,\dots ,8$$

(5)

where f is the particle density distribution function, $\mathit{r}=(x,y)$ is the space coordinate, ${\mathit{c}}_i$ is the discrete lattice velocity, $\Delta t$ is the time step, ${\Omega }_i$ is the collision operator, and $G_i$ is the source term representing the body force. A detailed description of this equation can be found in Reference [33]. f in the whole flow field can be acquired from a well-defined boundary condition, such as the no-slip velocity condition on the boundary of the swimmer model. Once f is known, the macroscopic physical quantity such as fluid density, pressure and velocity can be computed from

$$\rho =\sum f_i,p=\rho c_s^2,\mathit{u}=\frac{1}{\rho }\left(\sum f_i{\mathit{c}}_i+\frac{\Delta t\mathit{g}}{2}\right),$$

(6)

where $c_s$ is the lattice speed of sound in the fluid, and $\mathit{g}$ is the body force. Then the force and torque on the swimmer model can be computed from those macroscopic physical quantities. In addition, a diffusion immersed boundary method (IBM) [34,35,36] is utilized to handle the boundary condition at the fluid-structure interface. In this method, the influence of the boundary on the fluid is represented by a distribution of body force on the background Eulerian mesh nodes. Compared to body conformal methods [37,38,39], the grid generation in IBM is much easier for complicated shapes [35,40,41]. A multi-block geometry-adaptive Cartesian mesh (Figure 2) is coupled with the IB–LBM to accelerate the computation. A detailed description of this numerical scheme and its validation can be found in References [30,34,42,43,44,45].

Figure 2. Near-boundary grid structure of a fish-like body.

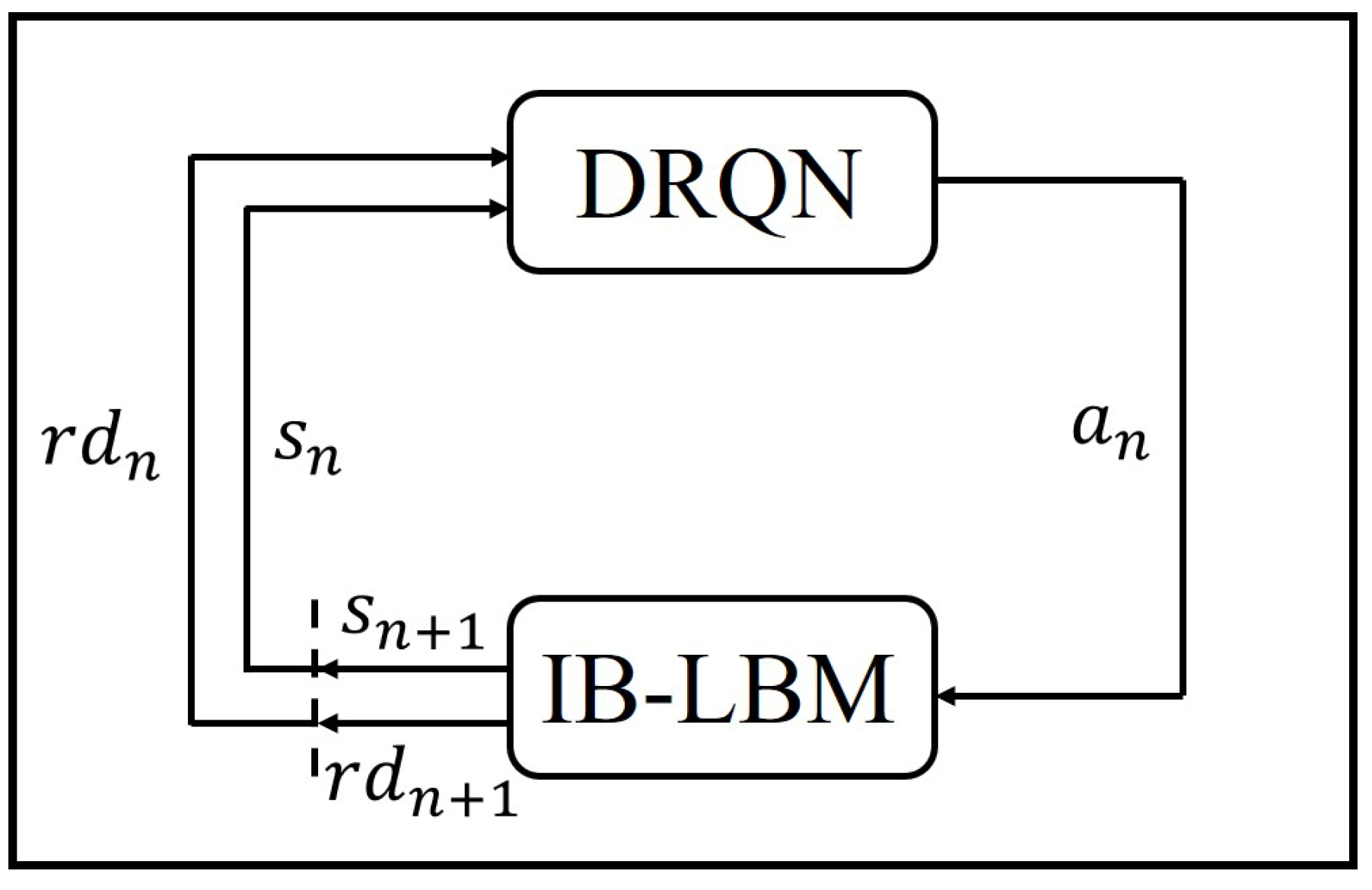
2.3. Deep Reinforcement Learning

DRL is a machine learning method combining reinforcement learning with an artificial neural network. DRL has gained extensive attention due to its success in complex real-world problems [46]. In this study, a specific DRL method called deep recurrent Q-network (DRQN) [47] is adopted, in which a long-short-term-memory recurrent neural network (LSTM-RNN) is used to process time-sequential data. In this method, a smart agent learns to achieve a specific goal by interacting with its environment [23]. The agent can sense the state of the environment (denoted by s) and take actions (denoted by a) to affect it. In addition, the agent will receive a reward (denoted by $rd$) for each action indicating how good the action is. The core idea is that the agent tries different actions in different states and finds a policy (denoted by $\pi (s,a)$, describing the probability of selecting each action in the different states) that maximizes the long-term reward.

The interaction procedure between the environment (IB-LBM) and the agent (DRL) is shown in Figure 3. The interaction is divided into a sequence of discrete steps $n=0,1,2,3,\cdots$. At steps n, the agents detect state $s_n$, and select action $a_n$, based on policy $\pi (s,a)$. Then the environment is changed under the influence of the action. At step $n+1$, in response to the change of the environment, the agent receives reward $r{d}_{n+1}$, and finds itself in a new state $s_{n+1}$. A detailed explanation of the procedure can be found in References [30,48]. Validations of the current solver can be found in Reference [30] for the hybrid method of DRL and IB-LBM.

Figure 3. The interaction procedure between IB-LBM and DRL.

3. Results and Discussion

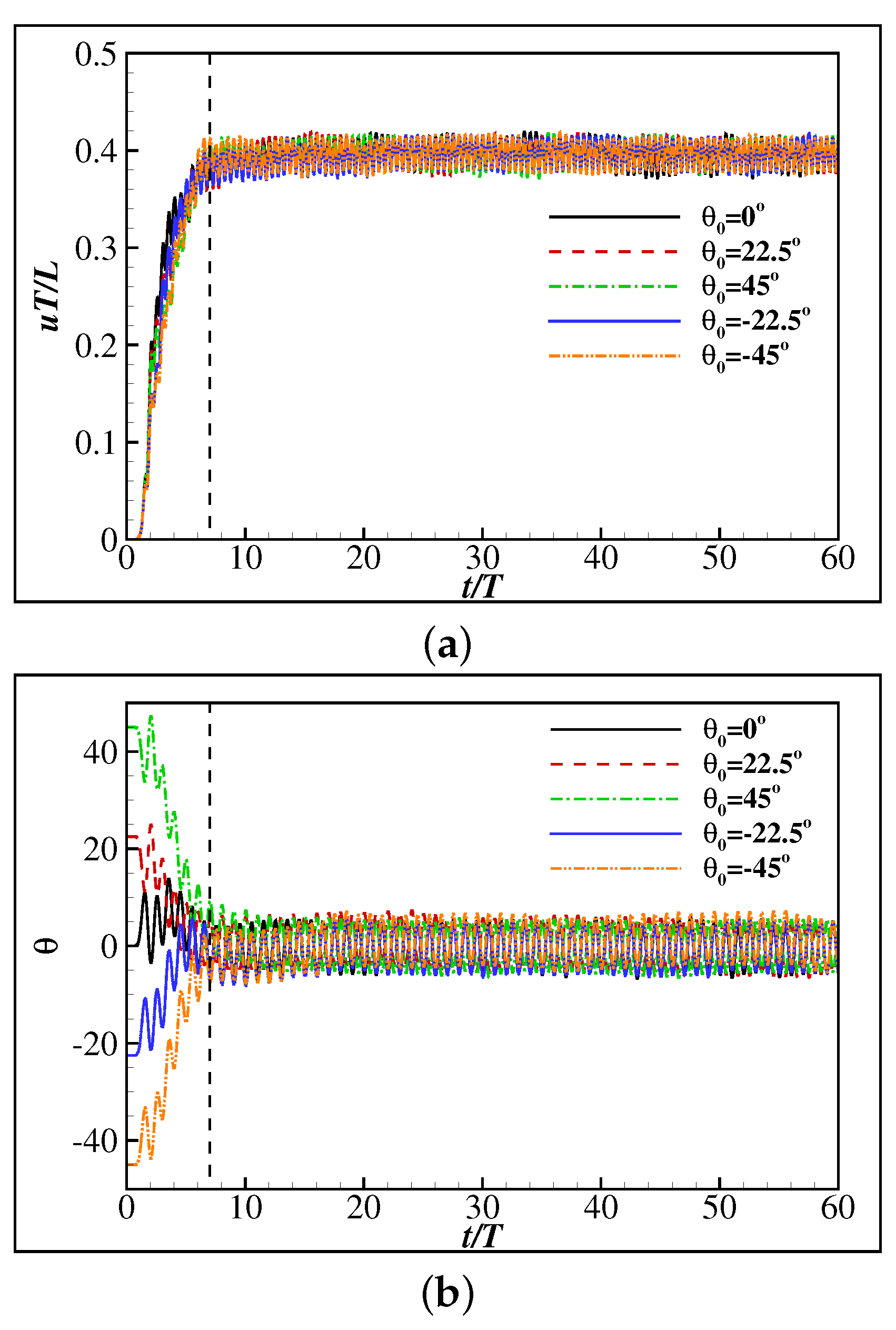
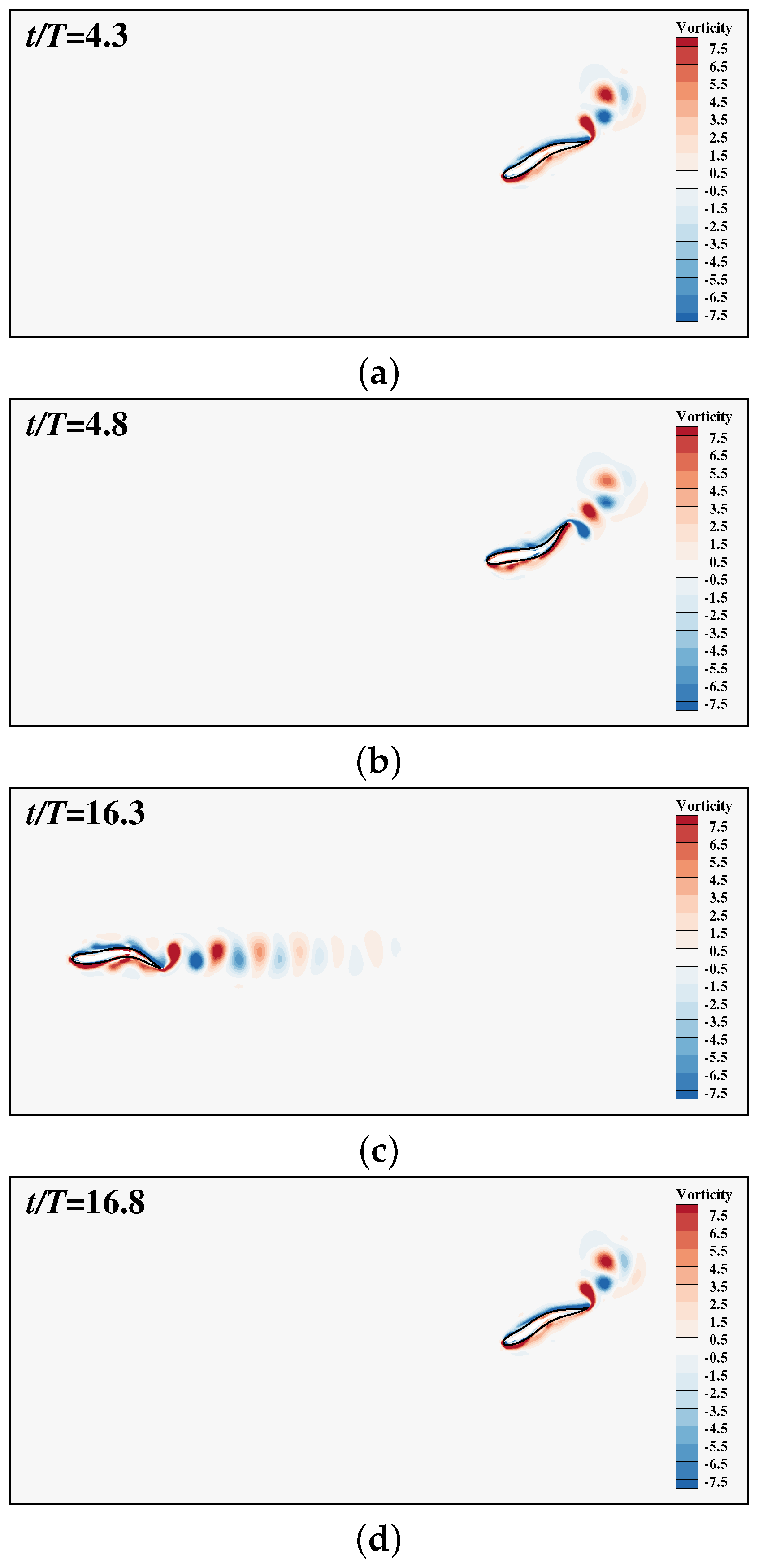
3.1. Learning to Maintain a Given Speed and Orientation

In this section, a fish is trained to maintain its swimming speed and orientation to a given value. Its body length is L and its waving period is T. The goal is to swim along the x-axis at a constant average speed $\overline{u}=0.4L/T$. The goal is reflected by defining a reward as

$$rd=-\sqrt{{({\overline{u}}_x-0.4L/T)}^2+{\overline{u}}_y^2},$$

(7)

where $rd$ is the reward of the swimmer, and ${\overline{u}}_x$ and ${\overline{u}}_y$ are the swimmer’s average speeds along x-axis and y-axis, respectively. In addition, the position of the leader $\mathit{r}$ is restricted to a confined area of $20L\times 10L$.

A comprehensive representation of the environment state is very important for accurate motion control. Theoretically, it should include the information of the fish itself and the ambient flow. The information of the fish includes the body kinematic parameters, position, orientation, velocity, angular velocity, acceleration and angular acceleration of the body. The flow information includes the flow velocity and pressure in the whole flow field. In addition, the historical evolution of the flow should also be considered. The information is too complicated to be considered in a simple definition of the state. Therefore, we have conducted tests with different environment information [30]. The results show that only considering the actions, orientations, and velocities in the last four periods is enough to capture the flow dynamics and can realize relatively high accurate motion control. Therefore, the state is defined by a tuple

$$s_n=\left[\begin{array}{cccc}{\left({\overline{u}}_x\right)}_n,& {\left({\overline{u}}_y\right)}_n,\hfill & {\theta }_n,\hfill & \\ {\left({\overline{u}}_x\right)}_{n-1},& {\left({\overline{u}}_y\right)}_{n-1},\hfill & {\theta }_{n-1},\hfill & a_{n-1}\hfill \\ \dots ,& \dots ,& \dots ,\hfill & \dots ,\hfill \\ {\left({\overline{u}}_x\right)}_{n-8},& {\left({\overline{u}}_y\right)}_{n-8},\hfill & {\theta }_{n-8},\hfill & a_{n-8}\hfill \end{array}\right].$$

(8)

The swimmer propels itself by periodically generating a traveling wave propagating from head to tail, as defined by Equations (2) and (3). The period is T and the body wavelength is fixed at $\lambda =L$. The amplitude set is defined as ${\theta }_{lmax}={10}^{\circ }$, ${15}^{\circ }$, ${20}^{\circ }$, ${25}^{\circ }$, ${30}^{\circ }$, ${35}^{\circ }$, ${40}^{\circ }$, ${45}^{\circ }$ and ${50}^{\circ }$. This parameter set forms an action base of nine components.

The simulation is performed for a Reynolds number of $Re=\rho L^2/T\mu =2500$. Considering the desired forward swimming speed $\overline{u}=0.4L/T$, this is equivalent to $R{e}_u=\rho \overline{u}L/\mu =1000$ for a steady swimmer. It should be noted that this is not a typical Reynolds number for an adult fish, rather it is representative of a juvenile fish less than 5 cm in length. This Reynolds number is used to reduce the computational cost by considering laminar flow, while still demonstrating the effectiveness of the control method. The computational domain of $80 L\times 80 L$ is divided into eight layers of the block with about $5.8\times {10}^4$ initial points. The minimum nondimensional mesh spacing is $\Delta x/L=\Delta y/L=0.01$ near the inner boundaries, and the nondimensional time step size is $\Delta t/T=0.001$. The learning rate is $\alpha =0.001$.

The learning process is divided into a series of episodes. In each episode, the leader is initially placed in the right boundary of the confined swimming area with the initial orientation angle ${\theta }_0$ varying between $-{60}^{\circ }$ and ${60}^{\circ }$. The positions and orientations of the swimmer are then determined by the FSI with the actions. Once the swimmers exceed the confined area, the episode ends and another starts. Figure 4 shows the change history of the speed u and orientation angle $\theta$ of the swimmer when the fish starts with different initial orientations after learning for 1000 episodes. In all cases, the fish successfully aligns itself with the x-axis and remains its average swimming speed close to $0.4L/T$.

Figure 4. Single smart swimmer: (a) The change history of the speed for different initial orientation angles; and (b) the change history of the orientation angle for different initial orientation angles.

Figure 5 shows the change history of the lateral displacement of the tail tip when the fish starts with an initial orientation angle ${\theta }_0={45}^{\circ }$. Figure 6 shows the gestures of the fish and the vorticity contours at different instants. As can be seen, the fish adopts a higher-right-amplitude flapping to turn clockwise to align with the x-axis. Then it adopts a symmetric and constant-amplitude flapping to maintain its orientation and speed. It is noted that asymmetric corrective movement is adopted occasionally.

Figure 5. The lateral movement of the tail of a single smart swimmer with an initial orientation angle ${45}^{\circ }$.

Figure 6. Vorticity contours behind a single smart swimmer at four typical instants: (a) $t/T=4.3$, (b) $t/T=4.8$, (c) $t/T=16.3$, (d) $t/T=16.8$. The range of the vorticity contours is from $-7.5$ to $7.5$. Note that the flow inside the body-occupied region is introduced by the IB-LBM, which however does not affect the solution in the physical region.

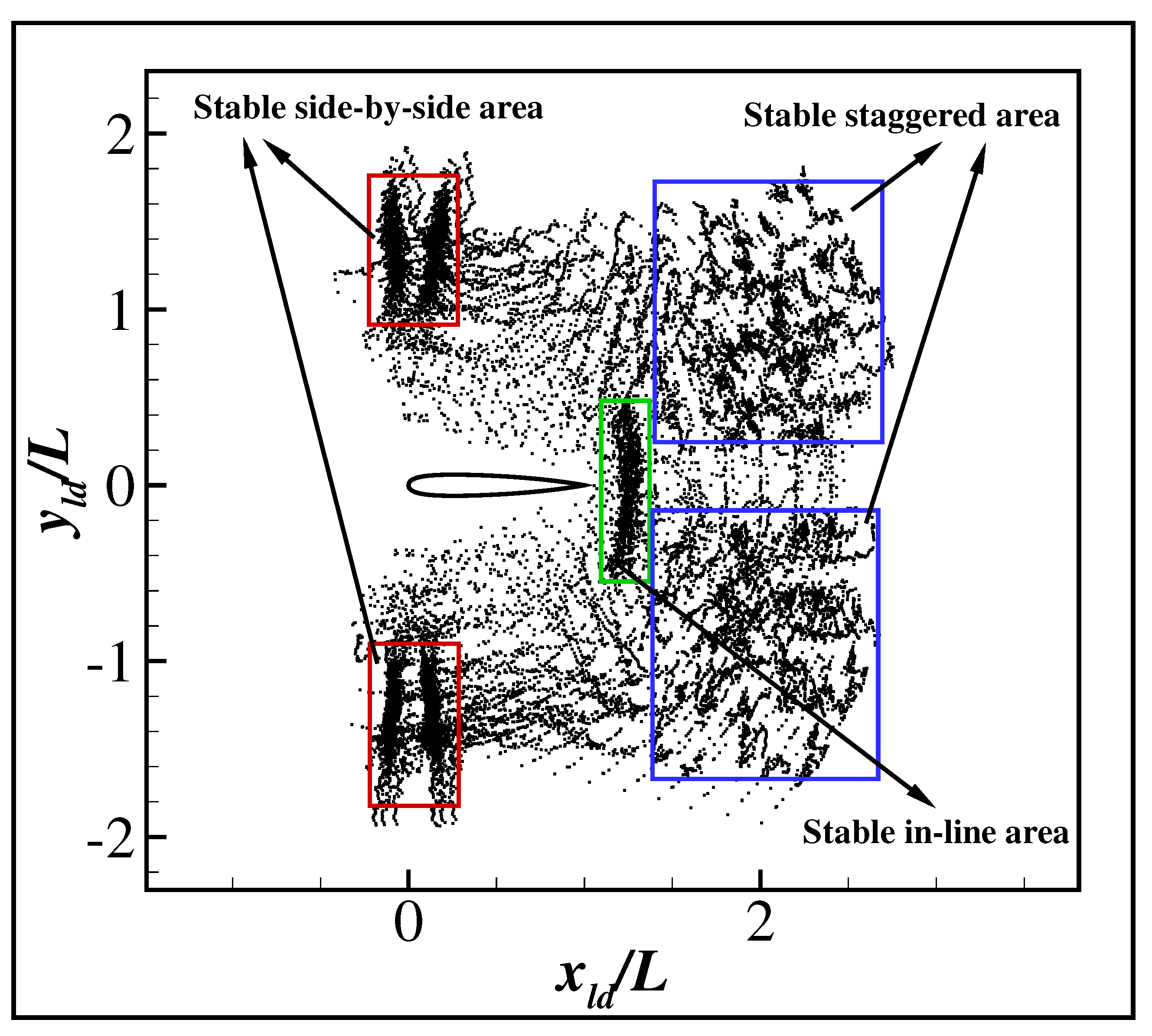
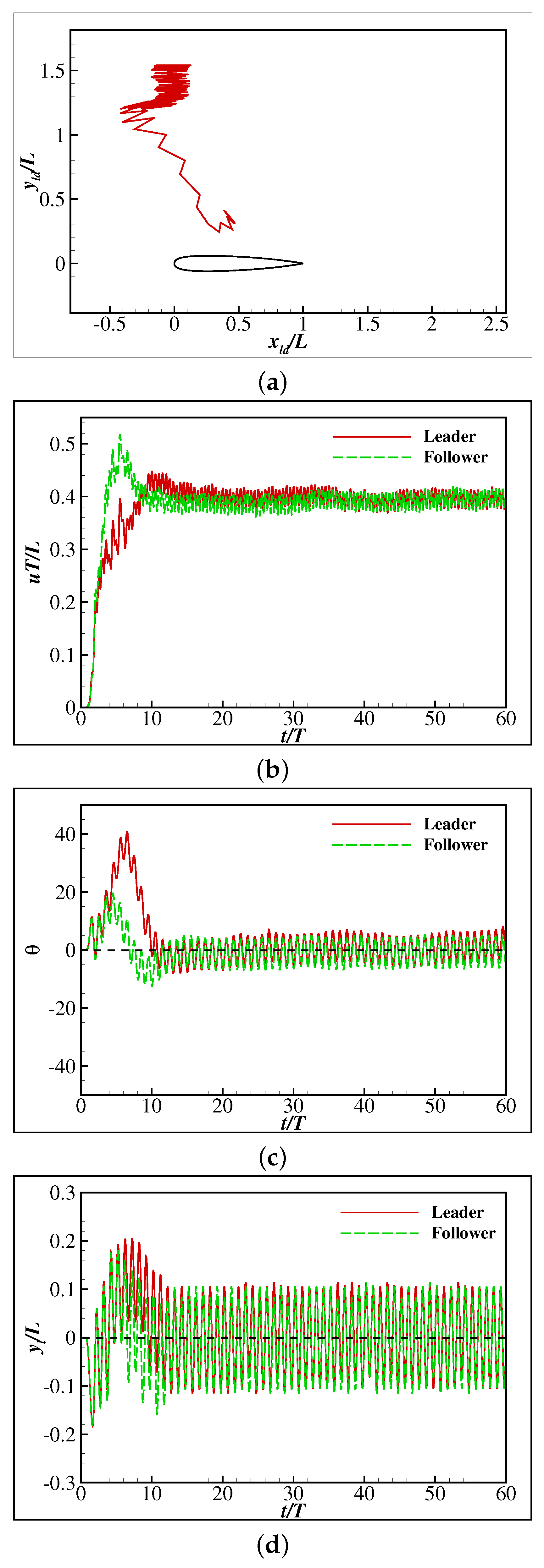
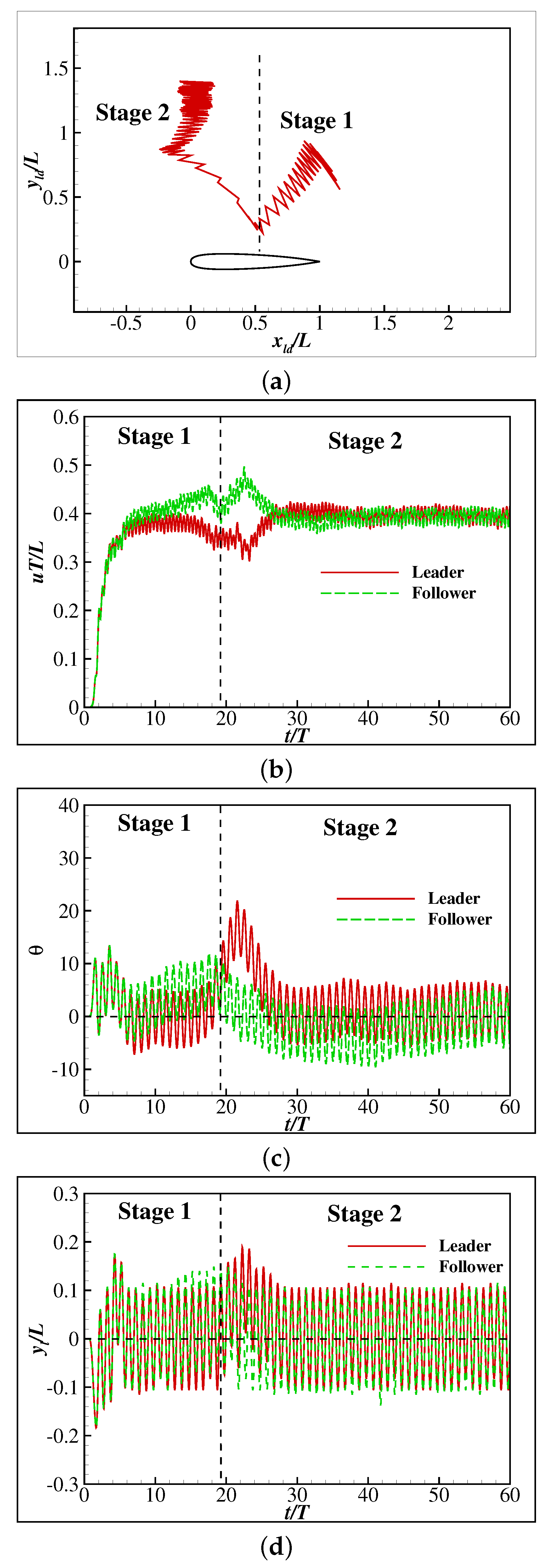
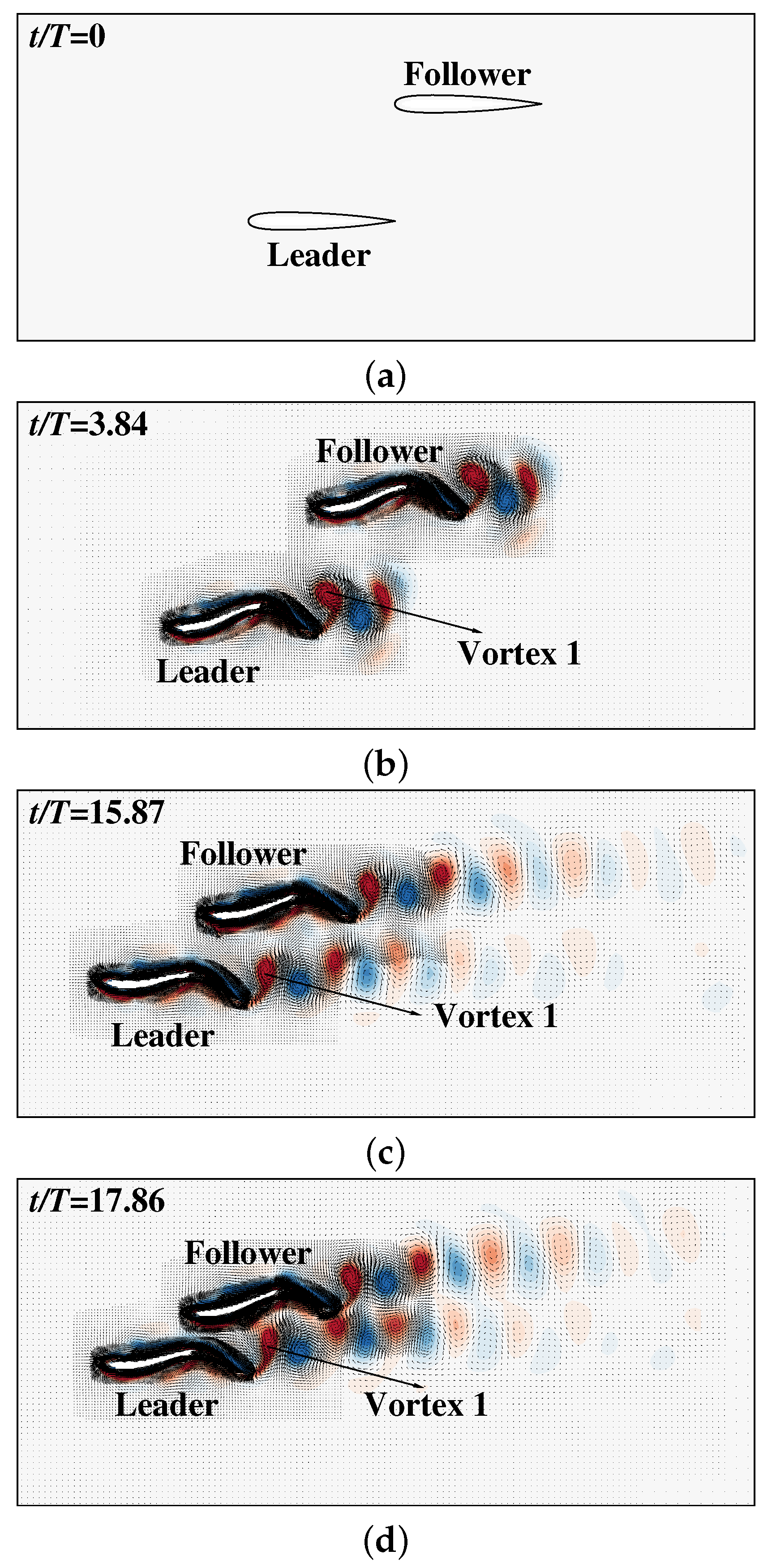
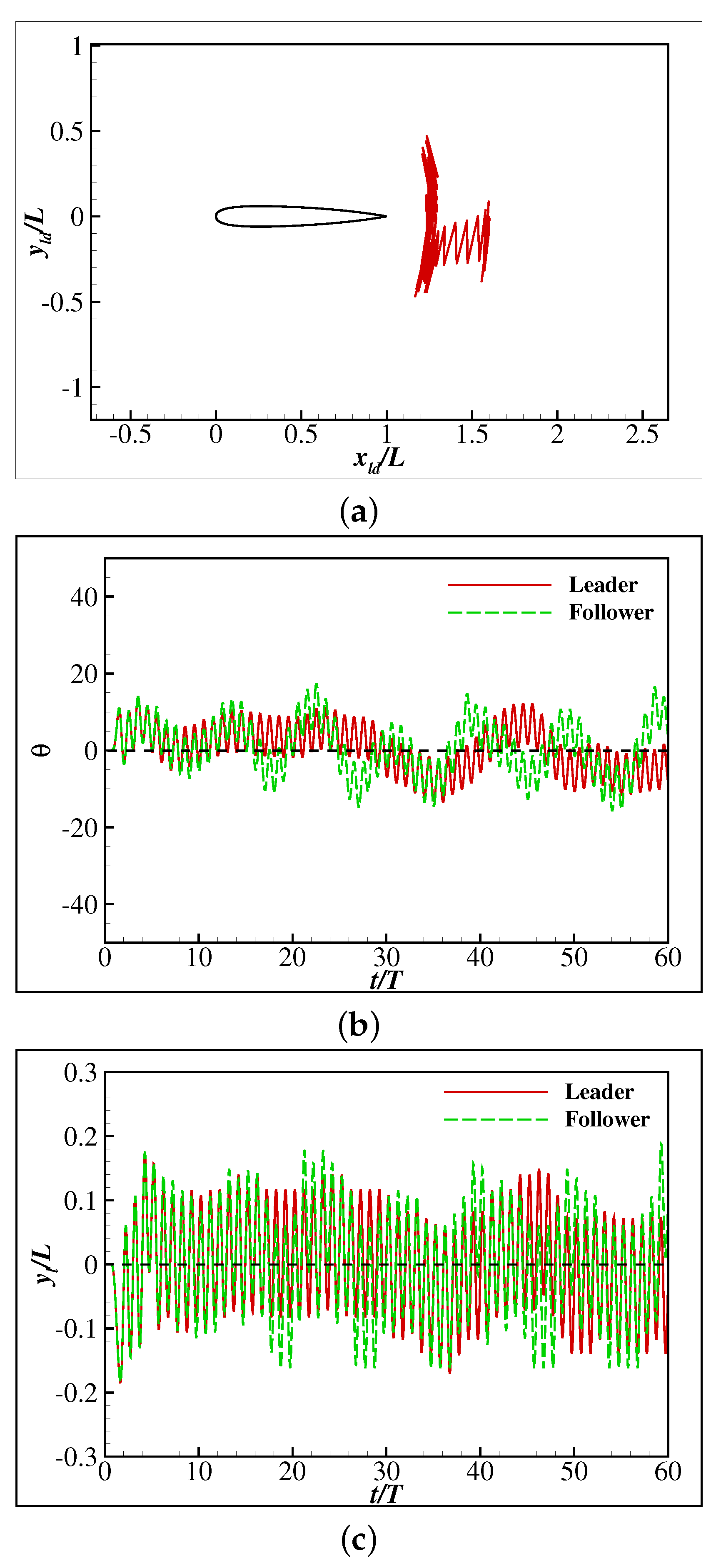
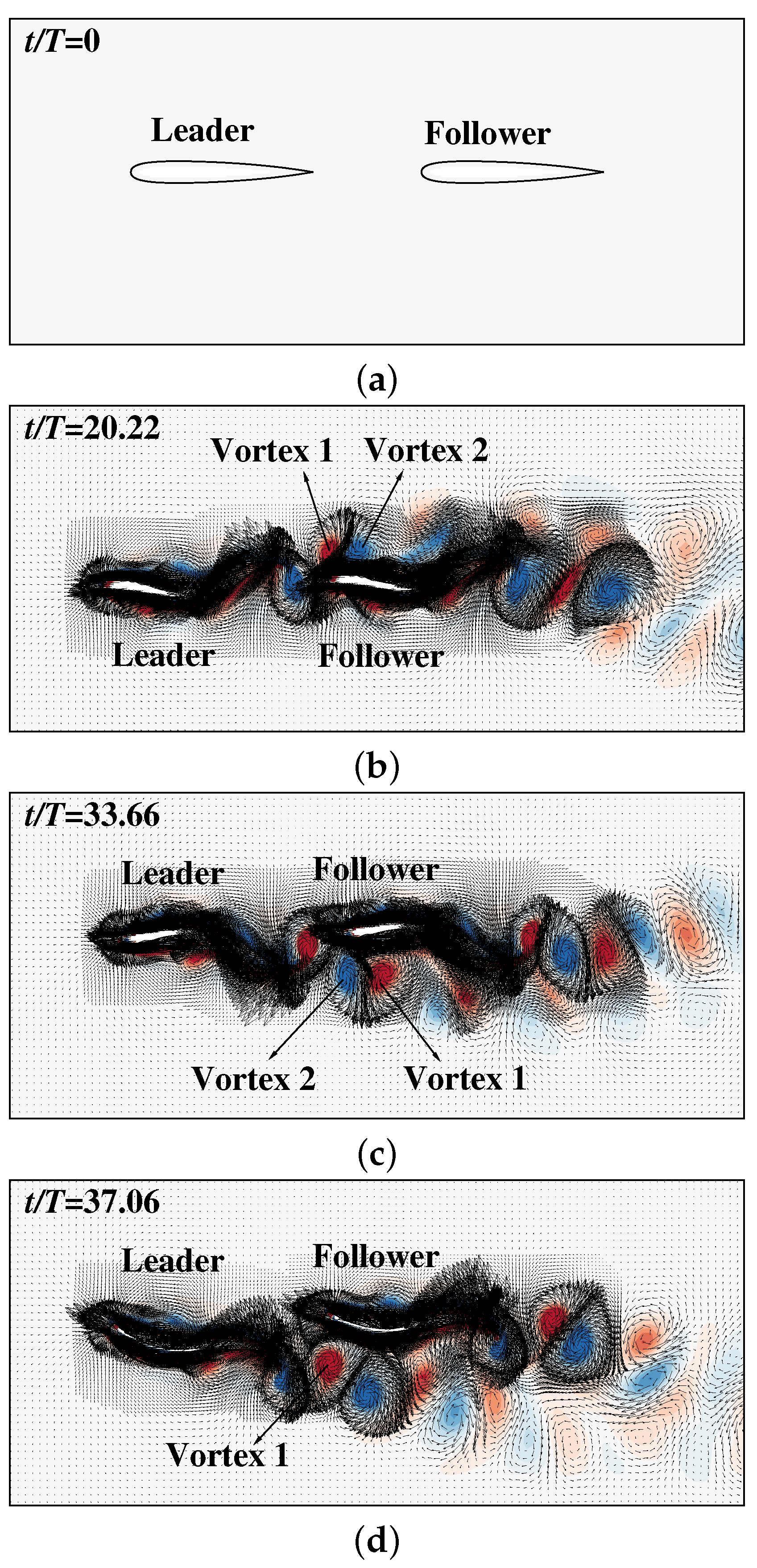
3.2. The Collective Motion of Two Smart Swimmers

In the last section, a swimmer learns a robust control policy to maintain its swimming speed and orientation. The logic of the control policy is simple: (1) if the fish is not swimming in the desired orientation, asymmetric flapping is used to turn into the desired orientation; (2) if the fish is in the desired orientation, appropriate symmetric flapping is used to achieve the desired speed and maintain the orientation. Theoretically, if two swimmers adopt the same control policy, it would be easier for them to swim together. Therefore, in this section, the collective motion of two identical smart swimmers with the same control policy is tested in the confined swimming area. As shown in Figure 7, a leader and a follower is identified, and the relative position and orientation of the follower with respect to the leader in the local coordinate system of the leader ($x_{ld}-y_{ld}$) are represented by $\delta x$, $\delta y$ and $\delta \theta$.

Figure 7. A schematic illustration of the relative position of the swimmers.

A total of 177 different cases are tested in which the initial relative orientation $\delta \theta =0^{\circ }$ and the initial relative positions are as shown in Figure 8. In all cases, the swimmers drive their body according to the policy learned in the above section. The relative positions of the swimmers recorded every half a period are shown in Figure 9. The result shows that different stable formations are achieved according to the initial relative position, as shown in Figure 9. For simplicity, the flow field around the leader is divided into five different areas: front, rear, close wake, far wake and far area, as shown in Figure 8. If the initial relative position is in the front or rear area, the swimmers will form stable side-by-side swimming. If the initial relative position is in the close wake area, the swimmers will form stable in-line swimming. If the initial relative position is in the far or far wake area, the swimmers will form stable staggered swimming. The stable staggered swimming area is located in the far area, and highly diverse formations arise according to the initial formations. We noted that this is because the swimmers can easily maintain their original formations when the hydrodynamic interaction between the swimmers is negligible. The stable side-by-side area is located in a small area left or right to the leader with a distance of about $1.35 L$. The stable in-line area is located in a small area about $0.25 L$ behind the leader. It is to be noticed that the emergence of the stable side-by-side and in-line formations from the highly diverse initial formations is due to the passive self-organization of hydrodynamics, since the swimmers always tend to maintain a given formation instead of actively alter it. In order to understand the hydrodynamic mechanism underlying the passive self-organization, three typical cases are studied in detail.

Figure 8. The initial relative positions of the follower in different test cases.

Figure 9. The traces of the follower in the local coordinate system of the leader in different test cases.

In the first case, the initial relative position is chosen as $\delta x=0.4L$ and $\delta y=0.4L$. The relative trace of the head tip recorded every half a period is shown in Figure 10a, and the change history of the swimming speed, orientation angle and the lateral movement of the tail tip are, respectively, shown in Figure 10b–d. As can be seen, the follower is firstly behind the leader. However, it accelerates rapidly and exceeds the leader in a few periods. Then the leader catches up with the follower gradually until they swim side-by-side in a stable formation. Meanwhile, the orientation angles of both swimmers grow quickly at the beginning and then gradually restore to the initial situation.

Figure 10. Collective swimming starts in front area: (a) The trace of the head tip, (b) the change of the speed, (c) the change of the orientation angle, (d) the lateral movement of the tail tip.

The gestures of the swimmers and the flow velocity and vorticity contours are shown in Figure 11. As can be seen, at the first few periods (Figure 11b,c), Vortex 1 (for simplicity, the newest generated counterclockwise vortex is called Vortex 1) has a strong influence on the posterior part of the leader and the middle part of the follower, making them rotating counterclockwise ($\theta$ becomes larger). In addition, the vortex triggers forward flow near the follower and backward flow near the leader, which significantly accelerates the follower and decelerates the leader, as shown in Figure 10b. A few periods later (Figure 11d), the follower is very close to the leader and Vortex 1 between the swimmers exerts strong attraction force to the posterior part of them, leading to the counterclockwise rotation of the leader and the clockwise rotation of the follower. These rotations cause the swimmers to move in different directions. It is noted that this process is irreversible, which means that the swimmers will continuously swim in different directions and eventually separate (see the videos of the swimmers without active control in the Supplementary Materials). In other words, the passive mechanism does not support stable 3-DoF side-by-side swimming. This highlights the importance of active control in maintaining the stable side-by-side swimming. However, in this case, the smart swimmers are able to adjust their orientations actively. As shown in Figure 10c,d, the swimmers adopt highly asymmetric flapping to restore their orientations when the swimmers are deviated from their original orientations. Due to those active adjustments, the swimmers gradually restore their orientations and move parallel to each other, as shown in Figure 11e,f. It is to be noticed that in Figure 11e, the follower has exceeded the leader. Meanwhile, Vortex 2 instead of Vortex 1 becomes the most influential vortex, gradually accelerating the leader until the swimmers move parallel to each other. It is noted that this is a passive balance mechanism since the swimmers do not actively chase each other.

Figure 11. Vorticity contours behind the fish during side-by-side swimming initiated in the front area at six typical instants: (a) $t/T=0$, (b) $t/T=3.84$, (c) $t/T=4.93$, (d) $t/T=6.66$, (e) $t/T=9.47$, and (f) $t/T=32$. The range of the vorticity contours is from $-7.5$ to $7.5$.

In the second case, the initial relative position is chosen as $\delta x=L$ and $\delta y=0.8L$. The relative trace of the head tip recorded every half a period is shown in Figure 12a, and the change history of the swimming speed, orientation angle and the lateral movement of the tail tip are, respectively, shown in Figure 12b–d. As can be seen, the relative motion of the follower can be divided into two stages. In Stage 1, the follower swims towards the middle part of the leader. In Stage 2, the follower swims away until it reaches the stable side-by-side position as in the first case. Considering the relative position in Stage 2 is close to that in the first case, the underlying mechanism is also similar. Therefore, the performance of the swimmers in Stage 2 is no longer discussed here. The follower is initially located parallel to the tail tip of the leader. However, it swims towards the leader with higher speed and reaches the middle part of the leader at the end of Stage 1. Meanwhile, the orientation angles of both swimmers grow gradually. Compared to the first case, the growth of the orientation angles is much smaller especially for the leader. In fact, the leader is rotating slower than the follower in this case, leading to the follower directly facing the leader.

Figure 12. Collective swimming starts in the rear area: (a) The trace of the head tip, (b) the change of the speed, (c) the change of the orientation angle, (d) the lateral movement of the tail tip.

The gestures of the swimmers and the flow velocity and vorticity contours are shown in Figure 13. As can be seen, Vortex 1 has a strong influence on the anterior part of the follower, making it rotate counterclockwise ($\theta$ becomes larger) to face the leader. The vortex also triggers forward flow near the follower, which accelerates it gradually. It is noticed that the influence on the leader is much smaller than in the first case and in Stage 2. This is because the distance between the swimmers is relatively large, thus weakening the hydrodynamic interaction. In addition, this motion could lead to the collision of the swimmers (see the video in the Supplementary Materials). However, the collision is avoided in this case because the swimmers continuously adjust their flapping to resist the rotations and restore their original orientations (parallel to the x-axis). As can be seen in Figure 12d, frequent asymmetric flapping is adopted by the swimmers to parallelize the orientations. Due to these adjustments, the follower enters the front area of the leader before running into it. Thereafter, the mechanism described in the first case automatically separates the swimmers and leads them to stable side-by-side swimming.

Figure 13. Vorticity contours behind the fish during side-by-side swimming initiated in the rear area at four typical instants in Stage 1: (a) $t/T=0$, (b) $t/T=3.84$, (c) $t/T=15.87$, (d) $t/T=17.86$. The range of the vorticity contours is from $-7.5$ to $7.5$.

It should also be noticed that the fishes take more than 30 periods to completely restore the speed and orientation, while in the single-fish case it takes less than 10 periods. It means that the control policy learned by the fish is not strong enough to quickly restore the speed and orientation in the presence of the hydrodynamic interaction between the fish. It can be speculated that if a more intense active adjustment strategy is utilized, the swimmers can better counteract the influence of hydrodynamic forces and restore their speeds and orientations more quickly. This mild adjustment strategy highlights the passive interaction of the fishes and thus is a good way to investigate the passive hydrodynamic mechanism of the schooling.

In the third case, the initial relative position is chosen as $\delta x=1.6L$ and $\delta y=0.0L$. The relative trace of the head tip recorded every half a period is shown in Figure 14a, and the change history of the orientation angle and the lateral movement of the tail tip are, respectively, shown in Figure 14b,c. As can be seen, the follower is drawn to the leader and oscillates around the tail tip of it. Meanwhile, the orientation angles of both swimmers vary frequently, leading to the frequent adjustment movement of the swimmers.

Figure 14. Collective swimming starts in close wake area: (a) The trace of the head tip, (b) the change of the orientation angle, (c) the lateral movement of the tail tip.

The gestures of the swimmers and the flow velocity and vorticity contours are shown in Figure 15. Two different situations can be identified. The first situation is when the follower is in direct contact with the leader’s wake vortices, as shown in Figure 15b,c. As can be seen, the vortices are pushed to one or the other side of the follower, forming vortex pairs. The vortex pairs strengthen the lateral wake flow along a particular direction, thus push the follower out of the wake area. The second situation is when the follower is out of the wake vortices, as shown in Figure 15d. As can be seen, the vortices no longer form vortex pairs, and Vortex 1 alone has a strong influence on the follower. This is similar to Stage 1 of the second case. As is discussed, the follower should be drawn to the tail. However, since the distance between the swimmers is larger, the follower is only drawn back to the first situation where it is in direct contact with the wake flow. It is noted that this is a passive balance mechanism relying on the strength of the vortices. If the follower is located in the far wake area where the vortices are vastly weakened, it cannot be pulled back to the wake flow by the vortices and eventually swims out of the wake flow.

Figure 15. Vorticity contours behind the fish during in-line swimming at four typical instants: (a) $t/T=0$, (b) $t/T=20.22$, (c) $t/T=33.66$, (d) $t/T=37.06$. The range of the vorticity contours is from $-7.5$ to $7.5$.

4. Conclusions

The collective motion of two freely-swimming smart swimmers has been numerically studied by a hybrid method of the deep reinforcement learning method (DRL) and the immersed boundary-lattice Boltzmann method (IB-LBM). An active control policy is developed by training a fish to swim in a specific speed and orientation. After training, the fish is able to restore the desired swimming speed and orientation from moderate external perturbation.

Then the control policy is adopted by two identical swimmers in the collective swimming. Results show that stable side-by-side, in-line and staggered formations are achieved according to the initial positions. The stable staggered formation is diverse since the hydrodynamic interaction between the swimmers is negligible. The stable side-by-side area is concentrated at a small area left or right to the leader with an average distance of about $1.35L$. The stable in-line area is concentrated in a small area about $0.25L$ behind the leader.

In the side-by-side swimming, the follower will gradually catch up with the leader until it enters the stable side-by-side area. A detailed analysis shows that both the active control and passive self-organization play an important role in this process. The active control works for maintaining the speed and orientation of the swimmers in case they collide or depart from each other. The passive self-organization works for emerging a stable schooling configuration. This result also shows that the side-by-side swimming is 2-DoF stable even though it is 3-DoF unstable. It means that less control effort is required for the fish to remain in the side-by-side formation since it only needs to actively adjust its orientation, and the relative position will be automatically decided by the self-organization.

In the in-line swimming, the follower is drawn to the close wake area of the leader. A passive balance mechanism is identified, in which the wake vortices periodically pull the follower out of and into the wake flow. However, the stable in-line swimming only exists in specific relative positions as the mechanism relies on the ability of the vortices to draw back the follower. We noted that if an active control could serve to pull back the follower to the wake flow, more stable formations can be acquired.

This research promotes our understanding of the hydrodynamic mechanism underlying the fish schooling, especially how the active control and passive self-organization combine to form stable schooling configurations. However, as a preliminary work, many important features of the real fish swimming are not considered, making it difficult to draw a direct conclusion about the real fish behavior. Ongoing work aims to make the simulation more realistic by introducing more real fish features. To be specific, the following aspects will be explored in the future: (1) the multi-agent deep reinforcement learning will be introduced to develop a more robust and subtle control policy, in which the fishes learn to respond to not only their own environmental states but also the actions of other individuals; (2) a structure solver will be considered to reveal the active and passive energy harvesting mechanism; (3) control based on the lateral line system (using hydrodynamic information as sensory input) will be covered; and (4) three-dimensional models will be investigated. Compared to the two-dimensional cases, more degrees of freedom need to be dealt with, including the translation and rotation in three different directions. In addition, the coordinate control of the tail and the pectoral and dorsal fins should also be considered in order to balance the three-dimensional forces and torques.