Numerical Simulation on Temperature and Moisture Fields Around Cooling Towers Used in Mine Ventilation System
Abstract
:1. Introduction
2. Numerical Simulation
2.1. Governing Equations
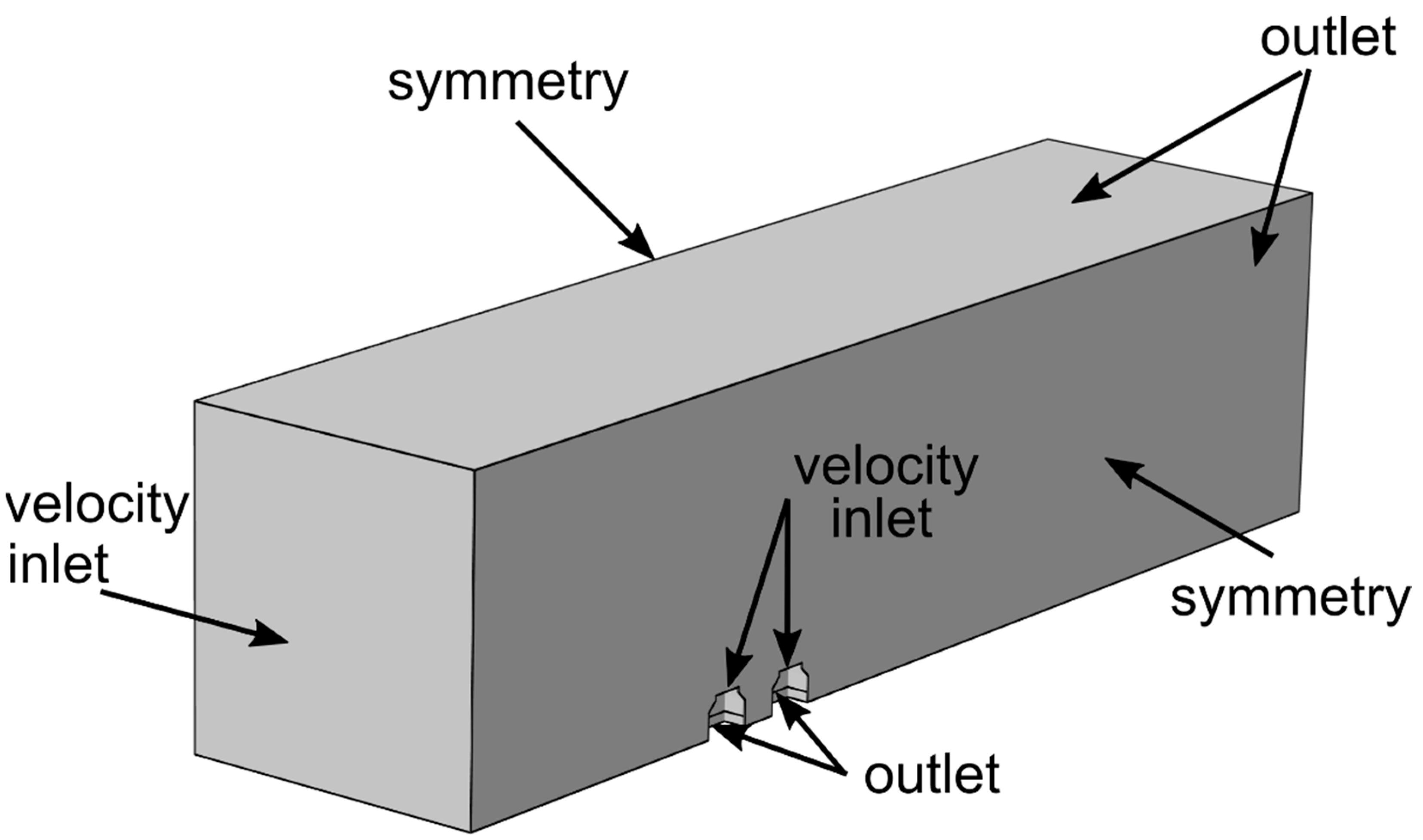
2.2. Geometry of Computational Domain and Boundary Conditions
2.3. Computer Implementation of the Model
3. Multiparametric Numerical Simulation of Dynamics of Airflow Around Cooling Towers
3.1. Parameters for Variation
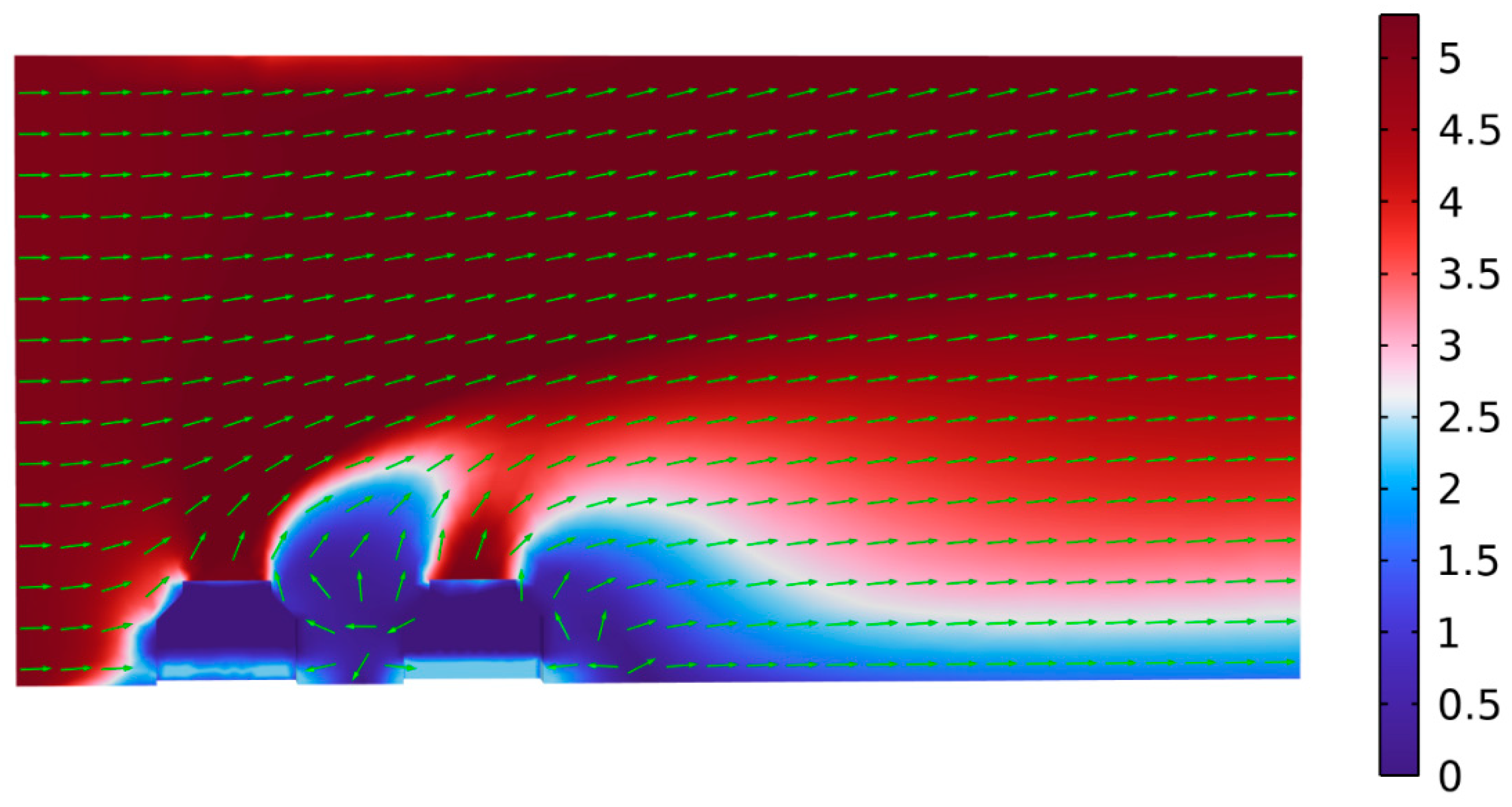
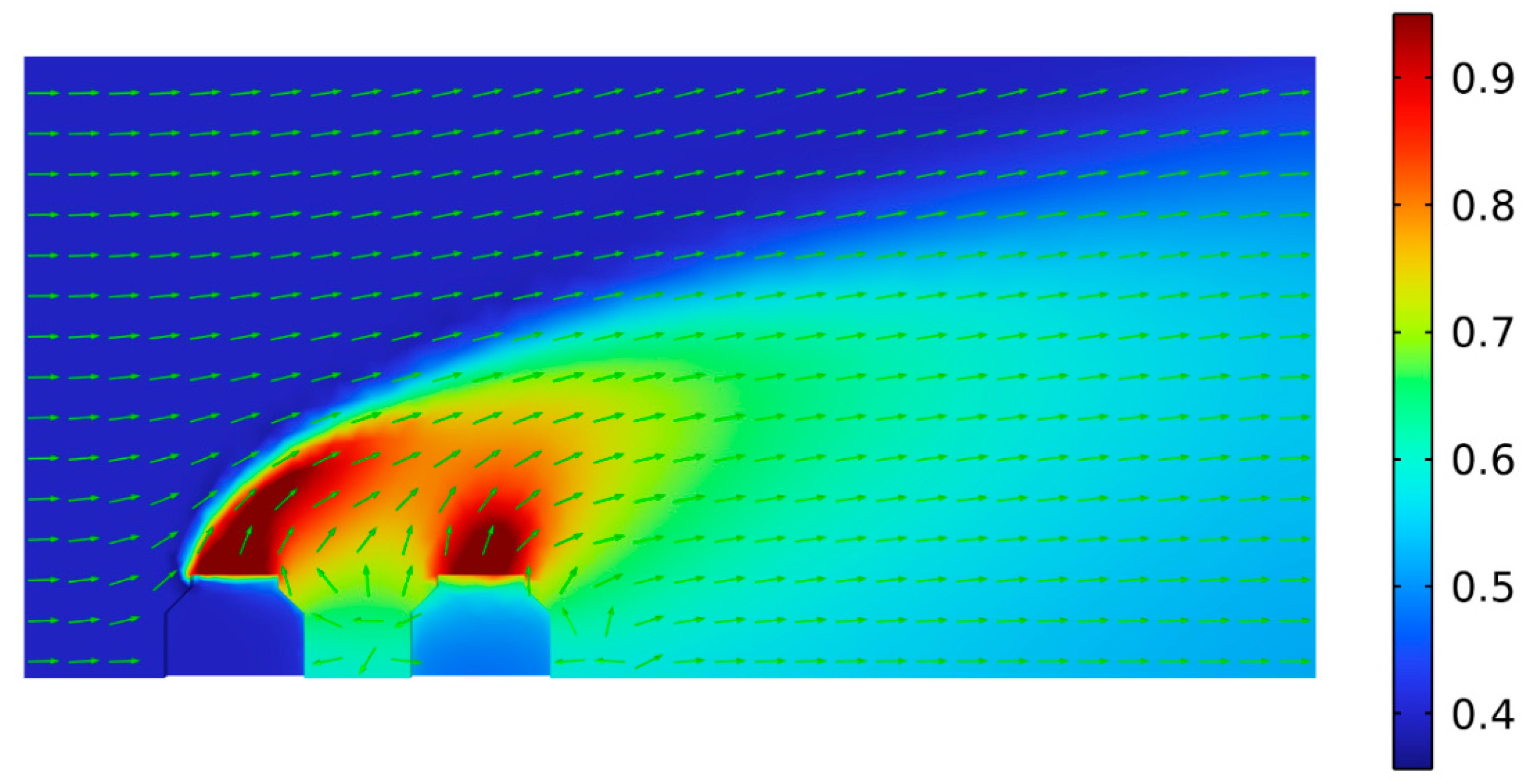
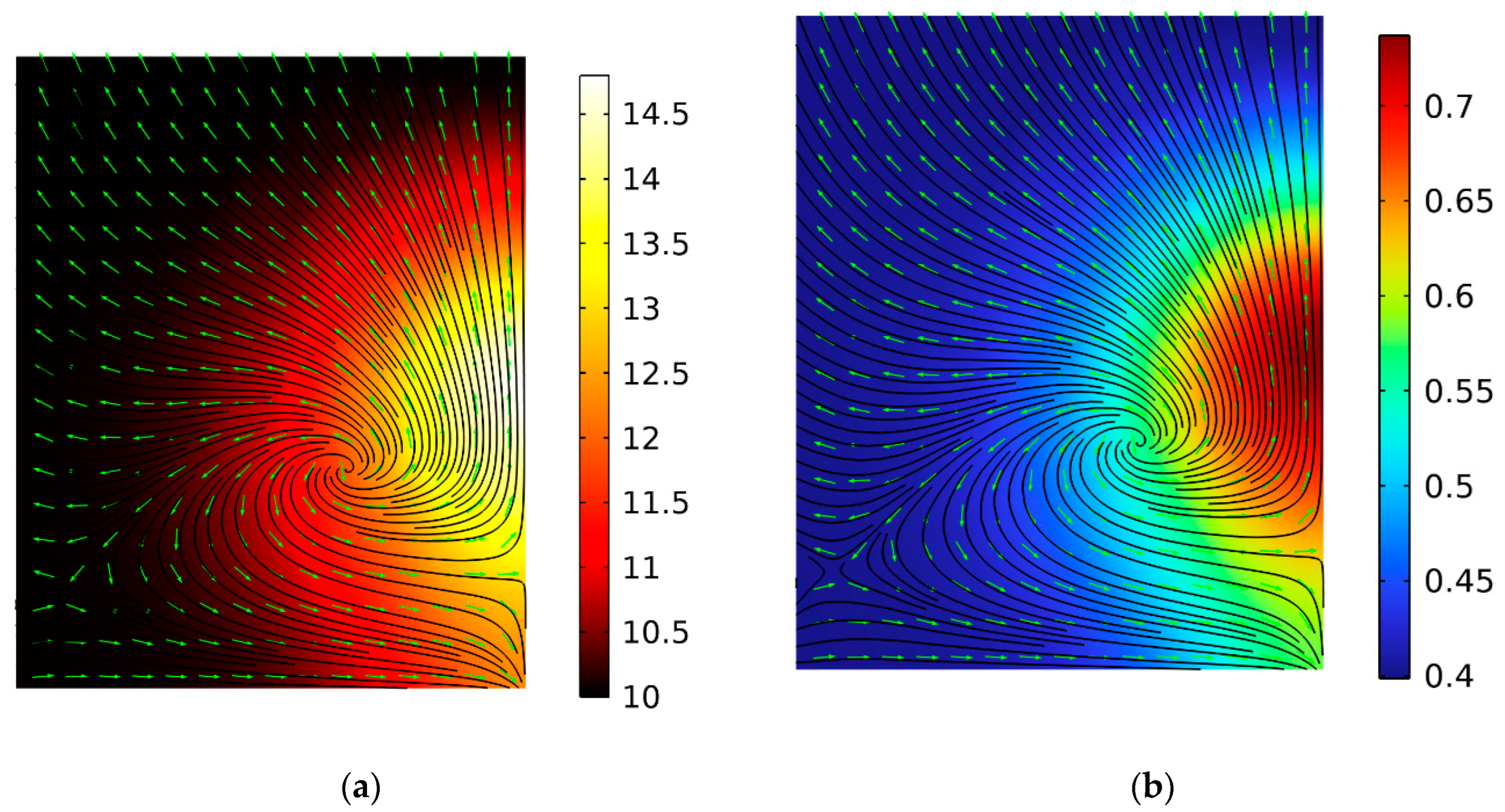
3.2. Simulation of Airflow for Two Cooling Towers
3.3. Simulation of Airflow for Three Cooling Towers
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Hill, G.B.; Pring, E.J.; Osborn, P.D. Cooling Towers: Principles and Practice; Butterworth-Heinemann: London, UK; Boston, MA, USA, 1990. [Google Scholar]
- García Cutillas, C.; Ruiz Ramírez, J.; Manuel Lucas, M. Optimum design and operation of an HVAC cooling tower for energy and water conservation. Energies 2017, 10, 299. [Google Scholar] [CrossRef]
- Zaitsev, A.V.; Levin, L.Y.; Butakov, S.V.; Semin, M.A. Normalization of microclimate in deep potash mines. Gorn. Zhurnal 2018, 8, 97–102. [Google Scholar] [CrossRef]
- Li, X.; Gurgenci, H.; Guan, Z.; Wang, X.; Xia, L. A review of the crosswind effect on the natural draft cooling towers. Appl. Therm. Eng. 2019, 150, 250–270. [Google Scholar] [CrossRef]
- Li, X.; Gurgenci, H.; Guan, Z.; Wang, X.; Duniam, S. Measurements of crosswind influence on a natural draft dry cooling tower for a solar thermal power plant. Appl. Energy 2017, 206, 1169–1183. [Google Scholar] [CrossRef]
- Ruiz, J.; Cutillas, C.G.; Kaiser, A.S.; Ballesta, M.; Zamora, B.; Lucas, M. Experimental study of drift deposition from mechanical draft cooling towers in urban environments. Energy Build. 2016, 125, 181–195. [Google Scholar] [CrossRef]
- Dang, Z.; Gao, M.; Long, G.; Zou, J.; He, S.; Sun, F. Crosswind influence on cooling capacity in different zones for high level water collecting wet cooling towers based on field test. J. Wind Eng. Ind. Aerodyn. 2019, 190, 134–142. [Google Scholar] [CrossRef]
- Gao, M.; Sun, F.Z.; Turan, A. Experimental study regarding the evolution of temperature profiles inside wet cooling tower under crosswind conditions. Int. J. Therm. Sci. 2014, 86, 284–291. [Google Scholar] [CrossRef]
- He, S.; Zhang, G.; Gao, M.; Sun, F.; Huang, X. Wind tunnel test on the flow resistance of U-type water collecting devices for natural draft wet cooling towers. J. Wind Eng. Ind. Aerodyn. 2019, 186, 234–240. [Google Scholar] [CrossRef]
- Yang, L.J.; Chen, L.; Du, X.Z.; Yang, Y.P. Effects of ambient winds on the thermo-flow performances of indirect dry cooling system in a power plant. Int. J. Therm. Sci. 2013, 64, 178–187. [Google Scholar] [CrossRef]
- Su, M.D.; Tang, G.F.; Fu, S. Numerical simulation of fluid flow and thermal performance of a dry-cooling tower under cross wind condition. J. Wind Eng. Ind. Aerodyn. 1999, 79, 289–306. [Google Scholar] [CrossRef]
- Al-Waked, R.; Behnia, M. The performance of natural draft dry cooling towers under crosswind: CFD study. Int. J. Energy Res. 2004, 28, 147–161. [Google Scholar] [CrossRef]
- Chen, L.; Yang, L.; Du, X.; Yang, Y. Performance improvement of natural draft dry cooling system by interior and exterior windbreaker configurations. Int. J. Heat Mass Transf. 2016, 96, 42–63. [Google Scholar] [CrossRef]
- Shirazi, M.; Jahangiri, A. 3D numerical study using three novel windbreak walls in natural draft dry cooling towers for performance enhancement under various crosswind conditions. Therm. Sci. Eng. Prog. 2021, 25, 100971. [Google Scholar] [CrossRef]
- Dong, P.; Li, X. A novel method integrating windbreak walls with water distribution to mitigate the crosswind effects on natural draft dry cooling towers. J. Wind Eng. Ind. Aerodyn. 2020, 205, 104318. [Google Scholar] [CrossRef]
- Ma, H.; Si, F.; Zhu, K.; Wang, J. The adoption of windbreak wall partially rotating to improve thermo-flow performance of natural draft dry cooling tower under crosswind. Int. J. Therm. Sci. 2018, 134, 66–88. [Google Scholar] [CrossRef]
- Wu, T.; Ge, Z.; Yang, L.; Du, X. Flow deflectors to release the negative defect of natural wind on large scale dry cooling tower. Int. J. Heat Mass Transf. 2019, 128, 248–269. [Google Scholar] [CrossRef]
- Goodarzi, M.; Ramezanpour, R. Alternative geometry for cylindrical natural draft cooling tower with higher cooling efficiency under crosswind condition. Energy Convers. Manag. 2014, 77, 243–249. [Google Scholar] [CrossRef]
- Liao, H.T.; Yang, L.J.; Du, X.Z.; Yang, Y.P. Influences of height to diameter ratios of dry-cooling tower upon thermo-flow characteristics of indirect dry cooling system. Int. J. Therm. Sci. 2015, 94, 178–192. [Google Scholar] [CrossRef]
- Chen, L.; Liao, H.T.; Huang, X.W.; Yang, L.J.; Du, X.Z.; Yang, Y.P. Thermo-flow characteristics of indirect dry cooling system with elliptically arranged heat exchanger bundles around a traditional circular cooling tower. Appl. Therm. Eng. 2017, 121, 419–430. [Google Scholar] [CrossRef]
- Li, Z.; Wei, H.; Wu, T.; Du, X. Optimization for Circulating Cooling Water Distribution of in-Direct Dry Cooling System in a Thermal Power Plant under Crosswind Condition with Evolution Strategies Algorithm. Energies 2021, 14, 1167. [Google Scholar] [CrossRef]
- Kashani, M.M.; Dobrego, K.V. Influence of flow rotation within a cooling tower on the aerodynamic interaction with crosswind flow. J. Eng. Phys. Thermophys. 2014, 87, 385–393. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, F.; Long, G.; Huang, X.; Huang, W.; Lyv, D. Comparative study on the cooling characteristics of high level water collecting natural draft wet cooling tower and the usual cooling tower. Energy Convers. Manag. 2016, 116, 150–164. [Google Scholar] [CrossRef]
- Chen, X.; Sun, F.; Chen, Y.; Gao, M. Novel method for improving the cooling performance of natural draft wet cooling towers. Appl. Therm. Eng. 2019, 147, 562–570. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, R.; Zhang, Z.; He, S.; Gao, M. Crosswind influence on heat and mass transfer performance for wet cooling tower equipped with an axial fan. Case Stud. Therm. Eng. 2021, 27, 101259. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, N.; Li, J.; Li, J.; He, S.; Gao, M. Effect of forced ventilation on the thermal performance of wet cooling towers. Case Stud. Therm. Eng. 2022, 35, 102116. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, M.; Liu, Y.; Gao, M.; He, S.; Shi, Y. An exploratory research on performance improvement of super-large natural draft wet cooling tower based on the reconstructed dry-wet hybrid rain zone, part 2: Crosswind effects. Int. J. Heat Mass Transf. 2020, 160, 120225. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, M.; Wang, Y.; He, S.; Gao, M. Influences of dry-wet hybrid rain zone on the heat and mass transfer characteristics of wet cooling towers: A case study. Case Stud. Therm. Eng. 2022, 30, 101784. [Google Scholar] [CrossRef]
- Jiang, L.; Han, Q.; Wang, N.; Gao, M.; He, S.; Guan, H.; Tan, X. The effects of water droplet diameter distribution in the rain zone on the cooling capacity and water-splashing noise for natural draft wet cooling towers. Int. J. Therm. Sci. 2021, 164, 106875. [Google Scholar] [CrossRef]
- Al-Waked, R. Crosswinds effect on the performance of natural draft wet cooling towers. Int. J. Therm. Sci. 2010, 49, 218–224. [Google Scholar] [CrossRef]
- Khamooshi, M.; Anderson, T.N.; Nates, R.J. A numerical study on interactions between three short natural draft dry cooling towers in an in-line arrangement. Int. J. Therm. Sci. 2021, 159, 106505. [Google Scholar] [CrossRef]
- Xiong, X.; Li, L.; Zhou, X.Q. Numerical Analysis and Optimization Research on Backflow Effect of Cooling Tower. Procedia Eng. 2017, 205, 2003–2010. [Google Scholar] [CrossRef]
- Kutateladze, S.S. Fundamentals of the Theory of Heat Transfer; Edward Arnold: London, UK, 1963. [Google Scholar]
- Goodarzi, M.A. Proposed stack configuration for dry cooling tower to improve cooling efficiency under crosswind. J. Wind Eng. Ind. Aerodyn. 2010, 98, 858–863. [Google Scholar] [CrossRef]
- Anderson, D.A.; Tannehill, J.C.; Pletcher, R.H. Computational Fluid Mechanics and Heat Transfer; Taylor & Francis: Boca Raton, FL, USA, 2016. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed.; DCW Indus.: La Cañada, CA, USA, 1998. [Google Scholar]
- Wilcox, D.C. Formulation of the kw turbulence model revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef]
- Comsol 5.4 CFD Module User’s Guide. Available online: https://doc.comsol.com/5.4/doc/com.comsol.help.cfd/CFDModuleUsersGuide.pdf (accessed on 25 September 2022).
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Tsilingiris, P.T. Thermophysical and transport properties of humid air at temperature range between 0 and 100 °C. Energy Convers. Manag. 2008, 49, 1098–1110. [Google Scholar] [CrossRef]
- Comsol 5.4 Heat Transfer. User’s Guide. Available online: https://doc.comsol.com/5.4/doc/com.comsol.help.heat/HeatTransferModuleUsersGuide.pdf (accessed on 25 September 2022).
- Monteith, J.L.; Unsworth, M.H. Principles of Environmental Physics; Edward Arnold: London, UK, 1990. [Google Scholar]
- Hughes, T.J.R.; Mallet, M. A New Finite Element Formulation for Computational Fluid Dynamics: III. The Generalized Streamline Operator for Multidimensional Advective-Diffusive System. Comput. Methods Appl. Mech. Eng. 1986, 58, 305–328. [Google Scholar] [CrossRef]
- Hauke, G.; Hughes, T.J.R. A Unified Approach to Compressible and Incompressible Flows. Comput. Methods Appl. Mech. Eng. 1994, 113, 389–395. [Google Scholar] [CrossRef]


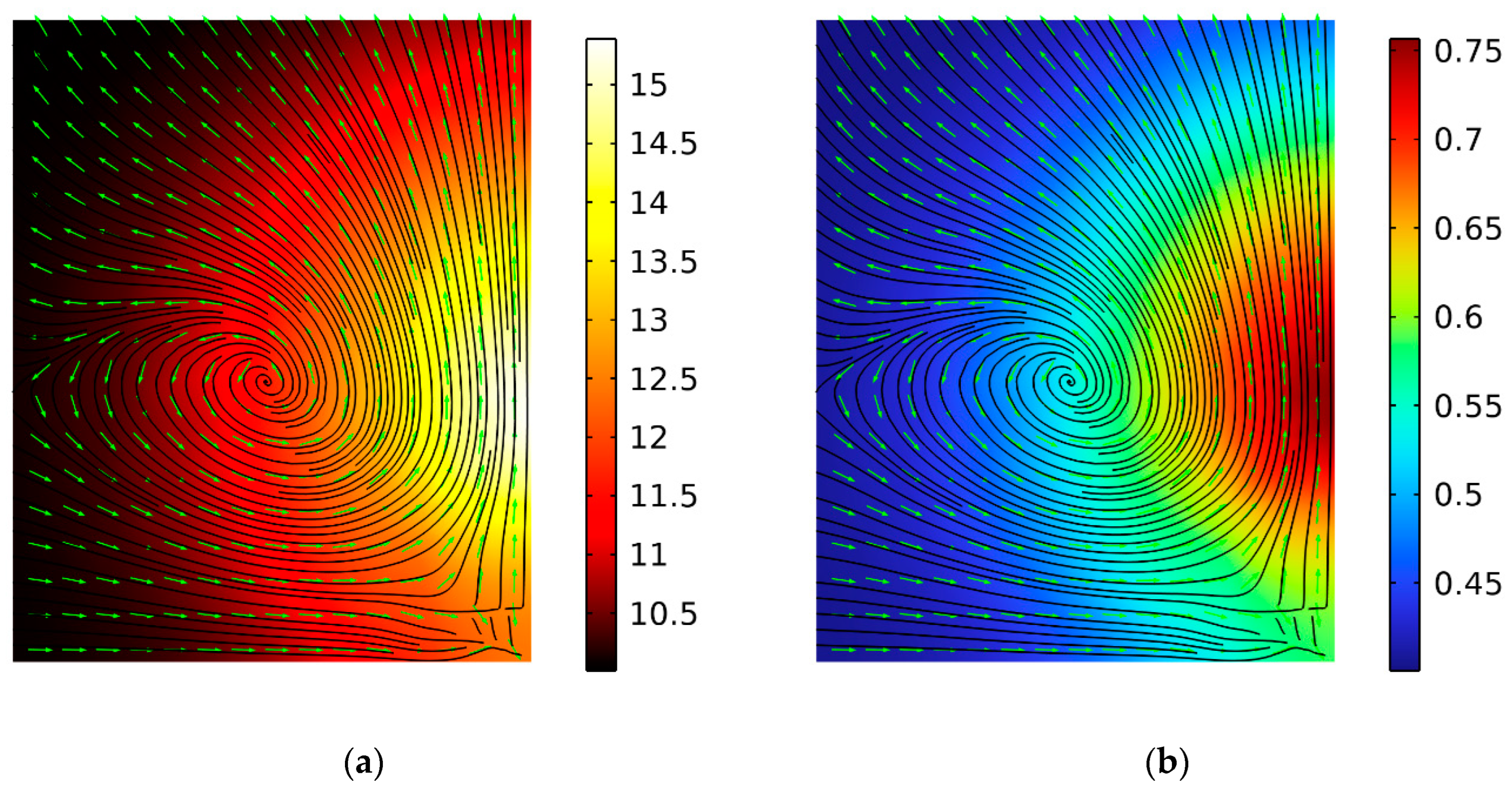

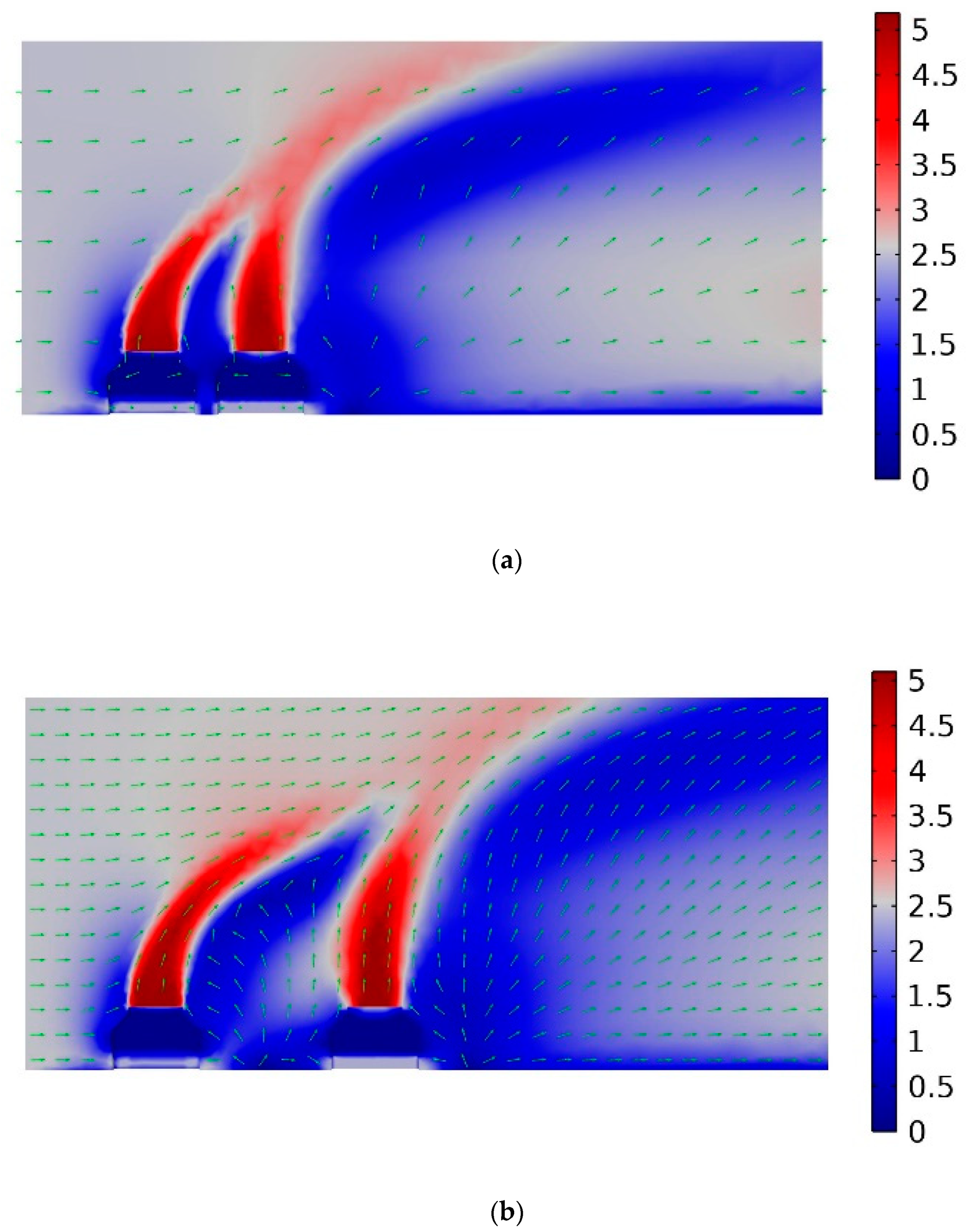
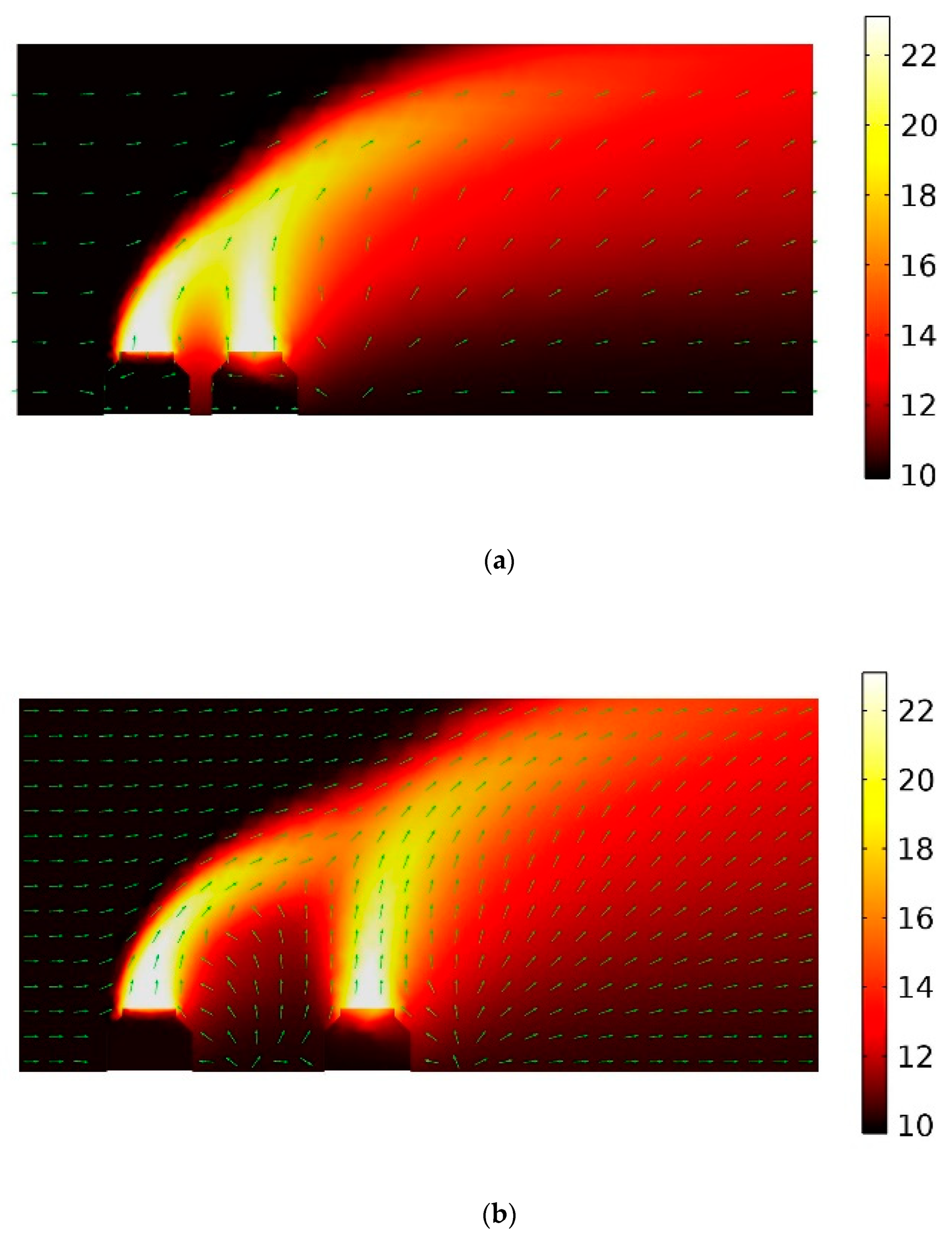

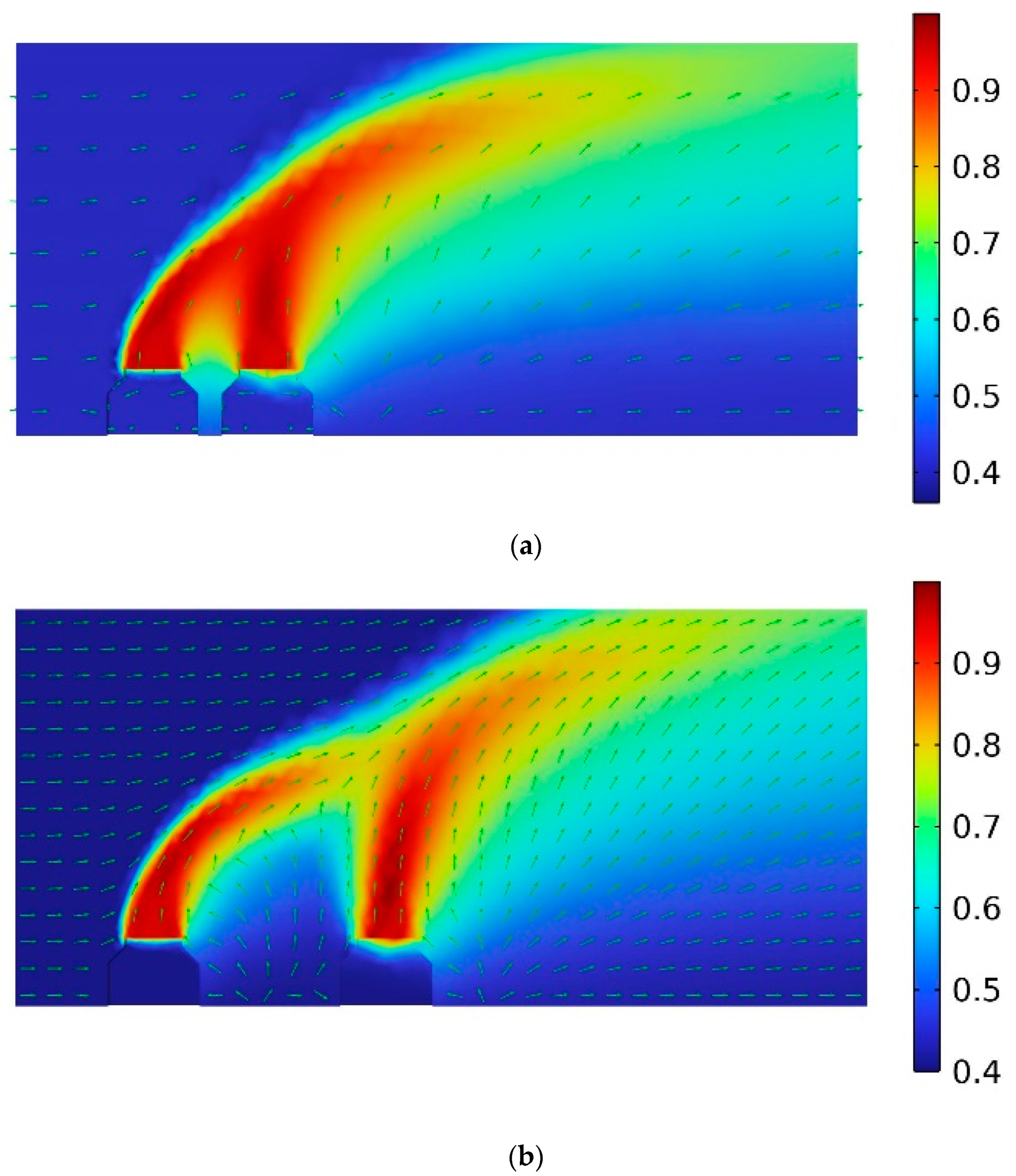

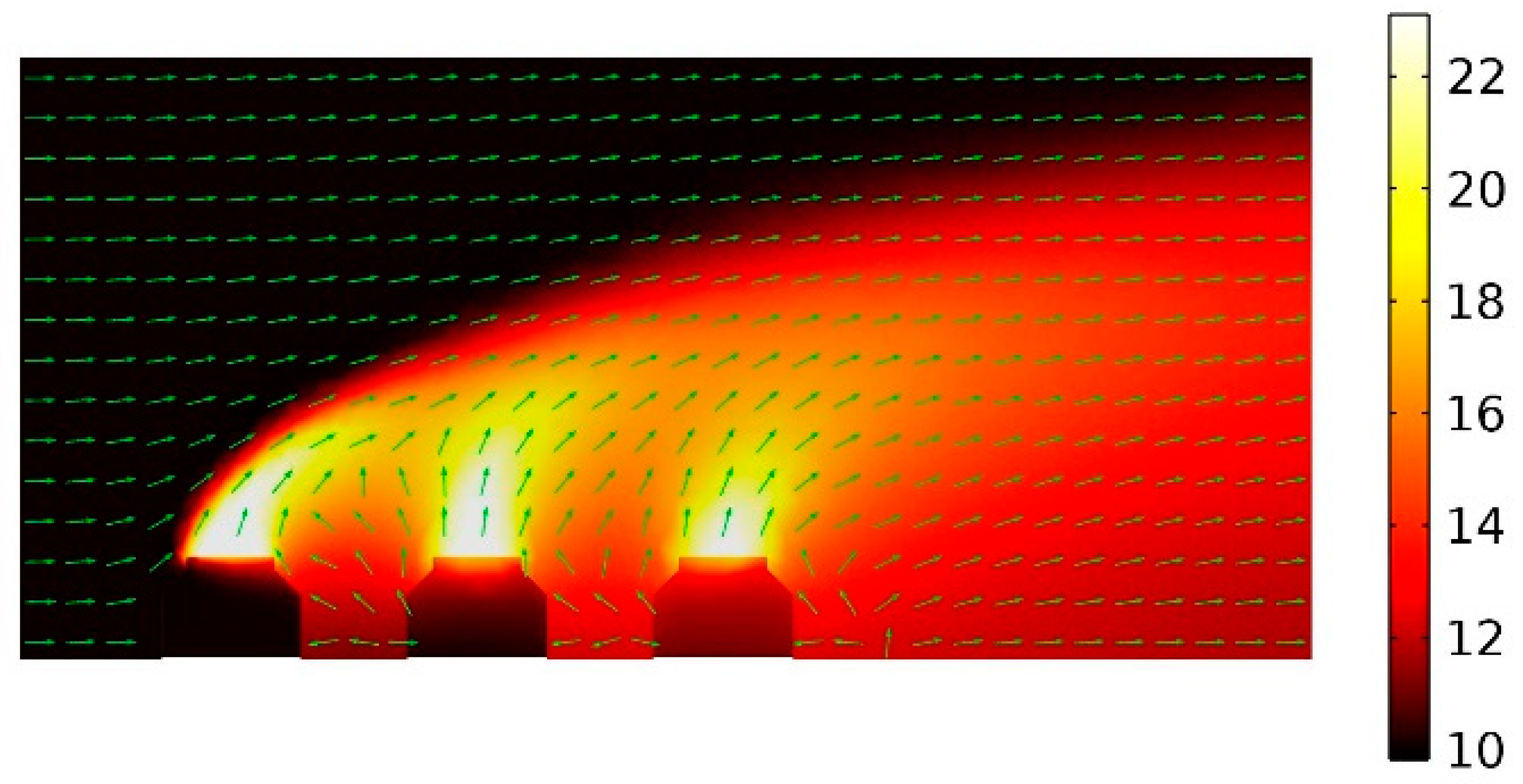
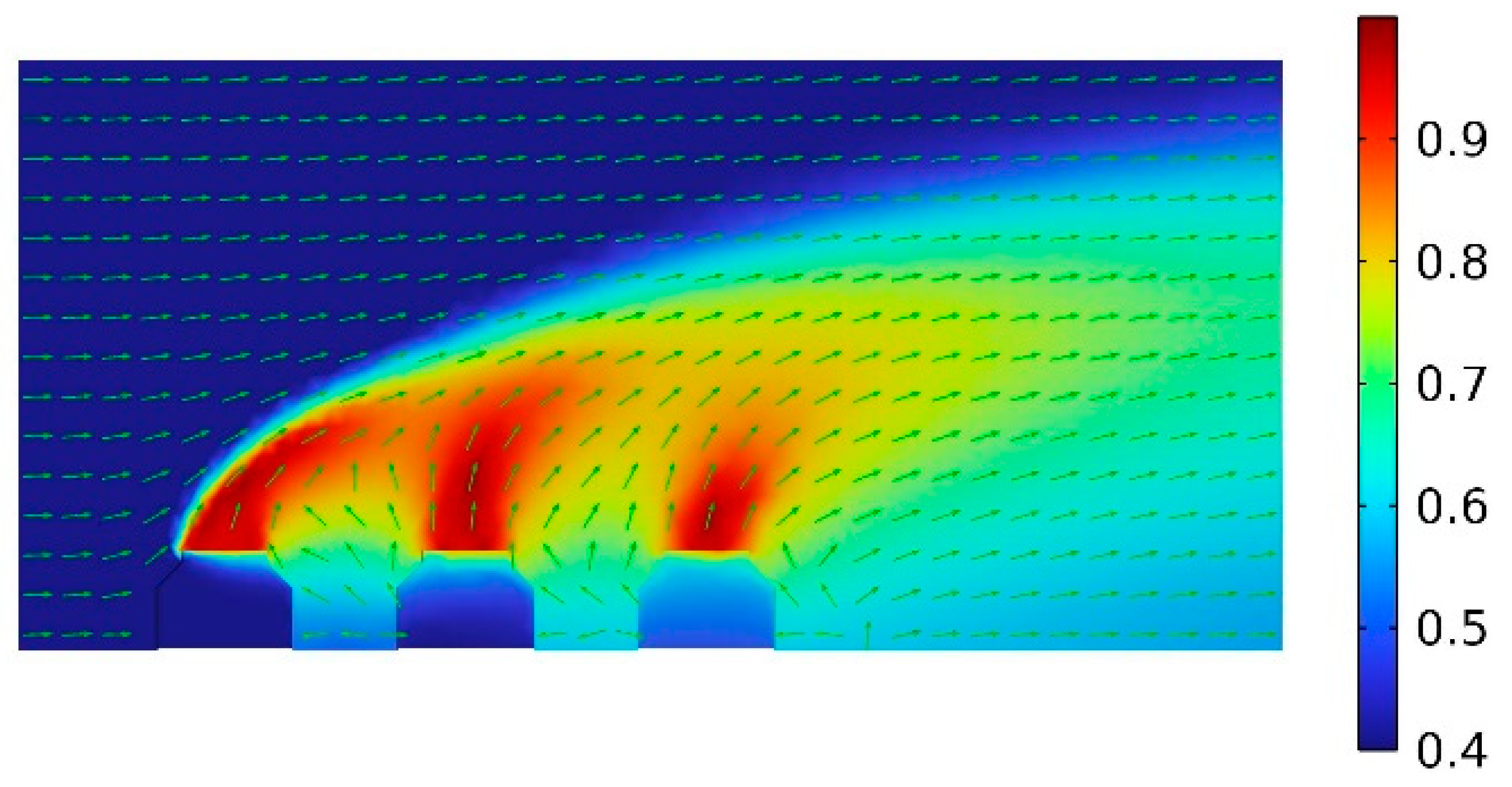
| Tamb(℃) | 10.0 |
| φamb(%) | 40 |
| Vin,t(m/s) | 5.1 |
| Tin,t(℃) | 23.1 |
| φin,t(%) | 95 |
| Qout(m3/s) | 120 |
| Intakes of the Second Tower in the Case of Two Towers | Intakes of the Second Tower in the Case of Three Towers | Intakes of the Third Tower in the Case of Three Towers |
|---|---|---|
| 10.47 | 14.58 | 29.91 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhelnin, M.; Kostina, A.; Plekhov, O.; Zaitsev, A.; Olkhovskiy, D. Numerical Simulation on Temperature and Moisture Fields Around Cooling Towers Used in Mine Ventilation System. Fluids 2022, 7, 317. https://doi.org/10.3390/fluids7100317
Zhelnin M, Kostina A, Plekhov O, Zaitsev A, Olkhovskiy D. Numerical Simulation on Temperature and Moisture Fields Around Cooling Towers Used in Mine Ventilation System. Fluids. 2022; 7(10):317. https://doi.org/10.3390/fluids7100317
Chicago/Turabian StyleZhelnin, Maxim, Anastasiia Kostina, Oleg Plekhov, Artem Zaitsev, and Dmitriy Olkhovskiy. 2022. "Numerical Simulation on Temperature and Moisture Fields Around Cooling Towers Used in Mine Ventilation System" Fluids 7, no. 10: 317. https://doi.org/10.3390/fluids7100317
APA StyleZhelnin, M., Kostina, A., Plekhov, O., Zaitsev, A., & Olkhovskiy, D. (2022). Numerical Simulation on Temperature and Moisture Fields Around Cooling Towers Used in Mine Ventilation System. Fluids, 7(10), 317. https://doi.org/10.3390/fluids7100317








