The Electrical Conductivity of Ionic Liquids: Numerical and Analytical Machine Learning Approaches
Abstract
1. Introduction
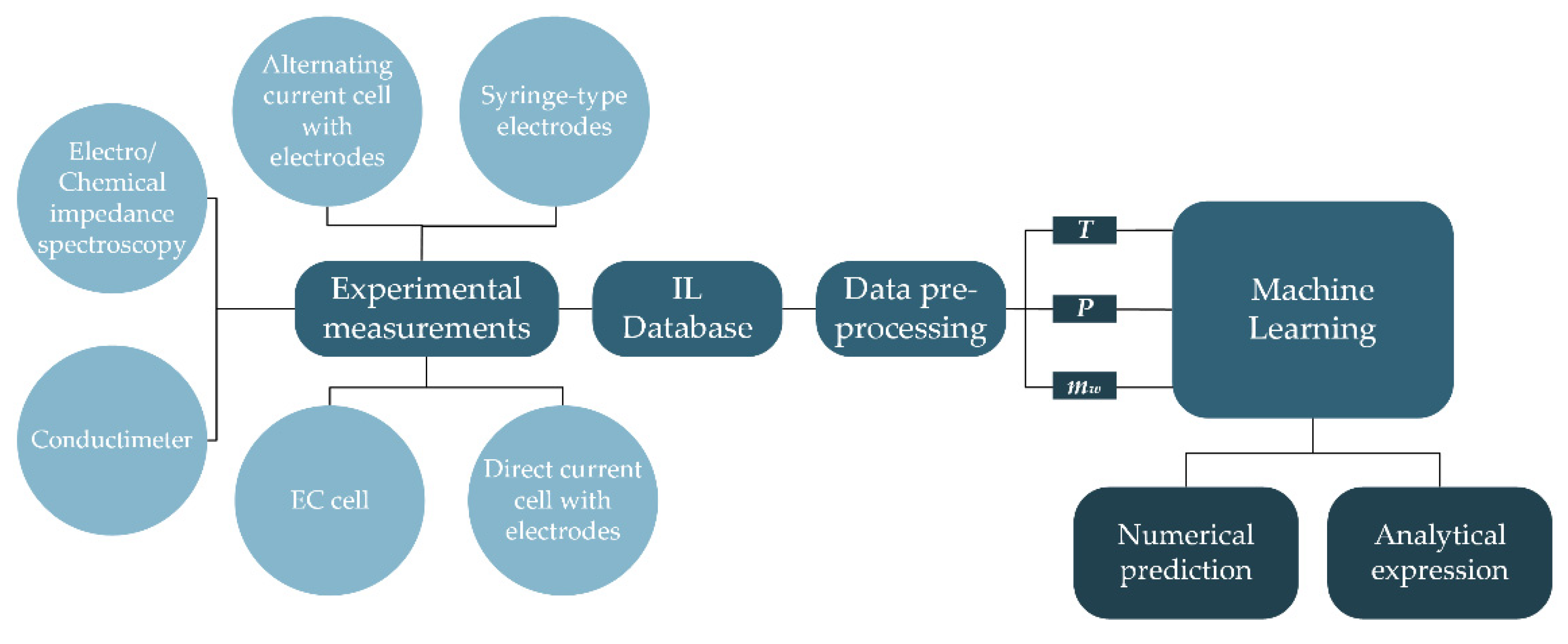
2. Materials and Methods
2.1. The Electrical Conductivity of Ionic Liquids
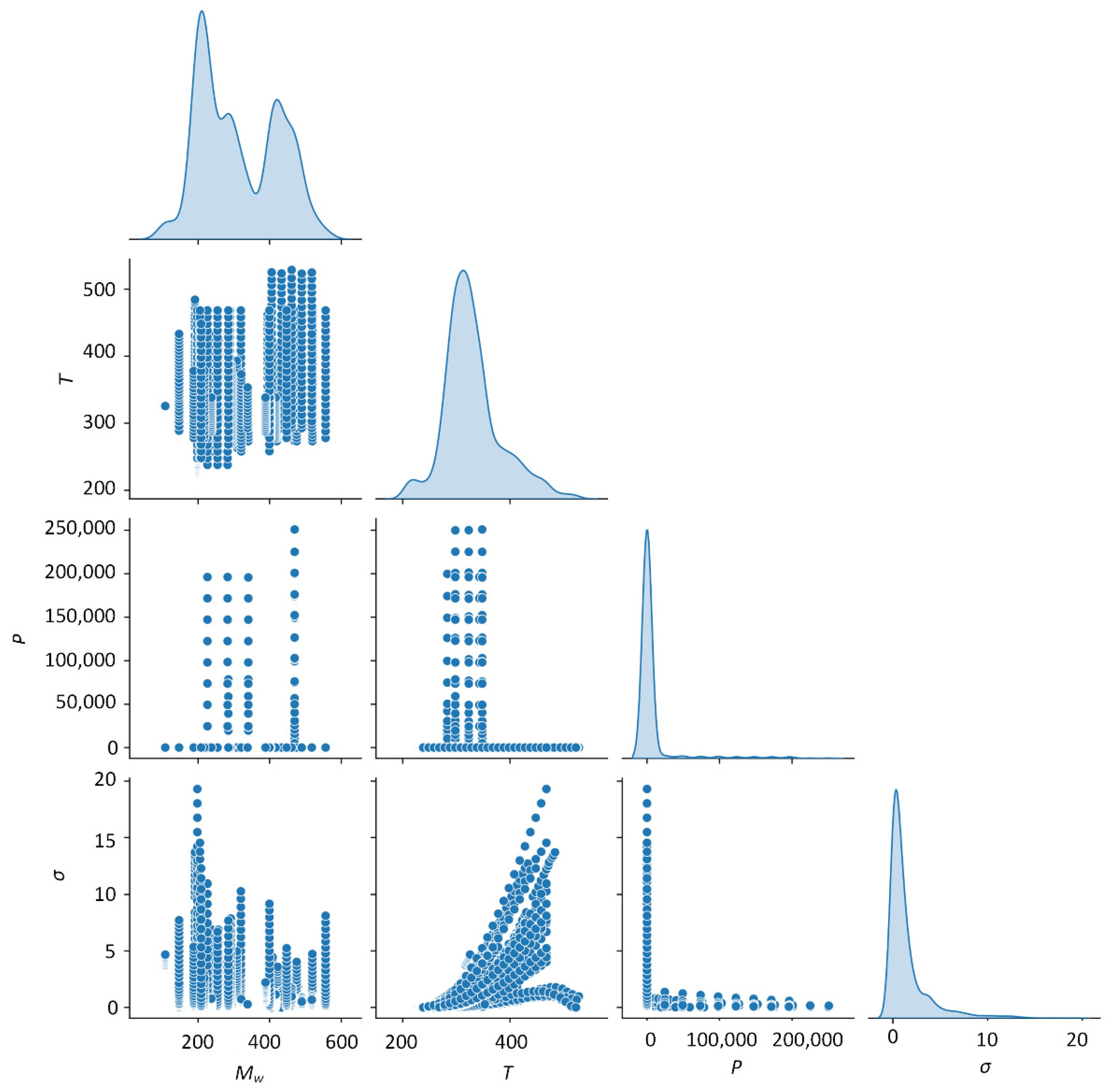
2.2. Electrical Conductivity Data
2.3. Pre-Processing
2.4. Machine Learning
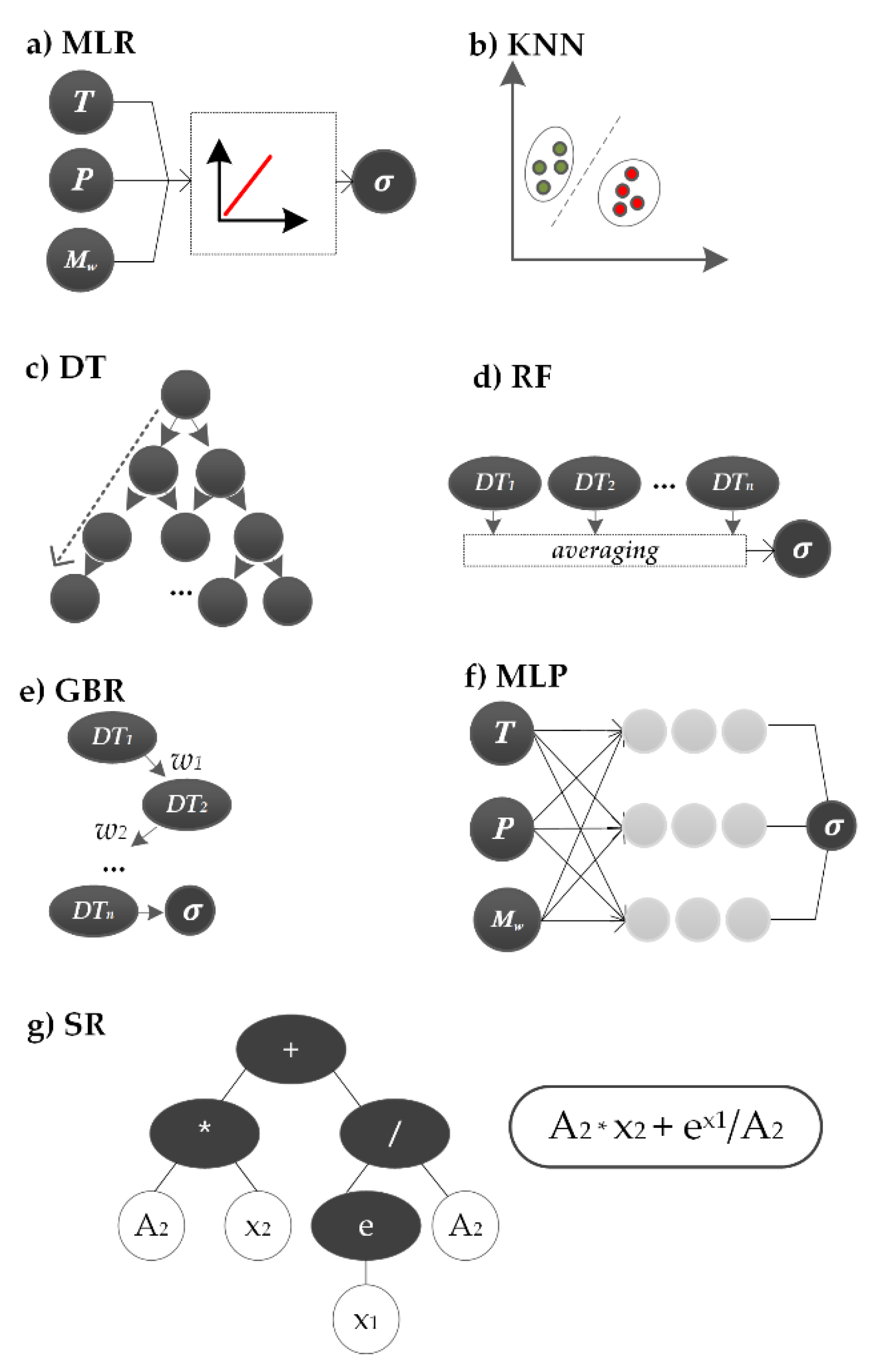
2.4.1. Multiple Linear Regression
2.4.2. k-Nearest Neighbors
2.4.3. Decision Trees
2.4.4. Random Forest
2.4.5. Gradient Boosting Regressor
2.4.6. Multi-Layer Perceptron
2.4.7. Symbolic Regression
2.4.8. Metrics of Accuracy
3. Results and Discussion
3.1. Partial Dependence
3.2. Machine Learning Results
3.3. Obtaining an Analytical Expression
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ward, L.; Wolverton, C. Atomistic calculations and materials informatics: A review. Curr. Opin. Solid State Mater. Sci. 2017, 21, 167–176. [Google Scholar] [CrossRef]
- Frank, M.; Drikakis, D.; Charissis, V. Machine-Learning Methods for Computational Science and Engineering. Computation 2020, 8, 15. [Google Scholar] [CrossRef]
- Ramprasad, R.; Batra, R.; Pilania, G.; Mannodi-Kanakkithodi, A.; Kim, C. Machine learning in materials informatics: Recent applications and prospects. npj Comput. Mater. 2017, 3, 54. [Google Scholar] [CrossRef]
- Gao, C.; Min, X.; Fang, M.; Tao, T.; Zheng, X.; Liu, Y.; Wu, X.; Huang, Z. Innovative Materials Science via Machine Learning. Adv. Funct. Mater. 2022, 32, 2108044. [Google Scholar] [CrossRef]
- Craven, G.T.; Lubbers, N.; Barros, K.; Tretiak, S. Machine learning approaches for structural and thermodynamic properties of a Lennard-Jones fluid. J. Chem. Phys. 2020, 153, 104502. [Google Scholar] [CrossRef]
- Sun, W.; Zheng, Y.; Yang, K.; Zhang, Q.; Shah, A.A.; Wu, Z.; Sun, Y.; Feng, L.; Chen, D.; Xiao, Z.; et al. Machine learning-assisted molecular design and efficiency prediction for high-performance organic photovoltaic materials. Sci. Adv. 2019, 5, eaay4275. [Google Scholar] [CrossRef]
- Voyles, P.M. Informatics and data science in materials microscopy. Curr. Opin. Solid State Mater. Sci. 2017, 21, 141–158. [Google Scholar] [CrossRef]
- Davies, M.B.; Fitzner, M.; Michaelides, A. Accurate prediction of ice nucleation from room temperature water. Proc. Natl. Acad. Sci. USA 2022, 119, e2205347119. [Google Scholar] [CrossRef]
- Deringer, V.L.; Bartók, A.P.; Bernstein, N.; Wilkins, D.M.; Ceriotti, M.; Csányi, G. Gaussian Process Regression for Materials and Molecules. Chem. Rev. 2021, 121, 10073–10141. [Google Scholar] [CrossRef]
- Boussaidi, M.A.; Ren, O.; Voytsekhovsky, D.; Manzhos, S. Random Sampling High Dimensional Model Representation Gaussian Process Regression (RS-HDMR-GPR) for Multivariate Function Representation: Application to Molecular Potential Energy Surfaces. J. Phys. Chem. A 2020, 124, 7598–7607. [Google Scholar] [CrossRef]
- Alber, M.; Buganza Tepole, A.; Cannon, W.R.; De, S.; Dura-Bernal, S.; Garikipati, K.; Karniadakis, G.; Lytton, W.W.; Perdikaris, P.; Petzold, L.; et al. Integrating machine learning and multiscale modeling—Perspectives, challenges, and opportunities in the biological, biomedical, and behavioral sciences. npj Digit. Med. 2019, 2, 115. [Google Scholar] [CrossRef] [PubMed]
- Sofos, F.; Stavrogiannis, C.; Exarchou-Kouveli, K.K.; Akabua, D.; Charilas, G.; Karakasidis, T.E. Current Trends in Fluid Research in the Era of Artificial Intelligence: A Review. Fluids 2022, 7, 116. [Google Scholar] [CrossRef]
- Schran, C.; Thiemann, F.L.; Rowe, P.; Müller, E.A.; Marsalek, O.; Michaelides, A. Machine learning potentials for complex aqueous systems made simple. Proc. Natl. Acad. Sci. USA 2021, 118, e2110077118. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Alam, T.M.; Allers, J.P.; Leverant, C.J.; Harvey, J.A. Symbolic regression development of empirical equations for diffusion in Lennard-Jones fluids. J. Chem. Phys. 2022, 157, 014503. [Google Scholar] [CrossRef] [PubMed]
- Papastamatiou, K.; Sofos, F.; Karakasidis, T.E. Machine learning symbolic equations for diffusion with physics-based descriptions. AIP Adv. 2022, 12, 025004. [Google Scholar] [CrossRef]
- Marsh, K.N.; Boxall, J.A.; Lichtenthaler, R. Room temperature ionic liquids and their mixtures—A review. Fluid Phase Equilibria 2004, 219, 93–98. [Google Scholar] [CrossRef]
- Gao, T.; Itliong, J.; Kumar, S.P.; Hjorth, Z.; Nakamura, I. Polarization of ionic liquid and polymer and its implications for polymerized ionic liquids: An overview towards a new theory and simulation. J. Polym. Sci. 2021, 59, 2434–2457. [Google Scholar] [CrossRef]
- Mousavi, S.P.; Atashrouz, S.; Nait Amar, M.; Hemmati-Sarapardeh, A.; Mohaddespour, A.; Mosavi, A. Viscosity of Ionic Liquids: Application of the Eyring’s Theory and a Committee Machine Intelligent System. Molecules 2021, 26, 156. [Google Scholar] [CrossRef]
- Earle, M.J.; Esperança, J.M.S.S.; Gilea, M.A.; Canongia Lopes, J.N.; Rebelo, L.P.N.; Magee, J.W.; Seddon, K.R.; Widegren, J.A. The distillation and volatility of ionic liquids. Nature 2006, 439, 831–834. [Google Scholar] [CrossRef]
- Armand, M.; Endres, F.; MacFarlane, D.R.; Ohno, H.; Scrosati, B. Ionic-liquid materials for the electrochemical challenges of the future. Nat. Mater. 2009, 8, 621–629. [Google Scholar] [CrossRef] [PubMed]
- Koutsoumpos, S.; Giannios, P.; Stavrakas, I.; Moutzouris, K. The derivative method of critical-angle refractometry for attenuating media. J. Opt. 2020, 22, 075601. [Google Scholar] [CrossRef]
- Tsuda, T.; Kawakami, K.; Mochizuki, E.; Kuwabata, S. Ionic liquid-based transmission electron microscopy for herpes simplex virus type 1. Biophys. Rev. 2018, 10, 927–929. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Cui, X.; Zhang, Y.; Feng, T.; Lin, R.; Li, X.; Jie, H. Measurement and correlation of electrical conductivity of ionic liquid [EMIM][DCA] in propylene carbonate and γ-butyrolactone. Electrochim. Acta 2015, 174, 900–907. [Google Scholar] [CrossRef]
- Koutsoukos, S.; Philippi, F.; Malaret, F.; Welton, T. A review on machine learning algorithms for the ionic liquid chemical space. Chem. Sci. 2021, 12, 6820–6843. [Google Scholar] [CrossRef]
- Duong, D.V.; Tran, H.-V.; Pathirannahalage, S.K.; Brown, S.J.; Hassett, M.; Yalcin, D.; Meftahi, N.; Christofferson, A.J.; Greaves, T.L.; Le, T.C. Machine learning investigation of viscosity and ionic conductivity of protic ionic liquids in water mixtures. J. Chem. Phys. 2022, 156, 154503. [Google Scholar] [CrossRef] [PubMed]
- Daryayehsalameh, B.; Nabavi, M.; Vaferi, B. Modeling of CO2 capture ability of [Bmim][BF4] ionic liquid using connectionist smart paradigms. Environ. Technol. Innov. 2021, 22, 101484. [Google Scholar] [CrossRef]
- Beckner, W.; Ashraf, C.; Lee, J.; Beck, D.A.C.; Pfaendtner, J. Continuous Molecular Representations of Ionic Liquids. J. Phys. Chem. B 2020, 124, 8347–8357. [Google Scholar] [CrossRef]
- Bulut, S.; Eiden, P.; Beichel, W.; Slattery, J.M.; Beyersdorff, T.F.; Schubert, T.J.S.; Krossing, I. Temperature Dependence of the Viscosity and Conductivity of Mildly Functionalized and Non-Functionalized [Tf2N]−Ionic Liquids. ChemPhysChem 2011, 12, 2296–2310. [Google Scholar] [CrossRef]
- Leys, J.; Wübbenhorst, M.; Preethy Menon, C.; Rajesh, R.; Thoen, J.; Glorieux, C.; Nockemann, P.; Thijs, B.; Binnemans, K.; Longuemart, S. Temperature dependence of the electrical conductivity of imidazolium ionic liquids. J. Chem. Phys. 2008, 128, 064509. [Google Scholar] [CrossRef]
- Rodil, E.; Arce, A.; Arce, A.; Soto, A. Measurements of the density, refractive index, electrical conductivity, thermal conductivity and dynamic viscosity for tributylmethylphosphonium and methylsulfate based ionic liquids. Thermochim. Acta 2018, 664, 81–90. [Google Scholar] [CrossRef]
- Bandrés, I.; Montaño, D.F.; Gascón, I.; Cea, P.; Lafuente, C. Study of the conductivity behavior of pyridinium-based ionic liquids. Electrochim. Acta 2010, 55, 2252–2257. [Google Scholar] [CrossRef]
- Slattery, J.M.; Daguenet, C.; Dyson, P.J.; Schubert, T.J.S.; Krossing, I. How to Predict the Physical Properties of Ionic Liquids: A Volume-Based Approach. Angew. Chem. Int. Ed. 2007, 46, 5384–5388. [Google Scholar] [CrossRef] [PubMed]
- Beichel, W.; Preiss, U.P.; Verevkin, S.P.; Koslowski, T.; Krossing, I. Empirical description and prediction of ionic liquids’ properties with augmented volume-based thermodynamics. J. Mol. Liq. 2014, 192, 3–8. [Google Scholar] [CrossRef]
- Ionic Liquids Database-ILThermo. NIST Standard Reference Database #147. Available online: https://ilthermo.boulder.nist.gov/ (accessed on 4 August 2022).
- Dong, Q.; Muzny, C.D.; Kazakov, A.; Diky, V.; Magee, J.W.; Widegren, J.A.; Chirico, R.D.; Marsh, K.N.; Frenkel, M. ILThermo: A Free-Access Web Database for Thermodynamic Properties of Ionic Liquids. J. Chem. Eng. Data 2007, 52, 1151–1159. [Google Scholar] [CrossRef]
- Zec, N.; Bešter-Rogač, M.; Vraneš, M.; Gadžurić, S. Physicochemical properties of (1-butyl-1-methylpyrrolydinium dicyanamide+γ-butyrolactone) binary mixtures. J. Chem. Thermodyn. 2015, 91, 327–335. [Google Scholar] [CrossRef]
- Vila, J.; Fernández-Castro, B.; Rilo, E.; Carrete, J.; Domínguez-Pérez, M.; Rodríguez, J.R.; García, M.; Varela, L.M.; Cabeza, O. Liquid–solid–liquid phase transition hysteresis loops in the ionic conductivity of ten imidazolium-based ionic liquids. Fluid Phase Equilibria 2012, 320, 1–10. [Google Scholar] [CrossRef]
- Harris, K.R.; Kanakubo, M.; Kodama, D.; Makino, T.; Mizuguchi, Y.; Watanabe, M.; Watanabe, T. Temperature and Density Dependence of the Transport Properties of the Ionic Liquid Triethylpentylphosphonium Bis(trifluoromethanesulfonyl)amide, [P222,5][Tf2N]. J. Chem. Eng. Data 2018, 63, 2015–2027. [Google Scholar] [CrossRef]
- Harris, K.R.; Kanakubo, M.; Tsuchihashi, N.; Ibuki, K.; Ueno, M. Effect of Pressure on the Transport Properties of Ionic Liquids: 1-Alkyl-3-methylimidazolium Salts. J. Phys. Chem. B 2008, 112, 9830–9840. [Google Scholar] [CrossRef]
- Vranes, M.; Dozic, S.; Djeric, V.; Gadzuric, S. Physicochemical Characterization of 1-Butyl-3-methylimidazolium and 1-Butyl-1-methylpyrrolidinium Bis(trifluoromethylsulfonyl)imide. J. Chem. Eng. Data 2012, 57, 1072–1077. [Google Scholar] [CrossRef]
- Kanakubo, M.; Harris, K.R.; Tsuchihashi, N.; Ibuki, K.; Ueno, M. Temperature and pressure dependence of the electrical conductivity of the ionic liquids 1-methyl-3-octylimidazolium hexafluorophosphate and 1-methyl-3-octylimidazolium tetrafluoroborate. Fluid Phase Equilibria 2007, 261, 414–420. [Google Scholar] [CrossRef]
- Kanakubo, M.; Harris, K.R.; Tsuchihashi, N.; Ibuki, K.; Ueno, M. Effect of Pressure on Transport Properties of the Ionic Liquid 1-Butyl-3-methylimidazolium Hexafluorophosphate. J. Phys. Chem. B 2007, 111, 2062–2069. [Google Scholar] [CrossRef] [PubMed]
- Oleinikova, A.; Bonetti, M. Critical Behavior of the Electrical Conductivity of Concentrated Electrolytes: Ethylammonium Nitrate in n-Octanol Binary Mixture. J. Solut. Chem. 2002, 31, 397–413. [Google Scholar] [CrossRef]
- Kanakubo, M.; Harris, K.R. Density of 1-Butyl-3-methylimidazolium Bis(trifluoromethanesulfonyl)amide and 1-Hexyl-3-methylimidazolium Bis(trifluoromethanesulfonyl)amide over an Extended Pressure Range up to 250 MPa. J. Chem. Eng. Data 2015, 60, 1408–1418. [Google Scholar] [CrossRef]
- Vila, J.; Ginés, P.; Pico, J.M.; Franjo, C.; Jiménez, E.; Varela, L.M.; Cabeza, O. Temperature dependence of the electrical conductivity in EMIM-based ionic liquids: Evidence of Vogel–Tamman–Fulcher behavior. Fluid Phase Equilibria 2006, 242, 141–146. [Google Scholar] [CrossRef]
- Machanová, K.; Boisset, A.; Sedláková, Z.; Anouti, M.; Bendová, M.; Jacquemin, J. Thermophysical Properties of Ammonium-Based Bis{(trifluoromethyl)sulfonyl}imide Ionic Liquids: Volumetric and Transport Properties. Chem. Eng. Data 2012, 57, 2227–2235. [Google Scholar] [CrossRef]
- Rad-Moghadam, K.; Hassani, S.A.R.M.; Roudsari, S.T. N-methyl-2-pyrrolidonium chlorosulfonate: An efficient ionic-liquid catalyst and mild sulfonating agent for one-pot synthesis of δ-sultones. J. Mol. Liq. 2016, 218, 275–280. [Google Scholar] [CrossRef]
- Fleshman, A.M.; Mauro, N.A. Temperature-dependent structure and transport of ionic liquids with short-and intermediate-chain length pyrrolidinium cations. J. Mol. Liq. 2019, 279, 23–31. [Google Scholar] [CrossRef]
- Nazet, A.; Sokolov, S.; Sonnleitner, T.; Makino, T.; Kanakubo, M.; Buchner, R. Densities, Viscosities, and Conductivities of the Imidazolium Ionic Liquids [Emim][Ac], [Emim][FAP], [Bmim][BETI], [Bmim][FSI], [Hmim][TFSI], and [Omim][TFSI]. J. Chem. Eng. Data 2015, 60, 2400–2411. [Google Scholar] [CrossRef]
- Abdurrokhman, I.; Elamin, K.; Danyliv, O.; Hasani, M.; Swenson, J.; Martinelli, A. Protic Ionic Liquids Based on the Alkyl-Imidazolium Cation: Effect of the Alkyl Chain Length on Structure and Dynamics. J. Phys. Chem. B 2019, 123, 4044–4054. [Google Scholar] [CrossRef]
- Bandrés, I.; Carmen López, M.; Castro, M.; Barberá, J.; Lafuente, C. Thermophysical properties of 1-propylpyridinium tetrafluoroborate. J. Chem. Thermodyn. 2012, 44, 148–153. [Google Scholar] [CrossRef]
- García-Mardones, M.; Bandrés, I.; López, M.C.; Gascón, I.; Lafuente, C. Experimental and Theoretical Study of Two Pyridinium-Based Ionic Liquids. J Solut. Chem. 2012, 41, 1836–1852. [Google Scholar] [CrossRef]
- Yamamoto, T.; Matsumoto, K.; Hagiwara, R.; Nohira, T. Physicochemical and Electrochemical Properties of K[N(SO2F)2]–[N-Methyl-N-propylpyrrolidinium][N(SO2F)2] Ionic Liquids for Potassium-Ion Batteries. J. Phys. Chem. C 2017, 121, 18450–18458. [Google Scholar] [CrossRef]
- Cabeza, O.; Vila, J.; Rilo, E.; Domínguez-Pérez, M.; Otero-Cernadas, L.; López-Lago, E.; Méndez-Morales, T.; Varela, L.M. Physical properties of aqueous mixtures of the ionic 1-ethl-3-methyl imidazolium octyl sulfate: A new ionic rigid gel. J. Chem. Thermodyn. 2014, 75, 52–57. [Google Scholar] [CrossRef]
- Stoppa, A.; Zech, O.; Kunz, W.; Buchner, R. The Conductivity of Imidazolium-Based Ionic Liquids from (−35 to 195) °C. A. Variation of Cation’s Alkyl Chain. J. Chem. Eng. Data 2010, 55, 1768–1773. [Google Scholar] [CrossRef]
- Zech, O.; Stoppa, A.; Buchner, R.; Kunz, W. The Conductivity of Imidazolium-Based Ionic Liquids from (248 to 468) K. B. Variation of the Anion. J. Chem. Eng. Data 2010, 55, 1774–1778. [Google Scholar] [CrossRef]
- Nazet, A.; Sokolov, S.; Sonnleitner, T.; Friesen, S.; Buchner, R. Densities, Refractive Indices, Viscosities, and Conductivities of Non-Imidazolium Ionic Liquids [Et3S][TFSI], [Et2MeS][TFSI], [BuPy][TFSI], [N8881][TFA], and [P14][DCA]. J. Chem. Eng. Data 2017, 62, 2549–2561. [Google Scholar] [CrossRef]
- Benito, J.; García-Mardones, M.; Pérez-Gregorio, V.; Gascón, I.; Lafuente, C. Physicochemical Study of n-Ethylpyridinium bis(trifluoromethylsulfonyl)imide Ionic Liquid. J Solut. Chem. 2014, 43, 696–710. [Google Scholar] [CrossRef]
- Kasprzak, D.; Stępniak, I.; Galiński, M. Electrodes and hydrogel electrolytes based on cellulose: Fabrication and characterization as EDLC components. J. Solid State Electrochem. 2018, 22, 3035–3047. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine Learning for Fluid Mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Cranmer, M.; Sanchez Gonzalez, A.; Battaglia, P.; Xu, R.; Cranmer, K.; Spergel, D.; Ho, S. Discovering symbolic models from deep learning with inductive biases. In Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS 2020), Vancouver, BC, Canada, 6–12 December 2020; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: New York, NY, USA, 2020; Volume 33, pp. 17429–17442. [Google Scholar]
- Uyanık, G.K.; Güler, N. A Study on Multiple Linear Regression Analysis. Procedia-Soc. Behav. Sci. 2013, 106, 234–240. [Google Scholar] [CrossRef]
- Rahman, J.; Ahmed, K.S.; Khan, N.I.; Islam, K.; Mangalathu, S. Data-driven shear strength prediction of steel fiber reinforced concrete beams using machine learning approach. Eng. Struct. 2021, 233, 111743. [Google Scholar] [CrossRef]
- Song, Y.; Liang, J.; Lu, J.; Zhao, X. An efficient instance selection algorithm for k nearest neighbor regression. Neurocomputing 2017, 251, 26–34. [Google Scholar] [CrossRef]
- Loh, W.-Y. Classification and regression trees. WIREs Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Schmidt, J.; Marques, M.R.G.; Botti, S.; Marques, M.A.L. Recent advances and applications of machine learning in solid-state materials science. npj Comput. Mater. 2019, 5, 83. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.E. Nanoscale slip length prediction with machine learning tools. Sci. Rep. 2021, 11, 12520. [Google Scholar] [CrossRef]
- Allers, J.P.; Harvey, J.A.; Garzon, F.H.; Alam, T.M. Machine learning prediction of self-diffusion in Lennard-Jones fluids. J. Chem. Phys. 2020, 153, 034102. [Google Scholar] [CrossRef]
- Sandhu, A.K.; Batth, R.S. Software reuse analytics using integrated random forest and gradient boosting machine learning algorithm. Softw Pract. Exp. 2021, 51, 735–747. [Google Scholar] [CrossRef]
- Jerome, H. Friedman Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Stathakis, D. How Many Hidden Layers and Nodes? Int. J. Remote Sens. 2009, 30, 2133–2147. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, 6908. [Google Scholar] [CrossRef]
- Wang, Y.; Wagner, N.; Rondinelli, J.M. Symbolic regression in materials science. MRS Commun. 2019, 9, 793–805. [Google Scholar] [CrossRef]
- Sofos, F.; Charakopoulos, A.; Papastamatiou, K.; Karakasidis, T.E. A combined clustering/symbolic regression framework for fluid property prediction. Phys. Fluids 2022, 34, 062004. [Google Scholar] [CrossRef]
- Agrawal, A.; Deshpande, P.D.; Cecen, A.; Basavarsu, G.P.; Choudhary, A.N.; Kalidindi, S.R. Exploration of data science techniques to predict fatigue strength of steel from composition and processing parameters. Integr. Mater. Manuf. Innov. 2014, 3, 90–108. [Google Scholar] [CrossRef]
- Bengfort, B.; Bilbro, R. Yellowbrick: Visualizing the Scikit-Learn Model Selection Process. J. Open Source Softw. 2019, 4, 1075. [Google Scholar] [CrossRef]


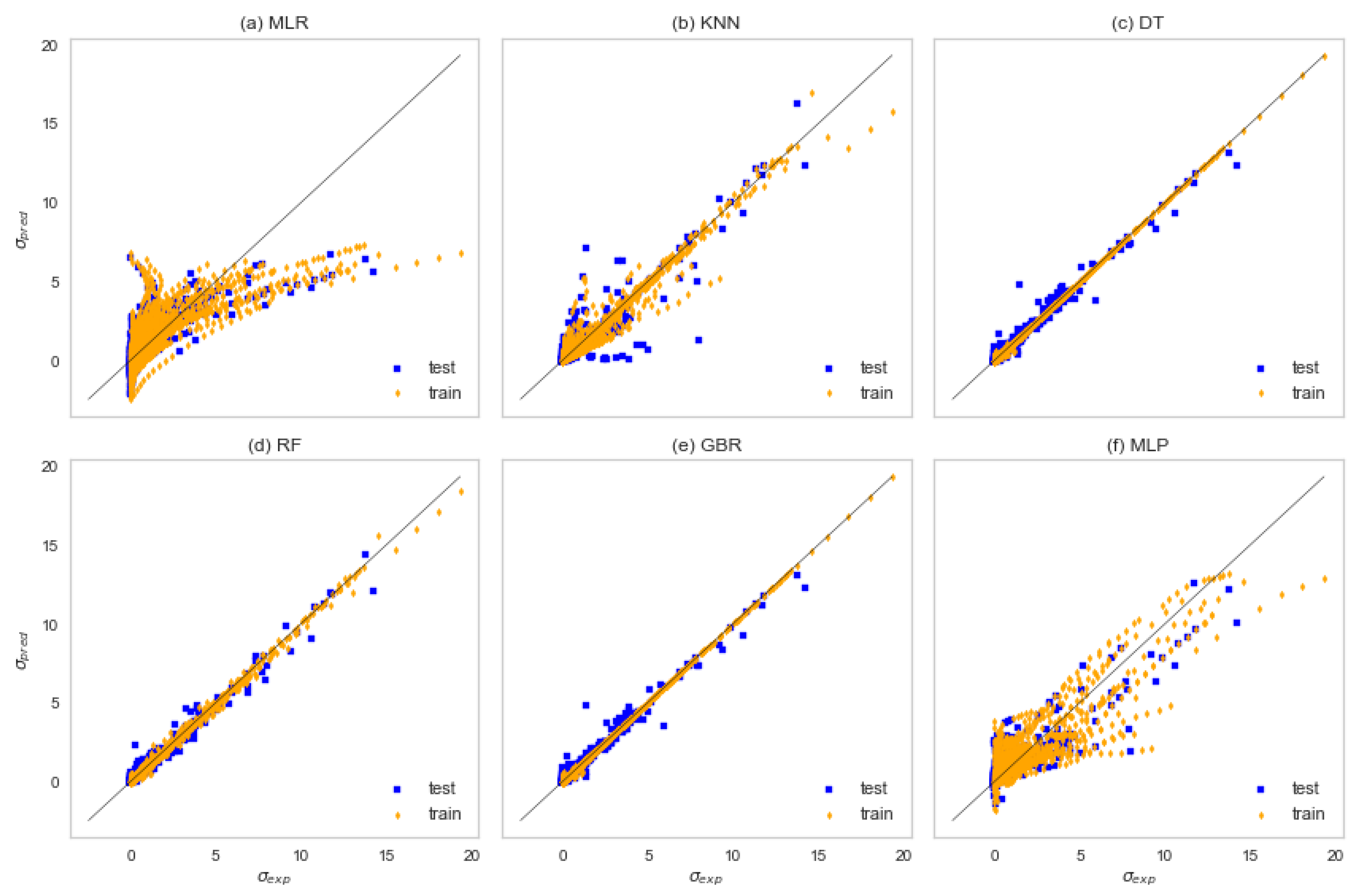

| Algorithm | R2 | MAE | MSE | AAD |
|---|---|---|---|---|
| MLR | 0.69701 | 1.02 | 2.287 | 663720.1 |
| KNN | 0.91344 | 0.381 | 0.755 | 1265.019 |
| DT | 0.98916 | 0.138 | 0.098 | 536.7186 |
| RF | 0.98919 | 0.16 | 0.097 | 1635.613 |
| GBR | 0.98886 | 0.137 | 0.1 | 271.6886 |
| MLP | 0.86707 | 0.706 | 1.107 | 35444.57 |
| Equation | Comp. | R2 | MAE | MSE | AAD |
|---|---|---|---|---|---|
| 6 | 0.760 | 1.234 | 2.846 | 2,660,488.8 | |
| 19 | 0.857 | 0.727 | 1.392 | 149,183.5 | |
| 20 | 0.883 | 0.728 | 1.160 | 3,551,375.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karakasidis, T.E.; Sofos, F.; Tsonos, C. The Electrical Conductivity of Ionic Liquids: Numerical and Analytical Machine Learning Approaches. Fluids 2022, 7, 321. https://doi.org/10.3390/fluids7100321
Karakasidis TE, Sofos F, Tsonos C. The Electrical Conductivity of Ionic Liquids: Numerical and Analytical Machine Learning Approaches. Fluids. 2022; 7(10):321. https://doi.org/10.3390/fluids7100321
Chicago/Turabian StyleKarakasidis, Theodoros E., Filippos Sofos, and Christos Tsonos. 2022. "The Electrical Conductivity of Ionic Liquids: Numerical and Analytical Machine Learning Approaches" Fluids 7, no. 10: 321. https://doi.org/10.3390/fluids7100321
APA StyleKarakasidis, T. E., Sofos, F., & Tsonos, C. (2022). The Electrical Conductivity of Ionic Liquids: Numerical and Analytical Machine Learning Approaches. Fluids, 7(10), 321. https://doi.org/10.3390/fluids7100321









