Dilational Rheology of Fluid/Fluid Interfaces: Foundations and Tools
Abstract
1. Introduction
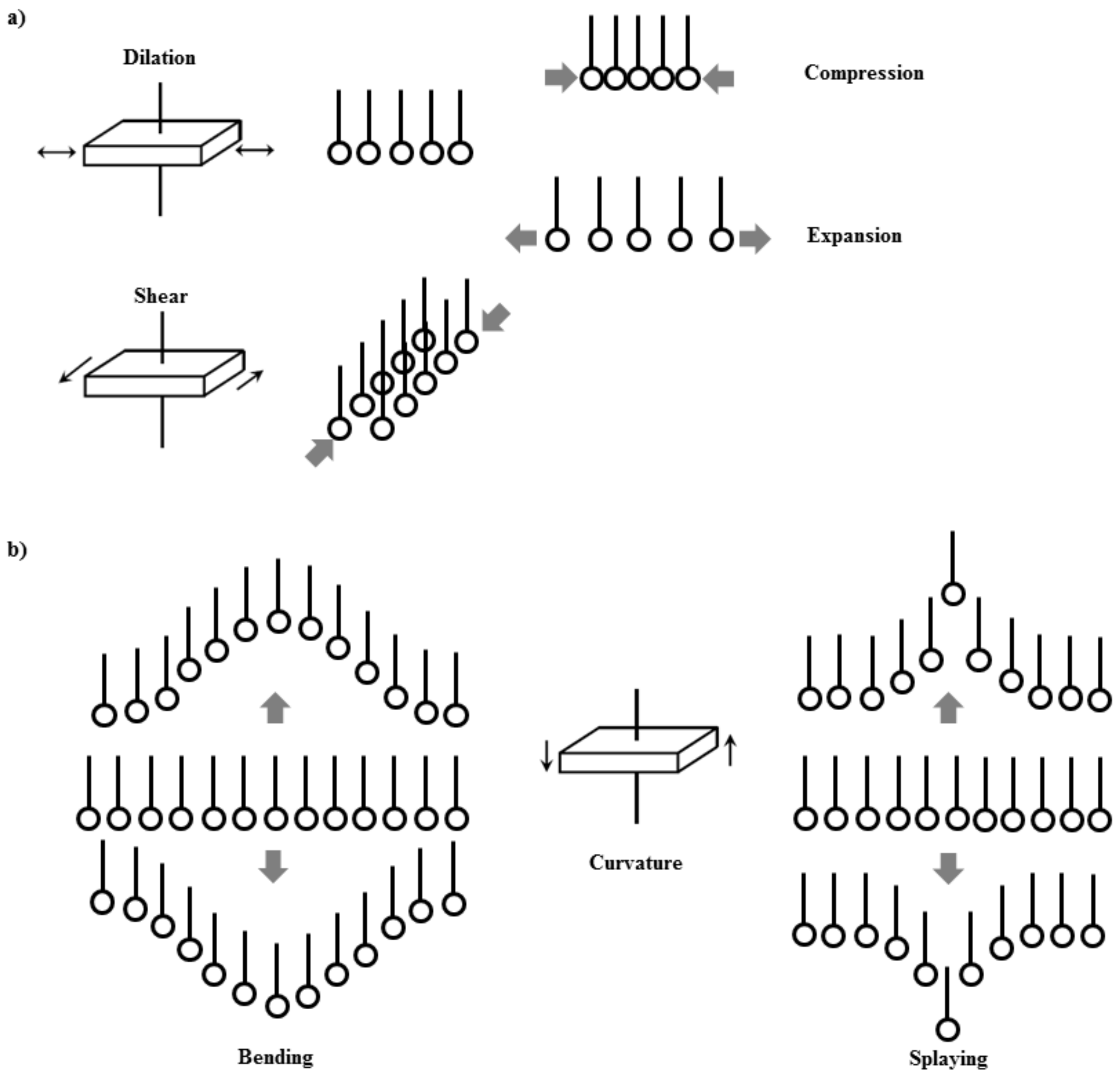
2. Interfacial Rheology: Foundations
3. Interfacial Dilational Rheology: General Aspects
4. Rheological Tools for Evaluating the Response of Planar Fluid/Fluid Interfaces against Dilation
4.1. Experimental Tools
4.1.1. Experimental Techniques
Drop/Bubble Shape Tensiometers
Capillary Pressure Tensiometers
Langmuir Troughs
Wave Damping
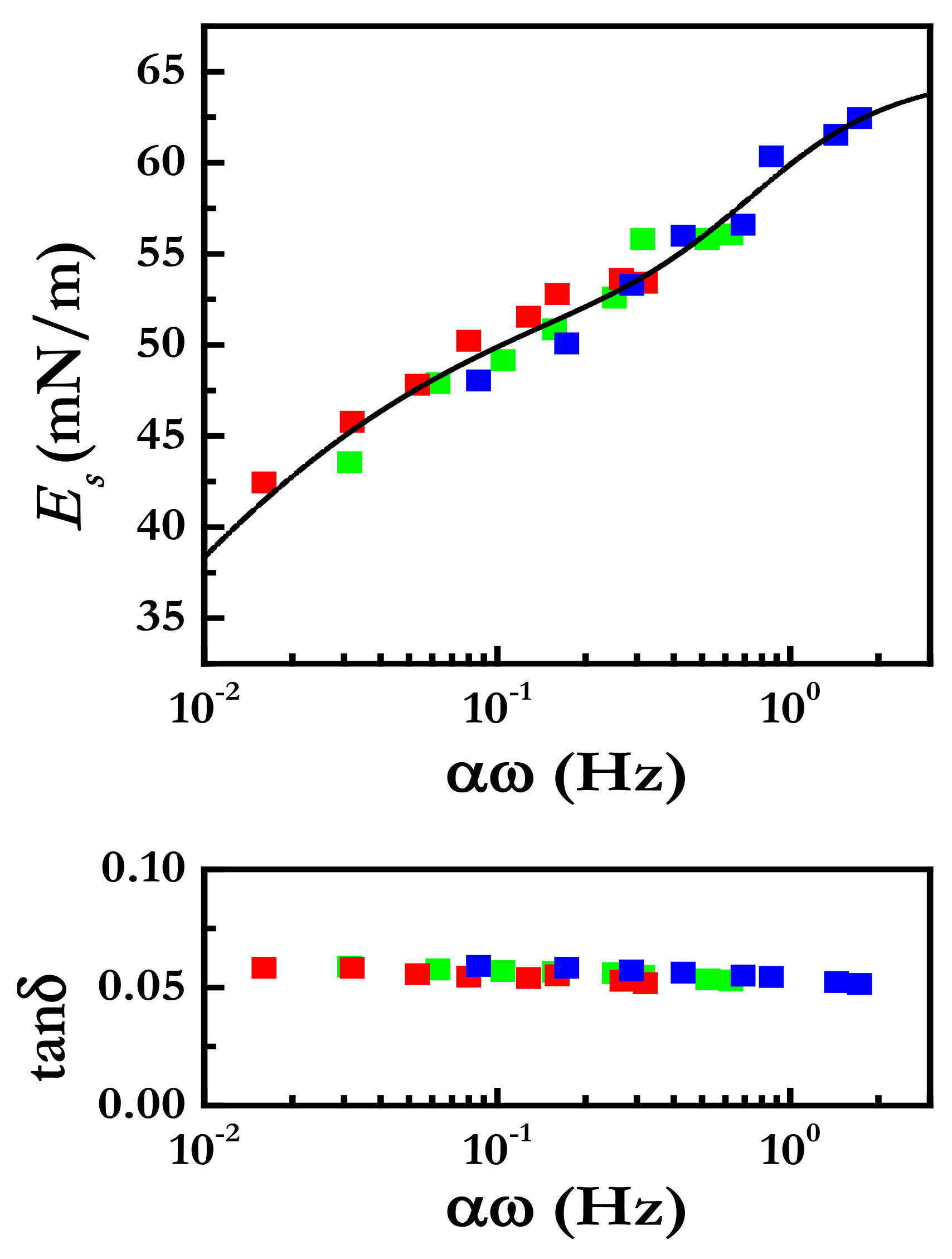
4.1.2. Experimental Methods
Stress Relaxation Experiments
Creep Experiments
Oscillatory Area Experiments
Surface Waves Experiments
4.2. Theoretical Models
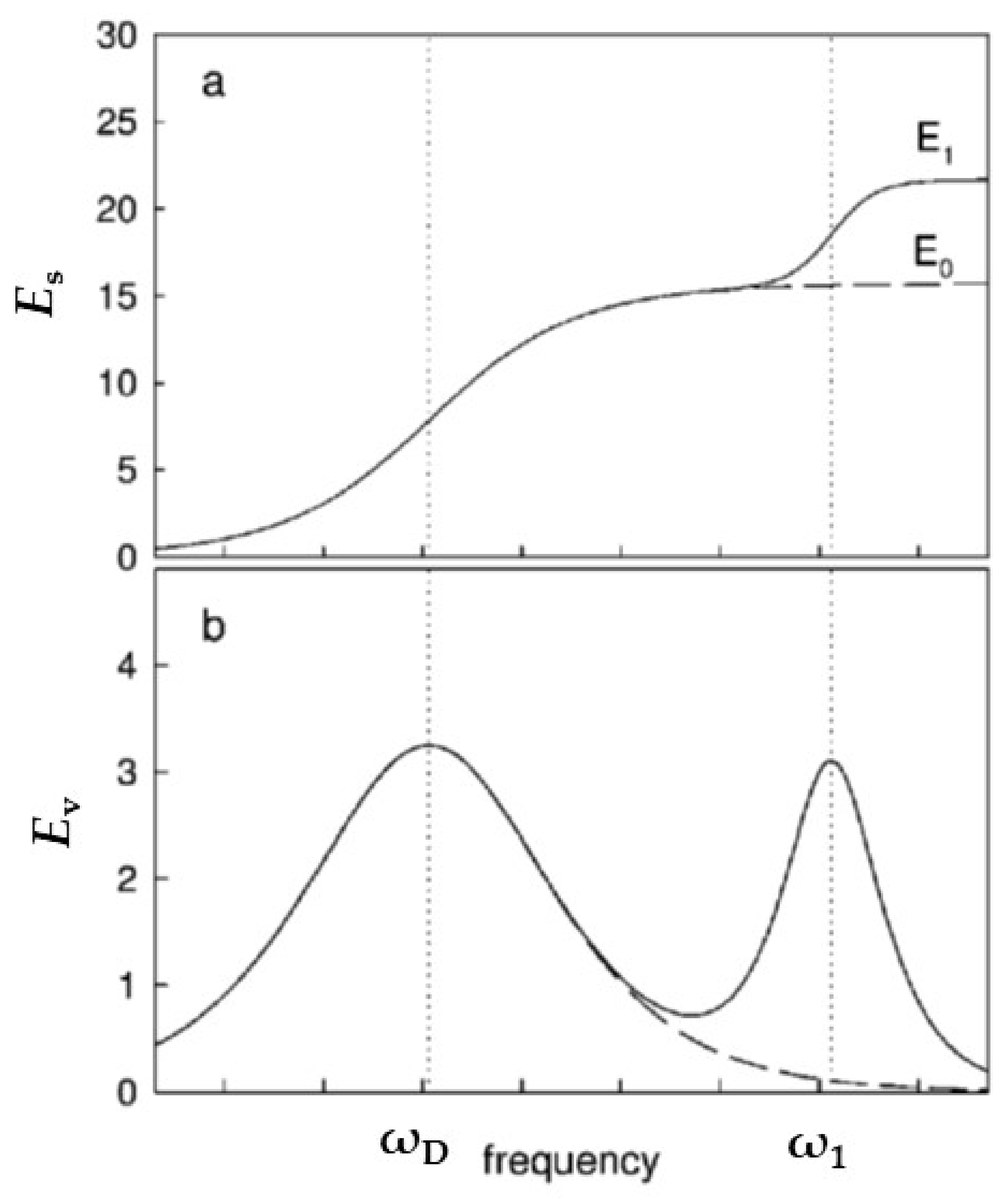
5. Evaluation of the Mechanical Relaxation Spectrum from Dilational Rheology Experiments
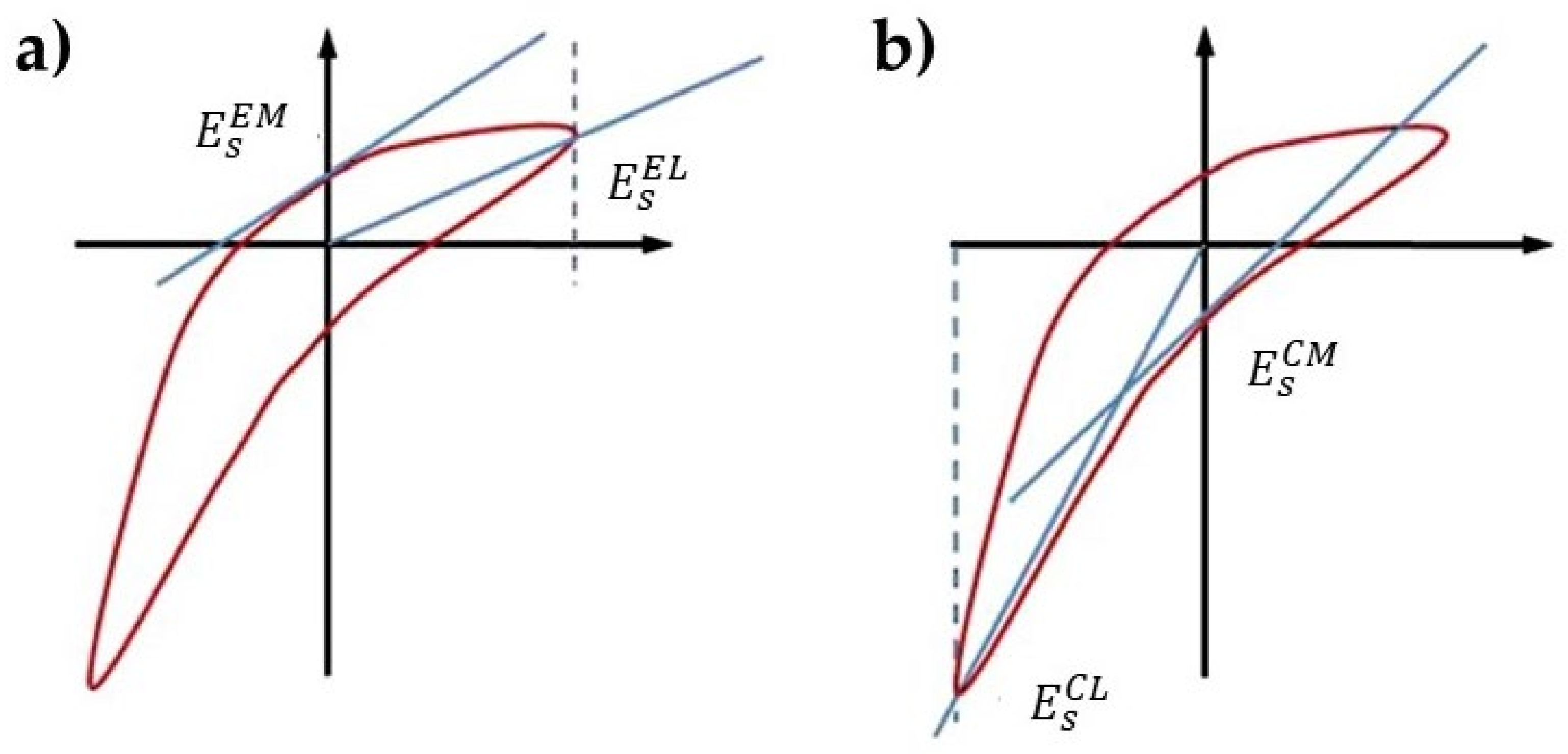
6. Non-Linear Dilational Interfacial Rheology
7. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Forth, J.; Kim, P.Y.; Xie, G.; Liu, X.; Helms, B.A.; Russell, T.P. Building Reconfigurable Devices Using Complex Liquid–Fluid Interfaces. Adv. Mater. 2019, 31, 1806370. [Google Scholar] [CrossRef] [PubMed]
- Guzmán, E. Current Perspective on the Study of Liquid–Fluid Interfaces: From Fundamentals to Innovative Applications. Coatings 2022, 12, 841. [Google Scholar] [CrossRef]
- Guzmán, E.; Martínez-Pedrero, F.; Calero, C.; Maestro, A.; Ortega, F.; Rubio, R.G. A broad perspective to particle-laden fluid interfaces systems: From chemically homogeneous particles to active colloids. Adv. Colloids Interface Sci. 2022, 302, 102620. [Google Scholar] [CrossRef] [PubMed]
- Guzmán, E. Fluid Films as Models for Understanding the Impact of Inhaled Particles in Lung Surfactant Layers. Coatings 2022, 12, 277. [Google Scholar] [CrossRef]
- Guzmán, E.; Santini, E. Lung surfactant-particles at fluid interfaces for toxicity assessments. Curr. Opin. Colloid Interface Sci. 2019, 39, 24–39. [Google Scholar] [CrossRef]
- Klein, C.O.; Theodoratou, A.; Rühs, P.A.; Jonas, U.; Loppinet, B.; Wilhelm, M.; Fischer, P.; Vermant, J.; Vlassopoulos, D. Interfacial Fourier transform shear rheometry of complex fluid interfaces. Rheol. Acta 2019, 58, 29–45. [Google Scholar] [CrossRef]
- Masuda, T.; Takai, M. Design of biointerfaces composed of soft materials using controlled radical polymerizations. J. Mater. Chem. B 2022, 10, 1473–1485. [Google Scholar] [CrossRef]
- Sagis, L.M.C.; Liu, B.; Li, Y.; Essers, J.; Yang, J.; Moghimikheirabadi, A.; Hinderink, E.; Berton-Carabin, C.; Schroen, K. Dynamic heterogeneity in complex interfaces of soft interface-dominated materials. Sci. Rep. 2019, 9, 2938. [Google Scholar] [CrossRef]
- Jaensson, N.; Vermant, J. Tensiometry and rheology of complex interfaces. Curr. Opin. Colloid Interface Sci. 2018, 37, 136–150. [Google Scholar] [CrossRef]
- Jaensson, N.O.; Anderson, P.D.; Vermant, J. Computational interfacial rheology. J. Non-Newton. Fluid Mech. 2021, 290, 104507. [Google Scholar] [CrossRef]
- Wei, Y.; Xie, Y.; Cai, Z.; Guo, Y.; Zhang, H. Interfacial rheology, emulsifying property and emulsion stability of glyceryl monooleate-modified corn fiber gum. Food Chem. 2021, 343, 128416. [Google Scholar] [CrossRef]
- Botti, T.C.; Hutin, A.; Quintella, E.; Carvalho, M.S. Effect of interfacial rheology on drop coalescence in water–oil emulsion. Soft Matter 2022, 18, 1423–1434. [Google Scholar] [CrossRef]
- Wang, H.; Wei, X.; Du, Y.; Wang, D. Experimental investigation on the dilatational interfacial rheology of dust-suppressing foam and its effect on foam performance. Process. Saf. Environ. Prot. 2019, 123, 351–357. [Google Scholar] [CrossRef]
- Thai, L.P.A.; Mousseau, F.; Oikonomou, E.K.; Berret, J.F. On the rheology of pulmonary surfactant: Effects of concentration and consequences for the surfactant replacement therapy. Colloids Surf. B 2019, 178, 337–345. [Google Scholar] [CrossRef]
- Haslbeck, K.; Schwarz, K.; Hohlfeld, J.M.; Seume, J.R.; Koch, W. Submicron droplet formation in the human lung. J. Aerosol Sci. 2010, 41, 429–438. [Google Scholar] [CrossRef]
- Svitova, T.F.; Lin, M.C. Tear lipids interfacial rheology: Effect of lysozyme and lens care solutions. Optom. Vis. Sci. 2010, 87, 10–20. [Google Scholar] [CrossRef]
- Rubio, R.G.; Guzmán, E.; Ortega, F.; Liggieri, L. Monolayers of Cholesterol and Cholesteryl Stearate at the Water/Vapor Interface: A Physico-Chemical Study of Components of the Meibum Layer. Colloids Interfaces 2021, 5, 30. [Google Scholar] [CrossRef]
- Zhang, H.; Lamnawar, K.; Maazouz, A. Fundamental studies of interfacial rheology at multilayered model polymers for coextrusion process. AIP Conf. Proc. 2015, 1664, 100008. [Google Scholar] [CrossRef]
- Perrin, L.; Akanno, A.; Guzman, E.; Ortega, F.; Rubio, R.G. Pattern Formation upon Evaporation of Sessile Droplets of Polyelectrolyte/Surfactant Mixtures on Silicon Wafers. Int. J. Mol. Sci. 2021, 22, 7953. [Google Scholar] [CrossRef]
- Sun, H.-Q.; Zhang, L.; Li, Z.-Q.; Zhang, L.; Luo, L.; Zhao, S. Interfacial dilational rheology related to enhance oil recovery. Soft Matter 2011, 7, 7601–7611. [Google Scholar] [CrossRef]
- Gade, M.; Byfield, V.; Ermakov, S.; Lavrova, O.; Mitnik, L. Slicks as Indicators for Marine Processes. Oceanography 2013, 26, 138–149. [Google Scholar] [CrossRef]
- Ermakov, S.A.; Khazanov, G.E. Resonance damping of gravity–capillary waves on water covered with a visco-elastic film of finite thickness: A reappraisal. Phys. Fluids 2022, 34, 092107. [Google Scholar] [CrossRef]
- Sánchez-Puga, P.; Tajuelo, J.; Pastor, J.M.; Rubio, M.A. Flow field-based data analysis in interfacial shear rheometry. Adv. Colloids Interface Sci. 2021, 288, 102332. [Google Scholar] [CrossRef]
- Guzmán, E.; Tajuelo, J.; Pastor, J.M.; Rubio, M.Á.; Ortega, F.; Rubio, R.G. Shear rheology of fluid interfaces: Closing the gap between macro- and micro-rheology. Curr. Opin. Colloid Interface Sci. 2018, 37, 33–48. [Google Scholar] [CrossRef]
- Wong, W.-H.B.; Hulsen, M.A.; Anderson, P.D. A numerical model for the development of the morphology of disperse blends in complex flow. Rheol. Acta 2019, 58, 79–95. [Google Scholar] [CrossRef]
- Nilsson, M.A.; Kulkarni, R.; Gerberich, L.; Hammond, R.; Singh, R.; Baumhoff, E.; Rothstein, J.P. Effect of fluid rheology on enhanced oil recovery in a microfluidic sandstone device. J. Non-Newton. Fluid Mech. 2013, 202, 112–119. [Google Scholar] [CrossRef]
- Perez, P.L.; Zaragoza, J.N.; Patel, N.K.; Dion, M.A. Impact of Asphaltene Stabilizers on the Elasticity of a Crude Oil–Water Interface and Its Correlation to Demulsification under Desalting Conditions. Energy Fuels 2022, 36, 275–289. [Google Scholar] [CrossRef]
- Guzmán, E.; Santini, E.; Ferrari, M.; Liggieri, L.; Ravera, F. Evaluating the Impact of Hydrophobic Silicon Dioxide in the Interfacial Properties of Lung Surfactant Films. ACS Environ. Sci. Technol. 2022, 56, 7308–7318. [Google Scholar] [CrossRef] [PubMed]
- Nagel, M.; Tervoort, T.A.; Vermant, J. From drop-shape analysis to stress-fitting elastometry. Adv. Colloids Interface Sci. 2017, 247, 33–51. [Google Scholar] [CrossRef] [PubMed]
- Mendoza, A.J.; Guzmán, E.; Martínez-Pedrero, F.; Ritacco, H.; Rubio, R.G.; Ortega, F.; Starov, V.M.; Miller, R. Particle laden fluid interfaces: Dynamics and interfacial rheology. Adv. Colloids Interface Sci. 2014, 206, 303–319. [Google Scholar] [CrossRef] [PubMed]
- Manikantan, H.; Squires, T.M. Surfactant dynamics: Hidden variables controlling fluid flows. J. Fluid Mech. 2020, 892, P1. [Google Scholar] [CrossRef]
- Krotov, V.V. Basics of Interfacial rheology. In Interfacial Rheology; Miller, R., Liggieri, L., Eds.; Brill: Leiden, The Netherlands, 2009; pp. 1–37. [Google Scholar]
- Garbin, V. Collapse mechanisms and extreme deformation of particle-laden interfaces. Curr. Opin. Colloid Interface Sci. 2019, 39, 202–211. [Google Scholar] [CrossRef]
- Maestro, A.; Guzmán, E. Colloids at Fluid Interfaces. Processes 2019, 7, 942. [Google Scholar] [CrossRef]
- Nitschke, I.; Voigt, A. Observer-invariant time derivatives on moving surfaces. J. Geom. Phys. 2022, 173, 104428. [Google Scholar] [CrossRef]
- Langevin, D. Light scattering by liquid surfaces, new developments. Adv. Colloids Interface Sci. 2021, 289, 102368. [Google Scholar] [CrossRef]
- Fuller, G.G.; Vermant, J. Complex Fluid-Fluid Interfaces: Rheology and Structure. Annu. Rev. Chem. Biomol. Eng. 2012, 3, 519–543. [Google Scholar] [CrossRef]
- Stone, H.A.; Leal, L.G. The effects of surfactants on drop deformation and breakup. J. Fluid Mech. 1990, 220, 161–186. [Google Scholar] [CrossRef]
- De Kinkelder, E.; Sagis, L.; Aland, S. A numerical method for the simulation of viscoelastic fluid surfaces. J. Comput. Phys. 2021, 440, 110413. [Google Scholar] [CrossRef]
- Pepicelli, M.; Verwijlen, T.; Tervoort, T.; Vermant, J. Characterization and modelling of Langmuir interfaces with finite elasticity. Soft Matter 2017, 13, 5977–5990. [Google Scholar] [CrossRef]
- Sagis, L. Dynamic surface tension of complex fluid-fluid interfaces: A useful concept, or not? Eur. Phys. J. Spec. Top. 2013, 222, 39–46. [Google Scholar] [CrossRef]
- Reichert, M.D.; Alvarez, N.J.; Brooks, C.F.; Grillet, A.M.; Mondy, L.A.; Anna, S.L.; Walker, L.M. The importance of experimental design on measurement of dynamic interfacial tension and interfacial rheology in diffusion-limited surfactant systems. Colloids Surf. A 2015, 467, 135–142. [Google Scholar] [CrossRef]
- Miller, R.; Ferri, J.; Javadi, A.; Krägel, J.; Mucic, N.; Wüstneck, R. Rheology of interfacial layers. Colloid Polym. Sci. 2010, 288, 937–950. [Google Scholar] [CrossRef]
- Karbaschi, M.; Lotfi, M.; Krägel, J.; Javadi, A.; Bastani, D.; Miller, R. Rheology of interfacial layers. Curr. Opin. Colloid Interface Sci. 2014, 19, 514–519. [Google Scholar] [CrossRef]
- Ravera, F.; Ferrari, M.; Santini, E.; Liggieri, L. Influence of surface processes on the dilational visco-elasticity of surfactant solutions. Adv. Colloids Interface Sci. 2005, 117, 75–100. [Google Scholar] [CrossRef]
- Guzmán, E.; Liggieri, L.; Santini, E.; Ferrari, M.; Ravera, F. Influence of silicananoparticles on dilational rheology of DPPC–palmitic acid Langmuir monolayers. Soft Matter 2012, 8, 3938–3948. [Google Scholar] [CrossRef]
- Guzmán, E.; Liggieri, L.; Santini, E.; Ferrari, M.; Ravera, F. Mixed DPPC–cholesterol Langmuir monolayers in presence of hydrophilic silica nanoparticles. Colloids Surf. B 2015, 105, 284–293. [Google Scholar] [CrossRef]
- Omari, Y.E.; Yousfi, M.; Duchet-Rumeau, J.; Maazouz, A. Recent Advances in the Interfacial Shear and Dilational Rheology of Polymer Systems: From Fundamentals to Applications. Polymers 2022, 14, 2844. [Google Scholar] [CrossRef]
- Ravera, F.; Miller, R.; Zuo, Y.Y.; Noskov, B.A.; Bykov, A.G.; Kovalchuk, V.I.; Loglio, G.; Javadi, A.; Liggieri, L. Methods and models to investigate the physicochemical functionality of pulmonary surfactant. Curr. Opin. Colloid Interface Sci. 2021, 55, 101467. [Google Scholar] [CrossRef]
- Firouzi, M.; Kovalchuk, V.I.; Loglio, G.; Miller, R. Salt effects on the dilational viscoelasticity of surfactant adsorption layers. Curr. Opin. Colloid Interface Sci. 2022, 57, 101538. [Google Scholar] [CrossRef]
- Akanno, A.; Guzmán, E.; Ortega, F.; Rubio, R.G. Behavior of the water/vapor interface of chitosan solutions with an anionic surfactant: Effect of polymer–surfactant interactions. Phys. Chem. Chem. Phys. 2020, 22, 23360–23373. [Google Scholar] [CrossRef]
- Bae, J.-E.; Jung, J.B.; Kim, K.; Lee, S.-M.; Kang, N.-G. A study on time-concentration superposition of dilatational modulus and foaming behavior of sodium alkyl sulfate. J. Colloid Interface Sci. 2019, 55, 704–716. [Google Scholar] [CrossRef]
- Suja, V.C.; Rodríguez-Hakim, M.; Tajuelo, J.; Fuller, G.G. Single bubble and drop techniques for characterizing foams and emulsions. Adv. Colloids Interface Sci. 2020, 286, 102295. [Google Scholar] [CrossRef]
- Akanno, A.; Perrin, L.; Guzmán, E.; Llamas, S.; Starov, V.M.; Ortega, F.; Rubio, R.G.; Velarde, M.G. Evaporation of Sessile Droplets of Polyelectrolyte/Surfactant Mixtures on Silicon Wafers. Colloids Interfaces 2021, 5, 12. [Google Scholar] [CrossRef]
- Noskov, B.A. Dilational surface rheology of polymer and polymer/surfactant solutions. Curr. Opin. Colloid Interface Sci. 2010, 15, 229–236. [Google Scholar] [CrossRef]
- Javadi, A.; Krägel, J.; Makievski, A.V.; Kovalchuk, V.I.; Kovalchuk, N.M.; Mucic, N.; Loglio, G.; Pandolfini, P.; Karbaschi, M.; Miller, R. Fast dynamic interfacial tension measurements and dilational rheology of interfacial layers by using the capillary pressure technique. Colloids Surf. A 2012, 407, 159–168. [Google Scholar] [CrossRef]
- Saad, S.; Neumann, A. Axisymmetric drop shape analysis (ADSA): An outline. Adv. Colloids Interface Sci. 2016, 238, 62–87. [Google Scholar] [CrossRef]
- Danov, K.; Stanimirova, R.; Kralchevsky, P.; Marinova, K.; Alexandrov, N.; Stoyanov, S.; Blijdenstein, T.; Pelan, E. Capillary meniscus dynamometry—method for determining the surface tension of drops and bubbles with isotropic and anisotropic surface stress distributions. J. Colloid Interface Sci. 2015, 440, 168–178. [Google Scholar] [CrossRef]
- Ravera, F.; Loglio, G.; Kovalchuk, V.I. Interfacial dilational rheology by oscillating bubble/drop methods. Curr. Opin. Colloid Interface Sci. 2010, 15, 217–228. [Google Scholar] [CrossRef]
- Kotula, A.P.; Anna, S.L. Regular perturbation analysis of small amplitude oscillatory dilatation of an interface in a capillary pressure tensiometer. J. Rheol. 2014, 59, 85–117. [Google Scholar] [CrossRef]
- Kovalchuk, V.I.; Krägel, J.; Makievski, A.V.; Loglio, G.; Ravera, F.; Liggieri, L.; Miller, R. Frequency characteristics of amplitude and phase of oscillating bubble systems in a closed measuring cell. J. Colloid Interface Sci. 2002, 252, 433–442. [Google Scholar] [CrossRef]
- Guzmán, E.; Santini, E.; Ferrari, M.; Liggieri, L.; Ravera, F. Evaluation of the impact of carbonaceous particles in the mechanical performance of lipid Langmuir monolayers. Colloids Surf. A 2022, 634, 127974. [Google Scholar] [CrossRef]
- Guzmán, E.; Santini, E.; Ferrari, M.; Liggieri, L.; Ravera, F. Interaction of Particles with Langmuir Monolayers of 1,2-Dipalmitoyl-Sn-Glycero-3-Phosphocholine: A Matter of Chemistry? Coatings 2020, 10, 469. [Google Scholar] [CrossRef]
- Petkov, J.; Gurkov, T.; Campbell, B.; Borwankar, R. Dilatational and shear elasticity of gel-like protein layers on air/water interface. Langmuir 2000, 16, 3703–3711. [Google Scholar] [CrossRef]
- Vora, S.; Bognet, B.; Patanwala, H.; Young, C.; Chang, S.; Daux, V.; Ma, A. Global strain field mapping of a particle-laden interface using digital image correlation. J. Colloid Interface Sci. 2018, 509, 94–101. [Google Scholar] [CrossRef]
- Alicke, A.; Simon, S.; Sjöblom, J.; Vermant, J. Assessing the interfacial activity of insoluble asphaltene layers: Interfacial rheology versus interfacial tension. Langmuir 2020, 36, 14942–14959. [Google Scholar] [CrossRef]
- Duncan, J.H.; Waxman, A.M.; Tulin, M.P. The dynamics of waves at the interface between a viscoelastic coating and a fluid flow. J. Fluid Mech. 1985, 158, 177–197. [Google Scholar] [CrossRef]
- Slavchov, R.I.; Peychev, B.; Ismail, A.S. Characterization of capillary waves: A review and a new optical method. Phys. Fluids 2021, 33, 101303. [Google Scholar] [CrossRef]
- Sergievskaya, I.; Ermakov, S.; Lazareva, T.; Guo, J. Damping of surface waves due to crude oil/oil emulsion films on water. Mar. Pollut. Bull. 2019, 146, 206–214. [Google Scholar] [CrossRef]
- Ermakov, S.A. Damping of gravity-capillary waves on water surface covered with a visco-elastic film of finite thickness. Izv. Atmos. Ocean. Phys. 2003, 39, 624–628. [Google Scholar]
- Ermakov, S.A.; Kijashko, S.V. Laboratory study of the damping of parametric ripples due to surfactant films. In Marine Surface Films. Chemical Characteristics, Influence on Air-Sea Interactions and Remote Sensing; Gade, M., Hühnerfuss, H., Korenowski, G.M., Eds.; Springer: Berlin, Germany, 2006; pp. 113–128. [Google Scholar]
- Langevin, D. Rheology of adsorbed surfactant monolayers at fluid surfaces. Annu. Rev. Fluid Mech. 2014, 46, 47–65. [Google Scholar] [CrossRef]
- Liu, X.; Duncan, J.H.; Korenowski, G.M.; Kelly, J.S. A laboratory study of longitudinal waves in surfactant films in a water wave tank. J. Geophys. Res. Oceans 2007, 122, C06005. [Google Scholar] [CrossRef]
- Rajan, G.K. Dissipation of interfacial Marangoni waves and their resonance with capillary-gravity waves. Int. J. Eng. Sci. 2020, 154, 103340. [Google Scholar] [CrossRef]
- Rajan, G.K. Solutions of a comprehensive dispersion relation for waves at the elastic interface of two viscous fluids. Eur. J. Mech. B Fluids 2021, 89, 241–258. [Google Scholar] [CrossRef]
- Derkach, S.R.; Krägel, J.; Miller, R. Methods of measuring rheological properties of interfacial layers (Experimental methods of 2D rheology). Colloid J. 2009, 71, 1–17. [Google Scholar] [CrossRef]
- Rajan, G.K. Damping rate measurements and predictions for gravity waves in an air–oil–water system. Phys. Fluids 2022, 34, 022113. [Google Scholar] [CrossRef]
- Lau, Y.M.; Westerweel, J.; Van De Water, W. Using Faraday Waves to Measure Interfacial Tension. Langmuir 2020, 36, 5872–5879. [Google Scholar] [CrossRef]
- Kharbedia, M.; Caselli, N.; Herráez-Aguilar, D.; López-Menéndez, H.; Enciso, E.; Santiago, J.A.; Monroy, F. Moulding hydrodynamic 2D-crystals upon parametric Faraday waves in shear-functionalized water surfaces. Nat. Commun. 2021, 12, 1130. [Google Scholar] [CrossRef]
- Henderson, D.M. Effects of surfactants on Faraday-wave dynamics. J. Fluid Mech. 1998, 365, 89–107. [Google Scholar] [CrossRef]
- Henderson, D.M.; Larsson, K.; Rao, Y.K. A study of wheat storage protein monolayers by Faraday wave damping. Langmuir 1991, 7, 2731–2736. [Google Scholar] [CrossRef]
- Monroy, F.; Ortega, F.; Rubio, R.G. Dilatational rheology of insoluble polymer monolayers: Poly(vinylacetate). Phys. Rev. E 1998, 58, 7629. [Google Scholar] [CrossRef]
- Guzmán, E.; Ritacco, H.; Ortega, F.; Svitova, T.; Radke, C.J.; Rubio, R.G. Adsorption Kinetics and Mechanical Properties of Ultrathin Polyelectrolyte Multilayers: Liquid-Supported versus Solid-Supported Films. J. Phys. Chem. B 2009, 113, 7128–7137. [Google Scholar] [CrossRef]
- Alexandrov, N.A.; Marinova, K.G.; Gurkov, T.D.; Danov, K.D.; Kralchevsky, P.A.; Stoyanov, S.D.; Blijdenstein, T.B.J.; Arnaudov, L.N.; Pelan, E.G. Interfacial layers from the protein HFBII hydrophobin: Dynamic surface tension, dilatational elasticity and relaxation times. J. Colloid Interface Sci. 2012, 376, 296–306. [Google Scholar] [CrossRef]
- Hilles, H.; Monroy, F. Dilational creep compliance in Langmuir polymer films. Soft Matter 2011, 7, 7790–7796. [Google Scholar] [CrossRef]
- Findley, W.N.; Lai, J.S.; Onaran, K. Creep and Relaxation of Nonlinear Viscoelastic Materials; Dover Publications, Inc.: New York, NY, USA, 1976. [Google Scholar]
- Ravera, F.; Liggieri, L.; Loglio, G. Dilational rheology of adsorbed layers by oscillating drops and bubbles. In Interfacial Rheology; Miller, R., Liggieri, L., Eds.; Brill: Leiden, The Netherlands, 2009; pp. 138–173. [Google Scholar]
- Lombardini, P.P.; Piazzese, F.; Cini, R. The Marangoni wave in ripples on an air-water interface covered by a spreading film. Il Nuovo Cimento C 1982, 5, 256–263. [Google Scholar] [CrossRef]
- Ghia, P.L.; Trivero, P. On the vibration modes of the air-water interface in the presence of surface films. Il Nuovo Cimento C 1988, 11, 305–315. [Google Scholar] [CrossRef]
- Fiscella, B.; Lombardini, P.P.; Trivero, P.; Cini, R. Ripple damping on water surface covered by a spreading film: Theory and experiment. Il Nuovo Cimento C 1985, 8, 491–500. [Google Scholar] [CrossRef]
- Monroy, F.; Ortega, F.; Rubio, R.G.; Velarde, M.G. Surface rheology, equilibrium and dynamic features at interfaces, with emphasis on efficient tools for probing polymer dynamics at interfaces. Adv. Colloids Interface Sci. 2007, 134–135, 175–189. [Google Scholar] [CrossRef]
- Cicuta, P.; Hopkinson, I. Recent developments of surface light scattering as a tool for optical-rheology of polymer monolayers. Colloids Surf. A 2004, 233, 97–107. [Google Scholar] [CrossRef]
- Sutherland, G.; Halsne, T.; Rabault, J.; Jensen, A. The attenuation of monochromatic surface waves due to the presence of an inextensible cover. Wave Motion 2017, 68, 88–96. [Google Scholar] [CrossRef]
- Jenkins, A.D.; Jacobs, S.J. Wave damping by a thin layer of viscous fluid. J. Fluid Mech. 1997, 9, 1256. [Google Scholar] [CrossRef]
- Monroy, F. Surface hydrodynamics of viscoelastic fluids and soft solids: Surfing bulk rheology on capillary and Rayleigh waves. Adv. Colloid Interface Sci. 2017, 247, 4–22. [Google Scholar] [CrossRef]
- Muñoz, M.G.; Monroy, F.; Hernández, P.; Ortega, F.; Rubio, R.G.; Langevin, D. Anomalous Damping of the Capillary Waves at the Air−Water Interface of a Soluble Triblock Copolymer. Langmuir 2003, 19, 2147–2154. [Google Scholar] [CrossRef]
- Baidakov, V.G.; Protsenko, S.P.; Bryukhanov, V.M. Relaxation processes at liquid-gas interfaces in one- and two-component Lennard-Jones systems: Molecular dynamics simulation. Fluid Ph. Equilibria 2019, 481, 1–14. [Google Scholar] [CrossRef]
- Lucassen, J.; Van Den Tempel, M. Dynamic measurements of dilational properties of a liquid interface. Chem. Eng. Sci. 1972, 27, 1283–1291. [Google Scholar] [CrossRef]
- Van den Tempel, M.; Lucassen-Reynders, E. Relaxation processes at fluid interfaces. Adv. Colloid Interface Sci. 1983, 18, 281–301. [Google Scholar] [CrossRef]
- Liggieri, L.; Miller, R. Interfacial rheology—The response of two-dimensional layers on external perturbations. Curr. Opin. Colloid Interface Sci. 2010, 15, 256–263. [Google Scholar] [CrossRef]
- Muñoz-López, R.; Guzmán, E.; Velázquez, M.M.; Fernández-Peña, L.; Merchán, M.D.; Maestro, A.; Ortega, F.; Rubio, R.G. Influence of Carbon Nanosheets on the Behavior of 1,2-Dipalmitoyl-sn-glycerol-3-phosphocholine Langmuir Monolayers. Processes 2020, 8, 94. [Google Scholar] [CrossRef]
- Guzmán, E.; Fernández-Peña, L.; Akanno, A.; Llamas, S.; Ortega, F.; Rubio, R.G. Two Different Scenarios for the Equilibration of Polycation—Anionic Solutions at Water–Vapor Interfaces. Coatings 2019, 9, 438. [Google Scholar] [CrossRef]
- Llamas, S.; Guzmán, E.; Akanno, A.; Fernández-Peña, L.; Ortega, F.; Campbell, R.A.; Miller, R.; Rubio, R.G. Study of the Liquid/Vapor Interfacial Properties of Concentrated Polyelectrolyte–Surfactant Mixtures Using Surface Tensiometry and Neutron Reflectometry: Equilibrium, Adsorption Kinetics, and Dilational Rheology. J. Phys. Chem. C 2018, 122, 4419–4427. [Google Scholar] [CrossRef]
- Liggieri, L.; Santini, E.; Guzmán, E.; Maestro, A.; Ravera, F. Wide-frequency dilational rheology investigation of mixed silica nanoparticle–CTAB interfacial layers. Soft Matter 2011, 7, 7699–7709. [Google Scholar] [CrossRef]
- Akanno, A.; Guzmán, E.; Fernández-Peña, L.; Llamas, S.; Ortega, F.; Rubio, R.G. Equilibration of a Polycation–Anionic Surfactant Mixture at the Water/Vapor Interface. Langmuir 2018, 34, 7455–7464. [Google Scholar] [CrossRef] [PubMed]
- Llamas, S.; Mendoza, A.J.; Guzmán, E.; Ortega, F.; Rubio, R.G. Salt effects on the air/solution interfacial properties of PEO-containing copolymers: Equilibrium, adsorption kinetics and surface rheological behavior. J. Colloid Interface Sci. 2013, 400, 49–58. [Google Scholar] [CrossRef] [PubMed]
- Maestro, A.; Kotsmar, C.; Javadi, A.; Miller, R.; Ortega, F.; Rubio, R.G. Adsorption of β-Casein–Surfactant Mixed Layers at the Air–Water Interface Evaluated by Interfacial Rheology. J. Phys. Chem. B 2012, 116, 4898–4907. [Google Scholar] [CrossRef] [PubMed]
- Maestro, A.; Ortega, F.; Rubio, R.G.; Rubio, M.A.; Krägel, J.; Miller, R. Rheology of poly(methyl methacrylate) Langmuir monolayers: Percolation transition to a soft glasslike system. J. Chem. Phys. 2011, 134, 104704. [Google Scholar] [CrossRef]
- Riande, E.; Diaz-Calleja, R.; Prolongo, M.G.; Masegosa, R.; Salom, C. Polymer Viscoelasticity: Stress and Strain in Practice; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Hilles, H.; Maestro, A.; Monroy, F.; Ortega, F.; Rubio, R.G. Polymer monolayers with a small viscoelastic linear regime: Equilibrium and rheology of poly(octadecyl acrylate) and poly(vinyl stearate). J. Chem. Phys. 2007, 126, 124904. [Google Scholar] [CrossRef]
- Hilles, H.; Monroy, F.; Bonales, L.J.; Ortega, F.; Rubio, R.G. Fourier-transform rheology of polymer Langmuir monolayers: Analysis of the non-linear and plastic behaviors. Adv. Colloid Interface Sci. 2006, 122, 67–77. [Google Scholar] [CrossRef]
- Guzmán, E.; Santini, E.; Ferrari, M.; Liggieri, L.; Ravera, F. Effect of the Incorporation of Nanosized Titanium Dioxide on the Interfacial Properties of 1,2-Dipalmitoyl-sn-glycerol-3-phosphocholine Langmuir Monolayers. Langmuir 2017, 33, 10715–10725. [Google Scholar] [CrossRef]
- Sagis, L.M.C.; Fischer, P. Nonlinear rheology of complex fluid–fluid interfaces. Curr. Opin. Colloid Interface Sci. 2014, 19, 520–529. [Google Scholar] [CrossRef]
- Ferri, J.K.; Fernandes, P.A.L.; McRuiza, J.T.; Gambinossi, F. Elastic nanomembrane metrology at fluid–fluid interfaces using axisymmetric drop shape analysis with anisotropic surface tensions: Deviations from Young–Laplace equation. Soft Matter 2012, 8, 10352–10359. [Google Scholar] [CrossRef]
- Bykov, A.G.; Guzmán, E.; Rubio, R.G.; Krycki, M.M.; Milyaeva, O.Y.; Noskov, B.A. Influence of temperature on dynamic surface properties of spread DPPC monolayers in a broad range of surface pressures. Chem. Phys. Lipids 2019, 225, 104812. [Google Scholar] [CrossRef]
- Loglio, G.; Pandolfini, P.; Miller, R.; Makievski, A.V.; Krägel, J.; Ravera, F.; Noskov, B.A. Perturbation–response relationship in liquid interfacial systems: Non-linearity assessment by frequency–domain analysis. Colloids Surf. A 2005, 261, 57–63. [Google Scholar] [CrossRef]
- Bykov, A.G.; Liggieri, L.; Noskov, B.A.; Pandolfinib, P.; Ravera, F.; Loglio, G. Surface dilational rheological properties in the nonlinear domain. Adv. Colloid Interface Sci. 2015, 222, 110–118. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guzmán, E.; Maestro, A.; Carbone, C.; Ortega, F.; Rubio, R.G. Dilational Rheology of Fluid/Fluid Interfaces: Foundations and Tools. Fluids 2022, 7, 335. https://doi.org/10.3390/fluids7100335
Guzmán E, Maestro A, Carbone C, Ortega F, Rubio RG. Dilational Rheology of Fluid/Fluid Interfaces: Foundations and Tools. Fluids. 2022; 7(10):335. https://doi.org/10.3390/fluids7100335
Chicago/Turabian StyleGuzmán, Eduardo, Armando Maestro, Carlo Carbone, Francisco Ortega, and Ramón G. Rubio. 2022. "Dilational Rheology of Fluid/Fluid Interfaces: Foundations and Tools" Fluids 7, no. 10: 335. https://doi.org/10.3390/fluids7100335
APA StyleGuzmán, E., Maestro, A., Carbone, C., Ortega, F., & Rubio, R. G. (2022). Dilational Rheology of Fluid/Fluid Interfaces: Foundations and Tools. Fluids, 7(10), 335. https://doi.org/10.3390/fluids7100335









