Efficiency and Aerodynamic Performance of Bristled Insect Wings Depending on Reynolds Number in Flapping Flight
Abstract
:1. Introduction
2. Materials and Methods
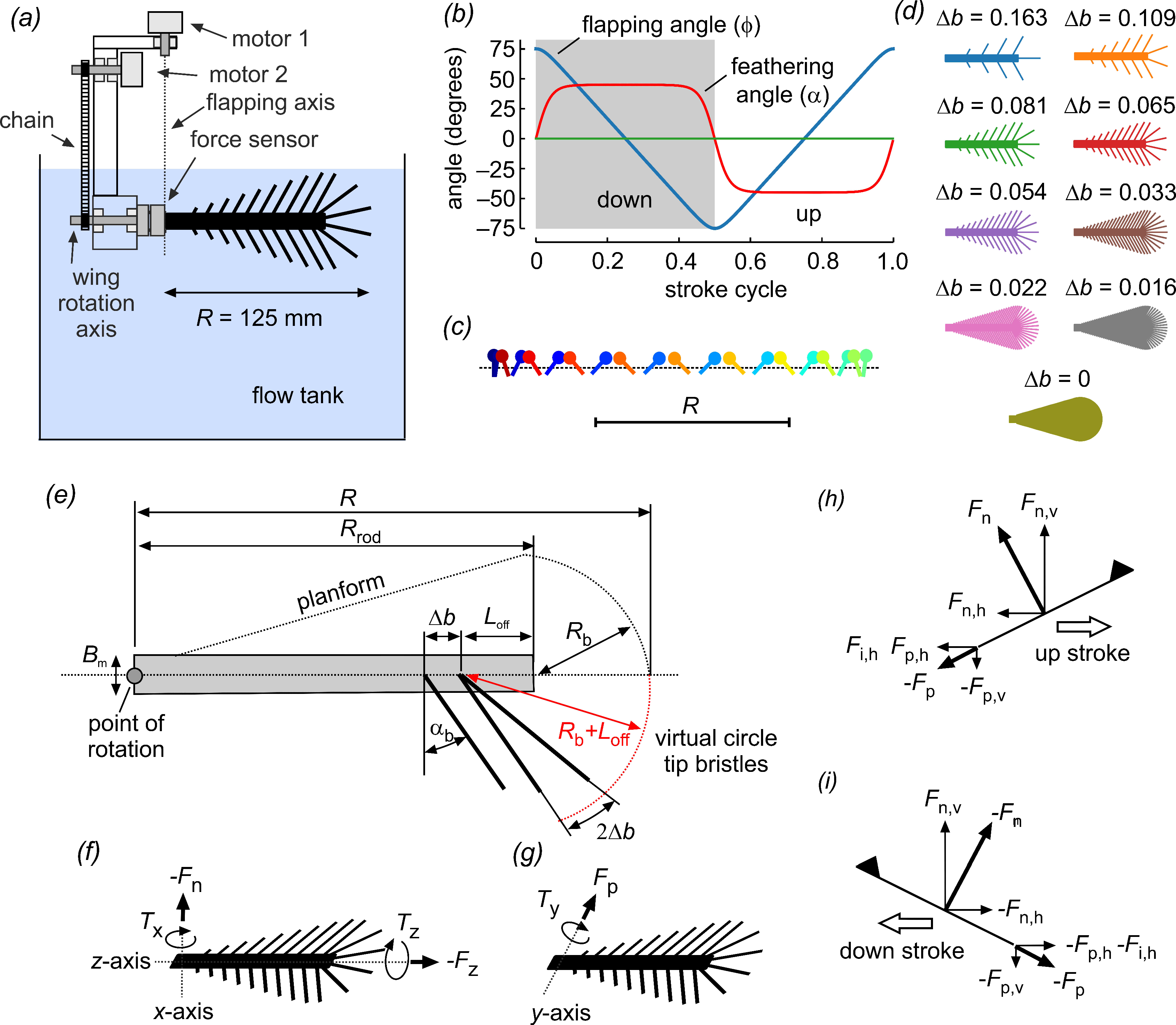
2.1. Wing Design and Kinematics
2.2. Experimental Setup
2.3. Power and Coefficients
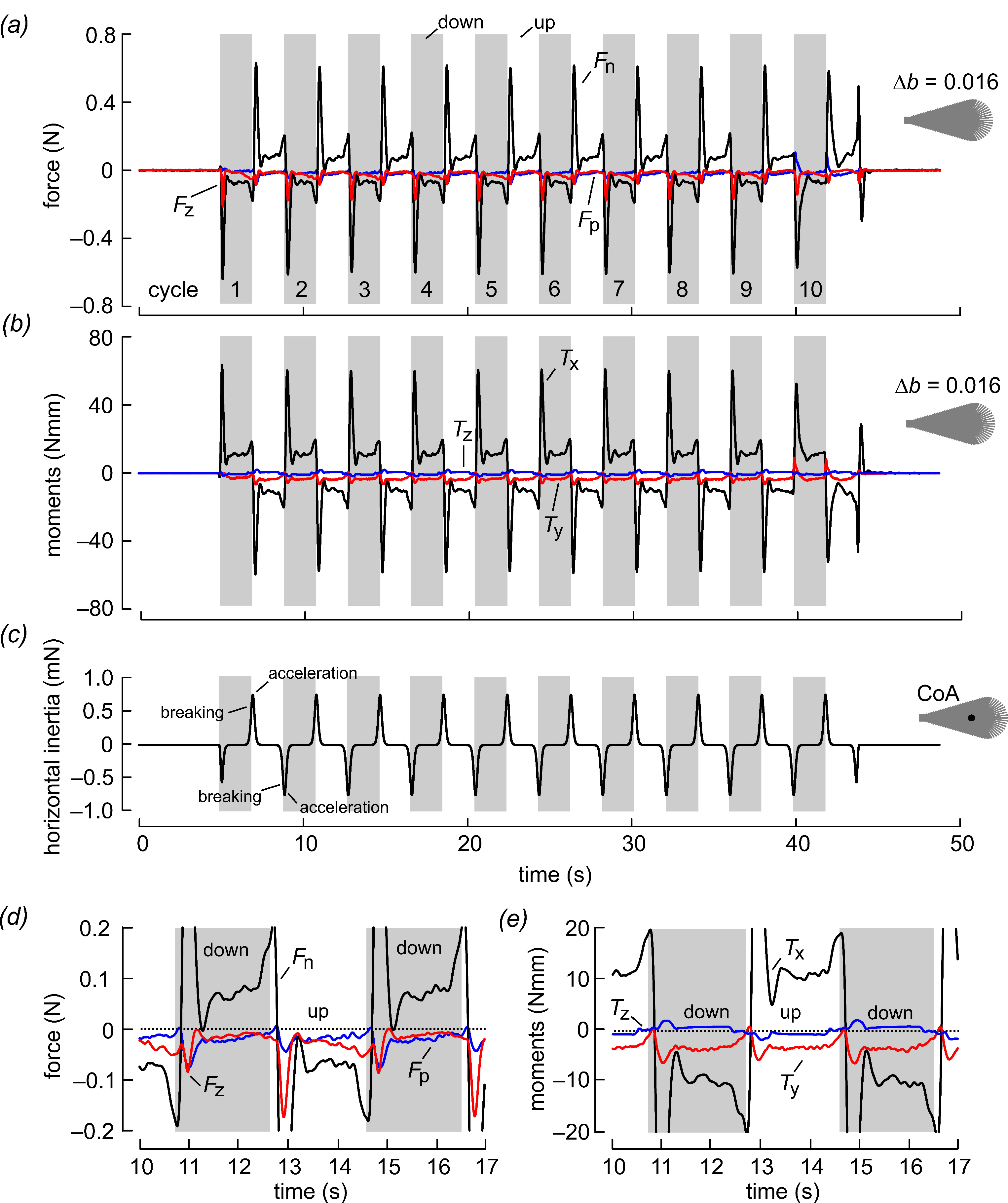
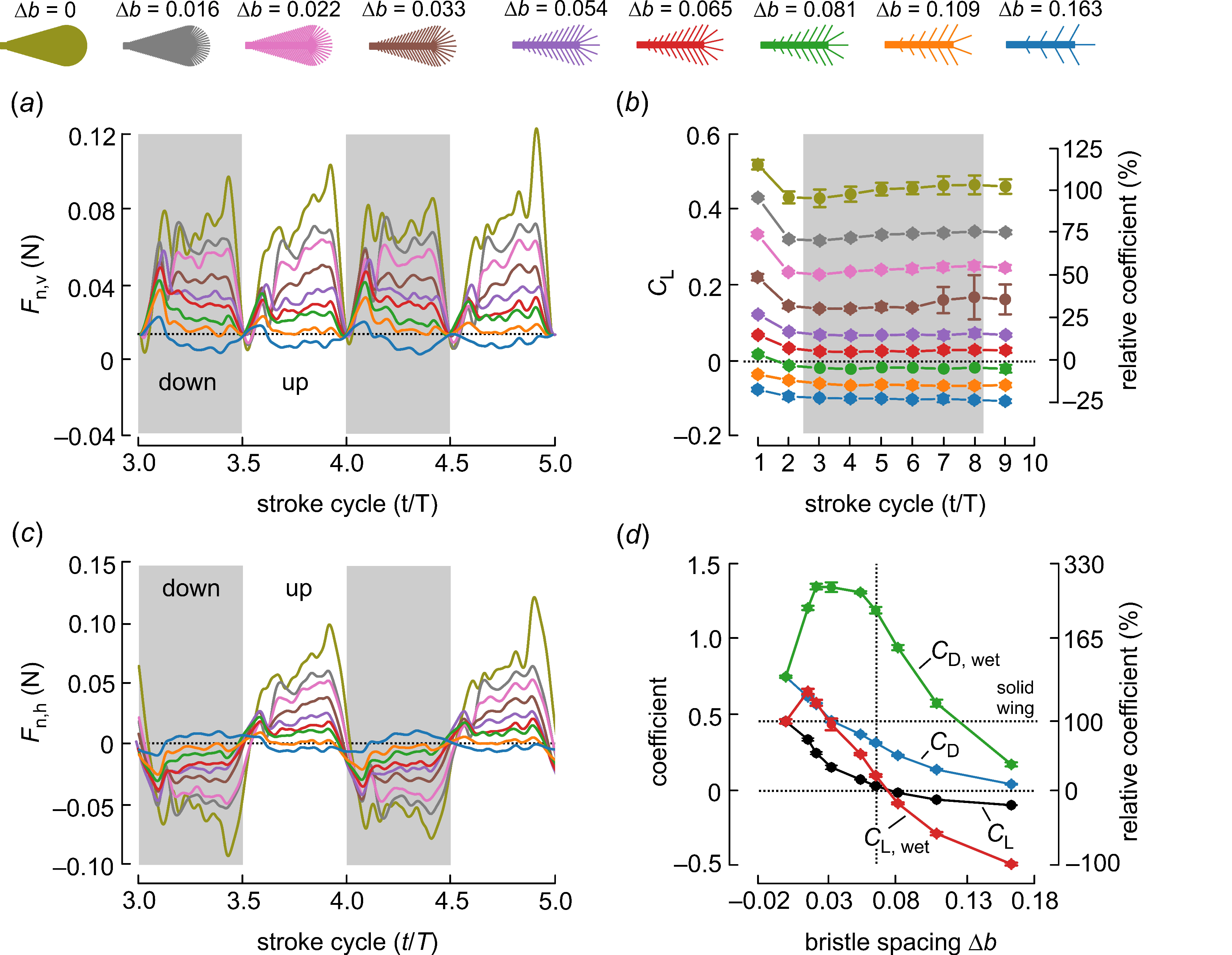
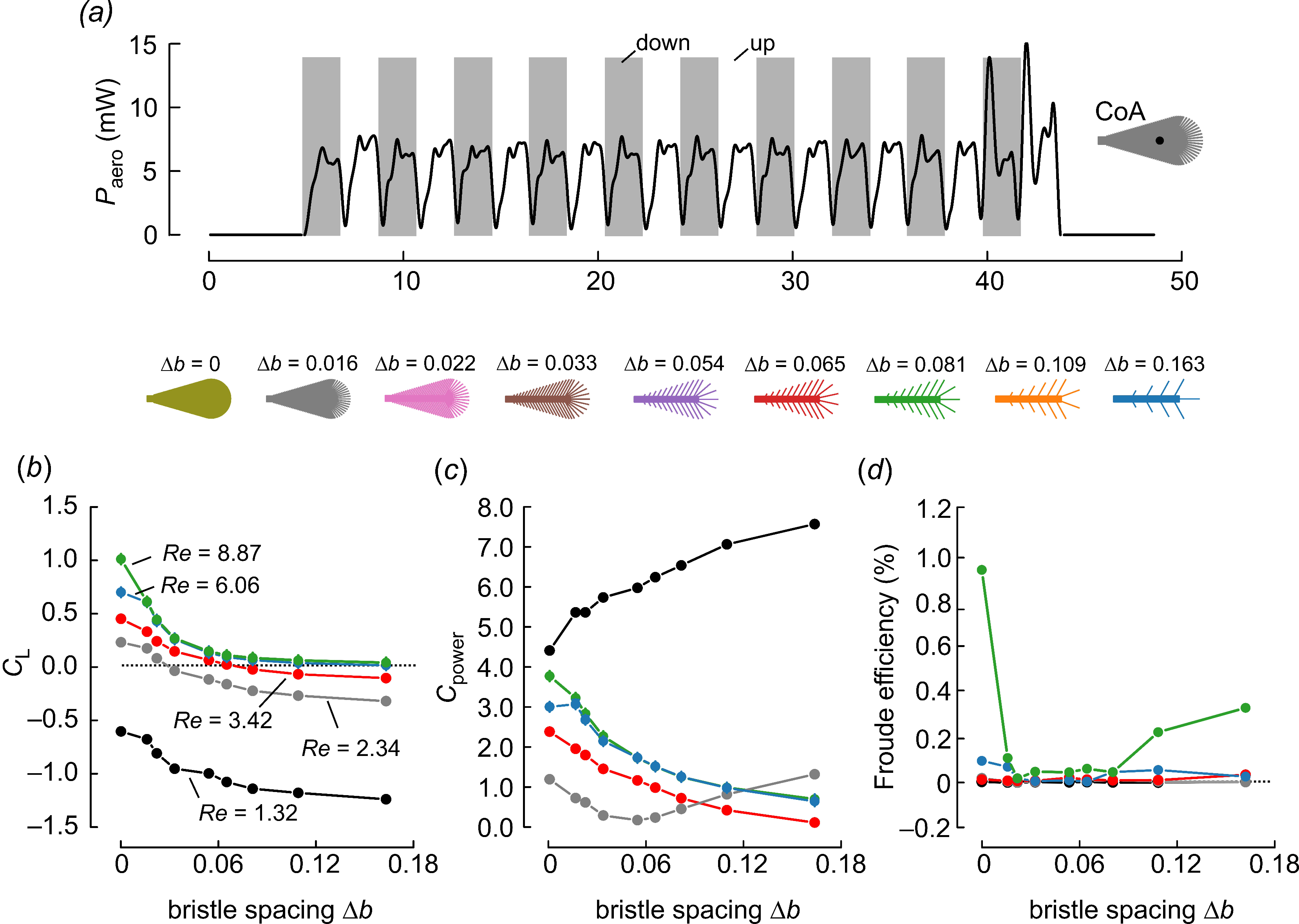
3. Results and Discussion
4. Conclusions
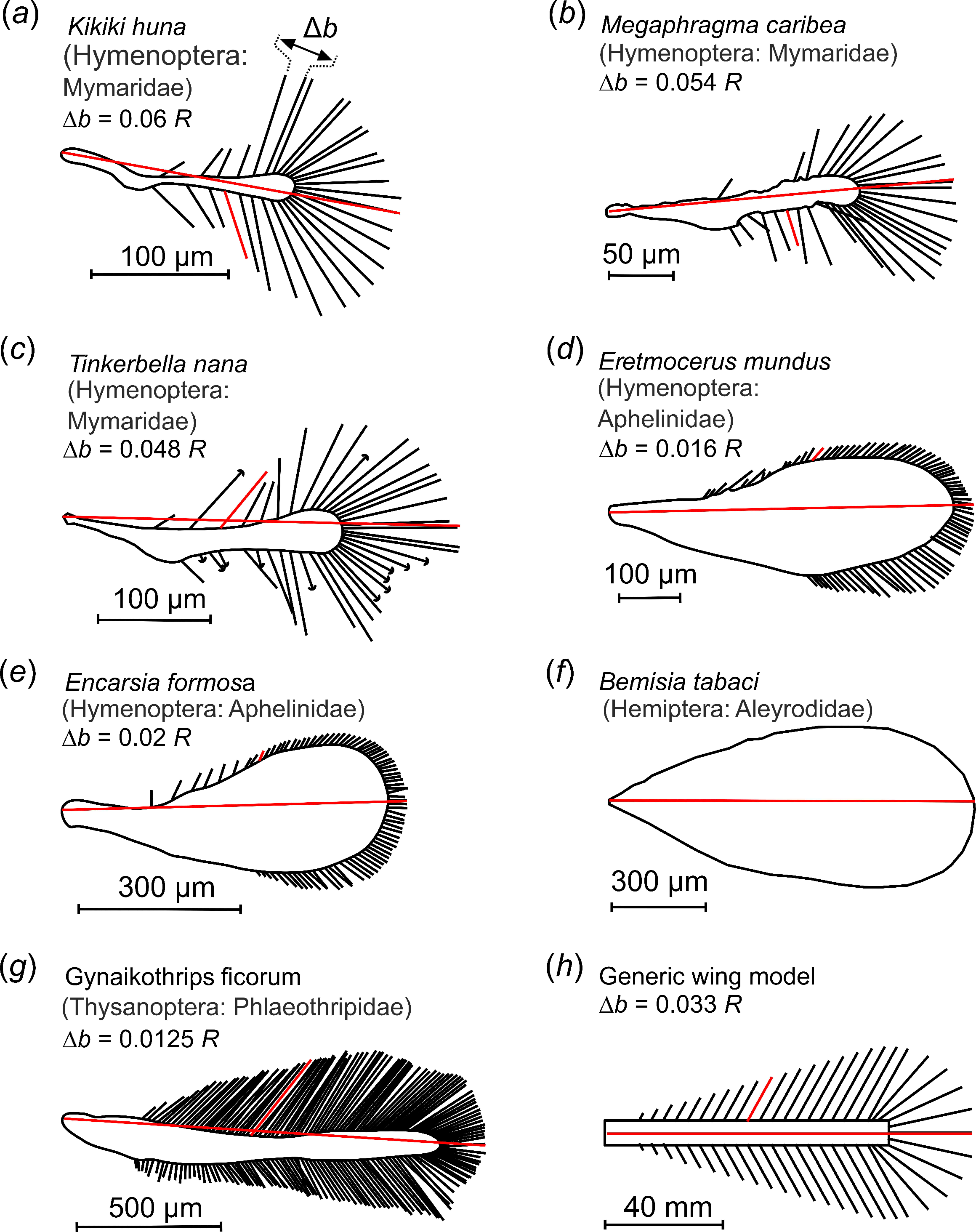
| Species | Ref | Wing Type | Wing Length (µm) | Bristle Number | Bristle Angle (Degrees) | Bristle Spacing ∆b | Bristle Length LB | Wingbeat Frequency (Hz) | Re |
|---|---|---|---|---|---|---|---|---|---|
| Kikiki huna | [41] | bristled | 245 | 30 | 61.6 | 0.06 R | 0.310 R | n.a. | n.a. |
| Megaphragma caribea | [42] | bristled | 286 | 32 | 77.9 | 0.054 R | 0.280 R | n.a. | n.a. |
| Tinkerbella nana | [41] | bristled | 354 | 40 | 50.6 | 0.048 R | 0.289 R | n.a. | n.a. |
| Eretmocerus mundus | [43], t.s. | hybrid | 600 | 78 | 46.6 | 0.016 R | 0.057 R | 273 | 7 |
| Encarsia formosa | [18,25] | hybrid | 642 | 82 | 64.8 | 0.02 R | 0.055 R | 361 | 10 |
| Bemisia tabaci | t.s. | solid | 1012 | 0 | n.a. | n.a. | n.a. | 131 | 7 |
| Gynaikothrips ficorum | t.s. | bristled | 1460 | 173 | 54.9 | 0.0125 R | 0.101 R | 196 | 24 |
| Model wing | t.s. | bristled | n.a. | 9–99 | 61 | see text | 0.224 R | see text | 1.3–8.9 |
| Bristle Spacing ∆b | 0.163 | 0.109 | 0.081 | 0.065 | 0.054 | 0.033 | 0.022 | 0.016 | 0 (Solid) |
|---|---|---|---|---|---|---|---|---|---|
| Area coverage | 0.21 | 0.23 | 0.24 | 0.26 | 0.28 | 0.34 | 0.42 | 0.51 | 1.0 |
| Number of bristles | 9 | 14 | 19 | 24 | 29 | 49 | 74 | 99 | 0 |
| Wing mass (g) | 1.58 | 1.71 | 1.79 | 1.89 | 1.99 | 2.33 | 2.83 | 3.34 | 12.7 |
| Fp,v (N) | −0.005 | −0.010 | −0.012 | −0.014 | −0.015 | −0.015 | −0.016 | −0.014 | −0.014 |
| Fn,v (N) | −0.005 | 0.003 | 0.010 | 0.016 | 0.021 | 0.030 | 0.040 | 0.047 | 0.059 |
| Tx (mNm) | 0.229 | 0.269 | 0.333 | 0.412 | 0.436 | 0.420 | 0.463 | 0.592 | 0.409 |
| Ty (mNm) | −2.48 | −3.21 | −3.65 | −3.95 | −4.06 | −3.84 | −3.84 | −3.49 | −3.61 |
| Paero (mW) | 0.358 | 1.30 | 2.30 | 3.20 | 3.70 | 4.70 | 5.80 | 6.30 | 7.60 |
| CL | −0.104 | −0.067 | −0.022 | 0.024 | 0.066 | 0.147 | 0.241 | 0.331 | 0.452 |
| CD | 0.035 | 0.131 | 0.226 | 0.309 | 0.365 | 0.455 | 0.564 | 0.613 | 0.747 |
| CL,wet | −0.495 | −0.292 | −0.092 | 0.092 | 0.235 | 0.431 | 0.574 | 0.650 | 0.452 |
| CD,wet | 0.167 | 0.571 | 0.940 | 1.19 | 1.31 | 1.34 | 1.34 | 1.20 | 0.747 |
| Cpower | 0.112 | 0.419 | 0.719 | 0.984 | 1.17 | 1.45 | 1.80 | 1.96 | 2.38 |
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| αb | Bristle angle with respect to rod |
| A0 | Area of actuator disc |
| Aw | Wing area |
| Bm | Width of solid wing rod |
| f | Wing flapping frequency |
| Re | Reynolds number |
| CL | Lift coefficient for wing translation based on solid wing area |
| CL,wet | Lift coefficient for wing translation based on wetted wing area |
| CD | Drag coefficient for wing translation based on solid wing area |
| CD,wet | Drag coefficient for wing translation based on wetted wing area |
| Cpower | Coefficient of aerodynamic power |
| Mean horizontal force (drag) | |
| ∆b | Bristle spacing |
| Fi | Wing inertia |
| Fn | Force normal to the wing surface |
| Fp | Force parallel to wing surface (chordwise direction) |
| Fn,v | Vertical force normal to wing surface |
| Fp,v | Vertical force parallel to wing surface |
| Fn,h,trans | Horizontal force component of Fn for wing translation |
| Fp,h,trans | Horizontal force component of Fp for wing translation |
| Φ | Wing beat amplitude |
| Cycle-averaged vertical force (lift) | |
| Loff | Distance between bristle root and rod tip |
| ν | Kinematic viscosity of the fluid |
| utip | Cycle-averaged wing tip velocity |
| uCoF | Cycle-averaged wing velocity at center of force |
| Paero,trans | Aerodynamic power for wing translation |
| R | Wing length |
| Rb | Bristle length |
| Rrod | Length of solid wing rod |
| ρ | Fluid density |
| Tx | Moment about the wing’s x-axis |
| Ty | Moment about the wing’s y-axis |
| Tz | Moment about the wing’s z-axis |
References
- Nijhout, H.; Davidowitz, G.; Roff, D. A quantitative analysis of the mechanism that control body size in Manduca sexta. J. Biol. 2006, 5, 16. [Google Scholar] [CrossRef] [Green Version]
- Polilov, A.A. Small is beautiful: Features of the smallest insects and limits to miniaturization. Annu. Rev. Entomol. 2015, 60, 103–121. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, F.-O. The efficiency of aerodynamic force production in Drosophila. Comp. Biochem. Physiol. A 2001, 131, 77–88. [Google Scholar] [CrossRef]
- Horridge, G.A. The flight of very small insects. Nature 1956, 178, 1334–1335. [Google Scholar] [CrossRef]
- Santhanakrishnan, A.; Robinson, A.K.; Jones, S.; Low, A.A.; Gadi, S.; Hedrick, T.L.; Miller, L.A. Clap and fling mechanism with interacting porous wings in tiny insect flight. J. Exp. Biol. 2014, 217, 3898–3909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sane, S.P. Neurobiology and biomechanics of flight in miniature insects. Curr. Opin. Neurobiol. 2016, 41, 158–166. [Google Scholar] [CrossRef]
- Yavorskaya, M.I.; Beutel, R.G.; Farisenkov, S.E.; Polilov, A.A. The locomotor apparatus of one of the smallest beetles—The thoracic skeletomuscular system of Nephanes titan (Coleoptera, Ptiliidae). Arthropod Struct. Dev. 2019, 48, 71–82. [Google Scholar] [CrossRef]
- Kolomenskiy, D.; Farisenkov, S.; Engels, T.; Lapina, N.; Petrov, P.; Lehmann, F.-O.; Onishi, R.; Liu, H.; Polilov, A.A. Aerodynamic performance of a bristled wing of a very small insect. Exp. Fluids 2020, 61, 194. [Google Scholar] [CrossRef]
- Weihs, D.; Barta, E. Comb wings for flapping flight at extremely low Reynolds numbers. AIAA J. 2007, 46, 285–288. [Google Scholar] [CrossRef]
- Kasoju, V.T.; Terrif, C.L.; Ford, M.P.; Santhanakrishnan, A. Leaky flow through simplified physical models of bristled wings of tiny insects during clap and fling. Fluids 2018, 3, 44. [Google Scholar] [CrossRef] [Green Version]
- Davidi, G.; Weihs, D. Flow around a comb wing in low-Reynolds-number flow. AIAA J. 2012, 50, 249–253. [Google Scholar] [CrossRef]
- Cheer, A.Y.L.; Koehl, M.A.R. Paddles and rakes: Fluid flow through bristled appendages of small organisms. J. Theor. Biol. 1987, 129, 17–39. [Google Scholar] [CrossRef]
- Lee, S.H.; Lahooti, M.; Kim, D. Aerodynamic characteristics of unsteady gap flow in a bristled wing. Phys. Fluids 2018, 30, 071901. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, M.; Kim, D. Optimal configuration of a two-dimensional bristled wing. J. Fluid Mech. 2020, 888, A23. [Google Scholar] [CrossRef]
- Sunada, S.; Takashima, H.; Hattori, T.; Yasuda, K.; Kawachi, K. Fluid-dynamic characteristics of a bristled wing. J. Exp. Biol. 2002, 2737–2744. [Google Scholar] [CrossRef]
- Lee, S.; Kim, D. Aerodynamic response of a bristled wing in gusty flow. J. Fluid Mech. 2021, 913, A4. [Google Scholar] [CrossRef]
- Ford, M.P.; Kasoju, V.T.; Gaddam, M.G.; Santhanakrishnan, A. Aerodynamic effects of varying solid surface area of bristled wings performing clap and fling. Bioinsp. Biomim. 2019, 14, 046003. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Sun, M. Very small insects use novel wing flapping and drag principle to generate the weight-supporting vertical force. J. Fluid Mech. 2018, 855, 646–670. [Google Scholar] [CrossRef] [Green Version]
- Shyy, W.; Lian, Y.; Tang, J.; Viieru, D.; Liu, H. Aerodynamics of Low Reynolds Number Flyers; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Ribak, G.; Dafni, E.; Gerling, D. Whiteflies stabilize their take-off with closed wings. J. Exp. Biol. 2016, 219, 1639–1648. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lehmann, F.-O.; Heymann, N. Dynamics of in vivo power output and efficiency of Nasonia asynchronous flight muscle. J. Biotechnol. 2006, 124, 93–107. [Google Scholar] [CrossRef] [PubMed]
- Lyu, Y.Z.; Zhu, H.J.; Sun, M. Flapping-mode changes and aerodynamic mechanisms in miniature insects. Phys. Rev. E 2019, 99, 012419. [Google Scholar] [CrossRef] [PubMed]
- Ristroph, L.; Bergou, A.J.; Guckenheimer, J.; Wang, Z.J.; Cohen, I. Paddling mode of forward fligth in insects. Phys. Rev. Lett. 2011, 106, 178103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jones, S.K.; Laurenza, R.; Hedrick, T.L.; Griffith, B.E.; Miller, L.A. Lift vs. drag based mechanisms for vertical force production in the smallest flying insects. J. Theor. Biol. 2015, 7, 105–120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weis-Fogh, T. Quick estimates of flight fitness in hovering animals, including novel mechanisms for lift production. J. Exp. Biol. 1973, 59, 169–230. [Google Scholar] [CrossRef]
- Chen, S.; Li, H.; Guo, S.; Tong, M.; Ji, B. Unsteady aerodynamic model of flexible flapping wing. Aero. Sci. Tech. 2018, 80, 354–367. [Google Scholar] [CrossRef] [Green Version]
- Santhanakrishnan, A.; Jones, S.K.; Dickson, W.B.; Peek, M.; Kasojo, V.T.; Dickinson, M.H.; Miller, L.A. Flow structure and force generation on flapping wings at low reynolds numbers relevant to the flight of tiny insects. Fluids 2018, 3, 45. [Google Scholar] [CrossRef] [Green Version]
- Jones, S.K.; Yun, Y.J.J.; Hedrick, T.L.; Griffith, B.E.; Miller, L.A. Bristles reduce the force required to ‘fling’ wings apart in the smallest insects. J. Exp. Biol. 2016, 219, 3759–3772. [Google Scholar] [CrossRef] [Green Version]
- Engels, T.; Kolomenskiy, D.; Lehmann, F.-O. Flight efficiency is a key to diverse wing morphologies in small insects. J. R. Soc. Interface 2021, 18, 20210518. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhao, P.; Cai, X.; Rong, J.; Dong, Z.; Chen, H.; Wu, P.; Hu, H.; Jin, X.; Zhang, D. Bristled-wing design of materials, microstructures and aerodynamics enables flapping flight in tiny wasps. iScience 2021, 103692. [Google Scholar] [CrossRef] [PubMed]
- Engels, T.; Wehmann, H.-N.; Lehmann, F.-O. Three-dimensional wing structure attenuates aerodynamic efficiency in flapping fly wings. J. R. Soc. Interface 2020, 17, 20190804. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, F.-O.; Dickinson, M.H. The control of wing kinematics and flight forces in fruit flies (Drosophila spp.). J. Exp. Biol. 1998, 201, 385–401. [Google Scholar] [CrossRef]
- Ramamurti, R.; Sandberg, W.C. A three-dimensional computational study of the aerodynamic mechanisms of insect flight. J. Exp. Biol. 2002, 205, 1507–1518. [Google Scholar] [CrossRef] [PubMed]
- Ellington, C.P. The aerodynamics of hovering insect flight. V. A vortex theory. Phil. Trans. R. Soc. Lond. B 1984, 305, 115–144. [Google Scholar]
- Ferral, N.; Gomez, N.; Holloway, K.; Neeter, H.; Fairfield, M.; Pollman, K.; Huang, Y.-W.; Hou, C. The extremely low energy cost of biosynthesis in holometabolous insect larvae. J. Insect Physiol. 2020, 120, 103988. [Google Scholar] [CrossRef]
- Dudley, R. The Biomechanics of Insect Flight: Form, Function, Evolution; Princeton University Press: Princeton, NJ, USA, 2000. [Google Scholar]
- Usherwood, J.R.; Lehmann, F.-O. Phasing of dragonfly wings can improve aerodynamic efficiency by removing swirl. J. R. Soc. Interface 2008, 5, 1303–1307. [Google Scholar] [CrossRef] [Green Version]
- Farisenkov, S.E.; Kolomenskiy, D.; Petrov, P.N.; Lapina, N.A.; Engels, T.; Lehmann, F.-O.; Onishi, R.; Liu, H.; Polilov, A.A. A novel flight style allowing the smallest featherwing beetles to excel. bioRxiv 2021. [CrossRef]
- Farisenkov, S.E.; Kolomenskiy, D.; Petrov, P.N.; Engels, T.; Lapina, N.A.; Lehmann, F.-O.; Onishi, R.; Liu, H.; Polilov, A.A. Novel flight style and light wings boost flight performance of tiny beetles. Nature 2022, 602, 96–100. [Google Scholar] [CrossRef] [PubMed]
- Tomoyasu, Y. What crustaceans can tell us about the evolution of insect wings and other morphologically novel structures. Curr. Opin. Genet. Dev. 2021, 69, 48–55. [Google Scholar] [CrossRef]
- Huber, J.T.; Noyes, J.S. A new genus and specied of fairyfly, Tinkerbella nana (Hymenoptera, Mymaridae), with comments on its sister genus Kikiki, and discussion on small size limits in arthropods. J. Hymenopt. Res. 2013, 32, 17–44. [Google Scholar] [CrossRef] [Green Version]
- Polilov, A.A. First record of Megaphragma (Hymenoptera, Trichogrammatidae) in Columbia, and third animal species known to have anucleate neurons. J. Hymenopt. Res. 2017, 60, 181–185. [Google Scholar] [CrossRef] [Green Version]
- Barro, P.J.D.; Driver, F.; Naumann, I.D.; Schmidt, S.; Clarke, G.M.; Curran, J. Descriptions of three species of Eretmocerus Haldeman (Hymenoptera: Aphelinidae) parasitising Bemisia tabaci (Gennadius) (Hemiptera: Aleyrodidae) and Trialeurodes vaporariorum (Westwood)(Hemiptera: Aleyrodidae) in Australia based on morphological and molecular data. Aust. J. Entomol. 2000, 39, 259–269. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
O’Callaghan, F.; Sarig, A.; Ribak, G.; Lehmann, F.-O. Efficiency and Aerodynamic Performance of Bristled Insect Wings Depending on Reynolds Number in Flapping Flight. Fluids 2022, 7, 75. https://doi.org/10.3390/fluids7020075
O’Callaghan F, Sarig A, Ribak G, Lehmann F-O. Efficiency and Aerodynamic Performance of Bristled Insect Wings Depending on Reynolds Number in Flapping Flight. Fluids. 2022; 7(2):75. https://doi.org/10.3390/fluids7020075
Chicago/Turabian StyleO’Callaghan, Felicity, Amir Sarig, Gal Ribak, and Fritz-Olaf Lehmann. 2022. "Efficiency and Aerodynamic Performance of Bristled Insect Wings Depending on Reynolds Number in Flapping Flight" Fluids 7, no. 2: 75. https://doi.org/10.3390/fluids7020075
APA StyleO’Callaghan, F., Sarig, A., Ribak, G., & Lehmann, F.-O. (2022). Efficiency and Aerodynamic Performance of Bristled Insect Wings Depending on Reynolds Number in Flapping Flight. Fluids, 7(2), 75. https://doi.org/10.3390/fluids7020075






