Experimental Techniques against RANS Method in a Fully Developed Turbulent Pipe Flow: Evolution of Experimental and Computational Methods for the Study of Turbulence
Abstract
:1. Introduction
Evolution of the Experimental and Computational Techniques
2. Materials and Methods
2.1. Experimental Set-Up
- A brass pipe with length to diameter ratio of 125:1, which was considered an adequate ratio for a high Reynolds number.
- A variable speed centrifugal fan, which was used at the inlet and forced air at ambient conditions to flow along the pipe.
- An analogue manometer, which was connected via a pressure switch to static pressure tapings in the wall of the pipe and also to a Preston tube placed at the pipe exit.
- A Preston tube, which was used at the outlet of the brass pipe to measure the dynamic pressure.
- Static pressure tappings, which were used at two points on the wall of the pipe to calculate the pressure drop along the pipe over a fixed distance.
- A set of two pressure switches, which were used to interconnect a digital manometer apparatus with the Preston tube.
- A hot-wire anemometer.
2.2. Instrumentation and Measurements
2.2.1. Anemometry Measuring System
- Two single hot-wire probes (one straight and one 45° hot-wire).
- A set of traverse gears, which were implemented to move the hot-wire to the required position in the pipe.
- Two Constant Temperature Anemometer (CTA) bridges.
- A linearizer, which was used to enhance the non-linear behavior of the amplifier and to filter down a portion of the noise interfering with the output data from hot-wire anemometry, mainly caused by the fluctuation of the probe in the pipe.
- Two separate digital voltage meters, which measured the mean and the Root Mean Square (RMS) velocities.
- AC amplifier, which was used to increase the signal of the time-varying voltage.
2.2.2. Hot-Wire Anemometer
2.3. Experimental Procedure
2.3.1. Measurement of the Velocity Field
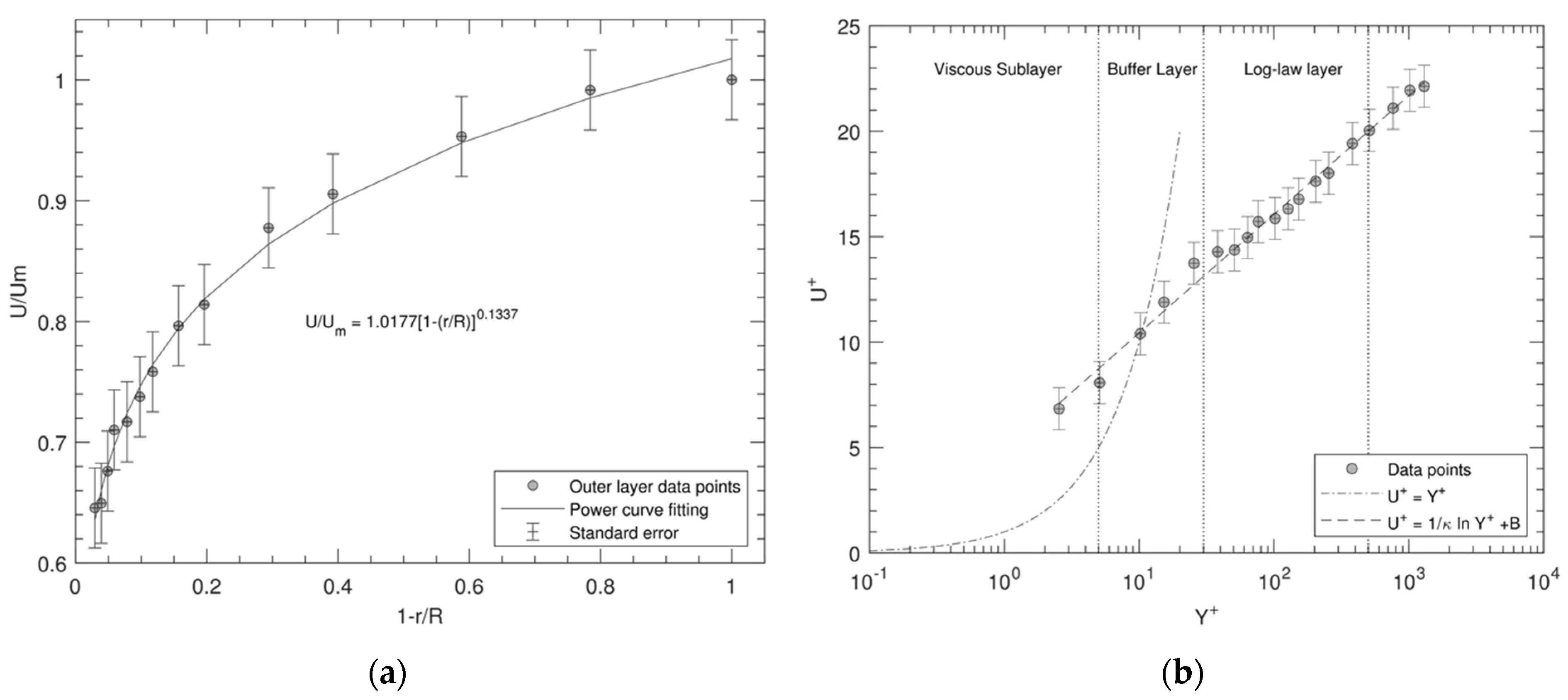
2.3.2. Power-Law Velocity Profile
2.3.3. Method 1: Static Pressure Drop
2.3.4. Method 2: Mean Square Signal (45° Hot-Wire)
2.3.5. Method 3: Preston Tube
2.3.6. Method 4: Clauser Plot
2.4. Computational Method
2.4.1. Grid Generation
2.4.2. Turbulence Modelling
Standard Model
Standard Model
Standard Model
2.4.3. Boundary Conditions
2.4.4. Discretization
2.4.5. Pressure-Velocity Coupling Scheme
2.4.6. Convergence Criteria
3. Results and Discussion
3.1. Experimental Results: Velocity Profile Analysis
3.2. Experimental Results: Wall Shear Stress Analysis
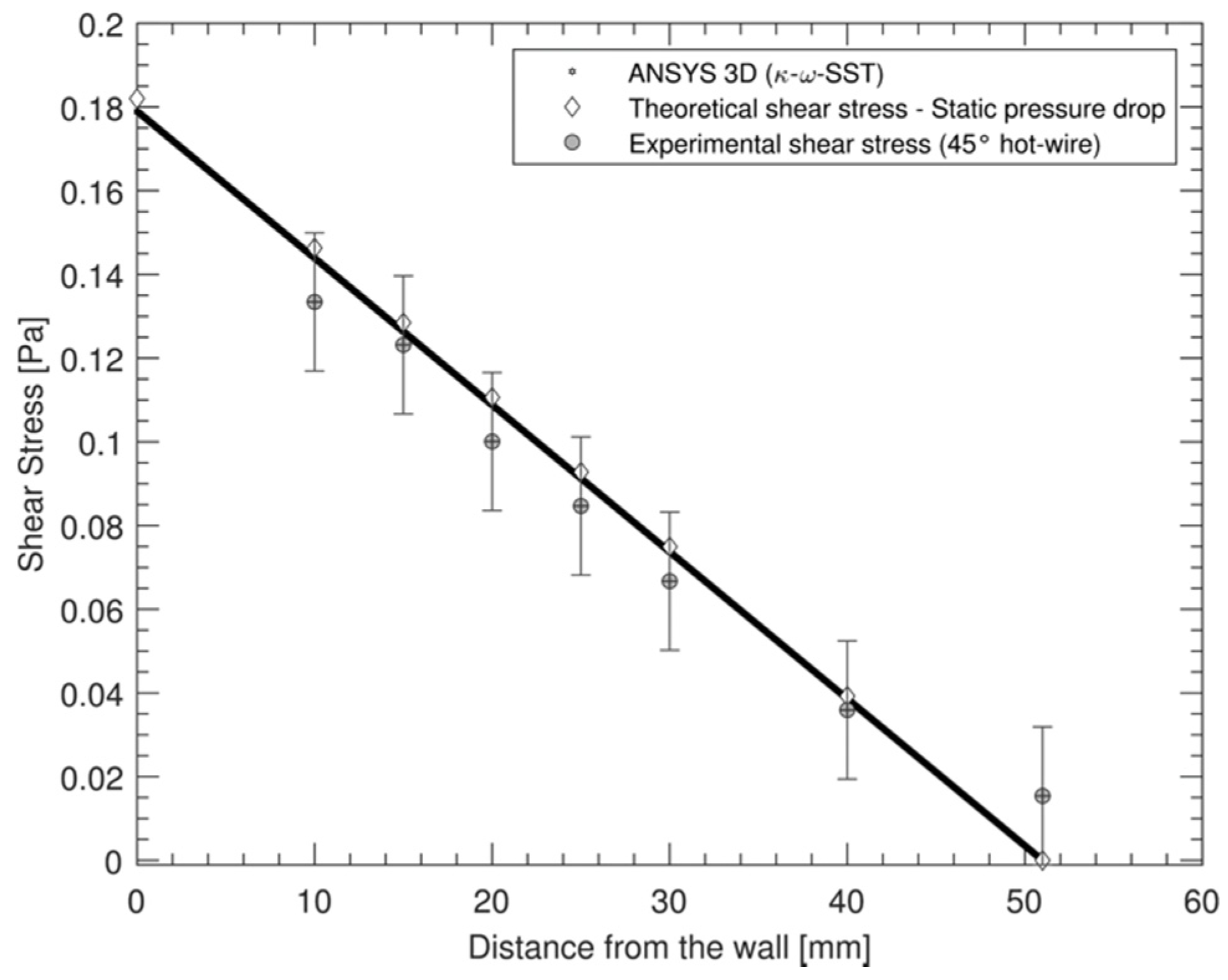
3.2.1. Static Pressure Drop
3.2.2. Mean Square Signal (45° Hot-Wire)
3.2.3. Preston Tube
3.2.4. Clauser Plot
3.2.5. Error of Measurement
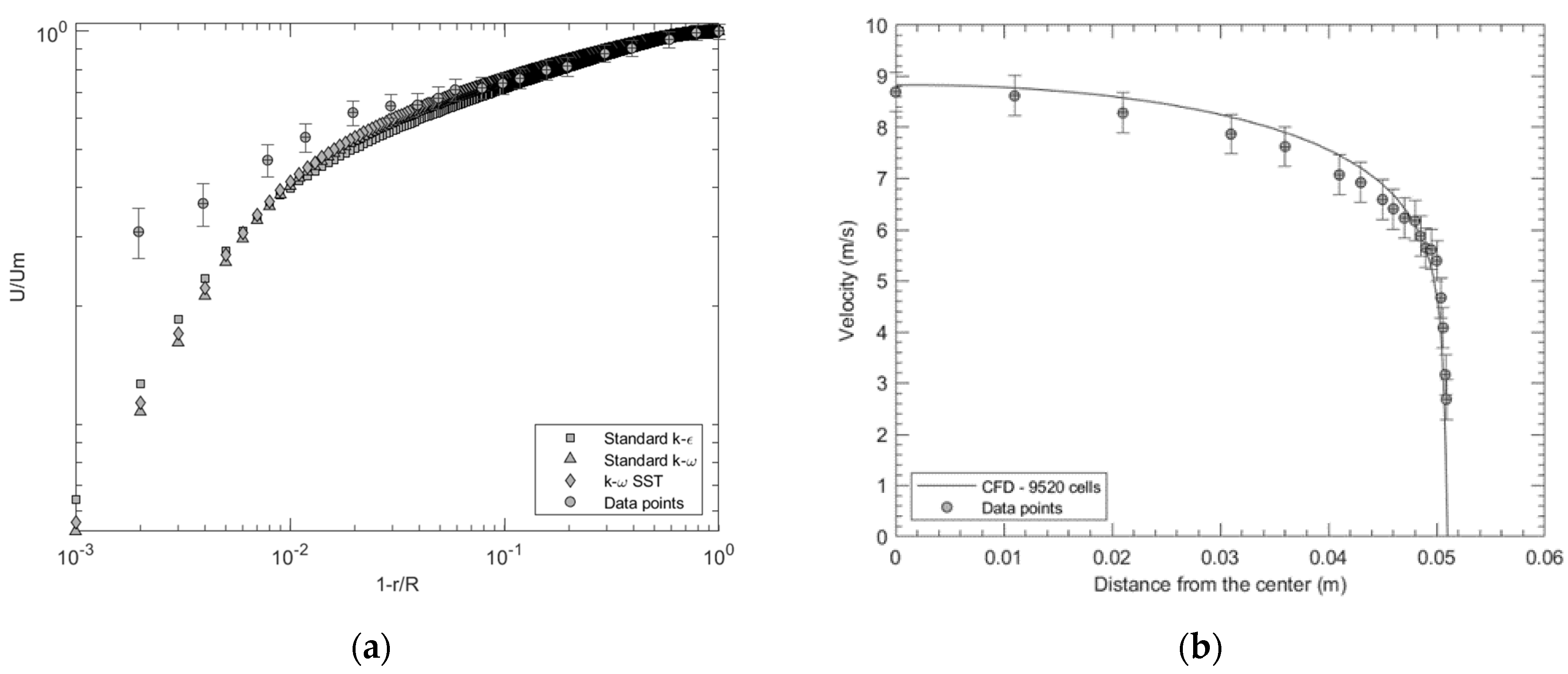
3.3. Computational Results
3.3.1. Mesh Independency
3.3.2. Turbulence Models Comparison
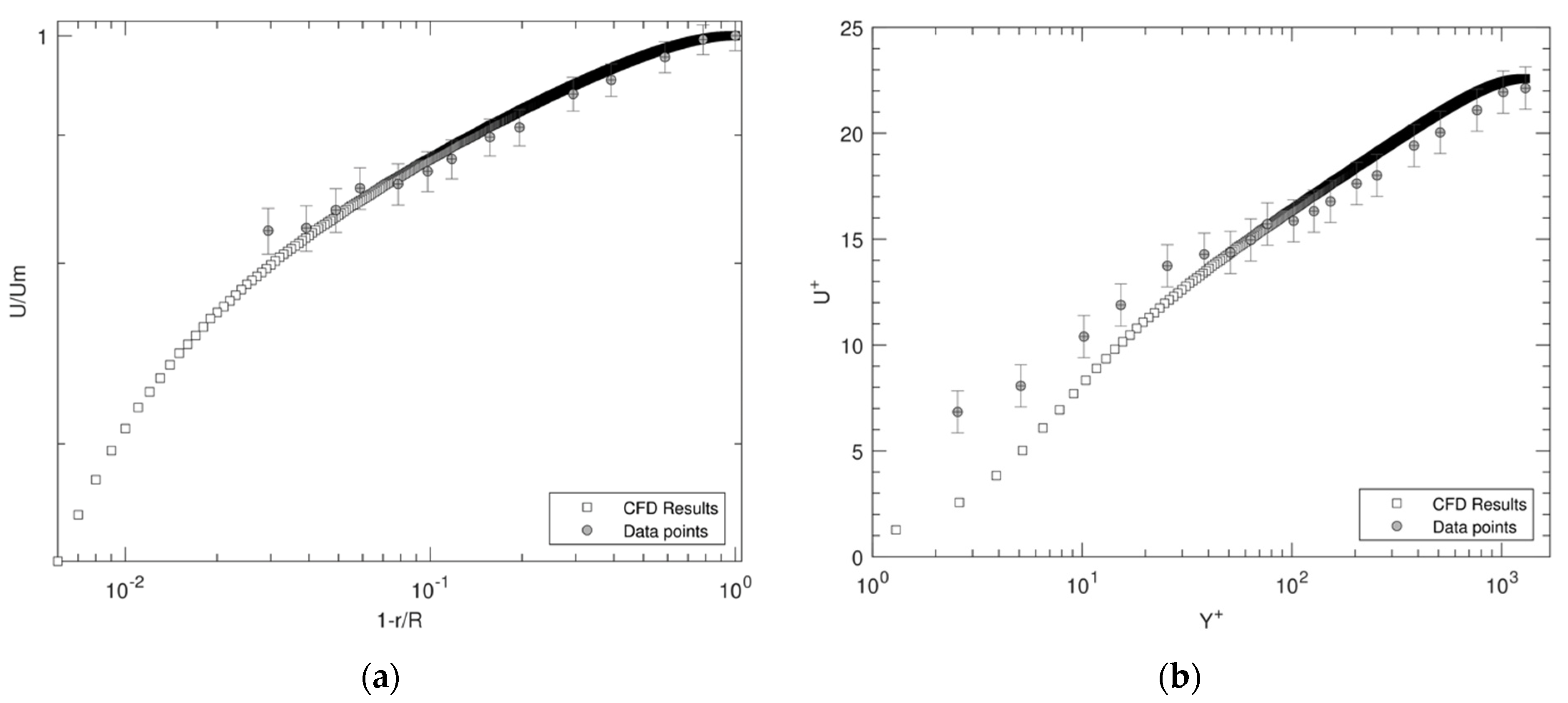
3.4. Experimental vs. Computational Results
3.4.1. Velocity Profiles Comparison
3.4.2. Wall Shear Comparison
3.5. Assessment of Errors
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Çengel, Y.; Turner, R.; Cimbala, J. Fundamentals of Thermal-Fluid Sciences, 3rd ed.; McGraw Hill: New York, NY, USA, 2008. [Google Scholar]
- Perry, A. Hot-Wire Anemometry; Oxford University Press: Oxford, UK, 1982. [Google Scholar]
- Vardy, A.; Brown, J. Transient Turbulent Friction in Smooth Pipe Flows. J. Sound Vib. 2003, 259, 1011–1036. [Google Scholar] [CrossRef]
- Reynolds, O. An Experimental Investigation of the Circumstances Which Determine Whether the Motion of Water Shall Be Direct or Sinuous, and of the Law of Resistance in Parallel Channels. Philos. Trans. R. Soc. 1883, 174, 935–982. [Google Scholar] [CrossRef] [Green Version]
- Turns, S. Thermal-Fluid Sciences; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Boussinesq, M. Calcul Du Pouvoir Refroidissant des Courants Fluids. J. Math Pures Appl. 1905, 6, 285–332. [Google Scholar]
- Russel, A. The Convection of Heat from a Body Cooled by a Stream of Fluid. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1911, 20, 591–610. [Google Scholar] [CrossRef]
- King, L. On the Convection of Heat from Small Cylinders in a Stream of Fluid: Determination of the Convection Constants of Small Platinum Wires with Applications to Hot-Wire Anemometry. Proc. R. Soc. A Math. Phys. Eng. Sci. 1914, 90, 373–432. [Google Scholar] [CrossRef] [Green Version]
- Dryden, H.; Kuethe, A. The Measurement of Fluctuations of Air Speed by the Hot-Wire Anemometer. Available online: https://ntrs.nasa.gov/search.jsp?R=19930091390 (accessed on 13 August 2018).
- Gad-el-Hak, M. Advances in Fluid Mechanics Measurements; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Head, M.; Rechenberg, I. The Preston Tube as a Means of Measuring Skin Friction. J. Fluid Mech. 2006, 14, 1–17. [Google Scholar] [CrossRef]
- Preston, J. The Determination of Turbulent, Skin Friction by Means of Pitot Tubes. J. R. Aeronaut. Soc. 1954, 58, 109–121. [Google Scholar] [CrossRef]
- Clauser, F. The Turbulent Boundary Layer. Adv. Appl. Mech. 1956, 4, 1–51. [Google Scholar] [CrossRef]
- Fernholz, H.; Finley, P. The Incompressible Zero-Pressure-Gradient Turbulent Boundary Layer: An Assessment of the Data. Prog. Aerosp. Sci. 1996, 32, 245–311. [Google Scholar] [CrossRef]
- Versteeg, H.; Malalasekera, W. An Introduction to Computational Fluid Dynamics; Pearson: London, UK, 1995. [Google Scholar]
- Kapelson, A. Computational of Mean Velocity Distribution in a Turbulent Flow. Available online: https://arxiv.org/abs/physics/9904030 (accessed on 12 November 2017).
- Deardorff, J. A Numerical Study of Three-Dimensional Turbulent Channel Flow at Large Reynolds Numbers. J. Fluid Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
- Menter, F. Two-Equations Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Orszag, S.; Patterson, G. Numerical Simulation of Turbulence: Statistical Models and Turbulence; Springer: Berlin/Heidelberg, Germany, 1972. [Google Scholar]
- Craft, T. Finite Difference Schemes, CFD Mechanical Aerospace and Civil Engineering Manchester Website. Available online: http://cfd.mace.manchester.ac.uk/twiki/pub/Main/TimCraftNotes_All_Access/cfd1-findiffs.pdf (accessed on 16 July 2018).
- Launder, B.; Spalding, D. Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Keshmiri, A. Numerical Sensitivity Analysis of 3- and 2-Dimensional Rib-Roughened Channels. Heat Mass Transf. 2012, 48, 1257–1271. [Google Scholar] [CrossRef]
- Keshmiri, A.; Cotton, M.; Addad, Y.; Rolfo, S.; Billard, F. RANS and LES Investigations of Vertical Flows in the Fuel Passages of Gas-Cooled Nuclear Reactors. In Proceedings of the 16th International Conference on Nuclear Engineering, Orlando, FL, USA, 11–15 May 2008; Volume 2, pp. 297–306. [Google Scholar] [CrossRef] [Green Version]
- Keshmiri, A.; Cotton, M.; Addad, Y.; Laurence, D. Turbulence Models and Large Eddy Simulations Applied to Ascending Mixed Convection Flows. Flow Turbul. Combust. 2012, 89, 407–434. [Google Scholar] [CrossRef]
- Keshmiri, A.; Osman, K.; Benhamadouche, S.; Shokri, N. Assessment of Advanced RANS Models against Large Eddy Simulation and Experimental Data in the Investigation of Ribbed Passages with Passive Heat Transfer. Numer. Heat Transf. Part B Fundam. 2016, 69, 96–110. [Google Scholar] [CrossRef] [Green Version]
- Keshmiri, A.; Revell, A.; Darabkhani, H. Assessment of a Common Nonlinear Eddy-Viscosity Turbulence Model in Capturing Laminarization in Mixed Convection Flows. Numer. Heat Transf. Part A Appl. 2016, 69, 146–165. [Google Scholar] [CrossRef] [Green Version]
- Keshmiri, A.; Uribe, J.; Shokri, N. Benchmarking of Three Different CFD Codes in Simulating Natural, Forced and Mixed Convection Flows. Numer. Heat Transf. Part A Appl. 2015, 67, 1324–1351. [Google Scholar] [CrossRef]
- Pope, S. Turbulent Flows, 7th ed.; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Hurst, D.; Vassilicos, J. Scaling and Decay of Fractal-Generated Turbulence. Phys. Fluids 2007, 19, 035103. [Google Scholar] [CrossRef] [Green Version]
- Chamorro, L.; Porte-Agel, F. A Wind-Tunnel Investigation of Wind-Turbine Wakes: Boundary-Layer Turbulence Effects. Bound. -Layer Meteorol. 2009, 132, 129–149. [Google Scholar] [CrossRef] [Green Version]
- Lomas, C. Fundamentals of Hot Wire Anemometry; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Bruun, H.H. Hot-Wire Anemometry: Principles and Signal Analysis; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Comte-Bellot, G. Hot-Wire Anemometry. Annu. Rev. Fluid Mech. 1976, 8, 209–231. [Google Scholar] [CrossRef]
- Neu, M. Hot-Wire and Hot-Film Anemometry. Available online: http://www.dept.aoe.vt.edu/~simpson/aoe4154/hotwirelab.pdf (accessed on 23 March 2021).
- McDonough, J. Introductory Lectures on Turbulence: Physics, Mathematics and Modeling. Available online: https://uknowledge.uky.edu/me_textbooks/2 (accessed on 23 March 2021).
- Harotinidis, J.H. The Measurement of Wall Shear Stress. Adv. Fluid Mech. Meas. 1989, 45, 229–261. [Google Scholar] [CrossRef]
- Tropea, C.; Yarin, A.; Foss, J. Springer Handbook of Experimental Fluid Mechanics; Springer: Chicago, IL, USA, 2007. [Google Scholar]
- Patel, V. Calibration of the Preston Tube and Limitations on Its Use in Pressure Gradients. J. Fluid Mech. 1965, 23, 185–208. [Google Scholar] [CrossRef]
- Wei, T.; Schmidt, R.; McMurtry, P. Comment on the Clauser Chart Method for Determining the Friction Velocity. Exp. Fluids 2005, 38, 695–699. [Google Scholar] [CrossRef]
- Sherman, F. Viscous Flow; McGraw-Hill: New York, NY, USA, 1990. [Google Scholar]
- Eggels, J.; Unger, F.; Weiss, M.; Westerweel, J.; Adrian, R.; Friedrich, R.; Nieuwstadt, F. Fully Developed Turbulent Pipe Flow: A Comparison between Direct Numerical Simulation and Experiment. J. Fluid Mech. 1994, 268, 175–209. [Google Scholar] [CrossRef]
- Evola, G.; Popov, V. Computational Analysis of Wind Driven Natural Ventilation in Buildings. Energy Build. 2006, 5, 491–501. [Google Scholar] [CrossRef]
- Khier, W.; Breuer, M.; Durst, F. Flow Structure around Trains under Side Wind Conditions: A Numerical Study. Comput. Fluids 2000, 29, 179–195. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Zhang, Z. Laminar-to-Turbulent Fluid-Particle Flows in a Human Airway Model. Int. J. Multiph. Flow 2003, 2, 271–289. [Google Scholar] [CrossRef]
- Umlauf, L.; Burchard, H.; Hunter, K. Extending the K-w Turbulence Model towards Oceanic Applications. Ocean Model. 2003, 3, 195–218. [Google Scholar] [CrossRef]
- Wilcox, D. Turbulence Modeling for CFD, 2nd ed.; DCW Industries: La Canada Flintridge, CA, USA, 1998. [Google Scholar]
- Menter, F. Zonal Two Equation K-ω Turbulence Models for Aerodynamic Flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993; Volume 32, pp. 1598–1605. [Google Scholar] [CrossRef]
- ANSYS 7.3.16. Periodic Boundary Conditions. Available online: www.afs.enea.it/project/neptunius/docs/fluent/html/ug/node252 (accessed on 29 January 2018).
- Craft, T. Turbulence and Related Modelling, CFD Mechanical Aerospace and Civil Engineering Manchester Website. Available online: http://cfd.mace.manchester.ac.uk/twiki/pub/Main/TimCraftNotes_All_Access/ms4-turbflow.pdf (accessed on 16 July 2018).
- Patankar, S. Numerical Heat Transfer and Fluid Flow; Taylor & Francis: New York, NY, USA, 1980. [Google Scholar]
- Keshmiri, A.; Gotts, J. Thermalhydraulic Analysis of Four Geometrical Design Parameters in Rib-Roughened Channels. Numer. Heat Transf. Part A Appl. 2011, 60, 305–327. [Google Scholar] [CrossRef]
- Keshmiri, A. Three-dimensional simulation of a simplified advanced gas-cooled reactor fuel element. Nucl. Eng. Des. 2011, 241, 4122–4135. [Google Scholar] [CrossRef]
- Laufer, J. The Structure of Turbulence in Fully Developed Pipe Flow. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19930083975.pdf (accessed on 13 August 2018).
- Keshmiri, A.; Addad, Y.; Cotton, M.A.; Laurence, D.R.; Billar, F.; Billard, F. Refined eddy viscosity schemes and large eddy simulations for ascending mixed convection flows. In Proceedings of the 4th International Symposium on Advances in Computational Heat Transfer, “CHT08”, Marrakech, Morocco, 11–16 May 2008; Paper CHT-08-407. Volume 44, pp. 1–22. [Google Scholar]
- Keshmiri, A. Effects of Various Physical and Numerical Parameters on Heat Transfer in Vertical Passages at Relatively Low Heat Loading. J. Heat Transf. 2011, 133, 092502. [Google Scholar] [CrossRef] [Green Version]
- Casey, M.; Wintergerste, T. European Research Community on Flow, Turbulence and Combustion] Special Interest Group on “Quality and Trust in Industrial CFD” Best Practice Guidelines; ERCOFTAC: London, UK, 2000. [Google Scholar]





| Coarse Mesh | Medium Mesh | Fine Mesh | Very Fine Mesh |
|---|---|---|---|
| 3060 cells | 9520 cells | 30,240 cells | 90,045 cells |
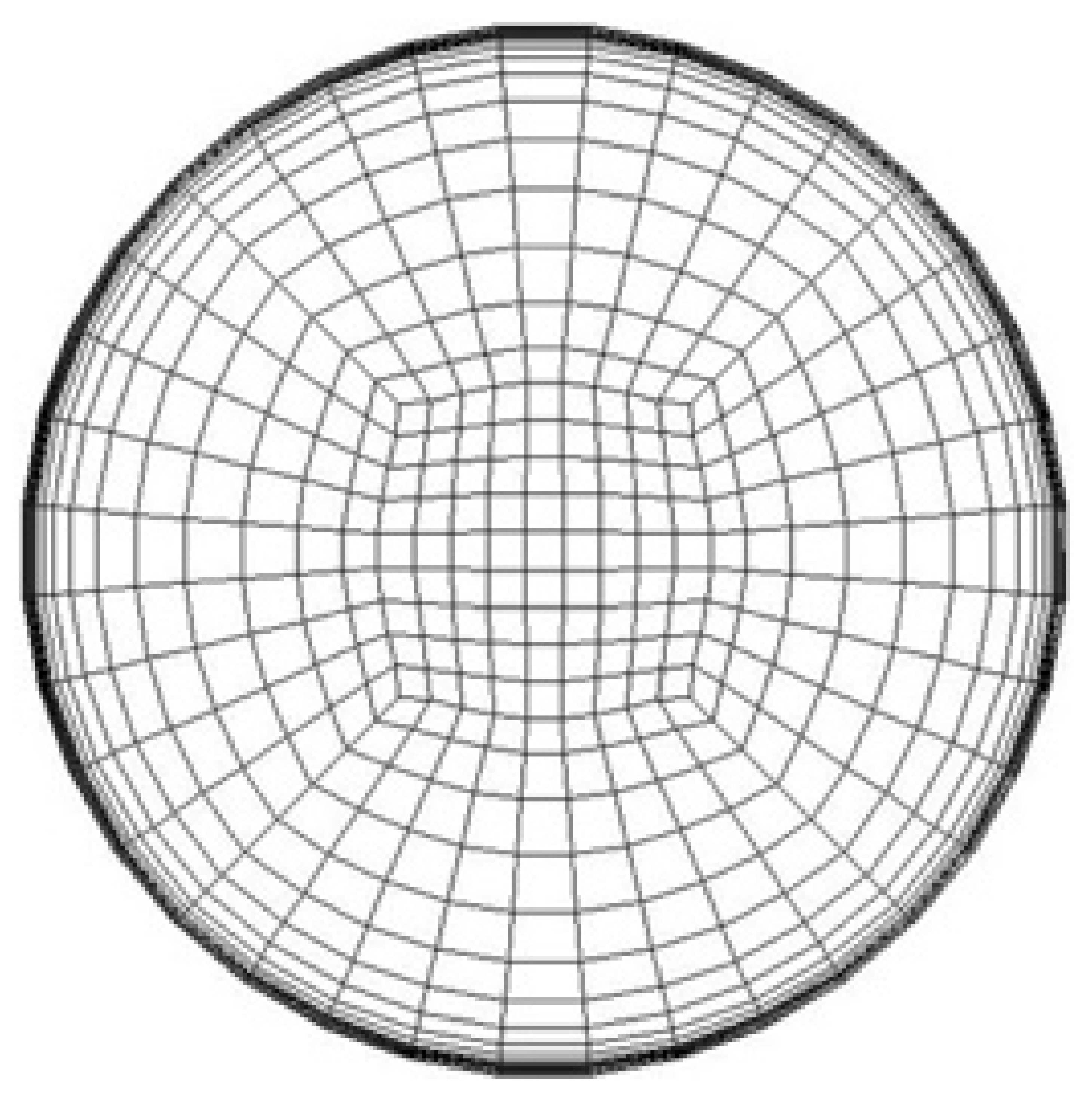 | 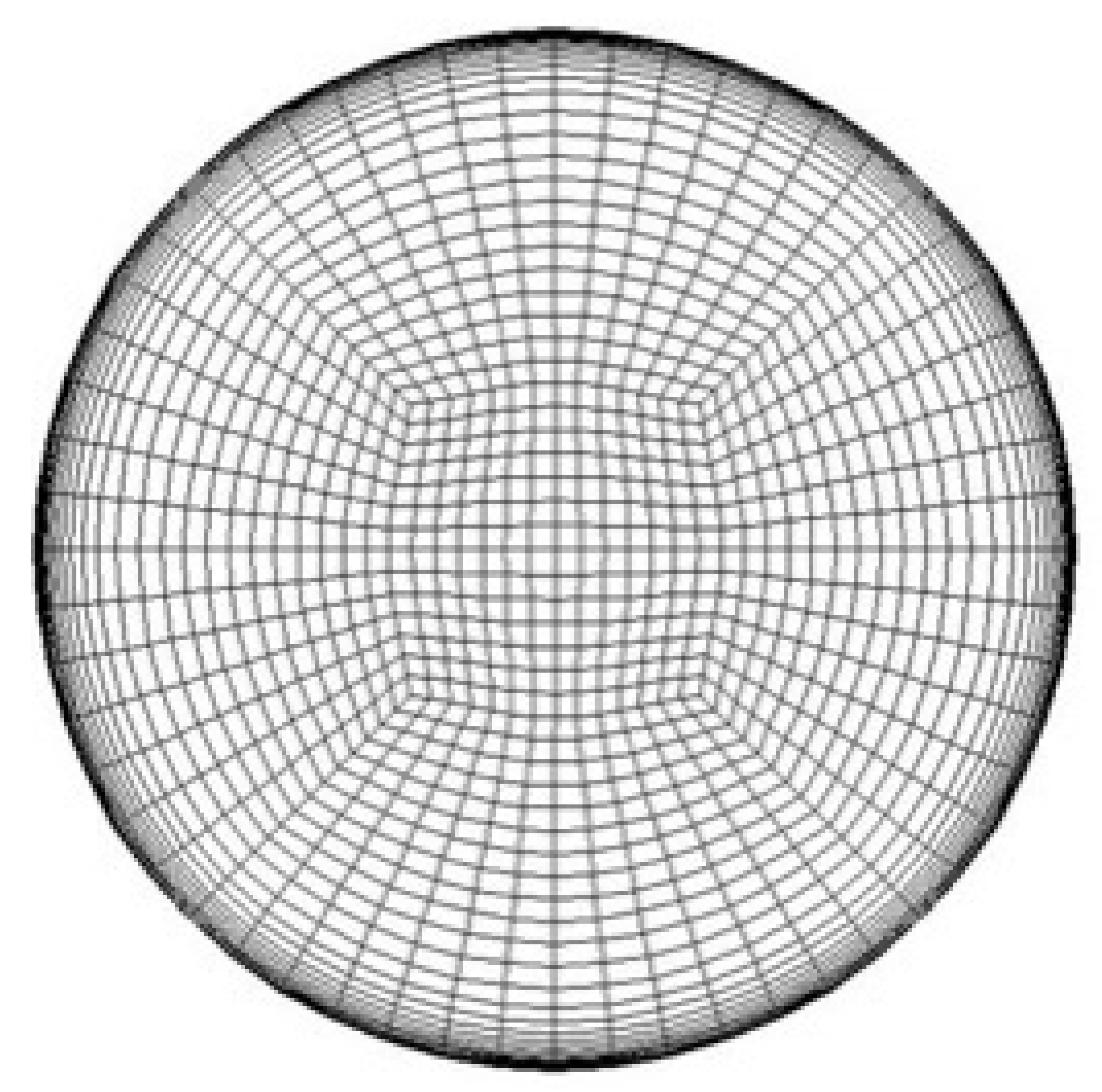 | 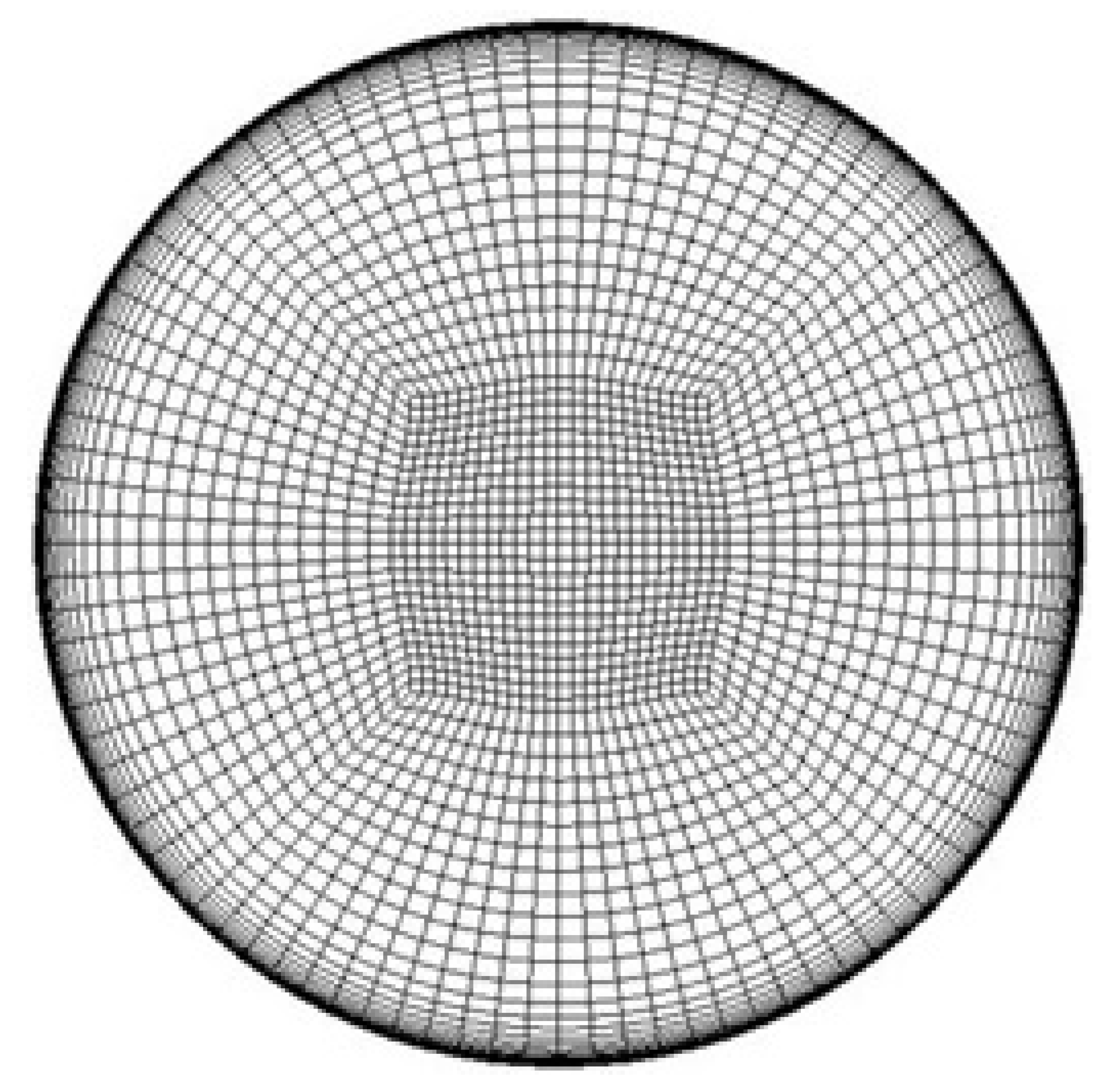 | 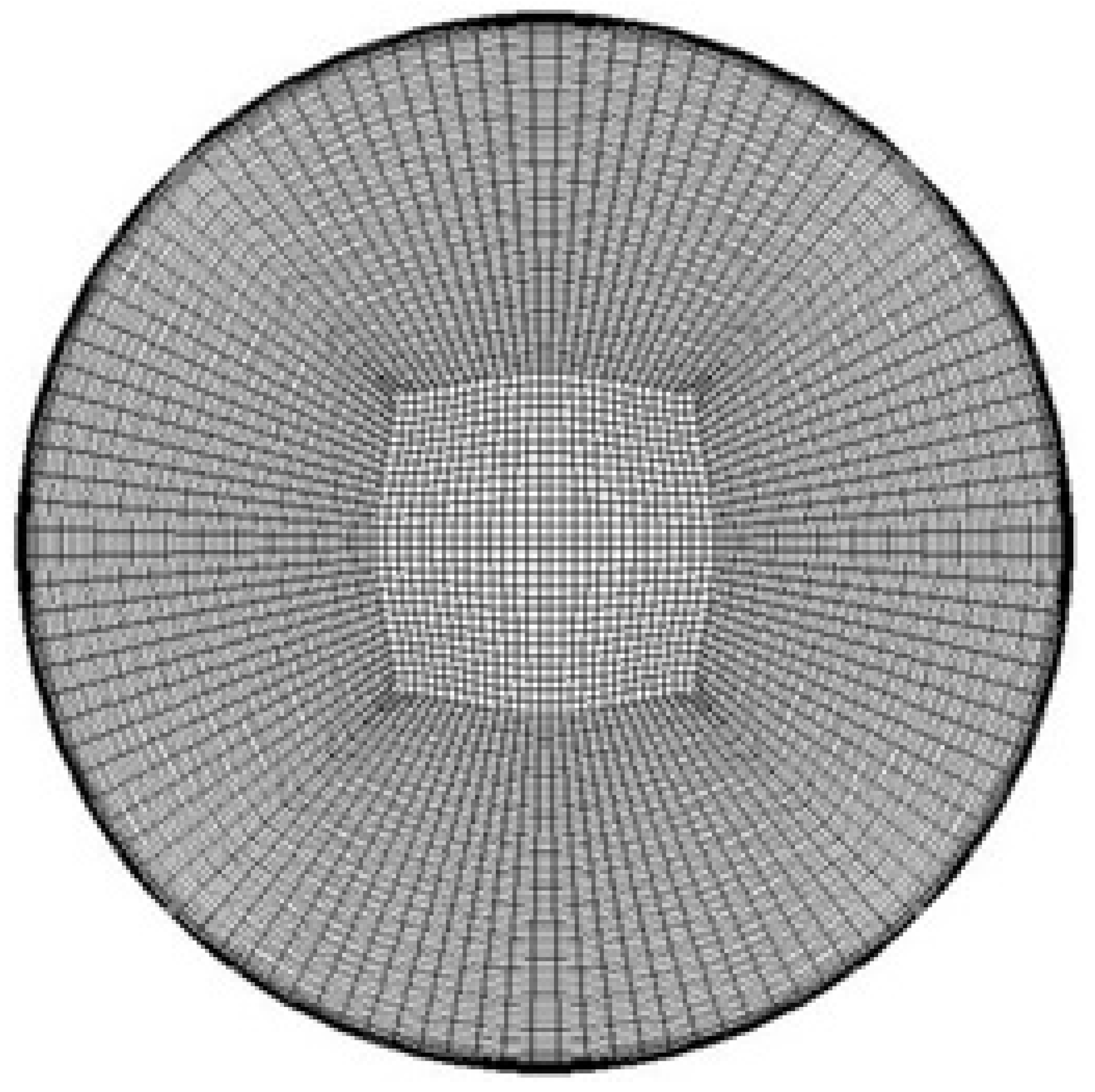 |
| Parameter | Value |
|---|---|
| Pipe inner diameter | 0.102 m |
| Length | 0.004 m |
| Reynolds number | 57,469 |
| Air density | 1.19 kg/m3 |
| Air viscosity | 1.82 × 10−5 kg/ms |
| Von-Karman constant | 0.41 (±0.1) |
| Mass flow rate | 7.5 × 10−2 kg/s |
| Velocity | 7.5 m/s |
| Nearest wall distance | 3.43 × 10−5 m |
| Turbulencemodel | ||||
| Discretization Scheme | Second-order upwind | |||
| Convergence Criteria | 1.0 × 10−6 | |||
| P-V Coupling Scheme | SIMPLE Scheme | |||
| Processors in Parallel | 4 | |||
| Boundary Conditions | -No-slip in the walls -Periodic inlet/outlet | |||
| Grid method | 3D Multiblock—Hexahedral mesh | |||
| Number of cells | 3060 (coarse) | 9520 (medium) | 30,240 (fine) | 90,045 (very fine) |
| Iterations to Converge | 13,589 | 4510 | 12,914 | 26,625 |
| Maximum Wall Y+ | 0.053 | 0.028 | 0.028 | 0.025 |
| CPU User time | 1463.88 s | 764.764 s | 4890.82 s | 55,457.7 s |
| Wall clock | 126.53 s | 99.75 s | 1016.62 s | 13,339.77 s |
| Mbytes used cells | 3 | 9 | 29 | 77 |
| Virtual Memory Usage | 0.258 GB | 0.279 GB | 0.366 GB | 0.414 GB |
| Turbulence Model | |||
|---|---|---|---|
| Grid method | 3D Multiblock—Hexahedral mesh | ||
| Number of cells | 9520 | ||
| Discretization Scheme | Second-order upwind | ||
| P-V Coupling Scheme | SIMPLE Scheme | ||
| Boundary Conditions | -No-slip in the walls-Periodic inlet/outlet | ||
| Residual Value | 1.0 × 10−6 | ||
| Processors in Parallel | 4 | ||
| Iterations | 5084 | 4668 | 4510 |
| Maximum Wall Y+ | 0.030 | 0.027 | 0.028 |
| CPU User time | 736.964 s | 643.301 s | 764.764 s |
| Wall clock | 92.241 s | 82.750 s | 99.751 s |
| Mbytes used cells | 6 | 6 | 9 |
| Virtual Mem Usage | 0.263 GB | 0.263 GB | 0.279 GB |
| Method | Wall Shear Stress [Pa] | Error |
|---|---|---|
| Mean Pressure—Gradient method | 0.182 | Reference |
| 3D CFD | 0.179 | +1.6% |
| The law of the wall | 0.178 | +2.2% |
| Preston tube | 0.188 | +3.3% |
| Mean square signal from a hot-wire | 0.162 | +10.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopez-Santana, G.; Kennaugh, A.; Keshmiri, A. Experimental Techniques against RANS Method in a Fully Developed Turbulent Pipe Flow: Evolution of Experimental and Computational Methods for the Study of Turbulence. Fluids 2022, 7, 78. https://doi.org/10.3390/fluids7020078
Lopez-Santana G, Kennaugh A, Keshmiri A. Experimental Techniques against RANS Method in a Fully Developed Turbulent Pipe Flow: Evolution of Experimental and Computational Methods for the Study of Turbulence. Fluids. 2022; 7(2):78. https://doi.org/10.3390/fluids7020078
Chicago/Turabian StyleLopez-Santana, Gabriela, Andrew Kennaugh, and Amir Keshmiri. 2022. "Experimental Techniques against RANS Method in a Fully Developed Turbulent Pipe Flow: Evolution of Experimental and Computational Methods for the Study of Turbulence" Fluids 7, no. 2: 78. https://doi.org/10.3390/fluids7020078
APA StyleLopez-Santana, G., Kennaugh, A., & Keshmiri, A. (2022). Experimental Techniques against RANS Method in a Fully Developed Turbulent Pipe Flow: Evolution of Experimental and Computational Methods for the Study of Turbulence. Fluids, 7(2), 78. https://doi.org/10.3390/fluids7020078






