Numerical Simulation of Departure from Nucleate Boiling in Rod Bundles under High-Pressure Conditions
Abstract
:1. Introduction
2. Mathematical Model
2.1. Heat Flux Partitioning Model
2.2. Boiling Closures
2.2.1. Bubble Departure Diameter and Frequency
2.2.2. Nucleation Site Density
2.3. Momentum Closures
2.4. Turbulence Closure
3. Benchmark Data
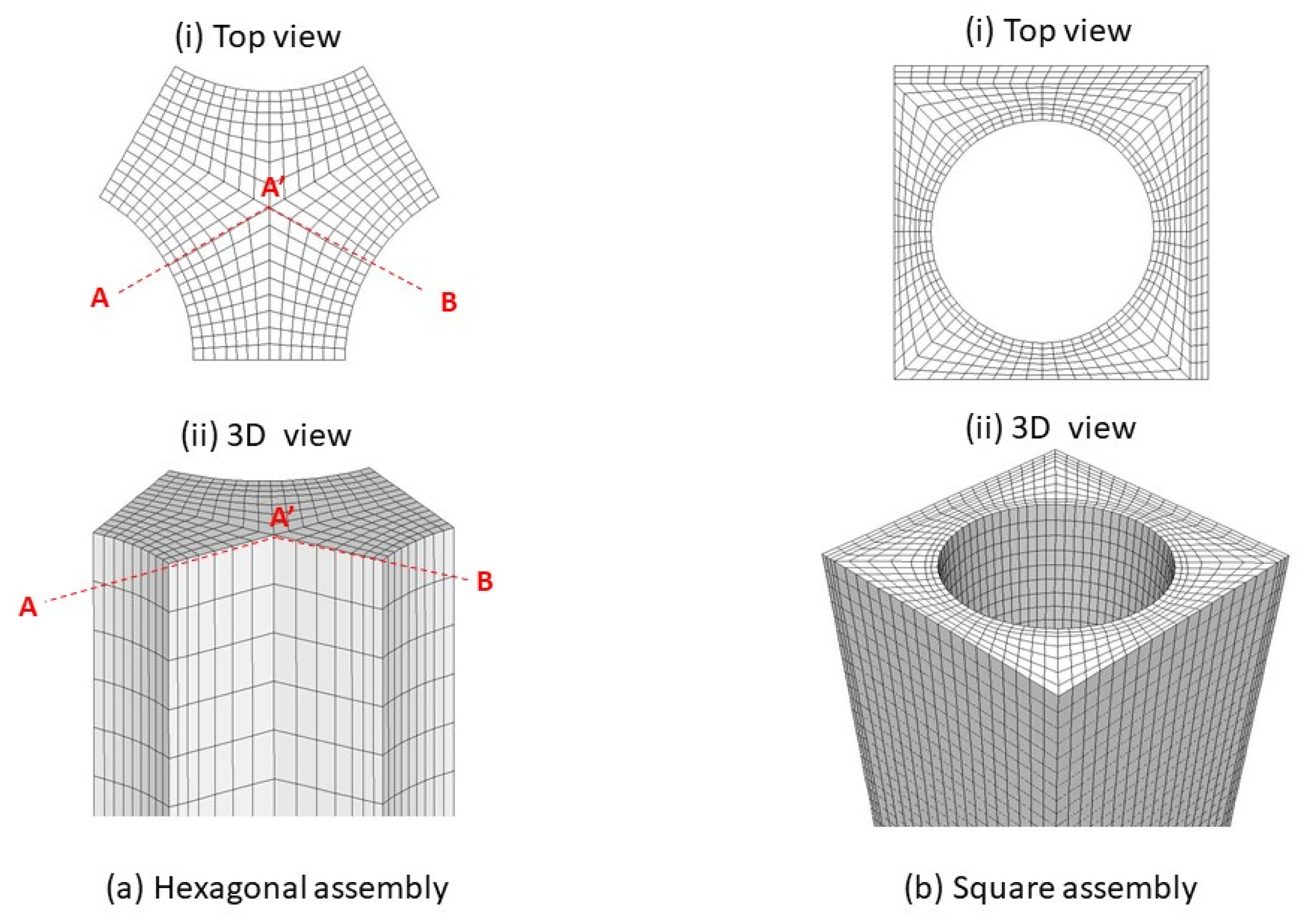
4. Modeling Strategy
5. Results and Discussions
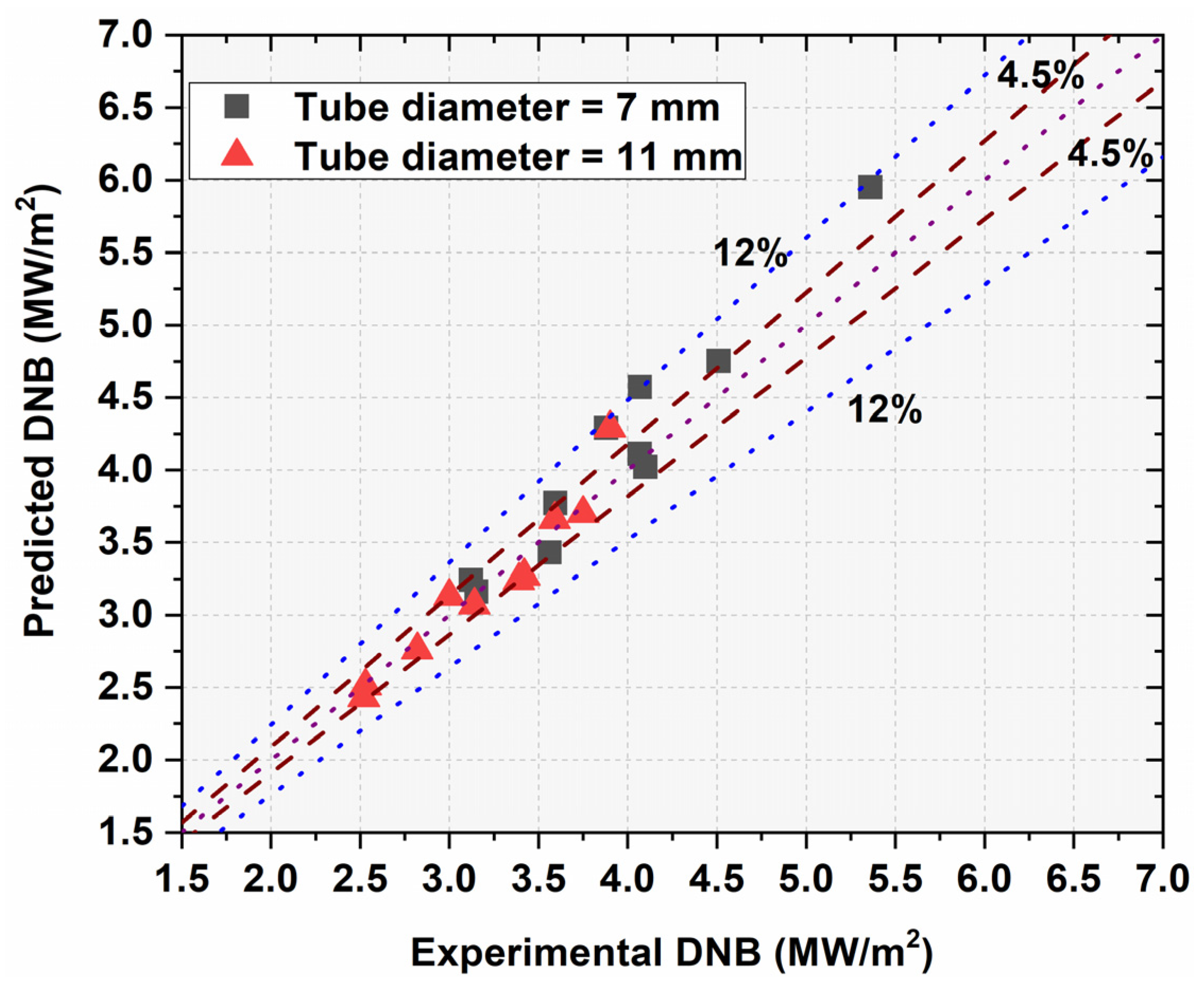
5.1. DNB in Tubes
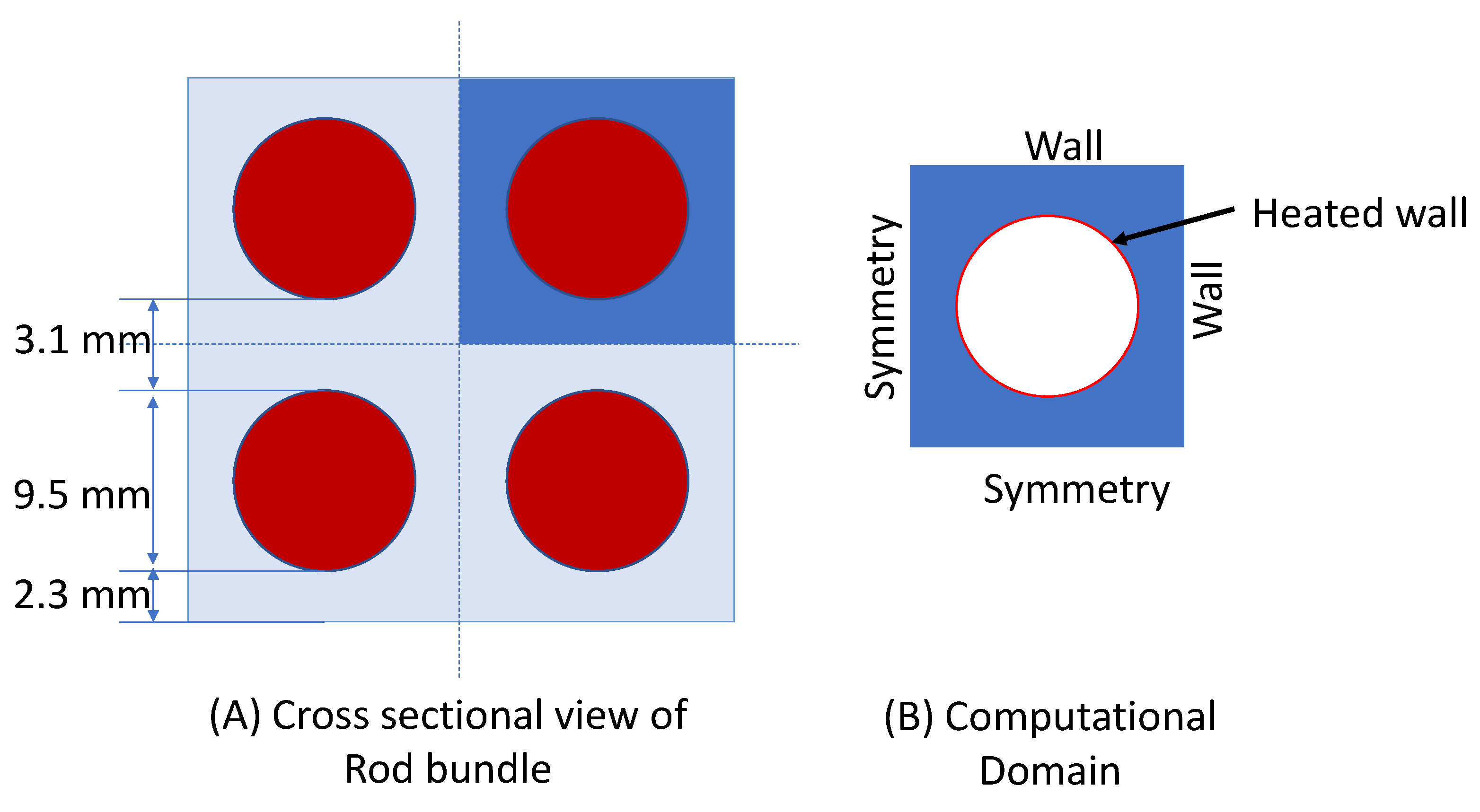
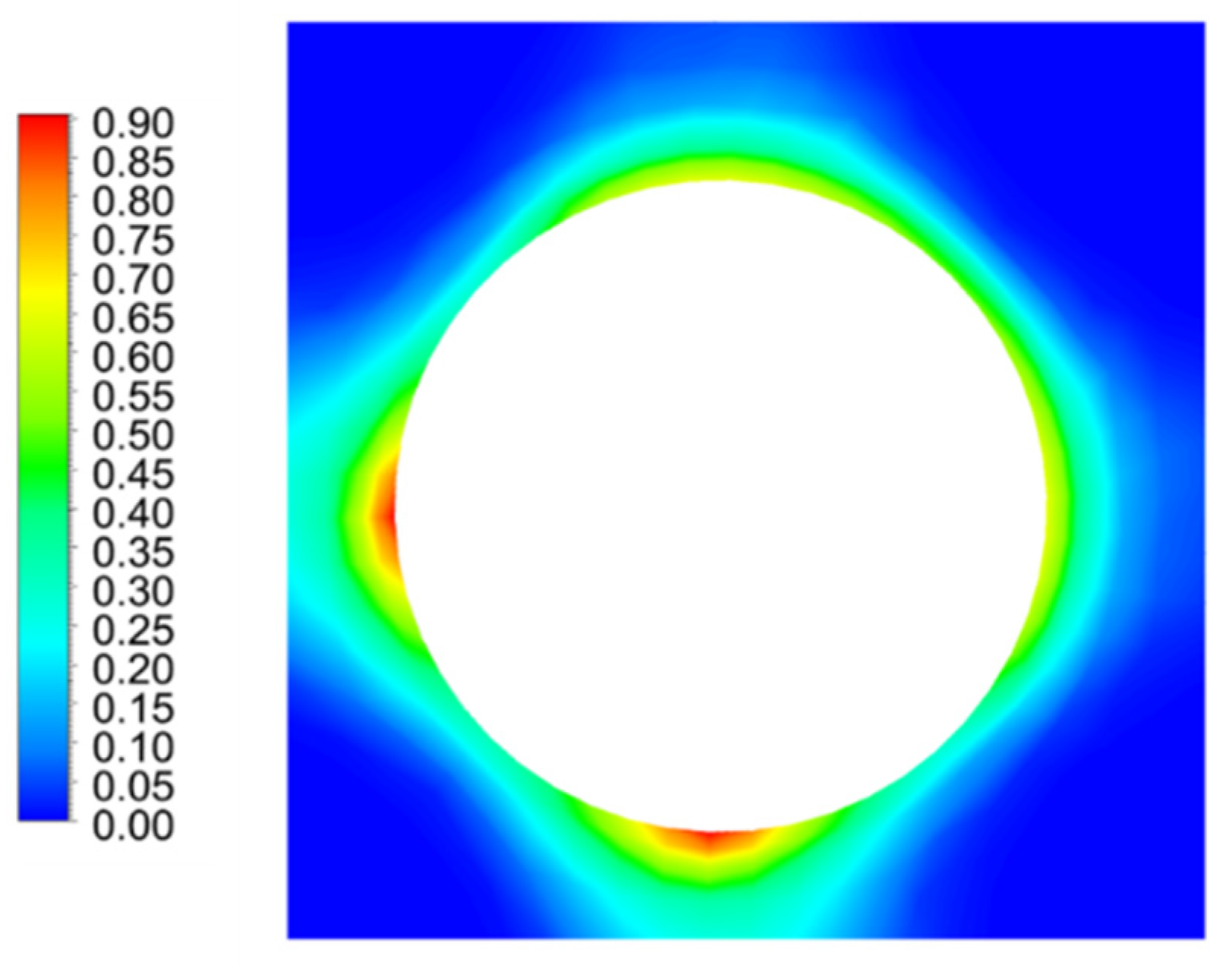
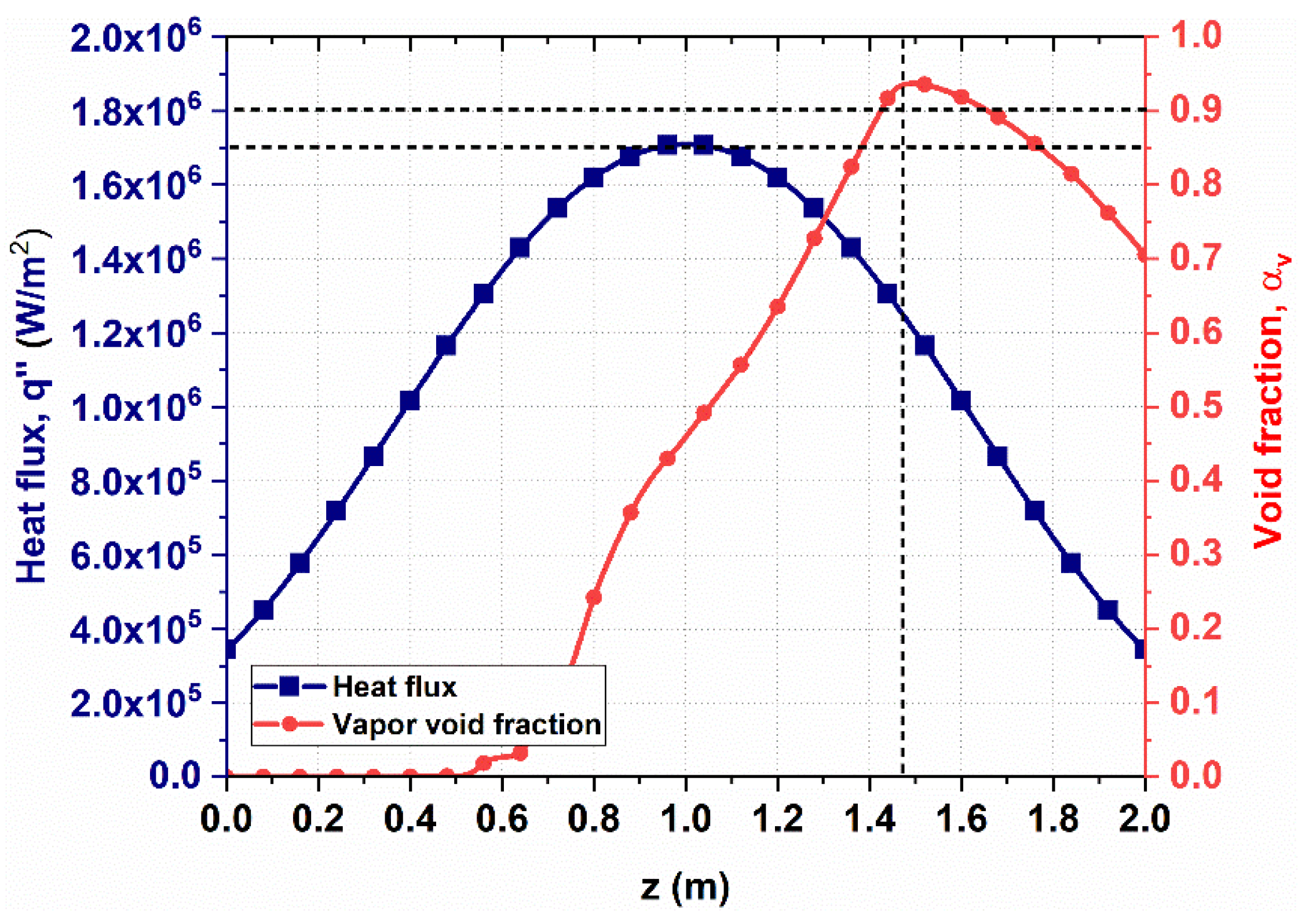
5.2. DNB in Rod Bundle (Square Lattice)
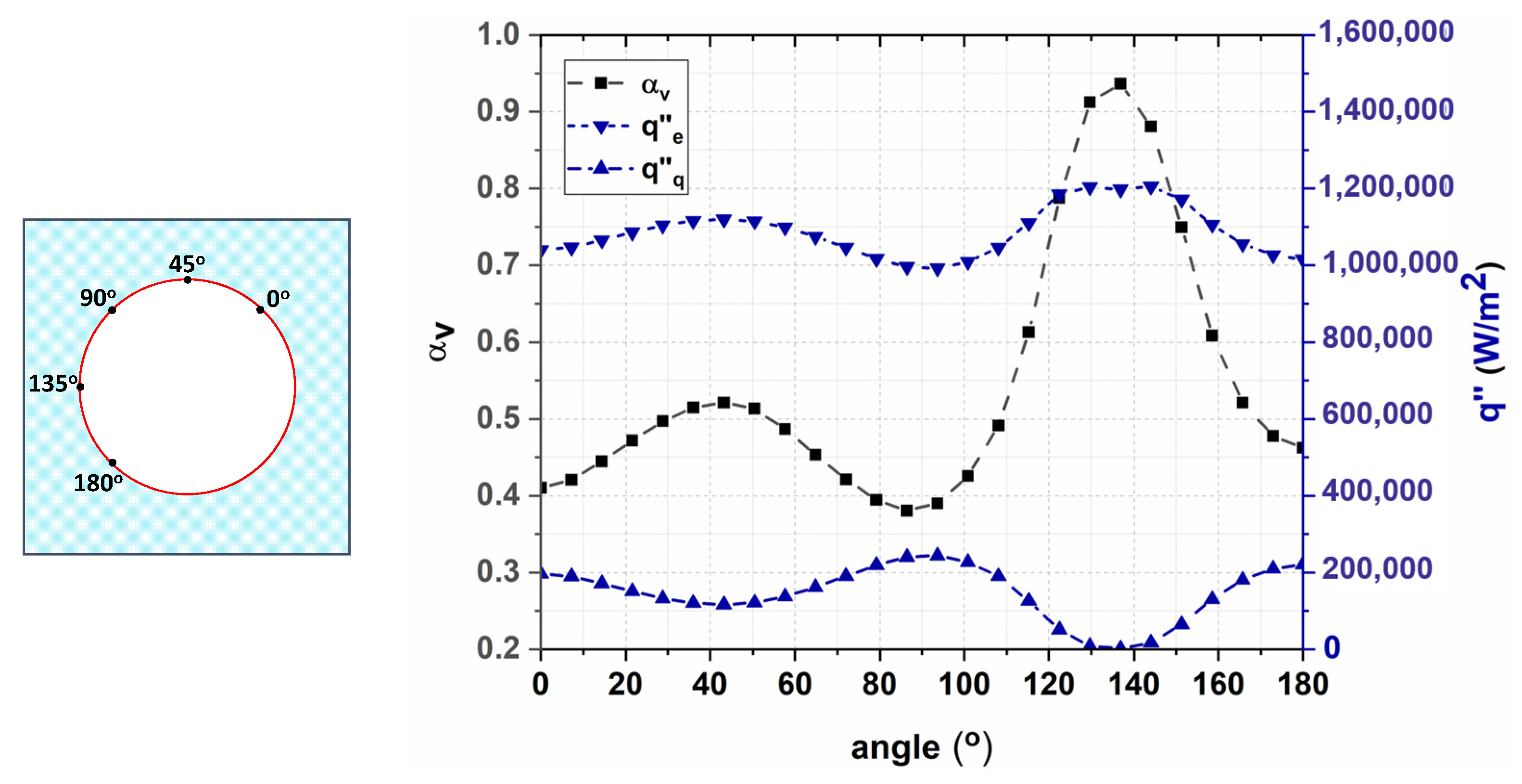
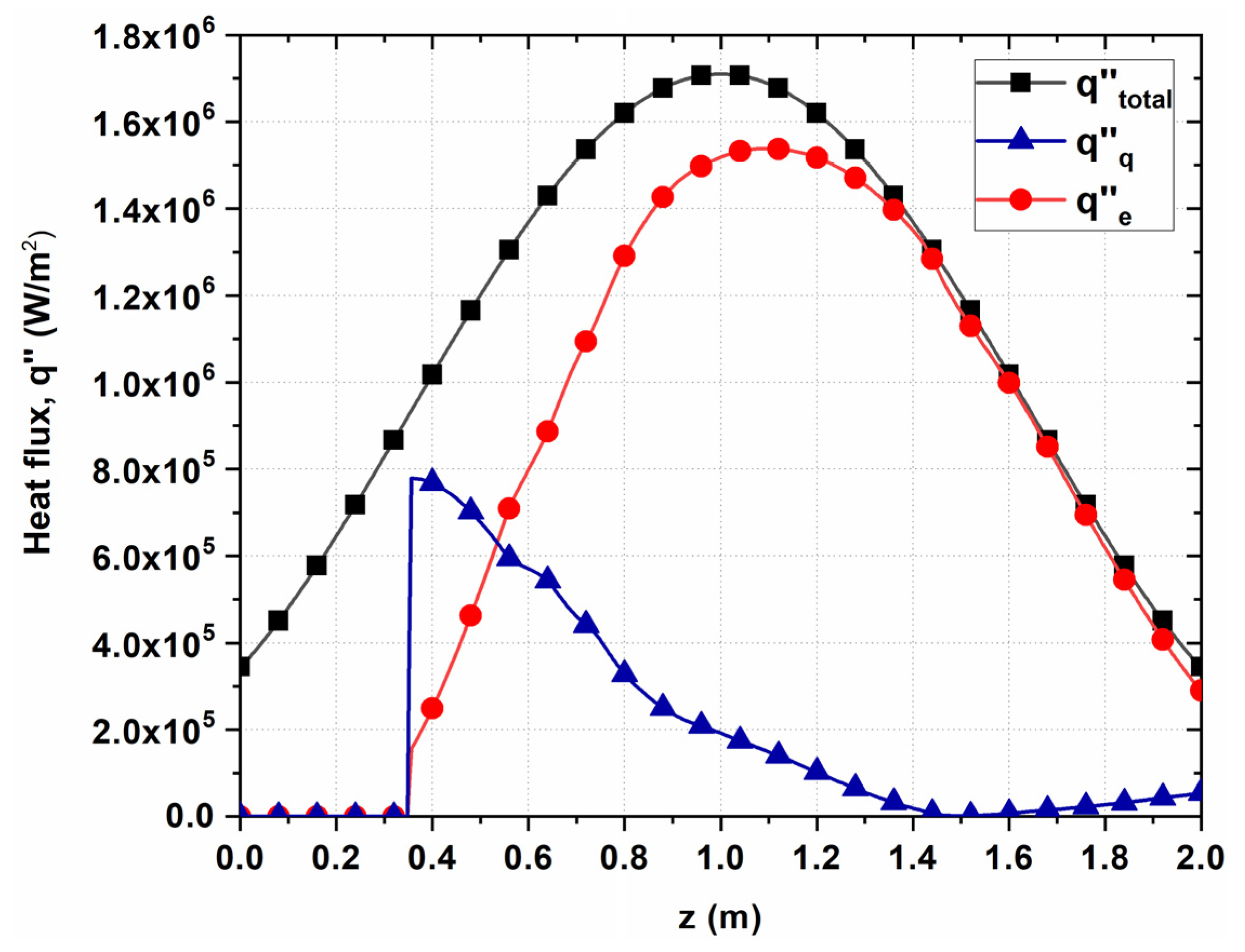
Heat Flux Partitioning Analysis
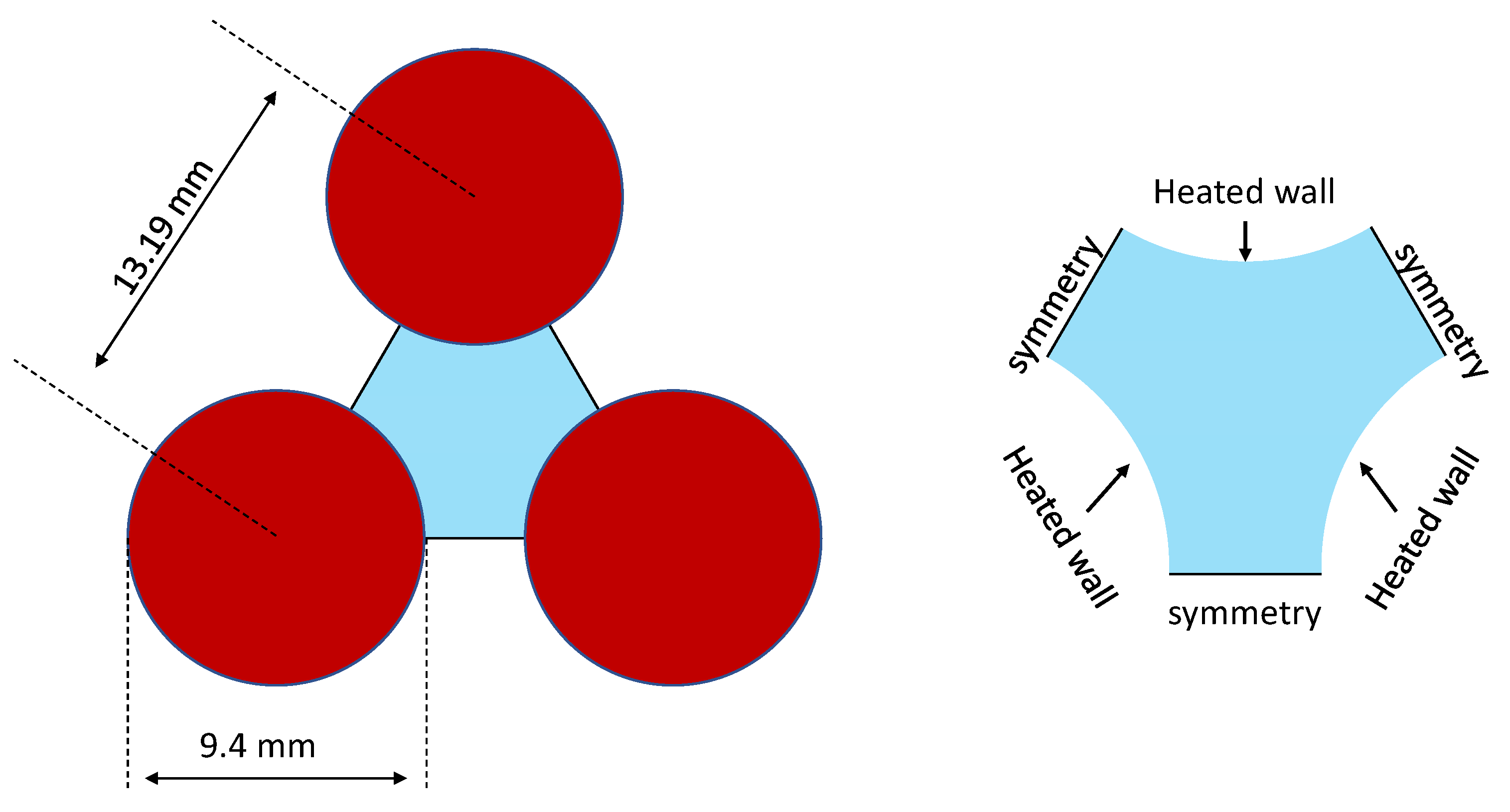
5.3. DNB in Rod Bundle (Hexagonal Lattice)
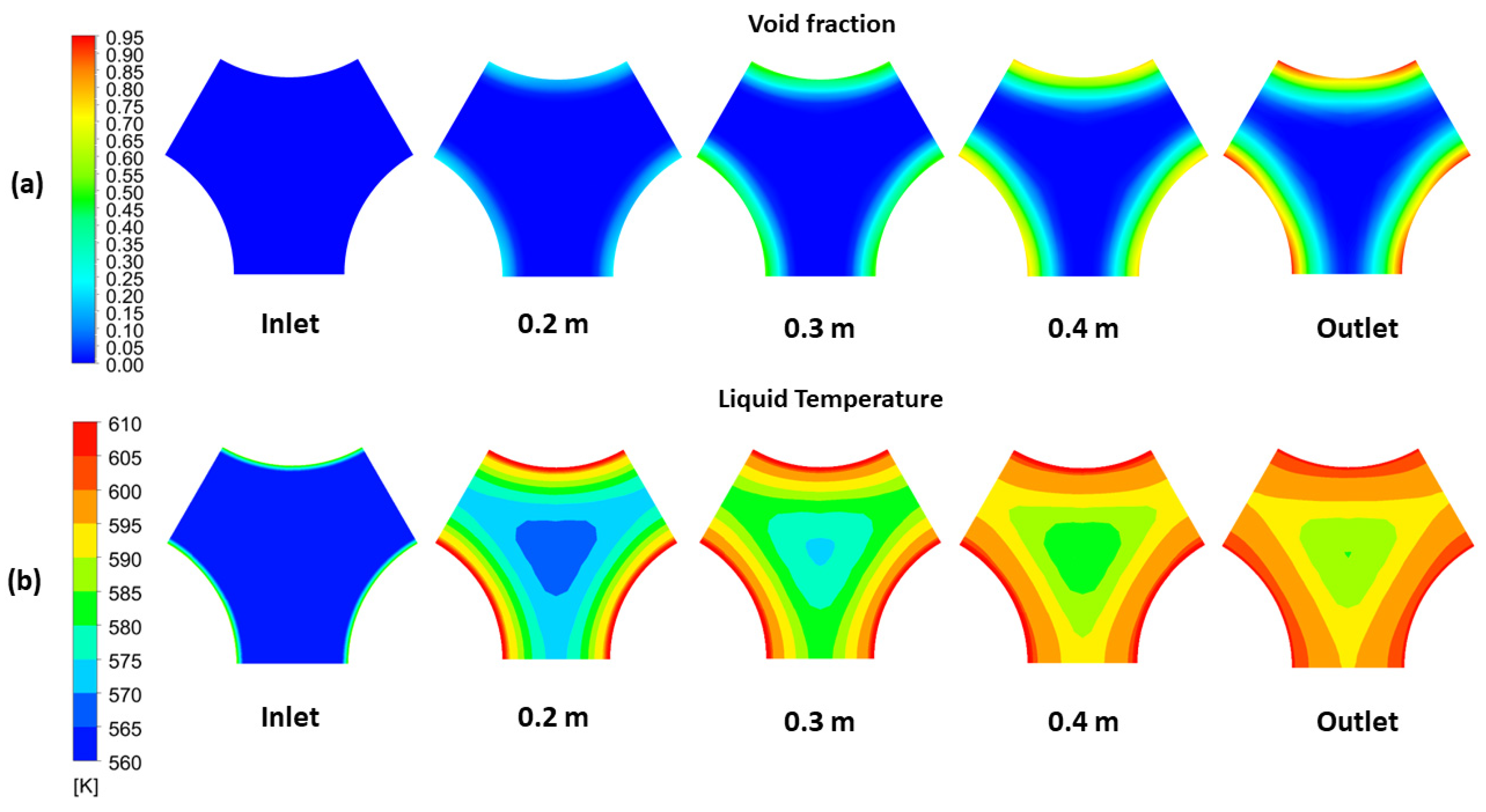
5.3.1. Void and Temperature Distribution in the Hexagonal Lattice
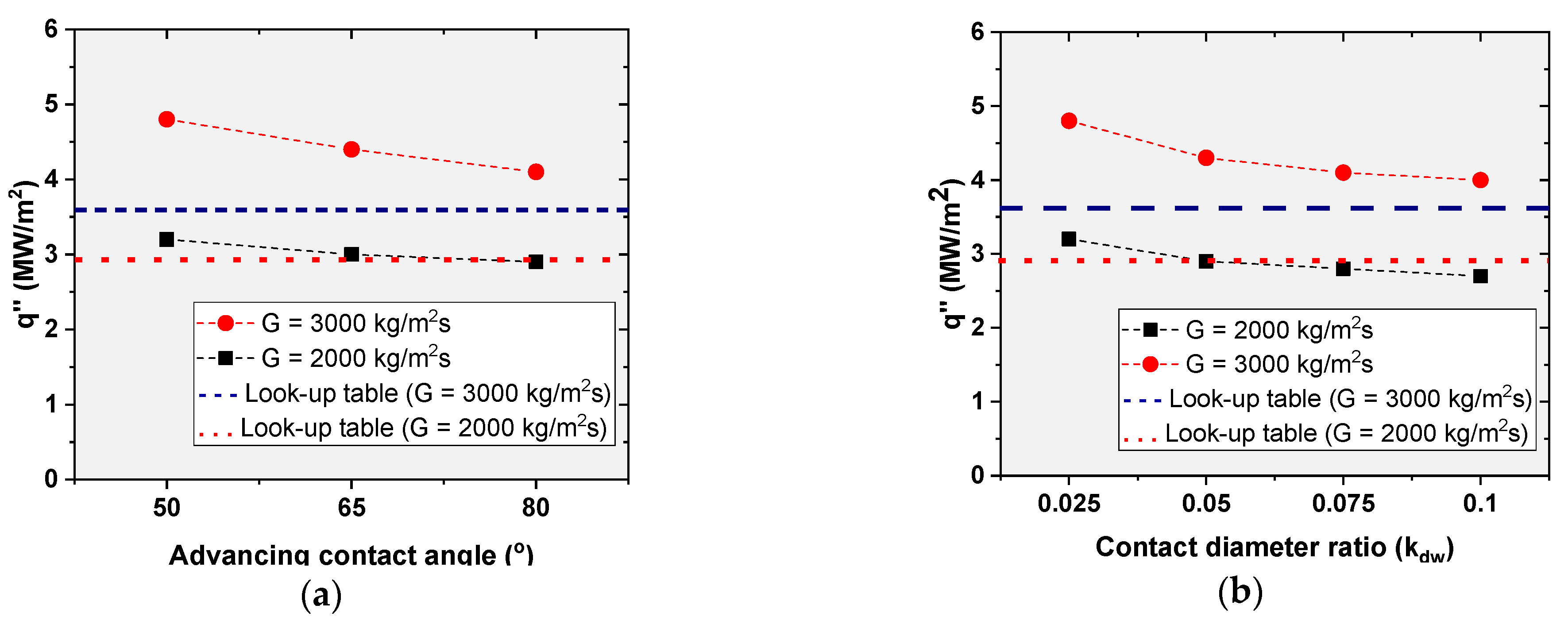
5.3.2. Comparison of Predicted DNB Values with Lookup Table
6. Conclusions
- Using the developed semi-mechanistic models for bubble departure characteristics, DNB has been predicted in tubes at high-pressure conditions with a mean error of 4.5% and maximum error of 12%, as opposed to the mean error of 7% and maximum error of 15% using the empirical models [24].
- The CFD model predicted the average heat flux at which DNB occurred with a minimum error of 11.5% and a maximum error of 19.6% compared to experimental average heat flux values in square lattices.
- CFD model has also been used to predict DNB in hexagonal subchannel at various mass flux values at 13.8 MPa. Predicted DNB values of hexagonal subchannel have been compared with both Bobkov and Groeneveld Look-up tables with appropriate correction factors. Predicted DNB deviations have been in the range of 1.8–13.9% for hexagonal lattices.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Fraction of the area influenced by bubbles |
| B | Parameter and function of pressure |
| C | Parameter and function of pressure |
| CFD | Computational fluid dynamics |
| CHF | Critical heat flux |
| Db | Bubble departure diameter (m) |
| Dh | Hydraulic diameter (m) |
| d | Diameter of the fuel rod (m) |
| dt | Thermal diameter (m) |
| DNB | Departure from nucleate boiling |
| f | Bubble departure frequency (s−1) |
| f(P) | Function of pressure |
| F | Force (N) |
| g | Acceleration due to gravity (m s−2) |
| hc | Liquid heat transfer coefficient (W m−2 K−1) |
| hv | Vapor heat transfer coefficient (W m−2 K−1) |
| K1 | Groeneveld correction factor for hydraulic diameter |
| K2 | Groeneveld bundle correction factor |
| K1,b | Bobkov correction factor for thermal diameter |
| K2,b | Bobkov bundle correction factor |
| K3,b | Bobkov correction factor for heating length |
| ka | Area influence factor |
| kdw | Contact diameter ratio |
| L | Heating length (m) |
| MVGs | Mixing vane grid configurations |
| N0 | Constant |
| Nw | Nucleation site density |
| NVMGs | Non-mixing vane grid configurations |
| P | Pressure (Pa) |
| p | Pitch between the fuel rods(m) |
| PWR | Pressurized water reactor |
| q″ | Heat flux (W m−2) |
| q | heater power |
| R | Bubble radius (m) |
| Reb | Bubble Reynolds number |
| T | Temperature (K) |
| Vb | Volume of the bubble (m3) |
| vr | Relative velocity (m/s) |
| x | Thermodynamic quality |
| z | Axial position |
| Greek letters | |
| α | Phase fraction |
| αl,crit | Critical liquid fraction |
| αv,1 | Constant |
| αv,2 | Constant |
| ε | Rate of dissipation of turbulent kinetic energy per unit mass (m2 s−3) |
| f(α) | Function of void fraction |
| θ | Contact angle |
| Advancing contact angle | |
| Receding contact angle | |
| ρ | Density (kg m−3) |
| Subscripts | |
| avg | Average |
| b | Buoyancy |
| c | Convective |
| cp | Contact pressure |
| du | Unsteady drag |
| e | Evaporative |
| exp | Experimental value |
| h | Hydrodynamic pressure |
| k | kth phase |
| l | Liquid |
| pre | Predicted value |
| q | Quenching |
| qs | Quasi-static drag |
| sat | saturation |
| sl | Shear lift |
| st | Surface tension |
| v | Vapor |
| w | Wall |
| x | x-direction (flow direction) |
| y | y-direction (normal to the wall direction) |
Appendix A
Look-Up Tables
References
- Todreas, N.E.; Kazimi, M.S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2012. [Google Scholar]
- Hall, D.D.; Mudawar, I. Critical Heat Flux (CHF) for Water Flow in Tubes-I. Compilation and Assessment of World CHF Data. Int. J. Heat Mass Transf. 2000, 43, 2573–2604. [Google Scholar] [CrossRef]
- Reddy, D.G.; Fighetti, C.F. Parametric Study of CHF Data. Volume 2. A Generalized Subchannel CHF Correlation for PWR and BWR Fuel Assemblies; Final Report No. EPRI-NP-2609-Vol. 2; Department of Chemical Engineering, Columbia University: New York, NY, USA, 1983. [Google Scholar]
- Hall, D.D.; Mudawar, I. Critical Heat Flux (CHF) for Water Flow in Tubes—II. Int. J. Heat Mass Transf. 2000, 43, 2605–2640. [Google Scholar] [CrossRef]
- Groeneveld, D.C.; Shan, J.Q.; Vasić, A.Z.; Leung, L.K.H.; Durmayaz, A.; Yang, J.; Cheng, S.C.; Tanase, A. The 2006 CHF Look-up Table. Nucl. Eng. Des. 2007, 237, 1909–1922. [Google Scholar] [CrossRef]
- Bobkov, V.P.; Efanov, A.D.; Pomet’ko, R.S.; Smogalev, I.P. A Modified Table for Calculating Critical Heat Fluxes in Assemblies of Triangularly Packed Fuel Rods. Therm. Eng. 2011, 58, 317–324. [Google Scholar] [CrossRef]
- Krepper, E.; Rzehak, R. CFD for Subcooled Flow Boiling: Simulation of DEBORA Experiments. Nucl. Eng. Des. 2011, 241, 3851–3866. [Google Scholar] [CrossRef]
- Krepper, E.; Končar, B.; Egorov, Y. CFD Modelling of Subcooled Boiling—Concept, Validation and Application to Fuel Assembly Design. Nucl. Eng. Des. 2007, 237, 716–731. [Google Scholar] [CrossRef]
- Colombo, M.; Fairweather, M. Accuracy of Eulerian–Eulerian, Two-Fluid CFD Boiling Models of Subcooled Boiling Flows. Int. J. Heat Mass Transf. 2016, 103, 28–44. [Google Scholar] [CrossRef]
- Murallidharan, J.S.; Prasad, B.V.S.S.S.; Patnaik, B.S.V.; Hewitt, G.F.; Badalassi, V. CFD Investigation and Assessment of Wall Heat Flux Partitioning Model for the Prediction of High Pressure Subcooled Flow Boiling. Int. J. Heat Mass Transf. 2016, 103, 211–230. [Google Scholar] [CrossRef]
- Baglietto, E.; Demarly, E.; Kommajosyula, R.; Lubchenko, N.; Magolan, B.; Sugrue, R. A Second Generation Multiphase-CFD Framework Toward Predictive Modeling of DNB. Nucl. Technol. 2019, 205, 1–22. [Google Scholar] [CrossRef]
- Tentner, A.; Lo, S.; Ioilev, A.; Melnikov, V.; Samigulin, M.; Ustinenko, V.; Kozlov, V. Advances in Computational Fluid Dynamics Modeling of Two Phase Flow in a Boiling Water Reactor Fuel Assembly. In Proceedings of the International Conference on Nuclear Engineering, Miami, FL, USA, 17–20 July 2006. [Google Scholar]
- Lavieville, J.; Quemerais, E.; Mimouni, S.; Boucker, M.; Mechitoua, N. NEPTUNE CFD V1. 0 Theory Manual. Rainterne EDF H-I81-2006-04377-EN. RaNEPTUNE Nept_2004_L, 1. Available online: https://scholar.google.com/scholar_lookup?hl=en&publication_year=2006&author=J.+Lavieville&title=NEPTUNE+CFD+V1.+0+theory+manual (accessed on 16 December 2021).
- Zhang, R.; Cong, T.; Tian, W.; Qiu, S.; Su, G. Prediction of CHF in Vertical Heated Tubes Based on CFD Methodology. Prog. Nucl. Energy 2015, 78, 196–200. [Google Scholar] [CrossRef]
- Ioilev, A.; Samigulin, M.; Ustinenko, V.; Kucherova, P.; Tentner, A.; Lo, S.; Splawski, A. Advances in the Modeling of Cladding Heat Transfer and Critical Heat Flux in Boiling Water Reactor Fuel Assemblies. In Proceedings of the 12th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-12), Pittsburgh, PA, USA, 30 September–4 October 2007. [Google Scholar]
- Li, Q.; Avramova, M.; Jiao, Y.; Chen, P.; Yu, J.; Pu, Z.; Chen, J. CFD Prediction of Critical Heat Flux in Vertical Heated Tubes with Uniform and Non-Uniform Heat Flux. Nucl. Eng. Des. 2018, 326, 403–412. [Google Scholar] [CrossRef]
- Kim, S.J.; Baglietto, E.; Demarly, E. Evaluation of DNB Predictive Capability in Multiphase Boiling Model of STAR-CCM+; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2018.
- Kim, S.J. Assessment on DNB Performance for High Pressure Subcooled Boiling with Modified CASL Boiling Model; Los Alamos National Laboratory: Los Alamos, NM, USA, 2019.
- Sugrue, R.M. A Robust Momentum Closure Approach for Multiphase Computational Fluid Dynamics Applications. Ph.D. Thesis, Massachusetts Institute of Technology, Boston, MA, USA, 2017. [Google Scholar]
- Lubchenko, N.; Magolan, B.; Sugrue, R.; Baglietto, E. A More Fundamental Wall Lubrication Force from Turbulent Dispersion Regularization for Multiphase CFD Applications. Int. J. Multiph. Flow 2018, 98, 36–44. [Google Scholar] [CrossRef]
- Thompson, B.; Macbeth, R.V. Boiling Water Heat Transfer Burnout in Uniformly Heated Round Tubes: A Compilation of World Data with Accurate Correlations; No. AEEW-R-356, United Kingdom Atomic Energy Authority, Reactor Group; Atomic Energy Establishment: Winfrith, UK, 1964.
- Xu, Y.; Brewster, R.A.; Conner, M.E.; Karoutas, Z.E.; Smith, L.D. CFD Modeling Development for DNB Prediction of Rod Bundle with Mixing Vanes Under PWR Conditions. Nucl. Technol. 2019, 205, 57–67. [Google Scholar] [CrossRef]
- Zhang, R.; Duarte, J.P.; Cong, T.; Corradini, M.L. Investigation on the Critical Heat Flux in a 2 by 2 Fuel Assembly under Low Flow Rate and High Pressure with a CFD Methodology. Ann. Nucl. Energy 2019, 124, 69–79. [Google Scholar] [CrossRef]
- Vadlamudi, S.R.G.; Nayak, A.K. CFD Simulation of Departure from Nucleate Boiling in Vertical Tubes under High Pressure and High Flow Conditions. Nucl. Eng. Des. 2019, 352, 110150. [Google Scholar] [CrossRef]
- Duarte, J.P.; Zhao, D.; Jo, H.; Corradini, M.L. Critical Heat Flux Experiments and a Post-CHF Heat Transfer Analysis Using 2D Inverse Heat Transfer. Nucl. Eng. Des. 2018, 337, 17–26. [Google Scholar] [CrossRef]
- Ishii, M.; Hibiki, T. Thermo-Fluid Dynamics of Two-Phase Flow; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Klausner, J.F.; Mei, R.; Bernhard, D.M.; Zeng, L.Z. Vapor Bubble Departure in Forced Convection Boiling. Int. J. Heat Mass Transf. 1993, 36, 651–662. [Google Scholar] [CrossRef]
- Tolubinsky, V.I.; Kostanchuk, D.M. Vapour Bubbles Growth Rate and Heat Transfer Intensity at Subcooled Water Boiling. In Proceedings of the International Heat Transfer Conference 4, Begellhouse, CT, USA, 31 August–5 September 1970; pp. 1–11. [Google Scholar]
- Yun, B.-J.; Splawski, A.; Lo, S.; Song, C.-H. Prediction of a Subcooled Boiling Flow with Advanced Two-Phase Flow Models. Nucl. Eng. Des. 2012, 253, 351–359. [Google Scholar] [CrossRef]
- Sugrue, R.; Buongiorno, J. A Modified Force-Balance Model for Prediction of Bubble Departure Diameter in Subcooled Flow Boiling. Nucl. Eng. Des. 2016, 305, 717–722. [Google Scholar] [CrossRef]
- Colombo, M.; Fairweather, M. Prediction of Bubble Departure in Forced Convection Boiling: A Mechanistic Model. Int. J. Heat Mass Transf. 2015, 85, 135–146. [Google Scholar] [CrossRef]
- Kurul, N.; Podowski, M.Z. Multidimensional Effects in Forced Convection Subcooled Boiling. In Proceedings of the 9th International Heat Transfer Conference, Jerusalem, Israel, 19–24 August 1990; pp. 21–26. [Google Scholar]
- Collier, J.G.; Thome, J.R. Convective Boiling and Condensation; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Tong, L.S.; Tang, Y.S. Boiling Heat Transfer and Two-Phase Flow; Series in Chemical and Mechanical Engineering; Taylor and Francis: Washington, DC, USA, 1997. [Google Scholar]
- Mikic, B.; Rohsenow, W.; Griffith, P. On Bubble Growth Rates. Int. J. Heat Mass Transf. 1970, 13, 657–666. [Google Scholar] [CrossRef]
- Forster, H.K.; Zuber, N. Growth of a Vapor Bubble in a Superheated Liquid. J. Appl. Phys. 1954, 25, 474–478. [Google Scholar] [CrossRef]
- Cooper, M.G. The Microlayer and Bubble Growth in Nucleate Pool Boiling. Int. J. Heat Mass Transf. 1969, 12, 915–933. [Google Scholar] [CrossRef]
- Sakashita, H. Bubble Growth Rates and Nucleation Site Densities in Saturated Pool Boiling of Water at High Pressures. J. Nucl. Sci. Technol. 2011, 48, 734–743. [Google Scholar] [CrossRef]
- Murallidharan, J.; Giustini, G.; Sato, Y.; Ničeno, B.; Badalassi, V.; Walker, S.P. Computational Fluid Dynamic Simulation of Single Bubble Growth under High-Pressure Pool Boiling Conditions. Nucl. Eng. Technol. 2016, 48, 859–869. [Google Scholar] [CrossRef] [Green Version]
- Plesset, M.S.; Zwick, S.A. The Growth of Vapor Bubbles in Superheated Liquids. J. Appl. Phys. 1954, 25, 493–500. [Google Scholar] [CrossRef] [Green Version]
- Vadlamudi, S.R.G.; Nayak, A.K. The Influence of Bubble Departure Characteristics on CHF Prediction at High-Pressure Conditions. Case Stud. Therm. Eng. 2020, 22, 100735. [Google Scholar] [CrossRef]
- Kocamustafaogullari, G.; Ishii, M. Interfacial Area and Nucleation Site Density in Boiling Systems. Int. J. Heat Mass Transf. 1983, 26, 1377–1387. [Google Scholar] [CrossRef]
- Hibiki, T.; Ishii, M. Active Nucleation Site Density in Boiling Systems. Int. J. Heat Mass Transf. 2003, 46, 2587–2601. [Google Scholar] [CrossRef]
- Li, Q.; Jiao, Y.; Avramova, M.; Chen, P.; Yu, J.; Chen, J.; Hou, J. Development, Verification and Application of a New Model for Active Nucleation Site Density in Boiling Systems. Nucl. Eng. Des. 2018, 328, 1–9. [Google Scholar] [CrossRef]
- Del Valle, V.H.; Kenning, D.B.R. Subcooled Flow Boiling at High Heat Flux. Int. J. Heat Mass Transf. 1985, 28, 1907–1920. [Google Scholar] [CrossRef]
- Ishii, M.; Zuber, N. Drag Coefficient and Relative Velocity in Bubbly, Droplet or Particulate Flows. AIChE J. 1979, 25, 843–855. [Google Scholar] [CrossRef]
- Vadlamudi, S.R.G.; Nayak, A.K. Investigations on Effect of Lift and Wall Lubrication Forces on the Subcooled Flow Boiling. ASME J. Nucl. Eng. Radiat. Sci. 2020, 6, 041109. [Google Scholar] [CrossRef]
- Burns, A.D.; Frank, T.; Hamill, I.; Shi, J.-M.M. The Favre Averaged Drag Model for Turbulent Dispersion in Eulerian Multi-Phase Flows. In Proceedings of the 5th International Conference on Multiphase Flow, ICMF-2004, Yokohama, Japan, 30 May–4 June 2004; pp. 1–17. [Google Scholar]
- Zhang, R.; Cong, T.; Tian, W.; Qiu, S.; Su, G. Effects of Turbulence Models on Forced Convection Subcooled Boiling in Vertical Pipe. Ann. Nucl. Energy 2015, 80, 293–302. [Google Scholar] [CrossRef]
- Sato, Y.; Sadatomi, M.; Sekoguchi, K. Momentum and Heat Transfer in Two-Phase Bubble Flow—I. Theory. Int. J. Multiph. Flow 1981, 7, 167–177. [Google Scholar] [CrossRef]
- Kim, S.J.; Johns, R.C.; Yoo, J.; Baglietto, E. Progress Toward Simulating Departure from Nucleate Boiling at High-Pressure Applications with Selected Wall Boiling Closures. Nucl. Sci. Eng. 2020, 194, 690–707. [Google Scholar] [CrossRef]
- Groeneveld, D.C.; Cheng, S.C.; Doan, T. 1986 AECL-UO Critical Heat Flux Lookup Table. Heat Transf. Eng. 1986, 7, 46–62. [Google Scholar] [CrossRef]
- Groeneveld, D.C.; Leung, L.K.H.; Guo, Y.; Vasic, A.; El Nakla, M.; Peng, S.W.; Yang, J.; Cheng, S.C. Lookup Tables for Predicting CHF and Film-Boiling Heat Transfer: Past, Present, and Future. Nucl. Technol. 2005, 152, 87–104. [Google Scholar] [CrossRef]
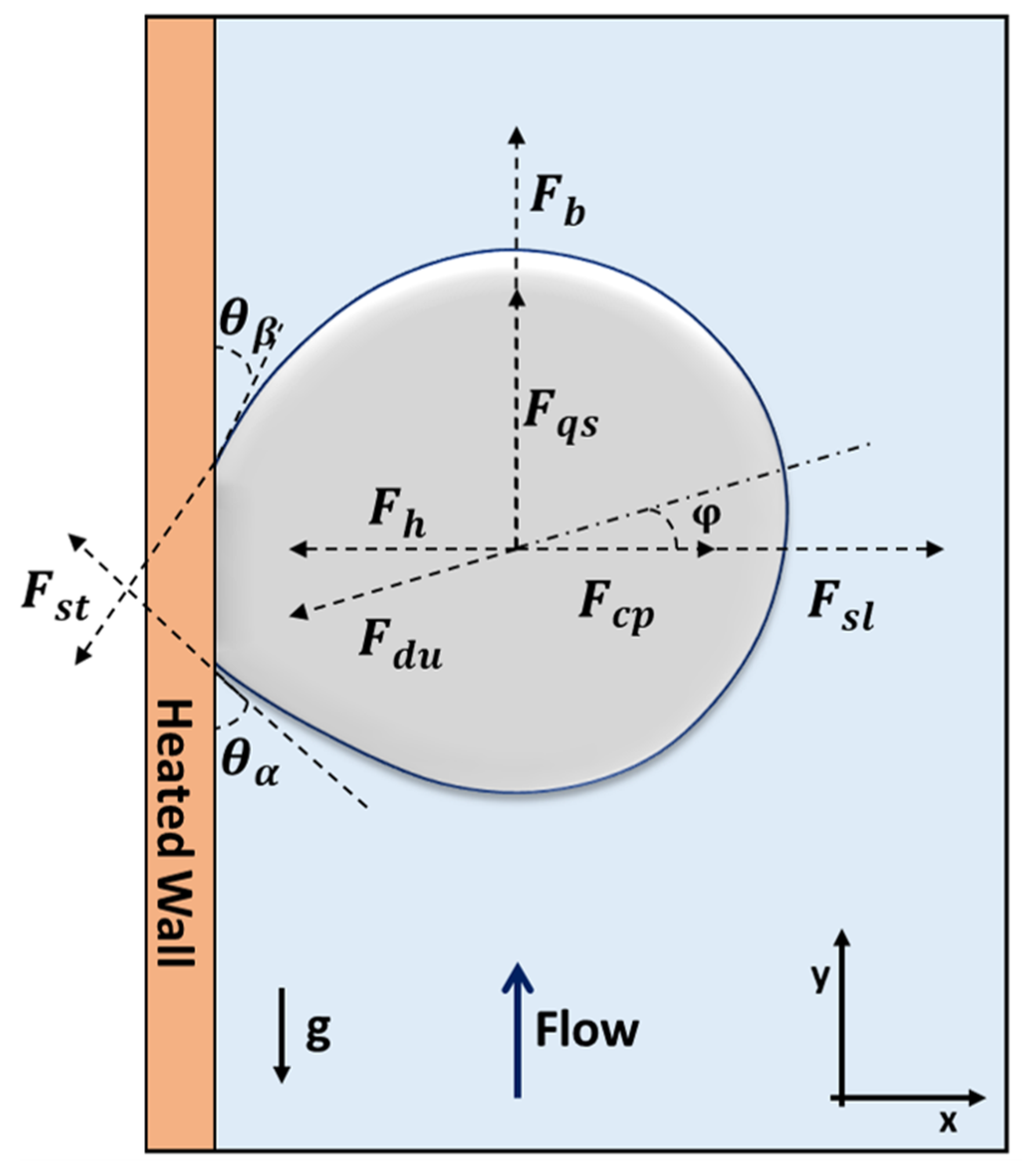


| x-Direction | y-Direction |
|---|---|
| Quasi-static drag force: where, n = 0.65 | Shear lift force: |
| Buoyancy force: | Hydrodynamic pressure force: |
| Unsteady drag force: | Unsteady drag force: |
| Surface tension force: | Surface tension force: |
| Contact pressure force: | |
| Contact diameter | Radius |
| Model | Radius |
|---|---|
| Forster and Zuber [36] | |
| Plesset and Zwick [40] | |
| Cooper [37] | |
| Mikic et al. [35] | |
| Yun et al. [29] | and b = 1.56 |
| Colombo and Fairweather [31] | |
| Sugrue and Buongiorno [30] | b = 1.56 |
| S No. | Inlet Subcooling Enthalpy (kJ/kg) | Inlet Pressure (MPa) | Mass Flux (kg/m2s) | Average DNB (MW/m2) |
|---|---|---|---|---|
| Case-1 | 343 | 16.1 | 1514 | 1.30 |
| Case-2 | 387 | 13.4 | 1526 | 1.58 |
| Case-3 | 425 | 14.2 | 1505 | 1.58 |
| Case-4 | 416 | 16.0 | 1506 | 1.44 |
| CFD Solver | Euler-Euler Two Phase Solver |
|---|---|
| Turbulence model | model with enhanced wall treatment |
| Boiling Closures | |
| Bubble Departure Diameter | Force balance model |
| Bubble Departure Frequency | Force balance model |
| Nucleation site density | Li et al. [44] |
| Area Influence Coefficient | Del Valle and Kenning [45] |
| Momentum Closures | |
| Drag force | Ishii and Zuber [46] |
| Turbulent Dispersion force | Burns et al. [48] |
| Boundary Conditions | |
| Inlet | Velocity inlet |
| Outlet | Pressure Outlet |
| Wall | Neumann condition (specified heat flux) |
| Solution Procedure | |
| Algorithm | Coupled |
| Schemes | 2nd order upwind for void distribution, momentum, energy, turbulent kinetic energy, and dissipation. |
| Grid Size | Average Heat Flux at DNB | Deviation (%) | ||
|---|---|---|---|---|
| Prediction (MW/m2) | Experimental (MW/m2) | |||
| Square assembly (Case 1) | ~1.5 million (187 × 4000) | 1.15 | 1.30 | 11.5 |
| ~2.5 million (306 × 4000) | 1.14 | 1.30 | 12.3 | |
| ~3 million (187 × 8000) | 1.15 | 1.30 | 11.5 | |
| Grid Size | Average Heat Flux at DNB | Deviation (%) | ||
| Prediction (MW/m2) | Look-Up Table (MW/m2) | |||
| Hexagonal assembly (G = 3000 kg/m2s) | ~0.08 million (180 × 425) | 4.10 | 3.58 | 14.5 |
| ~0.16 million (378 × 425) | 4.02 | 3.58 | 12.3 | |
| ~0.32 million (378 × 850) | 4.01 | 3.58 | 12.0 | |
| Case No. | Inlet Subcooling Enthalpy (kJ/kg) | Inlet Pressure (MPa) | Mass Flux (kg/m2s) | Average DNB (MW/m2) | Predicted (MW/m2) | Absolute Error (%) |
|---|---|---|---|---|---|---|
| Case-1 | 343 | 16.1 | 1514 | 1.30 | 1.15 | 11.5 |
| Case-2 | 387 | 13.4 | 1526 | 1.58 | 1.27 | 19.6 |
| Case-3 | 425 | 14.2 | 1505 | 1.58 | 1.32 | 16.4 |
| Case-4 | 416 | 16.0 | 1506 | 1.44 | 1.27 | 11.8 |
| Mass Flux (kg/m2s) | Predicted DNB (MW/m2) | Groeneveld Look-Up Table DNB (MW/m2) | Bobkov Look-Up Table (MW/m2) | Deviation from Groeneveld (%) | Deviation from Bobkov (%) |
|---|---|---|---|---|---|
| 1500 | 2.23 | 2.43 | 2.54 | 8.2 | 12.2 |
| 2000 | 2.87 | 2.82 | 2.97 | 1.8 | 3.4 |
| 2500 | 3.45 | 3.18 | 3.28 | 8.5 | 5.2 |
| 3000 | 4.02 | 3.53 | 3.58 | 13.9 | 12.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vadlamudi, S.R.G.; Nayak, A.K. Numerical Simulation of Departure from Nucleate Boiling in Rod Bundles under High-Pressure Conditions. Fluids 2022, 7, 83. https://doi.org/10.3390/fluids7020083
Vadlamudi SRG, Nayak AK. Numerical Simulation of Departure from Nucleate Boiling in Rod Bundles under High-Pressure Conditions. Fluids. 2022; 7(2):83. https://doi.org/10.3390/fluids7020083
Chicago/Turabian StyleVadlamudi, Sai Raja Gopal, and Arun K. Nayak. 2022. "Numerical Simulation of Departure from Nucleate Boiling in Rod Bundles under High-Pressure Conditions" Fluids 7, no. 2: 83. https://doi.org/10.3390/fluids7020083
APA StyleVadlamudi, S. R. G., & Nayak, A. K. (2022). Numerical Simulation of Departure from Nucleate Boiling in Rod Bundles under High-Pressure Conditions. Fluids, 7(2), 83. https://doi.org/10.3390/fluids7020083






