High-Speed Imaging of Water Hammer Cavitation in Oil–Hydraulic Pipe Flow
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Equipment
2.2. Wave Speed
2.3. Column Separation
3. Results
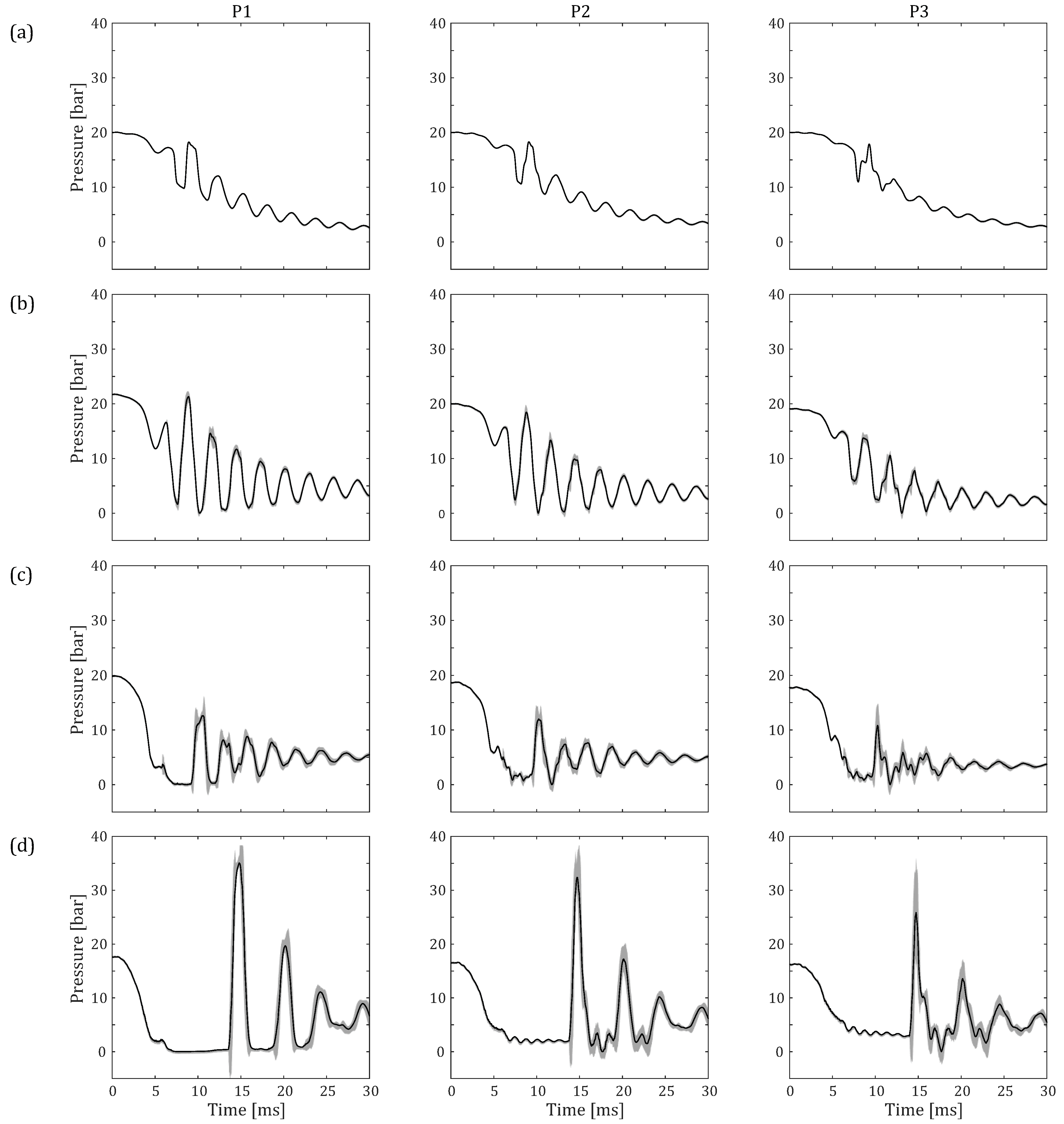
3.1. Wave Speed
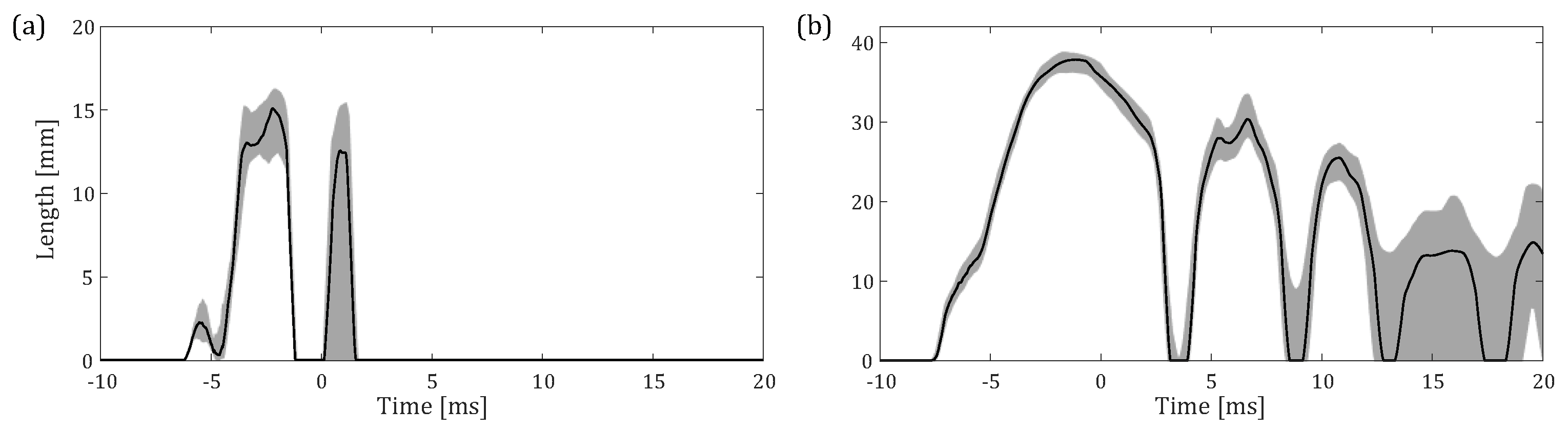
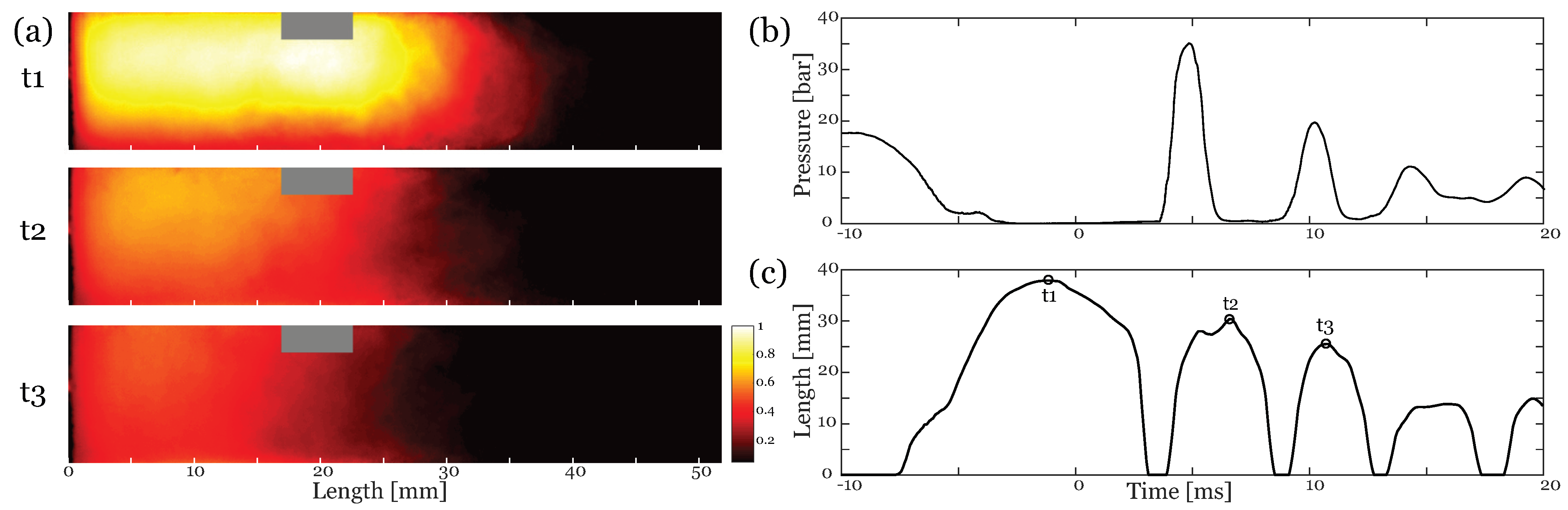
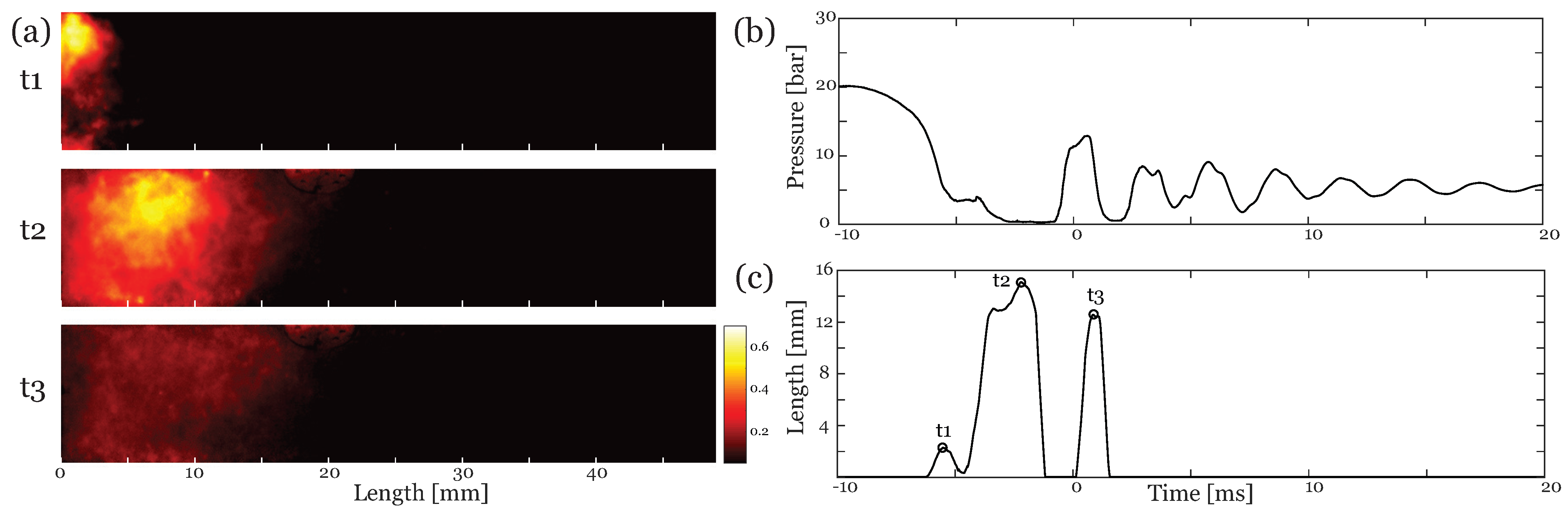
3.2. Column Separation Length
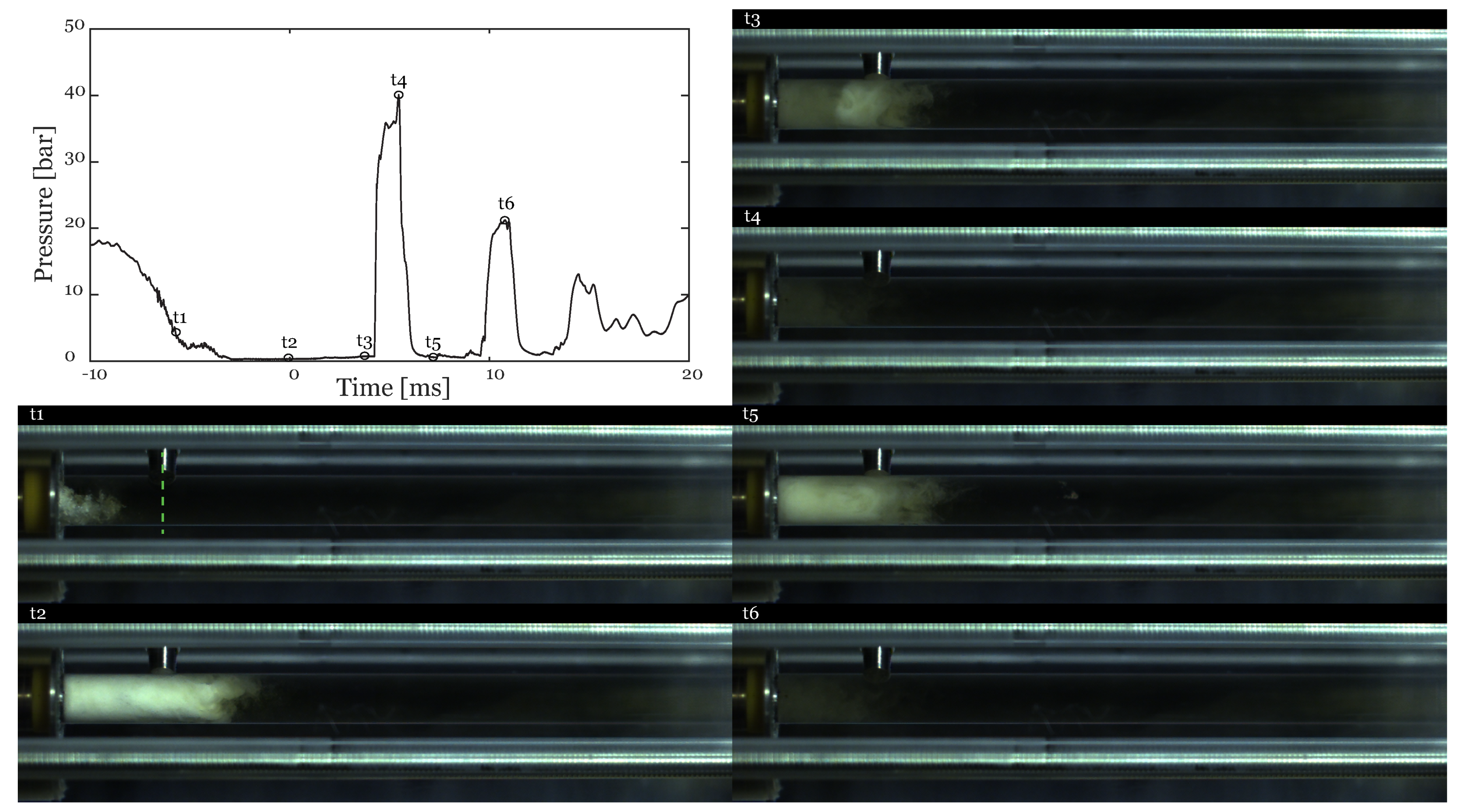
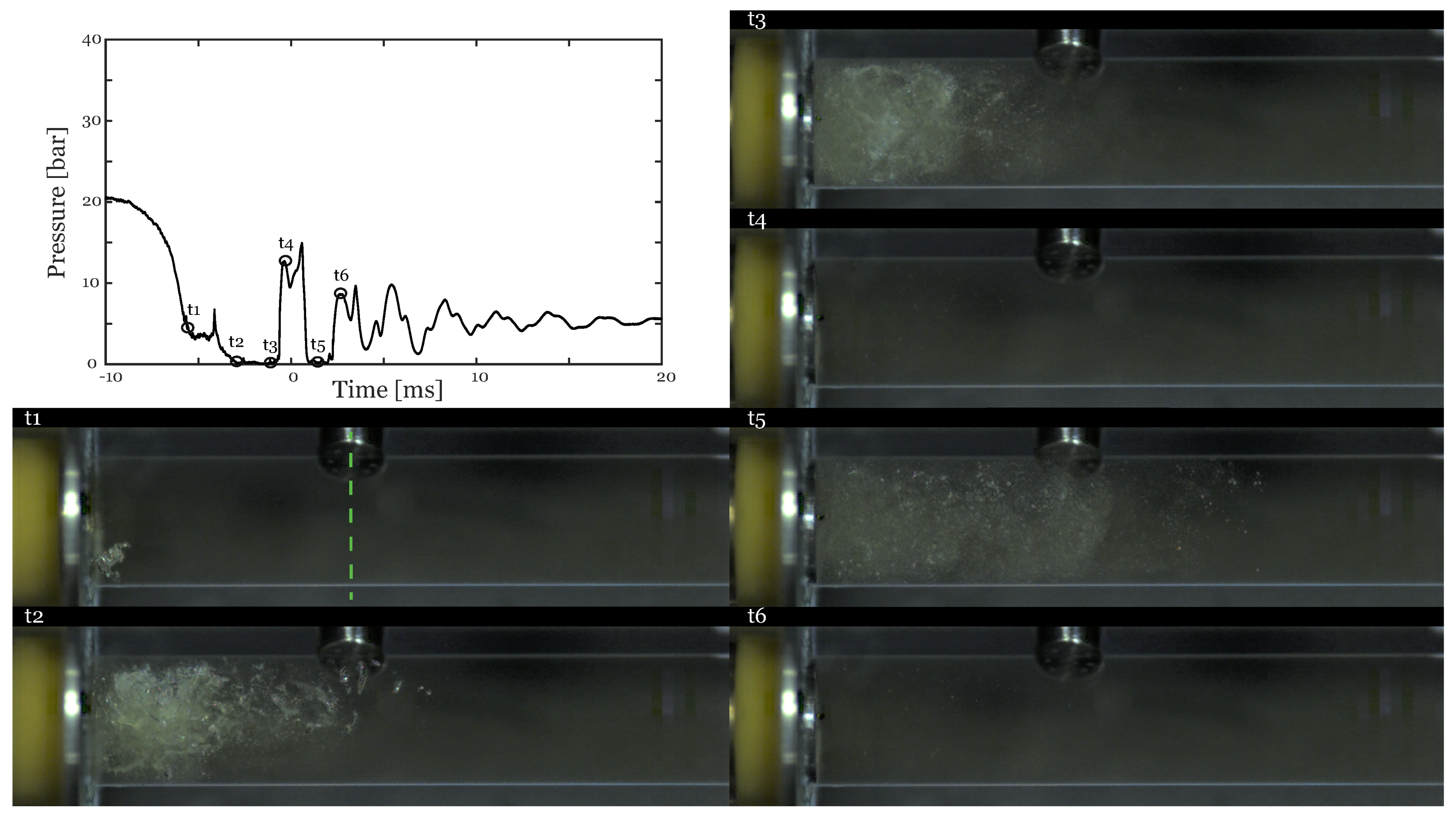
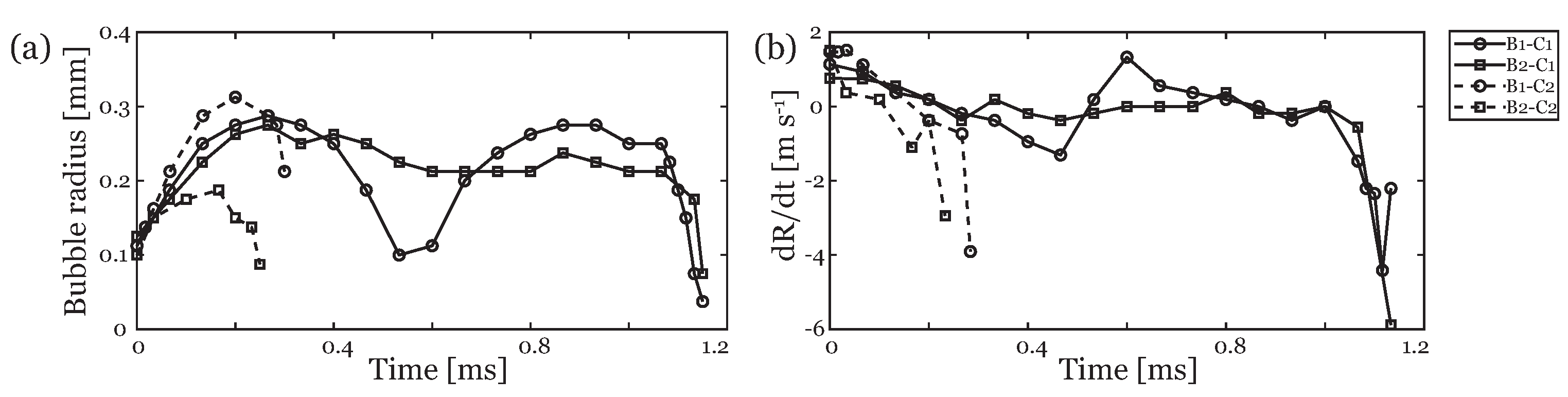
3.3. Bubble Dynamics
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, S. Cavitation of Hydraulic Machinery; World Scientific: Singapore, 2000; Volume 1. [Google Scholar]
- Dular, M.; Požar, T.; Zevnik, J. High speed observation of damage created by a collapse of a single cavitation bubble. Wear 2018, 418, 13–23. [Google Scholar] [CrossRef]
- Jansson, M.; Andersson, M.; Pettersson, M.; Karlsson, M. Experimental Assessment of Water Hammer-Induced Column Separation in Oil-Hydraulic Pipe Flow. J. Fluids Eng. 2019, 141, 101107. [Google Scholar] [CrossRef]
- Joukowsky, N. Über den Hydraulischen Stoss in Wasserleitungsrohren; Académie Impériale des Sciences: St. Petersbourg, Russia, 1900. [Google Scholar]
- Bergant, A.; Simpson, A. Pipeline Column Separation Flow Regimes. J. Hydraul. Eng. 1999, 125, 835–848. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A.R.; Tijsseling, A.S. Water hammer with column separation: A historical review. J. Fluids Struct. 2006, 22, 135–171. [Google Scholar] [CrossRef]
- Simpson, A.; Bergant, A. Interesting lessons from column separation experiments. In Proceedings of the 7th International Conference on Pressure Surges and Fluid Transients in Pipelines and Open Channels, Harrogate, UK, 16–18 April 1996; pp. 83–97. [Google Scholar]
- Fan, D.; Tijsseling, A. Fluid-Structure Interaction with Cavitation in Transient Pipe Flows. J. Fluids-Eng.-Trans. Asme-J. FLUID ENG 1992, 114, 268–274. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A. Visualisation of transient cavitating flow in piping systems. J. Mech. Eng. 1996, 42, 1–16. [Google Scholar]
- Streeter, V.L. Transient Cavitating Pipe Flow. J. Hydraul. Eng. 1983, 109, 1407–1423. [Google Scholar] [CrossRef]
- Simpson, A.R.; Bergant, A. Numerical Comparison of Pipe-Column-Separation Models. J. Hydraul. Eng. 1994, 120, 361–377. [Google Scholar] [CrossRef]
- Adamkowski, A.; Lewandowski, M. A new method for numerical prediction of liquid column separation accompanying hydraulic transients in pipelines. J. Fluids Eng. 2009, 131, 071302. [Google Scholar] [CrossRef]
- Urbanowicz, K.; Firkowski, M. Extended Bubble Cavitation Model to predict water hammer in viscoelastic pipelines. J. Phys. Conf. Ser. 2018, 1101, 012046. [Google Scholar] [CrossRef]
- Yang, J.; Yang, J.; Guo, W.; Luo, J.; Fu, G. Investigation of water column separation induced by pressure pulsation based on critical cavitation rate model. IOP Conf. Ser. Earth Environ. Sci. 2021, 774, 012055. [Google Scholar] [CrossRef]
- Patella, R.F.; Archer, A.; Flageul, C. Numerical and experimental investigations on cavitation erosion. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 022013. [Google Scholar] [CrossRef]
- Li, Z.; Pourquie, M.; Terwisga, T. Assessment of Cavitation Erosion With a URANS Method. J. Fluids Eng. 2014, 136, 041101. [Google Scholar] [CrossRef]
- Pinho, J.; Lema, M.; Rambaud, P.; Steelant, J. Multiphase Investigation of Water Hammer Phenomenon Using the Full Cavitation Model. J. Propuls. Power 2014, 30, 105–113. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, L.; Liu, D.; Karney, B.; Wang, P.; Xia, L.; Ma, J.; Xu, C. CFD Approach for Column Separation in Water Pipelines. J. Hydraul. Eng. 2016, 142, 04016036. [Google Scholar] [CrossRef]
- Gao, H.; Tang, X.; Li, X.; Shi, X. Analyses of 2D transient models for vaporous cavitating flows in reservoir-pipeline-valve systems. J. Hydroinformatics 2018, 20, 934–945. [Google Scholar] [CrossRef]
- Tang, X.; Duan, X.; Gao, H.; Li, X.; Shi, X. CFD Investigations of Transient Cavitation Flows in Pipeline Based on Weakly-Compressible Model. Water 2020, 12, 448. [Google Scholar] [CrossRef]
- Warda, H.A.; Wahba, E.M.; El-Din, M.S. Computational Fluid Dynamics (CFD) simulation of liquid column separation in pipe transients. Alex. Eng. J. 2020. [Google Scholar] [CrossRef]
- Adamkowski, A.; Lewandowski, M. Investigation of hydraulic transients in a pipeline with column separation. J. Hydraul. Eng. 2012, 138, 935–944. [Google Scholar] [CrossRef]
- Bunt, E. Preliminary study of valve cavitation in pipelines. J. S. Afr. Inst. Mech. Eng. 1953, 2, 235–260. [Google Scholar]
- Blind, H. Nichtstationäre Strömungen in Unterwasserstollen. In Veröffentlichungen zur Erforschung der Druckstoßprobleme in Wasserkraftanlagen und Rohrleitungen; Springer: Berlin/Heidelberg, Germany, 1956; pp. 67–108. [Google Scholar]
- Escande, L.; Nougaro, J. Etude théorique et expérimentale du fonctionnement en charge des canaux de fuite en l’absence de cheminée d’équilibre. La Houille Blanche 1953, 607–639. [Google Scholar] [CrossRef]
- Traudt, T.; Bombardieri, C.; Manfletti, C. High Speed Imaging of Water Hammer with Column Separation, BHR Group. In Proceedings of the 12th International Conference on Pressure Surges, Dublin, Ireland, 18–20 November 2015; pp. 47–57, ISBN 9781-85598-151-5-11.5-12. [Google Scholar]
- Kojima, E.; Shinada, M.; Shindo, K. Fluid Transient Phenomena Accompanied with Column Separation in Fluid Power Pipeline: 1st Report, On the Horizontal Pipeline Downstream of a Valve Instantaneously Closed. Bull. JSME 1984, 27, 2421–2429. [Google Scholar] [CrossRef]
- Fatjo, G.G.A. New Dimensionless Number To Predict Cavitation In Accelerated Fluid. Int. J. Comput. Methods Exp. Meas. 2016, 4, 484–492. [Google Scholar] [CrossRef][Green Version]
- Wylie, E.B.; Streeter, V.L. Fluid Transients; McGraw-Hill International Book Co.: New York, NY, USA, 1978; 401p. [Google Scholar]
- Watters, G.Z. Analysis and Control of Unsteady Flow in Pipelines; Butterworths: Boston, MA, USA, 1984. [Google Scholar]
- Jonkobilov, U.; Jonkobilov, S.; Bekjonov, R.; Norchayev, A. Shock wave velocity in two-phase pressure flow. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1030, 012129. [Google Scholar] [CrossRef]
- Covas, D.; Stoianov, I.; Ramos, H.; Graham, N.; Maksimovic, C. The dynamic effect of pipe-wall viscoelasticity in hydraulic transients. Part I—Experimental analysis and creep characterization. J. Hydraul. Res. 2004, 42, 517–532. [Google Scholar] [CrossRef]
- Ait Bouziad, Y.; Farhat, M.; Guennoun, F.; Kueny, J.L.; Avellan, F.; Miyagawa, K. Physical Modelling and Simulation of Leading Edge Cavitation, Application to an Industrial Inducer. In Proceedings of the Fifth International Symposium on Cavitation (CAV2003), Osaka, Japan, 4 November 2003. [Google Scholar]
- Vaz, G.; Hally, D.; Huuva, T.; Bulten, N.; Muller, P.; Becchi, P.; Herrer, J.; Whitworth, S.; Macé, R.; Korsström, A. Cavitating Flow Calculations for the E779A Propeller in Open Water and Behind Conditions: Code Comparison and Solution Validation. In Proceedings of the Fourth International Symposium on Marine Propulsors (Smp’15), Austin, TX, USA, 31 May–4 June 2015. [Google Scholar]
- Huan, Y.y.; Liu, Y.y.; Li, X.j.; Zhu, Z.c.; Qu, J.t.; Zhe, L.; Han, A.d. Experimental and numerical investigations of cavitation evolution in a high-speed centrifugal pump with inducer. J. Hydrodyn. 2021, 33, 140–149. [Google Scholar] [CrossRef]



| Orifice | 2 mm | 3 mm | 4 mm | 5 mm |
|---|---|---|---|---|
| p [bar] | 21.5 | 20.9 | 20.5 | 19.5 |
| [(mm s)] | 0.71 | 5.10 | 2.84 | 3.80 |
| [-] | 5.31 | 2.38 | 1.27 | 0.90 |
| Low | Int. | High | High | |
|---|---|---|---|---|
| Orifice size [mm] | 2 | 3 | 4 | 5 |
| Flow rate [L min] | 10.1 ± 0.05 | 21.7 ± 0.17 | 35.4 ± 0.21 | 48.5 ± 0.23 |
| Mean velocity [m s] | 2.14 ± 0.01 | 4.60 ± 0.04 | 7.51 ± 0.04 | 10.3 ± 0.05 |
| Reynolds number [-] | 465 | 1000 | 1633 | 2239 |
| Oil temperature [C] | 33.0 ± 0.30 | 33.1 ± 1.0 | 38.7 ± 0.28 | 40.5 ± 0.13 |
| Image resolution [pixels] | NA | 1024 × 256 | 1024 × 256 | 1024 × 256 |
| Frame rate [FPS] | NA | 75,000 | 75,000 | 75,000 |
| Shutter speed [s] | NA | 10 | 10 | 5/10 |
| Focal length [mm] | NA | 105 | 105 | 50/105 |
| Orifice Size | 2 mm | 3 mm | 4 mm | 5 mm |
|---|---|---|---|---|
| PSD | 920 | 935 | - | - |
| TD | - | - | 1061 | 946 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jansson, M.; Andersson, M.; Karlsson, M. High-Speed Imaging of Water Hammer Cavitation in Oil–Hydraulic Pipe Flow. Fluids 2022, 7, 102. https://doi.org/10.3390/fluids7030102
Jansson M, Andersson M, Karlsson M. High-Speed Imaging of Water Hammer Cavitation in Oil–Hydraulic Pipe Flow. Fluids. 2022; 7(3):102. https://doi.org/10.3390/fluids7030102
Chicago/Turabian StyleJansson, Marcus, Magnus Andersson, and Matts Karlsson. 2022. "High-Speed Imaging of Water Hammer Cavitation in Oil–Hydraulic Pipe Flow" Fluids 7, no. 3: 102. https://doi.org/10.3390/fluids7030102
APA StyleJansson, M., Andersson, M., & Karlsson, M. (2022). High-Speed Imaging of Water Hammer Cavitation in Oil–Hydraulic Pipe Flow. Fluids, 7(3), 102. https://doi.org/10.3390/fluids7030102






