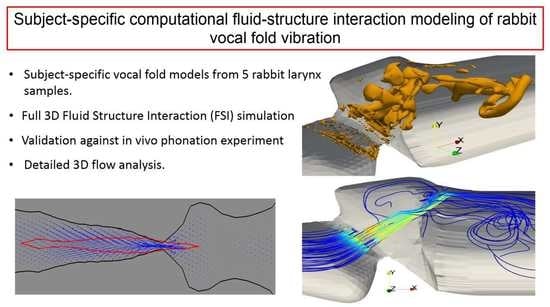
Subject-Specific Computational Fluid-Structure Interaction Modeling of Rabbit Vocal Fold Vibration
Abstract
:1. Introduction
2. Modeling Methods and Case Setup
2.1. Summary of the Previous Phonation Experiment
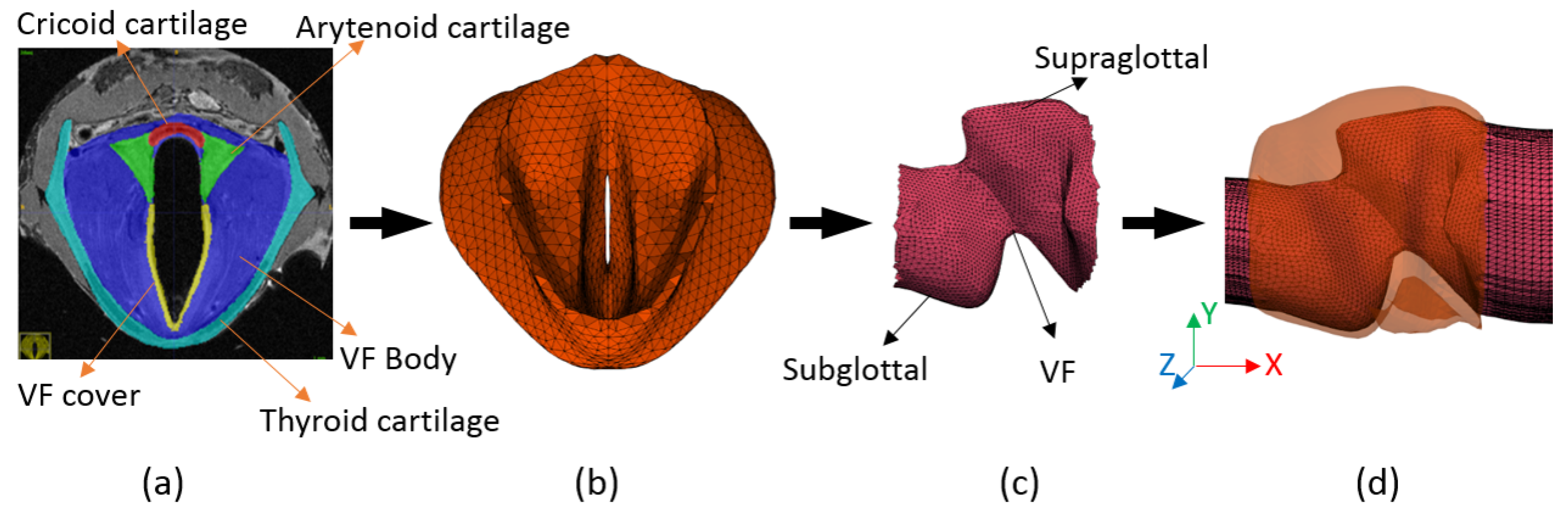
2.2. Subject-Specific Models of the Vocal Fold
2.3. Governing Equations and Computational Methods for the FSI
2.4. Simulation Setup
3. Results and Discussions
3.1. Vibration and Frequency Analysis
3.2. Power and Energy Analysis
3.3. Pressure Comparison between 1D and 3D FSI
3.4. Flow Field Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Additional Detail for the 1D-Flow Based FSI Model

Appendix B. Mesh Independence Study

References
- Titze, I.R.; Martin, D.W. Principles of Voice Production; Acoustical Society of America: Huntington, NY, USA, 1998. [Google Scholar]
- Mittal, R.; Iaccarino, G. Immersed boundary methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef] [Green Version]
- Mittal, R.; Erath, B.D.; Plesniak, M.W. Fluid dynamics of human phonation and speech. Annu. Rev. Fluid Mech. 2013, 45, 437–467. [Google Scholar] [CrossRef]
- Wilson, A.; Kimball, E.E.; Sayce, L.; Luo, H.; Khosla, S.M.; Rousseau, B. Medialization Laryngoplasty: A Review for Speech-Language Pathologists. J. Speech Lang. Hear. Res. 2021, 64, 481–490. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Wang, X.; Krane, M.; Zhang, L.T. Fully-coupled aeroelastic simulation with fluid compressibility—For application to vocal fold vibration. Comput. Methods Appl. Mech. Eng. 2017, 315, 584–606. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berry, D.A.; Herzel, H.; Titze, I.R.; Krischer, K. Interpretation of biomechanical simulations of normal and chaotic vocal fold oscillations with empirical eigenfunctions. J. Acoust. Soc. Am. 1994, 95, 3595–3604. [Google Scholar] [CrossRef] [PubMed]
- Alipour, F.; Berry, D.A.; Titze, I.R. A finite-element model of vocal-fold vibration. J. Acoust. Soc. Am. 2000, 108, 3003–3012. [Google Scholar] [CrossRef]
- Thomson, S.L.; Mongeau, L.; Frankel, S.H. Aerodynamic transfer of energy to the vocal folds. J. Acoust. Soc. Am. 2005, 118, 1689–1700. [Google Scholar] [CrossRef]
- Tao, C.; Zhang, Y.; Hottinger, D.G.; Jiang, J.J. Asymmetric airflow and vibration induced by the Coanda effect in a symmetric model of the vocal folds. J. Acoust. Soc. Am. 2007, 122, 2270–2278. [Google Scholar] [CrossRef]
- Zörner, S.; Kaltenbacher, M.; Döllinger, M. Investigation of prescribed movement in fluid-structure interaction simulation for the human phonation process. Comput. Fluids 2013, 86, 133–140. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharya, P.; Siegmund, T. A computational study of systemic hydration in vocal fold collision. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 1835–1852. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z. Vocal instabilities in a three-dimensional body-cover phonation model. J. Acoust. Soc. Am. 2018, 144, 1216–1230. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Yu, F.; Krane, M.; Zhang, L.T. The Perfectly Matched Layer absorbing boundary for fluid-structure interactions using the Immersed Finite Element Method. J. Fluids Struct. 2018, 76, 135–152. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Rasmussen, J.H.; Xue, Q.; Ding, M.; Zheng, X.; Elemans, C.P. High-fidelity continuum modeling predicts avian voiced sound production. Proc. Natl. Acad. Sci. USA 2020, 117, 4718–4723. [Google Scholar] [CrossRef] [PubMed]
- Bodaghi, D.; Xue, Q.; Zheng, X.; Thomson, S. Effect of Subglottic Stenosis on Vocal Fold Vibration and Voice Production Using Fluid-Structure-Acoustics Interaction Simulation. Appl. Sci. 2021, 11, 1221. [Google Scholar] [CrossRef]
- Triep, M.; Brücker, C.; Schröder, W. High-speed PIV measurements of the flow downstream of a dynamic mechanical model of the human vocal folds. Exp. Fluids 2005, 39, 232–245. [Google Scholar] [CrossRef]
- Döllinger, M.; Berry, D.A. Computation of the three-dimensional medial surface dynamics of the vocal folds. J. Biomech. 2006, 39, 369–374. [Google Scholar] [CrossRef]
- Krane, M.; Barry, M.; Wei, T. Unsteady behavior of flow in a scaled-up vocal folds model. J. Acoust. Soc. Am. 2007, 122, 3659–3670. [Google Scholar] [CrossRef]
- Khosla, S.; Muruguppan, S.; Gutmark, E.; Scherer, R. Vortical flow field during phonation in an excised canine larynx model. Ann. Otol. Rhinol. Laryngol. 2007, 116, 217–228. [Google Scholar] [CrossRef] [Green Version]
- Erath, B.D.; Plesniak, M.W. Three-dimensional laryngeal flow fields induced by a model vocal fold polyp. Int. J. Heat Fluid Flow 2012, 35, 93–101. [Google Scholar] [CrossRef]
- Xuan, Y.; Zhang, Z. Influence of embedded fibers and an epithelium layer on the glottal closure pattern in a physical vocal fold model. J. Speech Lang. Hear. Res. 2014, 57, 416–425. [Google Scholar] [CrossRef] [Green Version]
- Döllinger, M.; Kniesburges, S.; Berry, D.A.; Birk, V.; Wendler, O.; Dürr, S.; Alexiou, C.; Schützenberger, A. Investigation of phonatory characteristics using ex vivo rabbit larynges. J. Acoust. Soc. Am. 2018, 144, 142–152. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Zhang, Z. A parametric vocal fold model based on magnetic resonance imaging. J. Acoust. Soc. Am. 2016, 140, EL159–EL165. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xue, Q.; Zheng, X.; Mittal, R.; Bielamowicz, S. Subject-specific computational modeling of human phonation. J. Acoust. Soc. Am. 2014, 135, 1445–1456. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chan, R.W.; Fu, M.; Young, L.; Tirunagari, N. Relative contributions of collagen and elastin to elasticity of the vocal fold under tension. Ann. Biomed. Eng. 2007, 35, 1471–1483. [Google Scholar] [CrossRef]
- Riede, T.; Titze, I.R. Vocal fold elasticity of the Rocky Mountain elk (Cervus elaphus nelsoni)—Producing high fundamental frequency vocalization with a very long vocal fold. J. Exp. Biol. 2008, 211, 2144–2154. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.; Novaleski, C.K.; Kojima, T.; Mizuta, M.; Luo, H.; Rousseau, B. Subject-Specific Computational Modeling of Evoked Rabbit Phonation. J. Biomech. Eng. 2015, 138, 011005. [Google Scholar] [CrossRef] [Green Version]
- Novaleski, C.K.; Kojima, T.; Chang, S.; Luo, H.; Valenzuela, C.V.; Rousseau, B. Nonstimulated rabbit phonation model: Cricothyroid approximation. Laryngoscope 2016, 126, 1589–1594. [Google Scholar] [CrossRef] [Green Version]
- Ge, P.J.; French, L.C.; Ohno, T.; Zealear, D.L.; Rousseau, B. Model of evoked rabbit phonation. Ann. Otol. Rhinol. Laryngol. 2009, 118, 51–55. [Google Scholar] [CrossRef] [Green Version]
- Swanson, E.R.; Ohno, T.; Abdollahian, D.; Rousseau, B. Effects of raised-intensity phonation on inflammatory mediator gene expression in normal rabbit vocal fold. Otolaryngol.—Head Neck Surg. 2010, 143, 567–572. [Google Scholar] [CrossRef] [Green Version]
- Tian, F.B.; Dai, H.; Luo, H.; Doyle, J.F.; Rousseau, B. Fluid-structure interaction involving large deformations: 3D simulations and applications to biological systems. J. Comput. Phys. 2014, 258, 451–469. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.; Tian, F.B.; Luo, H.; Doyle, J.F.; Rousseau, B. The role of finite displacements in vocal fold modeling. J. Biomech. Eng. 2013, 135, 111008. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, H.; Dai, H.; de Sousa, P.J.F.; Yin, B. On the numerical oscillation of the direct-forcing immersed-boundary method for moving boundaries. Comput. Fluids 2012, 56, 61–76. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.; Chang, S.; Rousseau, B.; Luo, H. A one-dimensional flow model enhanced by machine learning for simulation of vocal fold vibration. J. Acoust. Soc. Am. 2021, 149, 1712–1723. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Chen, Y.; Chang, S.; Luo, H. A reduced-order flow model for fluid-structure interaction simulation of vocal fold vibration. J. Biomech. Eng. 2020, 142, 021005. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.; Chang, S.; Rousseau, B.; Luo, H. Reduced-order flow model for vocal fold vibration: From idealized to subject-specific models. J. Fluids Struct. 2020, 94, 102940. [Google Scholar] [CrossRef]
- Smith, S.L.; Thomson, S.L. Effect of inferior surface angle on the self-oscillation of a computational vocal fold model. J. Acoust. Soc. Am. 2012, 131, 4062–4075. [Google Scholar] [CrossRef] [Green Version]
- Khosla, S.; Murugappan, S.; Lakhamraju, R.; Gutmark, E. Using particle imaging velocimetry to measure anterior-posterior velocity gradients in the excised canine larynx model. Ann. Otol. Rhinol. Laryngol. 2008, 117, 134–144. [Google Scholar] [CrossRef]
- Luo, H.; Mittal, R.; Zheng, X.; Bielamowicz, S.A.; Walsh, R.J.; Hahn, J.K. An immersed-boundary method for flow-structure interaction in biological systems with application to phonation. J. Comput. Phys. 2008, 227, 9303–9332. [Google Scholar] [CrossRef] [Green Version]
- Zheng, X.; Bielamowicz, S.; Luo, H.; Mittal, R. A computational study of the effect of false vocal folds on glottal flow and vocal fold vibration during phonation. Ann. Biomed. Eng. 2009, 37, 625–642. [Google Scholar] [CrossRef] [Green Version]
- Zheng, X.; Mittal, R.; Bielamowicz, S. A computational study of asymmetric glottal jet deflection during phonation. J. Acoust. Soc. Am. 2011, 129, 2133–2143. [Google Scholar] [CrossRef]
- Xue, Q.; Mittal, R.; Zheng, X.; Bielamowicz, S. Computational modeling of phonatory dynamics in a tubular three-dimensional model of the human larynx. J. Acoust. Soc. Am. 2012, 132, 1602–1613. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, H.; Mittal, R.; Bielamowicz, S.A. Analysis of flow-structure interaction in the larynx during phonation using an immersed-boundary method. J. Acoust. Soc. Am. 2009, 126, 816–824. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biswas, R.; Strawn, R.C. Tetrahedral and hexahedral mesh adaptation for CFD problems. Appl. Numer. Math. 1998, 26, 135–151. [Google Scholar] [CrossRef]
- Valášek, J.; Kaltenbacher, M.; Sváček, P. On the application of acoustic analogies in the numerical simulation of human phonation process. Flow Turbul. Combust. 2019, 102, 129–143. [Google Scholar] [CrossRef]
- Zhang, Z. Characteristics of phonation onset in a two-layer vocal fold model. J. Acoust. Soc. Am. 2009, 125, 1091–1102. [Google Scholar] [CrossRef] [PubMed] [Green Version]










| Sample | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Elements | 40,394 | 63,070 | 84,368 | 101,166 | 81,386 |
| Sample | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Pressure (kPa) | 1.05 | 0.78 | 0.72 | 1.0 | 0.98 |
| (kPa) | 60 | 80 | 80 | 90 | 90 |
| (kPa) | 12 | 8 | 8 | 9 | 9 |
| Sample | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| (degrees) | 41 | 24 | 43 | 20 | 29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avhad, A.; Li, Z.; Wilson, A.; Sayce, L.; Chang, S.; Rousseau, B.; Luo, H. Subject-Specific Computational Fluid-Structure Interaction Modeling of Rabbit Vocal Fold Vibration. Fluids 2022, 7, 97. https://doi.org/10.3390/fluids7030097
Avhad A, Li Z, Wilson A, Sayce L, Chang S, Rousseau B, Luo H. Subject-Specific Computational Fluid-Structure Interaction Modeling of Rabbit Vocal Fold Vibration. Fluids. 2022; 7(3):97. https://doi.org/10.3390/fluids7030097
Chicago/Turabian StyleAvhad, Amit, Zheng Li, Azure Wilson, Lea Sayce, Siyuan Chang, Bernard Rousseau, and Haoxiang Luo. 2022. "Subject-Specific Computational Fluid-Structure Interaction Modeling of Rabbit Vocal Fold Vibration" Fluids 7, no. 3: 97. https://doi.org/10.3390/fluids7030097
APA StyleAvhad, A., Li, Z., Wilson, A., Sayce, L., Chang, S., Rousseau, B., & Luo, H. (2022). Subject-Specific Computational Fluid-Structure Interaction Modeling of Rabbit Vocal Fold Vibration. Fluids, 7(3), 97. https://doi.org/10.3390/fluids7030097