Aeroelastic Response of Wind Turbine Rotors under Rapid Actuation of Flap-Based Flow Control Devices

Abstract

The largest commercial wind turbines today are rated at powers between 12 MW to 16 MW, with rotor diameters between 220 m to 242 m, which are expected to grow beyond 250 m in the near future. Economies-of-scale factors suggest the advantages of upscaling in rotor size to effectively harvest the wind potential. An increased emphasis on studies related to improvements and innovations in aerodynamic load-control methodologies has led researchers to focus on overcoming the bottlenecks in size upscaling. Though conventional pitch control is an effective approach for long-term load variations, their application to mitigate short-term fluctuations has limitations. This is directly associated with the cubical dependence on the weight of the rotor with increasing diameter. Alternatively, active flow-control devices (FCDs) have the potential to alleviate load fluctuations through rapid aerodynamic trimming. Fractional light-weight attachments such as trailing-edge flaps promise the swift response of such rapid fluctuations and require low power of actuation. The current study investigates the performance of active in dynamic load control for utility-scale wind turbines through an aeroelastic evaluation of the turbine response to control actions in short time-scales relevant to rapid load fluctuations. The numerical platform used in the analysis is designed to consider the complex multi-physics dynamics of the wind turbine through a self-adaptive Ordinary Differential Equation (ODE) algorithm that integrates the dynamics presented by control system in to the coupled response of aerodynamics and structural deformations of the rotor. The benchmark case in consideration is the use of fractional trailing-edge flaps used on blades designed for the NREL-5MW Reference Wind Turbine, originally designed by the National Renewable Energy Laboratory.

1. Introduction

Wind is a major source of renewable energy that is clean, sustainable, and holds a promising share for the future of power generation. The largest commercial wind turbines today are rated at powers between 12 MW to 16 MW, with rotor diameters between 220 m to 242 m, which are expected to grow beyond 250 m in the near future. Economies-of-scale factors suggest the advantages of upscaling in rotor size to effectively harvest the wind potential. An increased emphasis on studies related to improvements and innovations in aerodynamic load-control methodologies has led researchers to focus on overcoming the bottlenecks in size upscaling. Some of the most recent research in the United States focuses on developing wind turbines capable of generating up to 50 MW from a single turbine [1,2], indicating a growing trend for upscale of rotor size to improve wind power potential through economies-of-scale. Longer and heavier blades used on these future machines make it more and more difficult to manage dynamically fluctuating aerodynamic loads, especially the high-frequency fluctuations occurring during normal operation of the turbines. Hence, there is a growing significance for studies focusing on load-control techniques and innovative approaches to manage dynamic load fluctuations in such huge machines.

Oscillating loads on wind turbines are the result of the highly complex non-linear interaction of structurally flexible blades (that could be considered as rotating wings) with the widely varying wind conditions. Fluctuations could also arise from operational characteristics of the turbines involving control decisions, dynamic alterations in the rotor, changing its orientation with the wind, or variations in the wind itself due to turbulence and terrain properties. Wind turbines implement control actions to counter such oscillations either as an active control decision through control systems, or through passively inbuilt features in the rotor/blade. Load fluctuations occurring in very short time-scales within the rotational cycle of wind turbine rotors are of key interest in this study. Aerodynamic loading peaks produced by wind gusts, and instantaneous drops in wind loads due to tower interference are some examples of short-term load fluctuations within the cycle of rotation. Situations such as tower shadow effects and the associated fluctuations in wind speed could prove detrimental due to the repetitive nature of loading, inducing blade fatigue and a consequent drop in performance. The sporadic power fluctuations resulting from such scenarios affect the safe operation of the electro-mechanical devices connected to the turbine, and the electric grid in general. Innovative load control techniques in the future should be capable of handling such short-term load peaks through rapid response action and swiftly returning to normal operation within a few seconds.

Several studies on load mitigation control approaches have been undertaken over the past couple of decades [3,4,5]. Some of the widely used control techniques are reviewed by Bianchi et al. [6]. Among these, pitch control is quite relevant to several contemporary commercial machines and is also widely studied for potential improvements. Most commercial turbines with pitch-control systems use a proportional-integral collective pitching with a dual purpose of reducing adverse structural loads and curtailing power to the rated value during above nominal conditions [7]. With respect to rapidly varying loads, pitching mechanisms should be fast enough to counter cyclical variations such as the ones associated with tower interference effects and/or the presence of gusts and turbulence. However, as pitching involves rotating the entire blade around its longitudinal axis, the actuation energy involved in the process presents certain bottlenecks in the upscaling of rotors [8]. Blades used on the Vestas V164-9.5 MW machine, for example, are 80 m long, and each one of them weighs up to 35 tonnes [9]. Pitching such massive turbine blades in very short time spans, while operating under full aerodynamic load, would demand a high power of actuation, and may induce aero-elasto-inertial instabilities that could compromise the structural integrity of the rotor or drastically shorten its lifespan. Alternatively, fractional devices that allow modification of the rotor airflow and hence the aerodynamics of the turbine itself, promise an effective technique in dynamic load control. The use of Flow Control Devices (FCDs) on turbine blades is heavily inspired from the parallels drawn with aeronautical and rotorcraft applications.

Active flow-control devices such as fractional chord trailing-edge flaps, micro-tabs, ailerons, and leading-edge slats are extensively used to improve the performance of airplane wings and helicopter rotor blades. These high-lift devices have a key role in the lift augmentation during take-off and landing procedures of airplanes, have been studied since early 1900s, and still form an integral part of commercial aircraft design [10,11]. The blades of a wind turbine being the driving force for converting the wind energy to electricity, studies related to active aerodynamic control of blades have always been important. The effective use of active and passive control devices on wind turbine blades have also gained significant attention [12,13,14], and brief highlights from interesting work in recent years are presented here. Pechlivanoglou et al. [15] does a detailed evaluation of the use of Gurney flaps in improving turbine blade performance. Berg et al. [16] presents an analysis of micro-tabs used on the pressure side of the blade to improve the aerodynamic performance of blades by effectively altering the camber of the airfoil sections. In an extensive parametric study of ‘smart rotor control ’, Lackner and van Kuik [17] evaluates the load reduction capabilities of trailing-edge flaps in comparison to pitch control. Another relevant aspect in this respect is the evaluation of the device interaction with the actuator and the design of predictive or responsive control decisions for the turbine [18].

The slotted-flap based concept in trailing-edge devices will be the focus of the current study. Their capabilities as actively controllable FCD will be evaluated on utility-scale wind turbines with relevance to mitigating load fluctuations occurring in short time-scales. Designed as fractional-chord and short-span attachments to the blade, these devices are considered much lighter than the entire blade. Activation of these devices as part of the control action will hence require much lesser energy in comparison to pitching the entire blade. However, as the wetted area of such FCDs are significantly lesser compared to the blades, the cumulative aerodynamic impact of a control action using FCD is not to be expected to replace the pitching action. On the other hand, bigger flow-control devices would defeat the purpose of using light-weight devices and could significantly impact the original blade efficiency. Hence, the focus would be to use fractional devices with the capability to finely trim the aerodynamics of the blade and hence mitigate rapid load fluctuations that occur at high-frequency. Moreover, as modular external attachments to existing blade designs, these devices propose minimal retooling to blade manufacturing process. Based on the slotted trailing-edge flap concept, these modular devices could be appended to an existing blade design, providing a cost-effective way of active control with low energy actuation. Understanding the aero-structural interaction of such an external device with a flexible turbine blade and the dynamic operating conditions of the rotor is significant to establishing an effective technique in dynamic load control. This emphasizes the need to study the aeroelastic response of wind turbine rotors under rapid loading scenarios to define the scope and limits of such rapid FCD-control actions.

The purpose of this study is the prognosis of flow-control devices (FCD) as dynamic load control techniques in scenarios relevant to mitigating rapid load fluctuations occurring in short time-scales, through an aeroelastic evaluation of the turbine response. External trailing-edge flaps will serve as the benchmark for the preliminary assessment of actively controllable devices used on flexible state-of-the-art blades. Time-scales in these evaluations are based on load fluctuations observed on a standard rotor subjected to tower shadow effects in nominal operating conditions, and will be discussed in more detail in Section 4. Observations made in this study will provide relevant information to implementing innovative load control techniques using active flow-control devices, and valuable information to researchers in the field of designing advanced control strategies. The outcomes of this research effort will also serve as a stepping platform for collaborative ventures to explore the capabilities of any flow-control device with a single parameter that defines the aerodynamic modifications.

2. The Numerical Model

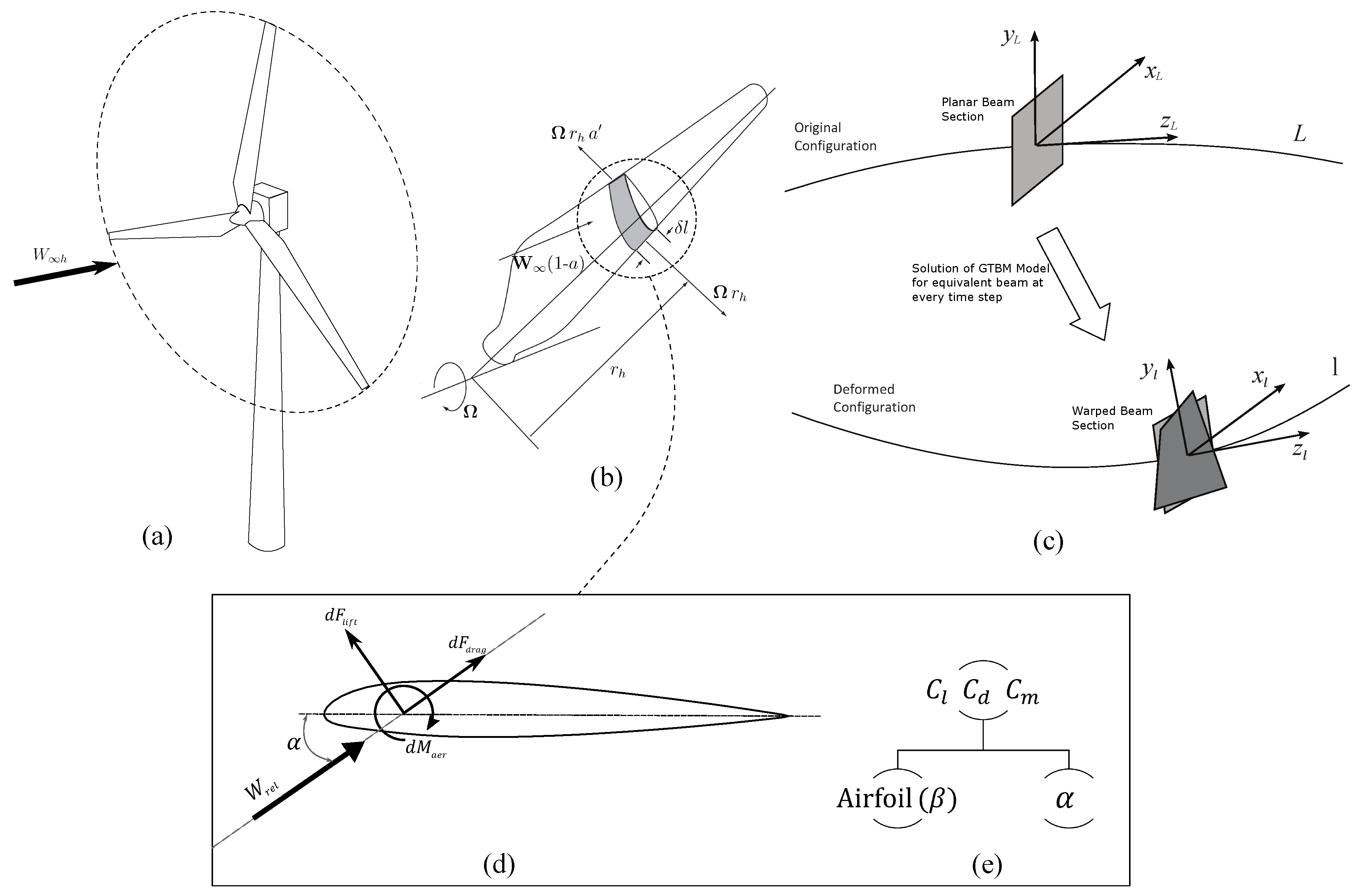
Wind turbine blades are complicated structures that undergo cyclical rotating loads in stochastic wind conditions, which makes wind turbines a complex, non-linear dynamic system. Modeling wind turbines require many degrees of freedom (DOFs) to capture all features of the dynamic behavior of the rotor. The increasing size of the state-of-the-art rotor and these interlinking factors make wind-tunnel studies of next generation super-turbines virtually impossible to extrapolate to the prototype scale, and thus prompt the need for full-scale studies using computer models. These models should also be capable of handling the complexities introduced by adding control systems that are coupled with aeroelastic modes of operation.

The present study uses a novel numerical model capable of handling the aforementioned complexities. We provide a brief description of the main features of the Dynamic Rotor Deformation–Blade Element Momentum (DRD-BEM) model [19], which is capable of representing the coupled phenomena of wind turbines using two advanced numerical schemes. Structural response is modeled using an innovative approach for heterogeneous composite blades that represents complex modes of blade deformation while reducing the computational efforts substantially [20]. A dimensional reduction technique for complex beams originally proposed by Prof. Hodges and his collaborators [21,22] known as the Generalized Timoshenko Beam Model (GTBM) approach is used in effect with some modifications. Second, the flow behavior is modeled using a novel aerodynamic technique based on the Blade Element Momentum (BEM) approach that allows representation of the instantaneous deformed configuration and the effects of rotor deformation on the computation of aerodynamic loads. This is achieved by the transformation of velocities acting at the rotor level through a series of orthogonal matrices projecting them on to the blade section, and in the same way re-projecting the forces acting at the blade section back to the rotor level where the interference is applied. These numerical schemes work in the context of a multi-physics solver called the Common Ordinary Differential Equation Framework (CODEF) [19], which also includes modules that model the dynamics of the control system and electromechanic devices on the drive-train.

For a detailed description of the implementation of the standard DRD-BEM model, the reader is referred to Ponta et al. [19] and the references therein. Details of the structural model can be found in Otero and Ponta [20] and Ponta et al. [19]. The latter also includes results of the application of the DRD-BEM model to the analysis of vibrational modes of composite laminate wind-turbine blades, and results to validate the DRD-BEM model against the works of Jonkman et al. [23] and Xudong et al. [24].

2.1. Blade Structural Model: Dimensional-Reduction Technique for Beams

The GTBM technique uses the same variables as the traditional Timoshenko beam theory but abandons the hypothesis that beam sections remain planar after deformation. Instead, a 2-D finite-element mesh is used to interpolate the real warping of the deformed section, and a mathematical procedure is used to rewrite the strain energy of the 3-D body in terms of the classical six variables of the traditional 1-D Timoshenko theory for beams (i.e., the extensional strain, the two transverse shear strains, the torsional curvature, and the two bending curvatures). The complexity of the blade-section geometry and/or its material properties are reduced into a stiffness matrix for the equivalent 1-D beam problem and this can be performed a priori in parallel for many blade cross sections. Elimination of the ad hoc kinematic assumptions of the traditional Timoshenko theory produces a fully populated 6 × 6 symmetric stiffness matrix for the 1-D beam, ensuring that the six modes of deformation are fully coupled. The non-linear, unsteady 1-D beam problem is then solved at each time step of the aeroelastic analysis through an advanced Ordinary Differential Equation (ODE) algorithm along a reference-line, L, that represents the axis of the beam on its original configuration. The procedure ensures that the strain energy of the reduced 1-D model is equivalent to the actual strain energy of the 3-D structure in an asymptotic sense. For a better understanding of the structural model approach, the reader is referred to Otero and Ponta [20] and the references therein.

2.2. Rotor Flow Model: DRD-BEM

The DRD-BEM is a numerical model representing the flow behavior on a wind turbine rotor based on the classical Blade Element Momentum model (BEM) [25]. Whereas the classical BEM approach misrepresents the aerodynamic forces due to a lack of complete representation of deformed cross-sections of the blade, the DRD-BEM model accounts for these deformations, and the resulting effects on aerodynamic loads itself. This is achieved through a series of orthogonal matrices that transform the velocities, and aerodynamic loads between coordinate systems representing specific aspects of the turbine. These aspects could be a pre-conformed manufacture setting such as a twist, cone angle, or pre-bending, or associated with a control action such as the pitching angle, yaw rotation, or rotor tilt.

We shall start from the velocity vector of the flow passing through an annular actuator disk aligned with the hub coordinate system, h. The components of this velocity vector are affected by an axial induction factor a, and a tangential induction factor $a^{\prime }$. These represent, respectively, the axial velocity deficit and the tangential velocity increase across the actuator disk. Then the velocity vector, ${\mathbf{W}}_h$, of the wind going through an annular actuator aligned with the hub coordinate system h is given by

$${\mathbf{W}}_h=\left[\begin{array}{c}{W}_{\infty h_x}(1-a)\hfill \\ W_{\infty h_y}+\Omega r_h{a}^{\prime }\hfill \\ W_{\infty h_z}\hfill \end{array}\right],$$

(1)

where ${{\mathbf{W}}_{\infty }}_h$ is the undisturbed wind velocity field referred to the hub coordinate system as shown in Figure 1a, $\Omega$ is the angular velocity of the rotor, and $r_h$ is the instantaneous radial distance of an annular disk traced by the rotating blade section (identified by $\delta l$ in Figure 1b) on the rotor plane. This 3-D construction of ${\mathbf{W}}_h$ reflects how the stream-tubes associated with each blade element, aligned with ${{\mathbf{W}}_{\infty }}_h$, are deflected by the forces exerted on them by the annular actuators. A set of orthogonal matrices transform the wind velocity defined in a coordinate system aligned with the wind itself, ${{\mathbf{W}}_{\infty }}_{wind}$, into the hub coordinate system, ${{\mathbf{W}}_{\infty }}_h$, to account for cases such as rotor tilt, and changes in yaw or wind direction. This unperturbed wind velocity in the hub coordinate system is obtained as:

$${{\mathbf{W}}_{\infty }}_h=\left({\mathbf{C}}_{{\theta }_{az}}{\mathbf{C}}_{{\theta }_{tlt}}{\mathbf{C}}_{\Delta {\theta }_{yaw}}{{\mathbf{W}}_{\infty }}_{wind}\right)$$

(2)

where ${\mathbf{C}}_{\Delta {\theta }_{yaw}}$ accounts for the misalignment between wind direction and nacelle orientation due to yaw, ${\mathbf{C}}_{{\theta }_{tlt}}$ accounts for the misalignment due to rotor tilt through a rotation around the horizontal axis of the nacelle system, and the azimuthal orthogonal matrix ${\mathbf{C}}_{{\theta }_{az}}$ transforms the wind velocity into the hub coordinate system h, by a rotation around the main shaft to the blade instantaneous position.

To compute the relative velocity of wind as seen by the instantaneous deformed blade section, ${\mathbf{W}}_h$ is projected through a few coordinate systems. This deformed configuration ($x_l$, $y_l$, $z_l$) is defined along the deformed reference-line l as depicted in the right panel of Figure 1, and the velocity of wind in this reference-frame, ${\mathbf{W}}_l$ is given as:

$${\mathbf{W}}_l=\left({\mathbf{C}}_{lL}{\mathbf{C}}_{Lb}{\mathbf{C}}_{{\theta }_p}{\mathbf{C}}_{{\theta }_{cn}}{\mathbf{W}}_h\right)+{\mathbf{v}}_{str}+{\mathbf{v}}_{mech}.$$

(3)

In Equation (3), ${\mathbf{C}}_{{\theta }_{cn}}$ denotes the transformation accounting for coning of the rotor, and ${\mathbf{C}}_{{\theta }_p}$ performs a rotation around the pitching axis of the blade. These two transformations result in the blade coordinate system indicated by the subscript b as per the IEC standards [26]. For a detailed description of the concept of coning rotors see [27,28,29]. Consequently, the orthogonal matrix ${\mathbf{C}}_{Lb}$ transforms the velocity of wind from blade coordinate system b to the non-deformed configuration system L, defined along the original reference line. Furthermore, the orthogonal matrix ${\mathbf{C}}_{lL}$ transforms from L to instantaneous deformed configuration system l, which is obtained from the solution of kinematic aspects of the structural model presented in Section 2.1. The intrinsic system L is aligned to the blade section in the chord-normal, chord-wise, and span-wise directions, and represents the longitudinal axis of the beam in its original configuration, as depicted in Figure 1c. In addition, ${\mathbf{v}}_{str}$ denotes the blade section vibrational velocities coming from the structural model, and ${\mathbf{v}}_{mech}$ is the velocity associated with the motion of the blade section due to combined action of mechanical devices such as yaw, pitch, and azimuthal rotation. Both these velocity vectors are already expressed in the l system. As an example of all the transformations, the pitching rotation matrix is shown here,

$${\mathbf{C}}_{{\theta }_p}=\left[\begin{array}{ccc}cos(-{\theta }_p)& sin(-{\theta }_p)& 0\\ -sin(-{\theta }_p)& cos(-{\theta }_p)& 0\\ 0& 0& 1\end{array}\right],$$

(4)

where ${\theta }_p$ is the pitch angle, which defines the angle of misalignment due to blade pitch that is either an operational parameter or the result of a control action.

Once wind velocity is transformed into the instantaneous blade section coordinate l, aerodynamic lift and drag forces can be computed using the sectional lift and drag coefficients, and the component of wind velocity in the blade section plane. Aerodynamic coefficients are defined for airfoil profiles (representing selected blade sections) based on the relative angle of attack, $\alpha$. Now, with the knowledge of the magnitude of wind velocity relative to the blade section, $|{\mathbf{W}}_l|$, and its angle of attack $\alpha$, the sectional lift and drag forces per unit length of span are computed as,

$$d{F}_{lift}=\frac{1}{2}\rho C_l{|{\mathbf{W}}_l|}^{2}c,$$

(5)

$$d{F}_{drag}=\frac{1}{2}\rho C_d{|{\mathbf{W}}_l|}^{2}c,$$

(6)

where $C_l$ and $C_d$ are the lift and drag coefficients, $\rho$ is the air density, and c is the chord length of the airfoil section. These non-dimensional coefficients quantify the aerodynamic behavior presented by the airfoil profiles and primarily depends on the angle of attack, $\alpha$. When the airfoils are equipped with a Flow-control Device (FCD), an updated set of aerodynamic coefficients are used based on an additional parameter defined by $\beta$. More about this will be discussed in Section 2.4. The total aerodynamic load acting on the sectional blade element aligned with relative wind direction has components corresponding to the lift and drag forces and is given by

$$\mathbf{\delta }{\mathbf{F}}_{rel}=\left[\begin{array}{c}d{F}_{lift}\\ d{F}_{drag}\\ 0\end{array}\right]\delta l,$$

(7)

where $\delta l$ is the span of the sectional blade element as shown in Figure 1b.

These forces aligned with direction of wind incidence are then projected onto the chord-normal and chord-wise directions before being projected back to the h coordinate system. The aerodynamic loads on the blade element expressed in the h coordinate system is given as

$$\mathbf{\delta }{\mathbf{F}}_h={\mathbf{C}}_{{\theta }_{cn}}^T{\mathbf{C}}_{{\theta }_p}^T{\mathbf{C}}_{Lb}^T{\mathbf{C}}_{lL}^T{\mathbf{C}}_{Lthal}{\mathbf{dF}}_{rel}\delta l$$

(8)

where ${\mathbf{C}}_{Lthal}$ is the transformation matrix to project lift and drag forces onto the chord-normal and chord-wise directions, aligned with the coordinates of l. The above expression (8) can also be written as $\mathbf{\delta }{\mathbf{F}}_h={\mathbf{dF}}_h\delta l$, or in component form as

$$\mathbf{\delta }{\mathbf{F}}_h=\left[\begin{array}{c}\delta F_{h_x}\\ \delta F_{h_y}\\ \delta F_{h_z}\end{array}\right]=\left[\begin{array}{c}d{F}_{h_x}\\ d{F}_{h_y}\\ d{F}_{h_z}\end{array}\right]\delta l,$$

(9)

where ${\mathbf{dF}}_h={\mathbf{C}}_{{\theta }_{cn}}^T{\mathbf{C}}_{{\theta }_p}^T{\mathbf{C}}_{Lb}^T{\mathbf{C}}_{lL}^T{\mathbf{C}}_{Lthal}{\mathbf{dF}}_{rel}$.

A major step in this model is equating the forces obtained from the Blade Element Theory to the change of momentum defined as per the Momentum Theory. Components of $\mathbf{\delta }{\mathbf{F}}_h$ are hence equated to the rate of change of momentum through the corresponding annular actuator. The component normal to the actuator, $\delta F_{h_x}$ is equated to the change in momentum on $W_{\infty h_x}$, which is associated with the axial interference factor a (see expression (1)), and the tangential component $\delta F_{h_y}$ is equated to the corresponding momentum change associated with tangential induction factor $a^{\prime }$. A set of equations are used to determine these interference factors in an iterative process for each blade section at every time-step of the analysis, adopting an advanced optimization algorithm to improve the stability and the speed of convergence of the iterative process.

The final step in the process of transitioning between the aeroelastic and structural modes is to compute the distributed loads and moments acting on the blade structure per unit span length. These forces expressed in the deformed configuration system l constitute both aerodynamic forces and gravitational loads and are required as inputs for the structural model. After determination of the induction factors, the process from Equation (1) through Equation (3) is repeated to compute the aerodynamic forces on each blade section, however, this time in the l system. That is, ${\mathbf{dF}}_l={\mathbf{C}}_{Lthal}{\mathbf{dF}}_{rel}$, whose first two components will give the chord-normal and chord-wise aerodynamic loads. Additionally, the aerodynamic moment on the airfoil section per unit span length acting around the first axis of l is computed at the blade sections as

$$d{M}_{aer}=\frac{1}{2}\rho C_m{W_{rel}}^2{c}^2$$

(10)

where $C_m$ is the aerodynamic pitch coefficient, which is the third non-dimensional characteristic of airfoils. As with the lift and drag coefficients, $C_m$ also now depends on both the angle of attack $\alpha$ and the FCD parameter $\beta$. The dependence of aerodynamic coefficients on these two parameters can be observed in an example of NACA 64₃-618 presented later in Figure 2, Section 2.4.

2.3. The Common ODE Framework (CODEF)

Hitherto, we have seen how our structural model will interact with our aerodynamic model, providing a comparable level of description in order to make full use of the advanced capabilities of both models. This notion of integral dynamic multi-physics modeling through an ODE solution in time could be extended to include other aspects that greatly affect the dynamics of the rotor and the overall performance of the wind-turbine, such as the response of the control-system and/or the turbine’s electromechanical devices.

As it was mentioned above, the equations of motion for the 1-D finite-element problem of the equivalent beam are solved using a nonlinear adaptive ODE solver. This type of solver is based on variable-timestep/variable-order ODE algorithms that check the solution by monitoring the local truncation error at every timestep, improving the efficiency and ensuring the stability of the time-marching scheme. The differential equations modeling the dynamics of the control system and electromechanical devices may be added to the general ODE system, with the control and the electromechanical dynamics modifying the boundary conditions for the aeroelastic solution and vice-versa. The use of a nonlinear adaptive ODE algorithm as a common framework provides a natural way of integrating the solution of all the multi-physics aspects of the problem. Figure 3 shows a flow-chart diagram of this global scheme, indicating the interrelation between the different modules. These modules may be treated individually, interfacing with the common ODE routine. Contrary to a monolithic approach, this modular design of our multi-physics model substantially simplifies further development of the code by the improvement and/or expansion of each submodel independently. This makes possible the simultaneous analysis of the aeroelastic problem, together with any innovative control strategy involving all physical aspects of the turbine dynamics (mechanical and electrical), by means of an integral computationally-efficient solution through a self-adaptive algorithm.

2.4. FCD Control Module

Fractional devices on turbine blades that can be triggered to alter the airflow dynamics near the rotor are known as flow-control devices (FCD). Use of such devices in controls bring a two-fold advantage of the ability to vary the control parameter for a range of values while making use of minimal power to execute the control action. An FCD essentially alters the aerodynamics of blade sections based on its relative configuration with respect to an airfoil section via the value of a control parameter. For instance, this could be the length of a micro-tab extension, the relative angle for a leading-edge slat, or the angle of actuation of a trailing-edge flap. The FCD module integrated in CODEF is designed to update the aerodynamic properties of each blade section based on the value of the control parameter that defines the relative configuration for the device, which is provided by the control module. In the example selected for this study, we defined the FCD control parameter as the angle of actuation of a trailing-edge slotted flap, $\beta$.

Fractional-chord trailing-edge flaps that can be fitted as modular attachments onto existing benchmark blades are of primary interest in the current study. The relative positioning and configurations of trailing-edge flaps play a significant role in modifying the flow around the airfoil, and hence the aerodynamic behavior. Among other properties, slotted flaps have the ability to revitalize the boundary layer on the upper airfoil surface to prevent separation near the trailing edge of blades sections if the relative positioning of the flap with respect to the original airfoil section is properly selected.

Figure 4 presents a schematic of the configuration adopted for a modular device externally attached on the turbine blade. This configuration for airfoil–flap assembly was adopted after an extensive study on optimization of the relative positioning of the $20\%$-chord Clark Y profile flap near the trailing edge (see Menon et al. [30]). The relative dimensions and positioning for the flap attachment are shown in Figure 4a. Figure 4b shows an example of the implementation of this configuration on a modified NACA 64₃-618, and Figure 4c presents a blade span view of a modular device externally attached on the turbine blade based on this concept.

Aerodynamic loads acting on the blade is the cumulative effect of forces and moments acting along each section of the blade, which are given by Equations (5), (6) and (10) (see Section 2.2 for details). At the sectional level, these forces are primarily determined based on the non-dimensional aerodynamic coefficients of lift $C_l$, drag $C_d$, and pitching moment $C_m$. These coefficients characterize each airfoil section, whose values vary with changing angle of attack $\alpha$. The aerodynamic forces acting at blade sections are modified when airfoil sections are fitted with trailing-edge flaps, and the behavioral alterations depend on the flap chord, flap span, and flow alterations based on the airfoil–flap configurations. Fractional FCDs such as the trailing-edge flap are capable of modifying airflow near the airfoil tail, causing noticeable variations in the aerodynamic characteristics of the airfoil sections and providing a new set of aerodynamic coefficients for each airfoil–flap configuration.

The modified aerodynamic coefficients were computed for two key airfoils typically used in the outer regions of the blade span: the NACA 64₃-618 and the DU 93-W-210, when attached with a $20\%$-chord Clark Y profile trailing-edge flap. These airfoil sections are among the more aerodynamically efficient sections and are widely used in contemporary wind turbine blade designs, such as the benchmark wind turbine designed by National Renewable Energy Laboratory (NREL), known as the NREL-5MW Reference Wind Turbine (RWT). On such a blade, these two airfoil sections cumulatively make up about $45\%$ of the span, as indicated in Figure 5. The inner regions of the blade (closer to the root) have airfoils that are thicker to ensure structural stability, whereas the outer regions (closer to the tip) use thinner airfoils, which contribute more to the aerodynamic efficiency of the blade when compared to the inner regions. A major share of this aerodynamic contribution to blade operation originate in the shaded regions in Figure 5, which are essentially the span region equipped to be attached with a trailing-edge flap. The relative positioning of the trailing-edge flap adopted in this study is depicted in Figure 4. As mentioned earlier, the configuration of the airfoil–flap assembly plays a key role in determining the quantitative modification in aerodynamic behavior. These airfoil sections were studied for a range of configurations of the airfoil–flap assembly, and is defined using the relative angle $\beta$ between the airfoil and flap chords. The repository for aerodynamic characteristics of these airfoil section are available for a range of $\beta =-5^{\circ }$ to $\beta =5^{\circ }$, evaluated at regular intervals of $\beta$.

The control system module in CODEF currently has the ability to integrate the dynamics of control techniques such as yaw, pitch, and coning. Using trailing-edge flaps as a prototype, the module is extended with the capability to incorporate the dynamics of flow-control devices (FCD), simulating the interaction of such control actions with the dynamic aeroelastic response of the rotor. This means that the effects on the rotor dynamics due to a control decision from the FCD module and vice-versa will be evaluated at every instant of the simulation. In the example analyzed here, the aerodynamic characteristics of the modified airfoil sections fitted with fractional trailing-edge flaps are made available to the control module, which has the capacity to interpolate the instantaneous values of the aerodynamic coefficients from the repository of aerodynamic data. At each instant of the time-step analysis (see Section 2.2), the adaptive algorithm evaluates the level of actuation of the trailing-edge flap $\beta$ for each section of the blade, based on the instantaneous input from the control module. Then, each blade section adopts an updated value for its aerodynamic coefficients. The flowchart shown in Figure 6 gives an overview of functional algorithm that is used by the control system module of CODEF.

The aerodynamic coefficients and the resulting loads and moments acting at each airfoil section will now depend on two instantaneous parameters: angle of attack $\alpha$ at the airfoil section, and angle of flap actuation $\beta$ defining the airfoil–flap configuration. The adaptive ODE framework ensures that structural deformations and their effects on the aerodynamic loads that arise as a result of such aerodynamic alterations, are also considered through the natural integration that CODEF makes of the multi-physics dynamics of the machine. One other aspect to note here is that this technique could be extended to other types of FCDs, besides flaps, just by selecting a different repository of aerodynamic data which provides the modified aerodynamic coefficients in function of the angle of attack $\alpha$ and the level of actuation of the FCD in question.

Figure 2 shows the non-dimensional sectional coefficients of lift, drag, and pitching moment characterized for NACA 64₃-618. These numerical computations and the resultant aerodynamic coefficients of two key airfoil sections with attached trailing-edge flaps present valuable data for the design of future innovative turbine blades with active FCDs. These characteristics were obtained from an extensive study on two-dimensional flow characterization for these airfoil–flap assemblies. A steady-state pressure-based computational fluid dynamic solver was used to this effect, and the range of flap configuration covers a substantial set of scenarios relevant to wind turbine operating conditions. For more details of this study, the reader is referred to Menon et al. [30] and the references therein.

3. Power of Flap Actuation

To understand the advantages of a flap actuation control over contemporary load control techniques, an evaluation of the rotor’s aero-elasto-inertial dynamic response was performed under potential scenarios of rapid load fluctuation. The power required to implement a certain control action, $P_{ctrl}$, was computed for both conventional pitch control and flap control, and the results compared. This section will discuss the analytical approach used to determine $P_{ctrl}$ for both pitch and flap control, and present the numerical results of the analysis. The power required for control action is determined at every instant of the turbine operation and is computed as

$$P_{ctrl}=M_{ctrl}{\omega }_{ctrl}$$

(11)

where $M_{ctrl}$ is the total control moment, and ${\omega }_{ctrl}$ is the angular velocity of the control action. Here, the control moment is defined as the total moment required to effectuate a control action that involves overcoming the instantaneous aerodynamic moment, $M_{aer}$, and the inertial moment $M_{iner}$ of the control device. In the case of pitch-control the device is the entire blade while only the fractional-span flap is considered as the device in flap-actuation control.

Flap-actuation as an active rapid-control action involves altering the airfoil–flap configuration by energizing the flap from one configuration to another. As in the case of pitch-control, a coupled effect of aerodynamic and inertial loads acting on the flap impact the power needs $P_{ctrl}$ of the control action. However, the computation of $P_{ctrl}$ in this case is slightly different and will be performed independently for overcoming the aerodynamic moments and inertial moments that are involved. As these FCDs are much lighter than the blade itself, the inertial effect on the rotor dynamics are negligible, hence the control module of CODEF integrates only the aerodynamic effects of trailing-edge flaps in the aeroelastic analysis. Computation of $P_{ctrl}$ is effectively based on the moment required to overcome both the aerodynamic and inertial loads at every instant of operation. The computation of aerodynamic moment, $M_{aer}$ and inertial moment, $M_{iner}$ are performed separately, considering the instantaneous aerodynamic loads and the inertial loads acting on the flap hinge, respectively. Figure 7 shows a schematic of the computation process. The rapidity of control action is defined by the velocity of flap-actuation ${\omega }_{ctrl}$, which is known from the design of the load-control scenarios. The total moment required for the control actuation is given as $M_{ctrl}=M_{aer}+M_{iner}$, which is then used in Equation (11) along with the rapidity of flap actuation to obtain the power required for flap-actuation control. The factors involved in the computations of $M_{aer}$ and $M_{iner}$ will be discussed in the following sub-sections.

3.1. Aerodynamic Moment

Aerodynamic loads acting on a turbine blades primarily depends on the instantaneous flow characteristics faced by the rotor such as the velocity of wind, rotor orientation, and rotational speed. The forces and moments acting on an attached trailing-edge flap depend also on the configuration of airfoil–flap assembly (provided by flap-actuation angle $\beta$), and the instantaneous angle of attack $\alpha$ observed at the respective blade sections. To enable a flap actuation in the direction desired by the control action, the actuation mechanisms should supply enough torque to overcome the aerodynamic loads acting at that instant. The most important information necessary to compute this aerodynamic torque (and hence the power required) is the coefficient of aerodynamic moment around the flap actuation hinge, denoted by $C_{m_{hng}}$.

The coefficient of pitching moment at the actuation hinge depends on various factors such as the airfoil–flap configuration $\beta$, instantaneous angle of attack $\alpha$, and the airfoil profile itself. Figure 8 presents coefficients of hinge moments computed for both NACA 64₃-618 and DU 93-W-210 airfoil sections with an attached $20\%$-chord Clark Y profile trailing-edge flap, for a range of configurations relevant to the present work.

These results were also obtained on the same computational study on airfoil–flap assemblies Menon et al. [30] mentioned before. The flow solutions were used to compute the normalized coefficients of moment around the flap hinge, at specific flap actuation angles and for the range of $\alpha$ relevant to wind power applications. These coefficients of hinge moment, $C_{m_{hng}}$ form a repository of normalized 2-dimensional characteristic of an active trailing-edge flap that can be configured across the span of the turbine blade. The instantaneous $C_{m_{hng}}$ value is obtained from the instantaneous configurations of airfoil–flap assembly, and the aerodynamic moment is then computed as,

$$M_{aer}=\left(\frac{1}{2}\rho c^2{W_{rel}}^2{C}_{m_{hng}}\right)S$$

(12)

where $\rho$ is the density of air, c is the design chord length of the trailing-edge flap at the blade section, $W_{rel}$ is the magnitude of instantaneous relative velocity of wind observed at the blade section, $C_{m_{hng}}$ is the instantaneous coefficient of aerodynamic moment around the flap-actuation hinge, and S is the total span of the trailing-edge flap.

3.2. Inertial Moment

The moment around the flap-actuation hinge due to inertia consist of two components: the translational inertia, $I_{t_z}$,which primarily depends on the flap’s mass and hinge position; and the barycentric polar moment of inertia, $I_{p_z}$, which primarily depends on the flap internal structure. The translational part is computed as $I_{t_z}=m{r}^2$, where m is the total mass of the flap and r is the distance from the point of load concentration to the actuation hinge. This study pertains to the Clark Y profile trailing-edge flap that has a reference line defined along the span at $37.5\%$ of the chord, measured from the leading-edge. The position of the flap-actuation hinge is adopted from an extensive experimental study for optimization of the Clark Y profile flap positioning on high-lift airfoils such as NACA 23012 [11]. Figure 4b shows a schematic of the airfoil–flap assembly that presents the relative location of flap-actuation hinge with distances marked in proportion of the chord lengths. The total sectional aerodynamic loads are considered to be concentrated along the reference line, which for the current study is defined at $12.5\%$ behind the quarter-chord length i.e., at $37.5\%$ of the flap chord. Hence, the distance r is calculated from this reference line to the flap-actuation hinge (as defined in Figure 4b).

The internal structure of the trailing-edge flap is designed in one of the most common approaches found on turbine blade designs, and is necessary to withstand the continued aerodynamic loads during turbine operation. The total mass of the flap is determined primarily from these manufacturing considerations. The intended use of flaps as fractional-chord devices and to be attached on shorter spans of the blade allows the design of strong internal structures without significantly adding weight. As these flaps are attached as modular devices (see Figure 4a) on the blade, the desired aerodynamic alterations are effective with minimal span-wise deflections. For NREL-5MW RWT turbine blades with Clark Y flaps, the span-wise (or chord-normal) deflection was designed to be $5\%$ of the distance between the trailing-edge of airfoil and nose of the flap in a configuration of $\beta =+5^{\circ }$. Higher span-wise deflections stand the risk of altering the design gap beyond their original configuration, causing a misrepresentation of the modified aerodynamic properties being used in the aeroelastic evaluation. Considering uniform aerodynamic loading along the span of an attached flap, the chord-normal stiffness was computed using the Equation (13) for uniformly loaded beams [31]. Due to their higher significance in aerodynamic span-wise bending, forces in the chord-normal direction were used to determine the chord-normal stiffness for a permissible bending deflection.

$$k_N=\frac{5}{384}\left(\frac{w{S}^4}{{\delta }_{flp}}\right)$$

(13)

where $k_N$ is the chord-normal stiffness of the flap considered as a uniformly-loaded one-dimensional beam, w is the uniform aerodynamic load acting on the flap, S is flap span, and ${\delta }_{flp}$ is the design deflection permissible on the flap such that the aerodynamic effects of the airfoil–flap assembly is not lost. A series of internal structures are numerically designed for the flaps to obtain a matching value of the design chord-normal stiffness $k_N$. A box-beam-spar internal structure designed for Clark Y profile provided the sectional inertial properties including the mass per unit span length, chord-wise stiffness, span-wise stiffness, and polar moment of inertia. The flap span from load-control design is used in determining the total mass of the flap, which in turn provides the translational inertia, $I_{t_z}$. The inertia of the flap around itself defined as the polar moment of inertia, $I_{p_z}$ is relevant to the final computations and is also obtained from the internal structure design. Finally, the total inertial moment acting on the flap is computed as

$$M_{iner}=\left(I_{t_z}+I_{p_z}\right){\Gamma }_{ctrl}$$

(14)

where ${\Gamma }_{ctrl}$ is the acceleration of flap-actuation during the control action. Having started the computation from the sectional properties of the flap profile, the value of $M_{iner}$ represents the total torque/moment required to overcome the inertial loads acting on the entire span of the re-dimensionalized trailing-edge flap. As described earlier in this section, this will contribute to the computations of instantaneous power required for control-actuation.

4. Numerical Experimentation

The primary objective of the numerical experiments shown in this section is the assessment of the dynamic aeroelastic response of a typical utility-scale rotor when undergoing active load control using flow-control devices such as trailing-edge flaps. The baseline turbine used in this study is the benchmark 5 MW Reference Wind Turbine (RWT) designed by the National Renewable Energy Laboratory (NREL) [23]. This is an upwind horizontal axis turbine with a rotor diameter of 126 m and a rated output power of 5 MW. The nominal operating conditions are defined at a wind speed of 11.4 m/s with a rotational speed of 12.1 rpm. Each one of the three blades used on the rotor are 61.5 m long and weighs approximately 18 tonnes. For the purpose of the current study, the blades were aerodynamically altered by the addition of constant chord trailing edge flaps covering $10\%$ of the span length. The actuation range for these devices and the blade span region where they are located were selected in order to maximize the interaction between the blade and the flow-control device. Blade sections closer to the tip are aerodynamically more efficient and are designed to have a high impact on driving torque, and thus on power generation. Hence, we modified the NREL-5MW RWT blades by fitting $20\%$-chord Clark Y profile flaps along $10\%$ of the blade span, starting at $75\%$ of the blade span and running outward to $85\%$. The devices are configured as external attachments to airfoil sections NACA 64₃-618 and DU 93-W-210, as explained in Section 2.4.

Preliminary assessment of the rotor response is used to characterize an active control technique in load management of a benchmark wind turbine in scenarios that require swift response to dynamic load fluctuations. A relevant example in this respect is the aerodynamic interference of the tower structure when the blades pass fore/aft of the tower. The dynamic response of a standard NREL-5MW RWT rotor was characterized for such fluctuations during nominal operating conditions. The time scales of such fluctuations are too small in these conditions to enable contemporary active load-control techniques to mitigate them effectively without exciting other modes of structural vibrations. The present study focuses on characterizing the response of the system to rapid control actions. Hence, we will focus on small time-scale fluctuations in operational conditions that require preemptive control actions that will reveal the complex aeroelastic interaction of the rotors under such highly dynamic situations.

Figure 9 is an indicative example of the short time-scales involved in such loading scenarios. The left panel depicts a typical control action of the trailing-edge flap actuated from a quasi-neutral setting $\beta =0^{\circ }$ to its full negative actuation $\beta =-5^{\circ }$, which will serve as the baseline to analyze the rapid control-actions covered in the current study. The time-scale for this baseline case is derived from studying the fluctuation of the angle of attack $\alpha$, observed at the 90% span section, when each blade passes in front of the tower for a standard NREL-5MW RWT rotor, which could be seen in the right panel of Figure 9. Selecting the $90\%$ span section ensures the capture of the intense vibrational and deformational effects occurring close to the tip, while avoiding too high aerodynamic effects due to tip vortices. This effectively takes into account the combined dynamics of the structural and aerodynamic effects on the blade.

The observations made by Menon and Ponta [8] about the rotor response to tower interference forms a starting point for time-scale considerations in designing control test cases. In a hypothetical attempt to mitigate aerodynamics effects of tower interference and other short-term load fluctuations, control actions are designed to simultaneously actuate trailing-edge flaps on all blades to change the aerodynamics of the entire rotor. Preemptive control actions are applied to change the flap actuation angle, $\beta$, from one state to another, where the former is considered a neutral position for the flap at $\beta =0^{\circ }$. The range of actuation scenarios in this study is intended to understand the complex aeroelastic response of the turbine rotor, and to asses the impact on the aerodynamic alterations possible within nominal operational conditions. The basic test control action is a positive/negative step change in flap-actuation defined by the angle, ${\beta }_{ctrl}$, where the action is completed within one rotation cycle. The simulation of the turbine operation continues for a few more cycles of rotation, as needed for the aeroelastic transient modes of the rotor to develop into a stable state of operation.

The primary test scenario is a negative flap-actuation control corresponding to a decrease in lift. Other control actions are studied alongside to define the range of control and corresponding response in the present context. Measurable properties studied in this section include the instantaneous power P, rotor thrust T, axial blade tip deflection $U_{h_{x_{tip}}}$, and the angle of attack $\alpha$ at the $90\%$ span section. The evolution of the instantaneous power represents the effects on energy production and torque loads acting on the machine, which have a more global impact in terms of understanding the turbine response. Additionally, the assessment of $U_{h_{x_{tip}}}$ and $\alpha$ at $90\%$-span gives a closer look at the rotor response from both the structural and aerodynamic perspectives. On the other hand, the effective aeroelastic loads acting on the rotor and hence the cumulative effect of the control action is well represented through the evolution of the instantaneous rotor thrust T. The first two sub-sections will discuss the behavior of these properties in various degrees in the context of rapid control actuation of trailing-edge flaps. Some of this behavior will also be presented in comparison to the rotor response to other contemporary control techniques such as pitching. Later, we will also discuss the power management aspects involved in such active control techniques, attempting to learn the benefits of flap actuation in the context of rapid control scenarios.

4.1. Rotor Response to Rapid Flap Actuation

The primary interest in most dynamic load control approaches are to curtail the power production and decrease the deformation causing aerodynamic loads on the rotor. Using trailing-edge flaps in rapid control situations proves to be an effective approach in this respect. As discussed earlier, the airfoil–flap configuration had an upper limit of $\beta =-5^{\circ }$ and a lower limit of $\beta =5^{\circ }$. This allowed the assessment of a wide range of flap-actuation control scenarios by actuating the flap from a configuration of $\beta =0^{\circ }$ to distinct configurations defined by the flap-actuation control angles, ${\beta }_{ctrl}=-5^{\circ },-2^{\circ },-1^{\circ },1^{\circ },2^{\circ }$, and $5^{\circ }$.

Analysis of the aeroelastic response of turbine rotors in trailing-edge flap configurations indicates that blade-spans with the flap have slightly different behavior compared to regions (without a flap) that are in their original configuration. This variation in response, primarily inferred through the angle of attack ($\alpha$), showed a dependency on the angle of flap-actuation ($\beta$) as well. As the aerodynamics of the rotor is now dependent on the flap configurations, the aeroelastic response to control actions cannot be entirely understood by the observation of $\alpha$ alone. The response is now the result of combined effects from the instantaneous $\beta$ and the resulting $\alpha$ observed at the blade section. Hence, the effects of such rapid control action are analyzed from a global perspective by evaluating four key aspects of the rotor response. The most important among these are the structural deformations due to axial loading and their effects on power production, which could be assessed by analyzing the rotor thrust, T, and the instantaneous power, P. The structural deformations on the blades are also studied from the changes in tip displacement observed in the axial direction of the hub coordinate system, and denoted as $U_{h_{x_{tip}}}$. The aerodynamic response at the rotor level is assessed from the changes in $\alpha$ observed at the $90\%$ span section of the blade.

Figure 10 shows the behavior of these four properties for two rapid-control cases where the flap is actuated for ${\beta }_{ctrl}=-5^{\circ }$, and for ${\beta }_{ctrl}=5^{\circ }$. They constitute an overall representation of the dynamic rotor response to rapid flap-actuation, when the respective control actions are implemented in approximately a 1 s time period (as depicted in the example on Figure 9).

The scenarios presented in Figure 10 show the outer limits for the range of flap actuation covered in this rapid-control study. Additionally, these properties illustrate the outer boundaries of effective alterations possible in the airfoil–flap configurations under consideration. In the case of ${\beta }_{ctrl}=-5^{\circ }$, Figure 10a shows a reduction in axial thrust on the rotor easing the aerodynamic loads acting on the rotor as the result of the control action. This reduction of about 17 kN is relevant for sudden fluctuations in wind, improving the reliability and life-span of turbines through better management of fatigue loads.

One of the most important effects is an overall power reduction as seen in Figure 10b, which is attained through a drop in lift created by the dissipation of flow energy. It shows a reduction of about 76 kW in generated power by actuating the flap in a nose-down direction of ${\beta }_{ctrl}=-5^{\circ }$. The ability to effect such power reduction, demonstrated by a light-weight fractional-chord device through a small angle of control actuation is significant in developing innovative control strategies.

The rotor response illustrated by tip deflection $U_{h_{x_{tip}}}$ in Figure 10c shows a reduction in the bending deformation of the blade. This is consistent with the reduced axial loading observed on the rotor as the result of the control action.

It is also noticeable from Figure 10d that actuating the flap in the nose-down direction effects a slight increase in the angle of attack ($\alpha$) observed at the $90\%$ span section of the blade. In understanding the overall rotor response, Figure 10d suggests that the amplitude of oscillations in instantaneous power is relatively higher compared to other properties presented. This is expected in a rotor that operates under various modes of vibrations, but the more important observation here is that these oscillations are quickly damped and it attains a stable value of power in the new configuration.

The oscillatory behavior of the turbine blades and their effect on the rotor was also evaluated by studying the dynamic response at four different time spans of control action, $\Delta t_{ctrl}$. Keeping $\Delta t_{ctrl}$ = 1 s as the reference for rapid variations in dynamic loads observed, three other time spans were adopted.

Figure 11 shows the behavior of the rotor thrust, T, during the rapid flap-control actuation, when the control action is implemented at four different time spans. The corresponding rates of flap actuation are also indicated as an inset in the respective panels. The reference case of $\Delta t_{ctrl}$ = 1 s resulted in a variation in T as shown in Figure 11b, which shows the presence of minor oscillations, noticeable as the effect of the control action that swiftly disappear. A slightly slower scenario was assessed with $\Delta t_{ctrl}$ = 2 s, which is still within one cycle of rotation of the rotor. The effect of the control action on T is shown in Figure 11a, where the intended T value is immediately achieved, and any residual oscillations are negligible in this scenario.

On the other hand, with increasing rates of flap actuation the oscillatory behavior becomes more noticeable with secondary and possibly tertiary frequencies that contribute significantly to the rotor response. These effects are reflected through increasing amplitudes of oscillations shown in Figure 11c,d. The final value of T is attained after noticeable oscillations showing rich spectral behavior of the various modes of vibrations resulting from the rapid control action. The most interesting aspect here are the higher rates of damping (relative to those observed in rapid-pitching) involved, which ensures the system stabilizes in its new configuration within a short period of time. The final values attained by these properties have a consistent characteristic that it is purely dependent on the final value of the flap-actuation control angle, ${\beta }_{ctrl}$, and does not vary with the rate of flap actuation.

4.2. Oscillatory Behavior of Generated Power

As the total alterations in instantaneous power through flap-actuation are lesser, the extreme case for power reduction was chosen and a corresponding effect through rapid-pitching was matched. Based on this idea it was determined that a power reduction effected by a nose-down ${\beta }_{ctrl}=-5^{\circ }$ can be matched by a feathering action of pitching with ${\theta }_{p_{ctrl}}=0.{35}^{\circ }$. In both cases, a reduction of about 76 kW is obtained irrespective of the rate of control action.

Figure 12 shows the evolution of generated power P during the rapid control actions, plotted against the time of turbine operation covering a span where the control action is completed. They are plotted top-down in increasing rapidity of control action, and comparing the effects from rapid-pitching presented on the left side to corresponding rapid flap-actuation depicted on the right side. That is, control action time span, $\Delta t_{ctrl}$ is the same for panels (a) and (b), (c) and (d), and (e) and (f).

Observing the plots top-down, it can be noticed that with growing rapidity of the control action, the increase in the amplitude of the oscillations is significantly higher for rapid pitch-control in comparison to rapid flap-actuation control. Both approaches introduce secondary modes of oscillation at higher rates of actuation, and this is attributed to the structural response of the rotor in this context. These oscillations are damped through the course of turbine operation after the control action is completed, but their presence is significant in understanding the effects on mechanical and electrical components associated with the turbine operation.

In a similar comparative assessment of rapid-pitch and rapid flap-actuation controls, scenarios were evaluated for an effective increase in generated power as the result of the control action. This increase will occur from a negative pitching (pitching to stall) or a positive flap actuation (nose-up). The limit in the opposite direction for flap-actuation would be given by a control action of ${\beta }_{ctrl}=5^{\circ }$ that will result in a proportional increase in instantaneous power generated P. However, due to the non-linear behavior in generated power against rapid flap-actuation angle, the increase in power from ${\beta }_{ctrl}=5^{\circ }$ is about 39 kW. This variation in power is matched by a pitching action of ${\theta }_{p_{ctrl}}=-0.2^{\circ }$.

Figure 13 shows the evolution of the instantaneous generated power P during the rapid control actions, plotted against the time of turbine operation covering a span where the control action is completed. They are plotted top-down in increasing rapidity of control action, and comparing the effects from rapid-pitching presented on the left side directly to rapid flap-actuation depicted on the right side. That is, control action time span, $\Delta t_{ctrl}$, is the same for panels (a) and (b), (c) and (d), and (e) and (f). In spite of the fact that a relatively small amount of pitching (${\theta }_{p_{ctrl}}=-0.2^{\circ }$) is compared to the upper limit of nose-up flap-actuation (${\beta }_{ctrl}=5^{\circ }$), the differences in amplitude of oscillations are noticeable. The observations about the dynamic effects on the rotor as a result of the rapid control action in this configuration are similar to the previous discussion for power reduction (based on Figure 12), and confirms the effectiveness of flap actuation as a rapid control methodology.

4.3. Control Actuation Power

Considering the short time spans in which these control actions are implemented, a more important aspect is an assessment of power required for actuation, and placing it in relation to the effective alteration in generated power. This section evaluates instantaneous power generated P and the instantaneous power required for control action $P_{ctrl}$ as a baseline reference for the comparative analysis of rapid-pitch control and rapid flap-actuation control.

First, we will study the instantaneous power P, which is the total power output from the turbine computed at each instant of time during operation. As the primary interest in load control is curtailment of power generation, the scenarios of control actuation primarily assessed will be for power reduction. Qualitatively, a positive pitching (feathering) and negative flap-actuation (nose-down) effect a reduction in power. While in both cases the control device (blade or flap) is actuated in a nose-down orientation, due the conventions the pitching action is considered positive and flap-actuation as negative. Quantitatively, however, as trailing-edge flaps are spread across smaller span sections of the blade, they are intended to produce lesser overall power reduction in comparison to conventional pitching. On the other hand, being lighter devices compared to the entire blade (in pitching), flap-actuation is expected to employ lesser power for the control action itself.

A more interesting aspect of these rapid control actions is the power involved in actuation of the control itself, which is designated as $P_{ctrl}$. As discussed in Section 3, exerting a control action involves overcoming both the aerodynamic loads acting on the flap device, and the inertial loads of moving the control device itself. The former are primarily determined from the instantaneous aerodynamic loads, which depends on various factors such as wind conditions, rotor orientation, and structural deformations. In nominal operating conditions, the NREL-5MW RWT blades are designed to operate with the axis for center of pressure slightly behind the pitching axis (i.e., reference-line of the blade). Consequently, the blades sections operate in a configuration with the tendency to naturally pitch nose-down (i.e., pitching to feather). What this means to pitching as a control action is that energy needs to be dissipated during the process of pitching the blades to feather (positive pitch action), and energy should be supplied in attempting pitching to stall (negative pitch action).

Based on the configuration for the Clark Y trailing-edge flap attached on the NREL-5MW RWT blades, they also have a natural nose-down orientation. This is attributed to the location of flap-actuation hinge ahead of the aerodynamic center of the flap section, and hence ensuring the center of pressure will always lie aft of the actuation hinge. Due to the convention differences in pitching and flap-actuation, a natural nose-down tendency for flaps naturally augments a negative flap-actuation control, requiring the system to dissipate energy to effect the actuation in a controlled manner. In contrast, a positive actuation would require overcoming the natural nose-down alignment and hence would extract energy from the system.

The power needed for control actuation was computed for pitching and flap-actuation for rapid load-control scenarios defined by the control time-span, $\Delta t_{ctrl}$ = 1 s, 0.2 s, and 0.1 s. Figure 14 shows the instantaneous power required for the control actions, where rapid-pitching is juxtaposed with rapid flap-actuation under comparable control scenarios. Each panel depicts the dynamic response for a specific time-span that defines the rapid control scenario, and is shown top-down with an increasing rapidity of control action. The cases shown here are for pitching to feather and nose-down flap-actuation, and correspond to scenarios presented in Figure 12 effecting the same amount of reduction in power generated by the turbine.

Referring to Figure 14, it can be observed that with increasing rapidity of control action (or decreasing $\Delta t_{ctrl}$), the power required $P_{ctrl}$ increases for both approaches. This increase is more pronounced for pitching action than for flap-actuation, and is associated with the higher inertia of the entire blade as compared to the short-span fractional-chord flap. Each of the NREL-5MW RWT blades weighs 17,740 kg [23] compared to a much smaller 28.1 kg of the flap used along $10\%$-span of the blade in the current design. These inertial differences become significant due to a dependence on the time-span of control action $\Delta t_{ctrl}$. The power required to overcome the aerodynamic moment $M_{aer}$, and inertial moment $M_{iner}$ have different dependencies on $\Delta t_{ctrl}$. While the aerodynamic moment remains quasi-constant for the consistent wind scenario that is being studied, the inertial moment depends on the rotational acceleration of the control device. This imposes a dependence for $P_{ctrl}$ only on the rotational velocity of the control actuation to overcome $M_{aer}$, and an additional dependence on the acceleration of control actuation to overcome $M_{iner}$.

With increasing rapidity of control actuation the inertial aspect overshadows the aerodynamic one, skewing the power requirement in favor of flap-actuation control that has significantly lesser inertial loads to overcome. This also exposes the limitations of pitching as a rapid load control approach with increasing rapidity, and suggests that trailing-edge flaps are more favorable in such situations.

These observations are further confirmed through the observation of differences between pitching and flap-actuation, presented using peaks of the power required in respective control actions. Figure 15 shows the peaks of power involved in rapid-pitching and rapid flap-actuation controls, plotted against increasing time-spans of control actuation for specific cases of $\Delta t_{ctrl}$ = 1 s, 0.2 s, and 0.1 s. The solid markers indicate the actual peak powers, irrespective of their application for braking or acceleration, and the solid lines present the respective best-fit curves. The direct comparison cases for power reduction would be between ${\beta }_{ctrl}=-5^{\circ }$ and ${\theta }_{p_{ctrl}}=0.{35}^{\circ }$; and for power augmentation would be between ${\beta }_{ctrl}=5^{\circ }$ and ${\theta }_{p_{ctrl}}=-0.2^{\circ }$. It is noticeable that with decreasing $\Delta t_{ctrl}$ values, the curves for ${\beta }_{ctrl}$ show a gradual increase presenting a manageable power requirement for rapid flap-actuation control, whereas the curves for ${\theta }_{p_{ctrl}}$ depict a drastic increase in the power required for rapid-pitching.

5. Conclusions and Outlook for Further Work

FCDs capable of altering the aerodynamics of turbine blades are valuable in expanding the scope of dynamic load-control techniques, especially in high frequency repetitive loading scenarios. Using a trailing-edge flap as a test case for an actively controlled FCD, this study evaluated utility-scale benchmark wind turbine rotors to obtain a good understanding of the aeroelastic response paying close attention to rapid loading scenarios in nominal operating conditions. The nonlinear adaptive ODE algorithm used in this work provides a natural way to integrate the various multi-physics aspects of wind turbine dynamics. The capacity of CODEF framework (described in Section 2.3) to reflect the coupled aeroelastic response is critical to properly capturing essential elements in the prognosis of turbine response against rapid control actions. A simple structural analysis of the vibrational response of the blades would not show this phenomenon, as the aerodynamic component of the coupled problem is missing. In an attempt to emulate load fluctuations in short time-scales, several preemptive control actions were studied to characterize the capabilities and limitations of innovative active control techniques. The various aspects of the turbine response discussed in Section 4 indicate direct relations between the dynamic response in the aeroelastic behavior of the rotor, and a quantitative measure of the control-action given, i.e., the amount of the flap-actuation angle ${\beta }_{ctrl}$, as well as characteristic response that depends on the control time-span $\Delta t_{ctrl}$.

Based on the aeroelastic solutions presented in this work, trailing-edge flap devices seem to emerge as effective flow-control devices that are useful in mitigating high frequency dynamic load fluctuations. Here, we shall elaborate on some fundamental aspects regarding the physical mechanisms underlying the observed rotor response:

The first aspect to note is the consistent response of the rotor to rapid flap-actuation control in various scenarios where the quantitative alterations to observable properties depend only on the extent of the control action ${\beta }_{ctrl}$ and not on its rapidity. This observation is further established from the study on several control time-spans $\Delta t_{ctrl}$ that defines the rapidity of the control action (see Figure 11). Even within the limitations of the nominal flap-actuation range, there are noticeable effects on the instantaneous power P, and axial rotor thrust T as the result of the control actions. This results from significant aerodynamic modifications possible through flow-control near the trailing-edge of the blade that allows for active management of flow separation or re-attachment, as required by the instantaneous loading requirements. To retain the maximum original efficiency of the standard NREL-5MW RWT rotor blade, the flap device was fitted only along 10% of the blade span, which constitutes a first attempt to understand the complicated multi-physics dynamics of the rotor under such conditions. However, the change in aerodynamic behavior brought about by the attached device is much more significant due to its location along the blade span, covering a significant portion of the “aerodynamically active” part of the blade.

The second significant aspect is related to the oscillatory response under the rapid control action. A control action implemented actively during the operation of the machine is expected to excite other modes of frequencies associated with the multidimensional interaction involved in a wind turbine rotor. As noted in Section 4.3, such secondary and tertiary modes of oscillations are excited with increasing rapidity of the flap-actuation control. However, a couple of interesting observations are the controlled growth in amplitude, and high damping factors associated with such oscillations. In comparison to active pitch control action under similar rapid loading condition, these factors project flap-actuation control as highly stable even in high frequency rapid loading. Additionally, evaluation of the instantaneous power P validates the first observation made earlier in terms of the final value of a property depending only on the flap-actuation control angle ${\beta }_{ctrl}$.

The final aspect of the numerical outcomes is based on understanding the power management for rapid control actions relevant to scenarios such as tower interference that results in high-amplitude, high-frequency fluctuations at the level of blade aerodynamics. While avoiding excitation of other modes of vibrations is important in the process of a control action attempting to mitigate these fluctuations, another key factor is the power involved in applying the control action itself. As observed from the evaluation of $P_{ctrl}$ for both flap-actuation and pitch control actions, increasing rapidity of the control action favors FCDs due to the much lower inertial loads involved in the control action being applied onto a light-weight device.

Quantitatively, however, as trailing-edge flaps are spread across smaller span sections of the blade, they are intended to produce lesser overall power reduction in comparison to conventional pitching. On the other hand, being lighter devices compared to the entire blade (in pitching), flap-actuation is expected to employ lesser power for the control action itself. This also exposes the limitations of pitching as a rapid load control approach with increasing rapidity, and suggests that trailing-edge flaps are more favorable in such situations. These aspects would become more critical as the size of the state-of-the art turbine increases. Upscaling of rotor size is a definitive trend for reduced cost-of-energy in the envisioned wind-power industry of the future. An increase in blade length results in a higher swept area, squaring the power generation, but there is also a cubical increase in the rotor weight as per the square-cube law (see Thresher et al. [32]).

With the massive blades associated with the larger rotors to be used on future wind super turbines, it is necessary to use control systems which are less energy intensive than the pitch actuators. In this respect, innovative control methods such as active FCDs deserve to be studied in more detail due to two specific advantages that they offer: first, they require low-energy inputs to the actuating mechanisms, and second, the fact that they can respond rapidly to high frequency variations without significantly exciting other modes of turbine operation. Moreover, they could be used along with the classic pitch actuators, or with alternative control methods such as variable-speed stall control, and flexo-torsional adaptive blades, to create a hybrid low actuation energy blade that could eventually react fast enough to mitigate the effects of rapidly changing aerodynamic conditions.

As an outlook for further work, we propose to continue the analysis of the rotor’s aeroelastic response for different variations of trailing-edge flap configuration fitted on NREL-5MW RWT blades, such as using longer flap-span or altering the device location along the blade span. Additionally, we also intend to perform such numerical assessments for the turbine operating under above nominal conditions, i.e., higher wind speeds, facilitating a preliminary case for combining active flow-control with static non-zero pitching of the blades. The stability of the flap-actuation control as a dynamic load control technique opens avenues for collaboration with research focusing on the design of control strategies to mitigate load fluctuations arising from tower interference, wind gusts, and similar operating conditions.