Abstract
This study proposes hybrid models to solve the Colebrook–White equation by combining explicit equations available in the literature to solve the Colebrook–White equation with an error function. The hybrid model is in the form of is the friction factor value f predicted by the hybrid model, is the value of f calculated using several explicit formulas for the Colebrook–White equation, and is the error function determined using the neural network procedures. The hybrid equation consists of a series of hyperbolic tangent functions whose number corresponds to the number of neurons in the hidden layer. The simulation results showed that the hybrid models using five hyperbolic tangent functions could produce reasonable predictions of friction factors, with the maximum absolute relative error (MAXRE) around one tenth, or ten times lower than that produced by the corresponding existing formula. The simplified hybrid models are also given using four and three tangent hyperbolic functions. These simplified models still provide accurate results with MAXRE of less than 0.1%.
1. Introduction
The friction factor f is an important parameter in flow analysis in pipes and open channels because it is related to head or energy loss. The loss of head ΔH in the pipe over a distance L along the flow direction is given by the Darcy Equation (1),
where f is the Darcy–Weisbach friction factor, L is the length of pipe, D is the hydraulic diameter or equivalent pipe diameter, V is the mean velocity, and g is gravity acceleration. An open channel can be considered as full flow in the pipe split in half [1], and the Darcy–Weisbach equation originally developed for pipe flow can be adopted for an open channel [1,2,3,4]. Thus, the friction factor in open channels could be related to the flow conditions in the pipe [1,2,3,4]. For uniform flow in an open channel, Equation (1) could be converted into Equation (2) by substituting D = 4R [1,2,3,4,5,6], where R = A/P = hydraulic radius, A = area of pipe cross-section = πD2/4, P = D = wet perimeters of pipe, and Sf = ΔH/L = energy slope. From Equation (2), we obtain Equation (3).
The value of f for flow in a pipe depends on relative roughness ε/D as a ratio of the sand grain size to the pipe diameter and Reynold numbers, , defined by
where = fluid density and μ is the dynamic viscosity. The relationship between f to ε/D and also depends on the flow conditions, laminar or turbulent. For laminar flow with < 2100, the f value can be computed from Equation (6) [1,2,3,4,5,6,7,8,9]
There are three types of turbulent flows: smooth, transitional, and fully rough [1,2,3,4,5,6,7,8,9]. They are distinguished according to the dimensionless Reynolds number based on roughness height ε and the shear velocity, defined as [1,2,3,4,5,6,7,8,9]
where is boundary shear stress and ϑ is the kinematic viscosity of the fluid. The flow is hydraulically smooth if < 4, transitional if < 60 for pipe flow, and < 100 for channel flow, respectively, and fully rough if > 60 for pipe flow and > 100 for flow in open channel, respectively [1,2,3,4,5,6,7,8,9]. When the flow is hydraulically smooth and < 100,000, the f value has a relatively small roughness effect. Therefore, the f value is directly related to [1,2,3,4,5,6,7,8,9] given by the Blasius formula defined by Equation (9).
When > 100,000 and the boundaries are still hydraulically smooth, the f value is given by the Karman–Prandtl Equation (10) [1,6] as
For fully roughly turbulent flow, f is more influenced by roughness or dependent on ε/D [1,2,6] and f can be computed by Karman–Prandtl ’s Equation (11) [1,2,3,4,5,6,7,8,9].
For transitional flow, the friction factor f may be estimated from the Colebrook–White formula defined by Equations (12) and (13) [1,2,3,4,5,6,7,8,9,10].
Equations (12) and (13) are the two forms of the Colebrook–White equation, one for full flow in pipes and another for partially full in pipes and open channels but these are essentially the same since D = 4R [3].
Equations (12) and (13) are implicit concerning f, which must be determined by trial-and-error method or by using an iterative procedure, such as the Newton–Raphson Method or the Secant Method [11,12]. Several explicit formulas to solve the Colebrook–White Equation (12) have been proposed to avoid the iteration procedure. The first attempt to make the friction factor calculation easier was made by Moody [13] by producing a f − plot based on Equation (12), generally called Moody’s diagram. Moody also proposed an explicit formula for f. After that, several explicit equations for solving the Colebrook–White Equation (12) have been proposed. The study and attempt to find an explicit form of the Colebrook–White equation is an interesting topic, as can be seen from many studies available relating to the approximation of the Colebrook–White equation. The comparison and performance of these equations were examined by some authors, including Brkic [14], Zeghadnia et al. [15], Plascendia et al. [16], and Perez Pupo et al. [17], compared 49 explicit equations, ranging from the old equation of Moody [13] to relatively new and complex equations. Moreover, the study and development of the approximation of the Colebrook–White equation are still going on today. Some of the latest studies on this can be seen in several kinds of literature [18,19,20,21,22,23].
Another approach to determine the value of f is to use an artificial neural network (ANN), widely applied in engineering and science. The ANN approach was inspired by the structure and workings of biological neural networks. It is used to find the correlation between large, complex, and non-linear independent and dependent variables without knowing the physical process defining the relationship between these parameters [24,25,26]. Therefore, ANN could be considered a black-box model representing the processes modeled by networks and weights. Its structure consists of the input, hidden, and output layers with several neurons. In the ANN networks, information is transferred from one neuron to another using a specific transform function.
The ANN method starts from the parameters in the input layer, where the neurons receive input from the outside environment. The inputs received are usually independent parameters that describe a problem under study. Their signals are transferred to neurons in the next hidden layer and transmitted through a specific transfer function. The output signal in neurons at the hidden layer is then transferred to the neurons in the output layer that sends it to the user. The application of ANN consists of training, validation, and testing. The training process aims to obtain the weighting coefficient through optimization to produce minimal prediction errors. The ANN model needs to be tested through validation and testing processes. The data for the ANN model generally consists of 70% training, 15% validation, and 15% testing.
The commonly used and simple neural network model is the multi-layered perceptron (MLP), consisting of three main layers: input, hidden, and output. Cahyono [27] proposed an explicit model of ANN-based on the MLP model for the output layer consisting of a single node. The model was applied to develop equations for estimating the setting velocity of natural sediment. The explicit ANN equation consists of a series of hyperbolic tangent functions with the sequence number according to the number of nodes in the hidden layer. Each hyperbolic tangent part contains coefficients whose number is equal to the input parameters. For example, the explicit ANN with two input parameters is defined by Equation (14).
where is the predicted output value; and are the normalized input values, and Ek and F are coefficients that depend on the weights ak, bk, and ck, where k = 1, 2, …, N with N = number of nodes in the hidden layer. These weight coefficients were obtained through a training process. The MATLAB software can determine the coefficient and the initial value for the optimization to obtain the best coefficient.
This study’s main objective is to develop explicit models of the Colebrook–White equation. Several explicit formulas available in the literature for solving the Colebrook–White equation are used to create the models. The developed models, called hybrid, are built by developing an error equation, which is the formula expressing the difference between the friction factor computed by the Colebrook–White equation and that obtained with the explicit formula. The error equation is derived using the ANN Equation (14). Thus, with this method, the hybrid models can improve the accuracy of the explicit formula. The study considers three hybrid models with differences in the number of neurons in the hidden layer.
The following section discusses the methodology of developing hybrid models; the creation of data points for training, validation, and testing; and the analysis of the simulation results for hybrid models, discussion, and conclusions.
2. Materials and Methods
2.1. Development of Hybrid Formula
Hybrid models are developed using a combination of explicit formulas available in the literature to solve the Colebrook–White equation and an error function. Consider Equation (15) below
where and are the friction factor computed by the Colebrook–White Equation (12) and that obtained by the explicit formula, and is an error that is the difference between and , i.e., = − . For every pair of and ε/D, one can compute , and . Therefore, there is a correlation between parameters and ε/D with . In this study, an equation to approximate as a function of and ε/D, i.e., , is developed by using the ANN model. The main objective of the contribution is to model accurately so that ≈ by minimizing the difference between the and . Thus, the hybrid model for the solution of the Colebrook–White Equation (12) can be defined by Equation (16) below:
where is the friction factor computed by the hybrid model. This study applied the ANN method with the multi-layered perceptron (MLP) architecture consisting of three main layers: the input layer, the hidden layer, and the output layer. The input layer consists of two neurons that receive two input parameters, X1 and X2, relating to and ε/D. These input parameters are in a logarithmic transformation of and ε/D, i.e., X1 = log () and X2 = log (ε/D). Choosing these types of input parameters is in line with Sablani et al. [28], showing that the accuracy of the ANN model is better when the input parameters used are logarithmic transformations of and ε/D.
The hidden layer has several neurons depending on the ANN model. The output layer has single neurons relating to . However, in this model, the output value is EA, which is the value multiplied by 106. The value needs to be multiplied by the number 106 to avoid significant error calculations dealing with a small value . Thus, applying Equation (14) for , the explicit ANN model for the error function , can be expressed in a series of hyperbolic tangent functions as stated by Equation (17) below.
where ζ and η are normalized input parameters X1 = log () and X2 = log (ε/D), respectively, and a, b, c, E, and F are the coefficients of the function. Substituting Equation (17) into Equation (16), the hybrid model function becomes
The coefficients a, b, c, E, and F depend on the value of the ANN weighting coefficients that are obtained through optimization in the training process. The optimization is carried out by using the following objective function
where = − is the error value defined by Equation (15), and = the error value predicted by the ANN model defined by Equation (17).
2.2. Existing Equation Considered
The five explicit formulas reviewed in this study were selected based on their simplicity in mathematical expression and rough accuracy, namely, the maximum absolute relative error value of less than 1.0% in line with the study by Pérez Pupo et al. [17]. The considered explicit formulas are shown below:
- Formula (1) of Chen [29],
- Formula (2) of Schorle et al. [30],
- Formula (3) of Bar and White [31],
- Formula (4) of Sousa et al. [32],
- Formula (5) of Offor and Alabi [33],
2.3. Statistical Measure
The performance of the hybrid model is assessed using the following error measures:
- The coefficient of determination, R2, of the linear regression line between represents the predicted friction factor by the hybrid model Equation (18) and the desired output friction factor obtained from iteration Equation (12).
- The mean absolute relative error, MRE, is defined by:where = RE is the absolute relative error, and M is the amount of data.
- The maximum absolute relative error, MAXRE, is defined by:
2.4. Data Generation
The data points for the training, validation, and testing of the ANN model are generated by applying an iterative procedure using the Secant method [11,12] on the Colebrook–White Equation (12). The data points consist of a combination of ranging from 2 × 103 to 2 × 109 and ε/D values ranging from 2.5 × 10−7 to 0.05. The first group of data points for the training process comprises 30,351 points resulting from the solution of Equation (12) with system log ()(i) × log (ε/D)(j) = 151 × 201 data grids with uniform intervals in each log () and log (ε/D). The second group of data points for validation were from 301 and 301 ε/D values, resulting in 90,601 data points. The validation data points have uniform intervals in and ε/D. The third data group for testing comprises 200,901 data points made from 401 log () and 501 log (ε/D) values using uniform intervals as in the training data. The total data points obtained for training, validation, and testing are 321,853 points. The number of data points is enlarged for the resulting robust model for the range of and ε/D under consideration. Generally, the development of the ANN model uses a more significant proportion of data for training than validation data. In contrast, the data for validation and testing in this study is greater than the training data to ensure the robustness of the model obtained. Each data point has and ε/D and the associated f value, i.e., (, ε/D, f). Solving Equation (12) results in the value of f for each pair and ε/D through an iterative process [11,12]. By using the initial value f = 0.01, ε1 = the error tolerance absolute relative error for f, ε1 < 10−8; and ε2 = the absolute value of implicit Equation (12), ε2 < 10−8. To get a solution f with these tolerances requires the iteration of Equation (12) between five and eight times, with an average iteration of seven.
3. Results and Discussion
The training process using the nntool facility in MATLAB software produced coefficients a, b, c, E, and F, defined in Equation (18). An Excel program was developed based on the ANN algorithm described using MS excel software to obtain the explicit defined by Equation (17). This Excel program refines the ANN model by further optimizing computations. The optimization with MATLAB uses the Levenberg–Marquardt method, while the excel program uses the nonlinear generalized reduced gradient (GRG) technique available in the solver engine. Further optimization with the Excel program uses the coefficient values of a, b, c, E, and F obtained from simulation with MATLAB version R2022a licence academic ITB as initial values. Furthermore, optimization with the excel program applies different objective functions. The objective function is to minimize Er defined by Equation (19), and two other objective functions including minimizing MRE defined by Equation (25) and minimizing MAXRE defined by Equation (26). However, based on the simulation results, the MRE and MAXRE values generated from these three objective functions did not significantly differ in the MRE and the MAXRE values. Therefore, this study provides the coefficients obtained using the objective function of minimizing MRE. The resulting hybrid models using five nodes in the hidden layer, called hybrid model 1, are given in Equations (27)–(31).
- a.
- The formula hybrid model 1 of Chen [29]where ζ log ()/3 − 2.1 and η = 0.37729 log(ε/D) + 1.49089, a1 = 1.24842, a2 = −1.67471, a3 = 3.21556, a4 = −1.46582, a5 = −6.74339, b1 = 1.95053, b2 = −1.97848, b3 = 1.11762, b4 = −1.93413, b5 = −0.21634, c1 = 0.45646, c2 = −0.19816, c3 = 1.09509, c4 = −0.31873, c5 = −6.91059, E1 = 710.654, E2 = −1039.726, E3 = 28.674, E4 = 1773.675, E5 = 378.630, and F = 363.173.
- b.
- The formula for hybrid model 1 of Schorle et al. [30],
- c.
- The formula for hybrid model of Bar and White [31],
- d.
- The formula for hybrid model 1 of 4 Sousa et al. [32],
- e.
- The formula for hybrid model 1 of Offor and Alabi [33],
The coefficients a, b, c, and E and F for hybrid models Equations (28)–(31) are shown in Table A1. In comparison, the models with more nodes in the hidden layer are also considered, including models 2 and 3 with nodes in the hidden layer of 7 and 10, respectively. The equations and coefficients a, b, c, E, and F for hybrid models 2 and 3 are given in Tables S1–S4 in Supplementary Materials. Table 1 shows statistical measures such as MRE and MAXRE for each considered explicit formula and its corresponding hybrid models. The value of R2 is not displayed because almost all simulation results have an R2 value close to 1. Furthermore, it was discovered that the hybrid models could significantly increase the existing formula’s accuracy in reducing the MAXRE value.

Table 1.
Statistical measures for considered explicit equations and the hybrid models developed in this study.
The hybrid models produce the MAXRE of about six to forty times lower than those provided by existing formulas, especially in a hybrid model 3 with 10 hidden neurons, as seen in Table 1. Thus, the hybrid model 3 gives very accurate results but is less attractive in terms of computational time because it contains 10 hyperbolic tangent functions. From Table 1, the difference between the MAXRE values for Sousa et al. and Offor and Alabi models 1 and that for hybrid models 2 and 3 is relatively small. The results of this simulation indicate that using five nodes in the hidden layer for these two models can produce very satisfactory results.
To evaluate the computational efficiency of the hybrid models, the models are applied to compute data points for validating (90,601 data points). Using Microsoft Developer Studio for Fortran Compiler with a processor specification of Intel® Core™ i7-10510U CPU @ 1.80 GHz–2.30 GHz, and installed memory (RAM) 160 GB, the CPU times for generating the data with hybrid models 1 of Chen, Schorle et al., Bar and White, Sousa et al., and Offor and Alabi are 0.069, 0.051, 0.069, 0.052, and 0.052 s, respectively. In contrast, the corresponding hybrid models 3 require 0.101, 0.087, 0. 094, 0.088, and 0.089 s, respectively. The simulation results indicate that the average CPU time required to compute validating data by applying model 3 is 0.092 s, and model 2 is 0.058 s. The simulation with the hybrid model 3 requires the CPU time to be around 160% longer than that of the hybrid model 2. The results also indicate that the hybrid model 2 of Sousa et al. and Offor and Alibi require shorter CPU time than the other hybrid models. As a comparison, the CPU times to compute the validating data using the existing formulas of Chen [29], Schorle et al. [30], Bar and White [31], Sousa et al. [32], and Offor and Alabi [33] are 0.042, 0.027, 0.042, 0.031, and 0.032 s, respectively, while the CPU time for iteration of Equation (12) is 1.567 s.
It can be seen in Table A1 that the coefficients E3 and E4 for model 1 of Sousa et al. are relatively small, so their effects on the overall function value are minor. These coefficients, E3 and E4, can be eliminated to get a simplified model. By removing the coefficient E3 and then applying the optimization technique, new coefficients a, b, c, E, and F are determined, resulting in a simplified Sousa et al. model with four tanh functions. Moreover, removing the coefficients E3 and E4 and then applying the same approach resulted in a simplified formula for hybrid model 1 of Sousa et al. with three tanh functions. The hybrid models of Sousa et al. using four and three hyperbolic tangent functions are given by Equations (32) and (33).
where ζ log ()/3 − 2.1 and η = 0.37729 log(ε/D) + 1.49089. Coefficients a, b, c, E, and F are given in Table 2. The values of MAXRE and MRE for Equation (32) are 0.079% and 0.032%, around one-fifth or five times lower than those of existing Sousa et al.’s formula, while Equation (33) gives the MAXRE and MRE of 0.107% and 0.045%, respectively, around one-third or three times lower than those of the existing formula. The computation of validating data with Equations (32) and (33) requires CPU times of 0.046 and 0.048 s, respectively.

Table 2.
Coefficients of the simplified hybrid model of Sousa et al. [32].
The coefficients E1 and E4 of Offor and Alabi model 1 in Table A1 are relatively small compared to other coefficients. By performing the same procedure to obtain the simplification of Sousa et al. model, simplified hybrid models of Offor and Alabi using four and three tangent hyperbolic functions are given by Equations (34) and (35).
where ζ log ()/3 − 2.1 and η = 0.37729 log(ε/D) + 1.49089. Coefficients a, b, c, E, and F are given in Table 3. The simplification of the Offor and Alabi hybrid model gives MAMXRE and MRE values of 0.039% and 0.009% (around one-seventh or seven times lower than those of the corresponding existing formula) for Equation (34), and 0.068% and 0.013% (one-third or three times lower) for Equation (35). The CPU times for computing data for validation with Equations (34) and (35) are 0.047 and 0.050 s, respectively.

Table 3.
Coefficients of the simplified hybrid model of Offor-Alabi [33].
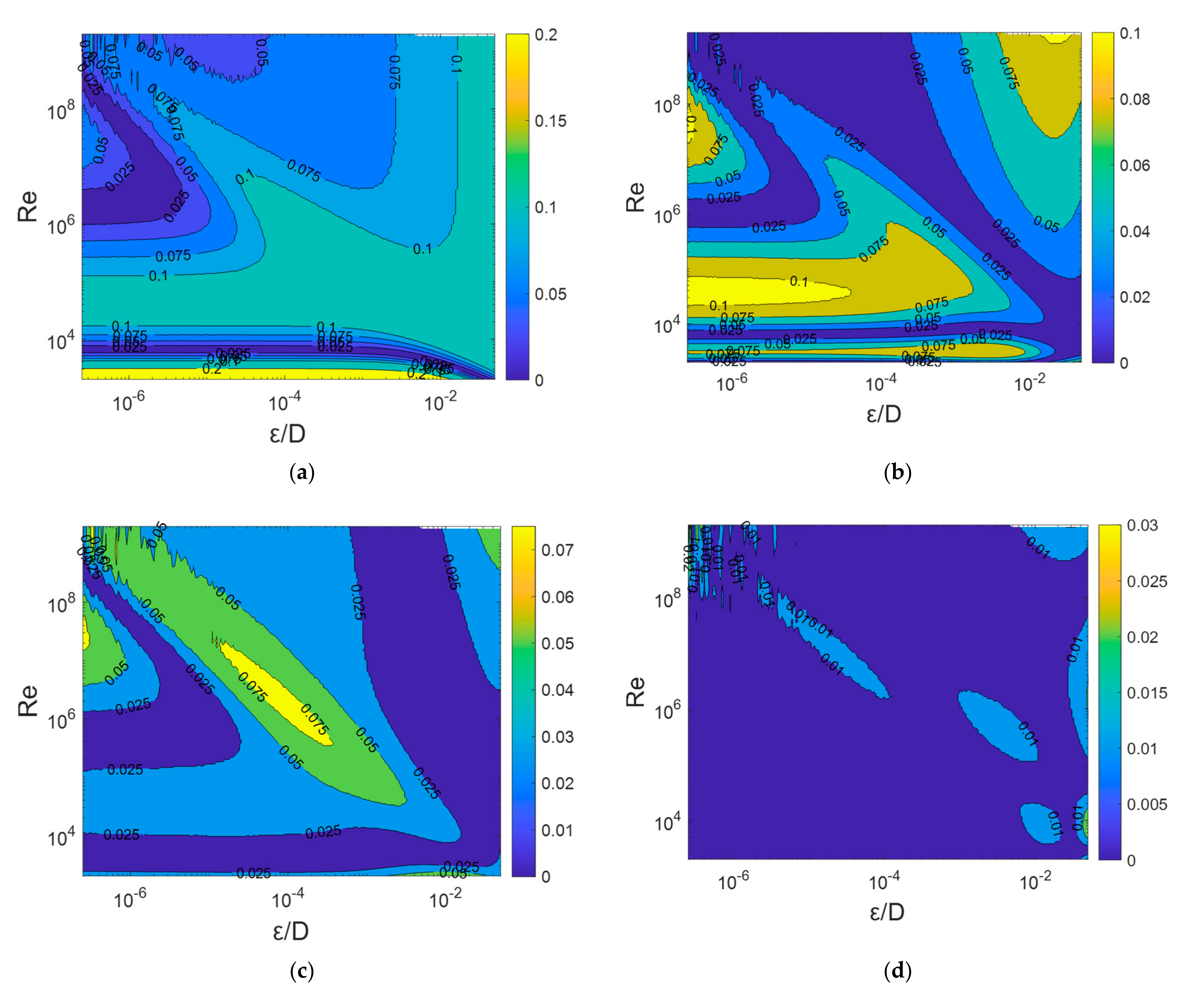
It is observed that the simplification of the Sousa et al. [32] and Offor-Alabi [33] hybrid models defined in Equations (32)–(35) still produces very accurate results with a MAXRE value of less than 0.1%, much more accurate than most of the more than 49 explicit formulas reviewed by Zeghadnia et al. [15] and Pérez Pupo et al. [17]. Therefore, Equations (32)–(35) are potentially used in practical applications, especially Equations (32) and (33), because they are more straightforward than Equations (34) and (35). However, to obtain more accurate results, the hybrid model 1 with five hyperbolic tangent functions should be used with small-time additional time computation. Figure 1 shows the spatial distribution of the absolute relative error RE of the existing formula of Sousa et al. [32] compared with RE predicted by its hybrid models with three, four, and five hyperbolic tangent functions. Figure 1 is generated by using MATLAB R2022a.
Figure 1.
Spatial distribution of absolute relative error RE (%) of friction factor f for (a) predicted by the original formula of Sousa et al. [32] and (b–d) predicted by the hybrid model of Sousa et al. with three, four, and five hyperbolic tangent functions, respectively.
4. Conclusions
Hybrid models have been developed using a combination of explicit formulas available in the literature to solve the Colebrook–White equation with an error equation, eA. The error equation eA estimates which is the difference between the friction factor computed by the Colebrook–White equation, fE, and that obtained by the explicit formula, fo. The existing formulas reviewed were those proposed by Chen [29], Schorle et al. [30], Bar and White [31], Sousa et al. [32], and Offor and Alabi [33]. The hybrid model is fH = fo + eA, where fH is the f value predicted by the hybrid model. This study applied the ANN method with the multi-layered perceptron (MLP) architecture consisting of three main layers—the input layer, the hidden layer, and the output layer—for modeling the error equation eA. The input layer consists of two input parameters: the logarithmic transformation of the Reynolds number , and the relative roughness ε/D. The output is the eA value for given and ε/D values. The error equation eA consists of a series of hyperbolic tangent functions whose number corresponds to the number of neurons in the hidden layer.
Three hybrid models are considered, including models 1, 2, and 3, with the number of hyperbolic tangent functions being 5, 7, and 10. Hybrid model 3 produces excellent results but is less attractive in computational time because it contains 10 hyperbolic tangent functions and requires a CPU time around 160% longer than hybrid model 2. However, the hybrid model 1 using five hyperbolic tangent functions could produce reasonable predictions of friction factors, with the MAXRE value one-tenth or ten times lower than that produced by the existing formula.
The equations for simplified hybrid models of Sousa et al. [32] and Offor-Alabi [33] using four and three tangent hyperbolic functions are also given. Simplifying these models still provides very accurate results, with a maximum absolute error MAXRE value of less than 0.1%, lower than that produced by most existing explicit formulas available in the literature. Therefore, these equations are potentially used in practical applications. However, for more precise results, hybrid model 1 with five hyperbolic tangent functions should be used with only small-time additional time computation, about 10 to 20% longer than that of the simplified model.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/fluids7070211/s1. Equations (S1)–(S10): listed the equations and coefficients for all hybrid formulas. Table S1: Coefficient of hybrid model 2 of Chen [29], Schorle et al. [30] and Barr and White [31] given by Equations (S1), (S2) and (S3), respectively; Tabel S2: Coefficient of hybrid model 2 of Sousa et al. [32] and Offor and Alabi [33] given by Equations (S4) and (S5), respectively; Tabel S3: Coefficient of hybrid model 3 of Chen [29], Schorle et al. [30] and Barr and White [31] given by Equations (S6), (S7) and (S8), respectively; Tabel S4: Coefficient of hybrid model 3 of Sousa et al. [32] and Offor and Alabi [33] given by Equations (S9) and (S10), respectively.
Funding
This research was funded by Faculty of Civil and Environmental Engineering, Bandung Institute of Technology, grant number: 453.11/IT1.C06/TA.00/2021.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
This appendix lists the coefficients for hybrid models (existing explicit formula + explicit ANN model for error function) to be used in Equations (28)–(31) for models 1 of Schorle et al. [30], Barr and White [31], Sousa et al. [32], and Offor and Alabi [33], respectively.

Table A1.
Coefficient of Equations (28)–(31) for hybrid models 1 of Schorle et al. [30], Barr and White [31], Sousa et al. [32], and Offor and Alabi [33].
Table A1.
Coefficient of Equations (28)–(31) for hybrid models 1 of Schorle et al. [30], Barr and White [31], Sousa et al. [32], and Offor and Alabi [33].
| Hybrid Model | Coefficients | ||||
|---|---|---|---|---|---|
| k | ak | bk | ck | Ek & F | |
| Schorle et al. [30] + ANN (2-5-1), Equation (28) | 1 | −2.26933 | −0.05760 | 0.74884 | 28.288 |
| 2 | 0.93914 | −0.66953 | 2.51097 | 25,423.641 | |
| 3 | −1.04822 | 0.70094 | −2.18636 | 11,387.088 | |
| 4 | 4.90973 | 0.04289 | 5.39717 | −1765.822 | |
| 5 | 2.66153 | 1.81116 | 0.83719 | 69.487 | |
| 6 | F = −12,307.506 | ||||
| Barr and White [31] + ANN (2-5-1), Equation (29) | 1 | 0.83941 | −2.98641 | 3.79362 | 3239.372 |
| 2 | 1.94701 | −3.08646 | 5.81603 | 9137.427 | |
| 3 | −0.37782 | −5.25154 | 1.95626 | 12.447 | |
| 4 | 0.90315 | −2.76715 | 4.22969 | −11,058.386 | |
| 5 | −4.51262 | 0.18143 | −5.95373 | 4272.718 | |
| 6 | F = 2942.393 | ||||
| Sousa et al. [32] + ANN (2-5-1), Equation (30) | 1 | −4.14477 | 3.26576 | −7.56141 | −203.631 |
| 2 | 0.13488 | 2.04836 | −3.88041 | −1598.224 | |
| 3 | 7.34543 | 6.94243 | 2.03779 | −5.643 | |
| 4 | −1.49063 | −0.02376 | −1.41946 | −77.800 | |
| 5 | 4.69215 | −0.00526 | 5.80950 | −1382.211 | |
| 6 | F = −494.097 | ||||
| Offor and Alabi [33] + ANN (2-5-1), Equation (31) | 1 | −6.74589 | −3.60800 | 1.99030 | 1.199 |
| 2 | −2.66078 | −0.61588 | −2.73123 | −457.489 | |
| 3 | 12.23306 | −3.42486 | 15.28631 | −134.388 | |
| 4 | 3.09142 | 0.68423 | 2.97875 | −415.722 | |
| 5 | 12.38692 | −0.21233 | 12.52520 | 192.577 | |
| 6 | F = −98.881 | ||||
References
- Subramanya, K. Flow in Open Channels, 3rd ed.; Tata McGraw-Hill Publishing Company Ltd.: New Delhi, India, 2009; pp. 86–91. [Google Scholar]
- Osman, A.A. Ópen Channel Hydraulics; Elsevier: Amsterdam, The Netherlands, 2006; pp. 67–74. [Google Scholar]
- Knight, D.W.; Hazlewood, C.; Lamb, R.; Samuels, P.G.; Shiono, K. Practical Channel Hydraulics Roughness, Conveyance and Afflux, 2nd ed.; CRC Press: Balkema, Leiden, 2018; pp. 29–33. [Google Scholar]
- White, F.M. Fluid Mechanics, 7th ed.; McGraw-Hill: New York, NY, USA, 2011; pp. 365–390. [Google Scholar]
- Çengel, Y.A.; Cimbala, J.M. Fluid Mechanics Fundamentals and Applications, 3rd ed.; McGraw-Hill: New York, NY, USA, 2014; pp. 367–374. [Google Scholar]
- Henderson, F.M. Open Channel Flow; The Macmillan Company: New York, NY, USA, 1966; pp. 90–101. [Google Scholar]
- Sturm, T.W. Open Channel Hydraulics, 2nd ed.; McGaw-Hill: New York, NY, USA, 2010; pp. 114–128. [Google Scholar]
- French, R.H. Open-Channel Hydrauics; McGraw-Hill Book Co.: Singapore, 1985; pp. 111–119. [Google Scholar]
- Chadwick, A.; Morfett, J.; Borthwick, M. Hydraulics in Civil and Environmental Engineering, 5th ed.; CRC Press: Abingdon, UK; Boca Raton, FL, USA, 2013; pp. 126–130. [Google Scholar]
- Colebrook, C.F. Turbulent Flow in Pipes with Particular Reference to the Transition Between the Smooth and Rough Pipe Laws. J. Inst. Civ. Eng. Lond. 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Chapra, S.C.; Canale, R.P. Numerical Method for Engineer; McGraw Hill Education: New York, NY, USA, 2010; pp. 151–161. [Google Scholar]
- Larock, B.E.; Jeppson, R.W.; Watters, G.Z. Hydraulics of Pipeline Systems; CRC Press LLC.: Boca Raton, FL, USA, 2002; pp. 17–22, 148–151. [Google Scholar]
- Moody, L.F. Friction Factors for Pipe Flow. Transactions of the American Society of Mechanical Engineers. J. Mater. Sci. Chem. Eng. 1944, 66, 671–681. [Google Scholar]
- Brkić, D. Review of Explicit Approximations to the Colebrook Relation for Flow Friction. J. Pet. Sci. Eng. 2011, 77, 34–48. [Google Scholar] [CrossRef]
- Zeghadnia, L.; Robert, J.L.; Achour, B. Explicit solutions for turbulent flow friction factor: A review, assessment and approaches classification. Ain Shams Eng. J. 2019, 10, 243–252. [Google Scholar] [CrossRef]
- Plascencia, G.; Díaz–Damacillo, L.; Robles-Agudo, M. On the estimation of the friction factor: A review of recent approaches. SN Appl. Sci. 2020, 2, 163. [Google Scholar] [CrossRef]
- Pérez Pupo, J.R.; Navarro-Ojeda, M.N.; Pérez-Guerrero, J.N.; Batista-Zaldívar, M.A. On the Explicit Expressions for the Determination of the Friction Factor in Turbulent Regime. Rev. Mex. Ing. Química 2020, 19, 313–334. [Google Scholar] [CrossRef]
- Qiu, M.; Ostfeld, A. A Head Formulation for the Steady-State Analysis of Water Distribution Systems Using an Explicit and Exact Expression of the Colebrook–White Equation. Water 2021, 13, 1163. [Google Scholar] [CrossRef]
- Choe, Y.W.; Sim, S.B.; Choo, Y.M. New Equation for Predicting Pipe Friction Coefficients Using the Statistical Based Entropy Concepts. Entropy 2021, 23, 611. [Google Scholar] [CrossRef]
- Brkić, D.; Pavel Praks, P. Colebrook’s Flow Friction Explicit Approximations Based on Fixed-Point Iterative Cycles and Symbolic Regression. Computation 2019, 7, 48. [Google Scholar] [CrossRef]
- Pavel Praks, P.; Brkić, D. Review of new flow friction equations: Constructing Colebrook’s explicit correlations accurately. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2020, 36, 41. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. What Can Students Learn While Solving Colebrook’s Flow Friction Equation? Fluids 2019, 4, 114. [Google Scholar] [CrossRef]
- Brkić, D.; Ćojbašić, Ž. Evolutionary Optimization of Colebrook’s Turbulent Flow Friction Approximations. Fluids 2017, 2, 15. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice-Hall: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Srinivasulu, S.; Jain, A.A. Comparative analysis of training methods for artificial neural network rainfall-runoff models. Appl. Soft Comput. 2006, 6, 295–306. [Google Scholar] [CrossRef]
- Huo, Z.; Feng, S.; Kang, S.; Huang, G.; Wang, F.; Guo, P. Integrated neural networks for monthly river flow estimation in arid inland basin of Northwest China. J. Hydrol. 2012, 420, 159–170. [Google Scholar] [CrossRef]
- Cahyono, M. The Development of Explicit Equations for Estimating Settling Velocity Based on Artificial Neural Networks Procedure. Hydrology 2022, 9, 98. [Google Scholar] [CrossRef]
- Sablani, S.S.; Shayya, W.H.; Kacimov, A. Explicit calculation of the friction factor in pipeline flow of Bingham plastic fluids: A neural network approach. Chem. Eng. Sci. 2003, 58, 99–106. [Google Scholar] [CrossRef]
- Chen, N.H. An explicit equation for friction factor in pipe. Ind. Eng. Chem. Fundam. 1979, 18, 296–297. [Google Scholar] [CrossRef]
- Schorle, B.J.; Churchill, S.W.; Shacham, M. Comments on: “An Explicit Equation for Friction Factor in Pipe”. Ind. Eng. Chem. Fundam. 1980, 19, 228–230. [Google Scholar] [CrossRef]
- Barr, D.; White, C. Technical note. solutions of the colebrook-white function for resistance to uniform turbulent flow. Proc. Inst. Civ. Eng. 1981, 71, 529–535. [Google Scholar] [CrossRef]
- Sousa, J.; Da Conceição, M.; Marques, A.S. An explicit solution of the Colebrook-White equation through simulated annealing. Water Ind. Syst. Model. Optim. Appl. 1999, 2, 347–355. [Google Scholar]
- Offor, U.H.; Alabi, S.B. An accurate and computationally efficient explicit friction factor model. Adv. Chem. Eng. Sci. 2016, 6, 237–245. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).