Amplification of Wave Groups in the Forced Nonlinear Schrödinger Equation
Abstract
:1. Introduction
2. Formulation
3. Numerical Simulations
3.1. Case 1
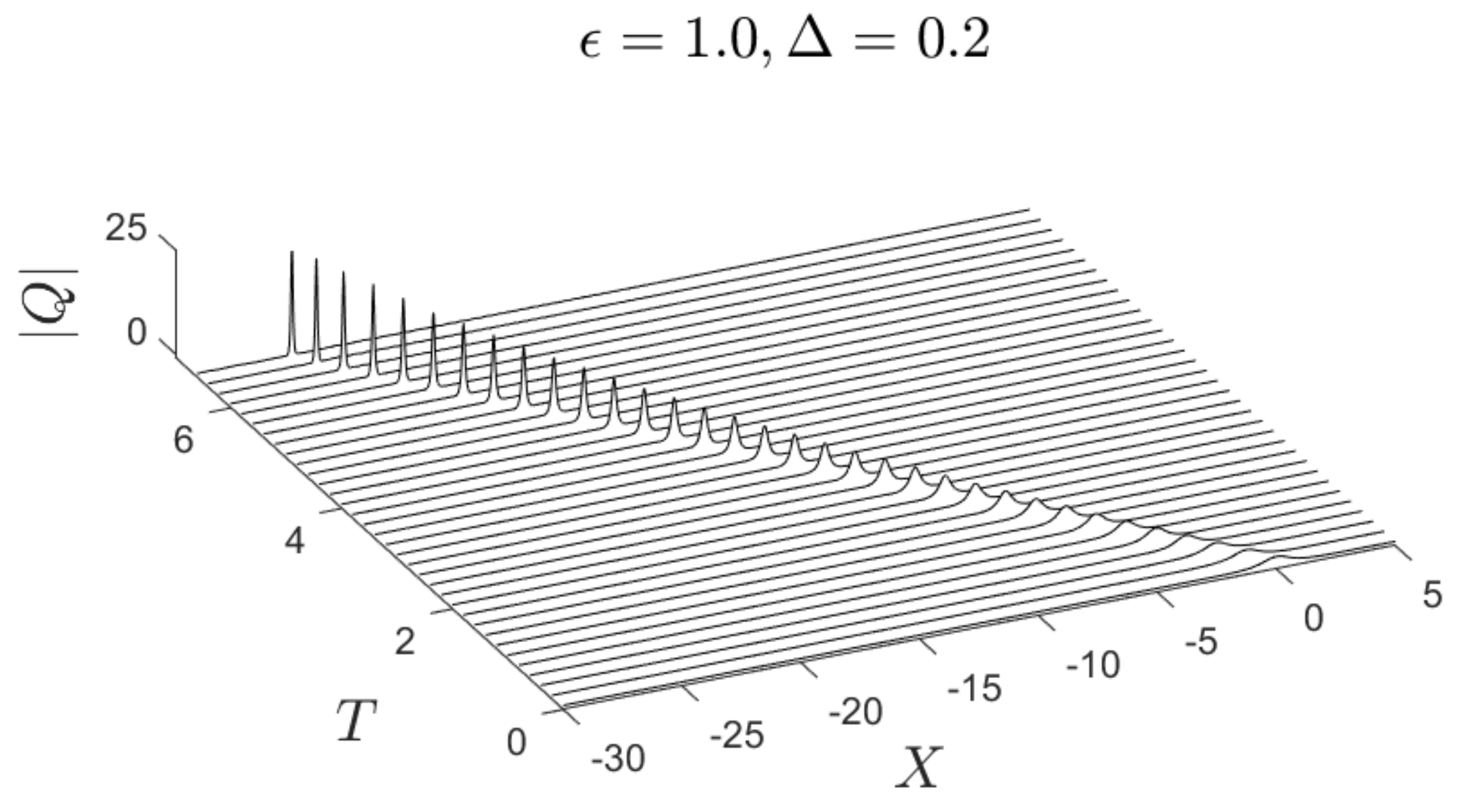
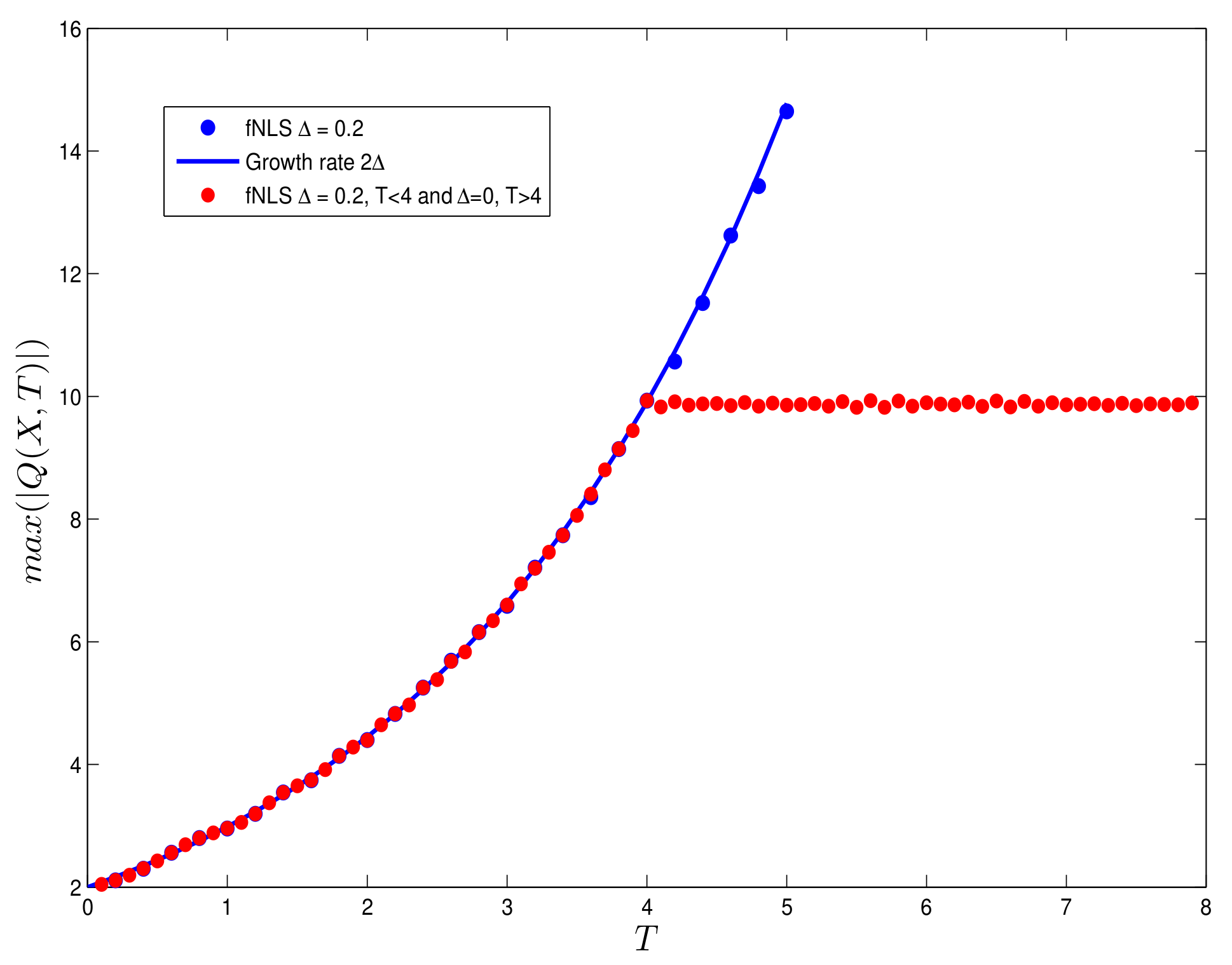
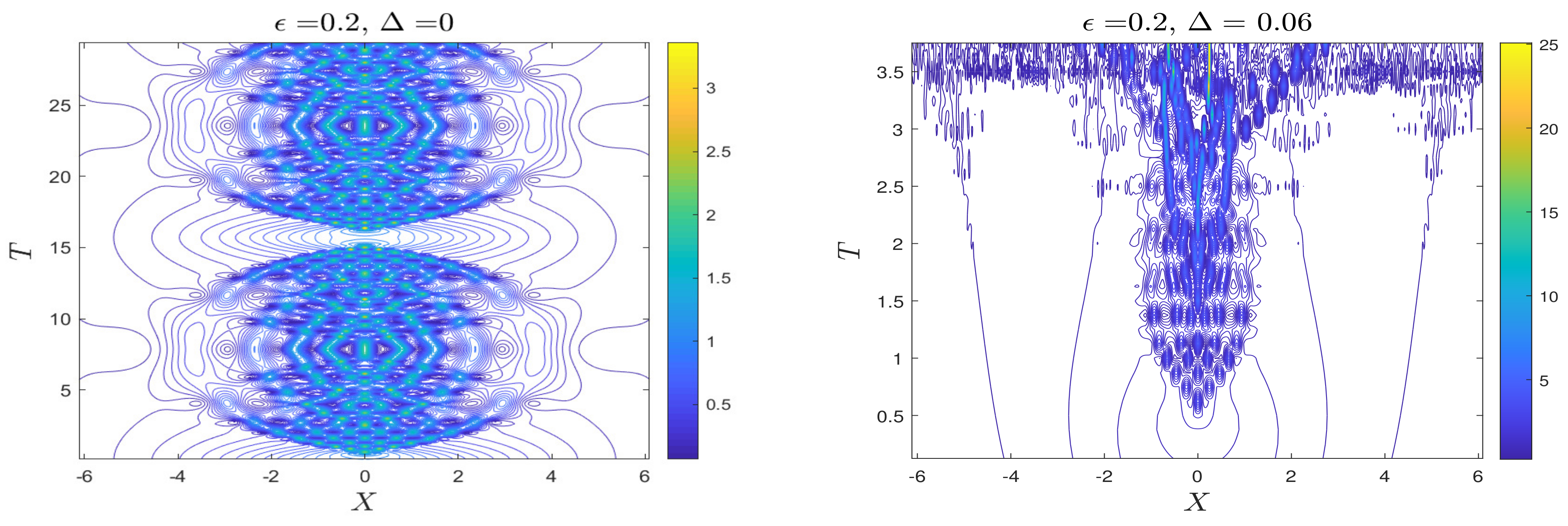
3.2. Case 2
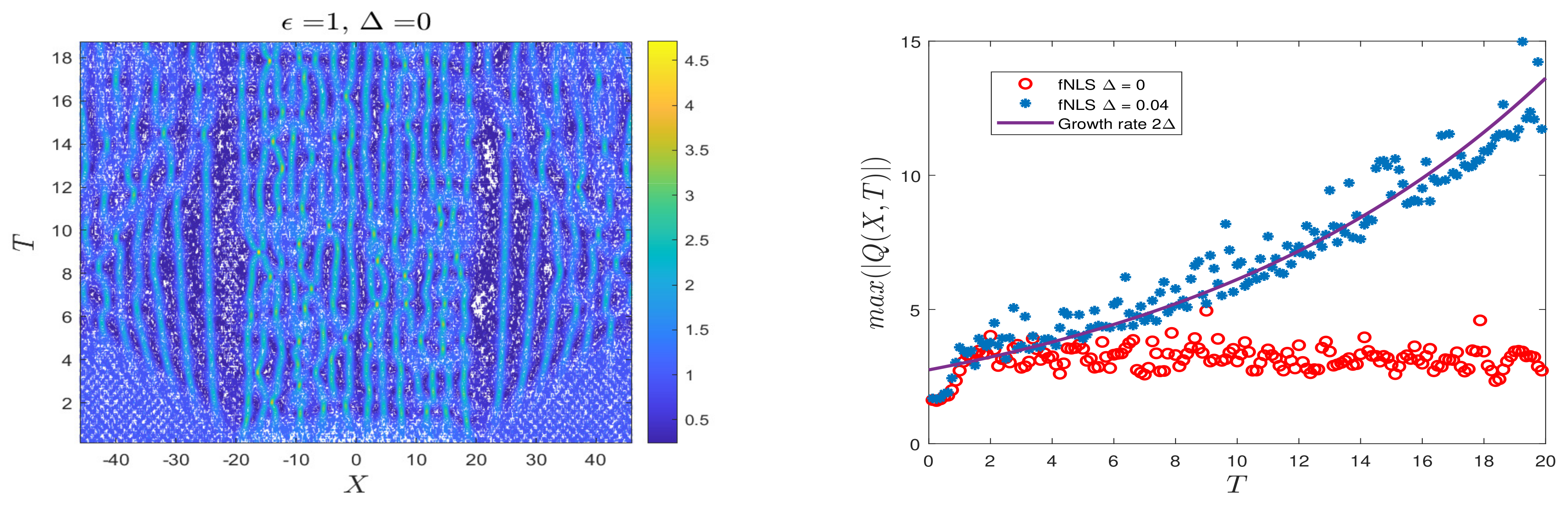
3.3. Case 3
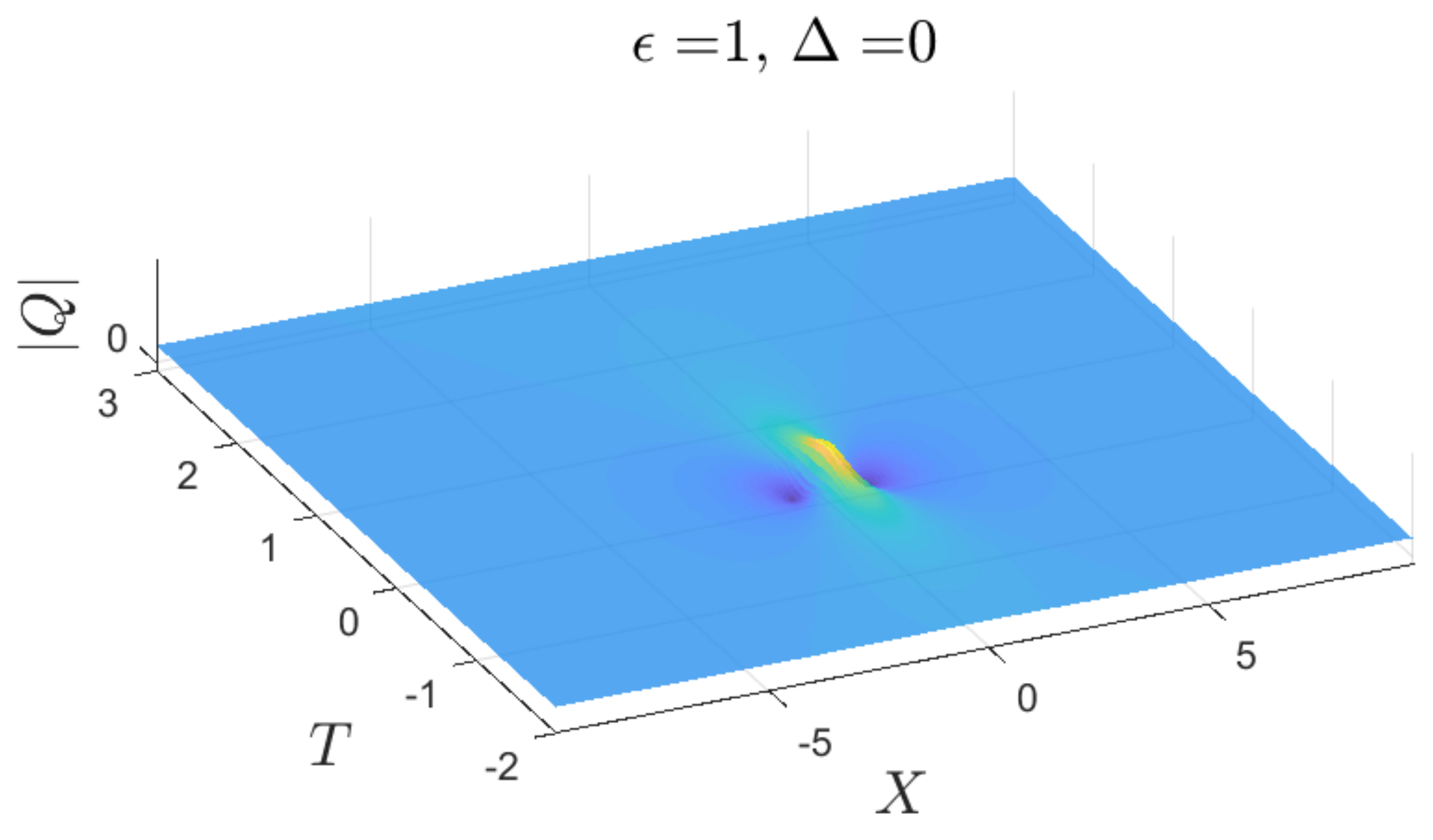
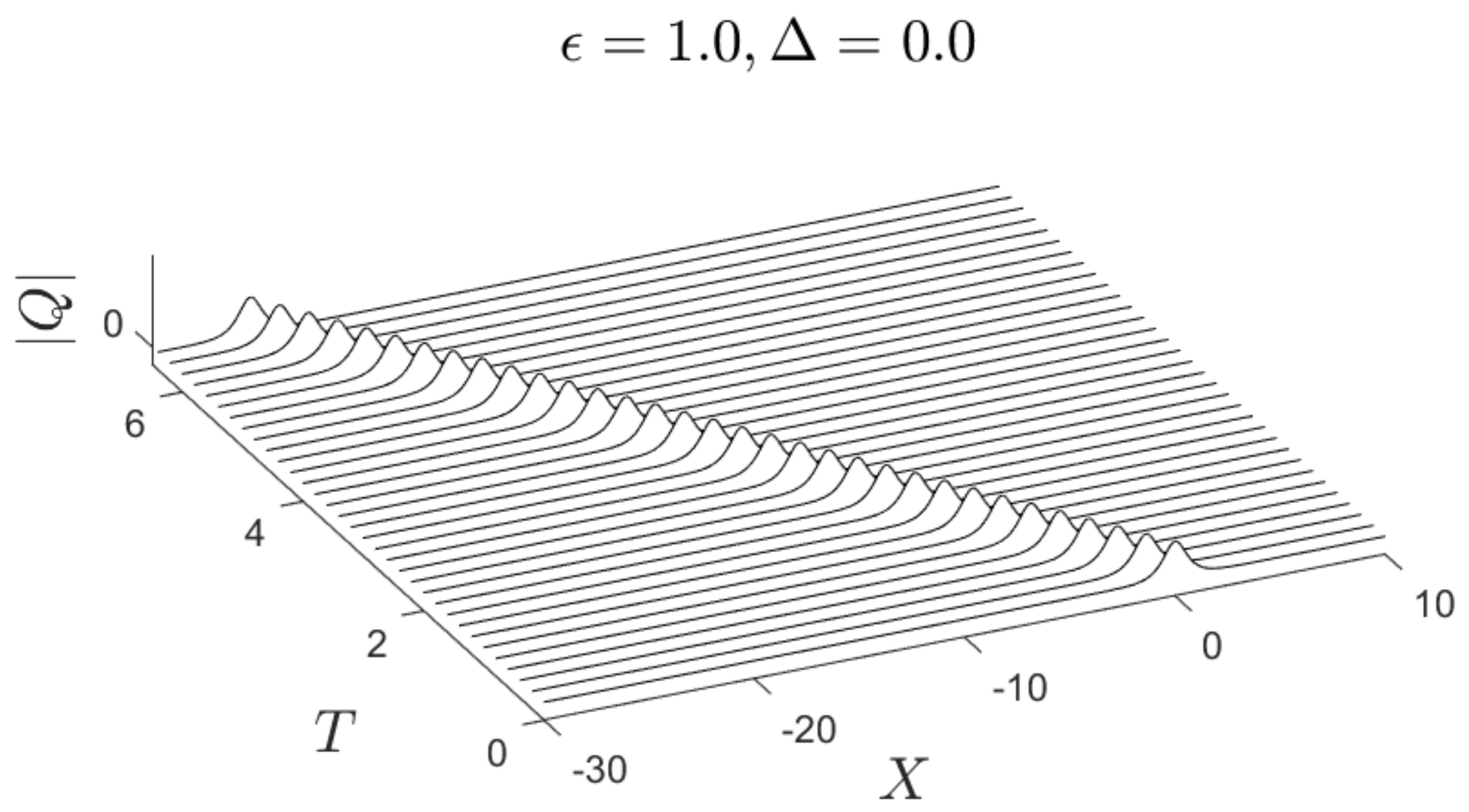
3.3.1. Without Forcing ()
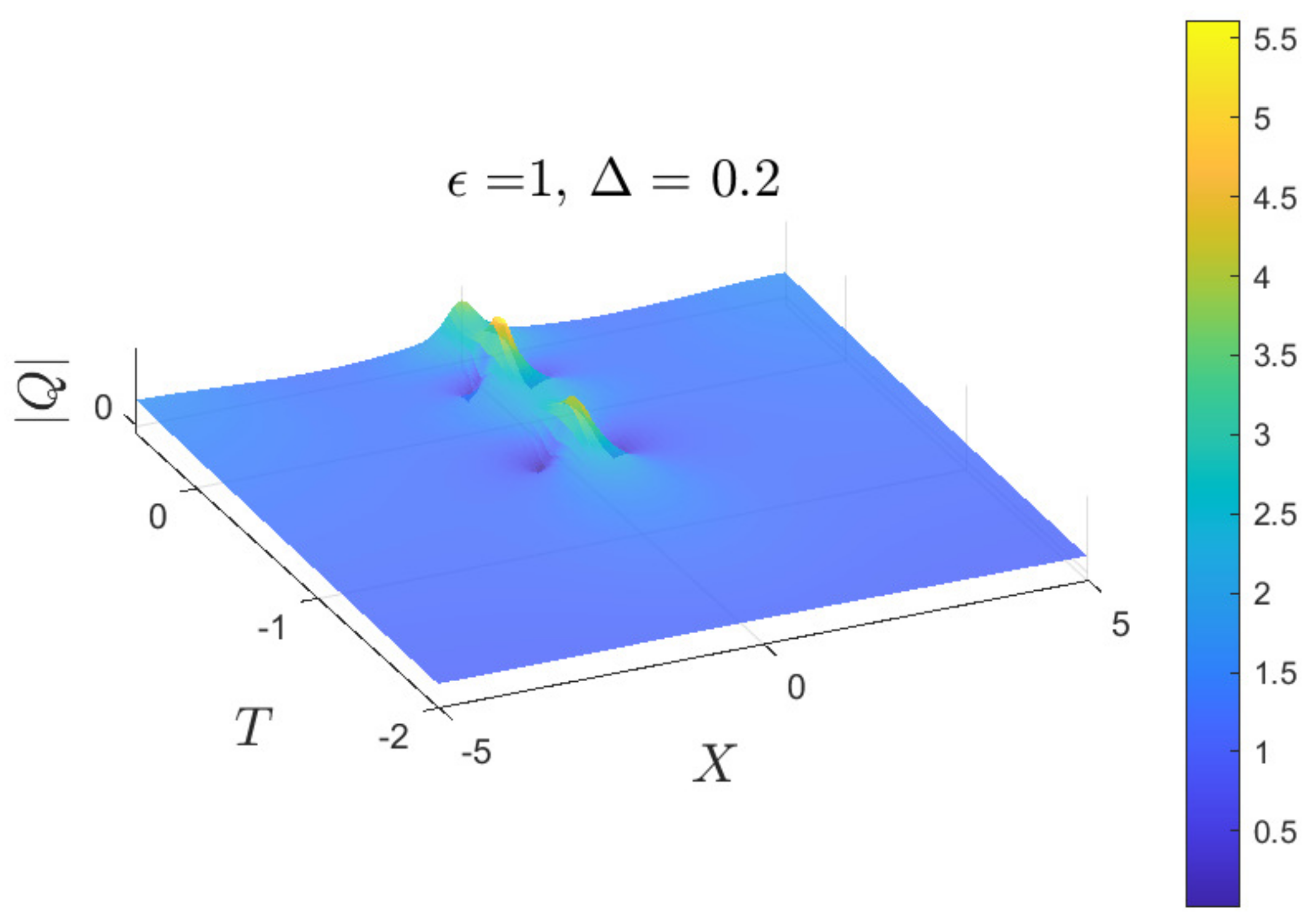
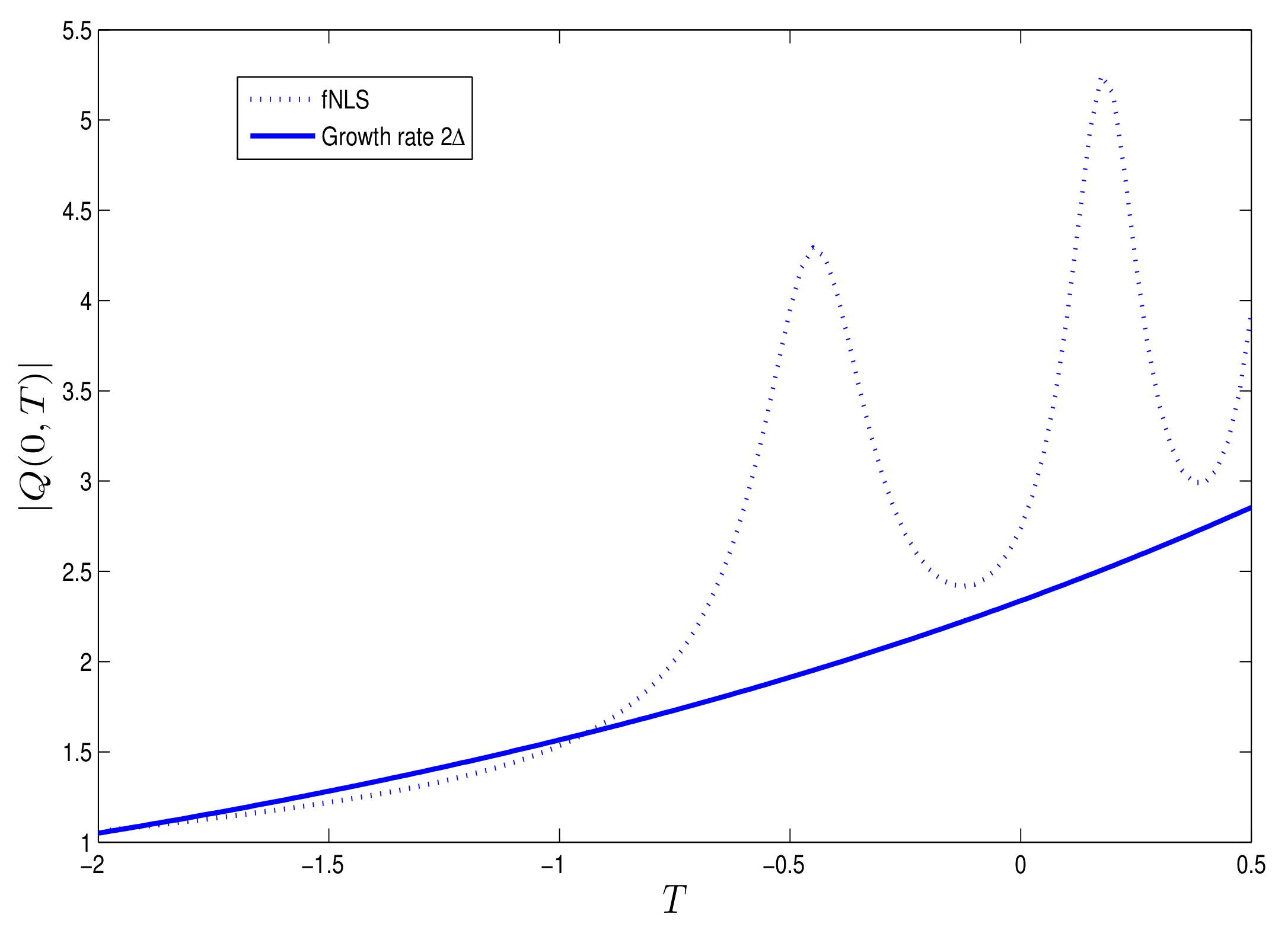
3.3.2. With Forcing ()
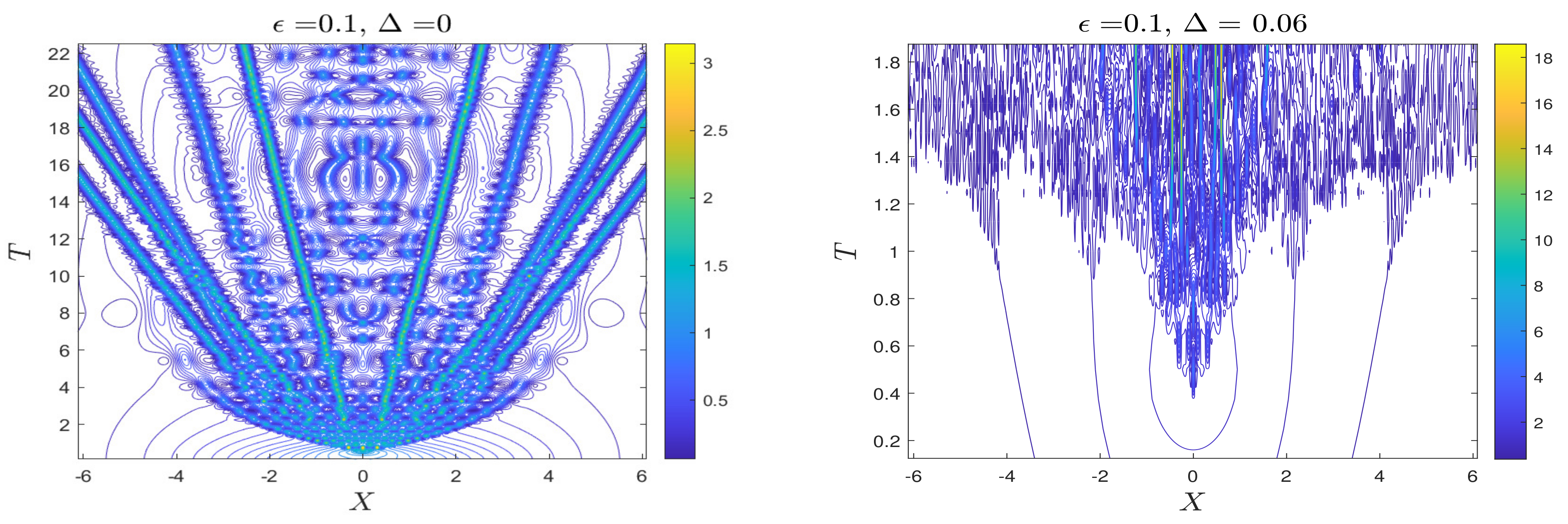
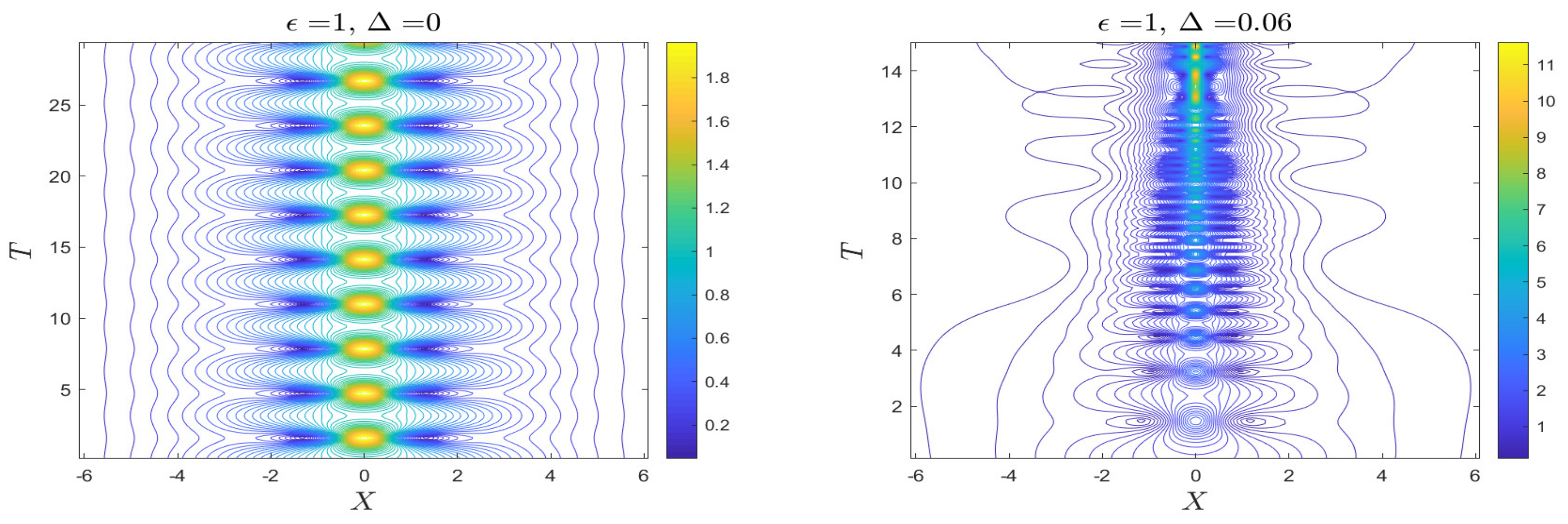
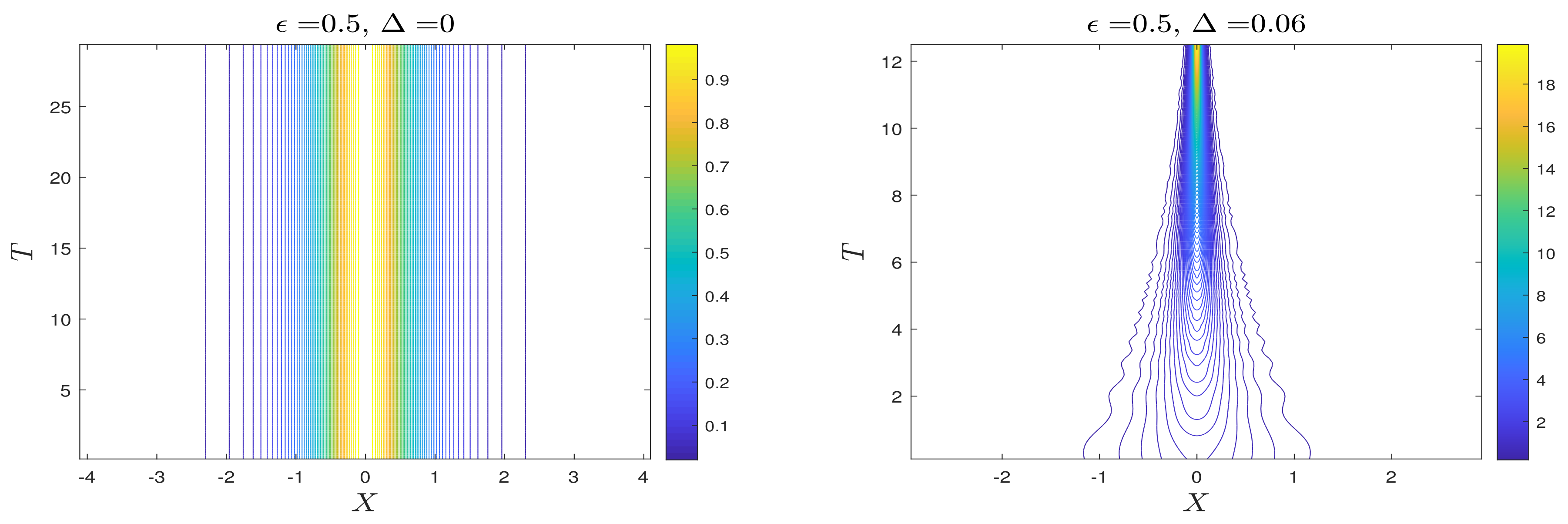
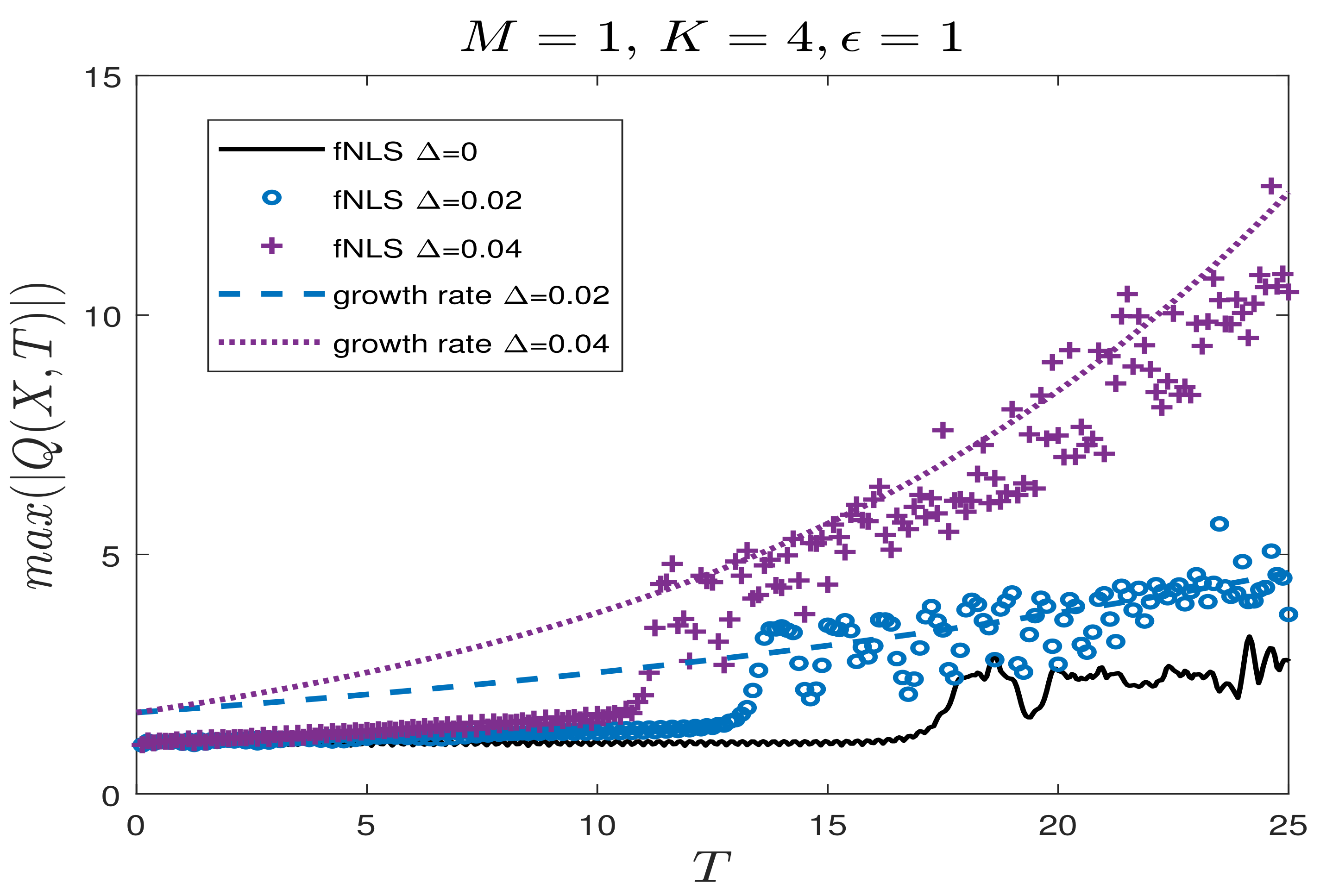
3.4. Case 4
3.4.1. Without Forcing ()
3.4.2. With Forcing ()
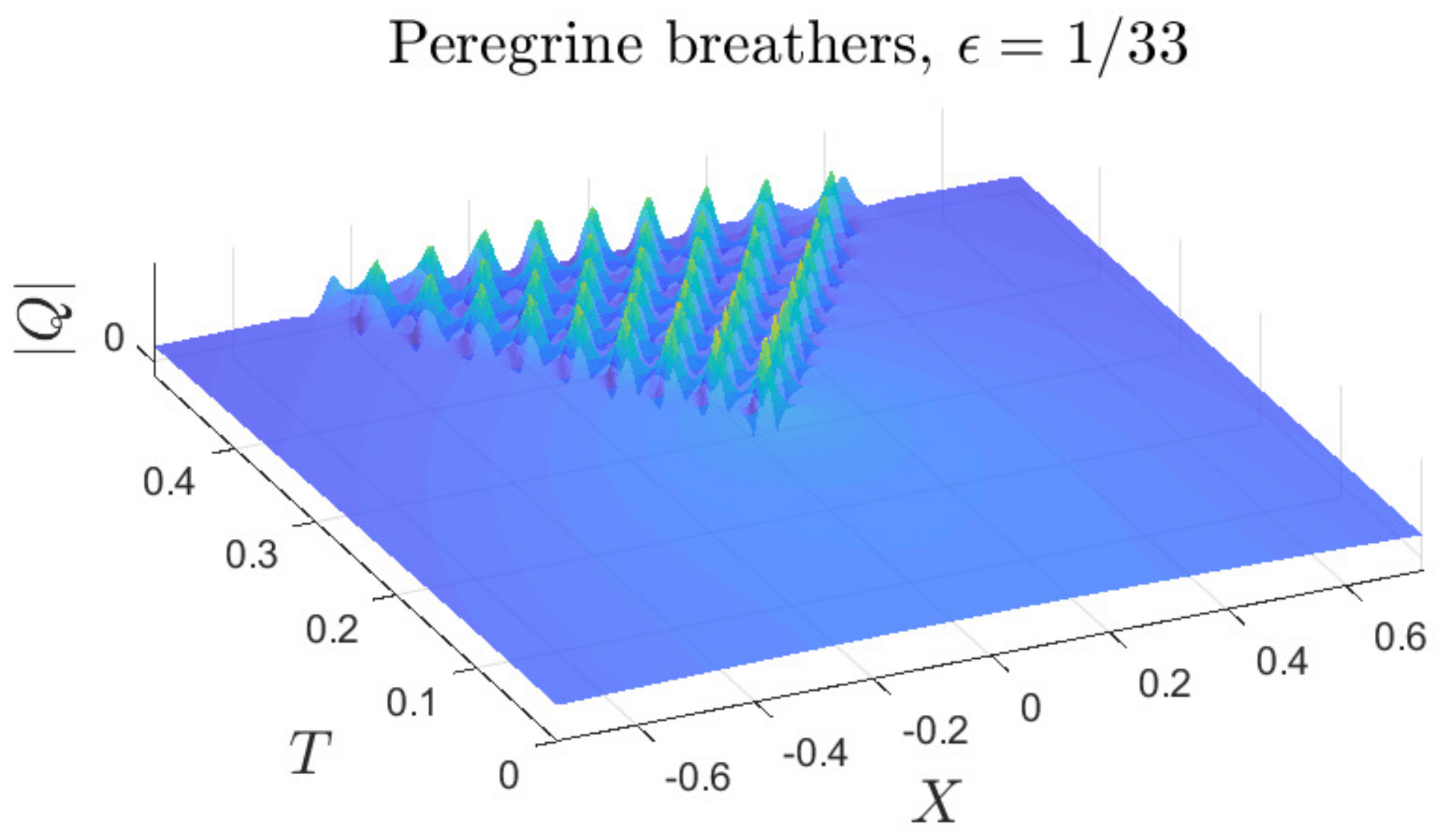
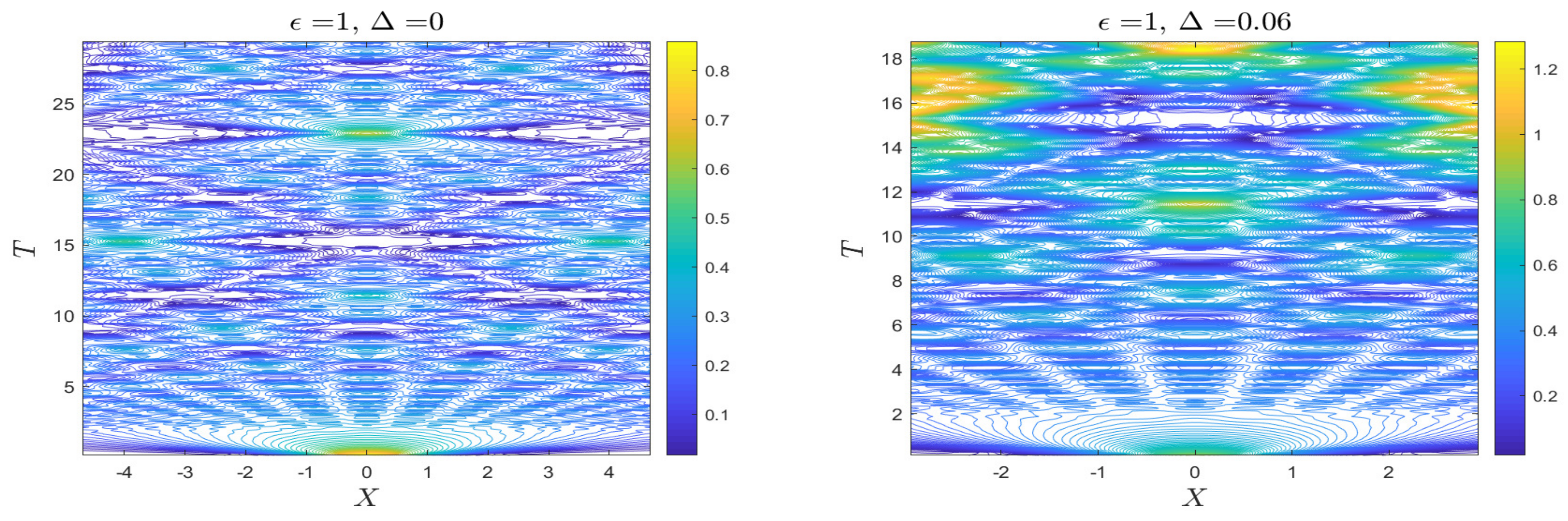
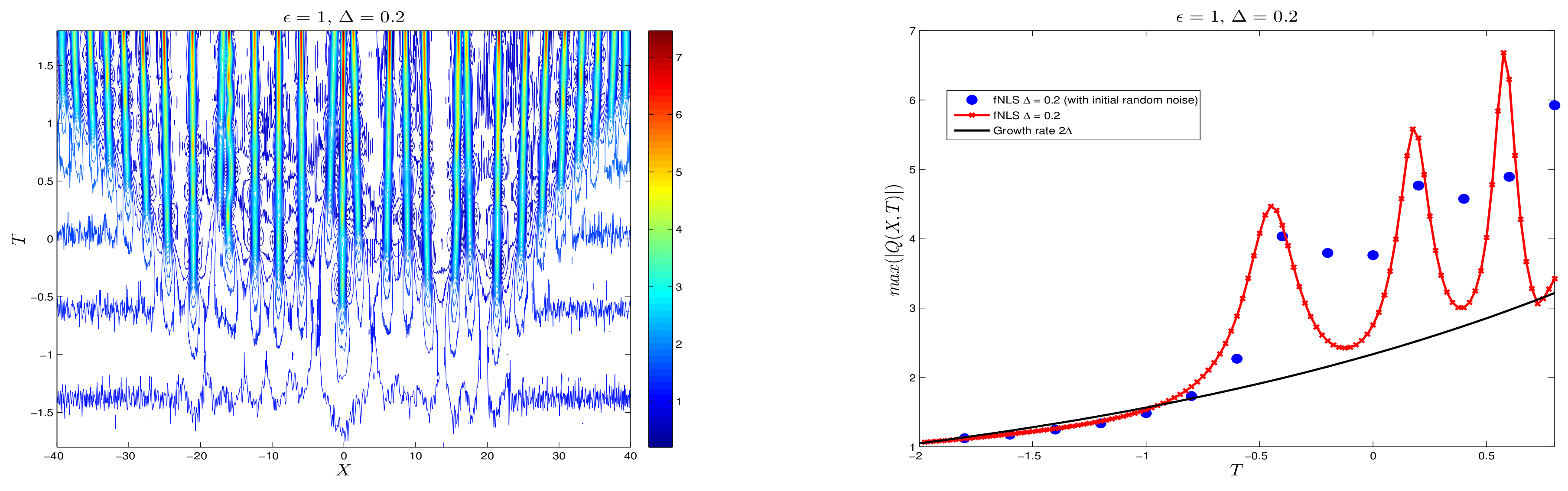
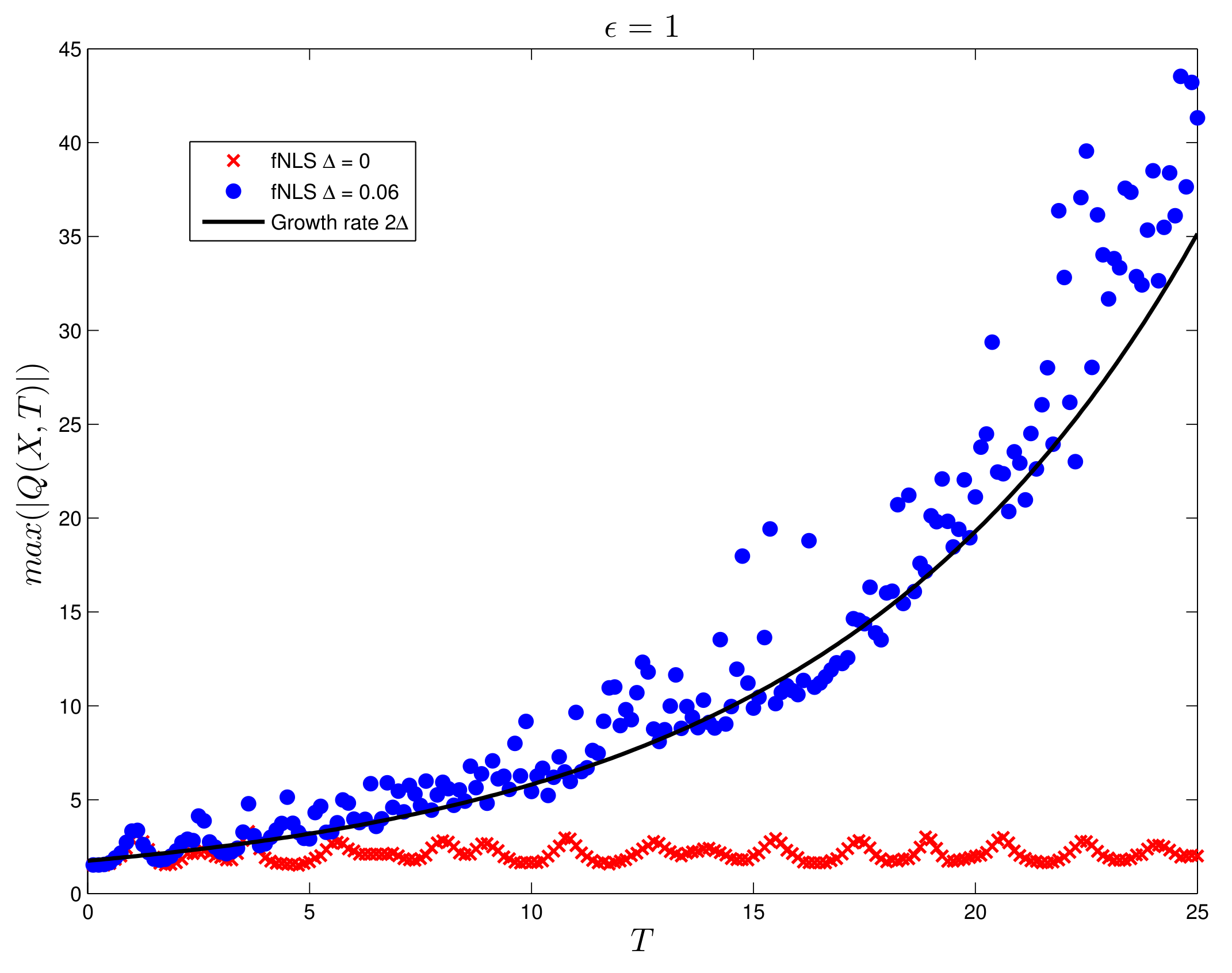
3.5. Initial Random Noise
4. Discussion and Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kharif, C.; Pelinovsky, E.; Slunyaev, A. Rogue Waves in the Ocean; Advances in Geophysical and Environmental Mechanics and Mathematics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Osborne, A.R. Nonlinear Ocean Waves and the Inverse Scattering Transform. In Scattering, 1st ed.; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Grimshaw, R.; Tovbis, A. Rogue waves: Analytical predictions. Proc. Royal Soc. 2013, 469, 20130094. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Talipova, T.; Sergeeva, A. Rogue internal waves in the ocean: Long wave model. Eur. Physical J. Special Topics 2010, 185, 195–208. [Google Scholar] [CrossRef]
- Chow, K.W.; Chan, H.N.; Grimshaw, R.H. Modulation instability of internal waves in a smoothly stratified shallow fluid with a constant buoyancy frequency. Nat. Hazards Earth Syst. Sci. Brief Comm. 2019, 19, 583–587. [Google Scholar] [CrossRef] [Green Version]
- Benney, D.J.; Newell, A.C. The propagation of nonlinear wave envelopes. J. Math. Phys. 1967, 46, 133–139. [Google Scholar] [CrossRef]
- Zakharov, V.E. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 1968, 9, 190–194. [Google Scholar] [CrossRef]
- Hasimoto, H.; Ono, H. Nonlinear modulation of gravity waves. J. Phys. Soc. Japan 1972, 33, 805–811. [Google Scholar] [CrossRef]
- Grimshaw, R. Envelope solitary waves. In Solitary waves in Fluids: Advances in Fluid Mechanics; Grimshaw, R., Ed.; WIT Press: Southampton, UK, 2007; Volume 45, pp. 159–179. [Google Scholar]
- Akhmediev, N.; Pelinovsky, E. Discussion and Debate: Rogue Waves-Towards a Unifying Concept? Eur. Physical J. Special Topics 2010, 185, 1–266. [Google Scholar] [CrossRef] [Green Version]
- Leblanc, S. Amplification of nonlinear surface waves by wind. Phys. Fluids 2007, 19, 101705. [Google Scholar] [CrossRef]
- Touboul, J.; Kharif, C.; Pelinovsky, E.; Giovanangeli, J.P. On the interaction of wind and steep gravity wave groups using Miles’ and Jeffreys’ mechanisms. Nonlin. Proc. Geophys. 2008, 15, 1023–1031. [Google Scholar] [CrossRef]
- Montalvo, P.; Kraenkel, R.; Manna, M.A.; Kharif, C. Wind-wave amplification mechanisms: Possible models for steep wave events in finite depth. Nat. Hazards Earth Syst. Sci. 2013, 13, 2805–2813. [Google Scholar] [CrossRef] [Green Version]
- Brunetti, M.; Marchiando, N.; Berti, N.; Kasparian, J. Nonlinear fast growth of water waves under wind forcing. Phys. Lett. A 2014, 378, 1025–1030. [Google Scholar] [CrossRef] [Green Version]
- Slunyaev, A.; Sergeeva, A.; Pelinovsky, E. Wave amplification in the framework of forced nonlinear Schrödinger equation: The rogue wave context. Phys. D 2015, 301, 18–27. [Google Scholar] [CrossRef] [Green Version]
- Grimshaw, R. Generation of wave groups. In IUTAM Symposium Wind Waves; Grimshaw, R., Hunt, J., Johnson, E., Eds.; Elsevier IUTAM Procedia Series; Elseveier: Amsterdam, The Netherlands, 2018; Volume 26, pp. 99–101. [Google Scholar]
- Grimshaw, R. Generation of wave groups by shear layer instability. Fluids 2019, 4, 39. [Google Scholar] [CrossRef] [Green Version]
- Grimshaw, R. Two-dimensional modulation instability of wind waves. J. Ocean. Eng. Mar. Energy 2019, 5, 413–417. [Google Scholar] [CrossRef] [Green Version]
- Miles, J.W. On the generation of surface waves by shear flows. J. Fluid Mech. 1957, 3, 185–204. [Google Scholar] [CrossRef]
- Miles, J.W. Surface wave generation revisited. J. Fluid Mech. 1993, 256, 427–441. [Google Scholar] [CrossRef]
- Morland, L.C.; Saffman, P.G. Effect of wind profile on the instability of wind blowing over water. J. Fluid Mech. 1993, 252, 383–398. [Google Scholar] [CrossRef]
- Janssen, P. The Interaction of Ocean Waves and Wind; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Stiassnie, M.; Agnon, Y.; Janssen, P.A.E.M. Temporal and spatial growth of wind waves. J. Phys. Ocean. 2007, 37, 106–114. [Google Scholar] [CrossRef] [Green Version]
- Sajjadi, S.G.; Hunt, J.C.R.; Drullion, F. Asymptotic multi-layer analysis of wind over unsteady monochromatic surface waves. J. Eng. Maths 2014, 84, 73–85. [Google Scholar] [CrossRef] [Green Version]
- Zakharov, V.E.; Resio, D.; Pushkarev, A. Balanced source terms for wave generation within the Hasselmann equation. Nonlin. Proc. Geophys. 2017, 24, 581–597. [Google Scholar] [CrossRef] [Green Version]
- Chabchoub, A.; Hoffmann, N.; Akhmediev, N. Rogue wave observation in a water wave tank. Phys. Rev. Lett. 2011, 106, 204502. [Google Scholar] [CrossRef] [PubMed]
- Chabchoub, A.; Slunyaev, A.; Hoffmann, N.; Dias, F.; Kibler, B.; Genty, G.; Dudley, J.M.; Akhmediev, N. The Peregrine breather on the zero-background limit as the two-Soliton degenerate solution: An experimental study. Front. Phys 2021, 9, 633549. [Google Scholar] [CrossRef]
- Onorato, M.; Osborne, A.R.; Serio, M. Modulational instability and non-Gaussian statistics in experimental random water-wave trains. Phys. Fluids 2005, 17, 078101. [Google Scholar] [CrossRef] [Green Version]
- León, S.P.; Osborne, A.R. Role of nonlinear four-wave interactions source term on the spectral shape. J. Mar. Sci. Eng. 2020, 8, 251. [Google Scholar] [CrossRef] [Green Version]
- Grimshaw, R.; Hunt, J.; Johnson, E. Preface. In IUTAM Symposium Wind Waves; Grimshaw, R., Hunt, J., Johnson, E., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 26, pp. 1–2. [Google Scholar]
- Grimshaw, R.H.J.; Maleewong, M. Transcritical flow over two obstacles: Forced Korteweg de Vries framework. J. Fluid Mech. 2016, 809, 918–940. [Google Scholar] [CrossRef]
- Peregrine, D.H. Water waves, nonlinear Schrödinger equations, and their solutions. J. Aust. Math. Soc. Series B 1983, 25, 16–43. [Google Scholar] [CrossRef] [Green Version]
- Chabchoub, A.; Grimshaw, R. The hydrodynamic nonlinear Schrödinger equation: Space and time. Fluids 2016, 1, 23. [Google Scholar] [CrossRef] [Green Version]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maleewong, M.; Grimshaw, R.H.J. Amplification of Wave Groups in the Forced Nonlinear Schrödinger Equation. Fluids 2022, 7, 233. https://doi.org/10.3390/fluids7070233
Maleewong M, Grimshaw RHJ. Amplification of Wave Groups in the Forced Nonlinear Schrödinger Equation. Fluids. 2022; 7(7):233. https://doi.org/10.3390/fluids7070233
Chicago/Turabian StyleMaleewong, Montri, and Roger H. J. Grimshaw. 2022. "Amplification of Wave Groups in the Forced Nonlinear Schrödinger Equation" Fluids 7, no. 7: 233. https://doi.org/10.3390/fluids7070233
APA StyleMaleewong, M., & Grimshaw, R. H. J. (2022). Amplification of Wave Groups in the Forced Nonlinear Schrödinger Equation. Fluids, 7(7), 233. https://doi.org/10.3390/fluids7070233





