A Numerical Analysis on the Unsteady Flow of a Thermomagnetic Reactive Maxwell Nanofluid over a Stretching/Shrinking Sheet with Ohmic Dissipation and Brownian Motion
Abstract
:1. Introduction
2. Mathematical Formulation
Similarity Transformations
3. Numerical Solution Using the Spectral Quasi-Linearization Method
4. Results and Discussions
5. Conclusions
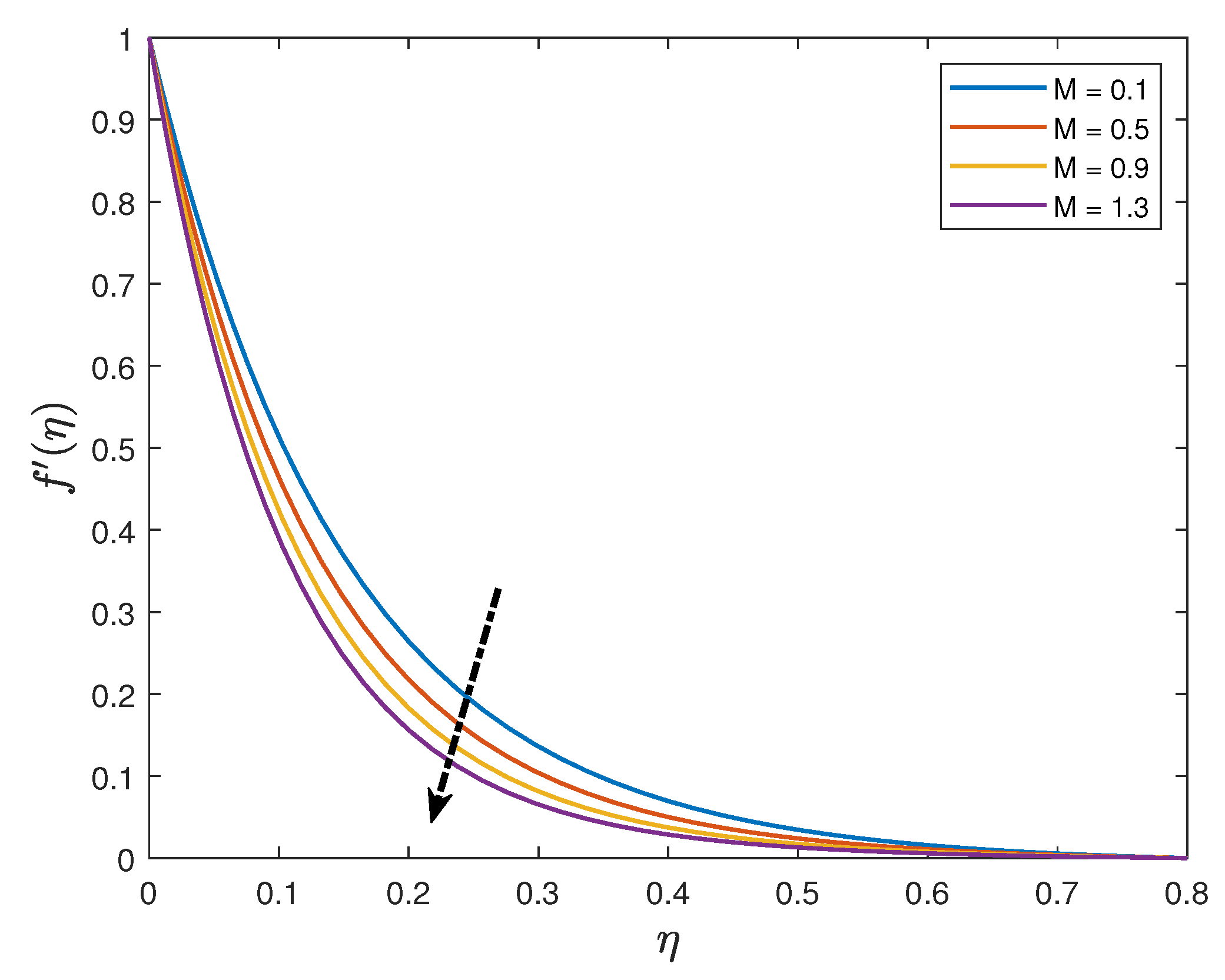
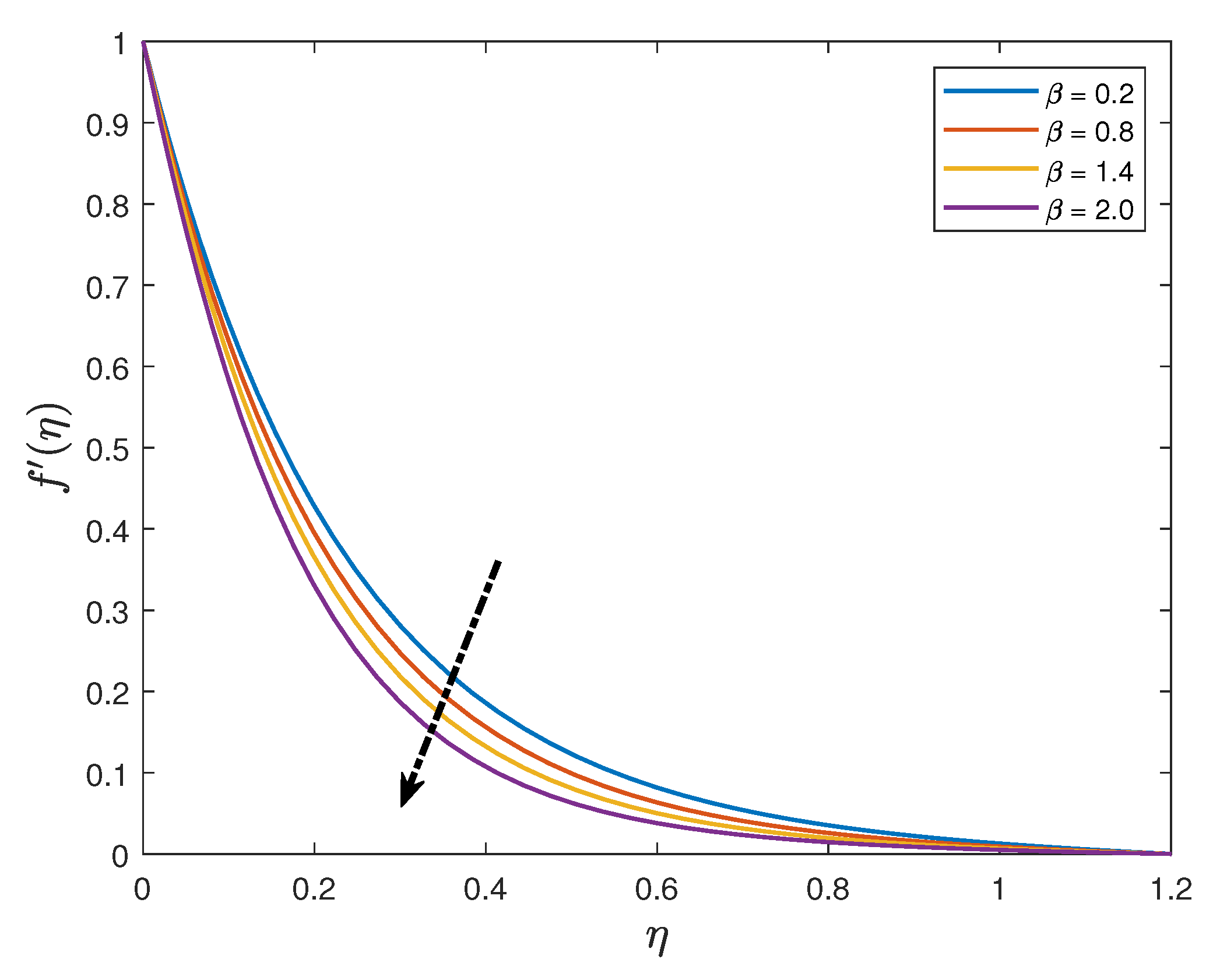
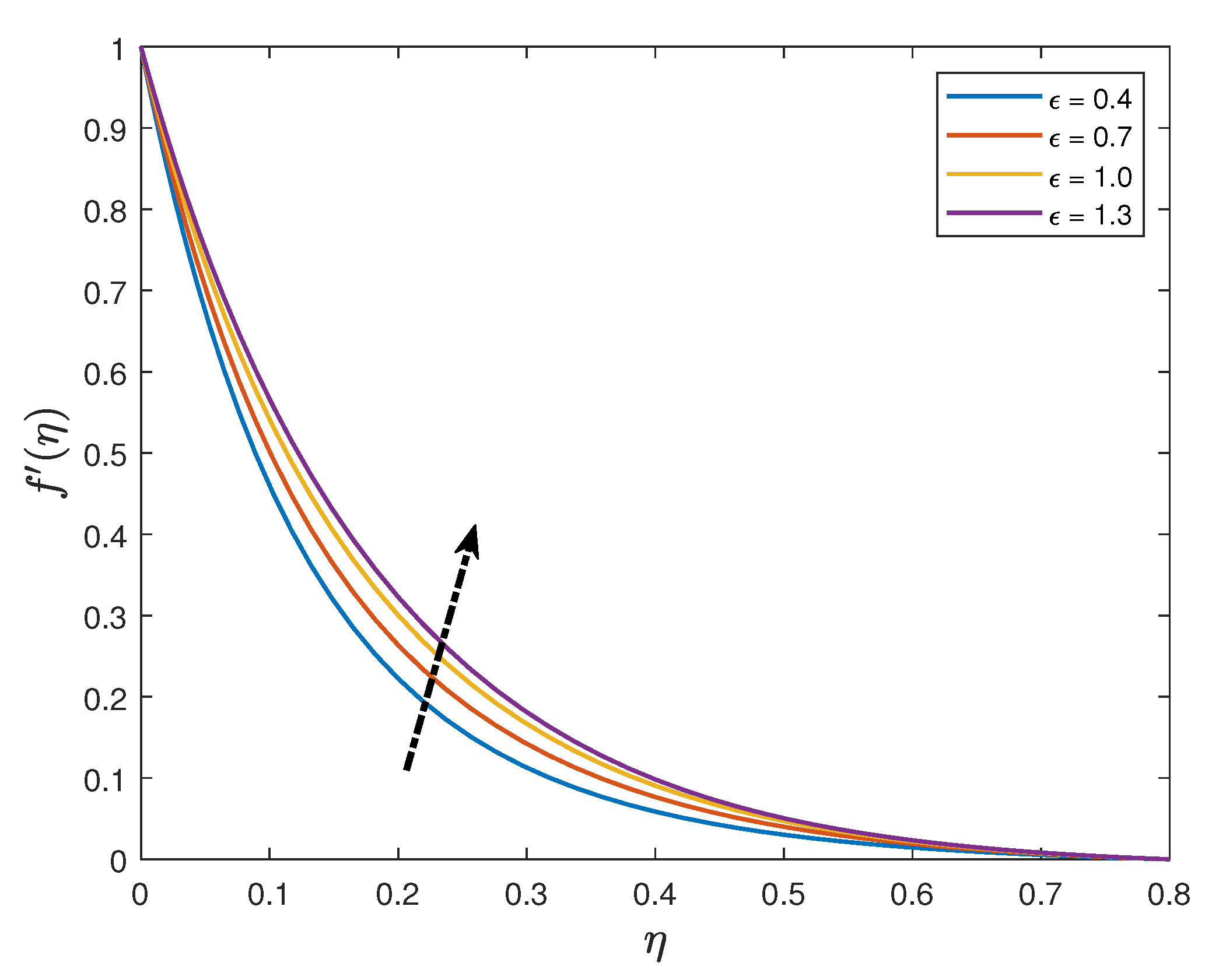
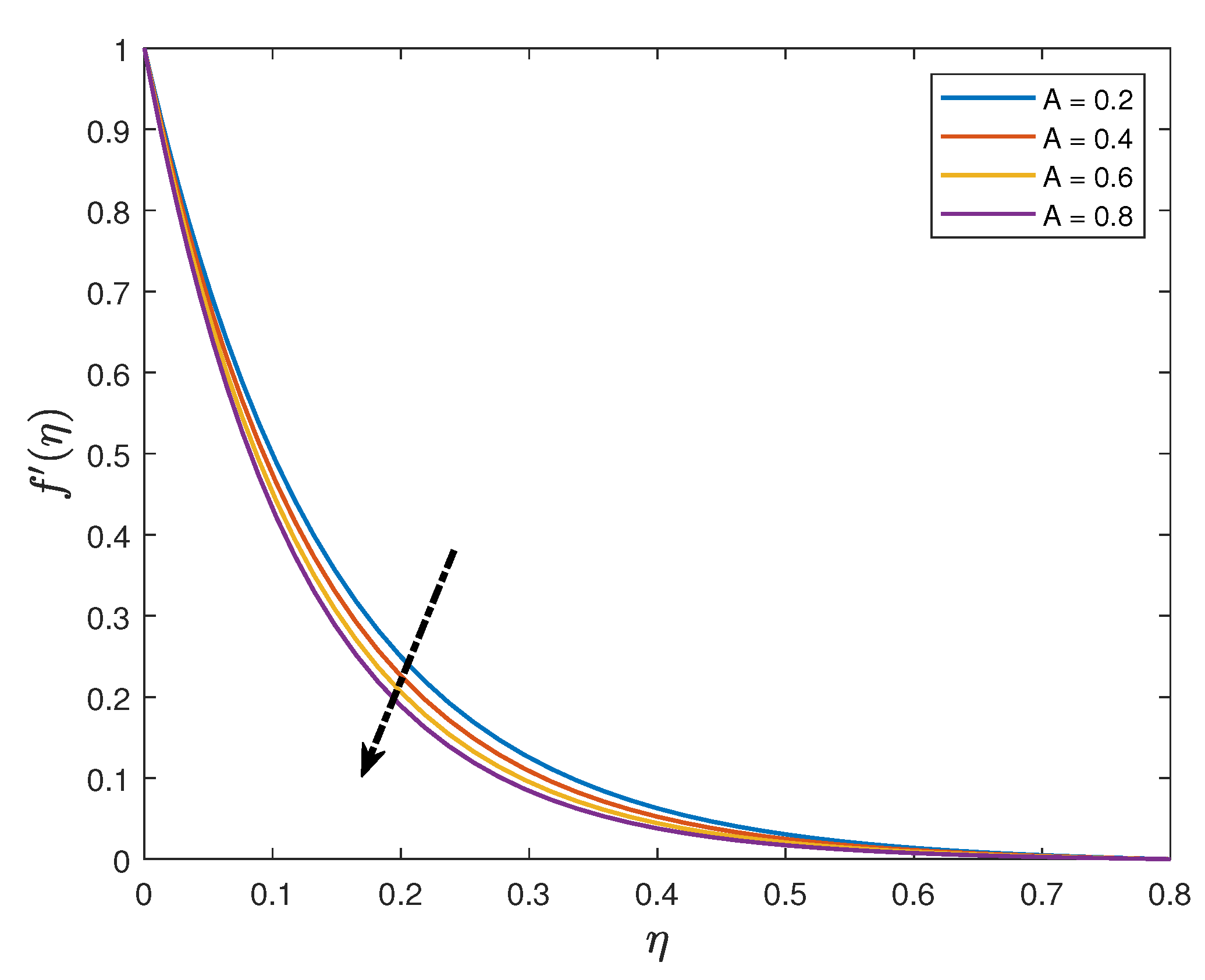
- The velocity distribution increases with an enhancement of the mixed convection parameter whilst it reduces when the values of the magnetic parameter, unsteadiness parameter and the Maxwell parameter are increased;
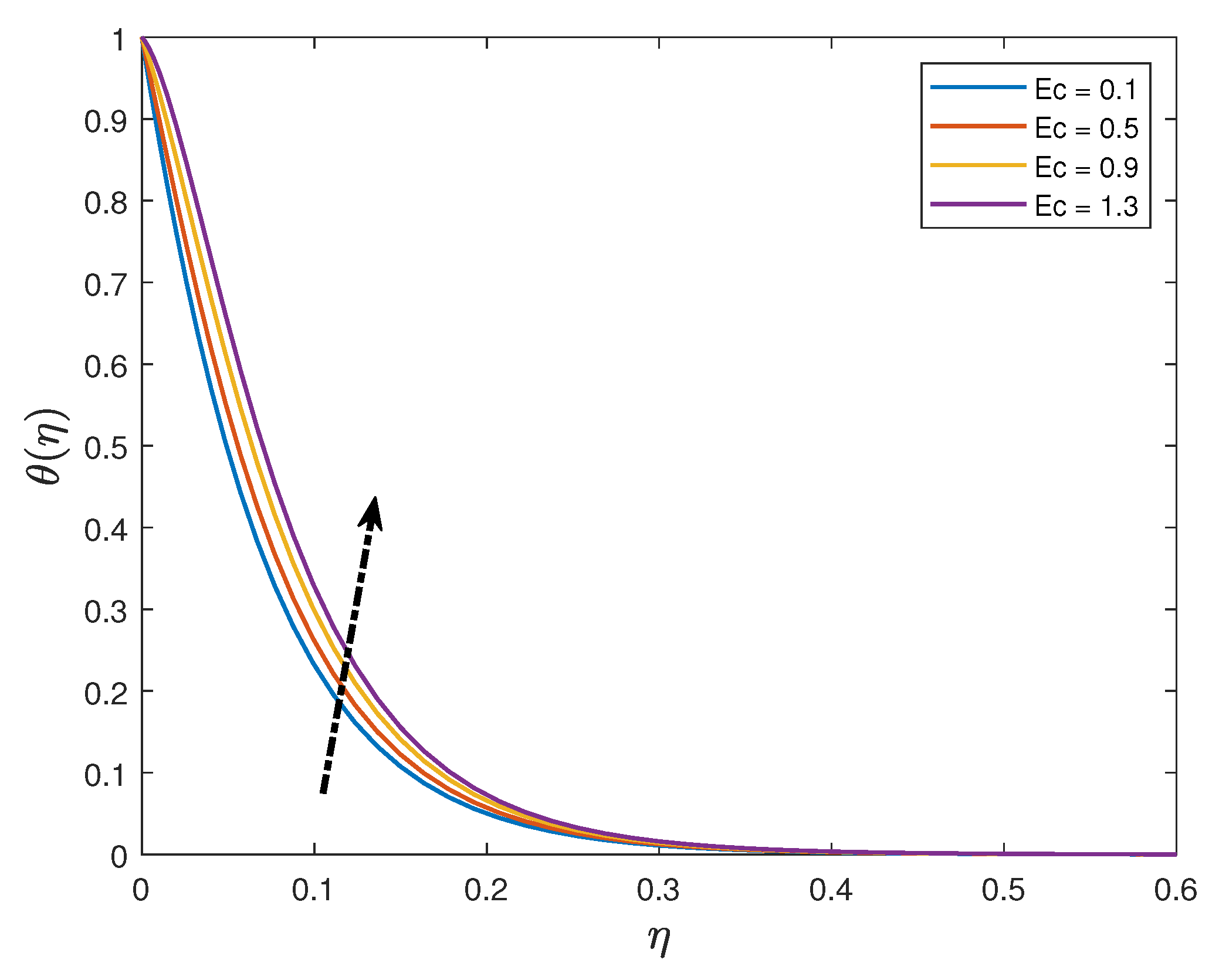
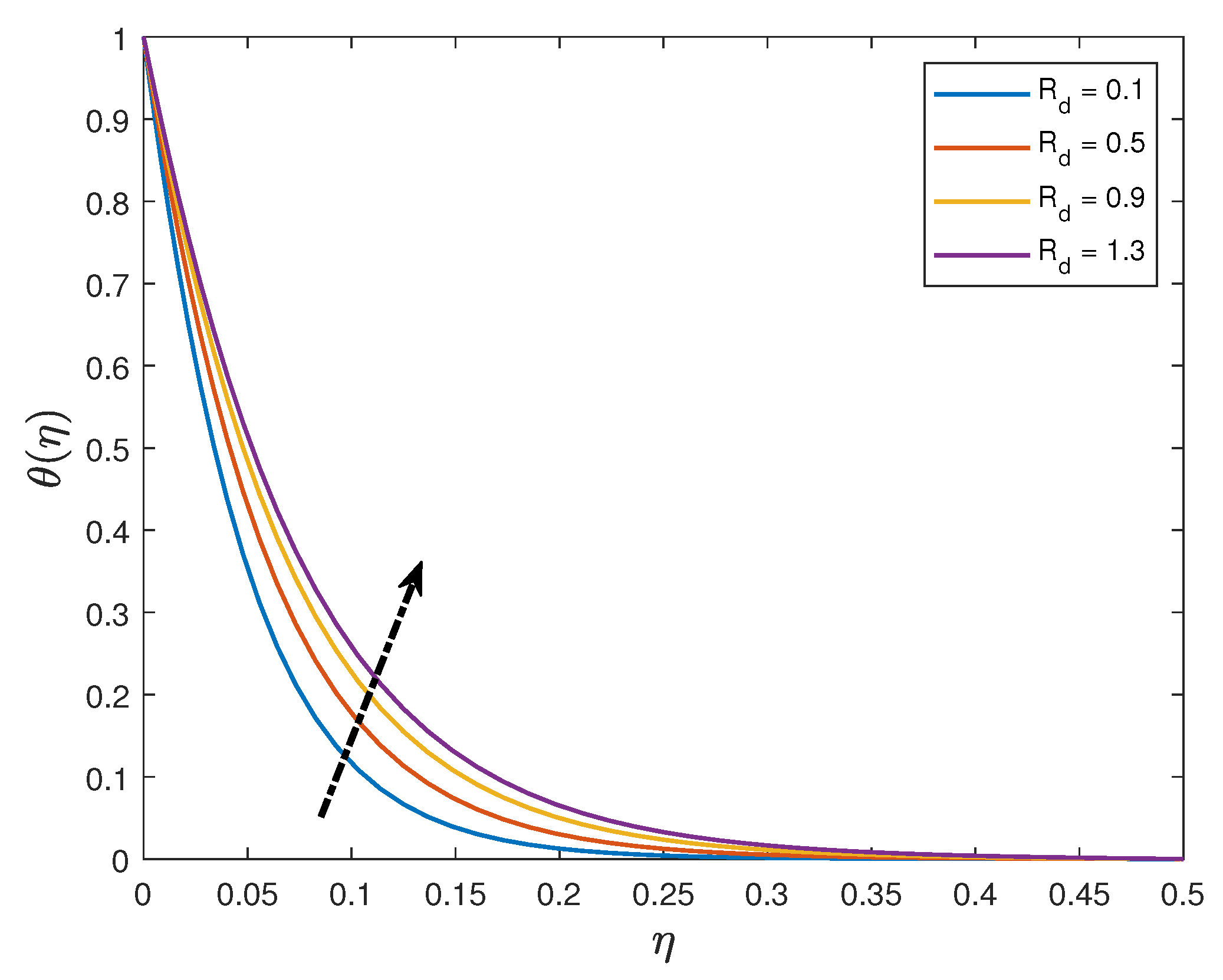
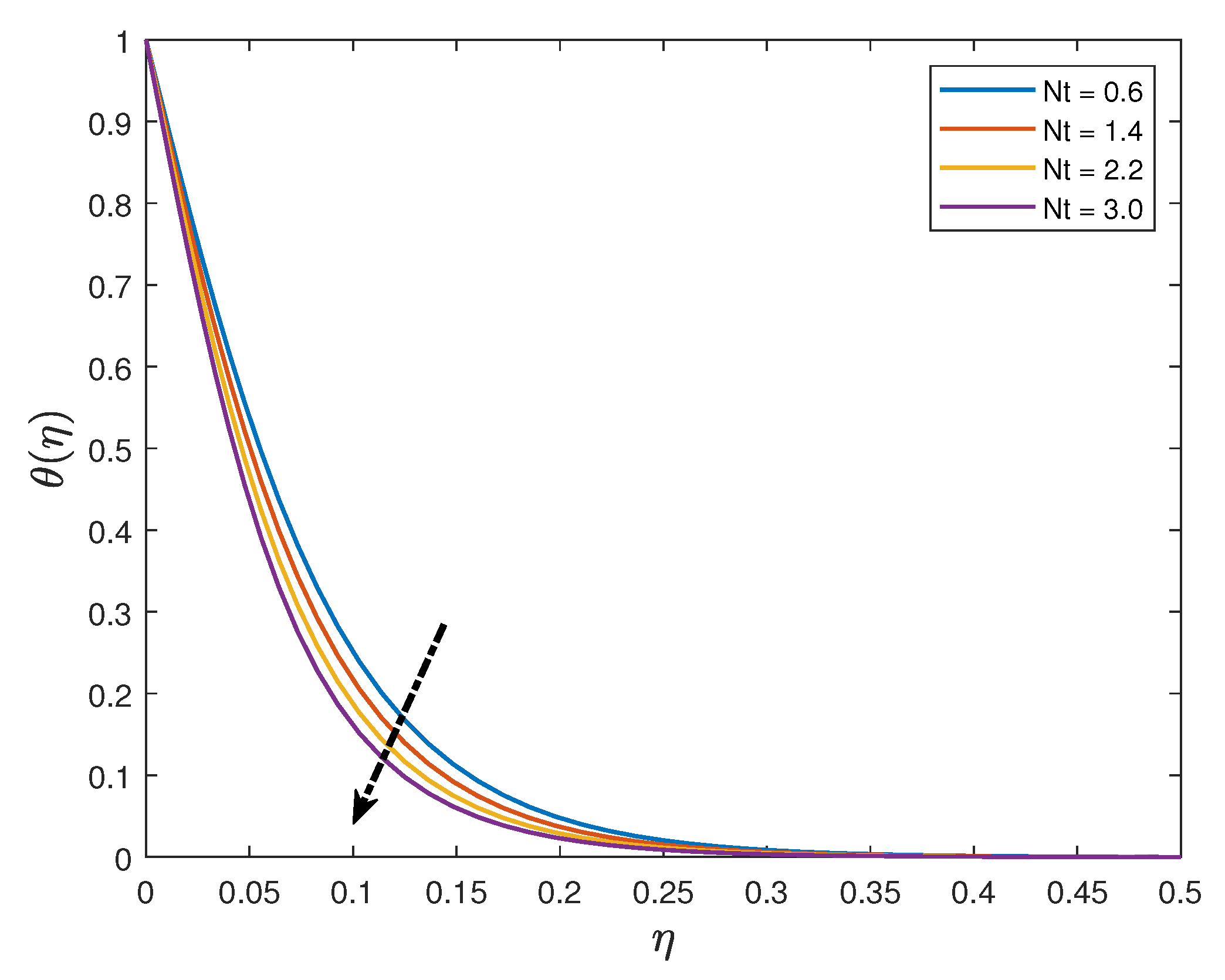
- Increasing the values of the Eckert number and thermal radiation parameter enhances the temperature profiles whilst the profiles are depressed when the Prandtl number and the thermophoresis parameter are increased;
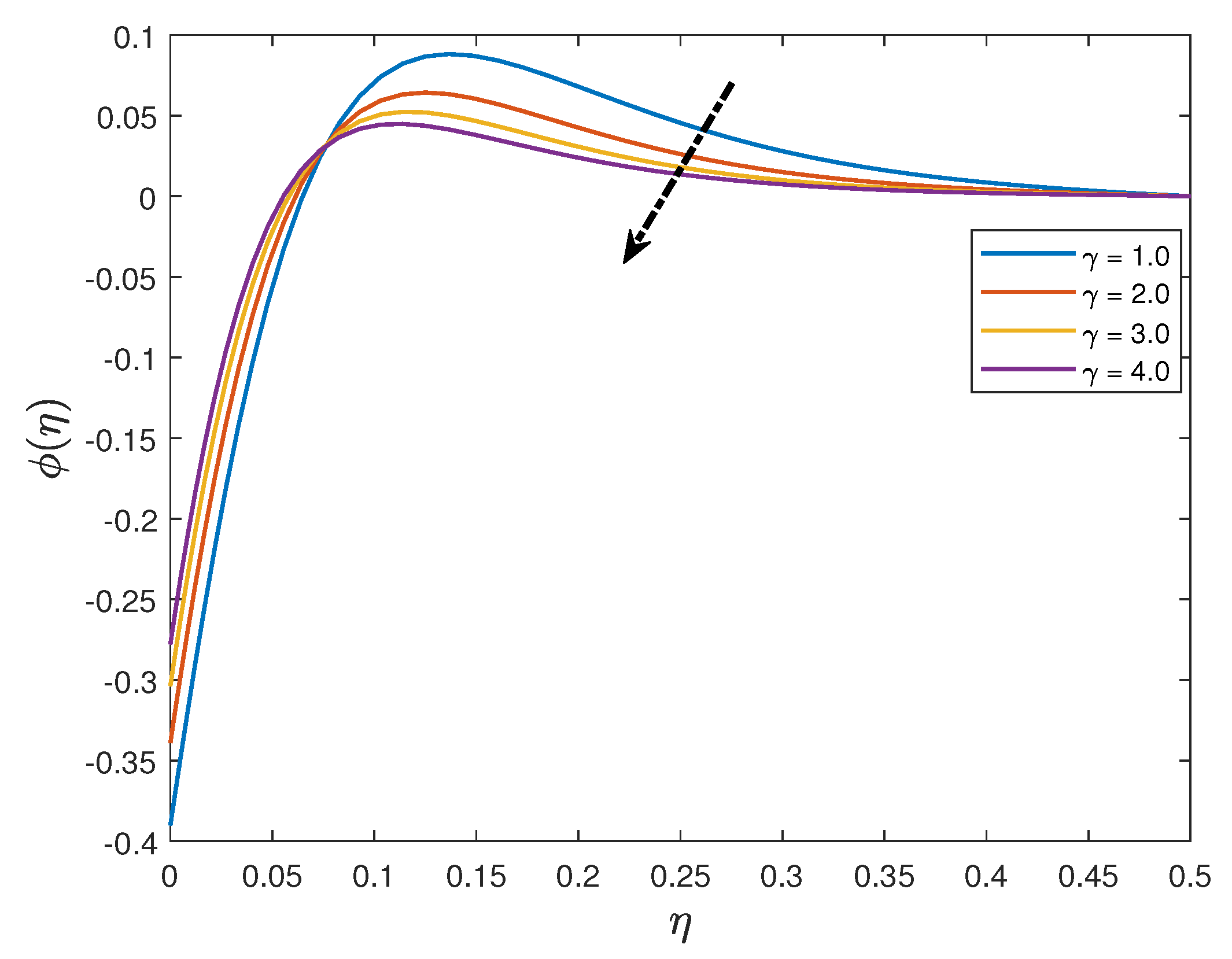
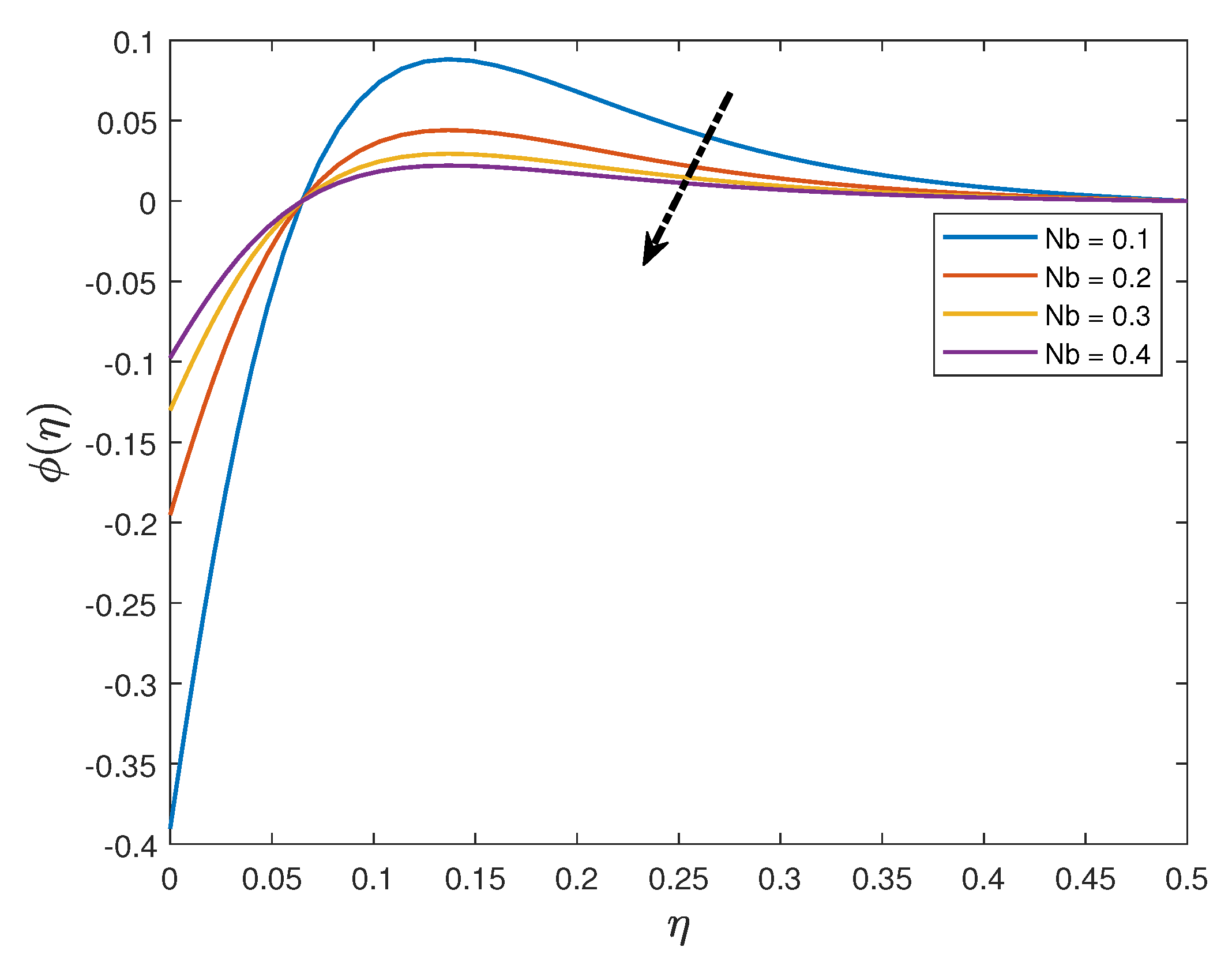
- The nanoparticle concentration distribution is an increasing function of the thermophoresis parameter and a decreasing function of thermal radiation parameter, Schmidt number and the Brownian motion parameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | stretching rate [s] |
| A | unsteadiness parameter |
| B | uniform magnetic field [T] |
| initial magnetic strength | |
| C | species concentration [mol m] |
| local skin friction coefficient | |
| specific heat capacity [J kg K] | |
| wall species concentration [mol m] | |
| free stream concentration [mol m] | |
| mass diffusivity [m s] | |
| Eckert number | |
| f | dimensionless stream function |
| g | acceleration due to gravity [m s] |
| chemical reaction rate | |
| mean absorption rate | |
| M | magnetic parameter |
| concentration-thermal buoyancy ratio | |
| Brownian motion parameter | |
| thermophoresis parameter | |
| local Nusselt number | |
| Prandtl number | |
| surface mass flux [kg s m] | |
| surface heat flux [W m] | |
| local Reynolds number | |
| thermal radiation parameter | |
| S | suction/injection parameter |
| Schmidt number | |
| local Sherwood number | |
| t | time |
| T | temperature of the Maxwell fluid [K] |
| wall temperature [K] | |
| ambient temperature [K] | |
| u | horizontal velocity component [m s] |
| sheet velocity component [m s] | |
| v | vertical velocity component [m s] |
| x | streamline coordinate [m] |
| y | transverse coordinate [m] |
| Greek Symbols | |
| constant [s] | |
| thermal diffusivity [m s] | |
| Maxwell parameter | |
| thermal expansion coefficient | |
| solutal expansion coefficient | |
| relaxation parameter | |
| retardation time | |
| dimensionless radial coordinate | |
| dynamic viscosity [kg m s] | |
| kinematic viscosity [m s] | |
| electrical conductivity [S m] | |
| Stefan-Boltzmann constant [W mK ] | |
| dimensionless temperature | |
| mixed convection parameter | |
| dimensionless concentration | |
| density [kg m] | |
| dimensionless stream function | |
| wall shear stress [kg m s] | |
| Subscripts | |
| w | wall conditions |
| ∞ | conditions far away from the plate |
References
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Laboratory (ANL): Argonne, IL, USA, 1995.
- Jakati, S.V.; Raju, T.B.; Nargund, A.L.; Sathyanarayana, S.B. Study of Maxwell Nanofluid Flow over a Stretching Sheet with Non-Uniform Heat Source/Sink with External Magnetic Field. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 55, 218–232. [Google Scholar]
- Hayat, T.; Qayyum, S.; Alsaedi, A. Mechanisms of nonlinear convective flow of Jeffrey nanofluid due to nonlinear radially stretching sheet with convective conditions and magnetic field. Results Phys. 2017, 7, 2341–2351. [Google Scholar] [CrossRef]
- Maxwell, J.C. On the Dynamical Theory of Gases. Philos. Trans. R. Soc. Lond. 1867, 157, 49–88. [Google Scholar] [CrossRef]
- Ellahi, R.; Raza, M.; Vafai, K. Series solutions of non-Newtonian nanofluids with Reynolds’ model and Vogel’s model by means of the homotopy analysis method. Math. Comput. Model. 2012, 55, 1876–1891. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Khan, S.; Selim, M.M.; Khan, A.; Ullah, A.; Abdeljawad, T.; Ikramullah; Ayaz, M.; Mashwani, W.K. On the Analysis of the Non-Newtonian Fluid Flow Past a Stretching/Shrinking Permeable Surface with Heat and Mass Transfer. Coatings 2021, 11, 566. [Google Scholar] [CrossRef]
- Kudenatti; Ramesh, B.; Misbah, N.-E. Hydrodynamic flow of non-Newtonian power-law fluid past a moving wedge or a stretching sheet: A unified computational approach. Sci. Rep. 2020, 101, 9445. [Google Scholar] [CrossRef]
- Gireesha, B.J.; Umeshaiah, M.; Prasannakumara, B.C.; Shashikumar, N.S.; Archana, M. Impact of nonlinear thermal radiation on magnetohydrodynamic three dimensional boundary layer flow of Jeffrey nanofluid over a nonlinearly permeable stretching sheet. Phys. A Stat. Mech. Appl. 2020, 549, 124051. [Google Scholar] [CrossRef]
- Shahzad, F.; Jamshed, W.; Nisar, K.S.; Nasir, N.A.A.M. Thermal analysis for Al2O3–sodium alginate magnetized Jeffrey’s nanofluid flow past a stretching sheet embedded in a porous medium. Sci. Rep. 2022, 12, 3287. [Google Scholar] [CrossRef]
- Jayachandra Babu, M.; Sandeep, N. MHD non-Newtonian fluid flow over a slendering stretching sheet in the presence of cross-diffusion effects. Alex. Eng. J. 2016, 55, 2193–2201. [Google Scholar] [CrossRef]
- Baranovskii, E.S. Flows of a polymer fluid in domain with impermeable boundaries. Comput. Math. Math. Phys. 2014, 54, 1589–1596. [Google Scholar] [CrossRef]
- Ibrahim, S.M.; Kumar, P.V.; Makinde, O.D. Chemical Reaction and Radiation Effects on Non-Newtonian Fluid Flow over a Stretching Sheet with Non-Uniform Thickness and Heat Source. Defect Diffus. Forum 2018, 387, 319–331. [Google Scholar] [CrossRef]
- Khan, W.; Idress, M.; Gul, T.; Khan, M.A.; Bonyah, E. Three non-Newtonian fluids flow considering thin film over an unsteady stretching surface with variable fluid properties. Adv. Mech. Eng. 2018, 10, 1687814018807361. [Google Scholar] [CrossRef]
- Sahoo, B. Flow and heat transfer of a non-Newtonian fluid past a stretching sheet with partial slip. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 602–615. [Google Scholar] [CrossRef]
- Mishra, S.R.; Baag, S.; Dash, G.C.; Acharya, M.R. Numerical approach to MHD flow of power-law fluid on a stretching sheet with non-uniform heat source. Nonlinear Eng. 2019, 9, 81–93. [Google Scholar] [CrossRef]
- Prasannakumara, B.C. Numerical simulation of heat transport in Maxwell nanofluid flow over stretching sheet considering magnetic dipole effect. Partial Differ. Equ. Appl. Math. 2021, 4, 100064. [Google Scholar] [CrossRef]
- Hussain, S.M.; Sharma, R.; Mishra, M.R.; Alrashidy, S.S. Hydromagnetic Dissipative and Radiative Graphene Maxwell Nanofluid Flow Past a Stretched Sheet-Numerical and Statistical Analysis. Mathematics 2020, 8, 1929. [Google Scholar] [CrossRef]
- Ibrahim, W.; Negera, M. MHD slip flow of upper-convected Maxwell nanofluid over a stretching sheet with chemical reaction. J. Egypt. Math. Soc. 2020, 28, 7. [Google Scholar] [CrossRef]
- Ahmad, S.; Khan, M.N.; Nadeem, S. Unsteady three dimensional bioconvective flow of Maxwell nanofluid over an exponentially stretching sheet with variable thermal conductivity and chemical reaction. Int. J. Ambient Energy 2022. [Google Scholar] [CrossRef]
- Jawad, M.; Saeed, A.; Gul, T.; Shah, Z.; Kumam, P. Unsteady thermal Maxwell power law nanofluid flow subject to forced thermal Marangoni Convection. Sci. Rep. 2021, 11, 7521. [Google Scholar] [CrossRef]
- Motsa, S.S.; Dlamini, P.G.; Khumalo, M. Spectral Relaxation Method and Spectral Quasilinearization Method for Solving Unsteady Boundary Layer Flow Problems. Adv. Math. Phys. 2014, 2014, 341964. [Google Scholar] [CrossRef]
- Rai, N.; Mondal, S. Spectral methods to solve nonlinear problems: A review. Partial Differ. Equ. Appl. Math. 2021, 4, 100043. [Google Scholar] [CrossRef]
- Alharbey, R.A.; Mondal, H.; Behl, R. Spectral Quasi-Linearization Method for Non-Darcy Porous Medium with Convective Boundary Condition. Entropy 2019, 21, 838. [Google Scholar] [CrossRef]
- Magodora, M.; Mondal, H.; Sibanda, P. Effect of Cattaneo-Christov Heat Flux on Radiative Hydromagnetic Nanofluid Flow between Parallel Plates using the Spectral Quasilinearization Method. J. Appl. Comput. Mech. 2022, 8, 865–875. [Google Scholar] [CrossRef]
- Mondal, H.; Sibanda, P. Spectral Quasi-Linearization Method for Entropy Generation Using the Cattaneo–Christov Heat Flux Model. Int. J. Comput. Methods 2018, 17, 1940002. [Google Scholar] [CrossRef]
- Mondal, H.; Bharti, S. Spectral Quasi-linearization for MHD Nanofluid Stagnation Boundary Layer Flow due to a Stretching/Shrinking Surface. J. Appl. Comput. Mech. 2020, 6, 1058–1068. [Google Scholar] [CrossRef]
- Nayak, R.E.; Rao, M.V.S.; Gangadhar, K. Mixed convection boundary layer flow of non-Newtonian nanofluid using the spectral quasi linearization. Math. Model. Eng. Probl. 2020, 7, 45–54. [Google Scholar] [CrossRef]
- Sahoo, A.; Nandkeolyar, R. Entropy generation and dissipative heat transfer analysis of mixed convective hydromagnetic flow of a Casson nanofluid with thermal radiation and Hall current. Sci. Rep. 2021, 11, 3926. [Google Scholar] [CrossRef]
- Kierzenka, J.; Shampine, L.F. A BVP solver based on residual control and the MATLAB PSE. ACM Trans. Math. Soft. 2001, 27, 299–316. [Google Scholar] [CrossRef]
- Madhu, M.; Kishan, N.; Chamkha, A.J. Unsteady flow of a Maxwell nanofluid over a stretching surface in the presence of magnetohydrodynamic and thermal radiation effects. Propuls. Power Res. 2017, 6, 31–40. [Google Scholar] [CrossRef]
- El-Aziz, M.A.; Yahya, A.S. Heat and Mass Transfer of Unsteady Hydromagnetic Free Convection Flow Through Porous Medium Past a Vertical Plate with Uniform Surface Heat Flux. J. Theor. Appl. Mech. 2017, 47, 25–58. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Thermal radiation on unsteady electrical MHD flow of nanofluid over stretching sheet with chemical reaction. J. King Saud Univ.—Sci. 2017, 31, 804–812. [Google Scholar] [CrossRef]
- Bellman, R.; Kalaba, R. Quasilinearization and Nonlinear Boundary-Value Problems; American Elsevier Publishing Company: New York, NY, USA, 1965. [Google Scholar]
- Trefethen, L.N. Spectral Methods in MATLAB; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Elbashbeshy, E.M.A.; Bazid, M.A.A. Heat transfer over an unsteady stretching surface. Heat Mass Transfer 2004, 41, 1–4. [Google Scholar] [CrossRef]
- Ibrahim, W.; Shankar, B. MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions. Comput. Fluids 2013, 75, 1–10. [Google Scholar] [CrossRef]

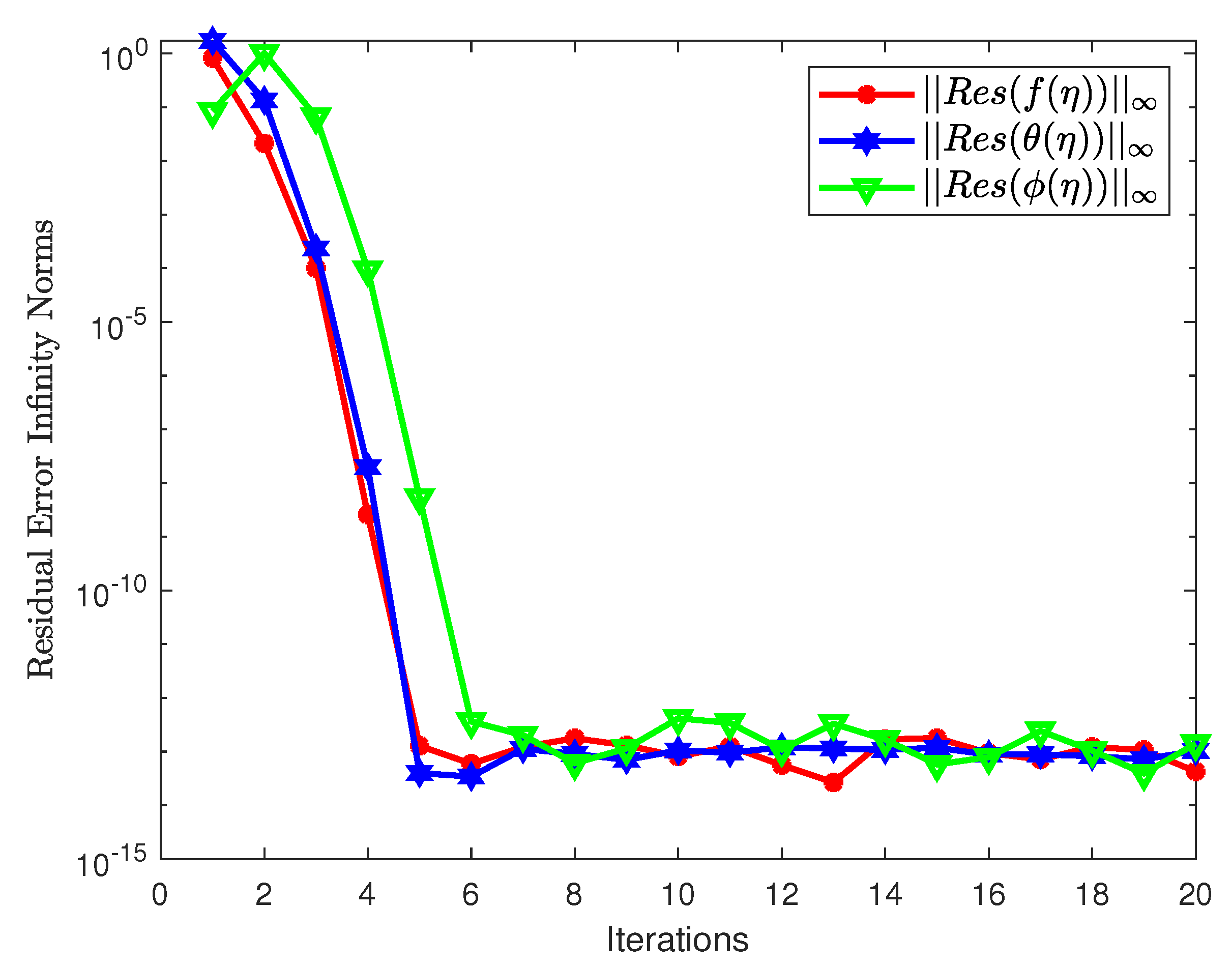
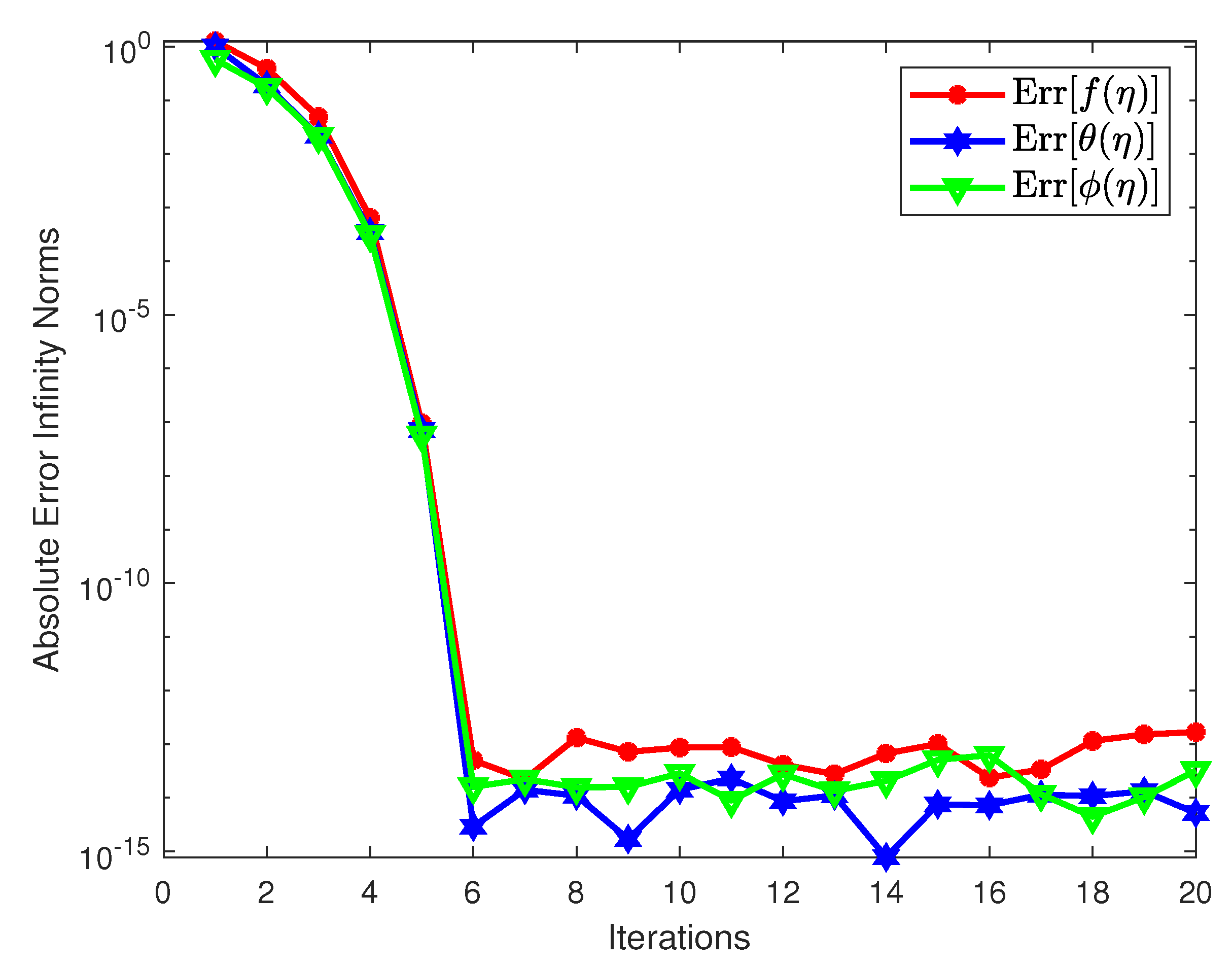



| A | Elbashbeshy and Bzid [36] | Hussain et al. [18] | Present Study |
|---|---|---|---|
| 0.8 | 1.3321 | 1.3333 | 1.331497109737629 |
| 1.2 | 1.4691 | 1.4684 | 1.469781692104270 |
| 2.0 | 1.7087 | 1.7090 | 1.713344535151333 |
| M | S | |||||
|---|---|---|---|---|---|---|
| Ibrahim and Shankar [37] | Matlab Bvp4c | SQLM | Matlab Bvp4c | SQLM | ||
| 0 | 0.5 | 1.2808 | 1.28077620 | 1.28077641 | 0.60136784 | 0.60136784 |
| 0.5 | 1.5000 | 1.50000000 | 1.50000000 | 0.55812915 | 0.55813015 | |
| 1.0 | 1.6861 | 1.68614066 | 1.68614066 | 0.52446025 | 0.52446152 | |
| 1.5 | 1.8508 | 1.85078106 | 1.85078106 | 0.49672490 | 0.49672670 | |
| 2.0 | 2.0000 | 2.00000000 | 2.00000000 | 0.47305633 | 0.47305881 | |
| 1.0 | 0 | 1.4142 | 1.41421356 | 1.41421356 | 0.29167318 | 0.29167374 |
| 0.2 | 1.5177 | 1.51774469 | 1.51774469 | 0.38145187 | 0.38145259 | |
| 0.7 | 1.8069 | 1.80688023 | 1.80688023 | 0.62431224 | 0.62431389 | |
| 1.0 | 2.0000 | 2.00000000 | 2.00000000 | 0.77943236 | 0.77942860 | |
| Ec | Pr | Nb | Nt | Sc | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.71 | 0.1 | 0.3 | 0.3 | 0.6 | 1.0 | 1.516610 | 0.686537 | −0.686537 |
| 0.3 | 1.515505 | 0.574942 | −0.574942 | ||||||
| 0.5 | 1.514401 | 0.463533 | −0.463533 | ||||||
| 1.0 | 1.519931 | 0.819431 | −0.819431 | ||||||
| 2.0 | 1.526872 | 1.171820 | −1.171820 | ||||||
| 3.0 | 1.530777 | 1.439856 | −1.439856 | ||||||
| 1.0 | 1.510498 | 0.479179 | −0.479179 | ||||||
| 1.5 | 1.508763 | 0.426789 | −0.426789 | ||||||
| 2.0 | 1.507540 | 0.391166 | −0.391166 | ||||||
| 0.5 | 1.516226 | 0.686539 | −0.411924 | ||||||
| 0.7 | 1.516061 | 0.686540 | −0.294231 | ||||||
| 0.9 | 1.515969 | 0.686540 | −0.228846 | ||||||
| 0.5 | 1.517497 | 0.695090 | −1.158483 | ||||||
| 0.7 | 1.518385 | 0.703747 | −1.642076 | ||||||
| 0.9 | 1.519272 | 0.712507 | −2.137521 | ||||||
| 0.8 | 1.516506 | 0.688506 | −0.688506 | ||||||
| 1.0 | 1.516438 | 0.690138 | −0.690138 | ||||||
| 1.2 | 1.516391 | 0.691529 | −0.691528 | ||||||
| 2.0 | 1.516512 | 0.690097 | −0.690097 | ||||||
| 3.0 | 1.516449 | 0.692653 | −0.692653 | ||||||
| 4.0 | 1.516405 | 0.694631 | −0.694631 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shateyi, S.; Muzara, H. A Numerical Analysis on the Unsteady Flow of a Thermomagnetic Reactive Maxwell Nanofluid over a Stretching/Shrinking Sheet with Ohmic Dissipation and Brownian Motion. Fluids 2022, 7, 252. https://doi.org/10.3390/fluids7080252
Shateyi S, Muzara H. A Numerical Analysis on the Unsteady Flow of a Thermomagnetic Reactive Maxwell Nanofluid over a Stretching/Shrinking Sheet with Ohmic Dissipation and Brownian Motion. Fluids. 2022; 7(8):252. https://doi.org/10.3390/fluids7080252
Chicago/Turabian StyleShateyi, Stanford, and Hillary Muzara. 2022. "A Numerical Analysis on the Unsteady Flow of a Thermomagnetic Reactive Maxwell Nanofluid over a Stretching/Shrinking Sheet with Ohmic Dissipation and Brownian Motion" Fluids 7, no. 8: 252. https://doi.org/10.3390/fluids7080252






