Dynamical Filtering Highlights the Seasonality of Surface-Balanced Motions at Diurnal Scales in the Eastern Boundary Currents

Abstract

Balanced motions (BM) and internal gravity waves (IGW) account for most of the kinetic energy budget and capture most of the vertical velocity in the ocean. However, estimating the contribution of BM to both issues at time scales of less than a day is a challenge because BM are obscured by IGW. To study the BM regime, we outlined the implementation of a dynamical filter that separates both classes of motion. This study used a high-resolution global simulation to analyze the Eastern Boundary Currents during the winter and summer months. Our results confirm the feasibility of recovering BM dynamics at short time scales, emphasizing the diurnal cycle in winter and its dampening in summer due to local stratification that prevents large vertical excursion of the surface boundary layer. Our filter opens up new possibilities for more accurate estimation of the vertical exchanges of any tracers at any vertical level in the water column. Moreover, it could be a valuable tool for studies focused on wave–turbulence interactions in ocean simulations.

1. Introduction

Eastern Boundary Currents (from now on EBC) have been of interest since they house large areas of net primary production [1]. Since wind runs equatorward alongshore on the EBC, Ekman dynamics transport rich-nutrient water to the mixed layer [2,3], feeding the trophic chain base [4], which explains why a large portion of the world fishery takes place within these regions. On the other hand, internal gravity waves (IGW) account for a higher portion of the total kinetic energy in EBC [5], unlike Western Boundary Currents [5] where balanced motions (BM) do. In addition, low-frequency relaxation of alongshore winds creates an undercurrent that flows poleward, following the continental slope [6].

In the present work, we analyze the four major Eastern Boundary Currents, namely the California, Canary, Peru-Benguela, and Benguela currents, as they can be studied as a whole, at least to a first approximation, and we discard other regions such as the Australian or Indian Eastern boundary currents since their size and geographical features make them not that similar to the four EBC mentioned above [7]. However, most differences can be found by comparing the Benguela current near $26°$ S and Canary current around $28°$ N: whereas bathymetric settings such the Walvis ridge on the former lead to the generation of strong internal waves regardless of the season, the latter experiments a high disturbance that is located near the Canary Island Archipielago, and therefore induces prominent mesoscale phenomena such as multi-scale, energetic eddies [8]. Despite these differences in the large-to-medium scale, the question remains open on which submesoscale characteristics behave similarly across the four current systems.

Balanced motions and internal gravity waves impact the ocean kinetic energy (KE) budget differently [9]. BM mostly experience an inverse KE cascade, with KE fluxing from sources toward larger scales. This cascade helps to sustain mesoscale eddy turbulence [10]. IGW, on the other hand, and in particular, the IGW continuum, experience a direct KE cascade with KE fluxing toward smaller scales, ultimately leading to irreversible mixing [11].

Within the BM regime, submesoscale oceanic currents ($Ro$∼1) play a crucial role in the vertical transport of tracers and heat in the upper ocean [12]. These motions occur predominantly within the mixed layer, where secondary circulations arise from lateral density gradients induced by larger-scale flows. Modeling studies have further emphasized that submesoscale BM can evolve over time scales of shorter than 1 day, contributing to the doubling of the amplitude of vertical heat flux [13]. A critical issue when assessing these fast-evolving submesoscale currents in the presence of an internal gravity field is that BM and IGW share similar temporal and spatial scales. Moreover, each has unique dynamical features [5,13,14,15].

Our motivation for this study was based on two intensive experiments that NASA is carrying out in the California Current System, the S-MODE (Sub-Mesoscale Ocean Dynamics Experiment, https://espo.nasa.gov/s-mode/content/S-MODE accessed on 5 May 2022) and the SWOT Cal/Val experiment (calibration and validation of the Surface and Water Ocean Topography mission) [16], in which in situ and airborne observations are being collected and high-resolution, submesoscale, and tidal resolving ocean numerical simulations are being run. The former experiment is testing the hypothesis that submesoscale-balanced motions (from now on SBM) make essential contributions to the vertical exchange of physical variables in the upper ocean. The latter is dedicated to calibrating and validating SWOT sea surface height (SSH) measurements at a high spatial resolution [16]. In anticipation of these experiments, using numerical simulations, the present study aims to further document the spatial and temporal characteristics of BM and IGW in the Eastern Boundary Currents (EBC).

The aim of this research work is to study the temporal variability of BM in the submesoscale regime (i.e., $Ro$∼1) in the EBC. However, the EBC pose an additional challenge to the analysis of submesoscales, since, compared to other more energetic regions in the ocean, kinetic energy from IGW dominates and tends to obscure other dynamical regimes, particularly in summer when higher stratification enhances the presence of internal waves [17].

There have been attempts to separate BM and IGW. Most recently, Qui et al [18] and Chereskin et al. [19] applied different strategies to find a transition scale in such a way motions smaller than it are labeled as submesoscale, and larger motions are considered on the regime of mesoscale or larger scale. Such approaches are more suitable for cases when only data from instruments with a low temporal resolution (e.g., satellite altimeters) are available. As it turns out, the main drawback of methods that go along the same line is that filtering submesoscale BM with a single horizontal scale will inevitably include internal gravity waves, regardless of the refinement of the considerations to calculate a transition scale. Additionally, there are cases where it is not always possible to determine a transition scale uniquely because, depending on the phenomenon being researched, IGW may be a high source of noise, particularly in regions such as the EBC, where IGW dominate [5,18].

Due to the need to separate BM and IWG more efficiently, we implemented a dynamical filter in the frequency–wavenumber domain based on the tenth baroclinic normal mode IGW dispersion relation and the permissible tides, following Qiu et al. [18]. After successfully separating BM and IGW, we analyzed the temporal variability of the intensity of the vertical vorticity, $\zeta$, and the divergence, $\delta$, fields within the EBC for both the BM and IGW regimes.

The methodology proposed here allowed us to recover BM at short time scales as well as recovering the vital properties of submesoscale BM in terms of intense $\zeta$ and $\delta$. Our findings include a lag between the intensities of the divergence and vorticity fields at around 2 to 3.5 h, in perfect agreement with the transient turbulent thermal wind balance (TTTW) system outlined by [20] for both the summer and winter seasons.

Furthermore, we report, for the first time, the seasonal dependency on these fields’ intensity, which is mainly induced by $KPP$ diagnostics. During the winter time, the diurnal cycle of $\zeta$ and $\delta$ exhibits marked changes between day and night, following the vertical excursion of the surface boundary layer, whereas in summer, the diurnal cycle is almost negligible, emphasizing the impact of the local stratification on the diurnal excursion of the surface boundary layer that modulates the diurnal cycle of $\zeta$ and $\delta$.

Our dynamical filter described here opens up the possibility of separating BM and IGW at any vertical level in the water column and estimating the contribution of deep-reaching submesoscale motions [21] on vertical transport of heat and any tracer. Moreover, it could be a valuable tool for use in studies focused on wave–turbulence interactions in realistic ocean simulations, an active topic nowadays.

2. Data and Methods

In this study, we characterized submesoscale relative vorticity (RV or $\zeta$) and divergence (DIV or $\delta$) fields in $6°\times 6°$ (∼500 km side at mid-latitudes) areas within the four major EBC: California, Peru, Canary, and Benguela currents (as displayed in Figure 1). We examined the time–space (x, y, t) and frequency–wavenumber ($\omega$, k, l) domains for the summer and winter months in 2012. Our starting point was the collection of $\omega -k_h$ ($k_h$ stands for the horizontal wavenumber, i.e., $k_h^2=k^2+l^2$) spectra from Torres et al. [5] to represent surface KE, along with its vortical ($\zeta$) and divergent ($\delta$) parts. As for the spatio-temporal data, we employed the output of a realistic high-resolution ocean simulation (LLC4320) based on the Massachusetts Institute of Technology general circulation model (MITgcm).

2.1. LLC4320

The primary data source is the LLC4320 global ocean simulation output, which uses the MITgcm. LLC4320 is a realistic, high-resolution simulation (24 s steps, $1/48°$ horizontal grid spacing, 90 vertical levels with $\mathcal{O}$ (1 m) resolution for the top 100 m) that spans 14 months from September 2011 to November 2012, for which hourly snapshots are available. The model is forced with 16 tidal constituents and high-frequency atmospheric boundary conditions. The interaction between wind and ocean occurs at the ocean surface, where energy and momentum are exchanged. Roughly speaking, surface wind stress is commonly parameterized as

$${\tau }_s={\rho }_{air}{C}_D\left|U_{wind}-U_{ocean}\right|(U_{wind}-U_{ocean}),$$

(1)

where ${\rho }_{air}$ is the density of the air, $C_D$ is known as the drag coefficient, $U_{wind}$ is the wind speed field, and $U_{ocean}$ is the surface ocean speed [23]. On the other hand, the ocean net heat flux is parameterized as

$$Q_{net}=Q_{rad}+Q_{lat}+Q_{sen},$$

(2)

where $Q_{rad}$, $Q_{lat}$, and $Q_{sen}$ are the radiation, latent, and sensible heat fluxes, respectively [24]. As we will see later in this paper, both wind stress and net heat flux modulate the mesoscale and submesoscale regimes. Therefore, evaluating the impact of atmospheric forcing on our observed variables is crucial.

Since $1/48°$ horizontal spacing is equivalent to ∼2 km at mid-latitudes, numerical diffusion yields an effective resolution of about four times the grid size (∼8 km) [17,25], so LLC4320 allows us to observe and study submesoscale features. In this study, as we aimed to compare the dynamics of EBC during the winter (January, February, March) and summer (August, September, October) months, we used hourly snapshots of LLC4320 for these months to examine the vorticity features of the EBC, resulting in about 2200 snapshots for each variable (e.g., U, V, $\theta$) as well as the season and depth. Data can be accessed by either directly downloading them from the ECCO Data Portal (see: https://data.nas.nasa.gov/ecco/data.php?dir=/eccodata/llc_4320, accessed on 10 November 2021) or by reading them using the xmitgcm Python package (see: https://github.com/MITgcm/xmitgcm, accessed on 3 March 2022).

2.2. Software for Data Processing

After we downloaded all the variables for our study, it was necessary to merge them into data collections that hold the information for each study area and season. Since managing and performing calculations over each of such collection would not be scalable, we used Python package https://www.dask.org/Dask (accessed on 5 May 2022) along with https://xarray.pydata.org/ (accessed on 5 May 2022); the former is a library that facilitates the creation of parallel calculations, with array functions similar to what https://numpy.org/ (accessed on 5 May 2022) offers, while the latter takes Dask variables and gathers them into data structures that are netCDF-friendly, while taking advantage of its lazy evalation scheme (i.e., it only reads data when it is required). In short, our workflow is as follows:

1.

Download hourly snapshots for each variable, area and season.

2.

Combine hourly data into time series for each variable and season, and the merge all variables into a single dataset per season and area.

3.

Calculate dynamical filter in 3D $\omega -k_h$ spectral space.

4.

Apply dynamical filter to each variable of interest, namely horizontal components of the ocean surface speed, from which one will obtain the low-pass (balanced motions) and high-pass (internal gravity waves) components.

5.

Compute derived quantities (i.e.,$\zeta$ and $\delta$) for further analyses.

In addition to this succinct summary, specific implementation details have been already shared in our sample Jupyter notebook (https://github.com/antonimmo/ebc-wk-spectral-analysis/blob/master/wk_3dfilter_.ipynb, accessed on 5 May 2022) [26].

2.3. $\omega -k_h$ Spectrum

For a given variable $\varphi \left(x,y,t\right)$ (e.g., kinetic energy, sea surface height), season (summer or winter), area (tiles in Figure 1), or vertical level, by performing a Fast Fourier Transform, we obtained the 3D spectral density in the wavenumber ($k,l$) and frequency ($\omega$) domains, $\mathrm{\Phi }\left(k,l,\omega \right)$. A close examination of $\mathrm{\Phi }\left(k,l,\omega \right)$ on the k–l plane confirmed that they are mostly azimuthally symmetric for all frequencies, so we were able to map the k–l plane into a horizontal wavenumber $k_h$; hence, the azimuthally averaged spectrum $\mathrm{\Phi }\left(k_h,\omega \right)$ was produced. An example of such isotropic 2D spectra in the $\omega -k_h$ space is shown in Figure 2, and the temporal and spatial reference scales are also displayed. An estimation of the average local buoyancy frequency N was used to calculate the dispersion relation curves corresponding to the first four and the tenth vertical modes of the IGW. The dispersion relation of IGW is:

$${\omega }_n^2\left(k_h\right)=\frac{N^2+f^2{\left(n\pi /k_{h}H\right)}^2}{1+{\left(n\pi /k_{h}H\right)}^2},$$

(3)

where H is the average depth at the area being studied, $k_h$ is the horizontal wavenumber, and n ($n=1,2,3\cdots$) is the IGW mode.

2.4. Temporal Variability of the Vorticity and Divergence Fields

In this work, we analyzed the rotational, $\zeta$, and divergent, $\delta$, components of horizontal motions, with $\zeta$ and $\delta$ being defined as $\zeta =v_x-u_y$, $\delta =u_x+v_y$, where u and v are the horizontal velocity components in Cartesian coordinates x and y. The relative vorticity $\zeta$ is related to the spin of horizontal motions, and the horizontal divergence $\delta$ is related to the vertical derivative of the vertical velocity via the 3D incompressibilty condition. Both $\zeta$ and $\delta$ are normalized by f, which corresponds to the local inertial period. We describe the analysis of the fields of $\zeta /f$ and $\delta /f$ in the following sections. Since both divergence ($\delta$) and vorticity ($\zeta$) have a spatial mean of almost zero in the ocean [27], the standard deviation of these quantities (S can be either $\zeta$ or $\delta$) $\sigma \left[S\right]\left(t\right)$ can be approximated by

$$\sigma \left[S\right]\left(t\right)\simeq \sqrt{\frac{1}{NM}{\displaystyle \sum _{n=0,m=0}^{N,M}}{\left(S_{n,m}\left(t\right)\right)}^2}=RMS\left[S\right]\left(t\right),$$

(4)

thus serving as a measure of the instantaneous average intensity of these fields. If one calculates the standard deviation of these variables for each hourly snapshot, a time series that shows the evolution of such fields’ intensity can be obtained.

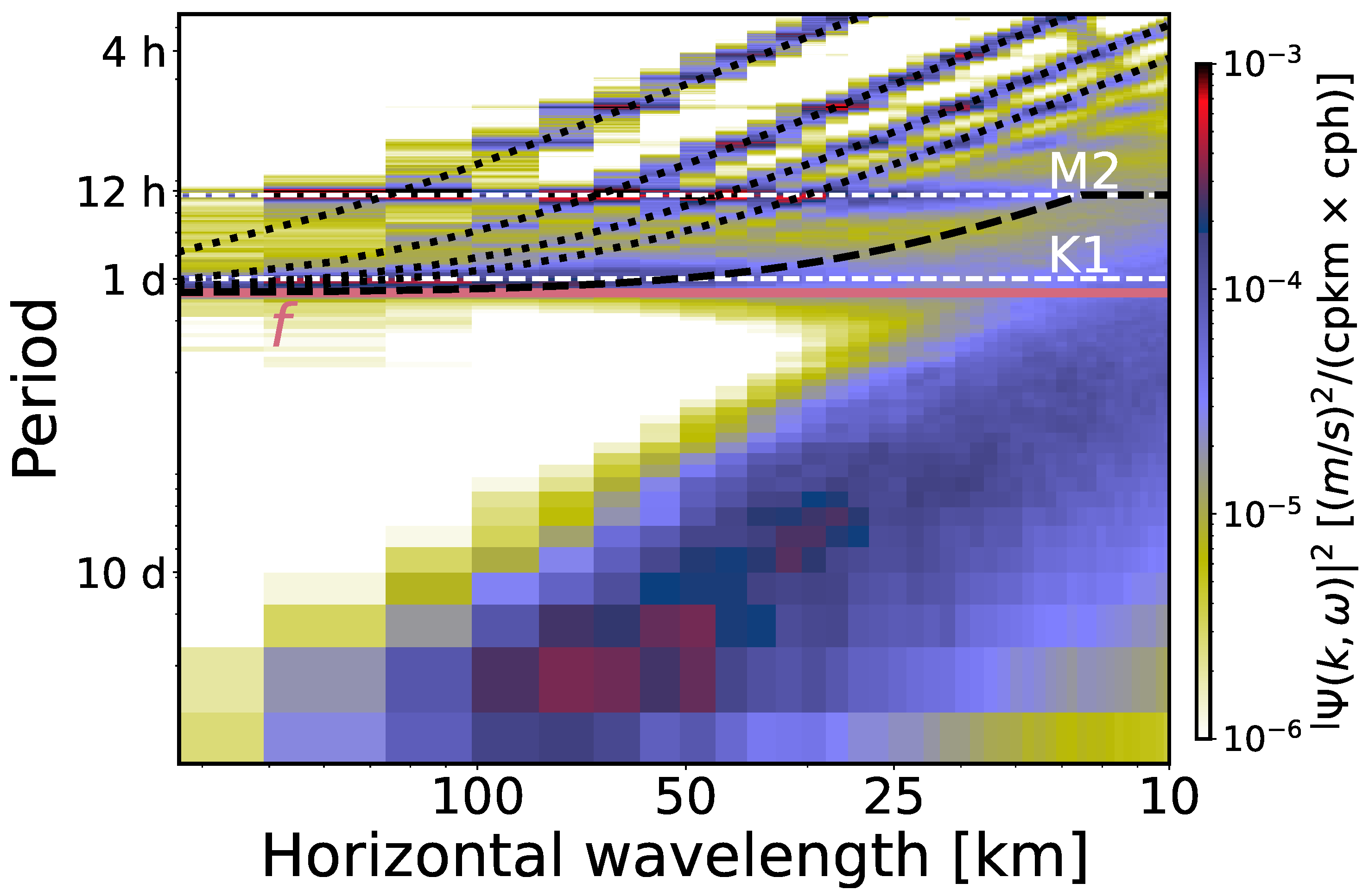
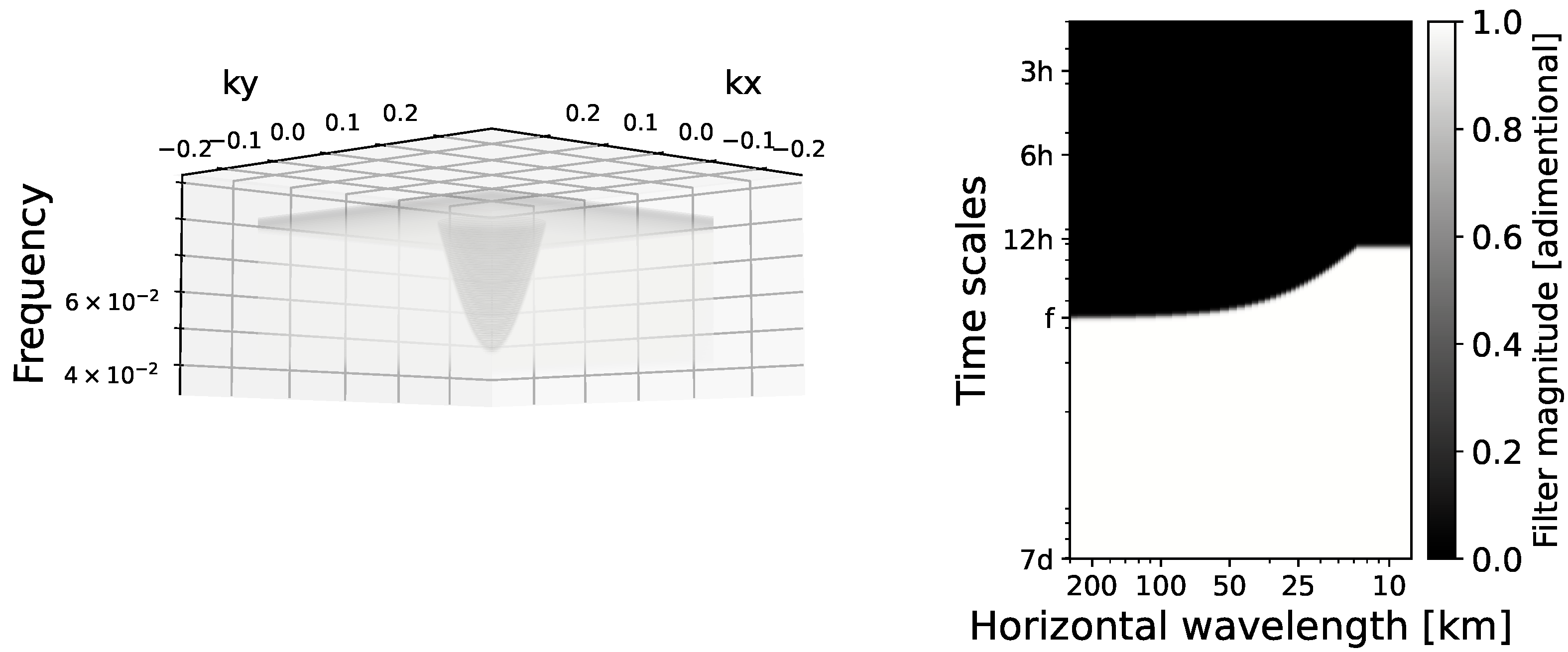
2.5. A Dynamical Filter to Discriminate BM from IGW

Chereskin et al. [19] reported a significant contribution of IGW to $\zeta$ and $\delta$ in the California Current System, and Torres et al. [5] reported IGW dominance in the EBC, where both studies were based on an LLC4320 simulation. In order to filter out IGW, we made use of a dynamical filter based on the dispersion relation of IGW in the frequency–wavenumber ($\omega -k_h$) space. The main feature of this filter is that it does not have a fixed cutoff frequency or horizontal wavenumber, $k_h$, but we designed it to filter as many internal waves and tides as possible. We achieved this by using a function in the $\omega -k_h$ spectral space to obtain a cutoff frequency for each $k_h$, ${\omega }_{cutoff}\left(k_h\right)$.

Our candidate function was the dispersion relation for the tenth vertical normal mode given by Equation (3) (i.e., ${\omega }_{10}$). Qiu et al. [18] and Torres et al. [5] used this tenth vertical normal to quantify the relative contributions of IGW and BM to the kinetic energy. As we can see in Figure 2, this criterion does not manage to filter out semidiurnal or diurnal tides at scales below 30 km. Hence, we included an additional constraint to discard them by considering the dominant tidal band below the ${\omega }_{10}$ (see Equation (3)) dispersion curve (M₂ in the cases we examined). The resulting filter is a function in the $\omega -k_h$ spectral space that obtains a cutoff frequency that depends on $k_h$ in the form

$${\omega }_{cutoff}\left(k_h\right)=min\left[{\omega }_{10},{\omega }_{tide}\left(k_h\right)\right],$$

(5)

where ${\omega }_{tide}$ corresponds to the frequency of the additional tidal band that needs to be discarded. The dispersion relation curve modified to discriminate BM from IGW (including M₂ tides in this example) is represented by the black dashed line in Figure 2.

BM and IGW are known to be present in a wide and similar range of horizontal scales, whereas IGW are, in general, faster than BM. Large BM are, in general, slow and can mostly be described by geostrophic dynamics, such as eddies. However, near the submesoscale ($Ro$∼1) regime, we found submesoscale BM (SMB) with horizontal scales of up to a couple of dozen kilometers, frequencies near the local Coriolis parameter, and enclosed motions, such as fronts, gradient wind (cyclostrophic) balance, and filaments. Since SBM tend to have frequencies and scales similar to the IGW domain, we needed to set a sensible threshold to allow us to study most SBM without interference from tides or higher IGW modes. This is the reason behind all choices made thus far in the design of the dynamical filter.

Figure 3 better illustrates how the filter separates IGW and tides from BM in the spectral space. The actual filtering should be performed in the three-dimensional spectral space (k, l, $\omega$) (Figure 3, left panel), which allows the inverse FFT to be applied to the filtered signal and then go back to the physical (x, y, t) space. Therefore, BM (IGW) are found below (above) the dispersion relation curve (Figure 3, right panel) or outside (inside) the cone shape (Figure 3, left panel).

Coherence and Phase Difference between Average Intensities of Divergence and Vorticity

Close inspection of both time series shows a temporal phase shift between them for the diurnal frequency component. As this shift might not be evident for time series with several frequency components, we calculated the cross power spectral density $P_{\zeta \delta }\left(\omega \right)$ [22], from which we obtained phase differences between both signals as a function of frequency. A positive shift implies that $\delta$ precedes $\zeta$, and the converse is true when the shift is negative. We then used Welch’s method to obtain the spectral coherence between $\delta$ and $\zeta$, $C_{\zeta \delta }\left(\omega \right)$ in the form

$$C_{\zeta \delta }\left(\omega \right)=\frac{{\left|P_{\zeta \delta }\left(\omega \right)\right|}^2}{P_{\zeta \zeta }\left(\omega \right)P_{\delta \delta }\left(\omega \right)},$$

(6)

where $P_{AB}\left(\omega \right)=\left|P_{AB}\left(\omega \right)\right|e^{i\theta \left(\omega \right)}$ is the cross spectral density between variables A and B. Spectral coherence is the frequency-domain analogue of the correlation coefficient [28], so values near 1 indicate a high correlation at a given frequency or, in other terms, such frequencies have major contributions to the total covariance. This methodology allowed us to confirm that diurnal divergence drives submesoscale vorticity in winter, but this result does not hold in summer.

3. Results

This section presents most of our results and provides comparisons between areas centered at the same latitude whenever possible. We compared areas at 26.64° (north or south) for the California, Canary, and Benguela currents and at 21.61 °S for the Peru current. Our results and conclusions were proved to be valid for all areas and seasons, except when we state otherwise.

3.1. Comparing $\zeta$ and $\delta$ at Seasonal and Diurnal Time Frames

Snapshots of vorticity and divergence in summer and winter are presented in Figure 4 as the first comparison between these two seasons. In winter, elongated positive and negative filaments with magnitudes of order 1 for $\zeta /f$ and $0.5$ for $\delta /f$ dominated the vorticity and divergence fields, respectively. Additionally, small-scale cyclonic eddies were all over the space, reaching magnitudes of order 1 for $\zeta /f$. On the other hand, internal gravity waves overshadowed balanced motions in the $\delta$ map in the summer season, whereas submesoscale BM features were weak but observable in the $\zeta$ map, compared to their winter counterpart.

To compare the diurnal variations in $\delta$ and $\zeta$, maps of vorticity and divergence can be visualized in Figure 5, which shows snapshots at times during the same day that are near the maximum and minimum $\delta$ and $\zeta$ values. In most cases, in all EBC, the maximum divergence occurred at around 5:00 p.m. local time (end of daytime), and the minimum divergence occurred at around 5:00 a.m. local time (end of night-time), with the only differences being the intensity of these fields and the exact time at which their minima and maxima occurred. Submesoscale structures strongly emerged during the afternoon with positive skewness for vorticity ($Ro>1$) and negative skewness for divergence. As revealed by comparing the 5:00 a.m. and 5:00 p.m. PDFs side by side, the skewness indicates that frontogenesis was more significant during the afternoon than late at night. This implies a change in the kinetic energy transfer, since small-scale motions intensified during the night.

Another point of dynamical comparison was the $\zeta -\delta$ joint probability distribution of both the divergence and vorticity fields for each season and area. Figure 4 and Figure 5, in addition to the comparison in the physical space, display their corresponding joint probability distribution functions (joint PDFs, or JPDFs). Each of these instantaneous JPDFs shows how one can translate dynamical differences in physical space into a JPDF that allows such differences to be described. Additionally, each of these four quadrants corresponds to different motion regimes. In particular, the higher probability densities found in the fourth quadrant (positive $\zeta$, negative $\delta$) and Rossby numbers $\zeta /f$ close to an order of 1 give us evidence of intense frontal activity, which is directly associated with submesoscale instabilities, such as fronts or filaments.

3.2. Rotational-Divergent Ratio in the Frequency–Wavenumber Space

We also calculated the corresponding $\omega -k_h$ kinetic energy spectral densities $K{E}_{\zeta }={\left|\widehat{\zeta }\right|}^2/k_h^2$ and $K{E}_{\delta }={\left|\widehat{\delta }\right|}^2/k_h^2$, where $\widehat{\zeta }$ and $\widehat{\delta }$ denote the Fourier transform of the relative vorticity and divergence fields. Figure 6 shows how the quotient of spectral densities $K{E}_{\zeta }/K{E}_{\delta }$ varies by current and season, making it evident that vorticity fields dominate over a broader range of frequencies in winter than they do in summer.

By inspecting Figure 6, we determined which temporal and spatial scales are dominant in each regime from these spectra. During summer, at periods of one day, both divergence and vorticity have roughly the same kinetic energy, where the ratio $K{E}_{\zeta }/K{E}_{\delta }\approx 1$. The kinetic energy for motions with periods longer than one day can be explained, mainly, by the divergent component (IGW); hence, in this case, $K{E}_{\zeta }/K{E}_{\delta }>>1$ (brown color). For motions with periods longer than one day, the vorticity component explains most of the variance (green color). During winter, the vorticity component tends to extend towards periods shorter than one day, particularly motions with horizontal wavelengths smaller than ∼50 km. This is consistent with our findings in Section 3.1, where Figure 4 provides evidence of which field dominates during each season.

From these spectra, one can argue that a temporal filter with a cut-off period of 1 day (or, in a more general case, the inertial period) is sufficient to discriminate BM from IGW. This procedure might work in summer, but not in winter due to the presence of submesoscale BM with periods of shorter than 1 day. It is precisely in winter that the scientific community has focused its efforts to discriminate both classes of motion. On the other hand, the implementation of a filter in the horizontal wavenumber space would rely on the definition of a transition scale (see, e.g., [18]), which cannot always be uniquely determined by area of study and season and also poses the challenge of choosing a dynamical criterion that suits all cases and does not depend on measurements of KE in the spectral space (which are, by themselves, sensitive to the selected timeframe or method). Here, we present a dynamical filter that intends to achieve such BM–IGW separation, whose performance is assessed in the next section.

3.3. Separating IGW and BM

The findings for the ratio of rotational to divergent components in the preceding section show that IGW and BM share the same small horizontal wavelengths and time scales as submesoscale BM, making their separation by applying a temporal or spatial filter difficult. In Section 2.4, we propose a dynamical filter that takes advantage of the dispersion relation of the tenth vertical normal mode limited to its maximum frequency at M₂ (1/12.42 h) (Figure 3). The fields presented before applying the filter are hereinafter referred to as unfiltered fields. After applying the filter, we follow the convention described in Section 2.4: BM (IGW) for motions below (above) the dispersion relation of the aforementioned vertical normal mode.

Figure 7 serves as a visual evaluation of how the dynamical filter works. The first row shows both $\zeta$ and $\delta$ unfiltered fields for a snapshot in summer, whereas the second and third rows showcase the ($\zeta$, $\delta$)-BM and ($\zeta$, $\delta$)-IGW components, respectively. By inspecting the unfiltered fields, it is noticeable that, on one hand, $\zeta$ partially filters out IGW. Blurry elongated cyclonic filaments can be identified visually. However, eddy-like structures are unclear. Torres et al. [5] and Torres et al. [15] reported that the signature of internal tides and their subharmonics is non-negligible. On the other hand, the impact of IGW is overwhelming in the unfiltered $\delta$ field. The typical dipole associated with elongated filaments [29] is visually undetectable. The IGW dominance over BM is well known during the summer season [18,30]: $\delta /f$ is characterized by having higher values than $\zeta /f$. This description is emphasized in the joint PDF (JPDF) by following a vertical distribution, with $\delta /f$ values from −1 to 1, whereas $\zeta /f$ is limited from −0.5 to 0.5.

This scenario changes after applying the dynamical filter. The second and third columns of Figure 7 demonstrate that the filter manages to separate BM and IGW regimes and preserve their respective relevant dynamical features in the $\zeta$-BM and $\delta$-BM fields, such as mesoscale cyclonic and anticyclonic eddies and elongated fronts and filaments, with their respective dipoles in $\delta$-BM. Additionally, the JPDF is slightly yet noticeably skewed towards the fourth quadrant, following a diagonal distribution. It is also noteworthy that the separation of BM is not sensitive to the intensity of the IGW component once the maximum cutoff frequency of the filter has been defined. As shown in Figure 8, the JPDF of the four EBC areas for the whole summer and winter seasons matches the distribution in Figure 7, regardless of the intensity of the IGW field. As expected, we found a stronger vorticity field in winter (yielding a diagonal distribution in the JPDF), whereas divergence (primarily associated with IGW) was more dominant in summer (yielding a vertical the distribution in the JPDF). Particularly in winter, the filter allows the leakage of information from the BM to the IGW component, as revealed by the gentile diagonal component in the JPDF of IGW (fourth column in Figure 8). This is explained by submesoscale motions with frequencies higher than the M₂ internal tides, since the dispersion relation used is limited at M₂. However, the JPDF associated with this leakage in the IGW component is three orders of magnitude smaller than the JPDF of BM.

3.4. Seasonal and Diurnal Variability of BM and IGW

We now examine the evolution of the RMS values of both $\zeta$ and $\delta$, as per Equation (4), for the BM and IGW regimes. These calculations are plotted along with the corresponding surface sea temperature (SST), surface net heat flux, magnitude of wind stress, and depth of the KPP boundary layer depth ($KP{P}_{hbl}$), since atmospheric forcing is known to impact the frontal dynamics through the vertical viscosity [31,32]. We show the findings for the Canary (Figure 9) and Benguela (Figure 10) currents, considering that these two currents have less common features, especially in winter. Canary has high temperature (and density) gradients and is located near a source of energetic eddies that are ejected towards the West Atlantic. The Benguela current around $26.64°$ S, on the other hand, has a weaker vorticity field and is mostly dominated by internal tides generated over topographic features at the Walvis Ridge.

The time series of RMS values of BM-$\zeta /f$ and BM-$\delta /f$ exhibits intermittency at daily to weekly time scales as well as strong seasonality (third and fourth panels in Figure 9 and Figure 10). In addition to the well-known seasonal variability in the $KP{P}_{hbl}$ (deeper in winter and shallower in summer), high-frequency variability can be detected in Figure 9 and Figure 10 (top panels red line). Simultaneously, $KP{P}_{hbl}$ displays a strong phase relationship with the ocean net heat flux (red line in the second row). The daily vertical excursion of $KP{P}_{hbl}$ in winter can be around ∼100 m, while in summer, this excursion gets weaker since the stratification increases during this season. The intensity of the $\delta$ and $\zeta$ fields in the BM regime follows the seasonal and diurnal variability of $KP{P}_{hbl}$. During winter, when $KP{P}_{hbl}$ reaches its maximum depth (around 250 m in the Canary Current and 150 m in the Benguela Current), the overall RMS values of $\zeta$ and $\delta$ increase and the high-frequency variability is intense, such that the RMS values of both BM-$\delta$ and BM-$\zeta$ increase and decrease drastically at diurnal time scales. From early spring to late summer, the diurnal pattern weakens (even vanishes), as revealed by a reduction in the amplitude of the diurnal variability (see panel g and the final part of panel h in Figure 9 and Figure 10). This dampening of the diurnal cycle follows the shallowness of $KP{P}_{hbl}$. The diurnal excursion of $KP{P}_{hbl}$ in summer is from 5 m to ∼50 m.

Regarding the IGW-$\zeta$ and IGW-$\delta$ time series, it is remarkable that the diurnal cycle is negligible, in both summer and winter. However, we should remark that dynamical filter is not $100\mathsf{\%}$ accurate. A comparison of panels f and h in both Figure 9 and Figure 10 indicated that there is leakage of high frequency BM onto the IGW component, which is more noticeable during the winter when the RMS values of BM-$\zeta$ (pink lines) are large. This is consistent with the IGW-$\zeta -\delta$ JPDFs in Figure 8, which shows a slight tendency towards the BM regime (fourth quadrant: positive $\zeta$ and negative $\delta$) near $Ro$∼1, although their JPDFs are three orders of magnitude smaller than those of their BM counterpart.

Figure 9 and Figure 10 illustrate the synchronization of the RMS values of BM-$\zeta$ and BM-$\delta$ with $KP{P}_{hbl}$ and the ocean net heat flux. Garrett and Loder [31] described that vertical viscosity forces are an effective divergent flow, ${\delta }_{\kappa }$ that further stimulates frontogenesis. A simple scaling analysis was conducted, following [31] and assuming that the vertical viscosity $\kappa$ was constant in space, which led to

$${\delta }_{\kappa }\approx \frac{\kappa }{f}{\zeta }_{zz}\approx \frac{\kappa }{f^2}\mathrm{\Delta }{b}_{zz}$$

(7)

with $\mathrm{\Delta }$ representing the horizontal Laplacian operator and b representing the buoyancy. This equation means that, through the modulation of the vertical viscosity, the wind intermittency and the diurnal cycle of surface heat fluxes impact the divergence and relative vorticity of BM. In our case, we did not have access to $\kappa$, but we show the time series of $KP{P}_{hbl}$, which was directly estimated from the vertical viscosity coefficient $\kappa$ under the KPP parameterization scheme [33]. One can infer that, when the net heat flux is maximal during the day, $\kappa$ is small because of heating (oceQnet < 0); therefore, $KP{P}_{hbl}$ is shallow, and $\zeta$ and $\delta$ increase. On the contrary, $\kappa$ increases during the night because of cooling (oceQnet > 0); therefore, $KP{P}_{hbl}$ is deeper, and $\zeta$ and $\delta$ decrease. This diurnal variation modifies the frontogenetic tendency. Torres et al. [15] reported that the frontogenesis tendency [34] exhibits a clear relationship with the net heat flux, with frontogenesis emphasized during the day and frontolysis emphasized during the night.

The time series of $\zeta$ and $\delta$ emphasizes the efficiency of the dynamical filter for separating BM and IGW and its ability to recover the BM dynamics on short time scales. Furthermore, the filtering highlights the seasonal variability of the diurnal cycle and its dependence on the seasonality of $KP{P}_{hbl}$. In the next section, we focus on the diurnal cycle of the filtered fields and its latitudinal dependence.

3.5. Diurnal Lag between Divergence and Vorticity

In addition to the seasonal differences in the diurnal cycle that were discussed in Section 3.4, we found a time lag between the $\delta$ and $\zeta$ instantaneous intensities in the BM regime. This lag became instantly noticeable in the BM regime by closely inspecting the time series of vorticity and divergence for arbitrary 8-day periods, as per Figure 11h. This pattern was observed for all EBC time series at diurnal scales, particularly in winter. In Figure 11, $\delta$ peaks first at around midday and $\zeta$ peaks later with a lag of ∼3 h. This behavior is consistent with previous studies based on numerical simulations with a higher horizontal resolution [15,20,32].

To provide a more quantitative perspective,

Table 1. Phase difference $\mathrm{\Delta }t$ (in hours) between normalized divergence $\left(\delta \right)$ and vorticity $\left(\zeta \right)$ by current, center (latitude, longitude), and season for each quadrangular area examined. The phase difference is the angle of the complex power spectral density, calculated with a 10-day window using Welch’s method [22]. All phase differences correspond to the diurnal (24 h) component. Positive values indicate that divergence occurs first and is then followed by the relative vorticity. Rows in bold mark the study areas compared in this paper. Values with an asterisk (*) correspond to cases when the coherence did not pass the F-test for the $90\mathsf{\%}$ confidence interval.

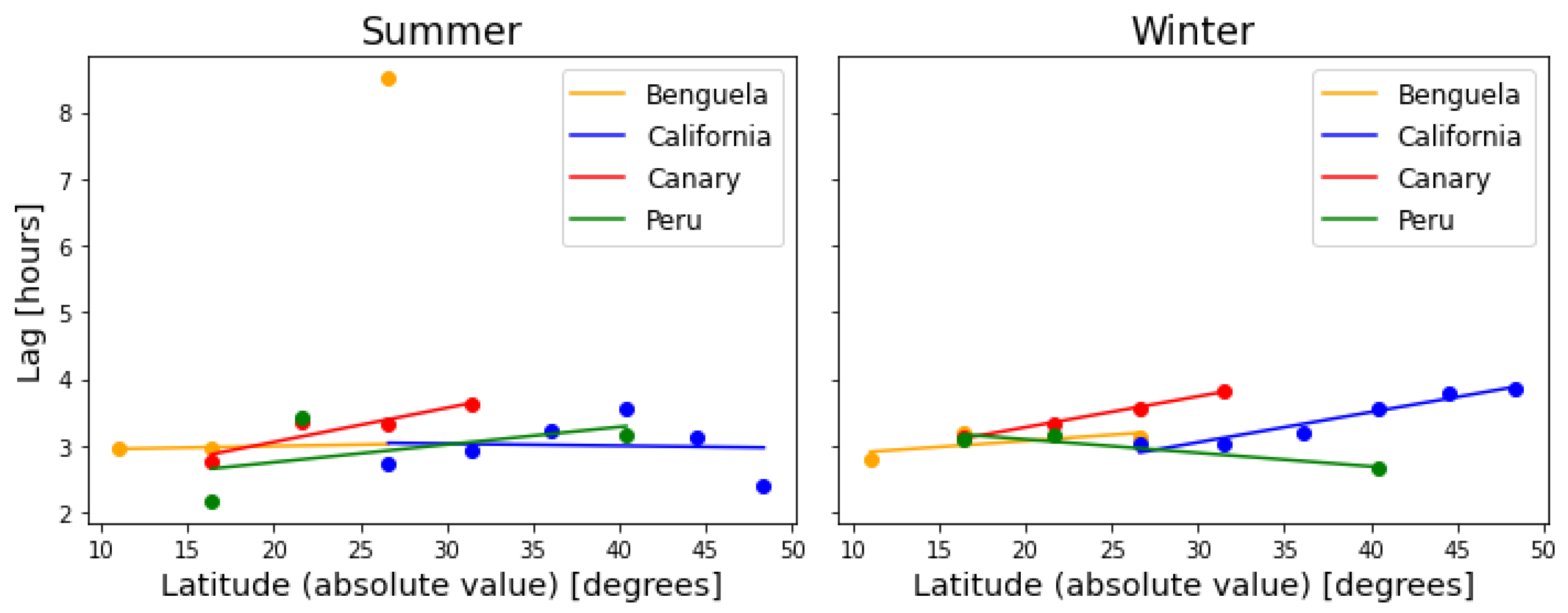
			Summer		Winter
Current	Latitude	Longitude	$\mathsf{\Delta }\mathit{t}$ [h]	${\mathit{C}}_{\mathit{\zeta }\mathit{\delta }}$	$\mathsf{\Delta }\mathit{t}$ [h]	${\mathit{C}}_{\mathit{\zeta }\mathit{\delta }}$
California	48.4° N	137° W	2.41	0.6	3.86	0.97
California	44.5° N	131° W	3.14	0.88	3.81	0.97
California	40.4° N	131° W	3.57	0.88	3.55	0.95
California	36.05° N	131° W	3.22	0.93	3.21	0.97
California	31.46° N	125° W	2.95	0.95	3.02	0.97
California	26.64° N	125° W	2.75	0.99	3.02	0.99
Canary	31.46° N	23° W	3.61	0.95	3.83	0.99
Canary	26.64° N	23° W	3.33	0.96	3.57	0.99
Canary	21.61° N	23° W	3.35	0.98	3.33	0.99
Canary	16.40° N	29° W	2.75	0.97	3.13	0.99
Peru	16.39° S	83° W	2.16	0.67	3.09	0.99
Peru	21.61° S	77° W	3.42	0.65	3.17	0.99
Peru	40.41° S	83° W	3.15	0.94	2.66	0.97
Benguela	11.03° S	7° E	2.96	0.76	2.79	0.99
Benguela	16.39° S	7° E	2.98	0.63	3.19	0.99
Benguela	26.64° S	7° E	8.5	0.19 *	3.13	0.99

shows the phase separation and coherence between $\zeta$ and $\delta$ calculated by season and area for the diurnal component. The first thing noted is that the coherence between $\delta$ and $\zeta$ is consistently high in winter with values above $0.95$ in all cases, while phase separation shows a trend towards larger values (around 3.5 h) as we approach high latitudes and lower values (around 2.5 h) as we get closer to the tropics. In summer, the picture is not that different, although the trend in the $\zeta -\delta$ lag is not as evident as in winter, along with the fact that coherence is considerably smaller in certain study areas, particularly in northern California and southern Benguela.

A complement to Table 1 is Figure 12, which illustrates the trend that the $\zeta -\delta$ lag follows as a function of latitude in the winter and summer seasons. These delays match what Dauhajre and McWilliams [20] found using their transient turbulent thermal wind balance (TTTW) model, which takes into consideration the difference between the maximum (${\kappa }_{max}$) and minimum (${\kappa }_{min}$) RMS values of the vertical viscosity ($\mathrm{\Delta }K={\kappa }_{max}-{\kappa }_{min}$), the period in which this varies ($T_{\kappa }$), and the mixed layer depth (H), described in its 1D formulation by a system of nondimensional equations:

$${\left(\begin{array}{c}u\\ v\end{array}\right)}_t+\mathrm{\Omega }\left(\begin{array}{c}-v\\ u\end{array}\right)-\mathrm{\Gamma }\left[\mathcal{K}\left(t\right)+k\right]{\left(\begin{array}{c}u\\ v\end{array}\right)}_{zz}=\mathcal{K}\left(t\right)\left(1-\mathrm{\Gamma }\right)\left(\begin{array}{c}\overline{u}\\ \overline{v}\end{array}\right),$$

(8)

where subscripts indicate partial derivatives, $\overline{\mathbf{u}}=\left(\overline{u},\overline{v}\right)$ is the steady solution, $\mathrm{\Omega }=T_{\kappa }{f}_0$, $\mathcal{K}\left(t\right)=cos\left(2\pi t/T_{\kappa }\right)$, $k=2K_0/\mathrm{\Delta }K$, and $\mathrm{\Omega }=T_{\kappa }\mathrm{\Delta }K/2H^2$, where $\mathrm{\Gamma }$ represents the ratio of the inertial frequency $f_o$ to the diurnal period, and $\mathrm{\Gamma }$ represents the ratio of the range of mixed time scales ($\mathrm{\Delta }K/2H^2$) relative to the diurnal period. These 1D Ekman layer dynamics are strongly determined by atmospheric forcings as well as by their impacts on the amplitude ($\mathrm{\Delta }K$) and frequency (or period $T_{\kappa }$) of the variability of the vertical viscosity. Equation (8) expresses that the amplitude and phase separation between $\zeta$ and $\delta$ are primarily controlled by inertial ($\mathrm{\Omega }$) and diffusive ($\mathrm{\Gamma }$) mechanisms. If the phase separation is zero, the diffusive mechanism is the main driver ($\delta$ and $\zeta$ evolve in phase with each other). As long as the phase separation is nonzero, there is competition between both mechanisms. Additionally, if the difference between ${\kappa }_{min}$ and ${\kappa }_{max}$ tends to zero, the amplitude of the diurnal cycle tends to zero as well. The above-mentioned scenario applies when the wind stress is weak and the surface net heat flux is the main atmospheric forcing. Table 1 indicates that both mechanisms play crucial roles in dictating the diurnal cycle. The variation between high latitudes and the lower latitude is about 1 h, indicating that the diffusive mechanism becomes slightly more relevant. In summer, the diurnal excursion of $KP{P}_{hbl}$ is not as dramatic as in winter. This indicates that the difference between ${\kappa }_{min}$ and ${\kappa }_{max}$ is small compared to in the winter season. This explains the weak signal of the diurnal cycle in $\zeta$ and $\delta$ for the summer season.

4. Discussion

BM and IGW are the two main classes of oceanic motion, since they encompass most of the different phenomena observed there and, consequently, account for most of the kinetic energy [9]. Although different in nature, there have been found to be interactions between these two dynamical regimes, so the interest in studying and understanding BM and IGW has increased in recent years [5,9,18,19].

BM explains most of the advective horizontal and vertical transport of heat and any tracers in the ocean [9,35]. However, diagnosing such transport in the presence of IGW requires, first, the partitioning of both classes of motion. Using low-pass temporal filters to remove IGW contributions also removes the high-frequency part of frontal dynamics [36]. A spatial filter that removes large horizontal scales results in incomplete removal of IGW (see supporting information in Torres et al. [15]). The challenge is that IGW and submesoscale BM share the same short time scale and small horizontal scale ranges. The application of dynamical filters is an alternative to accurately partition BM and IGW. In this research, we aimed to make improvements in two areas: (a) isolating IGW from BM regimes and (b) studying them separately within the four major EBC.

The dynamical filter presented in this study relies on the dispersion relation of IGW of the local tenth baroclinic normal mode. Qiu et al. [18] and Torres et al. [5] applied this approach in the spectral space. However, they did not recover BM in the physical space. Here, we tested the performance of this dynamical filter by recovering BM and IGW in the physical space in four EBC, where IGW showed a kinetic energy level close to the submesoscale BM [5,18,30]. Preliminary analyses (not shown) demonstrated that the correct way to use the dispersion relation of the tenth baroclinic is to combine it with the permissible tide as a cut-off wavenumber-dependent frequency [18].

Recently, Torres et al. [15] developed a simple approach to separate small-scale frontal dynamics from energetic internal gravity waves. Their method relies on two assumptions: IGW are mostly captured by low baroclinic normal modes and, therefore, by vertical scales larger than the mixed-layer depth. Second, small-scale frontal dynamics are trapped within the mixed-layer depth and, therefore, are explained by smaller vertical scales. The disadvantage of the method described by Torres et al (2022) is that BM and IGW cannot be separated below the mixed-layer depth. The method proposed here circumvents this constraint by relying on the local dispersion relation of IGW. The workflow used to apply our method to the ocean numerical simulation was as follows: (1) compute the frequency–wavenumber spectrum of KE; (2) compute the n-th local baroclinic normal modes as long as the spacing interval allows it; (3) identify the dispersion relation of the n-th baroclinic mode that best separates IGW and B; (4) use this dispersion relation as a criterion to separate BM and IGW in the Fourier space (3D spectral space (k, l, $\omega$)), and (5) compute the inverse Fourier transform to get back to the physical space (x, y, t). This workflow can be applied at any vertical level in the water column and to any component of the speed vector and tracer. Calculations over the filtered variables can be performed, always considering that there will be some noise as the complexity of such calculations grows, since handling slightly unevenly spaced, discrete, windowed data leads to some sort of spectral leakage.

The BM and IGW separation during winter poses a challenge due to the small-scale motions with frequencies larger than M₂ internal tides. In this paper, we used the model output of the LLC4320 simulation with a nominal horizontal resolution of ∼2 km ($1/48°$). Our method mitigates the leakage of information from BM to IGW during winter. Nevertheless, the horizontal and vertical resolutions of the LLC4320 prevent the proliferation of small-scale motions with frequencies larger than M₂ internal tides. Nelson et al. [37] demonstrated the strengthening of the kinetic energy frequency spectrum at frequencies greater than M₂ internal tides when the horizontal and vertical resolutions increase. However, this scenario needs to be tested by analyzing the Joint-PDF of $\zeta$ and $\delta$, as we did in this study.

Recovering high-frequency (>f) submesoscale motions in the presence of IGW is a critical issue for diagnosing vertical heat transport in the ocean. Su et al. [13] and Siegelman et al. [21] reported the impact of high-frequency motions on vertical heat fluxes using LLC4320, and Richards et al. [38] reported the impact using ROMS simulations, further confirming the contribution of such high-frequency motions as a doubling of the amplitude of the vertical heat flux when compared with low-frequency estimates (<1/36-h). The performance of our dynamical filter when recovering BM at short time scales was tested in four EBC and in two seasons. The Joint-PDF of $\zeta$-$\delta$ in the BM regime revealed $\zeta /f$ values close to or larger than one during winter, which reflects the presence of ageostrophic motions [39]. The time series of the same variables displays diurnal variability, which is a distinctive characteristic of submesoscale motions [15,20,40]. Previous studies have described the dependency of the diurnal cycle on the vertical eddy viscosity $\kappa$ [41]. Here, we reveal, for the first time, the seasonal variability of the diurnal cycle of $\zeta$ and $\delta$, which is mainly modulated by $KPP$ diagnostics. The model output of LLC4320 does not provide $\kappa$, but one can use $KP{P}_{hbl}$ as a proxy for the seasonal and diurnal variability of the strength of $\kappa$.

5. Conclusions and Perspectives

This work contributes to an improvement in the understanding of the Eastern Boundary Currents in the BM regime. The temporal evolution of BM within these currents was characterized. To achieve our objective, we developed a criterion based on dynamical filtering to separate IGW from BM, even in the presence of high-frequency submesoscale BM. Additionally, we identified the air–sea coupling factors with the most impact on short time scale motions—namely, diurnal changes in the eddy viscosity induced by ocean surface heat flux.

The main lesson from our work is twofold. First, within relative low-energy regions such as the EBC, IGW overshadows strong, quasi diurnal submesoscale activity, mainly driven by atmospheric and seasonal forcings. Second, when high resolution tidal-resolving and submesoscale-resolving ocean numerical simulations are available, it is possible to isolate IGW from BM by means of the dynamical filtering we propose in this paper.

Currently, highly realistic ocean numerical simulations are continuously running, both regionally and globally. Simulations are capable of resolving submesoscale dynamics and the internal gravity wave continuum. It is critical to separate BM from IGW to achieve accurate vertical heat flux estimates induced by BM at low and high frequencies. The method proposed here can be applied at any vertical level in the water column, opening up the possibility of separating IGW and deep-reaching submesoscale balanced motions [21,42] (whose vertical scale is larger than the mixed-layer depth) and quantifying their respective contributions to vertical heat fluxes. Additional concerns may exist regarding the interaction between IGW and BM motions, such as inertial (or near-inertial) waves that are trapped by eddies. These interactions, however, would not have any impact on the filter. Conversely, analyses in the physical or spectral spaces of BM–IGW interactions could benefit from the separation of the dynamical regimes achieved by our method.