Unsteady Fluid Flows in the Slab Mold Using Anticlogging Nozzles
Abstract
:1. Introduction
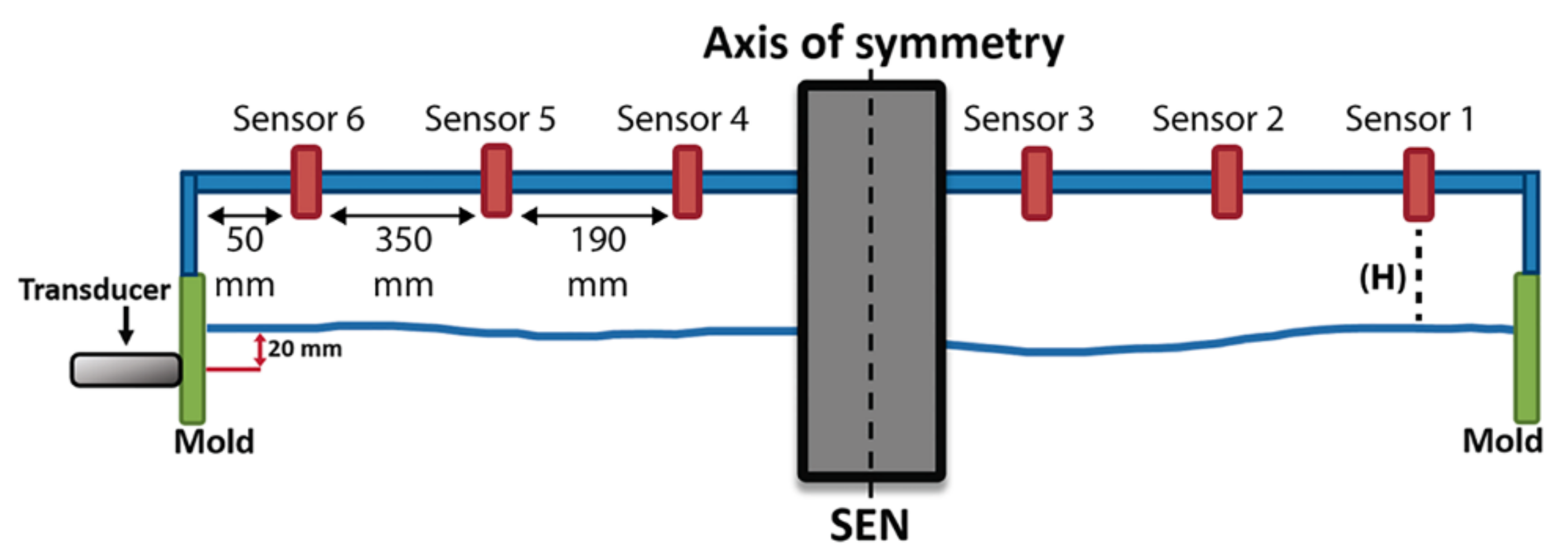
2. Experimental Work
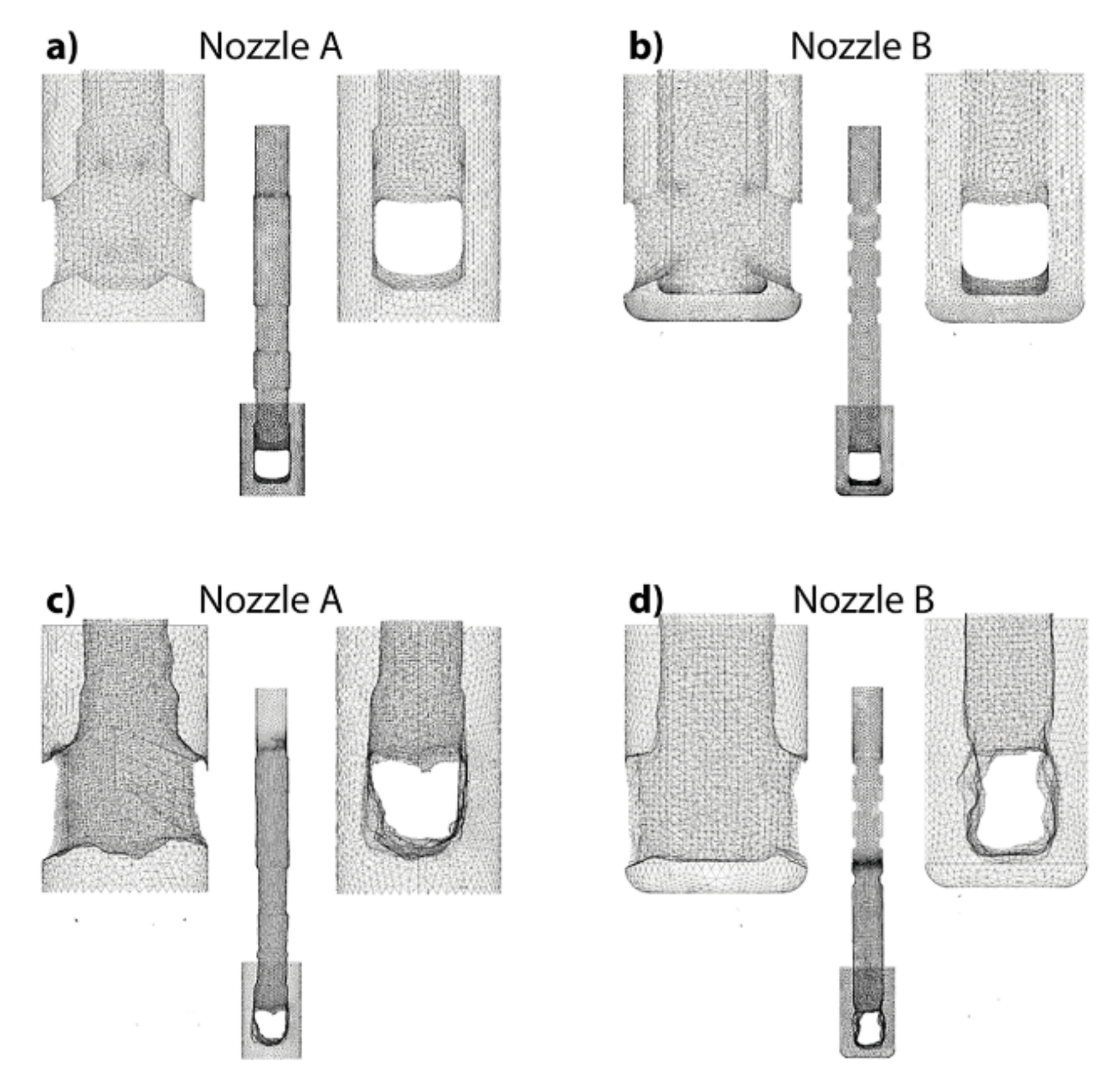
- A resin poured in the used nozzles permitted the capture of the topography of the clog surfaces adhering to the interior surfaces of the two industrial SENs. The solidified pieces work as cores (see Figure 5).
- The next step consists of cutting the industrial SENs along their lengths, yielding two halves, using a circular saw to extract the cores from the nozzles.
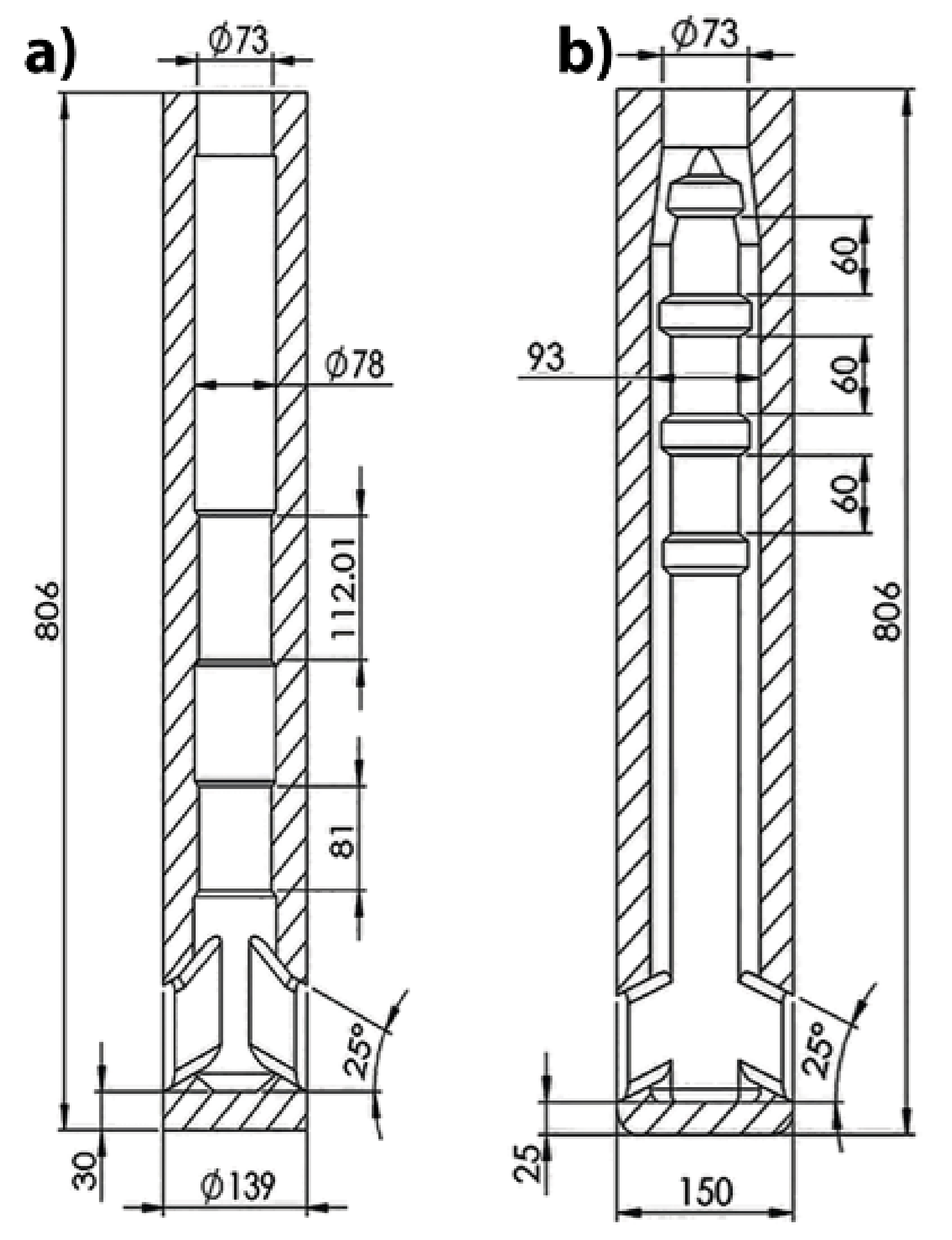
- Each nozzle is composed of a body, split in two halves and previously machined, and a 3D-printed tip with two bifurcated ports. Figure 5 shows the dissembled nozzles.
- The wrapped extracted core with the pieces of each disassembled model, including the tips of each SEN, conformed to a new casting system. With the core fixed into the assembled nozzle, there is a gap left between the clog and the core.
- A liquid rubber poured in the new casting filled the gap left between the nozzle surface and the core, forming an exact replica of the clog’s topography.
- By disassembling the nozzle, the core is again taken out; a final reassembling operation of the model nozzle yields a replica of the actual nozzle, with its respective alumina clogging adhering to the interior walls.
- A laser scanner introduced inside each assembled nozzle model, with their respective clog-models, supplied digital files of the surface’s topographies. These digital files were later used in building the computational meshes of the mathematical models.
3. Mathematical Model
4. Results and Discussion
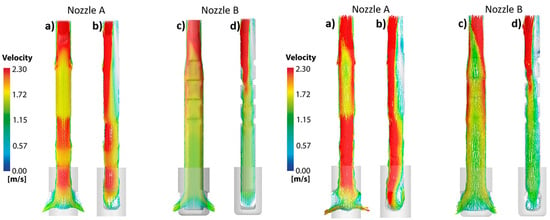
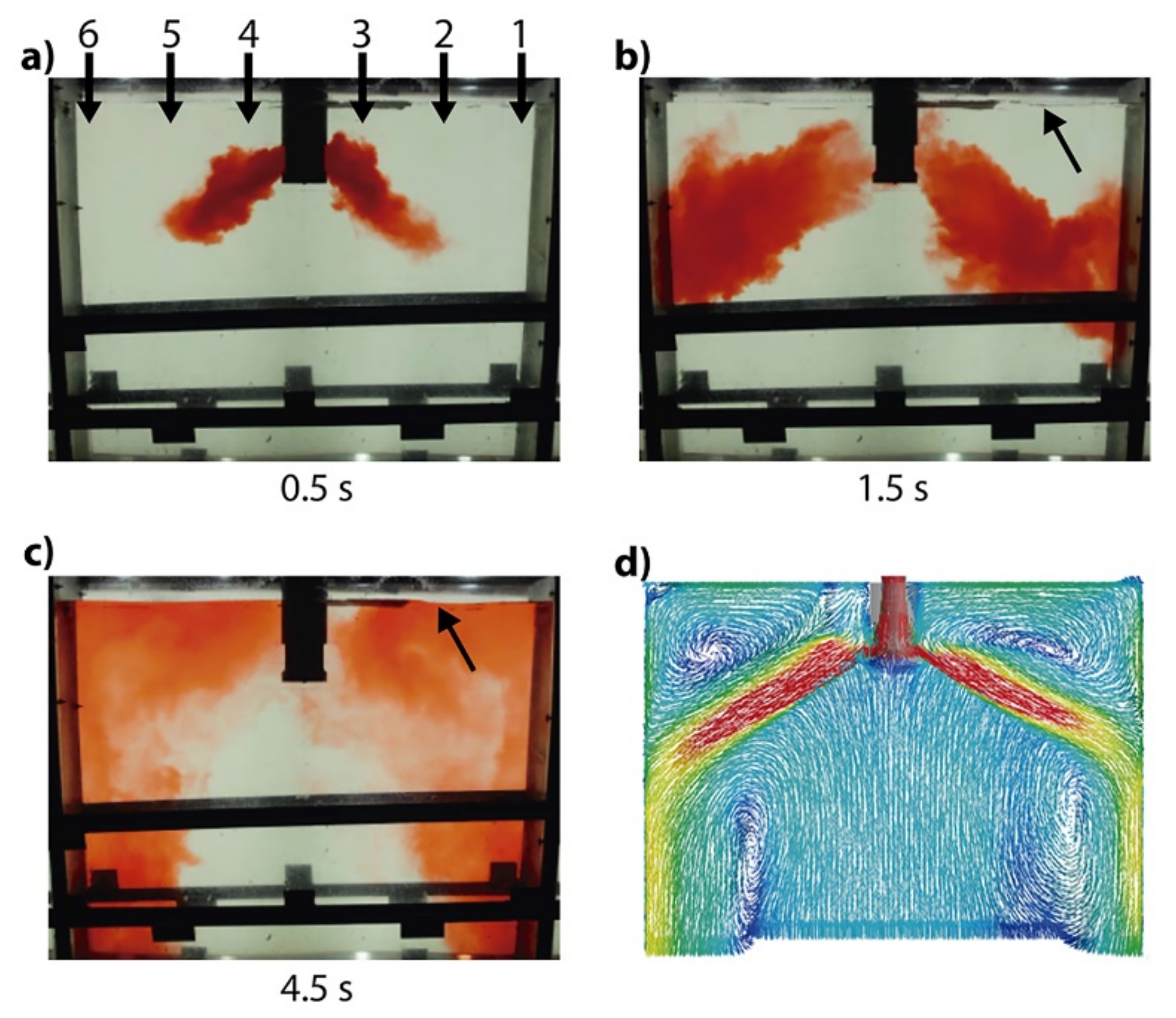
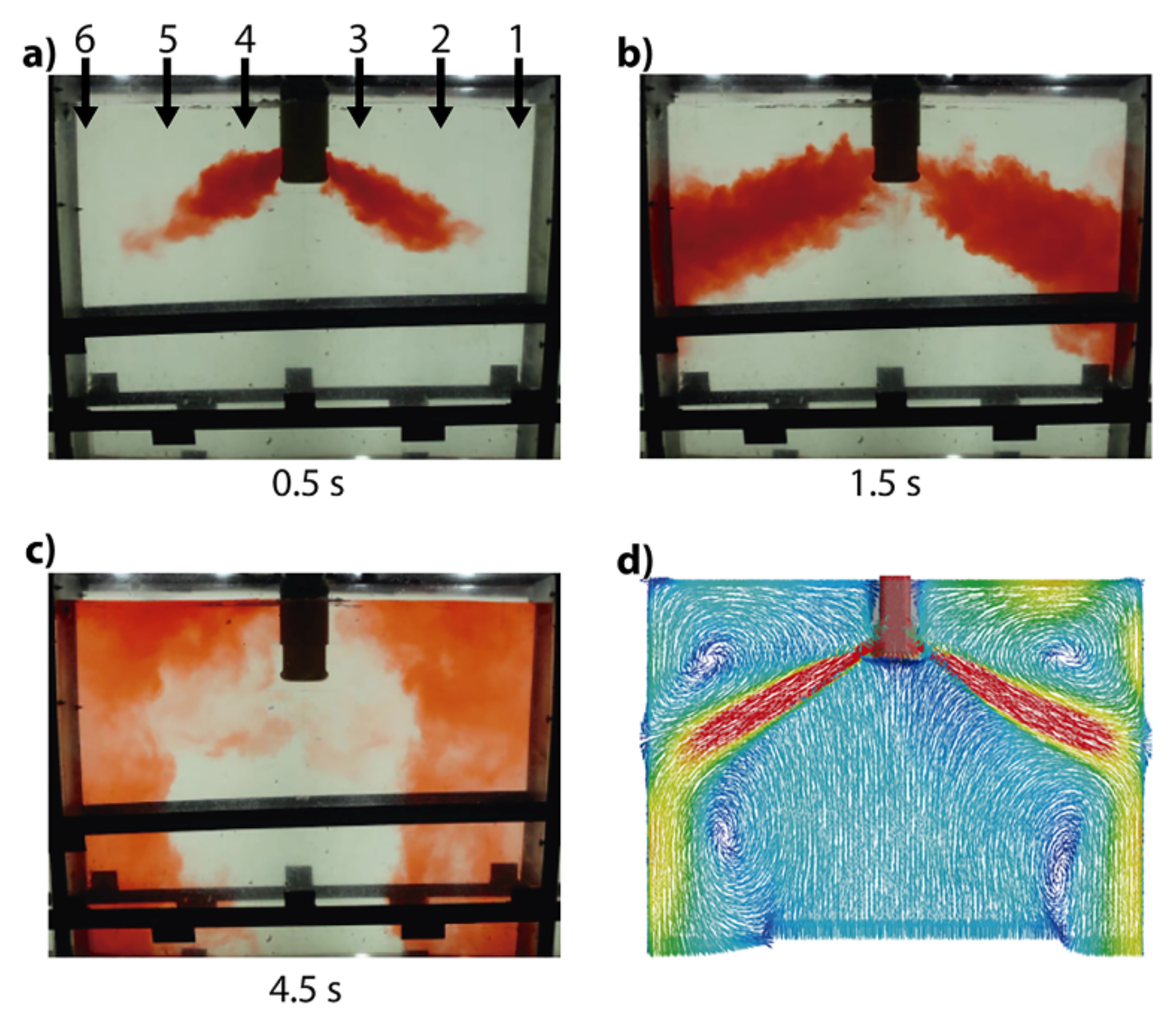
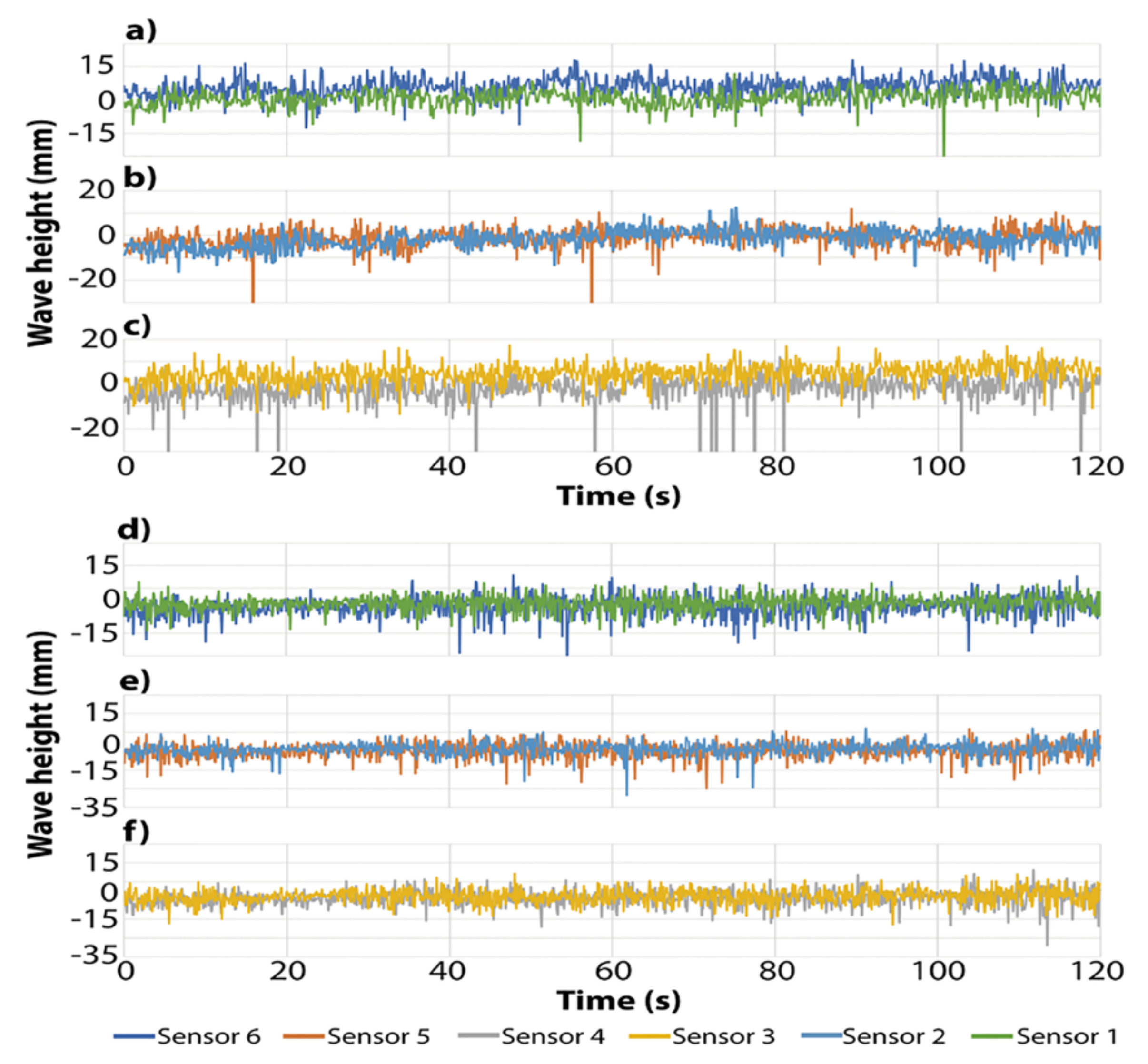
4.1. Fluid Flow Using Unclogged Nozzles
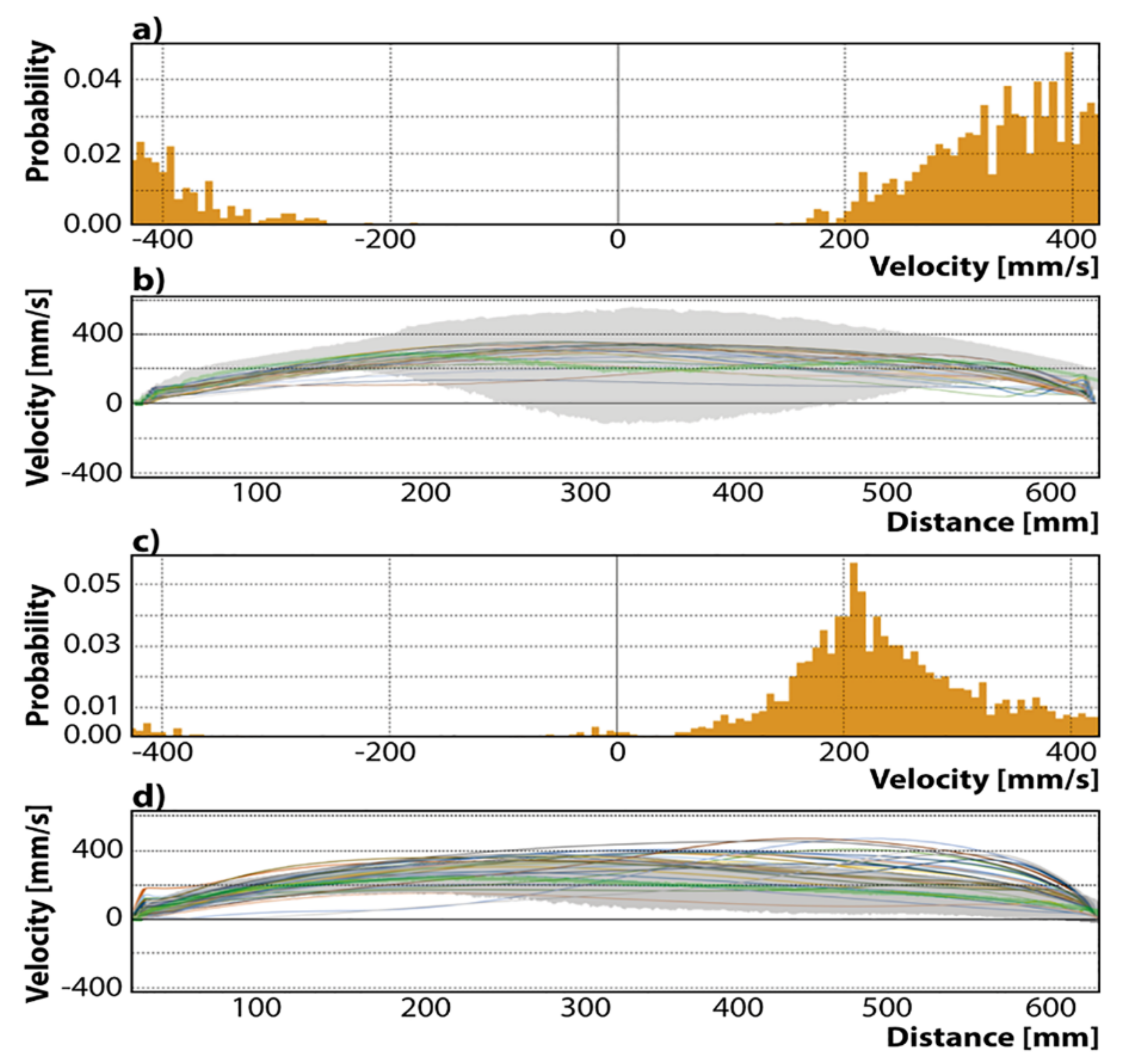
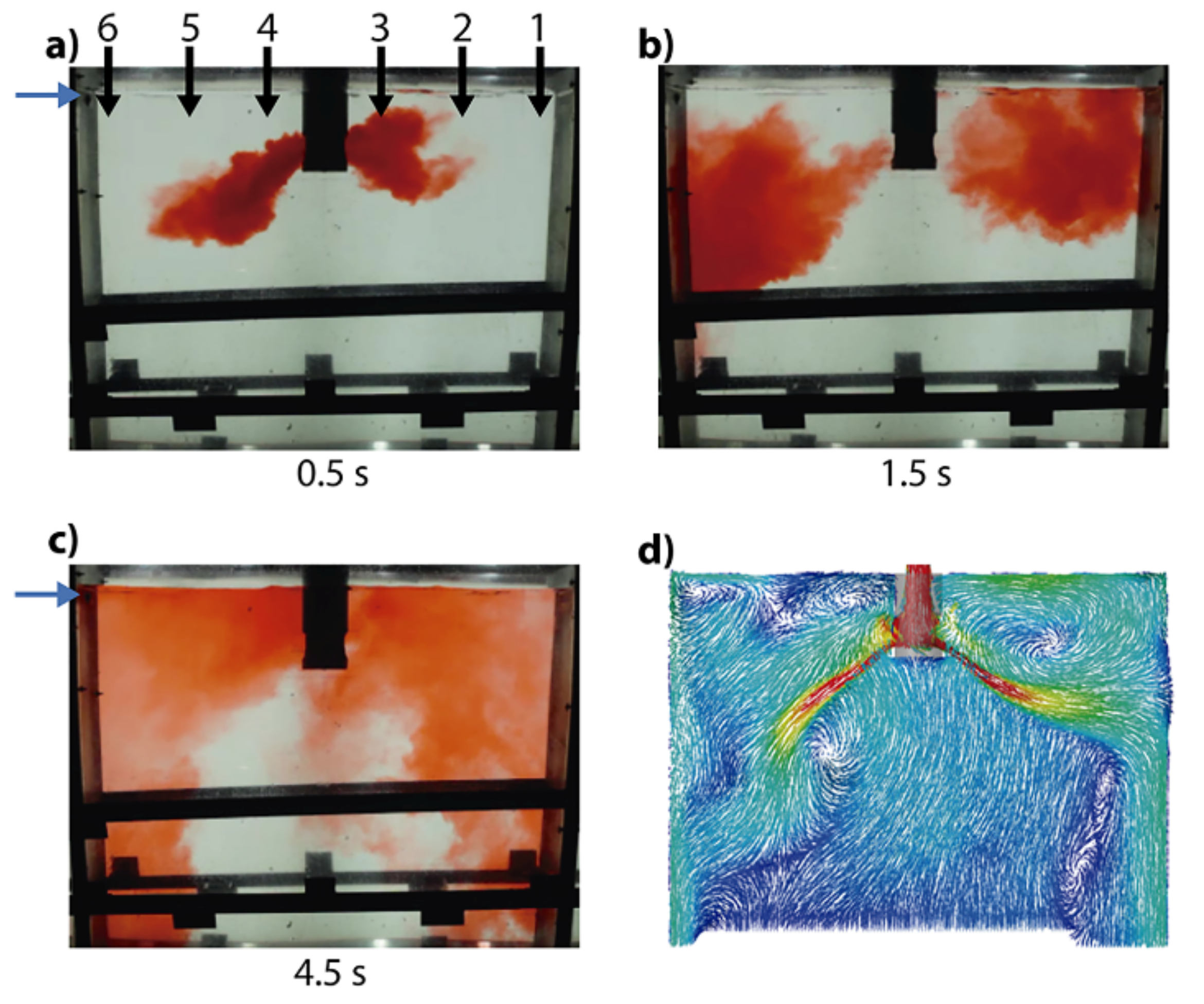
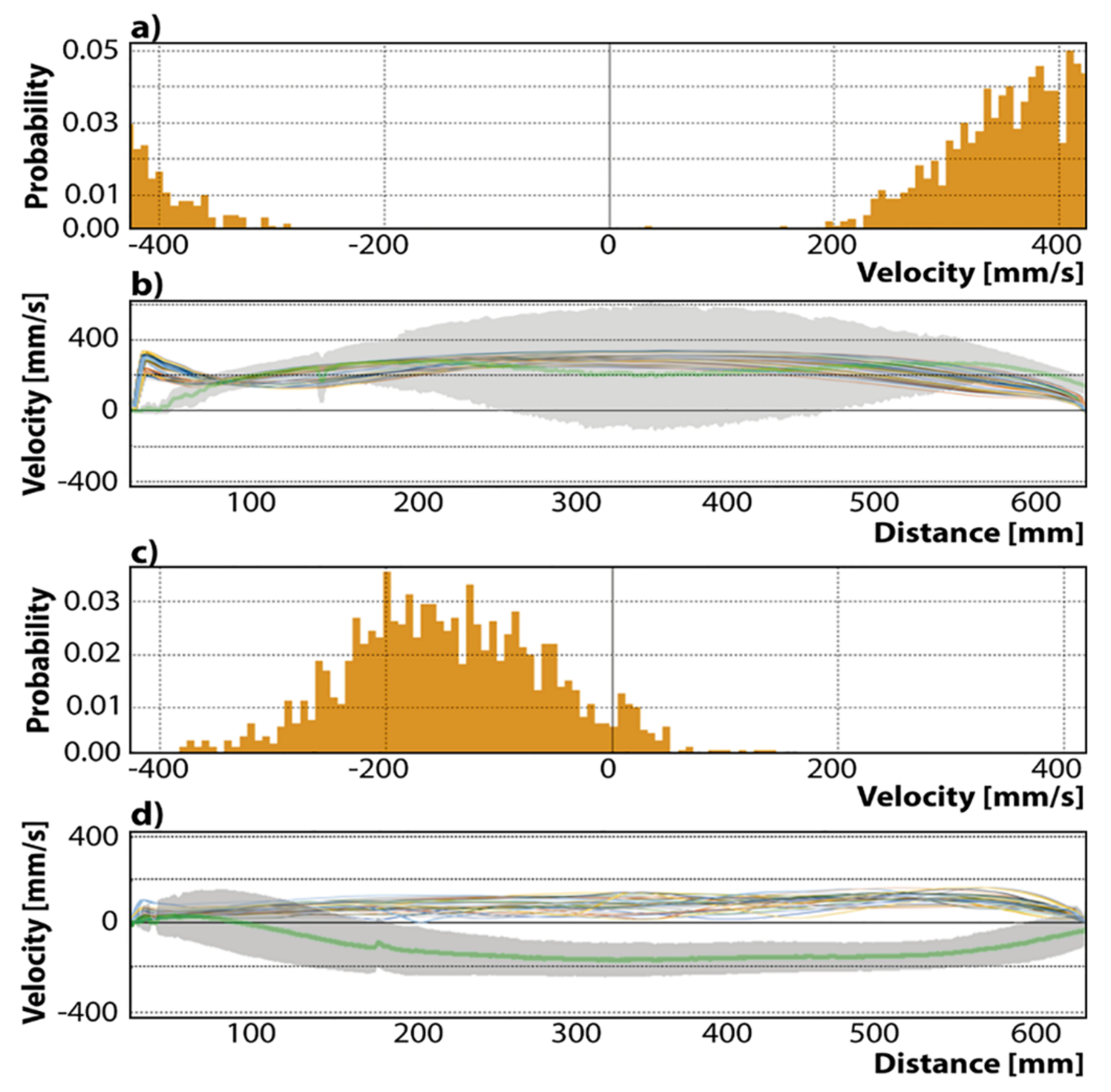
- The experimental velocities obtained using nozzle A include wide variations, reporting even negative velocities. The numerical results remain embodied inside the gray band region, lacking any numerical predictions with negative velocities.
- The numerical and experimental results yield radical time-changing velocity profiles, emphasizing the turbulent nature of the flow.
- The experimental velocities obtained using nozzle B yield a narrower band of variations, and the numerical results show some profiles outside, upwards in the region close to the SEN. However, some other instantaneous numerical results fall inside the gray experimental band, matching the experimental measurements well.
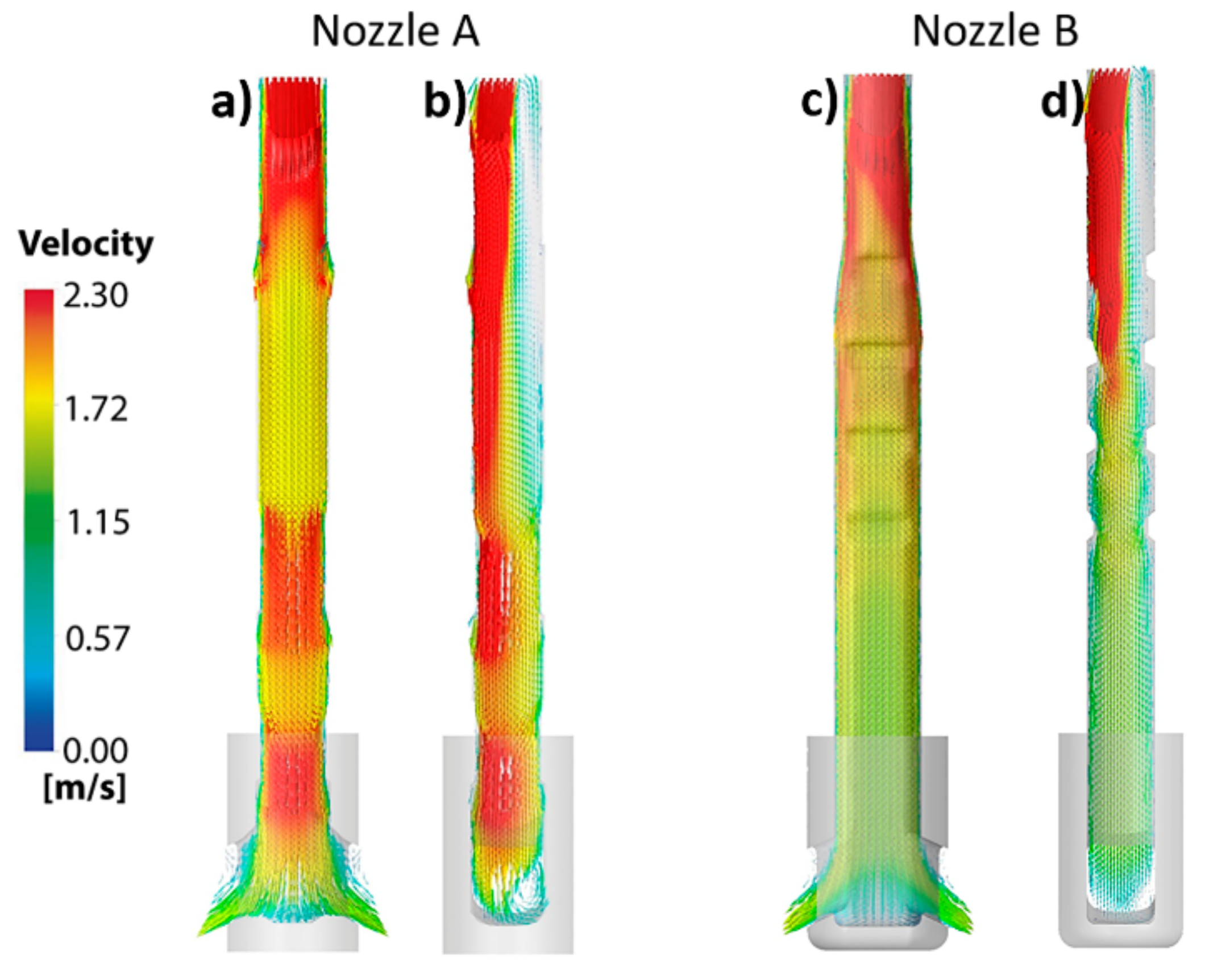
- The peak or spike velocities, predicted numerically for both nozzles, change to different positions between the narrow mold face and the nozzle, with time seldom falling in the middle position between the narrow mold wall and the outer nozzle’s wall.
- The numerical and experimental magnitudes of the velocity profiles are smaller in the flows yielded by nozzle B than in those yielded by nozzle A.
- The numerical predictions broadly predict the experimental measurements matching the overall dynamics of the subsurface flow.
4.2. Fluid Flow Using Clogged Nozzles
5. Conclusions
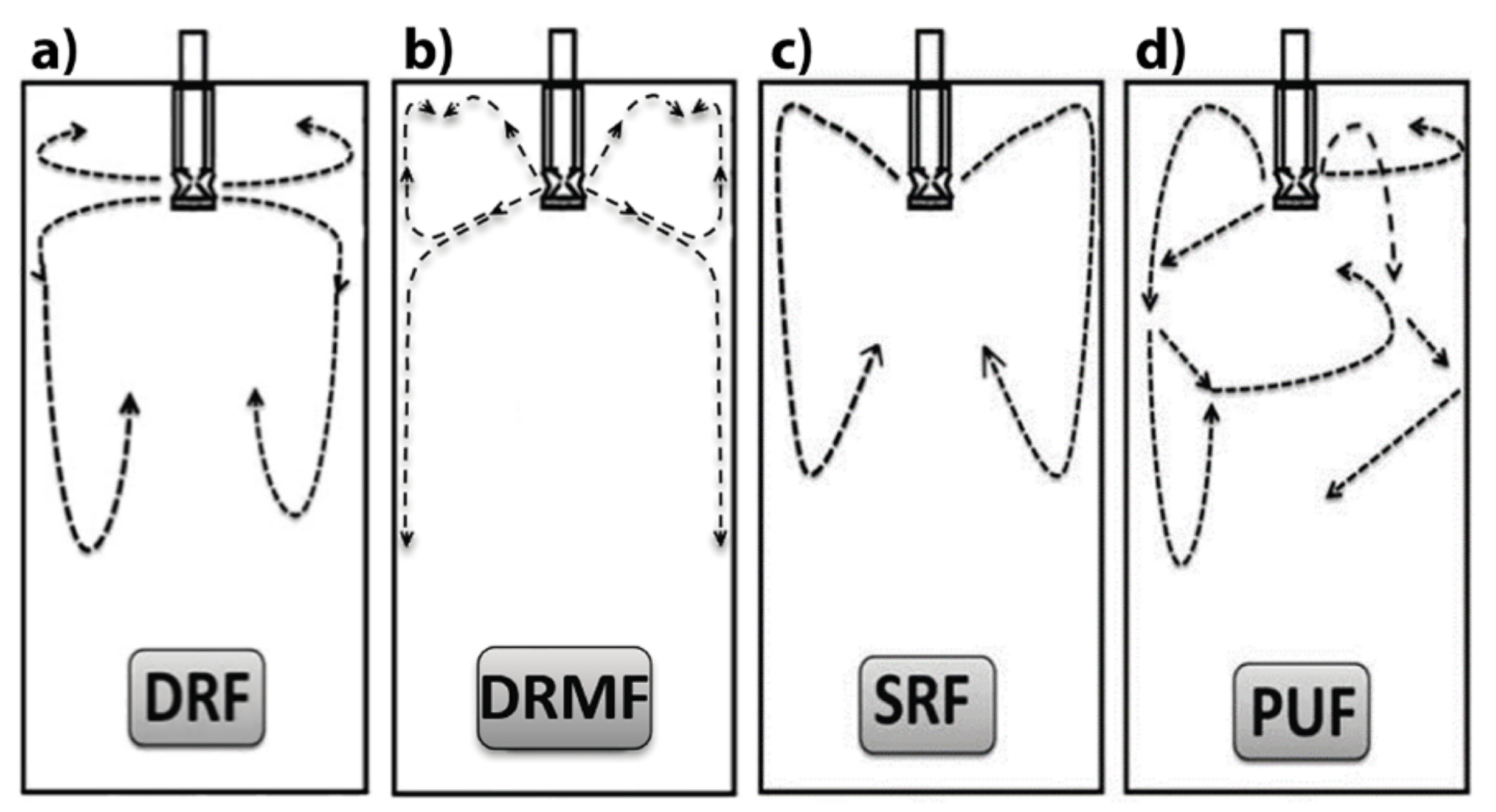
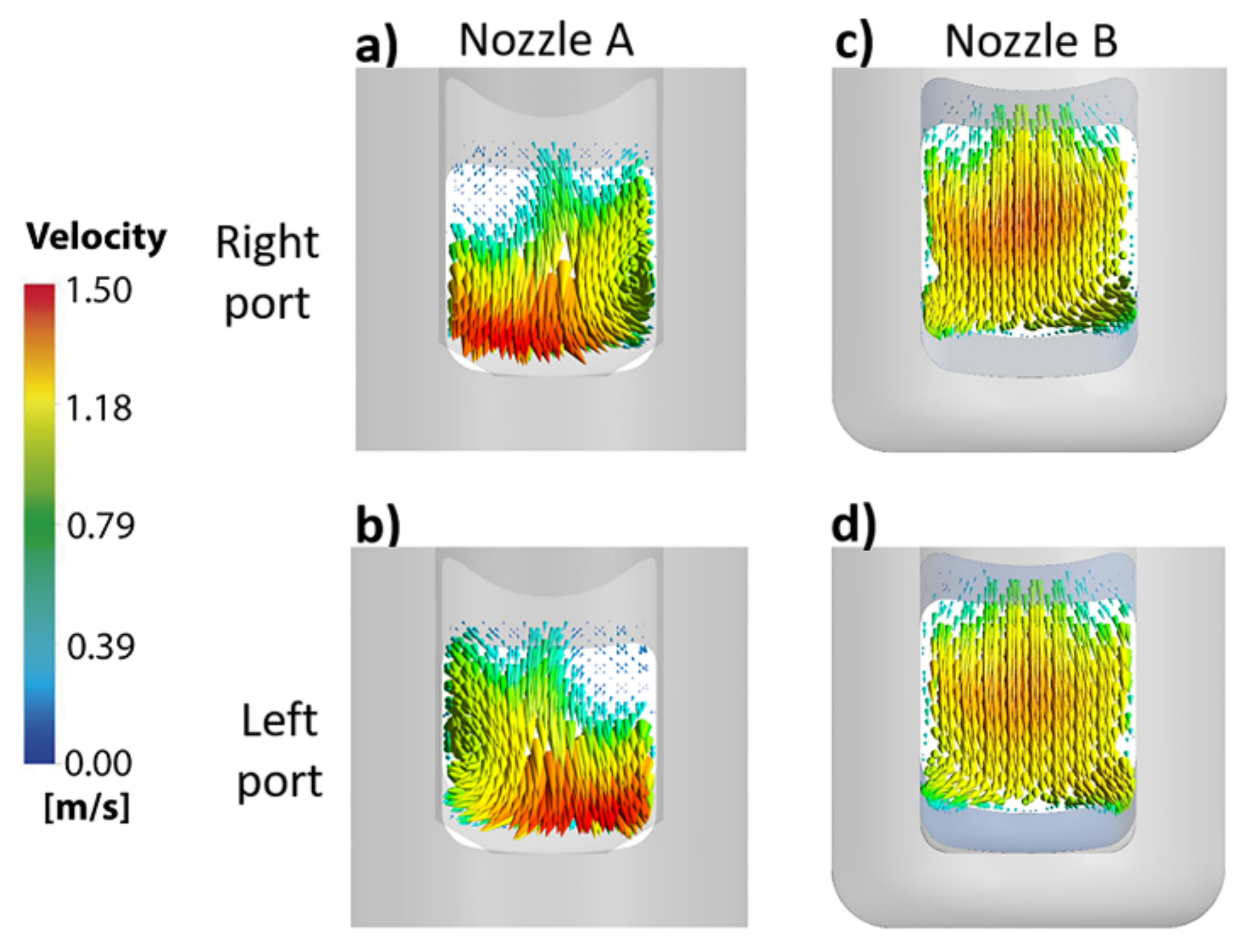
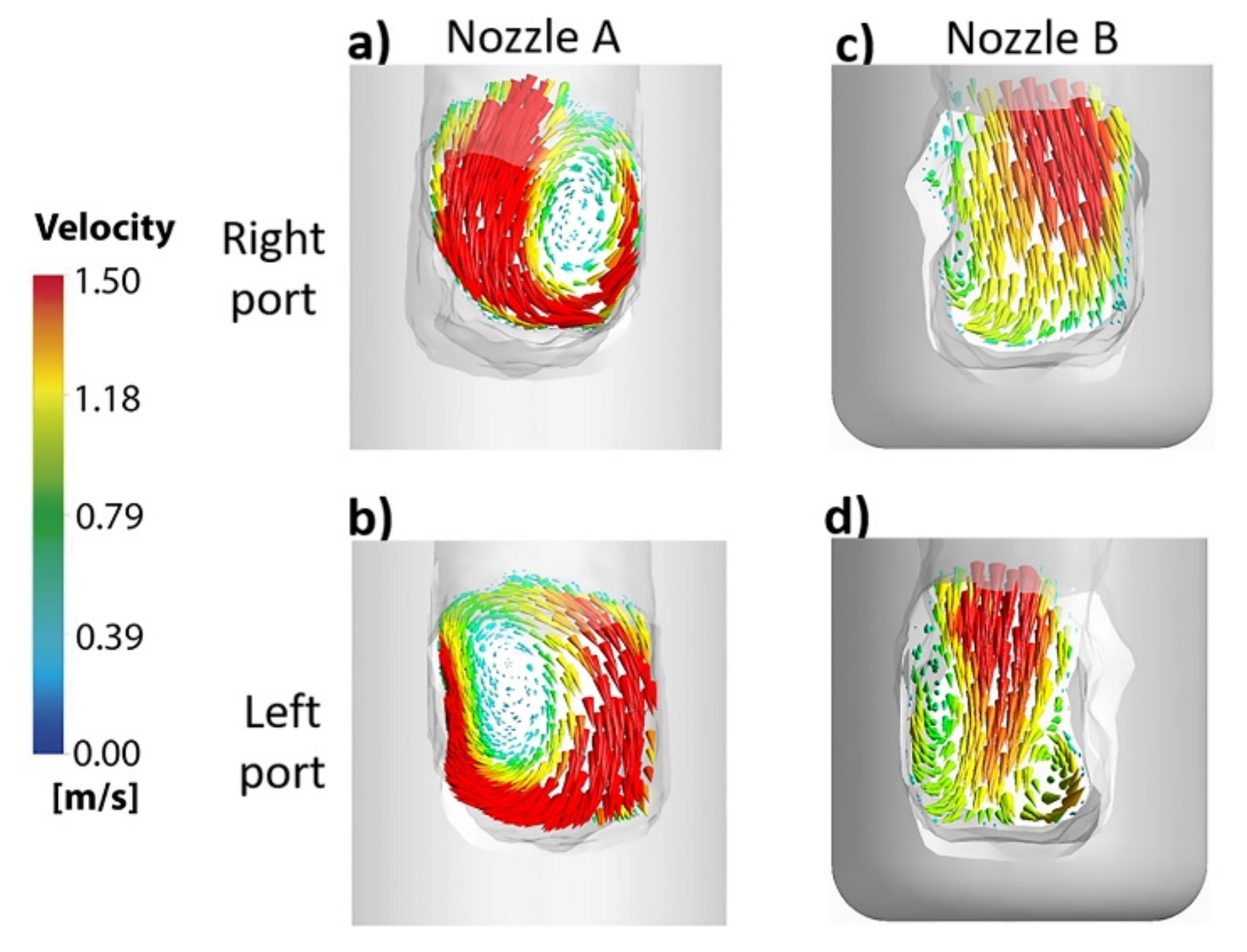
- The bath sub-surface velocity profiles using nozzle A are higher than the velocity profiles obtained through nozzle B.
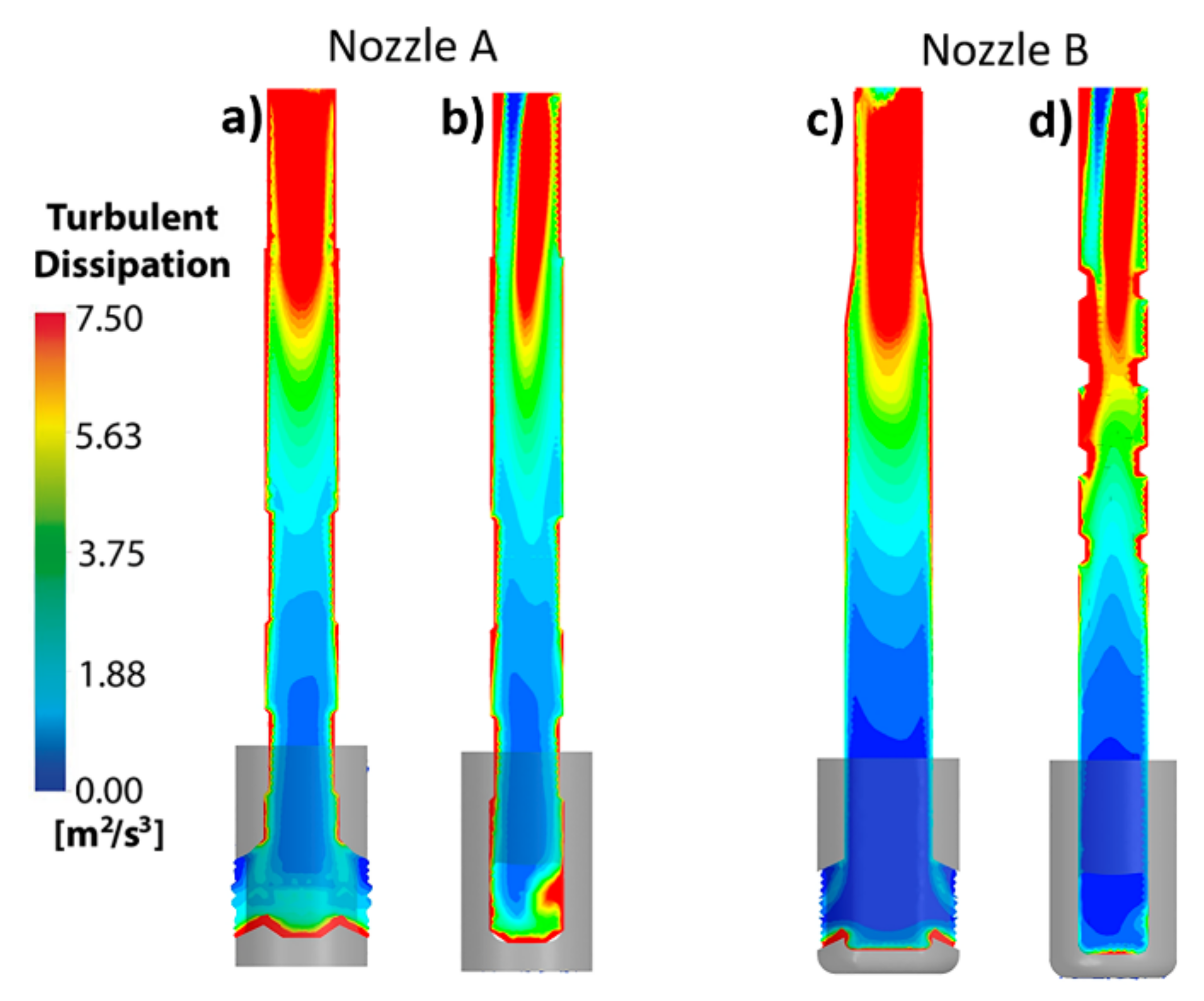
- The dissipation rate of kinetic energy is larger in the upper region of nozzle B than in nozzle A, resulting in smaller velocities through the bifurcated ports.
- The use of internal deflectors in nozzle B diminishes the internal biased flow, resulting in a larger port utilization area than that in nozzle A.
- The use of internal deflectors considerably decreases the amount of clogging alumina due to the existence of high turbulence manifested by the large dissipation rates of kinetic energy in the region.
- The existence of clogging induces crossed flows in the mold. Eventually, these flows will affect the thermal evenness of the heat flow through the copper plates in the actual mold.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Scale factor | |
| Gravity constant | |
| Thickness and height | |
| Kinetic energy (m2/s2) | |
| Length | |
| Pressure (Pa) | |
| Mean rate of strain tensor (s−1) | |
| Velocity magnitude (m/s) | |
| Velocity (m/s) | |
| Greek letters | |
| Turbulent dissipation rate (m2/s3) | |
| Dynamic viscosity (Pa-s) | |
| Viscosity (Pa-s) | |
| Density (kg/m3) | |
| Surface tension and turbulent Prandtl number | |
| Stress tensor | |
| Mean rate of rotation tensor | |
| Angular velocity | |
| Sub-Indexes | |
| Critical | |
| Metal | |
| Reynolds | |
| Slag and steel | |
| Turbulent | |
| Water | |
Appendix A. Equivalence between Wave Heights in Water and Waves Heights in Steel

References
- Cho, S.M.; Liang, M.; Olia, H.; Das, L.; Thomas, B.G. Multiphase flow-related defects in continuous casting of steel slabs. In TMS 2020 149th Annual Meeting & Exhibition Supplemental Proceedings; Springer: Cham, Switzerland, 2020; pp. 1161–1173. [Google Scholar]
- Chen, W.; Zhang, L.; Wang, Y.; Ji, S.; Ren, Y.; Yang, W. Mathematical simulation of two-phase flow and slag entrainment during steel bloom continuous casting. Powder Technol. 2021, 390, 539–554. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; Zhang, H. Zhang. The Study of Breakout and Crack Formation in Continuous Casting Mold. Metall. Mater. Trans. B 2016, 47B, 2244–2252. [Google Scholar] [CrossRef]
- Bo, K.; Cheng, G.; Wu, J.; Zhao, P.; Wang, J. Mechanism of oscillation mark formation in continuous casting of steel. Inter-national Journal of Minerals. Metall. Mater. 2000, 7, 189–192. [Google Scholar]
- Pütz, O.; Breitfeld, O.; Rödl, S. Investigations of flow conditions and solidification in continuous casting moulds by advanced simulation techniques. Steel Res. Int. 2003, 74, 686–692. [Google Scholar] [CrossRef]
- Sengupta, J.; Shin, H.J.; Thomas, B.G.; Kim, S.H. Micrograph evidence of meniscus solidification and sub-surface microstructure evolution in continuous-cast ultralow-carbon steels. Acta Mater. 2006, 54, 1165–1173. [Google Scholar] [CrossRef]
- Schmidt, K.D.; Friedel, F.; Imlau, K.P.; Jäger, W.; Müller, K.T. Consequent improvement of surface quality by systematic analysis of slabs. Steel Res. Int. 2003, 74, 659–666. [Google Scholar] [CrossRef]
- Kasai, N.; Iguchi, M. Water model experiment on melting powder trapping by vortex in the continuous casting mold. ISIJ Int. 2007, 47, 982–987. [Google Scholar] [CrossRef]
- Harman, J.M.; Cramb, A.W. 79 Steelmaking Conference Proceedings; The Iron and Steel Society: Warrendale, PA, USA, 1996; pp. 773–784. [Google Scholar]
- Lee, G.G.; Thomas, B.G.; Kim, S.H.; Shin, H.J.; Baek, S.K.; Choi, C.H.; Yu, S.J. Microstructure near corners of continuous-cast steel slabs showing three-dimensional frozen meniscus and hooks. Acta Mater. 2007, 55, 6705–6712. [Google Scholar] [CrossRef]
- Sengupta, J.; Thomas, B.G.; Shin, H.J.; Lee, G.G.; Kim, S.H. A new mechanism of hook formation during continuous casting of ultra-low-carbon steel slabs. Metall. Mater. Trans. A 2006, 37A, 1597–1611. [Google Scholar] [CrossRef]
- Birat, J.P.; Larrecg, M.; Lamant, J.Y.; Petegnief, J. Steelmaking Conference Proceedings; The Iron and Steel Society: Warrendale, PA, USA, 1991; pp. 39–40. [Google Scholar]
- Li, Z.; Zhang, L.; Bao, Y.; Ma, D. Numerical simulation on the brake effect of FAC-EMBr and EMBrRuler in the continuous casting mold. Processes 2020, 8, 1620. [Google Scholar] [CrossRef]
- Takeuchi, E.; Brimacombe, J.K. Effect of oscillation-mark formation on the surface quality of continuously cast steel slabs. Metall. Mater. Trans. B 1985, 16B, 605–625. [Google Scholar] [CrossRef]
- Leão, P.B.; Klug, J.L.; de Abreu, H.F.; Carneiro, C.A.; Ferreira, H.C.; Bielefeldt, W.V. Sliver defects in an ultra-low carbon Al-killed steel caused by low steel level in the tundish. Ironmak. Steelmak. 2021, 48, 978–985. [Google Scholar] [CrossRef]
- Cui, H.; Zhang, K.; Wang, Z.; Chen, B.; Liu, B.; Qing, J.; Li, Z. Formation of surface depression during continuous casting of High-Al TRIP steel. Metals 2019, 9, 204. [Google Scholar] [CrossRef]
- Yamashita, S.; Iguchi, M. Mechanism of mold powder entrapment caused by large argon bubble in continuous casting mold. ISIJ Int. 2001, 41, 1529–1531. [Google Scholar] [CrossRef]
- Watanabe, T.; Iguchi, M. Water model experiments on the effect of an argon bubble on the meniscus near the immersion nozzle. ISIJ Int. 2009, 49, 182–188. [Google Scholar] [CrossRef]
- Jin, K.; Vanka, S.P.; Thomas, B.G. Large eddy simulations of the effects of EMBr and SEN submergence depth on turbulent flow in the mold region of a steel caster. Metall. Mater. Trans. B 2017, 48B, 162–178. [Google Scholar] [CrossRef]
- Esaka, H.; Kuroda, Y.; Shinozuka, K.; Tamura, M. Interaction between argon gas bubbles and solidified shell. ISIJ Int. 2004, 44, 682–690. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, L. Materials Processing Fundamentals; Springer: Cham, Switzerland, 2019; pp. 37–47. [Google Scholar]
- Thomas, B.G.; Huang, X.; Sussman, R.C. Simulation of argon gas flow effects in a continuous slab caster. Metall. Mater. Trans. B 1994, 25B, 527–547. [Google Scholar] [CrossRef]
- Sánchez-Pérez, R.; Morales, R.D.; Díaz-Cruz, N.; Olivares-Xometl, O.; Palafox-Ramos, J. A physical model for the two-phase flow in a continuous casting mold. ISIJ Int. 2003, 43, 637–646. [Google Scholar] [CrossRef]
- Calderón-Ramos, I.; Morales, R.D.; García-Hernández, S.; Ceballos-Huerta, A. Effects of immersion depth on flow turbulence of liquid steel in a slab mold using a nozzle with upward angle rectangular ports. ISIJ Int. 2014, 54, 1797–1806. [Google Scholar] [CrossRef]
- Calderón-Ramos, I.; Morales, R.D.; Salazar-Campoy, M. Modeling flow turbulence in a continuous casting slab mold comparing the use of two bifurcated nozzles with square and circular ports. Steel Res. Int. 2015, 86, 1610–1621. [Google Scholar] [CrossRef]
- ANSYS Inc. FLUENT 6.2, User’s Guide; Centerra Resource Park: Cavendish Court, Lebanon, 2005; p. 51. [Google Scholar]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW industries: La Canada, CA, USA, 1998; p. 103. [Google Scholar]
- Issa, R.I.; Gosman, A.D.; Watkins, A.P. The computation of compressible and incompressible recirculating flows by a non-iterative implicit scheme. J. Comput. Phys. 1986, 62, 66–82. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1985, 62, 40–65. [Google Scholar] [CrossRef]
- Najjar, F.M.; Thomas, B.G.; Hershey, D.E. Numerical study of steady turbulent flow through bifurcated nozzles in continuous casting. Metall. Mater. Trans. B 1995, 26B, 749–765. [Google Scholar] [CrossRef]
- Hershey, D.E.; Thomas, B.G.; Najjar, F.M. Turbulent flow through bifurcated nozzles. Int. J. Numer. Methods Fluids 1993, 17, 23–47. [Google Scholar] [CrossRef]
- Thomas, B.G.; Zhang, L. Mathematical modeling of fluid flow in continuous casting. ISIJ Int. 2001, 41, 1181–1193. [Google Scholar] [CrossRef]
- Mishra, P.; Ajmani, S.; Kumar, A.; Shrivastava, K.K. Numerical modelling of Sen and mould for continuous slab. Int. J. Eng. Sci. Technol. 2012, 4, 2234–2242. [Google Scholar]
- Thomas, B.G.; Yuan, Q.; Sivaramakrishnan, S.; Shi, T.; Assar, M.B. Comparison of four methods to evaluate fluid velocities in a continuous slab casting mold. ISIJ Int. 2001, 41, 1262–1271. [Google Scholar] [CrossRef]
- Honeyands, T.; Hebertson, J. Flow dynamics in thin slab caster moulds. Steel Res. Int. 1995, 66, 287–293. [Google Scholar] [CrossRef]
- Calderón-Ramos, I.; Morales, R.D. Influence of turbulent flows in the nozzle on melt flow within a slab mold and stability of the metal-flux interface. Metall. Mater. Trans. B 2016, 47B, 1866–1881. [Google Scholar] [CrossRef]
- Kalter, R.; Tummers, M.J.; Wefers Bettink, J.B.; Righolt, B.W.; Kenjeres, S.; Kleijn, C.R. Aspect Ratio Effects on Fluid Flow Fluctuations in Rectangular Cavities. Metall. Mater. Trans. B 2014, 45B, 2186–2193. [Google Scholar] [CrossRef]


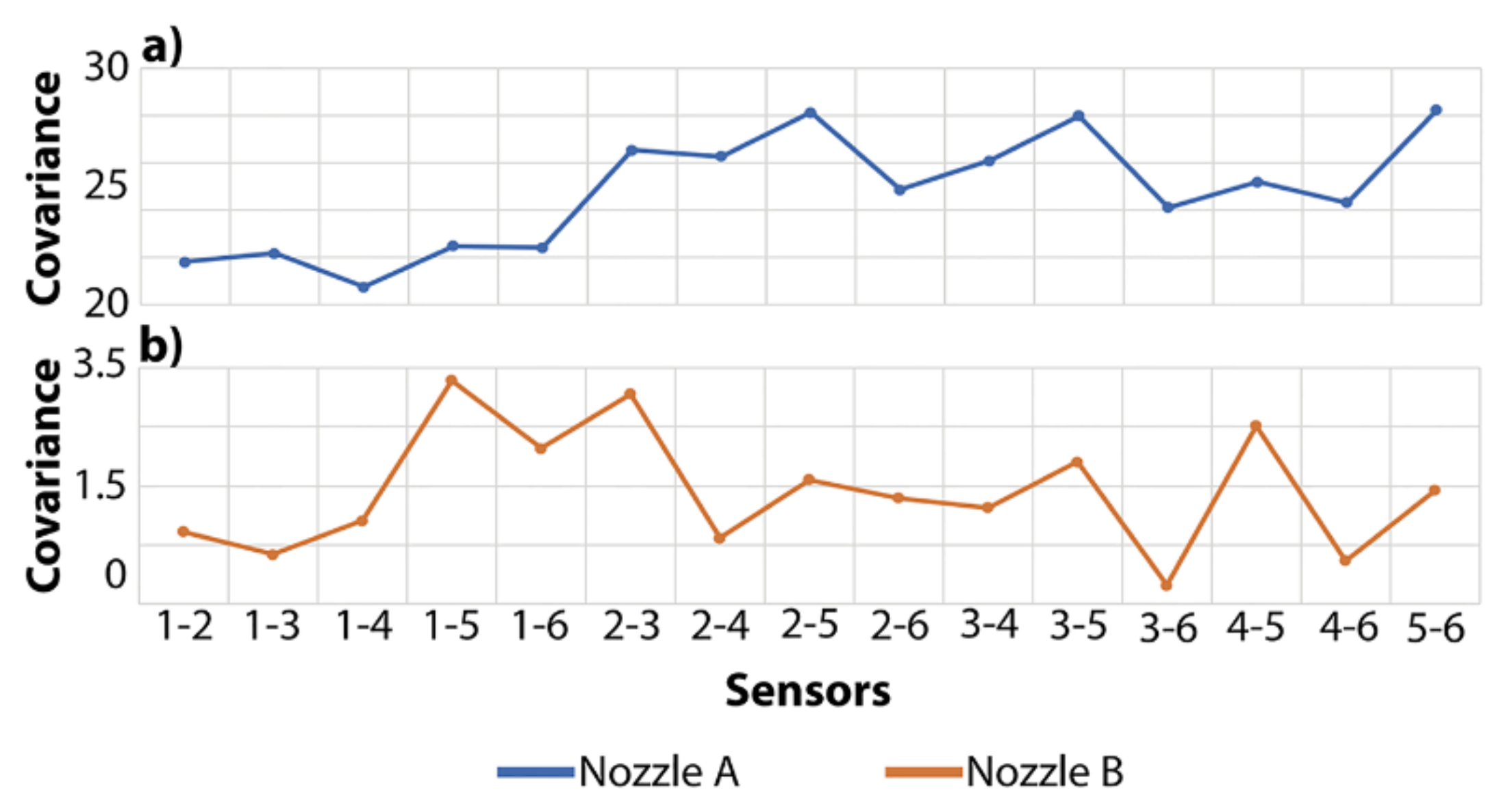






| Parameter | Value |
|---|---|
| Casting speed, (m/min) | 1.4 |
| Liquid flow rate, (L/min) | 8.56 |
| Mold size, (mm2) | 250 × 1450 |
| Nozzle immersion, (m) | 0.120 |
| Valve opening length, (m2) | 2.57 × 10−3 |
| Pressure inlet, (Pa) | 101 325 |
| Viscosity of the water, (Pa s) | 0.001003 |
| Density of the water, (kg/m3) | 998.2 |
| Nozzle A | Nozzle B | |
|---|---|---|
| Parameter | Description/Value | Description/Value |
| Gradient derivates | Green-Gauss Node-based | Green-Gauss Node-based |
| Pressure field | Body Force-weighted | Body Force-weighted |
| Pressure-velocity couple | PISO [29,30] | PISO [29,30] |
| Convergence criterion | 0.001 | 0.001 |
| Mesh type | Unstructured tetrahedral | Unstructured tetrahedral |
| Nodes | 486,328 | 398,488 |
| Elements | 2,591,343 | 2,276,970 |
| Skewness | Average: 0.20588 | Average: 0.10852 |
| Standard Deviation: 0.16652 | Standard Deviation: 9.982 × 10−002 | |
| Orthogonal quality | Average: 0.88292 | Average: 0.92652 |
| Standard Deviation: 8.713 × 0−002 | Standard Deviation: 6.097 × 10−002 |
| Left Side | |
|---|---|
| Nozzle A without clogging | 3.46 |
| Nozzle B without clogging | 3.80 |
| Nozzle A with clogging | 2.96 |
| Nozzle B with clogging | 3.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Solórzano, M.G.; Dávila, R.M.; Guarneros, J.; Calderón-Ramos, I.; Muñiz-Valdés, C.R.; Nájera-Bastida, A. Unsteady Fluid Flows in the Slab Mold Using Anticlogging Nozzles. Fluids 2022, 7, 288. https://doi.org/10.3390/fluids7090288
González-Solórzano MG, Dávila RM, Guarneros J, Calderón-Ramos I, Muñiz-Valdés CR, Nájera-Bastida A. Unsteady Fluid Flows in the Slab Mold Using Anticlogging Nozzles. Fluids. 2022; 7(9):288. https://doi.org/10.3390/fluids7090288
Chicago/Turabian StyleGonzález-Solórzano, María Guadalupe, Rodolfo Morales Dávila, Javier Guarneros, Ismael Calderón-Ramos, Carlos Rodrigo Muñiz-Valdés, and Alfonso Nájera-Bastida. 2022. "Unsteady Fluid Flows in the Slab Mold Using Anticlogging Nozzles" Fluids 7, no. 9: 288. https://doi.org/10.3390/fluids7090288
APA StyleGonzález-Solórzano, M. G., Dávila, R. M., Guarneros, J., Calderón-Ramos, I., Muñiz-Valdés, C. R., & Nájera-Bastida, A. (2022). Unsteady Fluid Flows in the Slab Mold Using Anticlogging Nozzles. Fluids, 7(9), 288. https://doi.org/10.3390/fluids7090288