Nucleus-Acoustic Solitary Waves in Warm Degenerate Magneto-Rotating Quantum Plasmas

Abstract

A warm degenerate magneto-rotating quantum plasma (WDMRQP) model consisting of a static heavy nucleus, inertial non-degenerate light nucleus, and warm non-relativistic or ultra-relativistic electrons has been considered to observe the generation of nucleus-acoustic (NA) solitary waves (NASWs). A Korteweg–de-Vries-type equation is derived by using the reductive perturbation method to describe the characteristics of the NASWs. It has been observed that the temperature of warm degenerate species, rotational speed of the plasma system, and the presence of heavy nucleus species modify the basic features (height and width) of NASWs in the WDMRQP system and support the existence of positive NA wave potential only. The applications of the present investigation have been briefly discussed.

1. Introduction

Recently, the study of degenerate plasmas has attracted the attention of many plasma physicists [1,2,3,4,5,6,7,8,9] due to their abundance in space (viz. white dwarf and neutron star) [1,2,3,4,5,6] as well as in laboratory experiments (viz. tokamak and laser intense microelectronic devices) [10]. The astrophysical compact objects (viz. white dwarf and neutron star) have ceased burning their thermonuclear fuel. Therefore, they are unable to generate thermal pressure, and contain extremely highly dense plasma species known as degenerate plasma species. The degenerate plasma is formed when it is compressed by increasing the pressure to such an extent that it cannot be compressed any more because of Pauli’s exclusion principle, which states that no two electrons can have exactly the same set of quantum numbers. This means that there is no extra space for the existence of more particles in that plasma system and that the space among the particles is extremely small. This corresponds to an extremely high-density plasma with $▵x\to 0$ and $▵p\to \infty$, where $▵x$ ($▵p$) is the uncertainty in position (momentum). This gives rise to an extremely high pressure known as degenerate pressure [11,12,13,14] in the highly dense astrophysical objects consisting of electrons, a light nucleus (viz. ${ }_1^1\mathrm{H}$ [14] or ${ }_2^4\mathrm{He}$ [15,16] or ${ }_{ 6}^{12}\mathrm{C}$ [17]), and a heavy nucleus (viz. ${ }_{26}^{56}\mathrm{Fe}$ [18] or ${ }_{37}^{85}\mathrm{Rb}$ [19] or ${ }_{42}^{96}\mathrm{Mo}$ [19]), which can be defined for absolute cold (zero temperature) plasma species j by the following equation [11,12,13]:

$$\begin{array}{c}\hfill P_j=k_j{n}_j^{{\gamma }_j},\end{array}$$

where $P_j$ is the degenerate pressure exerted by the degenerate species j and $n_j$ is the plasma species number density. $k_j\approx 3\pi {\hslash }^2/5m_j$ and ${\gamma }_j=5/3$ ($k_j\approx 3\hslash c/4 and {\gamma }_j=4/3)$ are valid for non-relativistic (ultra-relativistic) degenerate plasma species j, where ℏ is the reduced Planck constant, $m_j$ is the mass of the degenerate plasma species, and c is the speed of light. It may be noted here that the values of ${\gamma }_j$ ARE dependent on the dimension of the considered plasma system (${\gamma }_j=1+2/D$ for the non-relativistic limit [20] and ${\gamma }_j=1+1/D$ for the ultra-relativistic limit [20], where D is the dimension of the degenerate quantum system). Therefore, the values considered here (${\gamma }_j=5/3$ for the non-relativistic limit [20] and ${\gamma }_j=4/3$ for the ultra-relativistic limit [20]) are valid for three-dimensional degenerate plasmas. A new acoustic mode known as nucleus-acoustic (NA) waves is generated due to the combined effects of inertia provided by light or heavy nucleus species and the restoring force provided by the cold electron species degenerate pressure in such highly dense plasma systems. Unlike the usual ion-acoustic waves, the NA waves can exist at zero temperature [21]. The phase velocity $v_p$ for long-wavelength NA waves can be given by [1,2,3,4]:

$$\begin{array}{c}\hfill v_p=\frac{\omega }{k}={\left(\frac{z_l{n}_{l0}+z_h{n}_{h0}}{{\gamma }_e{z}_l{n}_{l0}{C}_l^2}\right)}^{-1/2},\end{array}$$

where $z_l$ ($n_{l0}$), $z_h$ ($n_{h0}$), and $c_l(=\sqrt{k_e{n}_{e0}^{{\gamma }_e-1}/m_e})$ are the charge state (unperturbed number density) of light nucleus species, charge state (number density) of heavy nucleus species, and NA wave speed, respectively.

Over the many years, a number of theoretical investigations have been conducted by the authors to observe the nonlinear features of NA waves in degenerate plasma systems. Mamun et al. [2,3] observed NA solitary waves considering strongly coupled heavy nucleus species [2], and studied heavy NA shock waves considering weakly coupled heavy nucleus species [3] in a cold degenerate plasma system (CDPS) containing cold degenerate electron and light nucleus species. These nonlinear structures generated in the cold degenerate plasma are associated with the heavy nucleus in the system. Therefore, the inertia is provided by the heavy nucleus mass density to generate heavy nucleus-acoustic waves in degenerate plasmas. Zaman et al. [22] considered a cold degenerate plasma system to investigate the generation and propagation characteristics of non-planar NA shock waves. Sultana et al. [7] considered inertial heavy nucleus species to observe the generation and propagation of NA rogue waves in a cold and highly dense quantum plasma system. In another investigation, Sultana and Schlickeiser [23] observed the basic features of NA solitons in a multi-ion quantum plasma system. Chowdhury et al. [6] analyzed the modulational instability of NA waves, and observed the characteristics of NA envelope solitons in a cold highly dense plasma medium using the nonlinear Schrödinger equation. A CDPS was considered by Zaman et al. [8] to investigate the basic features of cylindrical and spherical NA solitary waves. The effects of heavy immobile nucleus species on the characteristics of NA solitary waves were examined by Jannat and Mamun [5].

The highly dense charged particles in white dwarfs, neutron stars, pulsars, etc., give rise to a strong magnetic field [24]. A rapid rotation in the magnetized dense plasma system is produced whenever the angular momentum is conserved due to the decrease in the moment of inertia of collapsing stars [25]. Thus, the effect of the rotational magnetic field in highly dense plasma, such as neutron stars and pulsars, is very prominent. In the last few decades, the study of space plasmas has been made considering [10,26,27,28,29] or neglecting [30,31,32] the rotation of the magnetic field. Saini and Kaur [29] derived a Korteweg–de Vries (KdV) equation to analyze the basic features (viz. height and width) of ion-acoustic solitary and rogue waves in a quantum plasma. Hussain et al. [28] observed the nonlinear waves in a rotational two-component plasma consisting of inertial positive ions and inertialess non-extensive electrons. Saini et al. [27] examined the heavy nucleus-acoustic waves in three components (viz. non-degenerate heavy nucleus, degenerate light nucleus, and electron species) in a CDPS with the effect of the rotational magnetic field. Sahu et al. [10] also investigated the nonlinear electrostatic mode in a degenerate QP.

The investigations discussed above have some limitations that can be corrected in the following way:

• The works [1,2,3,4] neglected the presence of the magnetic field in various space plasmas. The pressure exerted due to the presence of the magnetic field in the degenerate quantum system is given by

  $$\begin{array}{c}{\mathcal{P}}_{MF}(magnetic field)=\frac{q_j}{m_j}(\overrightarrow{u_j}\times \overrightarrow{B}),\hfill \end{array}$$

  where $q_j$, $m_j$, $u_j$, and $B(=B_0\widehat{z})$ are the magnitude of the charge of the plasma species j, mass of j, velocity of plasma fluid species j, and the magnetic field acting on the plasma system, respectively.
• The investigations made in [30,31,32] neglected the effects of the rotational magnetic field in CDPS, for which, the applications of these works are limited to the non-rotational astrophysical objects (viz. white dwarfs). Neutron stars, pulsars, magnetars, etc., are highly dense quantum systems as well as rotational plasma systems. Therefore, in order to completely understand the characteristics of the said CDPS, one must consider the rotation of the plasma system at an angle around the direction axis of a constant magnetic field. A Coriolis force was used by the authors for describing the effect of the rotational ionized plasma system [27,28,29]. The Coriolis force effect can be introduced as [27,28,29]

  $$\begin{array}{c}{\mathcal{P}}_{RMF}(rotational magnetic field)=2m_j{n}_j(\overrightarrow{u_j}\times \overrightarrow{\Omega }),\hfill \end{array}$$

  where $n_j$ and $\overrightarrow{\Omega }$ are the number density of the plasma species j, and angular velocity of the rotational plasma system. It may be noted here that the higher order terms, viz. $\overrightarrow{\Omega }\times (\overrightarrow{\Omega }\times \overrightarrow{r})$, which describe the strong rotation, may be neglected in case of slow rotation.
• The degenerate pressure ($P_j$) exerted by the highly dense plasma species is given by the Chandrasekhar limit [11,12,13,14], which was introduced earlier in this section. The works [1,2,3,4,10,26,27,28,29] considered the Chandrasekhar limit for describing the degenerate pressure, which is only valid for CDPS (zero temperature). Astrophysical objects such as a hot white dwarf [33,34,35,36] have degenerate plasma species of finite temperature [37,38,39]. Therefore, the effect of the finite temperature of the degenerate plasma species must be considered to overcome the limitations of the previous works. The Chandrasekhar equation of state at a finite temperature can be introduced as [9,39]

  $$\begin{array}{c}{\mathcal{P}}_{Tj}=P_j\left(\frac{2\sqrt{1+{\sigma }_j^2}(1+24{\sigma }_{Tj}^2)-3{\sigma }_j^2{\sigma }_{kj}^2}{2\sqrt{1+{\sigma }_j^2}-3{\sigma }_j^2{\sigma }_{kj}^2}\right),\hfill \end{array}$$

  where ${\sigma }_j=m_j{c}^2/{\epsilon }_{Fj}$, ${\sigma }_{Tj}=k_B{T}_j/{\epsilon }_{Fj}$, and ${\sigma }_{kj}^2=\sqrt{1+{\sigma }_j^2}+{\sigma }_j^{2}log\frac{{\sigma }_j}{1+\sqrt{1+{\sigma }_j^2}}$. $k_B$, ${\epsilon }_{Fj}$, $T_j$, and $1/{\sigma }_j$ represent the Boltzmann constant, Fermi energy of plasma species j, plasma species temperature, and relativity parameter [9,39,40], respectively. At a value of ${\sigma }_j\gg 1$ and ${\gamma }_e=5/3$, the equation describes a warm non-relativistic degenerate plasma state [9,39,40]. On the other hand, to describe an ultra-relativistic degenerate plasma state, ${\sigma }_j\ll 1$ and ${\gamma }_e=4/3$ should be considered in the Chandrasekhar equation of state [9,39,40]. It is clear from the above equation that, at zero temperature, viz. $T_j=0 \mathrm{and} {\sigma }_{Tj}=0$, the equation reduces to Chandrasekhar’s cold degenerate plasma limit.
• The authors [6,10,28,29] considered a two-component plasma system containing cold degenerate electrons and an inertial light nucleus. A heavy nucleus such as ${ }_{26}^{56}\mathrm{Fe}$ [18] or ${ }_{37}^{85}\mathrm{Rb}$ [19] or ${ }_{42}^{96}\mathrm{Mo}$ [19] is found at the core of highly dense astrophysical plasmas. The heavy nucleus in such a degenerate plasma system can play a vital role in modifying the characteristics of the wave mode generated in the system. Due to their massive size compared to the light nucleus $\left(m\right(Fe)\approx 56m(H), m(Rb)\approx 85(H), \mathrm{and}$ $m\left(Mo\right)\approx 96m\left(H\right))$, and low number density, the heavy nucleus may be considered immobile. The presence of a heavy nucleus gives rise to the neutrality condition for a warm degenerate quantum plasma as $n_{e0}+Z_l{n}_{l0}+Z_h{n}_{h0}\approx 0$.

Therefore, our present investigation is concentrated on analyzing the NA solitary waves (NASWs) in a warm degenerate magneto-rotating quantum plasma (WDMRQP) consisting of warm degenerate electron species, inertial light nucleus species, and immobile heavy nucleus species. Inertia is provided by the light nucleus mass density and restoring force is provided by the degenerate pressure of the warm electrons to generate the NASWs in our WDQP system.

The outline of the paper is as follows: the theoretical model describing our plasma model is presented in Section 2. The Korteweg–de Vries (KdV) equation is derived to examine the characteristics of NASWs in Section 3. Results and discussion are summarized in Section 4.

2. Warm Degenerate Magnetized Plasma Model

We consider a WDMRQP system consisting of an immobile (low-density) heavy nucleus, inertial non-degenerate light nucleus, and warm degenerate electron to analyze the basic features of NASWs. It is considered that the said plasma system has a rotational magnetic field (constant magnetic field, $\overrightarrow{B}=B_0\widehat{z}$) acting at an angle of $\theta$ around the z-axis. The charge neutrality condition for the three-dimensional magneto-rotating quantum plasma can be written as $Z_h{n}_{h0}+Z_l{n}_{l0}\approx n_{e0}$, where $Z_h$, $Z_l$, $n_{h0}$, $n_{l0}$, and $n_{e0}$ are the heavy nucleus charge state, light nucleus charge state, unperturbed heavy nucleus number density, unperturbed light nucleus number density, and unperturbed electron number density, respectively. It should be mentioned here that the number density of the heavy nucleus is very low compared to that of the light nucleus and electrons. In addition, the heavy nucleus is considered static/immobile due to the low number density in the degenerate plasma system. The dynamics of nonlinear NA waves is governed by the following set of basic normalized equations

$$\begin{array}{c}\frac{\partial n_l}{\partial t}+\overrightarrow{\nabla }.\left(n_l{\overrightarrow{u}}_l\right)=0,\hfill \end{array}$$

(1)

$$\begin{array}{c}\frac{1}{2}\left(\frac{\partial u_l}{\partial t}+({\overrightarrow{u}}_l.\overrightarrow{\nabla }){\overrightarrow{u}}_l\right)=-\frac{1}{2}\overrightarrow{\nabla }\psi +\frac{{\Omega }_{cl}}{2}({\overrightarrow{u}}_l\times \widehat{z})+({\overrightarrow{u}}_l\times {\overrightarrow{\Omega }}_r),\hfill \end{array}$$

(2)

$$\begin{array}{c}{\nabla }^2\psi =(1+\delta )n_e-n_l-\delta ,\hfill \end{array}$$

(3)

where $n_l$, $n_e$, $n_h$, $u_l$, ${\Omega }_r$, t, and $\psi$ are the normalized light nucleus number density, electron number density, heavy nucleus number density, velocity of light nucleus fluid, angular frequency due to the rotation, normalized time variable, and normalized space variable, respectively, and are normalized by $n_{l0}$, $n_{e0}$, $n_{h0}$, light nucleus wave speed $c_l{(=k_e{n}_{e0}^{{\gamma }_e-1}/m_l)}^{1/2}$, light nucleus plasma frequency ${\Omega }_{pl}(=\sqrt{4\pi n_{l0}{Z}_l^2{e}^2/m_l})$ (with $Z_l$ being the charge state of light nucleus), ${\Omega }_{pl}^{-1}$, light nucleus Debye length ${\lambda }_{Dl}=c_l/{\Omega }_{pl}$, and ($e/k_e{n}_{e0}^{{\gamma }_e-1}$), respectively. The value of ${\Omega }_{cl}$ and $\delta$ is given by

$$\begin{array}{c}\hfill {\Omega }_{cl}={\Omega }_c/{\Omega }_{pl} \mathrm{and} \delta =\frac{Z_h{n}_{h0}}{Z_l{n}_{l0}},\end{array}$$

where ${\Omega }_c=e{B}_0/m_{l}c$. $Z_h$ and $n_{h0}$ are the charge state and unperturbed number density of the static immobile heavy nucleus species. The normalized Equations (1)–(3) govern the nonlinear dynamics of the three dimensional magneto-rotating quantum plasma system. The first Equation (1) describes the continuity equation for the light nucleus number density. The second Equation (2) interprets the momentum balance equation in which the second (comes from constant magnetic field) and third (comes from Coriolis force) term of the right hand side describe the pressure arisen due to the presence of the rotational magnetic field. It may be noted here that the warm degenerate pressure has been ignored for the light nucleus species as the magnetic field is very strong. In addition, the degeneracy of the light nucleus is much less than the degeneracy of electron species. We can clearly dictate from Equation (2) that, if we ignore the rotation of the magnetic field (i.e., ${\Omega }_r=0$), the warm degenerate plasma system is only dependent on the constant external magnetic field, and, if we ignore the gyro-frequency of the light nucleus species (i.e., ${\Omega }_{cl}=0$), the plasma becomes a three-component warm degenerate quantum system. The third equation is known as the Poisson equation, which describes the potential for NAWs in the three-dimensional magneto-rotating quantum plasma, and closes Equations (1) and (2). The physical parameter $\delta$ is present in this equation due to the assumption of stationary heavy nucleus species. The heavy nucleus number density is assumed to be unperturbed throughout the degenerate plasma system. It may also be noted here that nonlinear electrostatic waves such as NAWs propagate through the WDMRQP system in the $x-z$ plane (obliquely to the external magnetic field). We assume here that the number density of the light nucleus is comparatively more than the number density of the heavy nucleus species (i.e., $n_{l0}>n_{h0}$), for which, the value of $\delta$ becomes less than 1 ($\delta <1$). In addition, the mass of the heavy and light nucleus is much larger than the mass of the electron (i.e., $m_e\ll m_l,m_h$). The warm degenerate electron number density can be given as [9]

$$\begin{array}{c}{n}_e={\left[1+({\gamma }_e-1){\left({\gamma }_e{k}_{Te}\right)}^{-1}\psi \right]}^{{({\gamma }_e-1)}^{-1}},\hfill \end{array}$$

(4)

where ${\gamma }_e=5/3$ (${\gamma }_e=4/3$) for non-relativistic (ultra-relativistic) electron species and

$$\begin{array}{c}{k}_{Te}=\frac{(2\sqrt{1+{\sigma }_e^2}(1+24{\sigma }_{Te}^2)-3{\sigma }_e^2{\sigma }_{ke}^2)}{(2\sqrt{1+{\sigma }_e^2}-3{\sigma }_e^2{\sigma }_{ke}^2)},\hfill \end{array}$$

where ${\sigma }_e=m_e{c}^2/{\epsilon }_{Fe}$, ${\sigma }_{Te}=k_B{T}_e/{\epsilon }_{Fe}$, and ${\sigma }_{ke}^2=\sqrt{1+{\sigma }_e^2}+{\sigma }_e^{2}log\frac{{\sigma }_e}{1+\sqrt{1+{\sigma }_e^2}}$. $k_B$, ${\epsilon }_{Fe}$, $T_e$, and $1/{\sigma }_e$ represent the Boltzmann constant, Fermi energy of degenerate electrons, electron temperature, and relativity parameter [9,39,40], respectively. At a value of ${\sigma }_e\gg 1$ and ${\gamma }_e=5/3$, the equation describes a warm non-relativistic degenerate plasma state [9,39,40]. On the other hand, to describe the ultra-relativistic degenerate plasma state, ${\sigma }_e\ll 1$ and ${\gamma }_e=4/3$ should be considered in the Chandrasekhar equation of state [9,39,40]. It is clear that, for a value of $k_{Te}=1$, which occurs in the event of zero temperature (i.e., $T_e=0$ and ${\sigma }_{Te}=0$), the electron number density equation reduces to the cold degeneracy limit. For a value of $k_{Te}=1$ and ${\gamma }_e=1$ (which represents a relativistic plasma system), the electron number density follows the usual Maxwell–Boltzmann velocity distribution function. As the nonlinear propagation of NAWs is assumed in the $x-z$ plane, the components (x, y, and z) of Equations (1)–(3) for the three-dimensional propagation can be written as

$$\begin{array}{c}\frac{\partial n_l}{\partial t}+\frac{\partial }{\partial x}\left(n_l{u}_{lx}\right)+\frac{\partial }{\partial z}\left(n_l{u}_{lz}\right)=0,\hfill \end{array}$$

(5)

$$\begin{array}{c}\frac{\partial u_{lx}}{\partial t}+\left(u_{lx}\frac{\partial }{\partial x}+u_{lz}\frac{\partial }{\partial z}\right)u_{lx}+\frac{\partial \psi }{\partial x}-u_{ly}({\Omega }_{cl}+2{\Omega }_{0}sin\theta )=0,\hfill \end{array}$$

(6)

$$\begin{array}{c}\frac{\partial u_{ly}}{\partial t}+\left(u_{lx}\frac{\partial }{\partial x}+u_{lz}\frac{\partial }{\partial z}{u}_{ly}\right)u_{ly}+u_{lx}{\Omega }_{cl}+2{\Omega }_0(u_{lx}cos\theta -u_{lz}sin\theta )=0,\hfill \end{array}$$

(7)

$$\begin{array}{c}\frac{\partial u_{lz}}{\partial t}+\left(u_{lx}\frac{\partial }{\partial x}+u_{lz}\frac{\partial }{\partial z}\right)u_{lz}+\frac{\partial \psi }{\partial z}+2u_{ly}{\Omega }_{0}sin\theta =0,\hfill \end{array}$$

(8)

$$\begin{array}{c}\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial z^2}\right)\psi =(1+\delta )n_e-n_l-\delta .\hfill \end{array}$$

(9)

Here, the angular frequency of the rotational magnetic field in the two dimensions (due to the propagation of NAWs in the $x-z$ plane) can be expressed as ${\Omega }_{rx}={\Omega }_{0}sin\theta$ and ${\Omega }_{rz}={\Omega }_{0}cos\theta$, where ${\Omega }_0$ is the rotational frequency of the warm degenerate quantum plasma.

3. Derivation of KdV Equation

The stretch coordinates $\xi$ and $\tau$ were used to derive the KdV equation for observing the NASWs in a WDMRQP system, and are given by [10,26,27,28,29,41]

$$\begin{array}{c}\xi ={ϵ}^{1/2}(l_{x}x+l_{z}z)-{ϵ}^{1/2}\left(M\tau \right),\hfill \end{array}$$

(10)

$$\begin{array}{c}\tau ={ϵ}^{3/2}t,\hfill \end{array}$$

(11)

where $l_x^2+l_z^2=1$ ($l_x$ and $l_z$ are the direction cosines along the x and z axis, respectively) and $0<ϵ<1$ ($ϵ$ is the smallness parameter describing the degree of perturbation). The expansion of the dependent variables, such as $n_l$, $u_{lx}$, $u_{ly}$, $u_{lz}$, and $\psi$, are given by [10,26,27,28,29,41]

$$\begin{array}{c}{n}_l=1+ϵn_l^{\left(1\right)}+{ϵ}^2{n}_l^{\left(2\right)},\hfill \\ u_{lx}=0+{ϵ}^2{u}_{lx}^{\left(1\right)}+{ϵ}^3{u}_{lx}^{\left(2\right)},\hfill \\ u_{ly}=0+{ϵ}^{3/2}{u}_{ly}^{\left(1\right)}+{ϵ}^{5/2}{u}_{ly}^{\left(2\right)},\hfill \\ u_{lz}=0+ϵu_{lz}^{\left(1\right)}+{ϵ}^2{u}_{lz}^{\left(2\right)},\hfill \\ \psi =0+ϵ{\psi }^{\left(1\right)}+{ϵ}^2{\psi }^{\left(2\right)}.\hfill \end{array}$$

(12)

Putting the stretch coordinates, i.e., Equations (10) and (11), and the expanded depending variables, i.e., Equation (12), into Equations (1)–(3), we can write the values of $n_l$, $u_{lx}$, $u_{ly}$, and $u_{lz}$ for the lowest order of $ϵ$ as

$$\begin{array}{c}{n}_l^{\left(1\right)}=\frac{{\Omega }_l^{\prime }{l}_z^2+2{\Omega }_{0}sin\theta l_x{l}_z}{{\Omega }_l^{\prime }{M}^2}{\psi }^{\left(1\right)},\hfill \end{array}$$

(13)

$$\begin{array}{c}{u}_{lx}^{\left(1\right)}=\frac{M{u}_{ly}^{\left(1\right)}}{{\Omega }_l^{\prime }}\frac{\partial {\psi }^{\left(1\right)}}{\partial \xi },\hfill \end{array}$$

(14)

$$\begin{array}{c}{u}_{ly}^{\left(1\right)}=\frac{l_x}{{\Omega }_l^{\prime }}\frac{\partial {\psi }^{\left(1\right)}}{\partial \xi },\hfill \end{array}$$

(15)

$$\begin{array}{c}{u}_{lz}^{\left(1\right)}=\frac{M}{l_z}{n}_l^{\left(1\right)}.\hfill \end{array}$$

(16)

Combining Equations (13)–(16) with Equation (12), we obtain the value of the phase velocity of the NAWs in the WDMRQP system as

$$\begin{array}{c}M=l_z{\left[{\left(\frac{1+\delta }{{\gamma }_e{k}_{Te}}\right)}^{-1}\left(1+\frac{2{\Omega }_{0}sin\theta l_x}{{\Omega }_l^{\prime }{l}_z}\right)\right]}^{1/2}\hfill \end{array}$$

(17)

where ${\Omega }_l^{\prime }={\Omega }_{cl}+2{\Omega }_{0}cos\theta$. As we can see, the phase velocity of NAWs in a WDMRQP systems depends on the physical parameters related to the systems. For an irrotational magnetized warm degenerate plasma system, i.e., ${\Omega }_0=0$, the phase velocity of the NAWs can be written as

$$\begin{array}{c}M=l_z{\left(\frac{{\gamma }_e{k}_{Te}}{1+\delta }\right)}^{1/2}.\hfill \end{array}$$

(18)

The phase velocity of NAWs in a irrotational magnetized cold degenerate plasma system, i.e., $k_{Te}=1$, can be represented as

$$\begin{array}{c}M=l_z{\left(\frac{{\gamma }_e}{1+\delta }\right)}^{1/2}.\hfill \end{array}$$

(19)

For a two-component (inertial non-degenerate light nucleus and non-inertial degenerate electrons) irrotational magnetized cold degenerate plasma system, i.e., $\delta =0$, Equation (19) becomes

$$\begin{array}{c}M=l_z{\gamma }_e^{1/2}.\hfill \end{array}$$

(20)

The effects of the presence of non-relativistic ${\gamma }_e=5/3$, ultra-relativistic ${\gamma }_e=4/3$, and relativistic ${\gamma }_e=1$ electron species have been shown in a cold (Figure 1) and warm (Figure 2) magneto-rotating degenerate plasma system. In a cold (warm) degenerate magneto-rotating plasma system, the phase velocity of the NAWs is seen to be maximum in the presence of non-relativistic (ultra-relativistic) electron species. The effects of warm ultra-relativistic and warm non-relativistic electrons on the NA wave speed (Figure 2) are different from the effects of cold ultra-relativistic and cold non-relativistic electrons (Figure 1) due to the non-zero temperature assumption in our WDMRQP system.

The second-order equations are obtained in a similar manner and are expressed as

$$\begin{array}{c}\frac{\partial n_l^{\left(1\right)}}{\partial \tau }+\frac{\partial }{\partial \xi }\left[-M{n}_l^{\left(2\right)}+l_x{u}_{lx}^{\left(1\right)}+l_z{u}_{lz}^{\left(1\right)}+\frac{l_z}{M}{n}_l^{\left(1\right)}{u}_{lz}^{\left(1\right)}\right]=0,\hfill \end{array}$$

(21)

$$\begin{array}{c}\frac{\partial }{\partial \xi }\left[\frac{\partial u_{lx}^{\left(1\right)}}{\partial \xi }-\frac{l_x}{M}{\psi }^{\left(2\right)}+\frac{{\Omega }_l^{\prime }}{M}{u}_{ly}^{\left(2\right)}\right]=0,\hfill \end{array}$$

(22)

$$\begin{array}{c}\frac{\partial u_{lz}^{\left(1\right)}}{\partial \tau }+\frac{\partial }{\partial \xi }\left[-M{u}_{lz}^{\left(2\right)}+\frac{1}{2}{l}_z{\left[u_{lz}^{\left(1\right)}\right]}^2+l_z{\psi }^{\left(2\right)}\right]+2{\Omega }_{0}sin\theta u_{ly}^{\left(2\right)}=0,\hfill \end{array}$$

(23)

$$\begin{array}{c}\frac{{\partial }^2\psi }{\partial {\xi }^2}=(1+\delta )\left[\frac{1}{{\gamma }_e{k}_{Te}}{\psi }^{\left(2\right)}+\frac{2-{\gamma }_e}{{\gamma }_e^2{k}_{Te}^2}{\left({\psi }^{\left(1\right)}\right)}^2\right]-n_l^{\left(2\right)},\hfill \end{array}$$

(24)

Finally, the KdV equation for the WDMRQP system was derived as [41]

$$\begin{array}{c}\frac{\partial {\psi }^{\left(1\right)}}{\partial \tau }+A{\psi }^{\left(1\right)}\frac{\partial {\psi }^{\left(1\right)}}{\partial \xi }+B\frac{{\partial }^3{\psi }^{\left(1\right)}}{\partial {\xi }^3}=0,\hfill \end{array}$$

(25)

where A is known as the nonlinear coefficient, and is given by

$$\begin{array}{c}A=\frac{M}{2}\left[2(1+M)\frac{1+\delta }{{\gamma }_e{k}_{Te}}-\frac{2-{\gamma }_e}{{\gamma }_e{k}_{Te}}\right],\hfill \end{array}$$

(26)

and B is the dispersion coefficient and is given by

$$\begin{array}{c}B=\frac{{\gamma }_e{k}_{Te}M}{2(1+\delta )}\left[1+\frac{l_x^2}{{\Omega }_l^{{\prime }^2}}-\frac{2{\Omega }_{0}sin\theta l_x{l}_z}{{\Omega }_l^{{\prime }^3}}\right].\hfill \end{array}$$

(27)

Equation (25) represents the KdV equation, which describes the NAWs with the nonlinear A and dispersion B coefficient defined by Equations (26) and (27), respectively. Both the nonlinear and dispersion coefficient have values greater than zero (i.e., $A>0$ and $B>0$) for all of the possible values of the physical parameters of the WDMRQP system. Therefore, only positive NA solitary waves exist in the considered plasma medium. By assuming the moving frame and boundary conditions as $\zeta =\xi -U_0\tau$ and ${\psi }^{\left(1\right)}\to 0, \partial {\psi }^{\left(1\right)}/\partial \zeta \to 0$ at $\zeta \to \pm \infty$, respectively, we obtain the stationary NA solitary wave (NASW) solution as [41]

$$\begin{array}{c}\psi ={\psi }_0{\mathrm{sech}}^2\left(\frac{\zeta }{▵}\right),\hfill \end{array}$$

(28)

where the amplitude and the width are, respectively, given by ${\psi }_0=3U_0/A$ and $▵=2\sqrt{B/U_0}$.

4. Discussion

A warm degenerate magneto-rotating quantum plasma system containing warm non-relativistic or warm ultra-relativistic electron species, non-degenerate light nucleus species, and a static heavy nucleus was taken into consideration to investigate the basic nonlinear properties (viz. amplitude and width) of NASWs. The rotation speed of the plasma system around the z-axis was considered small. The effects of the degenerate electrons (via ${\gamma }_e$), warm degenerate parameter (via ${\sigma }_{Te}$), rotational frequency of the plasma system (via ${\Omega }_0$), inclination angle (via $\theta$), and the static heavy nucleus (via $\delta$) were observed on the generation, propagation, and the basic characteristics of the NASWs in the WDMRQP system. The values of the physical parameters of the system, such as ${\sigma }_{Te}$ [9], ${\Omega }_0$ [10], $\theta$ [10], and $\delta$ [9], were taken as corresponding to hot white dwarfs [33,34,35,36] and neutron stars. The findings are listed below:

• The presence of non-relativistic or ultra-relativistic electron species in the WDMRQP system supports the existence and propagation of compressional NASWs.
• The amplitude of the NASW potential decreases as the temperature is increased in the degenerate non-relativistic plasma medium as shown in Figure 3. The potential height and width of NASWs is maximum for the cold degenerate system (i.e., ${\sigma }_{Te}=0$) in the presence of non-relativistic electron species.
• As depicted in Figure 4, due to the presence of ultra-relativistic electrons, the potential height becomes maximum as the temperature of the system is increased. Hence, it can be said that the strength of the NASWs increases in the warm degenerate ultra-relativistic magneto-rotating plasma system. Both the amplitude and width of the NASW potential decrease for the cold degenerate ultra-relativistic system. It is evident from Figure 3 and Figure 4 that the temperature effect on the strength of NAWs is different in the case of the non-relativistic (Figure 3) and ultra-relativistic plasma system (Figure 4). The amplitude and width of the NAWs increase (decrease) with the increase in temperature of the ultra-relativistic (non-relativistic) electrons in the three-dimensional magneto-rotating degenerate plasma system.
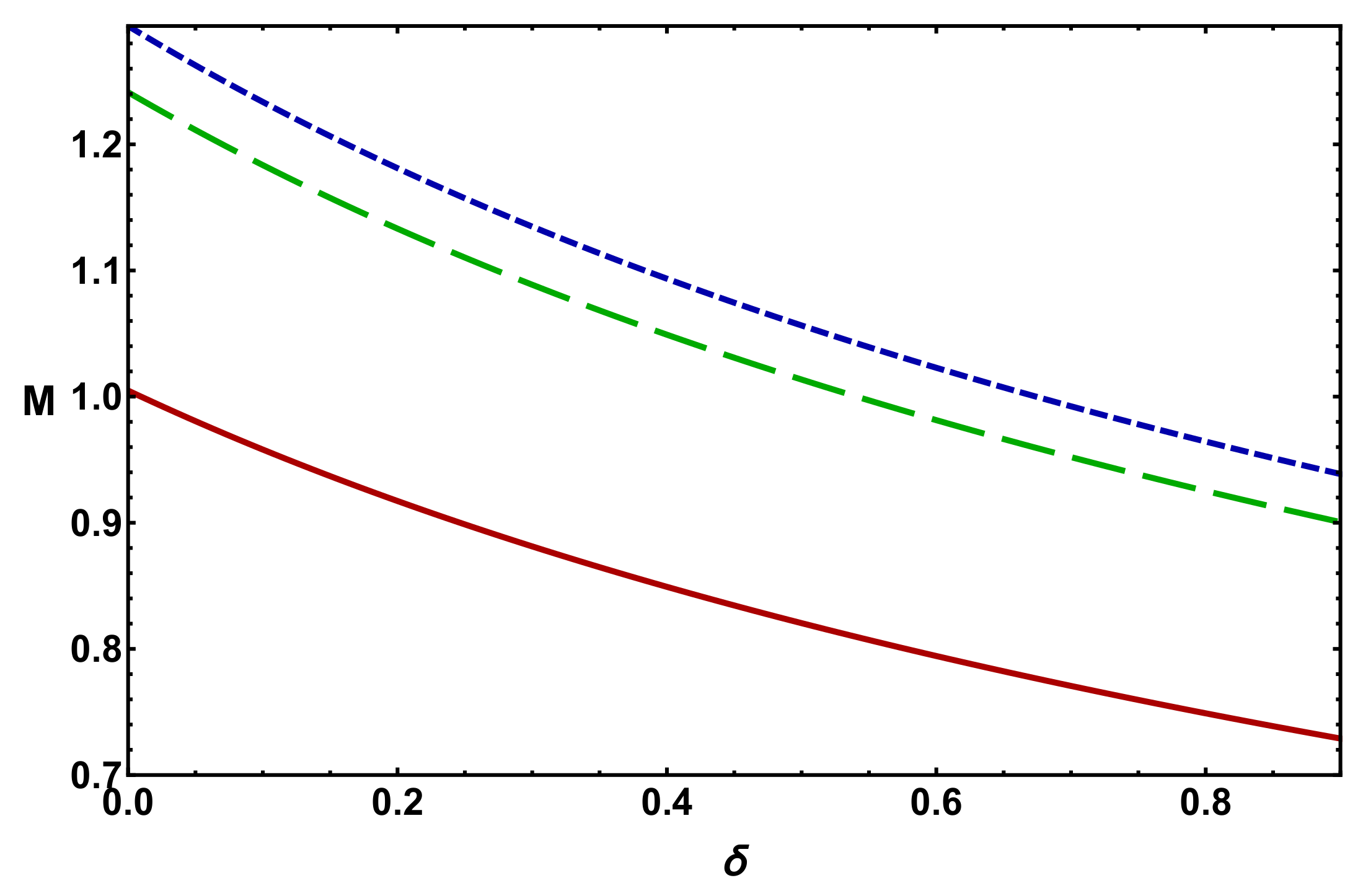
• The rotational frequency ${\Omega }_0$ of the plasma system does not affect the amplitude of the NASWs. However, the width of the NA wave potential decreases with an increasing rotational speed of the plasma system as shown in Figure 5.
• The width of the NASWs is observed to increase with the increase in the inclination angle of the rotation of the warm degenerate plasma system. As the rotation angle increases, the height of the positive potential decreases (Figure 6).
• The presence of a static heavy nucleus not only supports the existence of a positive NASW potential but also modifies the basic features of NASWs as shown in Figure 7. The amplitude and width of the NASW potential are decreased with the increase in the heavy nucleus number density and charge state. On the other hand, the amplitude and width of the NASWs increase with the decrease in the light nucleus number density and charge state.

The WDMRQP model presented in this paper is applicable to the hot white dwarf [33,34,35,36], as well as useful in describing the solitary wave potential generated in the magneto-rotating warm degenerate systems, such as neutron star and pulsars. The simple assumptions of this model allow us to broaden the area of the investigation of a cold/warm degenerate magneto-rotating/magnetized plasma system. However, the investigation of non-planar NA wave potential in the WDMRQP system was not included in this work. In addition, the arbitrary amplitude NA wave was not observed in the WDMRQP system, as it is beyond the scope of our present work. It should be mentioned here that the Bohm quantum term or the quantum diffraction term (arising from the kinetic term in the Schrödinger equation) [10], as well as the spin effects, such as exchange-correlation effects [42,43], were ignored in this present investigation. It may also be noted that the inclusion of the temperature effect in the Bohm potential undoubtedly provides a better observation for wave-like behaviour in the quantum regime, and also requires a new mathematical analysis that is currently beyond the scope of our present investigation. Finally, we hope that our investigation can a make a difference to the understanding of the nonlinear phenomenon observed in magneto-rotating space plasma such as hot white dwarfs (such as DQ white dwarfs, white dwarfs H1504 + 65, white dwarf PG 0948 + 534, etc.) [33,34,35,36] and neutron stars.