Self-Propelled Swimming of a Flexible Propulsor Actuated by a Distributed Active Moment
Abstract
1. Introduction
2. Physical Models and Governing Equations
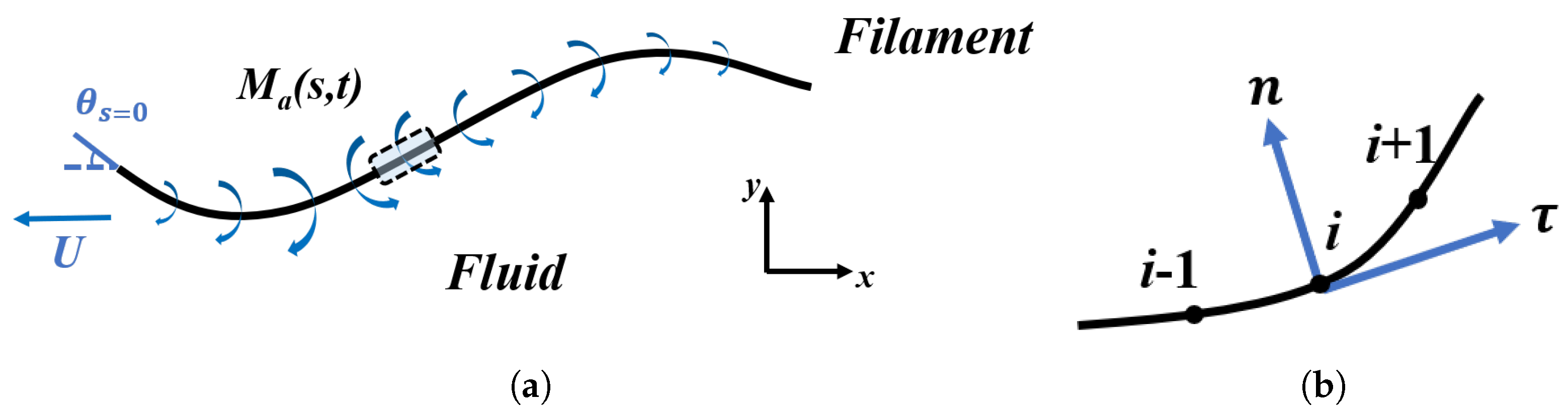
2.1. Physical Models
2.2. Governing Equations
3. Numerical Method and Settings
3.1. Numerical Method
3.2. Numerical Settings
4. Results and Discussion
4.1. Controls Parameters and Netrics of Performance
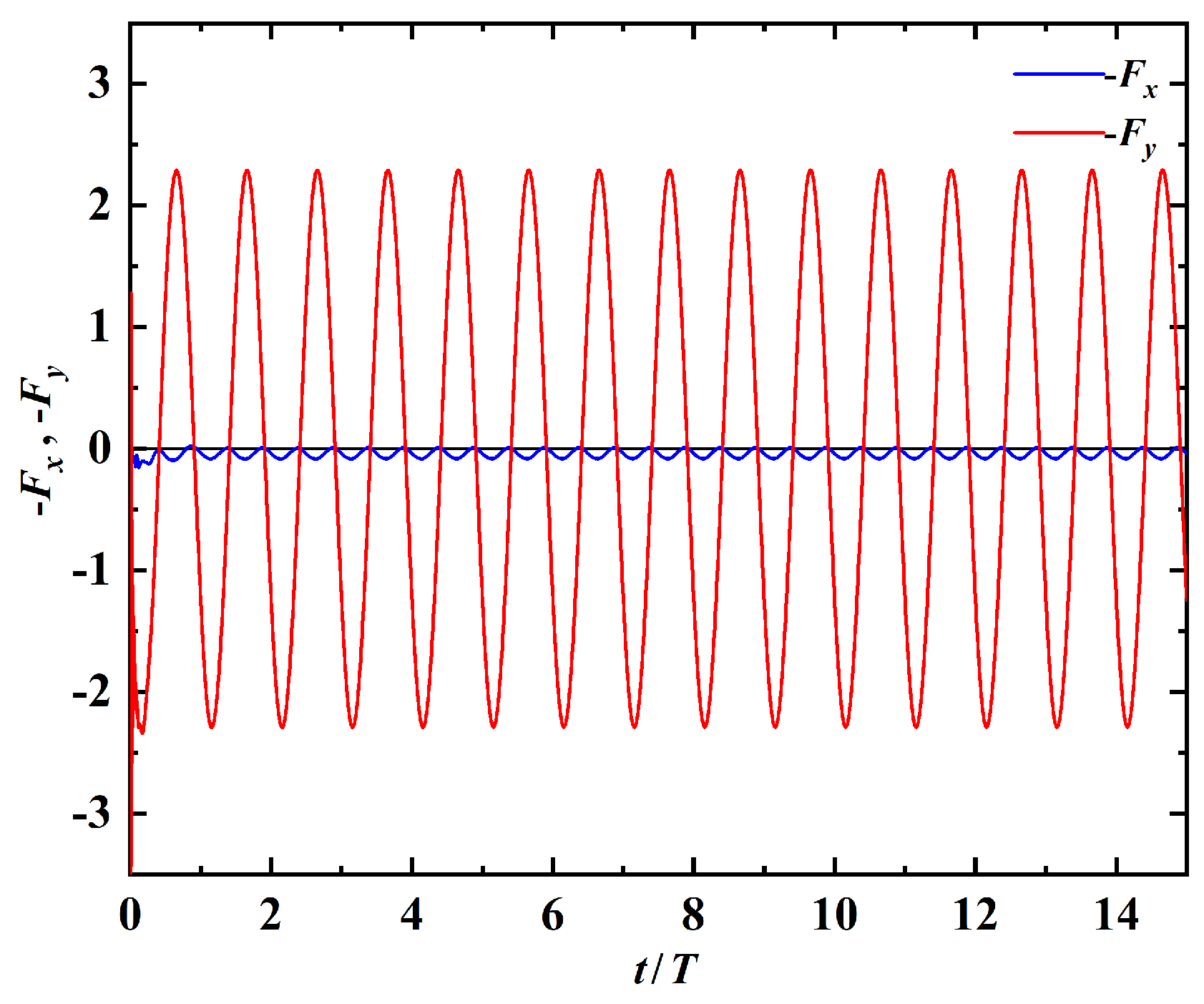
4.2. Straight-Line Swimming
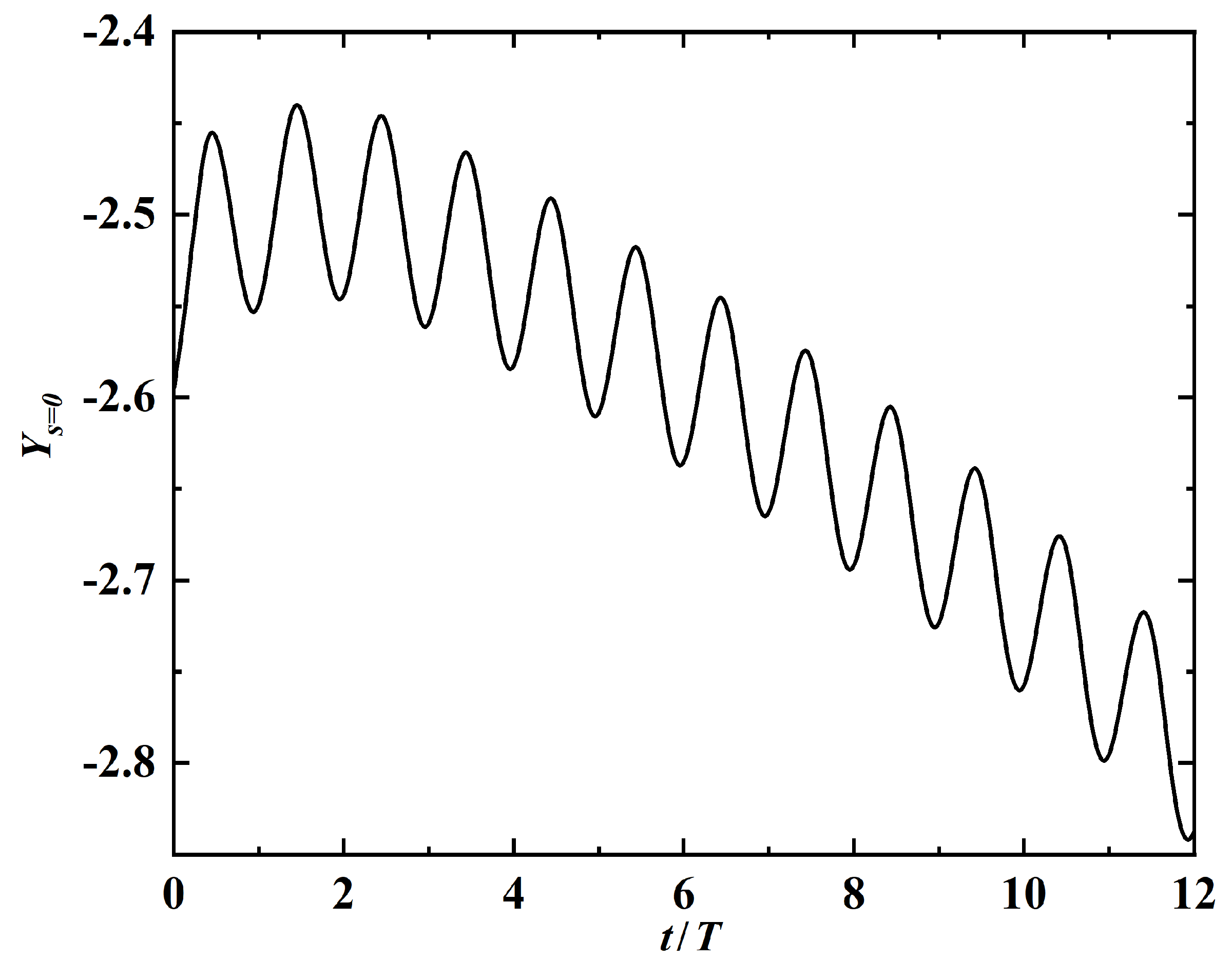
4.3. Locomotion near a Solid Wall
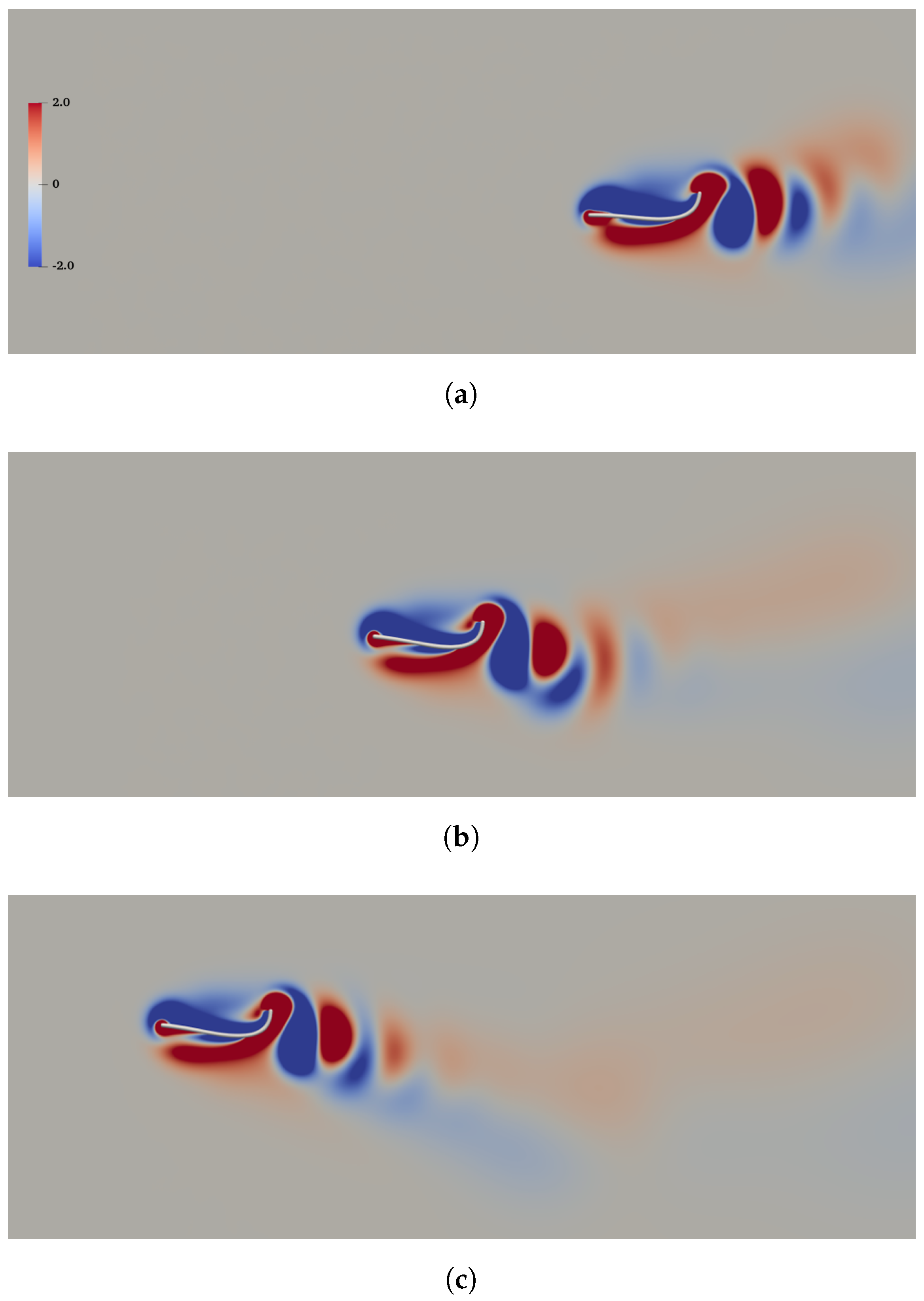
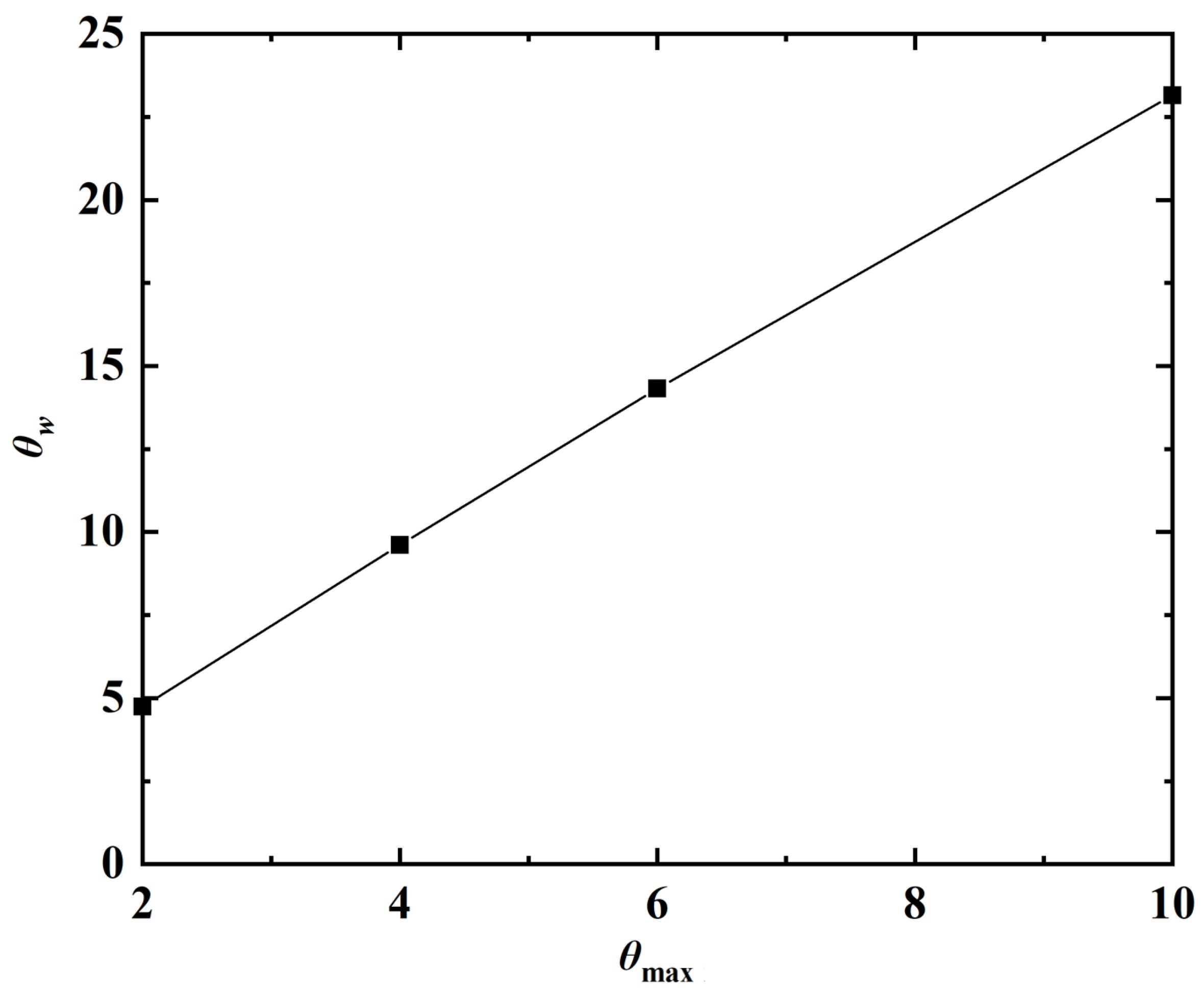
4.4. Turning Maneuver
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
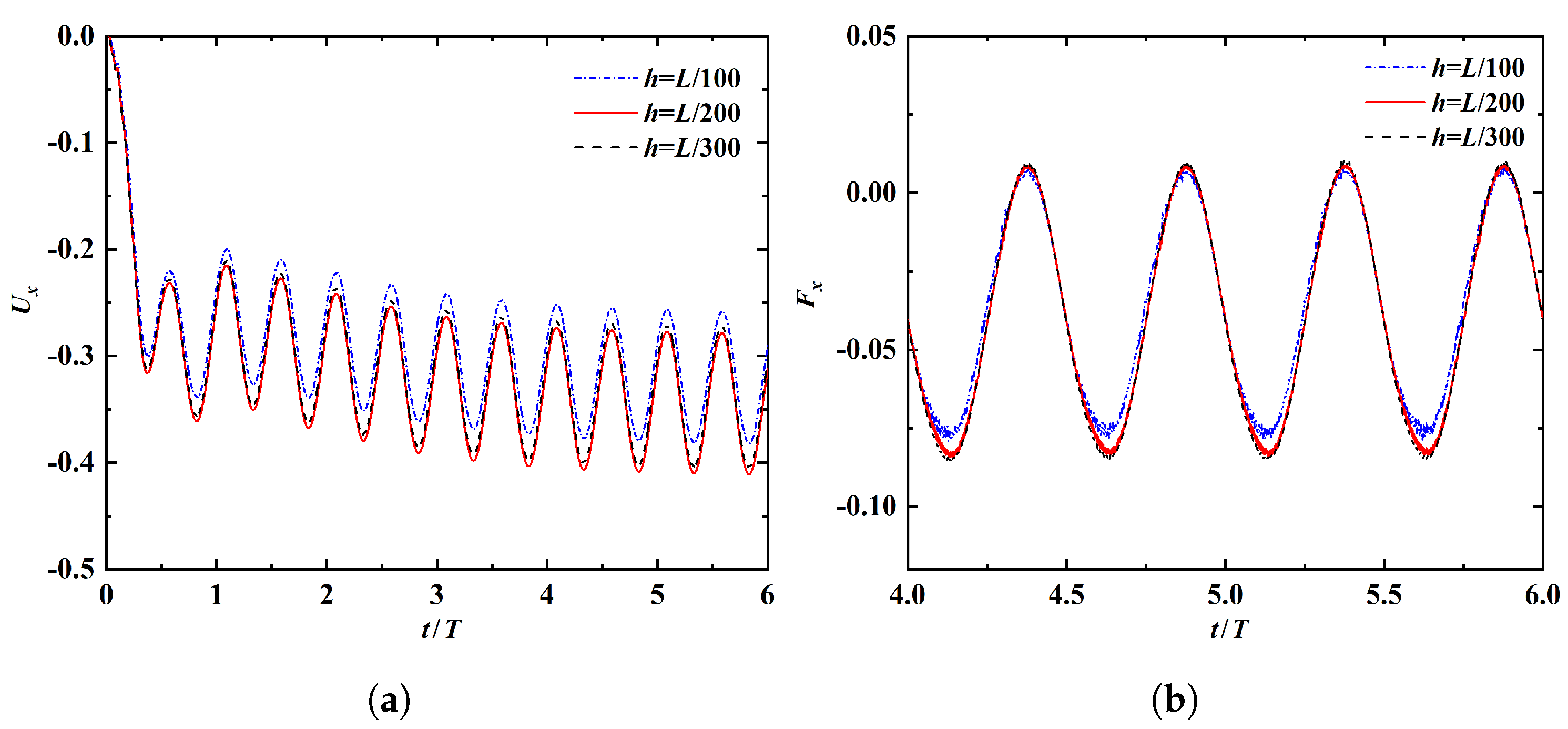
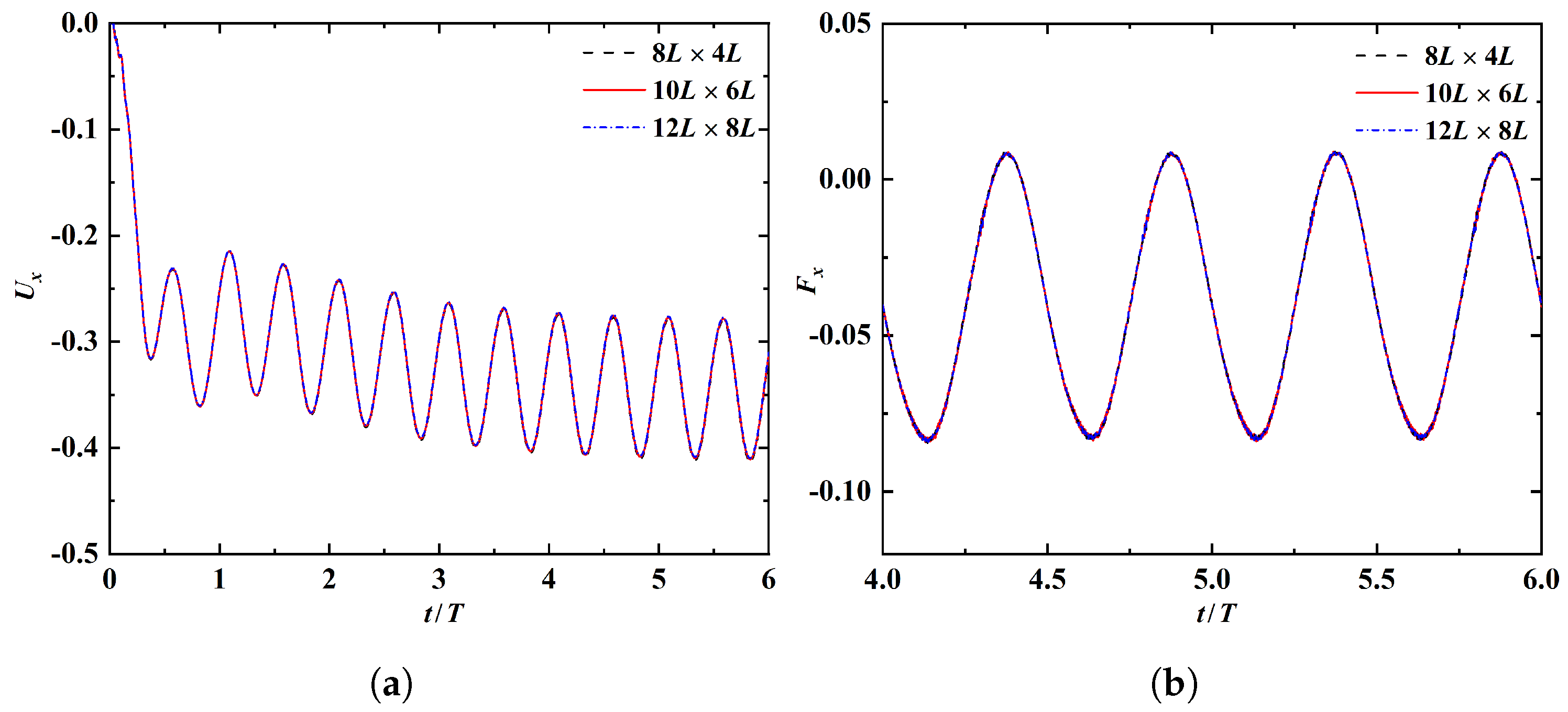
Appendix A. Mesh, Time-Step and Domain Independence Tests
| Mesh 1 | Points per Chord Length | Total Grid Points (Million) |
|---|---|---|
| C | 101 | 0.6 |
| M | 201 | 2.4 |
| F | 301 | 5.4 |

References
- Wu, X.; Zhang, X.; Tian, X.; Li, X.; Lu, W. A review on fluid dynamics of flapping foils. Ocean. Eng. 2020, 195, 106712. [Google Scholar] [CrossRef]
- Lauder, G.V.; Anderson, E.J.; Tangorra, J.; Madden, P.G. Fish biorobotics: Kinematics and hydrodynamics of self-propulsion. J. Exp. Biol. 2007, 210, 2767–2780. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.Z.; He, G.W.; Zhang, X. Self-propulsion of flapping bodies in viscous fluids: Recent advances and perspectives. Acta Mech. Sin. 2016, 32, 980–990. [Google Scholar] [CrossRef]
- Lin, X.J.; Wu, J.; Zhang, T.W. Self-directed propulsion of an unconstrained flapping swimmer at low Reynolds number: Hydrodynamic behaviour and scaling laws. J. Fluid Mech. 2020, 907, R3. [Google Scholar] [CrossRef]
- Lucas, K.N.; Johnson, N.; Beaulieu, W.T.; Cathcart, E.; Tirrell, G.; Colin, S.P.; Gemmell, B.J.; Dabiri, J.O.; Costello, J.H. Bending rules for animal propulsion. Nat. Commun. 2014, 5, 3293. [Google Scholar] [CrossRef]
- Erturk, A.; Delporte, G. Underwater thrust and power generation using flexible piezoelectric composites: An experimental investigation toward self-powered swimmer-sensor platforms. Smart Mater. Struct. 2011, 20, 125013. [Google Scholar] [CrossRef]
- Gao, B.F.; Guo, S.X. Dynamic mechanics and electric field analysis of an ICPF actuated fish-like underwater microrobot. In Proceedings of the 2011 IEEE International Conference on Automation and Logistics (ICAL), Chongqing, China, 15–16 August 2011; pp. 330–335. [Google Scholar]
- Wang, C.; Tang, H.; Zhang, X. Fluid-structure interaction of bio-inspired flexible slender structures: A review of selected topics. Bioinspiration Biomim. 2022, 17, 041002. [Google Scholar] [CrossRef]
- Kern, S.; Koumoutsakos, P. Simulations of optimized anguilliform swimming. J. Exp. Biol. 2006, 209, 4841–4857. [Google Scholar] [CrossRef]
- Hua, R.N.; Zhu, L.D.; Lu, X.Y. Locomotion of a flapping flexible plate. Phys. Fluids 2013, 25, 121901. [Google Scholar] [CrossRef]
- Zhu, X.J.; He, G.W.; Zhang, X. Numerical study on hydrodynamic effect of flexibility in a self-propelled plunging foil. Comput. Fluids 2014, 97, 1–20. [Google Scholar] [CrossRef]
- Kim, B.; Park, S.G.; Huang, W.; Sung, H.J. Self-propelled heaving and pitching flexible fin in a quiescent flow. Int. J. Heat Fluid Flow 2016, 62, 273–281. [Google Scholar] [CrossRef]
- Li, B.L.; Wang, Y.W.; Yin, B.; Zhang, X.; Zhang, X. Self-propelled swimming of a flexible filament driven by coupled plunging and pitching motions. J. Hydrodyn. 2021, 33, 157–169. [Google Scholar] [CrossRef]
- Wu, W. Study on the propulsion of the rigid-flexible composite plate driven on two points. Fluid Dyn. Res. 2022, 54, 035501. [Google Scholar] [CrossRef]
- Luo, Y.; Wright, M.; Xiao, Q.; Yue, H.; Pan, G. Fluid-structure interaction analysis on motion control of a self-propelled flexible plate near a rigid body utilizing PD control. Bioinspiration Biomim. 2021, 16, 066002. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.; Park, S.G.; Huang, W.; Sung, H.J. An autonomous flexible propulsor in a quiescent flow. Int. J. Heat Fluid Flow 2017, 68, 151–157. [Google Scholar] [CrossRef]
- Lin, Z.; Hess, A.; Yu, Z.; Cai, S.; Gao, T. A fluid-structure interaction study of soft robotic swimmer using a fictitious domain/active-strain method. J. Comput. Phys. 2019, 376, 1138–1155. [Google Scholar] [CrossRef]
- Hess, A.; Tan, X.; Gao, T. CFD-based multi-objective controller optimization for soft robotic fish with muscle-like actuation. Bioinspiration Biomim. 2020, 15, 035004. [Google Scholar] [CrossRef]
- Curatolo, M.; Teresi, L. Modeling and simulation of fish swimming with active muscles. J. Theor. Biol. 2016, 409, 18–26. [Google Scholar] [CrossRef]
- Hoover, A.P.; J. Daniels, J.; Nawroth, J.C.; Katija, K. A computational model for tail undulation and fluid transport in the giant larvacean. Fluids 2021, 6, 88. [Google Scholar] [CrossRef]
- Cheng, J.Y.; Pedley, T.J.; Altringham, J.D. A continuous dynamic beam model for swimming fish. Philos. Trans. R. Soc. London. Ser. Biol. Sci. 1998, 353, 981–997. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Y.L.; Tong, B.G. Fish swimming: Patterns in the mechanical energy generation, transmission and dissipation from muscle activation to body movement. AIP Conf. Proc. 2011, 1376, 476–479. [Google Scholar]
- Gazzola, M.; Argentina, M.; Mahadevan, L. Gait and speed selection in slender inertial swimmers. Proc. Natl. Acad. Sci. USA 2015, 112, 3874–3879. [Google Scholar] [CrossRef] [PubMed]
- Gross, D.; Roux, Y.; Argentina, M. Curvature-based, time delayed feedback as a means for self-propelled swimming. J. Fluids Struct. 2019, 86, 124–134. [Google Scholar] [CrossRef]
- Dai, L.; He, G.; Zhang, X. Self-propelled swimming of a flexible plunging foil near a solid wall. Bioinspiration Biomim. 2016, 11, 046005. [Google Scholar] [CrossRef]
- Dai, L.; He, G.; Zhang, X.; Zhang, X. Stable formations of self-propelled fish-like swimmers induced by hydrodynamic interactions. J. R. Soc. Interface 2018, 15, 20180490. [Google Scholar] [CrossRef]
- Dai, L.; He, G.; Zhang, X.; Zhang, X. Intermittent locomotion of a fish-like swimmer driven by passive elastic mechanism. Bioinspiration Biomim. 2018, 13, 056011. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X. An immersed boundary method based on discrete stream function formulation for two-and three-dimensional incompressible flows. J. Comput. Phys. 2011, 230, 3479–3499. [Google Scholar] [CrossRef]
- Zhu, X.; He, G.; Zhang, X. An improved direct-forcing immersed boundary method for fluid-structure interaction simulations. J. Fluids Eng. 2014, 136, 040903. [Google Scholar] [CrossRef]
- Wang, S.; He, G.; Zhang, X. Parallel computing strategy for a flow solver based on immersed boundary method and discrete stream-function formulation. Comput. Fluids 2013, 88, 210–224. [Google Scholar] [CrossRef]
- Liu, L.; Zhong, Q.; Han, T.; Moored, K.W.; Quinn, D.B. Fine-tuning near-boundary swimming equilibria using asymmetric kinematics. Bioinspiration Biomim. 2022, 18, 016011. [Google Scholar] [CrossRef]


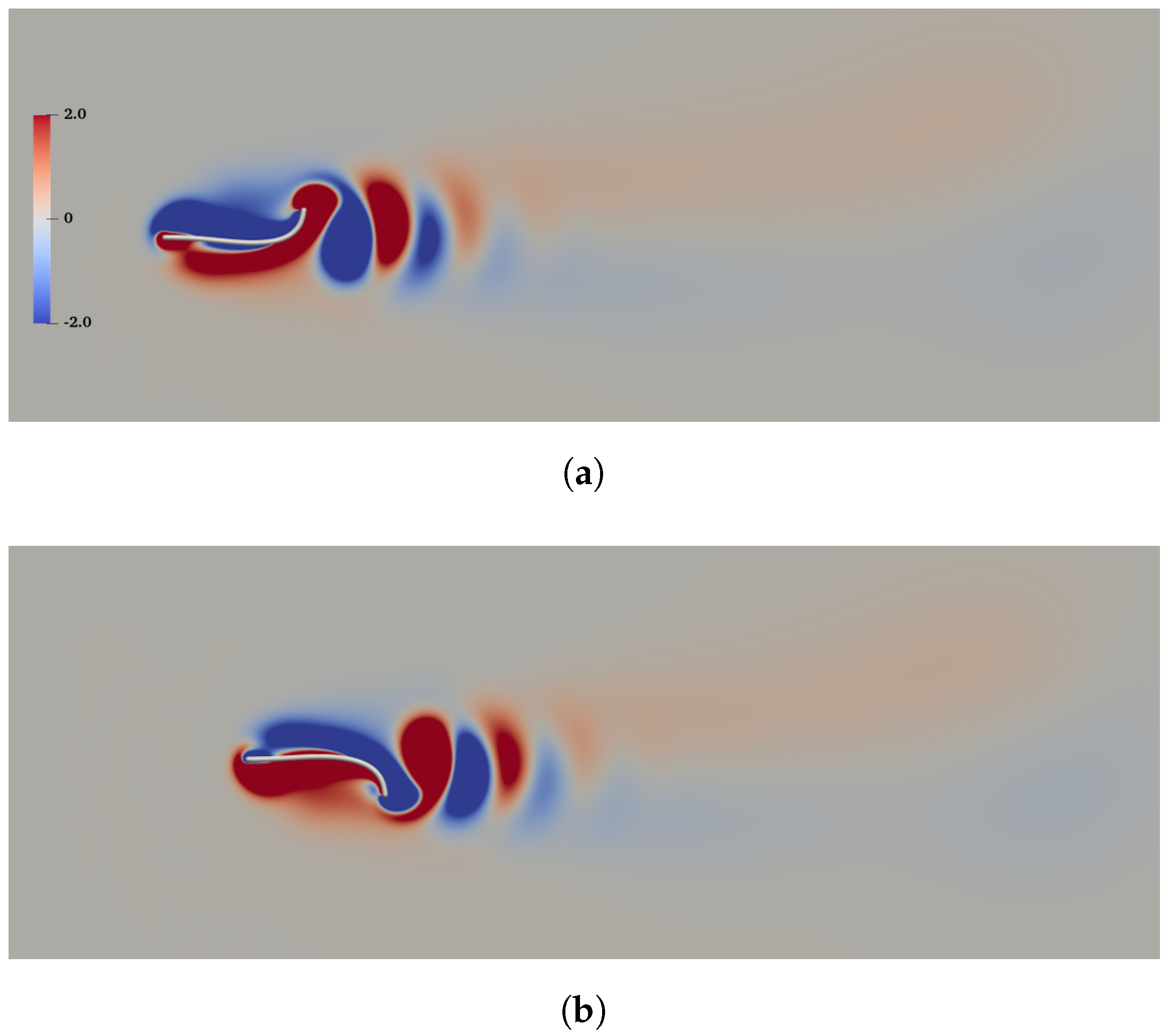
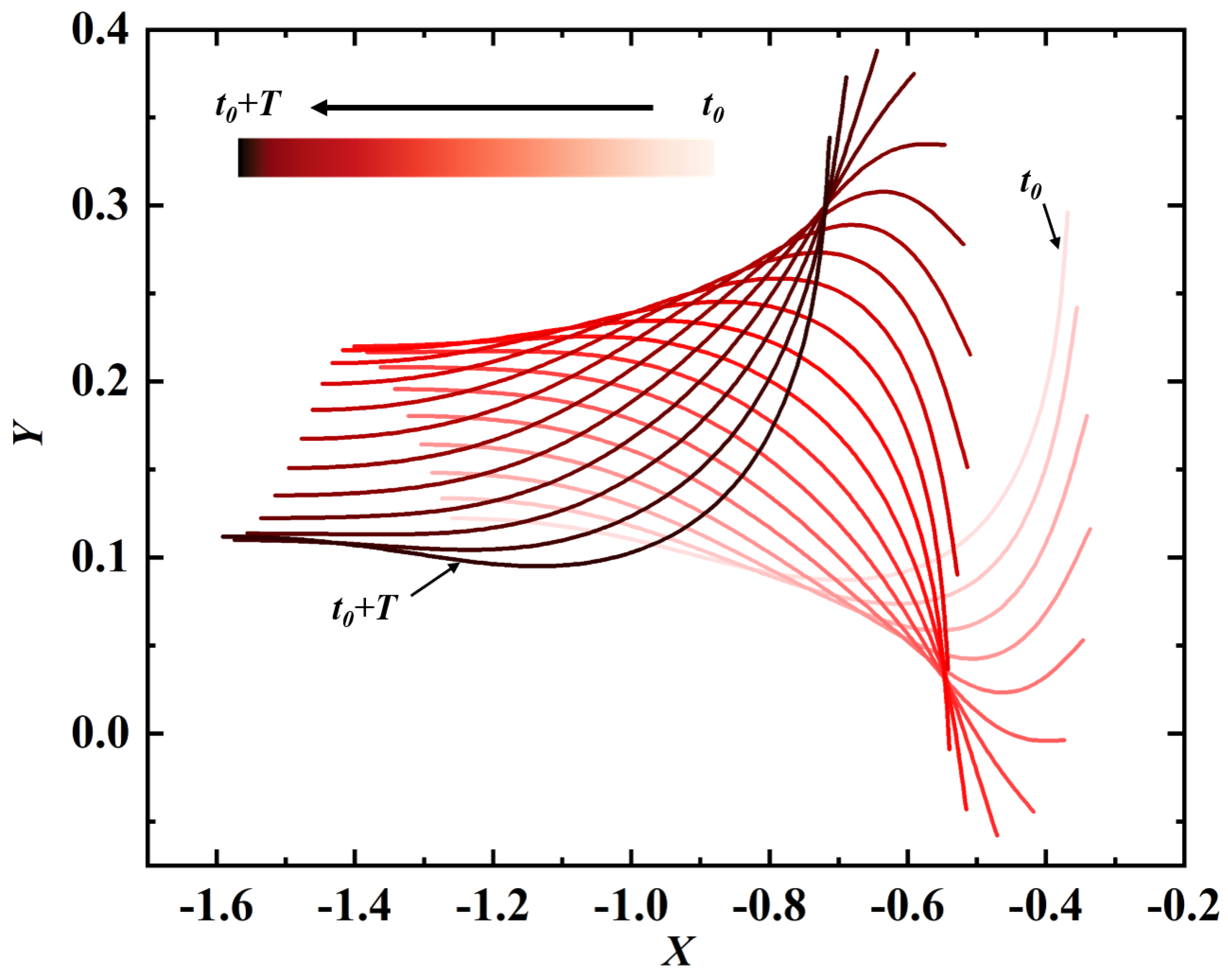
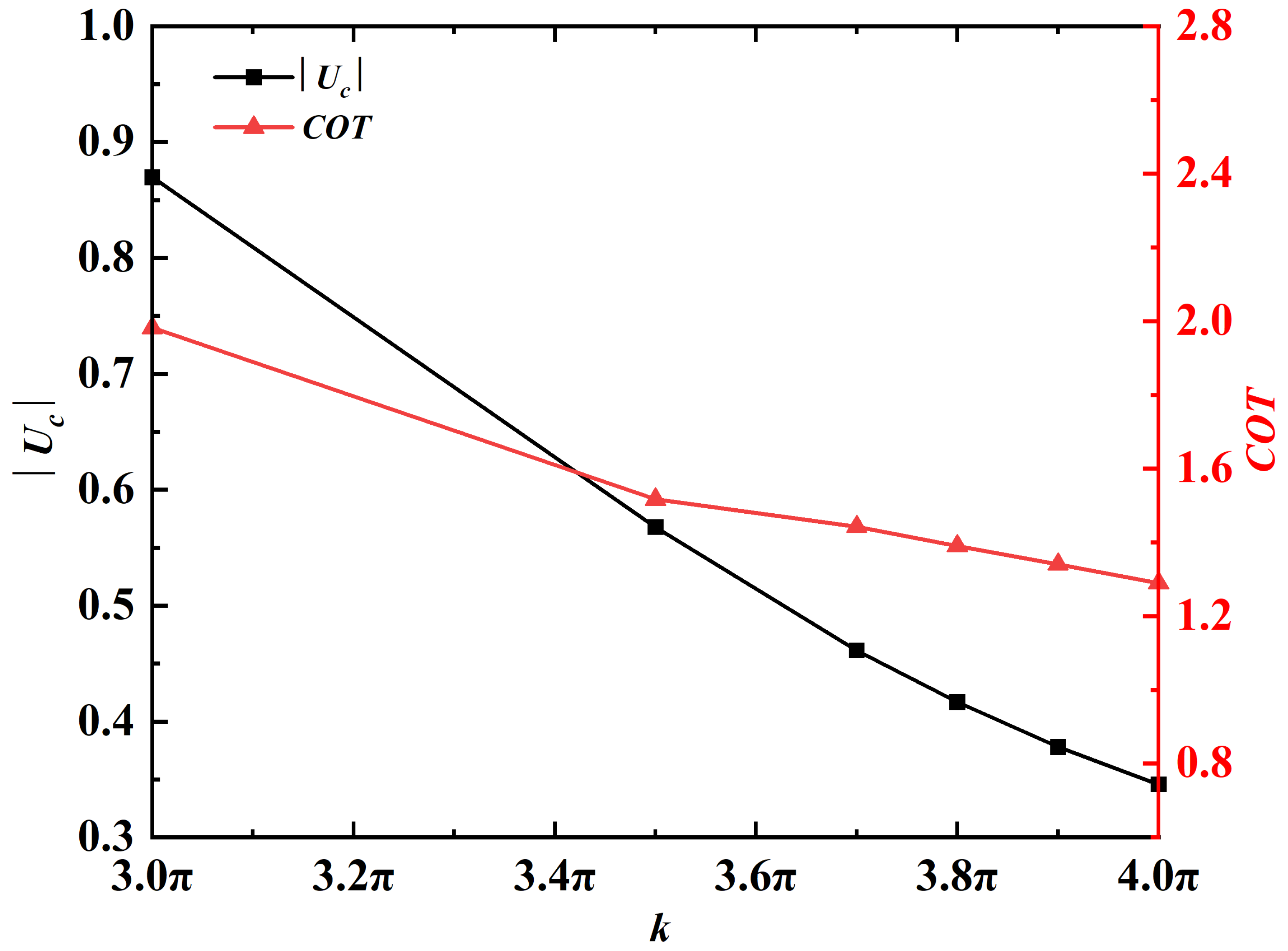
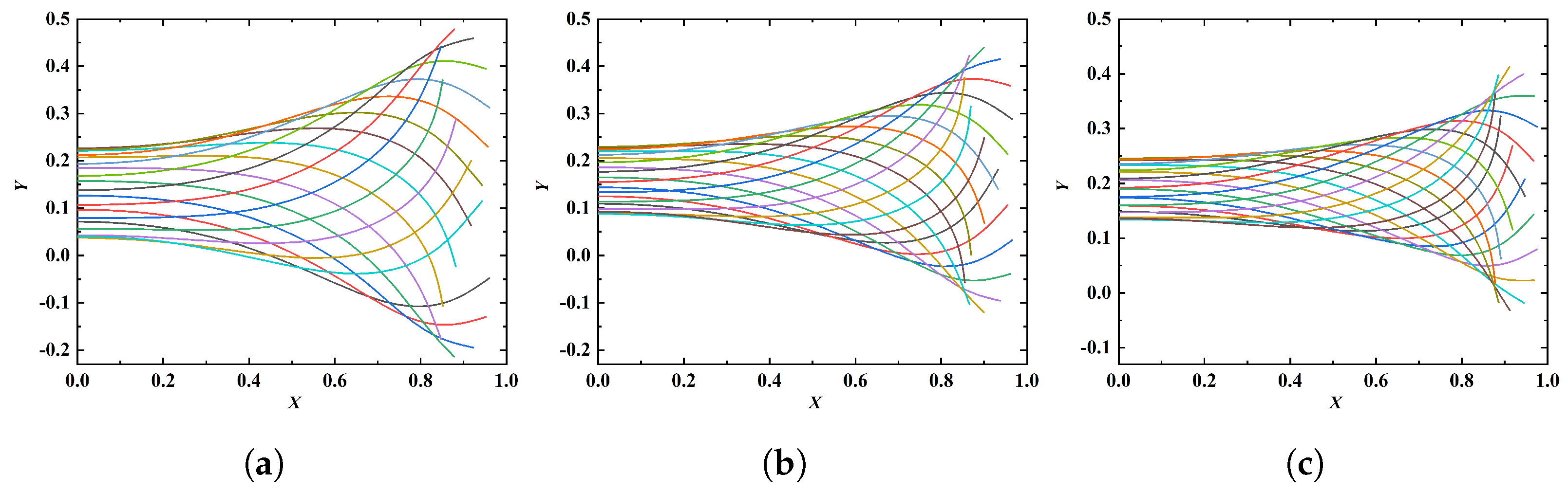
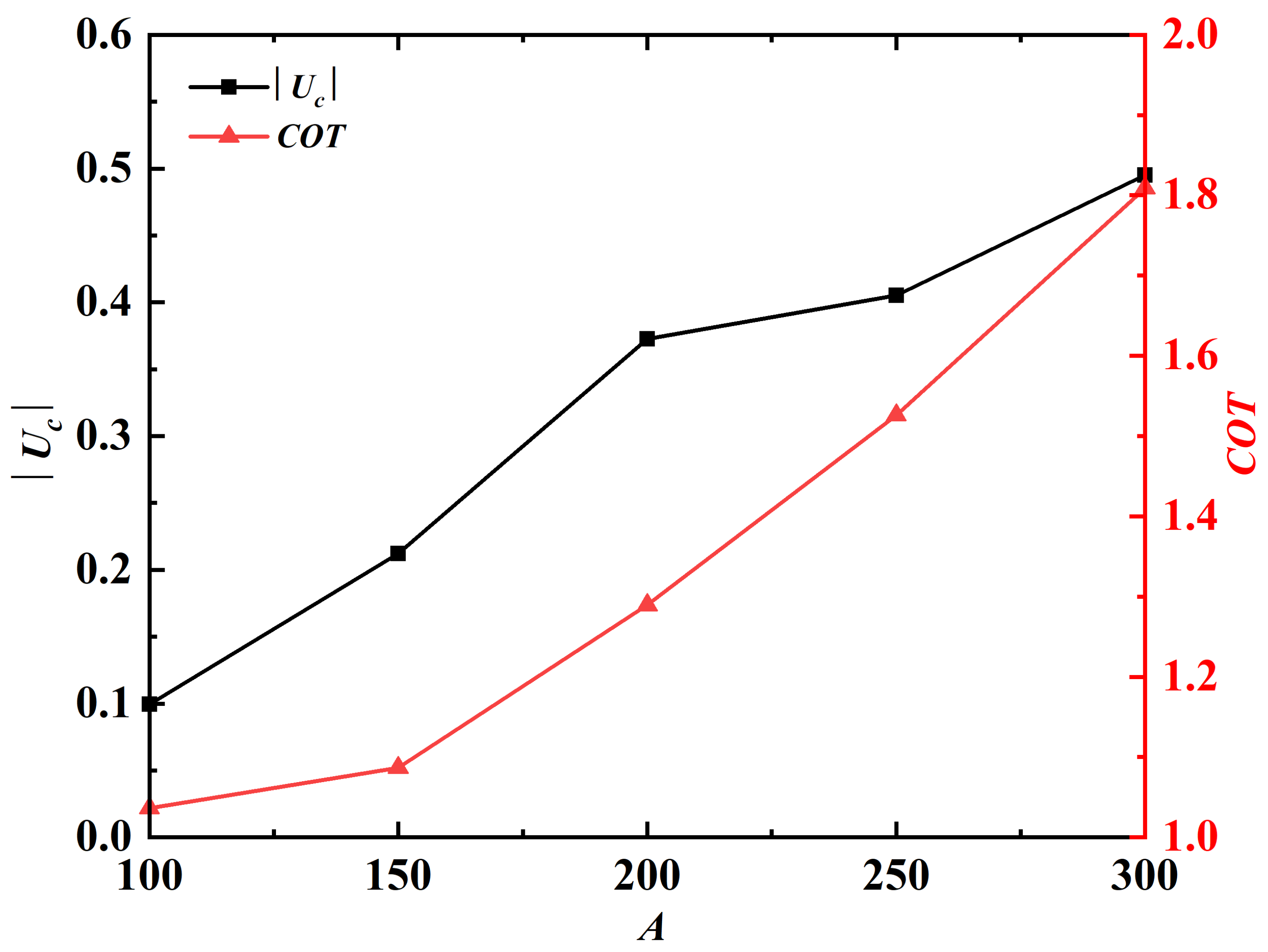
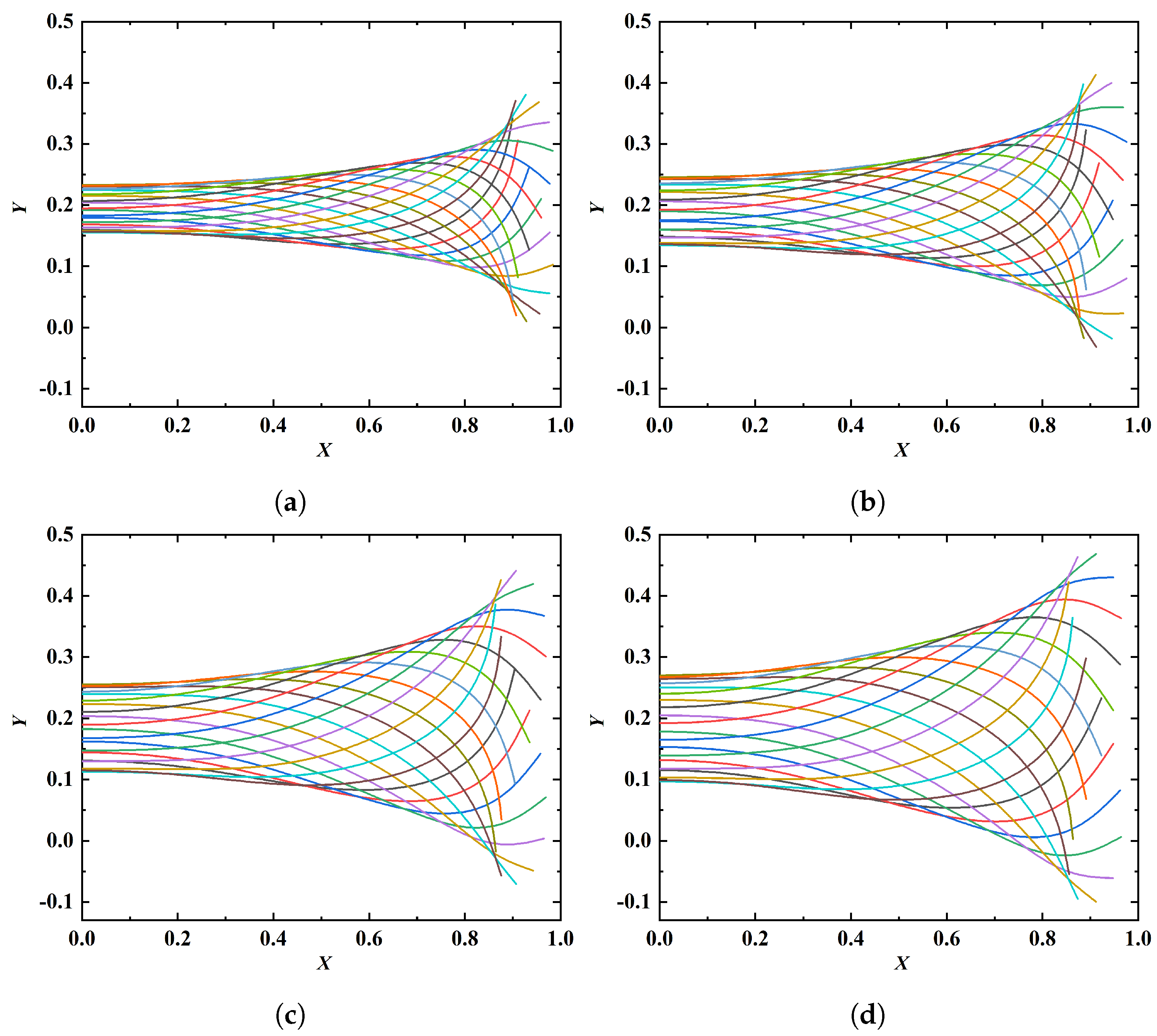

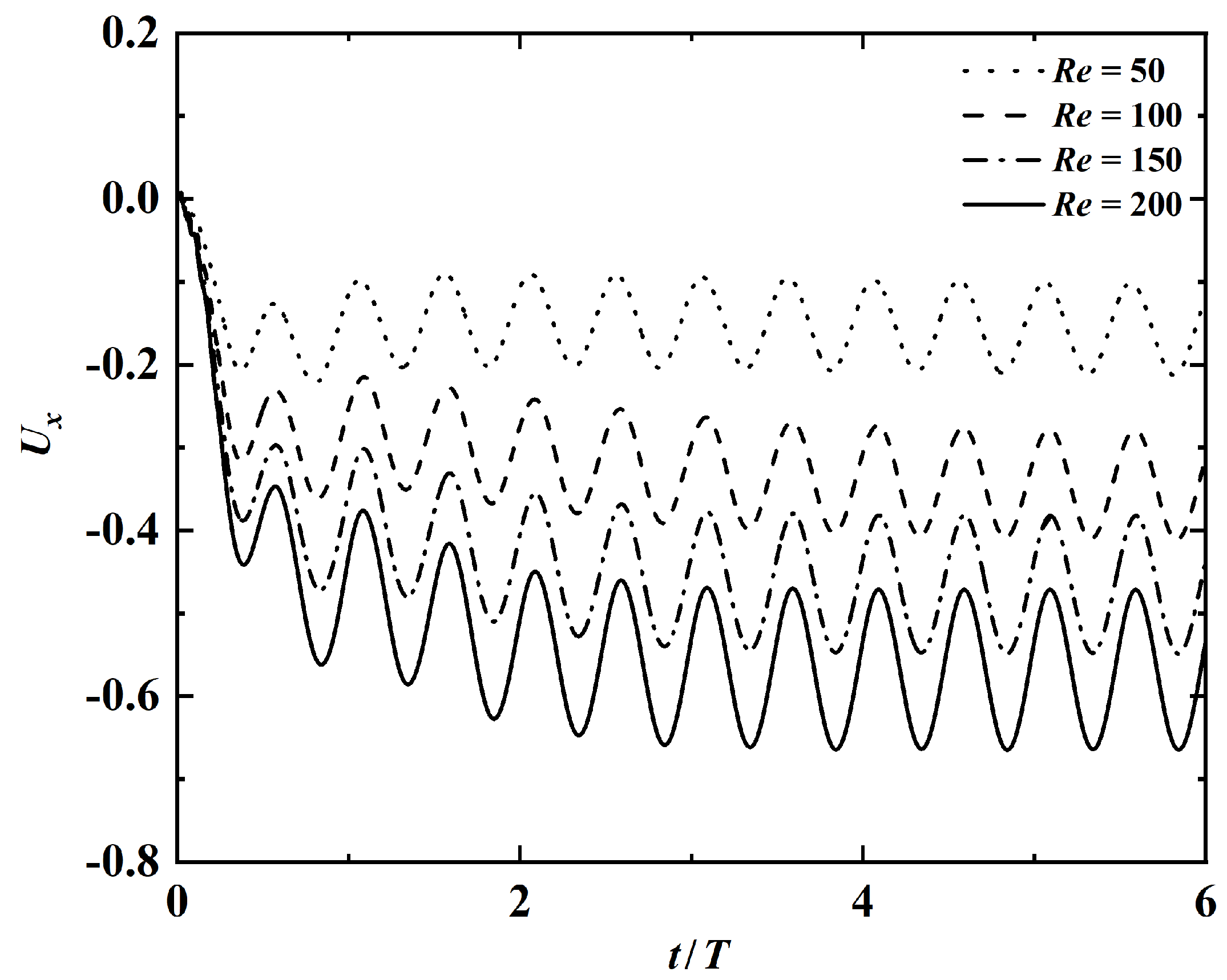
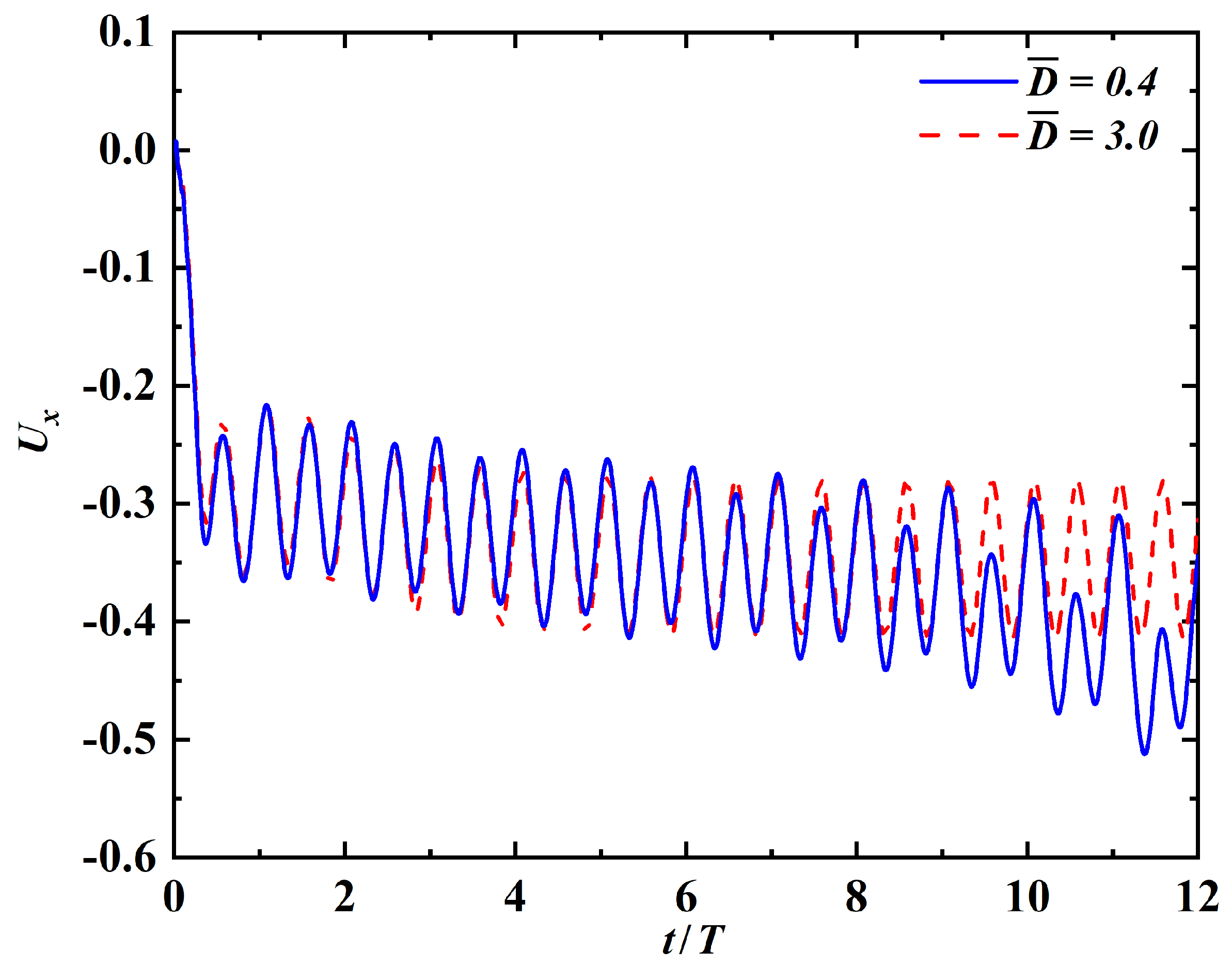





| k | , , , , , |
| A | 100, 150, 200, 250, 300 |
| Re | 50, 100, 150, 200 |
| k | Amplitude Ratio |
|---|---|
| 0.250 | |
| 0.254 | |
| 0.274 |
| A | Amplitude Ratio |
|---|---|
| 100 | 0.289 |
| 150 | 0.319 |
| 200 | 0.360 |
| 250 | 0.403 |
| 300 | 0.448 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, C.; Zhang, Z.; Zhang, X. Self-Propelled Swimming of a Flexible Propulsor Actuated by a Distributed Active Moment. Fluids 2023, 8, 29. https://doi.org/10.3390/fluids8010029
Han C, Zhang Z, Zhang X. Self-Propelled Swimming of a Flexible Propulsor Actuated by a Distributed Active Moment. Fluids. 2023; 8(1):29. https://doi.org/10.3390/fluids8010029
Chicago/Turabian StyleHan, Changhong, Zhiyu Zhang, and Xing Zhang. 2023. "Self-Propelled Swimming of a Flexible Propulsor Actuated by a Distributed Active Moment" Fluids 8, no. 1: 29. https://doi.org/10.3390/fluids8010029
APA StyleHan, C., Zhang, Z., & Zhang, X. (2023). Self-Propelled Swimming of a Flexible Propulsor Actuated by a Distributed Active Moment. Fluids, 8(1), 29. https://doi.org/10.3390/fluids8010029








