Experimental Observations on Flow Characteristics around a Low-Aspect-Ratio Wall-Mounted Circular and Square Cylinder
Abstract
:1. Introduction
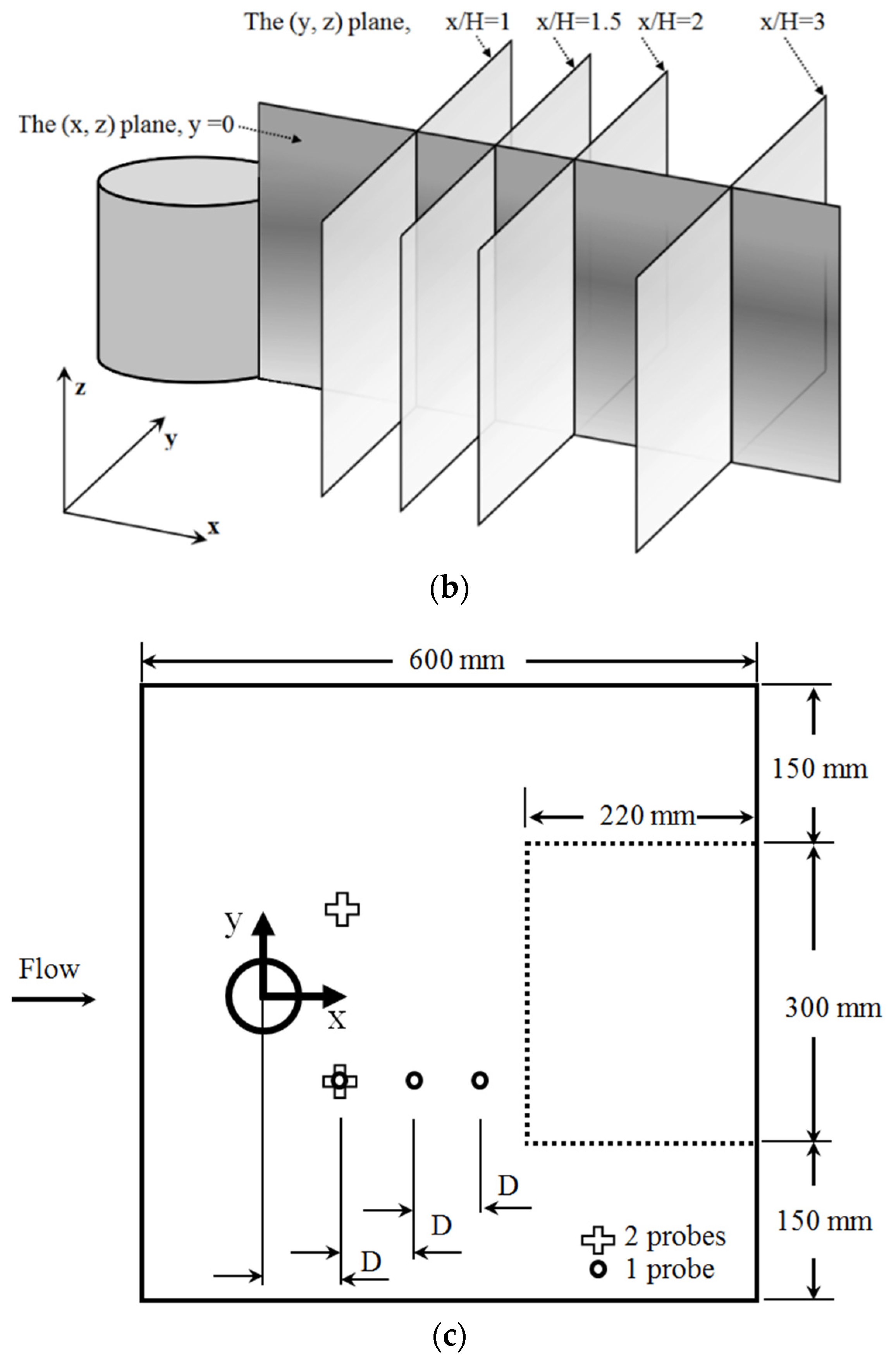
2. Experimental Setup and Methods
3. Results
3.1. Flow Patterns in the Streamwise Symmetry-Plane
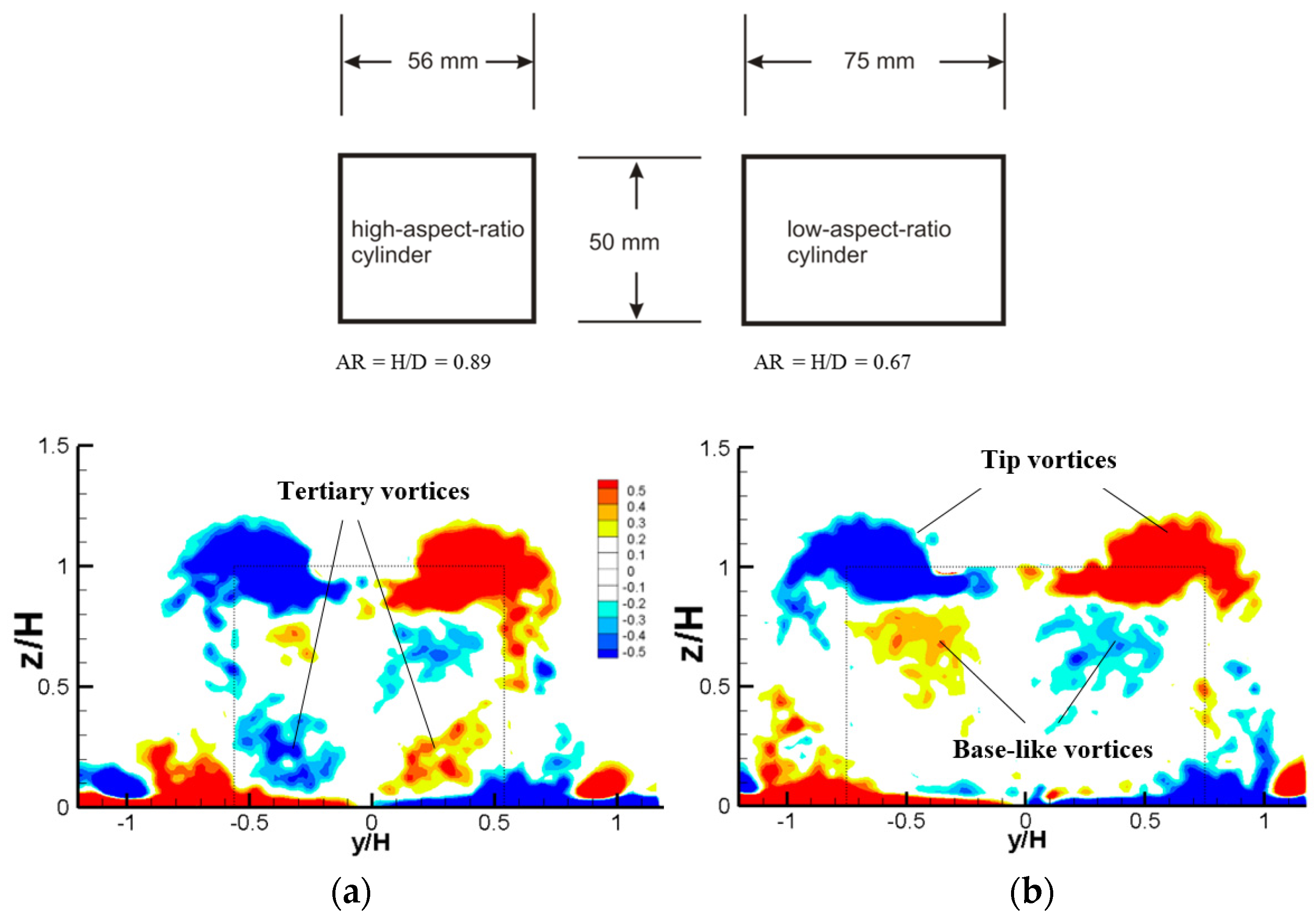
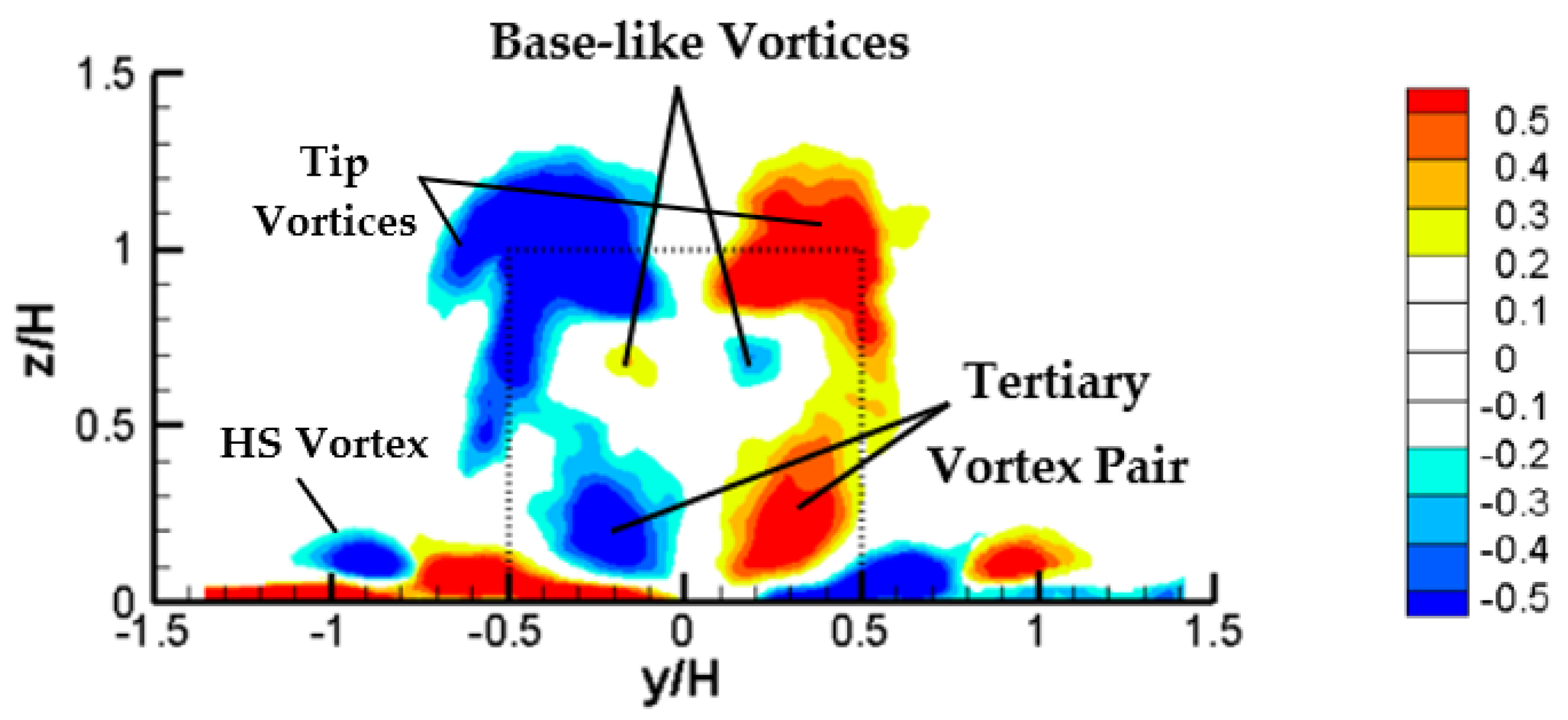
3.2. Flow Patterns in the Wake of Cube
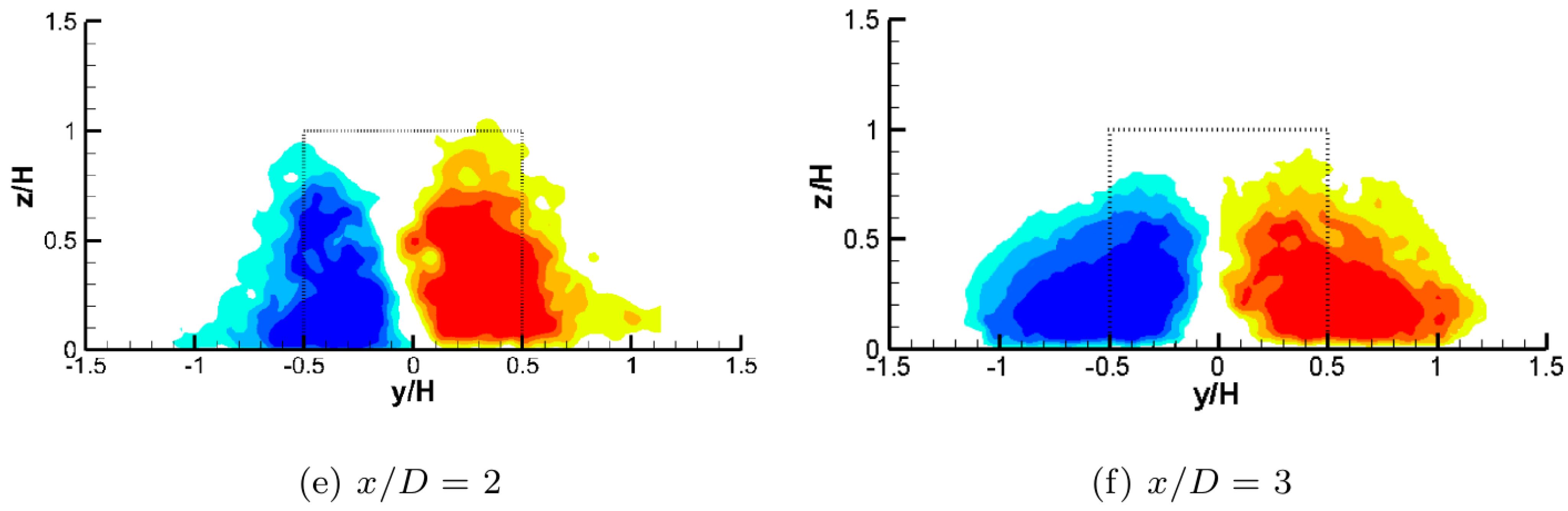
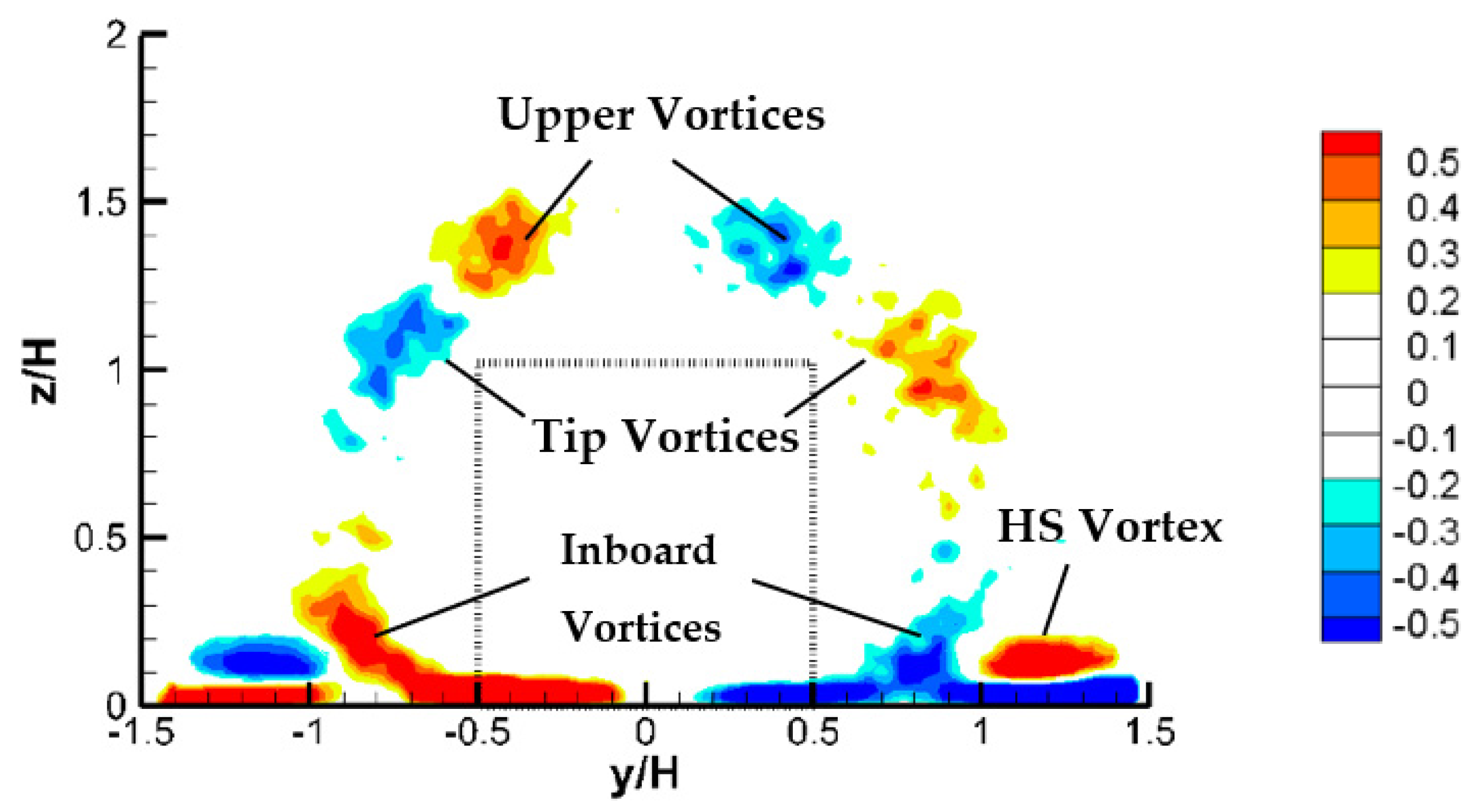
3.3. Flow Patterns in the Wake of Cylinder
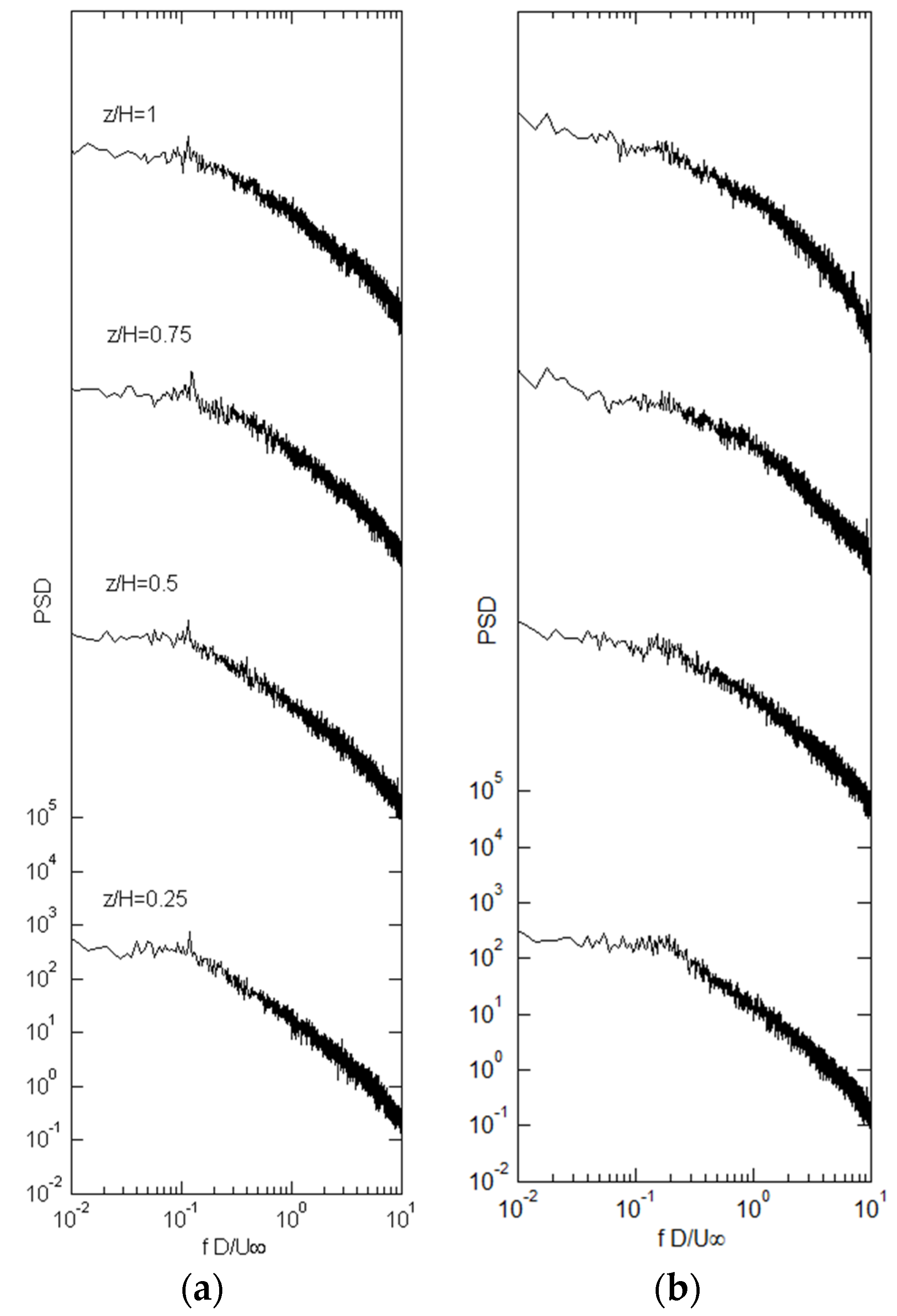
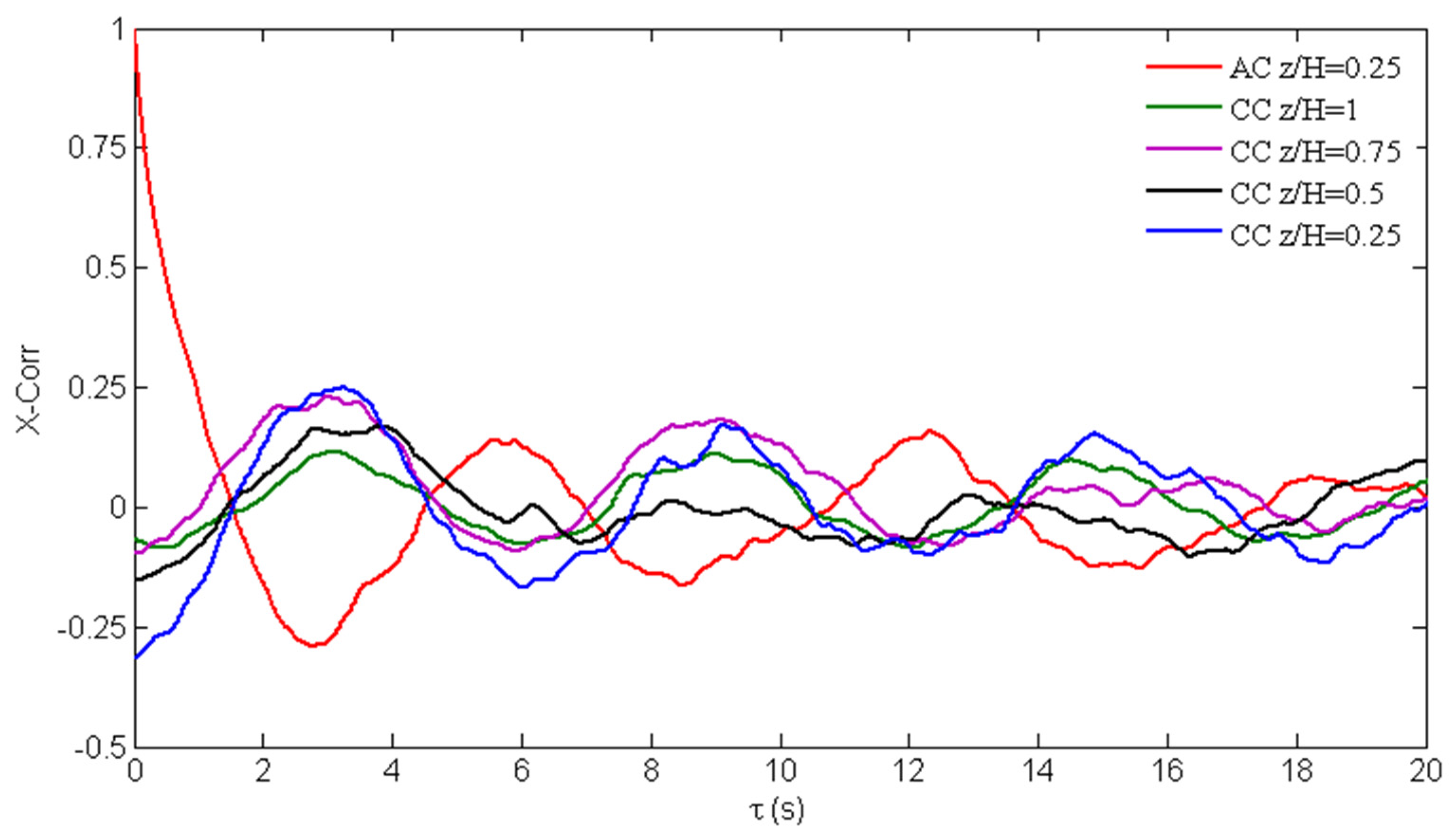
3.4. Shedding Characteristics
4. Discussion
5. Summary and Conclusions
- (1)
- Is the base-vortex connected with other known vortical structures in the mean flow-wake?
- (2)
- What is the nature of the base-vortices in low-aspect-ratio cylinders and their interactions with the instantaneous flow-structures?
- (3)
- Must base-vortices exist concurrently with anti-symmetric Karman-shedding, assuming the existence of intermittent Karman-shedding?
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| x: y, z | Streamwise, transverse (lateral), and spanwise (vertical or wall-normal) directions |
| AR | Aspect Ratio = H/D = 1.0 |
| H | Obstacle height (mm) = 50 |
| D | Obstacle diameter (mm) = 50 |
| d | Flow depth above the base plate (mm) = 175 |
| RS | Relative submergence = d/H = 3.5 |
| δ99/D | Relative thickness of the boundary-layer = 0.14 |
| U∞ | Free-stream velocity (m/s) = 0.35 |
| ReD | Reynolds number = U∞D/υ |
| υ | Kinematic viscosity (m2/s) |
| f | Frequency of velocity fluctuations in the wake (Hz) |
| fD/U∞ | Dimensionless frequency |
| f0 | Dominant frequency |
| St | Strouhal number = f0D/U∞ |
| ω | Vorticity (s−1) |
| ω* | Dimensionless vorticity, ω* = ωD/U∞ |
| Γ | Circulation (mm2/s) |
| Γ* | Dimensionless circulation Γ* = Γ/(U∞D) |
References
- Wang, H.F.; Zhou, Y. The finite-length square cylinder near wake. J. Fluid Mech. 2009, 638, 453–490. [Google Scholar] [CrossRef] [Green Version]
- Kindree, M.G.; Shahroodi, M.; Martinuzzi, R.J. Low-frequency dynamics in the turbulent wake of cantilevered square and circular cylinders protruding a thin laminar boundary layer. Exp. Fluids 2018, 59, 186. [Google Scholar] [CrossRef]
- Hosseini, Z.; Bourgeois, J.A.; Martinuzzi, R.J. Large Scale Structures in Dipole and Quadrupole Wakes of a Wall Mounted Finite Rectangular Cylinder. Exp. Fluids 2013, 54, 1595–1610. [Google Scholar] [CrossRef]
- Sumner, D.; Heseltine, J.L.; Dansereau, P. Wake structure of a finite circular cylinder of small aspect ratio. Exp. Fluids 2004, 37, 720–730. [Google Scholar] [CrossRef]
- Yauwenas, Y.; Porteous, R.; Moreau, D.J.; Doolan, C.J. The effect of aspect ratio on the wake structure of finite wall-mounted square cylinders. J. Fluid Mech. 2019, 875, 929–960. [Google Scholar] [CrossRef]
- Essel, E.; Tachie, M.; Balachandar, R. Time-resolved wake dynamics of finite wall-mounted circular cylinders submerged in a turbulent boundary layer. J. Fluid Mech. 2021, 917, A8. [Google Scholar] [CrossRef]
- Crane, R.; Popinhak, A.; Martinuzzi, R.; Morton, C. Tomographic PIV investigation of vortex shedding topology for a cantilevered circular cylinder. J. Fluid Mech. 2022, 931, R1. [Google Scholar] [CrossRef]
- Pattenden, R.J.; Turnock, S.R.; Zhang, Z. Measurements of the flow over a low-aspect-ratio cylinder mounted on a ground plane. Exp. Fluids 2005, 39, 10–21. [Google Scholar] [CrossRef]
- Hajimirzaie, S.M. Flow Structure in the Wake of a Low-Aspect-Ratio Wall-Mounted Bluff Body. Ph.D. Thesis, University of Iowa, Iowa City, IA, USA, 2013. [Google Scholar] [CrossRef] [Green Version]
- Hajimirzaie, S.M.; Wojcik, C.J.; Buchholz, J.H.J. The role of shape and relative submergence on the structure of wakes of low-aspect-ratio wall-mounted bodies. Exp. Fluids 2012, 53, 1943–1962. [Google Scholar] [CrossRef]
- Gildersleeve, S.; Amitay, M. Vortex dynamics of a low aspect ratio cantilevered cylinder immersed in a boundary layer. J. Fluid Mech. 2020, 901, A18. [Google Scholar] [CrossRef]
- Palau-Salvador, G.; Stoesser, T.; Fröhlich, J.; Kappler, M.; Rodi, W. Large eddy simulations and experiments of flow around finite-height cylinders. Flow Turbul. Combust. 2010, 84, 239. [Google Scholar] [CrossRef]
- Krajnovic, S. Flow around a tall finite cylinder explored by large eddy simulation. J. Fluid Mech. 2011, 676, 294–317. [Google Scholar] [CrossRef] [Green Version]
- Roh, S.; Park, S. Vortical flow over the free end surface of a finite circular cylinder mounted on a flat plate. Exp. Fluids 2003, 34, 63–67. [Google Scholar] [CrossRef]
- Hain, R.; Kahler, C.J.; Michaelis, D. Tomographic and time resolved PIV measurements on a finite cylinder mounted on a flat plate. Exp. Fluids 2008, 45, 715–724. [Google Scholar] [CrossRef]
- Okamoto, S.; Sunabashiri, Y. Vortex shedding from a circular cylinder of finite length placed on a ground plane. ASME J. Fluids Eng. 1992, 112, 512–521. [Google Scholar] [CrossRef]
- Okamoto, S.; Uemura, N. Effect of rounding side-corners on aerodynamic forces and turbulent wake of a cube placed on a ground plane. Exp. Fluids 1991, 11, 58–64. [Google Scholar] [CrossRef]
- Da Silva, B.L.; Chakravarty, R.; Sumner, D.; Bergstrom, D.J. Aerodynamic forces and three-dimensional flow structures in the mean wake of a surface mounted finite-height square prism. Int. J. Heat Fluid Flow 2020, 83, 108569. [Google Scholar] [CrossRef]
- Cao, Y.; Tamura, T.; Zhou, D.; Bao, Y.; Han, Z. Topological description of near-wall flows around a surface-mounted square cylinder at high Reynolds numbers. J. Fluid Mech. 2022, 933, A39. [Google Scholar] [CrossRef]
- Rastan, M.R.; Sohankar, A.; Alam, M.M. Low-Reynolds-number flow around a wall-mounted square cylinder: Flow structures and onset of vortex shedding. Phys. Fluids 2017, 29, 103601. [Google Scholar] [CrossRef]
- Wang, H.F.; Zhou, Y.; Chan, C.K.; Lam, K.S. Effect of initial conditions on interaction between a boundary layer and a wall-mounted finite-length-cylinder wake. Phys. Fluids 2006, 18, 065106. [Google Scholar] [CrossRef] [Green Version]
- Bourgeois, J.A.; Sattari, P.; Martinuzzi, R.J. Alternating half-loop shedding in the turbulent wake of a finite surface-mounted square cylinder with a thin boundary layer. Phys. Fluids 2011, 23, 095101. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hajimirzaie, S.M. Experimental Observations on Flow Characteristics around a Low-Aspect-Ratio Wall-Mounted Circular and Square Cylinder. Fluids 2023, 8, 32. https://doi.org/10.3390/fluids8010032
Hajimirzaie SM. Experimental Observations on Flow Characteristics around a Low-Aspect-Ratio Wall-Mounted Circular and Square Cylinder. Fluids. 2023; 8(1):32. https://doi.org/10.3390/fluids8010032
Chicago/Turabian StyleHajimirzaie, Seyed M. 2023. "Experimental Observations on Flow Characteristics around a Low-Aspect-Ratio Wall-Mounted Circular and Square Cylinder" Fluids 8, no. 1: 32. https://doi.org/10.3390/fluids8010032
APA StyleHajimirzaie, S. M. (2023). Experimental Observations on Flow Characteristics around a Low-Aspect-Ratio Wall-Mounted Circular and Square Cylinder. Fluids, 8(1), 32. https://doi.org/10.3390/fluids8010032







