Simulating Flow in an Intestinal Peristaltic System: Combining In Vitro and In Silico Approaches
Abstract
:1. Introduction
2. Materials and Methods
2.1. The In Vitro Model
2.1.1. Materials
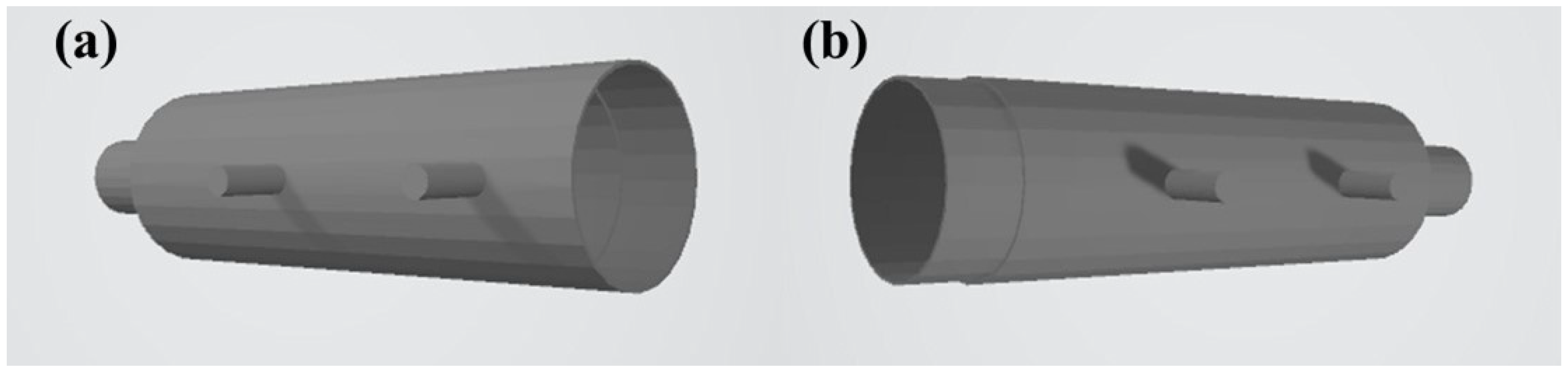
2.1.2. Manufacturing the TPU Model
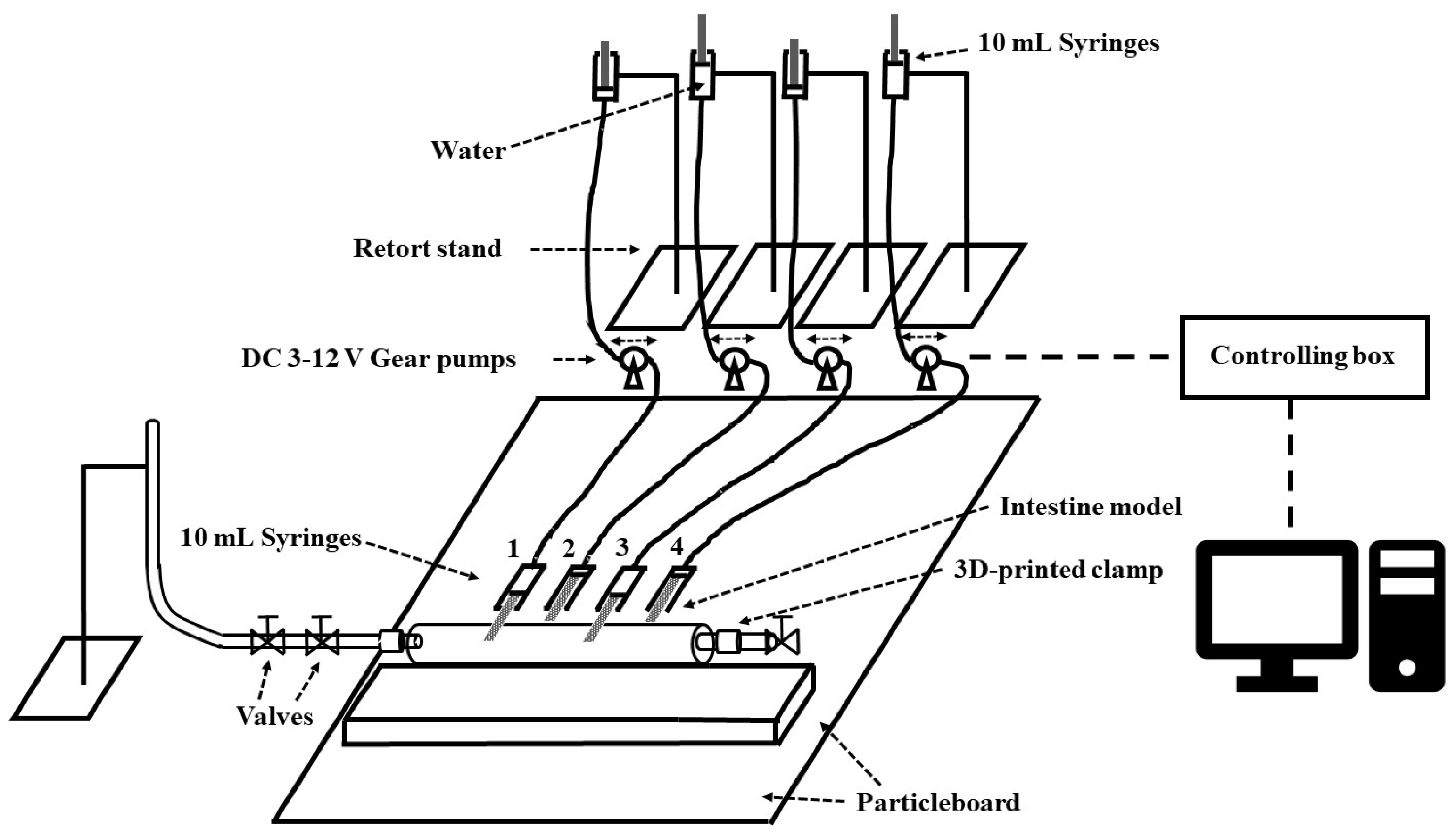
2.1.3. Arrangement of the In Vitro Intestine System
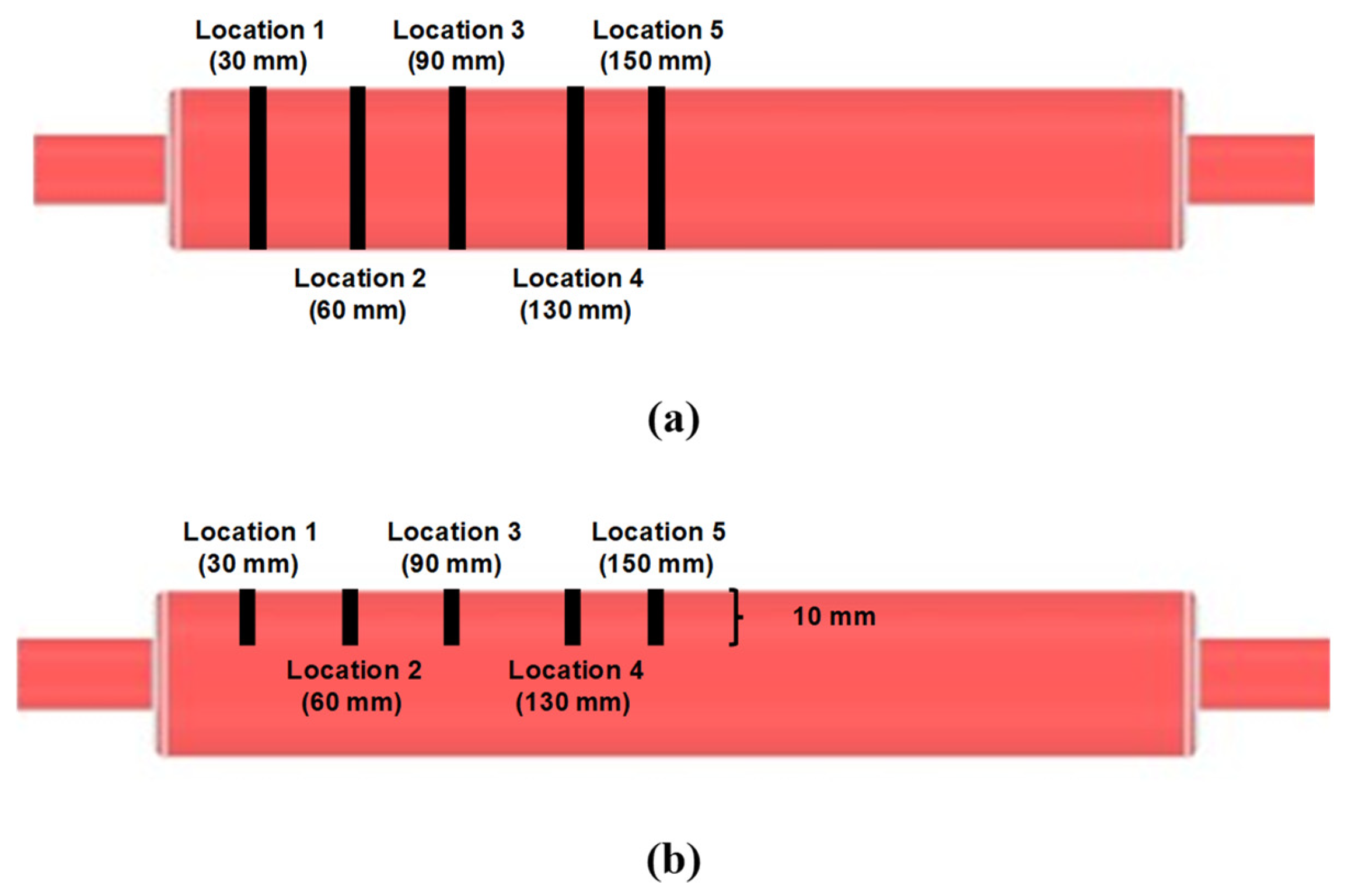
2.1.4. Flow Visualization Tests
2.1.5. Color Analysis
2.1.6. Tensile Tester
2.2. The In Silico Model
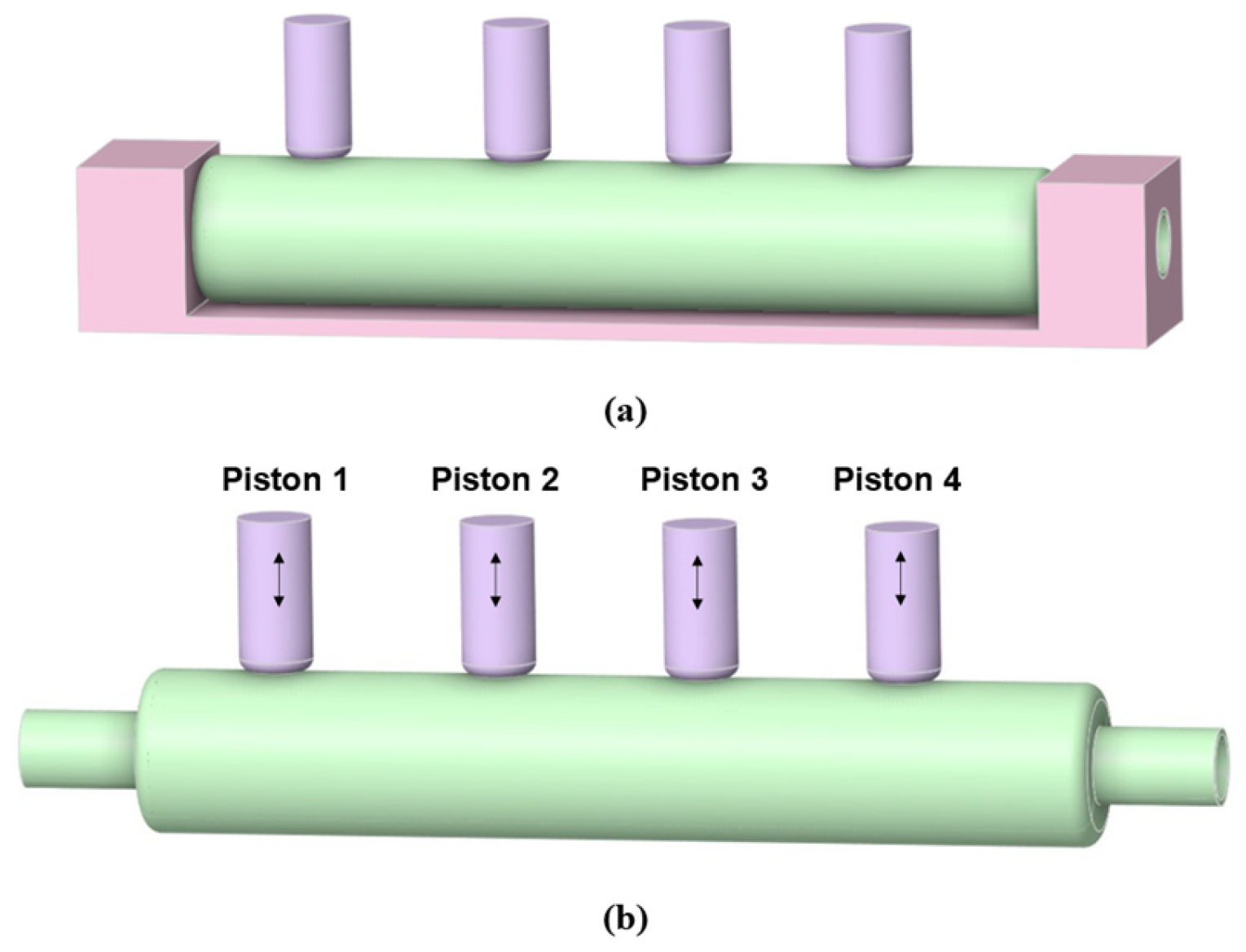
2.2.1. The Fluid Domain Model
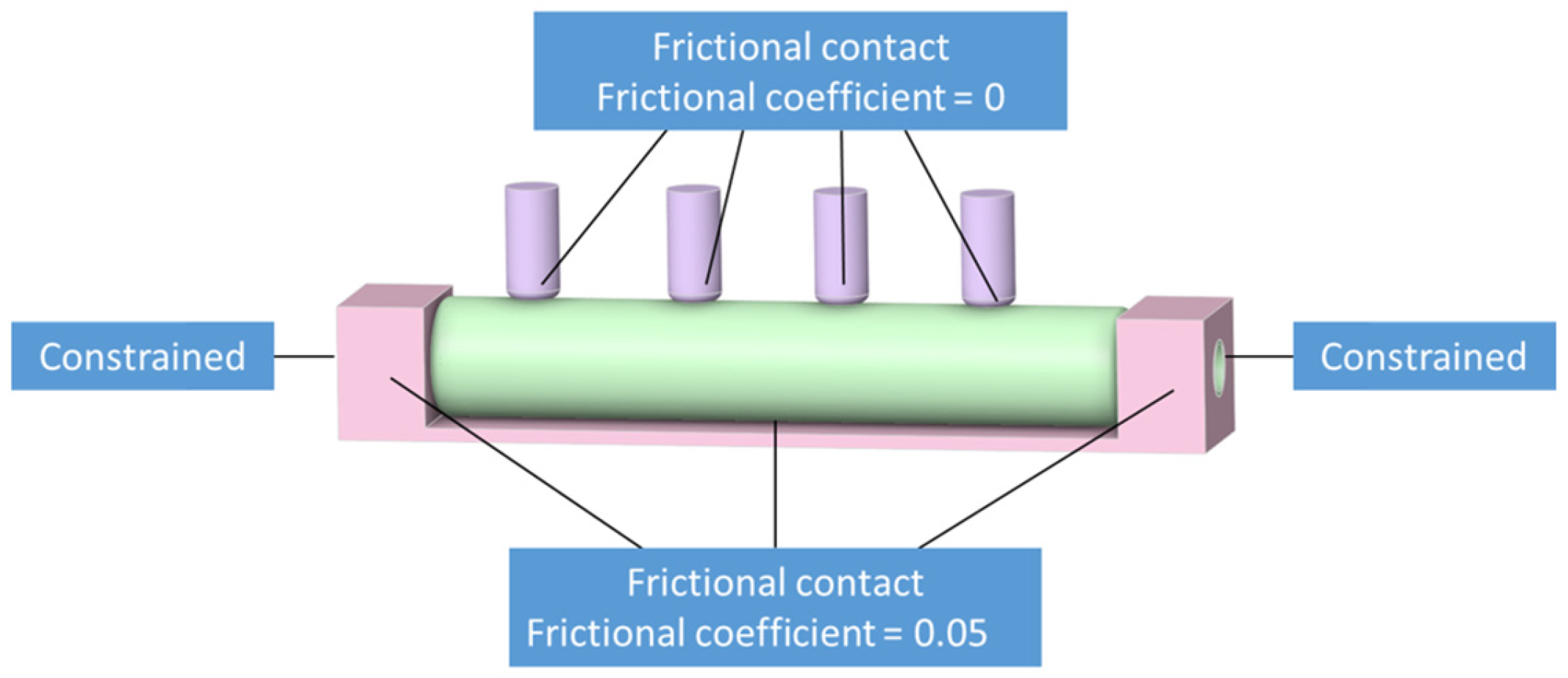
2.2.2. The Structural Domain Model
2.2.3. System Coupling
3. Results and Discussion
3.1. Physical Features of the Intestine Model
3.2. Experimental Results
3.3. Simulation Results
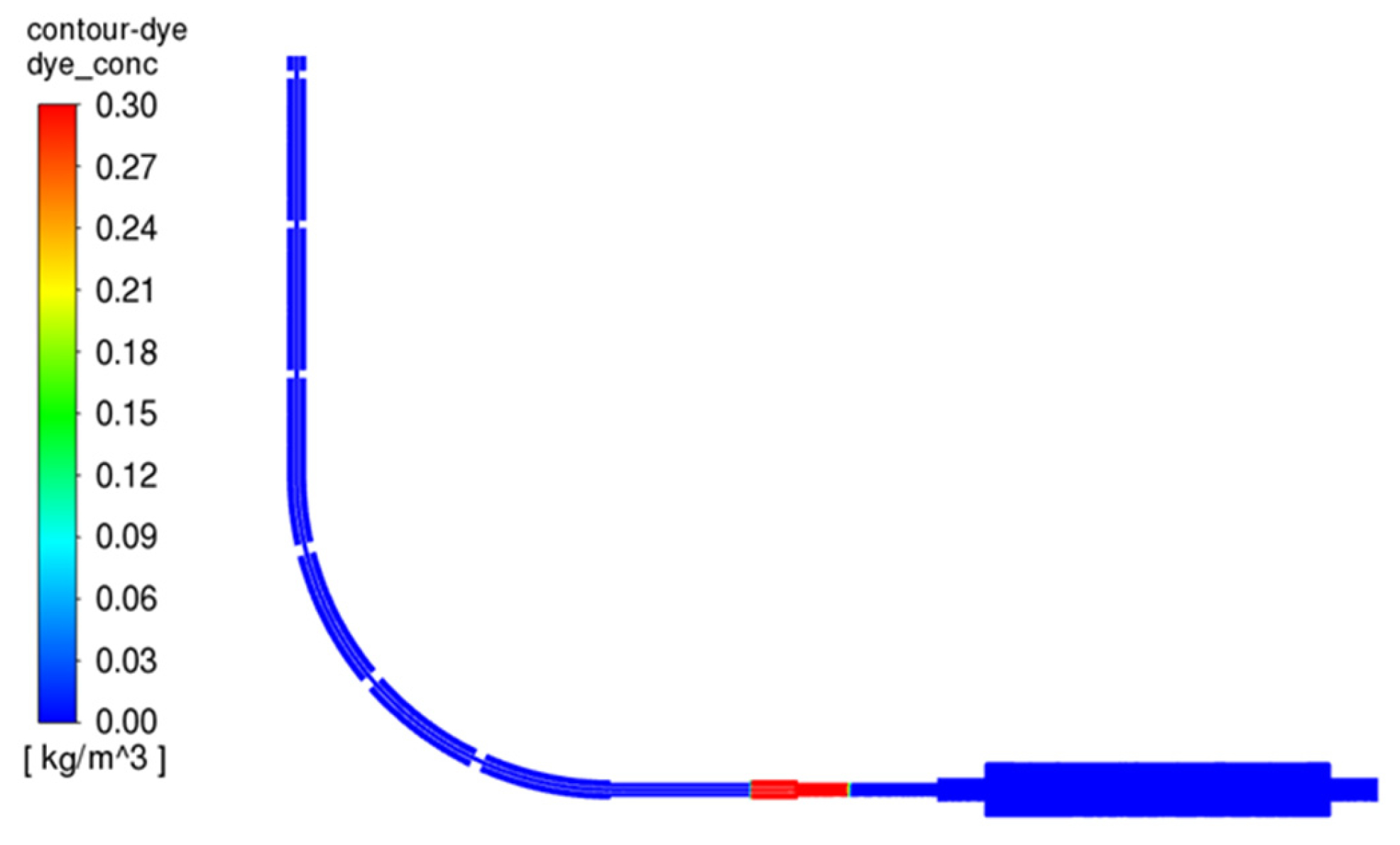
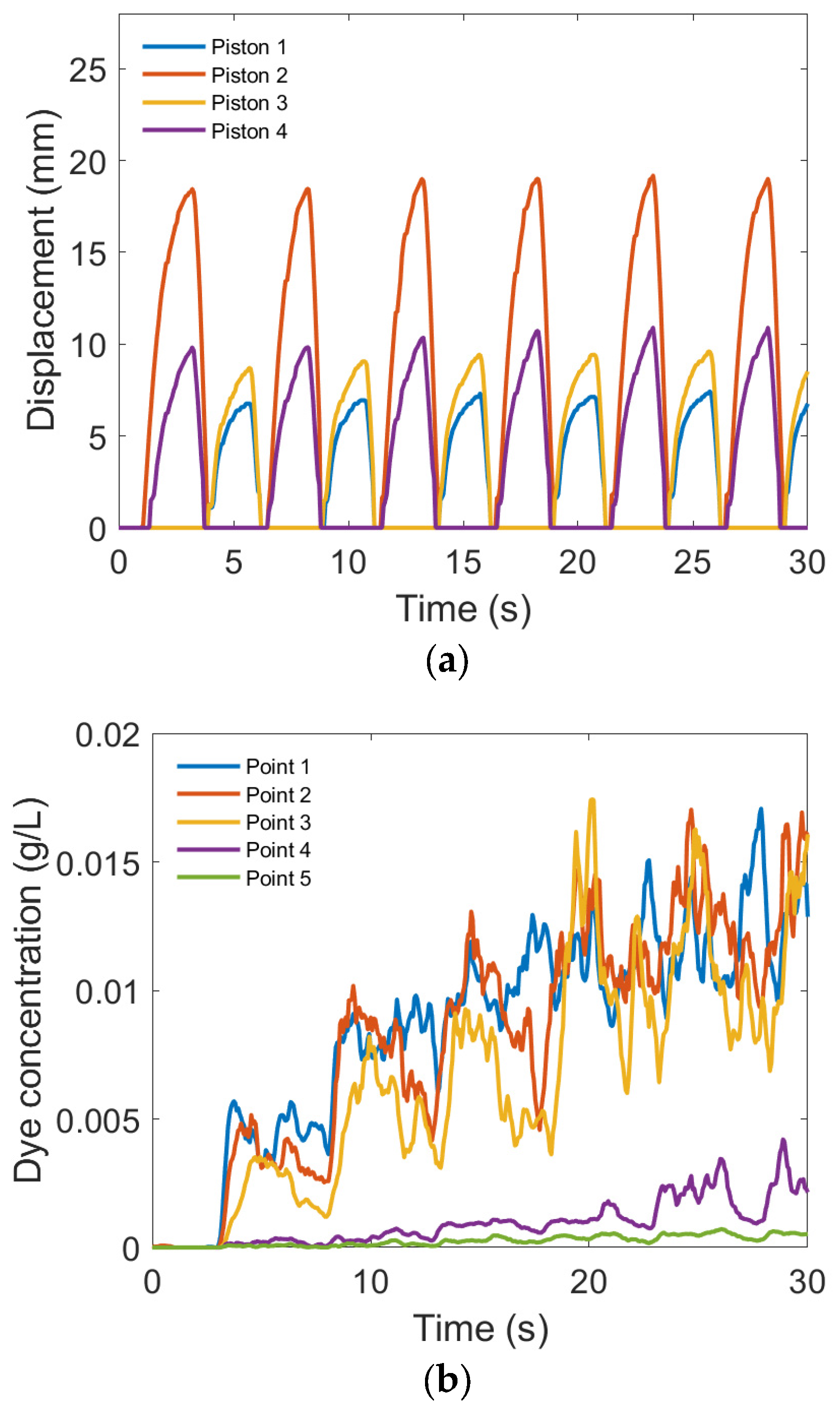
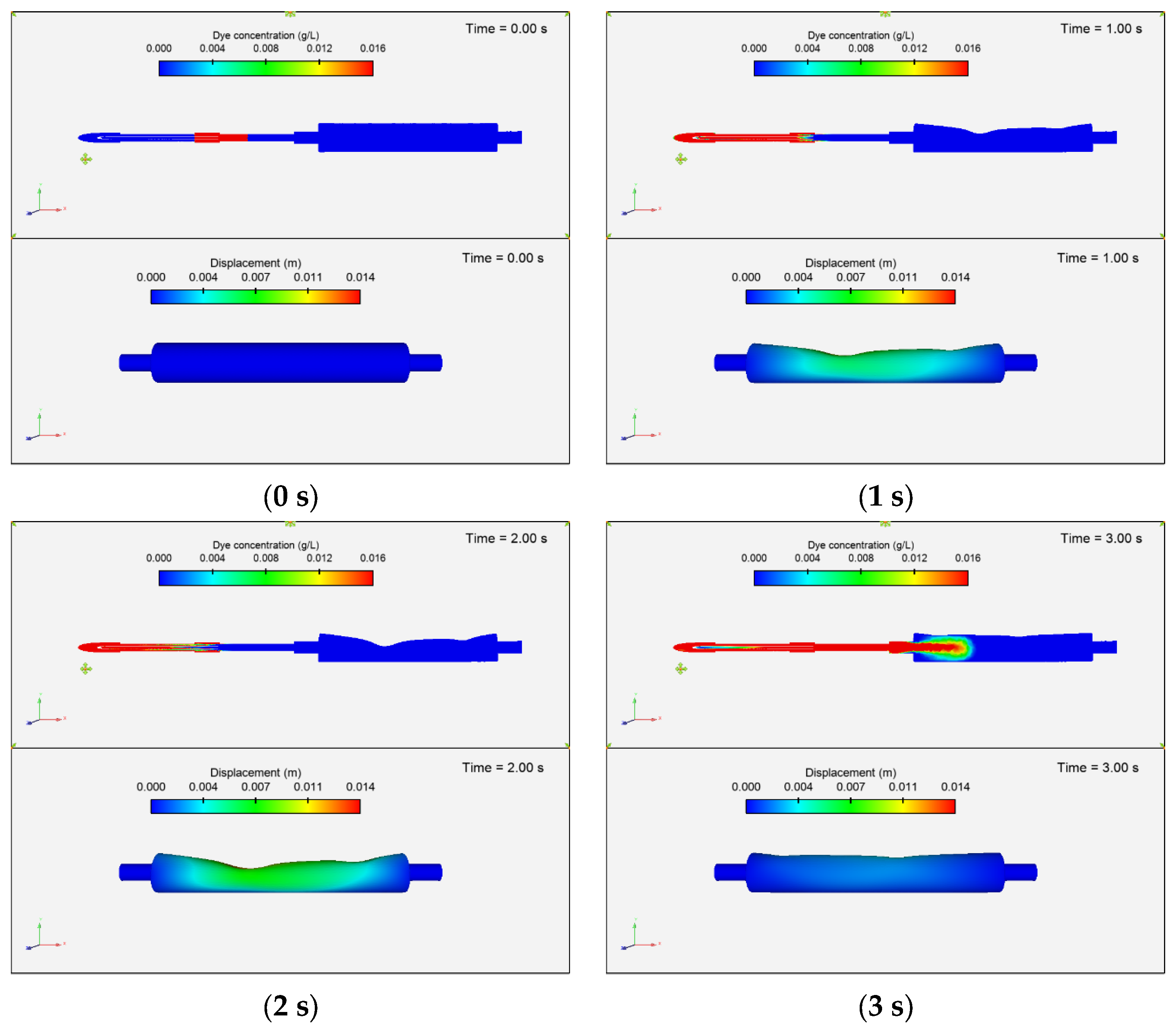
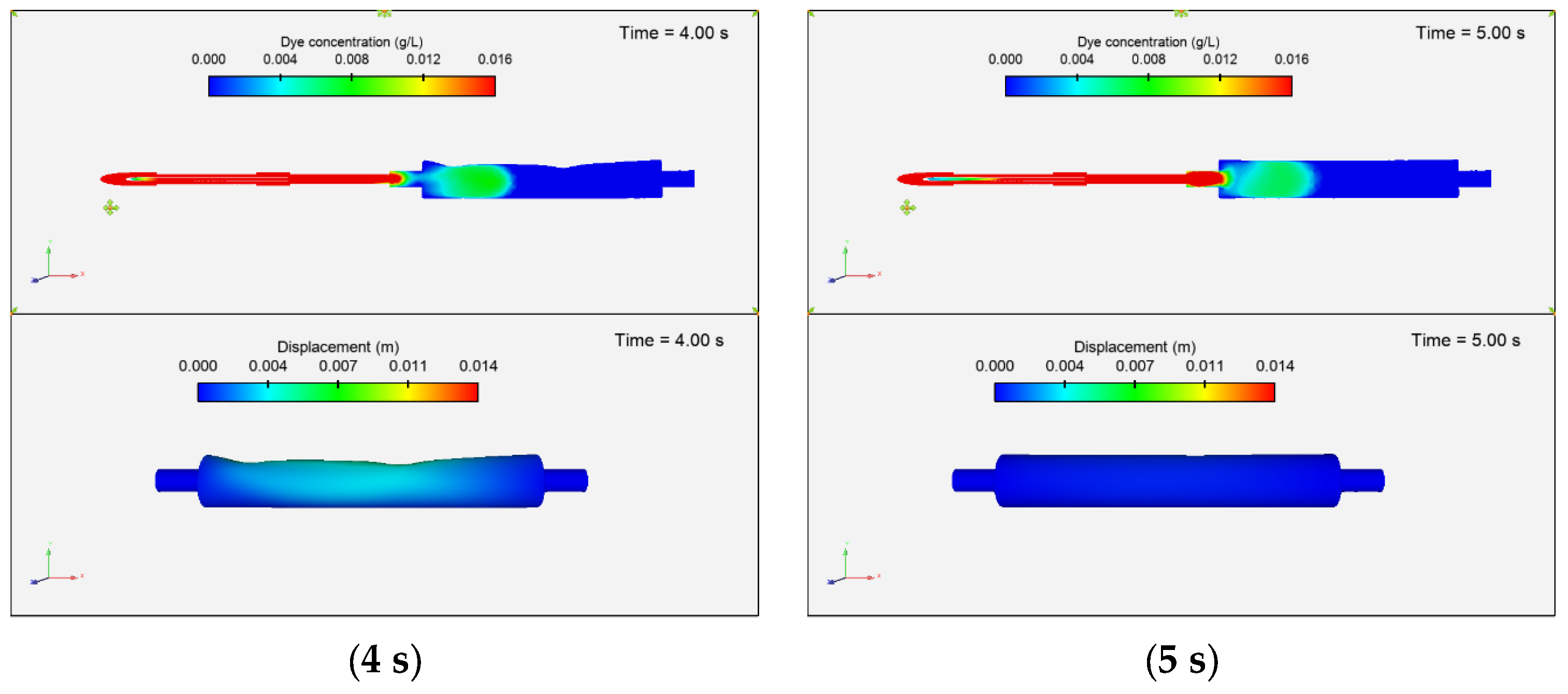
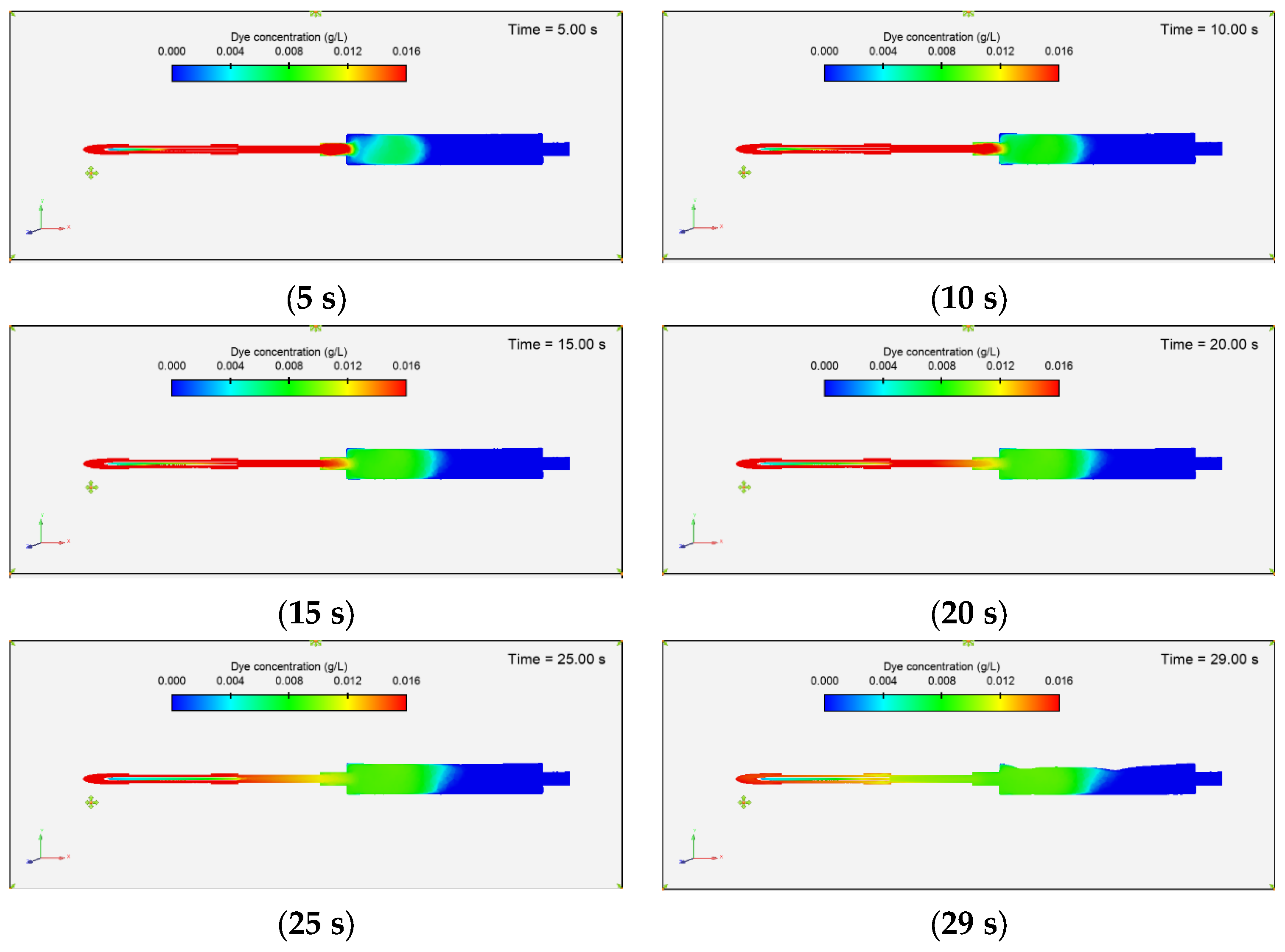
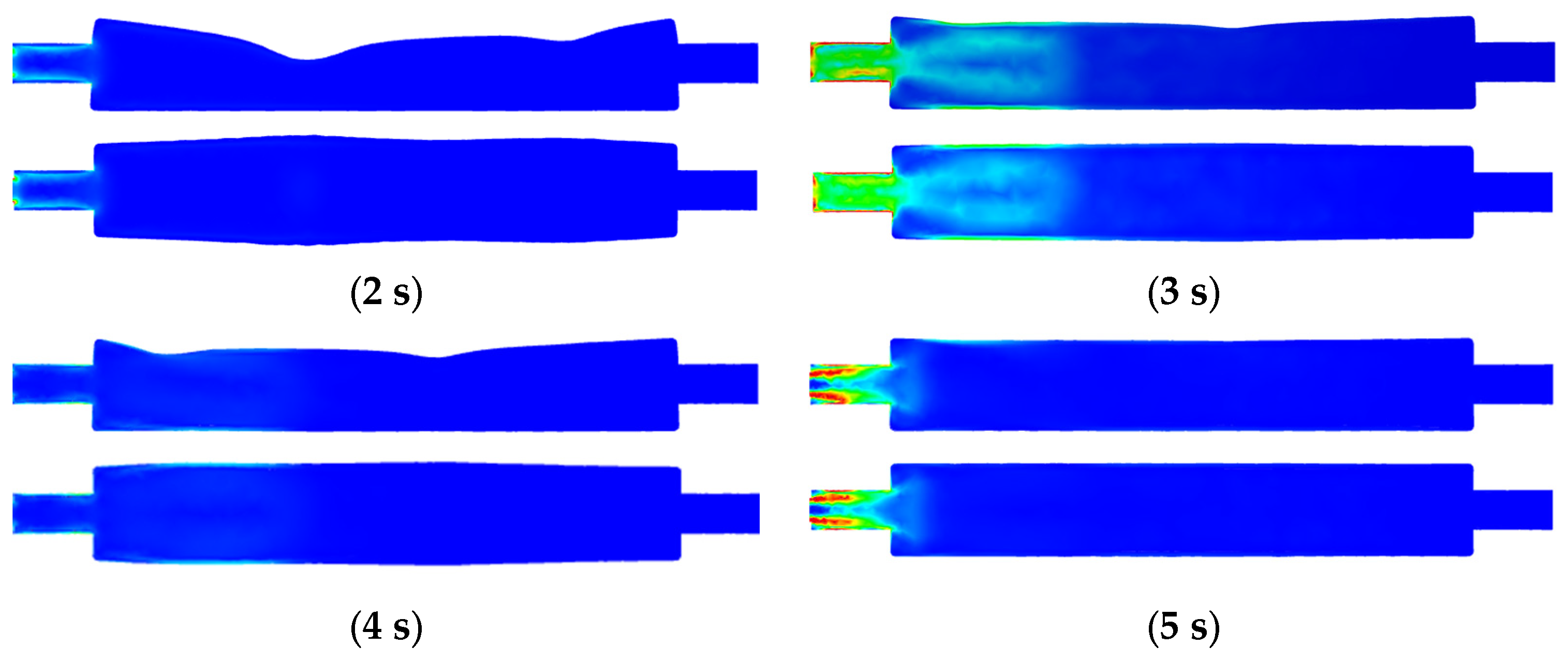
3.3.1. Dye Concentration and Chamber Displacement
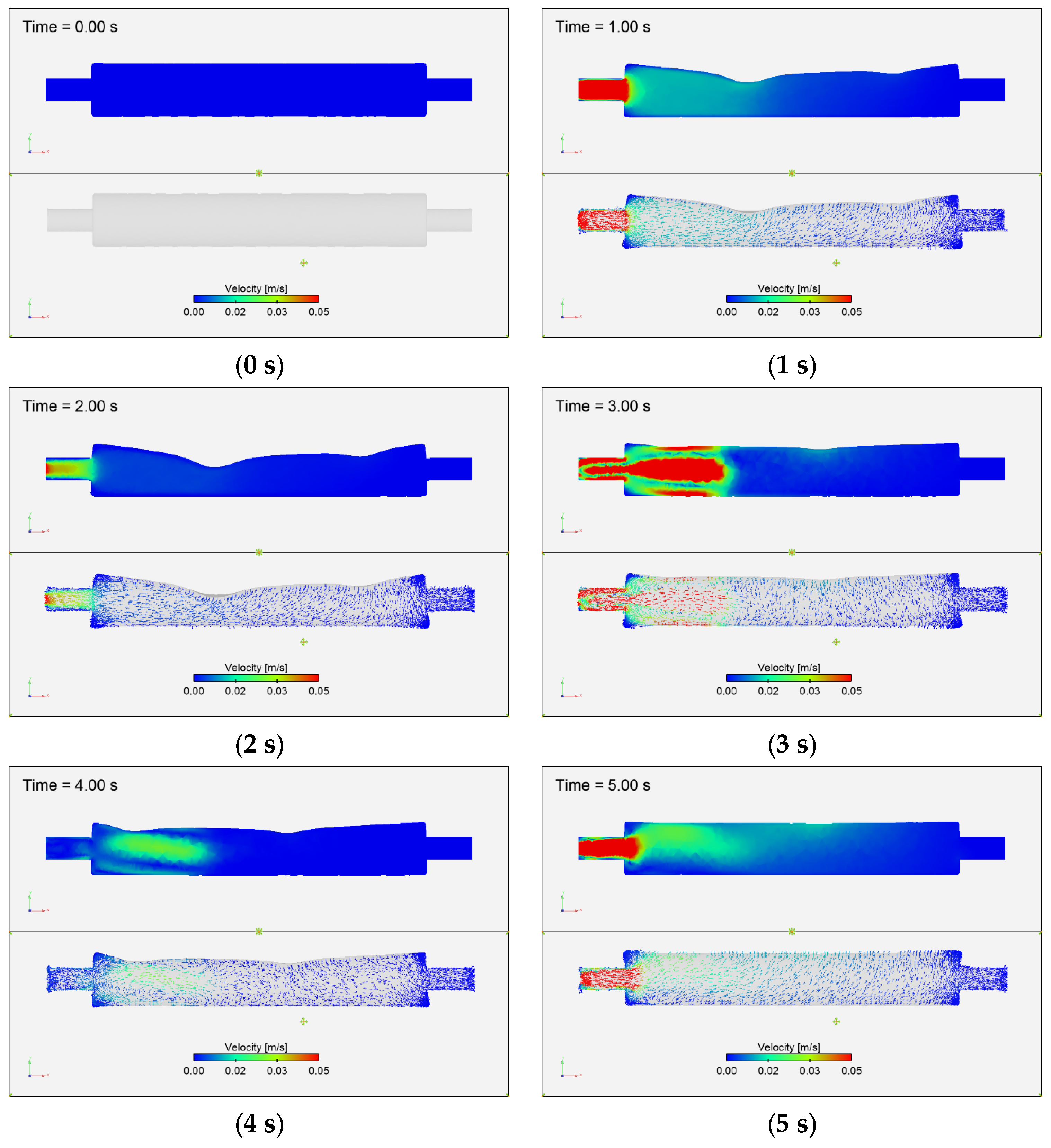
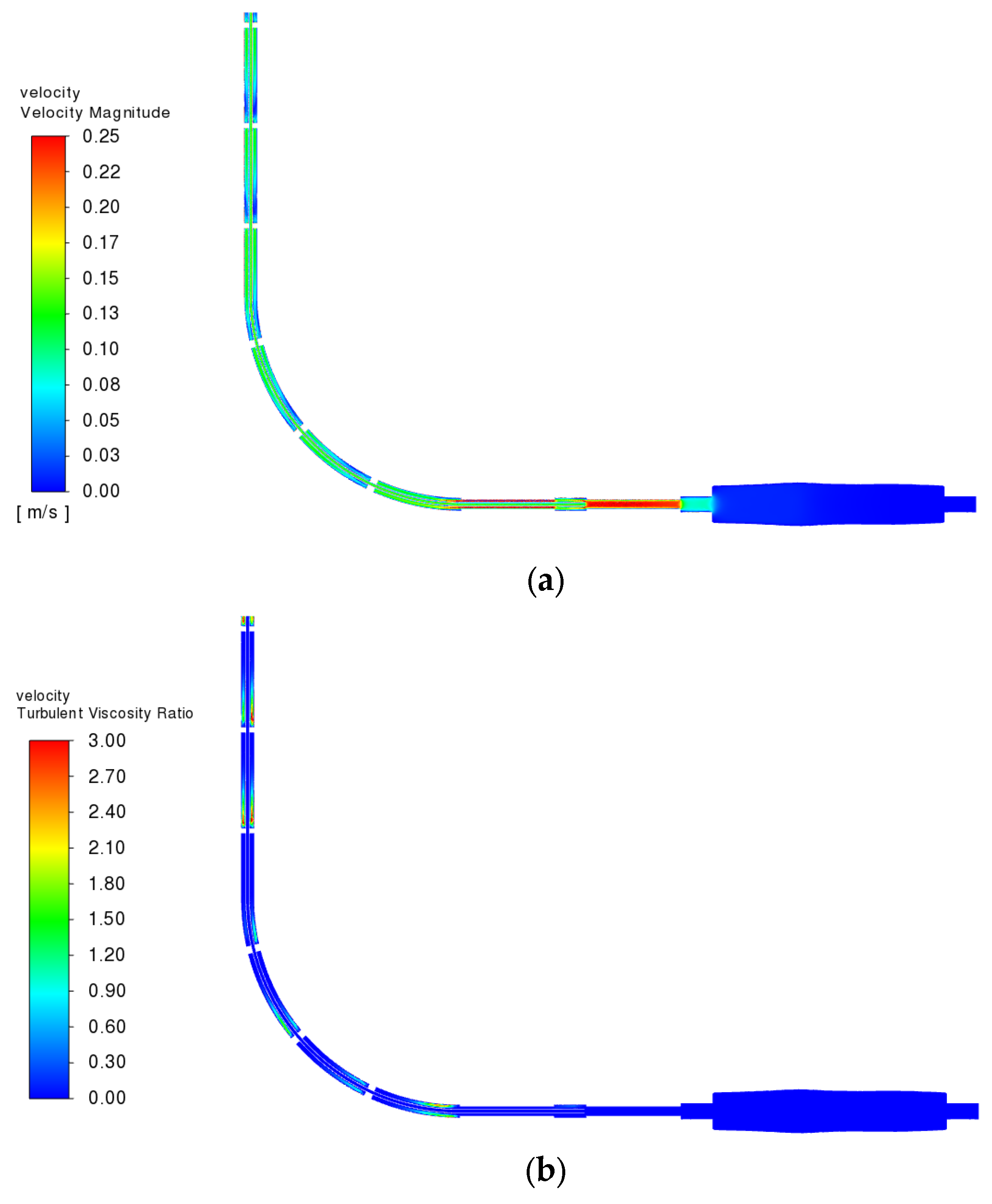
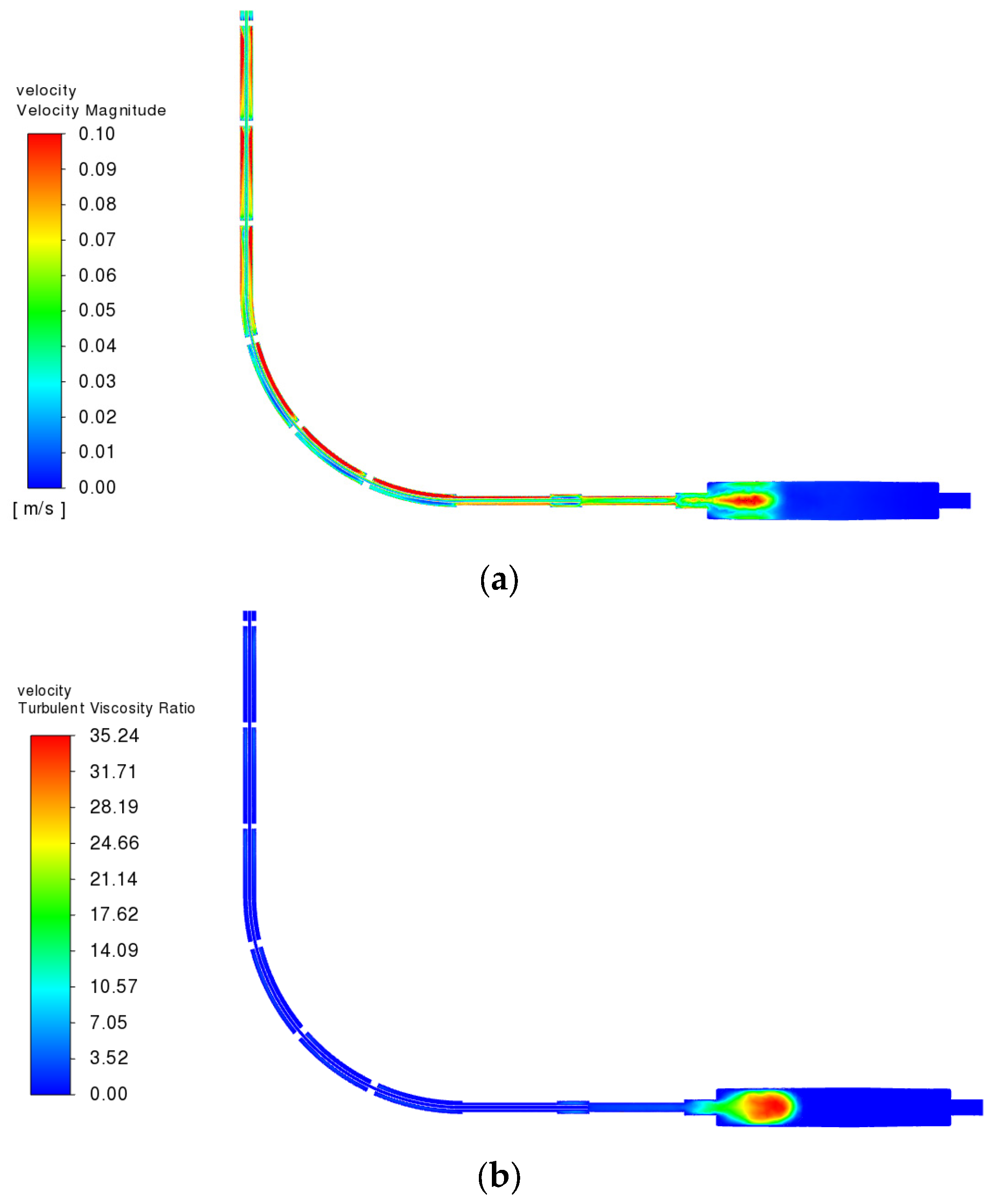
3.3.2. Fluid Velocity Field
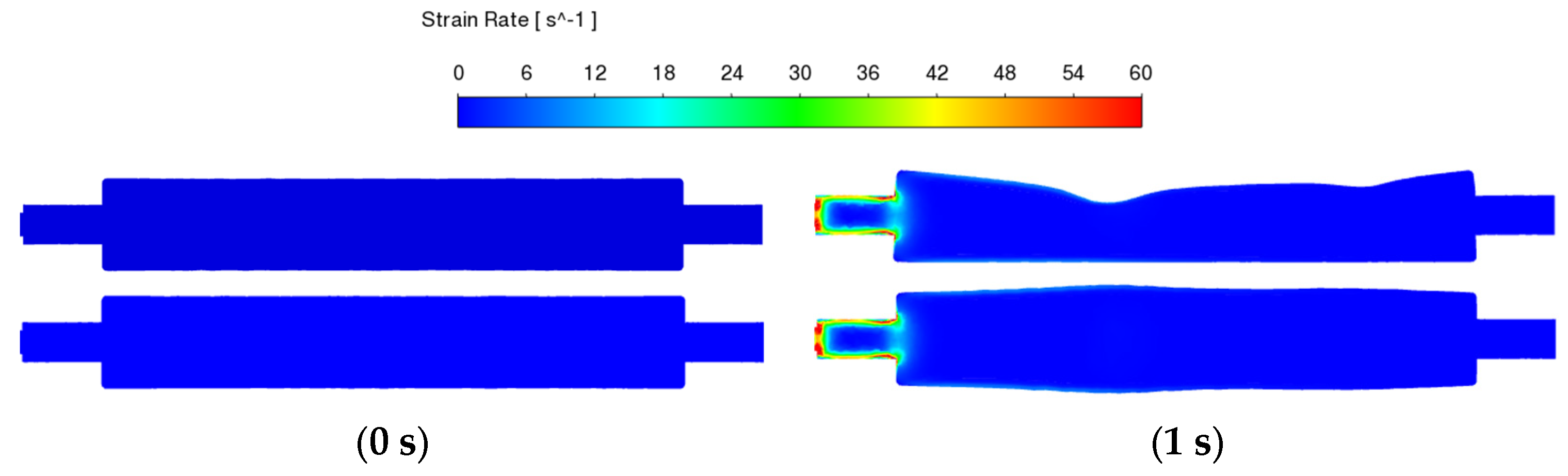
3.3.3. Fluid Strain Rate Changes
3.3.4. Reynolds Number and Turbulence Behavior in the Flow Regime
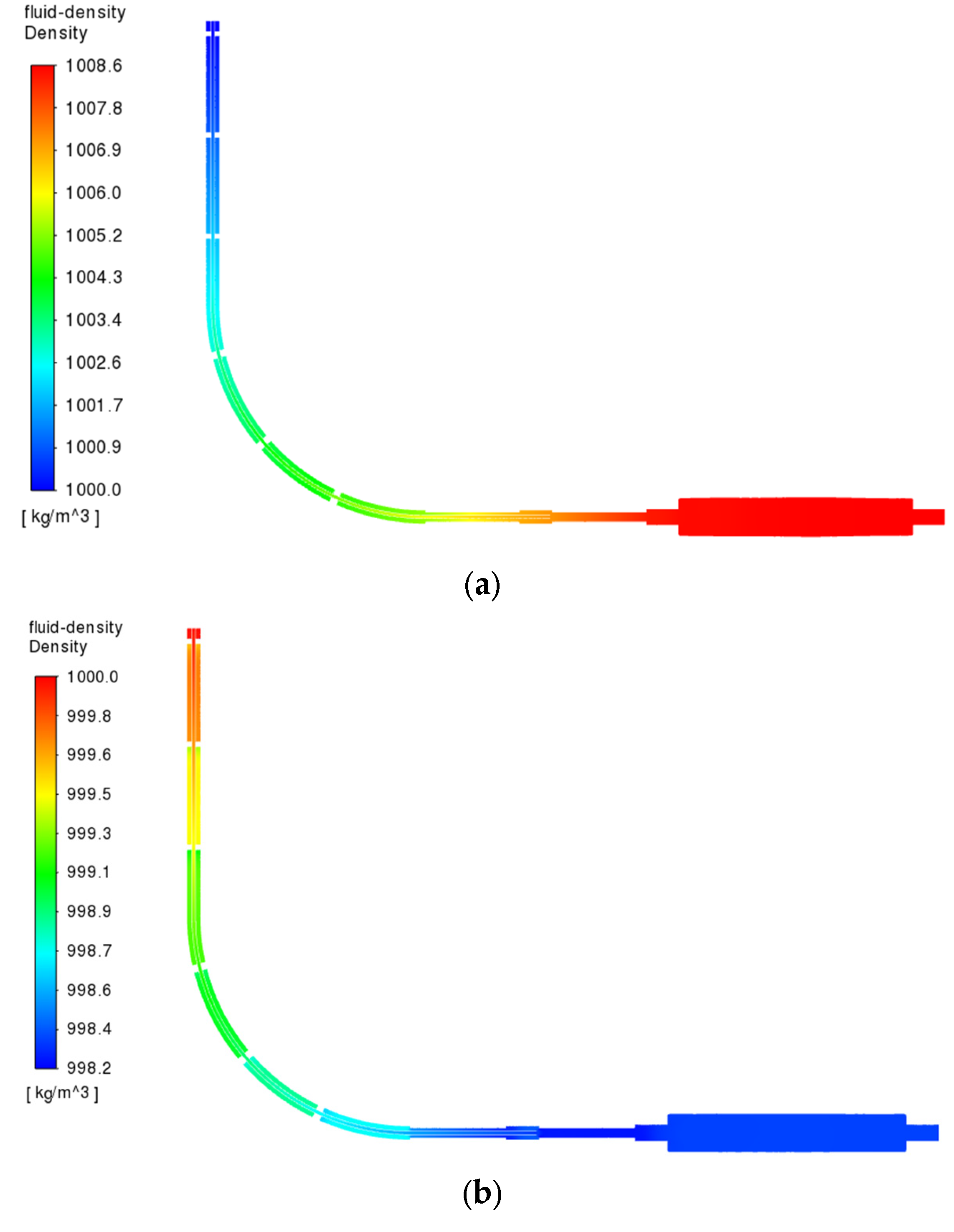
3.3.5. Fluid Density Changes in the Simulation
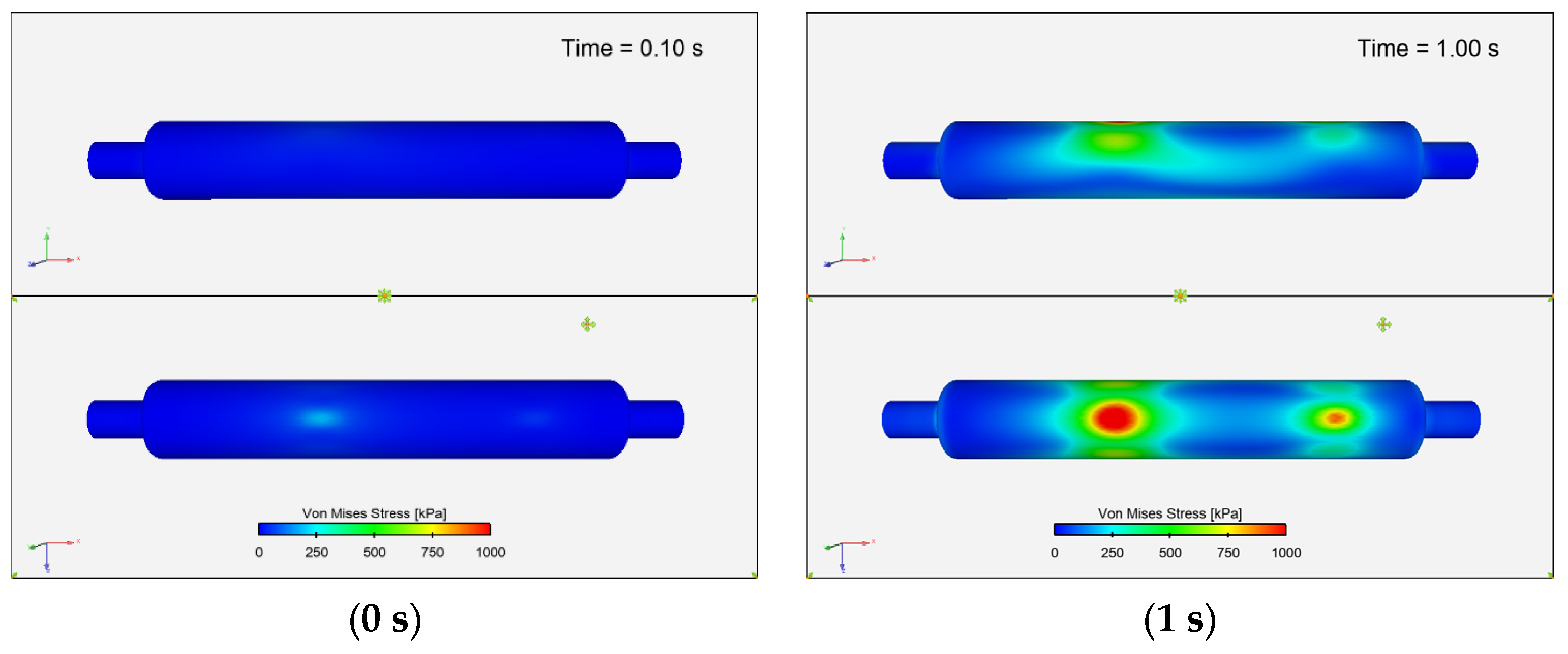
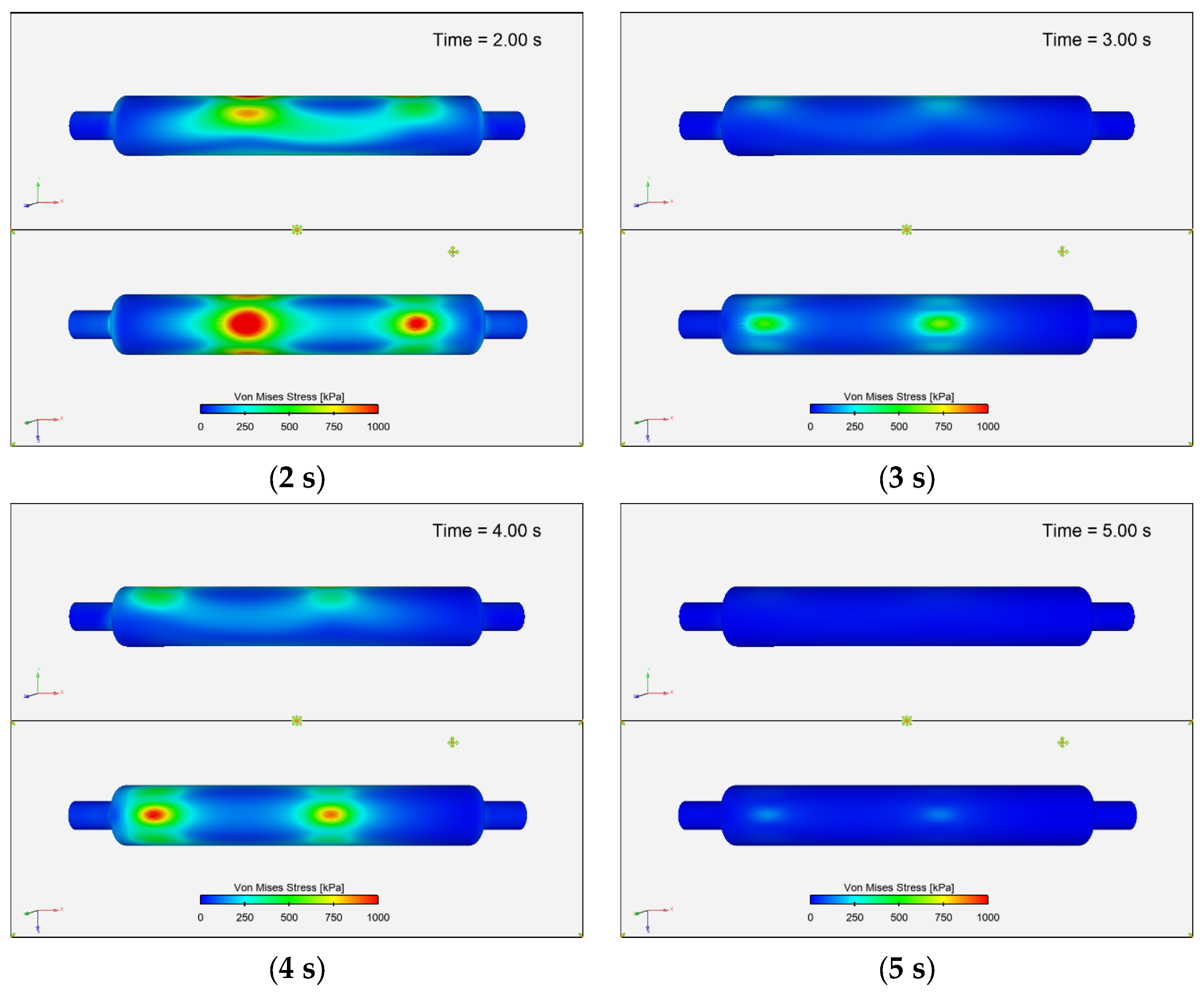
3.3.6. Von Mises Stress Distribution
3.4. Comparison of Flow and Mixing Data between Experiment and Simulation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van de Wiele, T.R.; Oomen, A.G.; Wragg, J.; Cave, M.; Minekus, M.; Hack, A.; Cornelis, C.; Rompelberg, C.J.; De Zwart, L.L.; Klinck, B.; et al. Comparison of five in vitro digestion models to in vivo experimental results: Lead bioaccessibility in the human gastrointestinal tract. J. Environ. Sci. Health A Toxic Hazard. Subst. Environ. Eng. 2007, 42, 1203–1211. [Google Scholar] [CrossRef] [PubMed]
- Dupont, D.; Alric, M.; Blanquet-Diot, S.; Bornhorst, G.; Cueva, C.; Deglaire, A.; Denis, S.; Ferrua, M.; Havenaar, R.; Lelieveld, J.; et al. Can dynamic in vitro digestion systems mimic the physiological reality? Food Sci. Nutr. 2018, 59, 1546–1562. [Google Scholar] [CrossRef]
- Gouseti, O.; Jaime-Fonseca, M.R.; Fryer, P.J.; Mills, C.; Wickham, M.S.J.; Bakalis, S. Hydrocolloids in human digestion: Dynamic in vitro assessment of the effect of food formulation on mass transfer. Food Hydrocoll. 2014, 42, 378–385. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, R.; Zhang, H.; Yang, D.; Liu, S.; Song, Z.; Gu, Y.; Ramalingam, M. Topological structure design and fabrication of biocompatible PLA/TPU/ADM mesh with appropriate elasticity for hernia repair. Macromol. Biosci. 2021, 21, 2000423. [Google Scholar] [CrossRef] [PubMed]
- Alves, P.; Cardoso, R.; Correia, T.R.; Antunes, B.P.; Correia, I.J.; Ferreira, P. Surface modification of polyurethane films by plasma and ultraviolet light to improve haemocompatibility for artificial heart valves. Colloids Surf. B Biointerfaces 2014, 113, 25–32. [Google Scholar] [CrossRef]
- Fallahiarezoudar, E.; Ahmadipourroudposht, M.; Idris, A.; Yusof, N.M. Optimization and development of Maghemite (γ-Fe2O3) filled poly-l-lactic acid (PLLA)/thermoplastic polyurethane (TPU) electrospun nanofibers using Taguchi orthogonal array for tissue engineering heart valve. Mater. Sci. Eng. C 2017, 76, 616–627. [Google Scholar] [CrossRef]
- Pal, A.; Indireshkumar, K.; Schwizer, W.; Abrahamsson, B.; Fried, M.; Brasseur, J.G. Gastric flow and mixing studied using computer simulation. Proc. R. Soc. B Biol. Sci. 2004, 271, 2587–2594. [Google Scholar] [CrossRef]
- Li, C.; Gasow, S.; Jin, Y.; Xiao, J.; Chen, X.D. Simulation based investigation of 2D soft-elastic reactors for better mixing performance. Eng. Appl. Comput. Fluid. Mech. 2021, 15, 1229–1242. [Google Scholar] [CrossRef]
- Karthikeyan, J.S.; Salvi, D.; Karwe, M.V. Modeling of fluid flow, carbohydrate digestion, and glucose absorption in human small intestine. J. Food Eng. 2021, 292, 110339. [Google Scholar] [CrossRef]
- Palmada, N.; Hosseini, S.; Avci, R.; Cater, J.E.; Suresh, V.; Cheng, L.K. A systematic review of computational fluid dynamics models in the stomach and small intestine. Appl. Sci. 2023, 13, 6092. [Google Scholar] [CrossRef]
- Ishida, S.; Miyagawa, T.; O’Grady, G.; Cheng, L.K.; Imai, Y. Quantification of gastric emptying caused by impaired coordination of pyloric closure with antral contraction: A simulation study. J. R. Soc. Interface 2019, 16, 157. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Jin, Y. A CFD model for investigating the dynamics of liquid gastric contents in human-stomach induced by gastric motility. J. Food Eng. 2021, 296, 110461. [Google Scholar] [CrossRef]
- Ferrua, M.J.; Singh, R.P. Modeling the fluid dynamics in a human stomach to gain insight of food digestion. J. Food Sci. 2010, 75, R151–R162. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, S.L.; Rozenblit, A.; Ricci, Z.; Roberts, J.; Milikow, D.; Chernyak, V.; Wolf, E. Small bowel faeces sign in patients without small bowel obstruction. Clin. Radiol. 2007, 62, 353–357. [Google Scholar] [CrossRef]
- Sant’Anna, V.; Gurak, P.D.; Ferreira Marczak, L.D.; Tessaro, I.C. Tracking bioactive compounds with colour changes in foods—A review. Dye Pigment. 2013, 98, 601–608. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- La Spina, A.; Förster, C.; Kronbichler, M.; Wall, W.A. On the role of (weak) compressibility for fluid-structure interaction solvers. Int. J. Numer. Methods Fluids 2020, 92, 129–147. [Google Scholar] [CrossRef]
- Rani, S.A.; Pitts, B.; Stewart, P.S. Rapid diffusion of fluorescent tracers into staphylococcus epidermidis biofilms visualized by time lapse microscopy. Antimicrob. Agents Chemother. 2005, 49, 728–732. [Google Scholar] [CrossRef]
- Ansys Inc. Ansys Fluent 2021R1 Manual. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v211/en/flu_th/flu_th.html (accessed on 1 December 2022).
- Liu, X.; Harrison, S.M.; Cleary, P.W.; Fletcher, D.F. Evaluation of SPH and FVM models of kinematically prescribed peristalsis-like flow in a tube. Fluids 2023, 8, 6. [Google Scholar] [CrossRef]
- Liu, X.; Fletcher, D.F. Verification of fluid-structure interaction modelling for wave propagation in fluid-filled elastic tubes. J. Algorithms Comput. Technol. 2023, 17, 1–13. [Google Scholar] [CrossRef]
- Zhong, C.; Langrish, T. A comparison of different physical stomach models and an analysis of shear stresses and strains in these system. Food Res. Int. 2020, 135, 109296. [Google Scholar] [CrossRef] [PubMed]
- Baxter, J.L.; Kukura, J.; Muzzio, F.J. Hydrodynamics-induced variability in the USP apparatus II dissolution test. Int. J. Pharm. 2005, 292, 17–28. [Google Scholar] [CrossRef] [PubMed]
- Nadia, J.; Olenskyj, A.G.; Stroebinger, N.; Hodgkinson, S.M.; Estevez, T.G.; Subramanian, P.; Singh, H.; Singh, R.P.; Bornhorst, G.M. Tracking physical breakdown of rice- and wheat-based foods with varying structures during gastric digestion and its influence on gastric emptying in a growing pig model. Food Funct. 2021, 12, 4349–4372. [Google Scholar] [CrossRef] [PubMed]





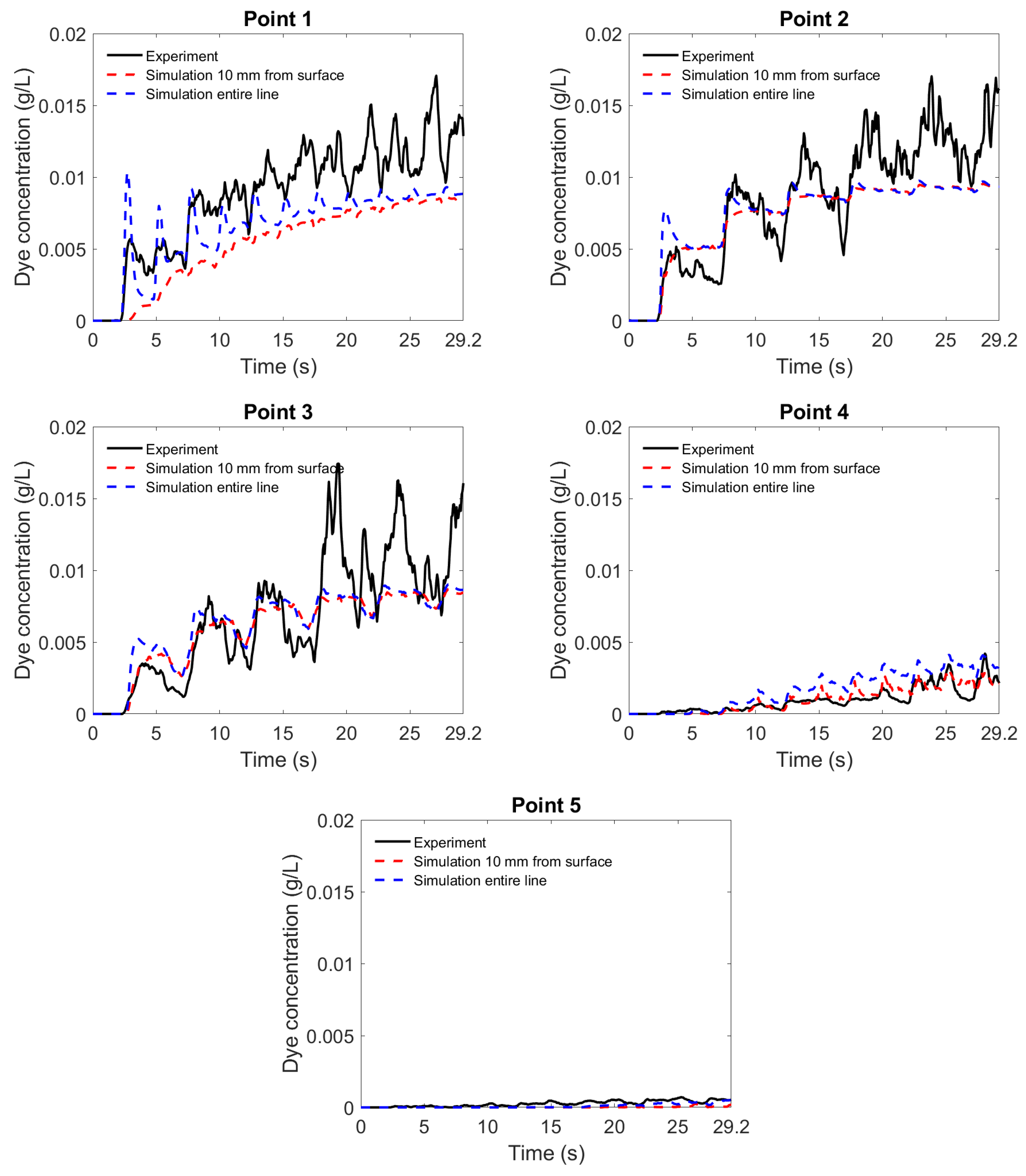
| Point 1 | Point 2 | Point 3 | Point 4 | Point 5 |
|---|---|---|---|---|
| 2.5 × 10−3 | 3.4 × 10−3 | 3.2 × 10−3 | 7.8 × 10−4 | 1.4 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhong, C.; Fletcher, D.F.; Langrish, T.A.G. Simulating Flow in an Intestinal Peristaltic System: Combining In Vitro and In Silico Approaches. Fluids 2023, 8, 298. https://doi.org/10.3390/fluids8110298
Liu X, Zhong C, Fletcher DF, Langrish TAG. Simulating Flow in an Intestinal Peristaltic System: Combining In Vitro and In Silico Approaches. Fluids. 2023; 8(11):298. https://doi.org/10.3390/fluids8110298
Chicago/Turabian StyleLiu, Xinying, Chao Zhong, David F. Fletcher, and Timothy A. G. Langrish. 2023. "Simulating Flow in an Intestinal Peristaltic System: Combining In Vitro and In Silico Approaches" Fluids 8, no. 11: 298. https://doi.org/10.3390/fluids8110298
APA StyleLiu, X., Zhong, C., Fletcher, D. F., & Langrish, T. A. G. (2023). Simulating Flow in an Intestinal Peristaltic System: Combining In Vitro and In Silico Approaches. Fluids, 8(11), 298. https://doi.org/10.3390/fluids8110298









