Reducing Scour around Semi-Elliptical Bridge Abutments: Application of Roughness Elements
Abstract
:1. Introduction
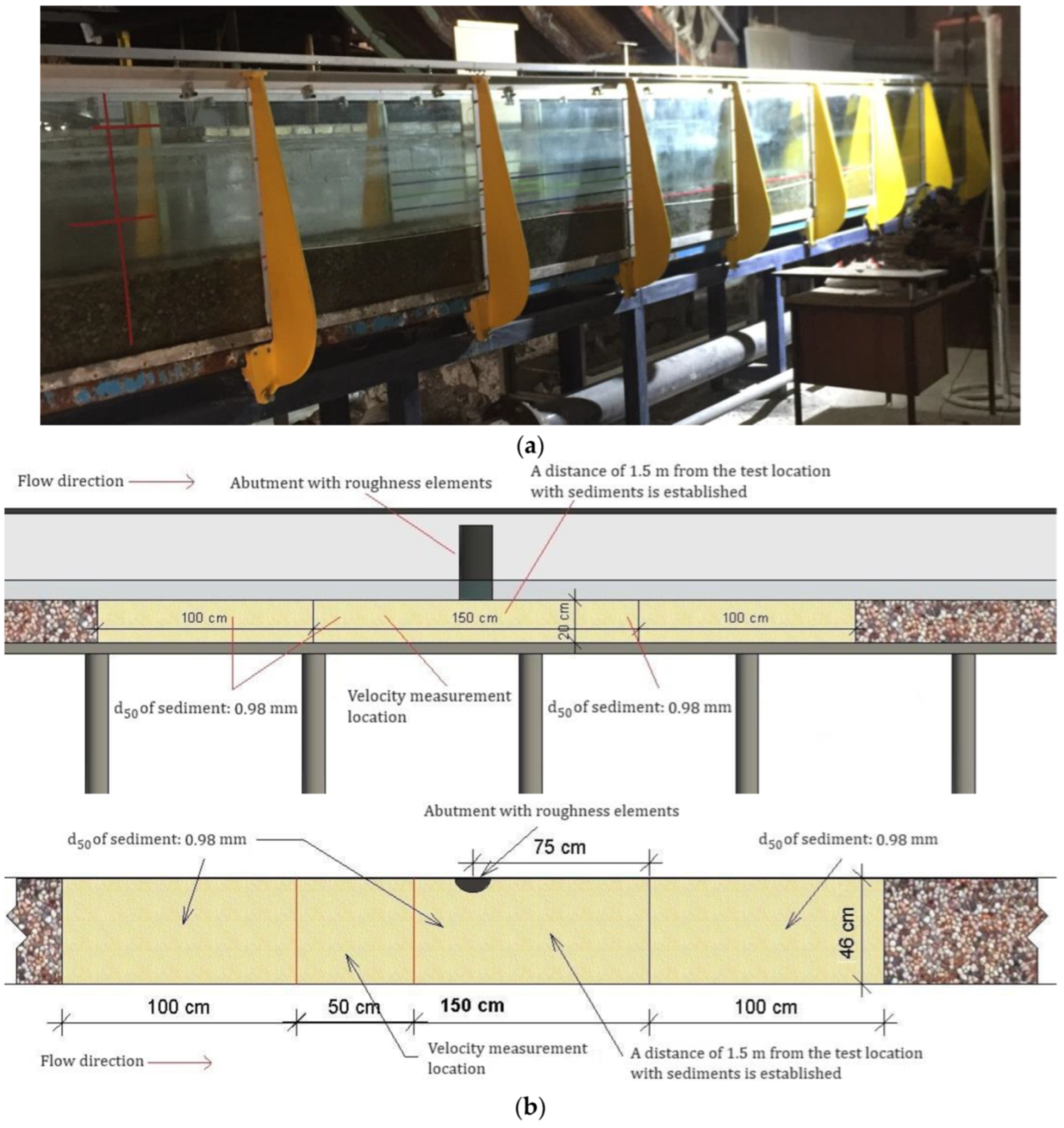
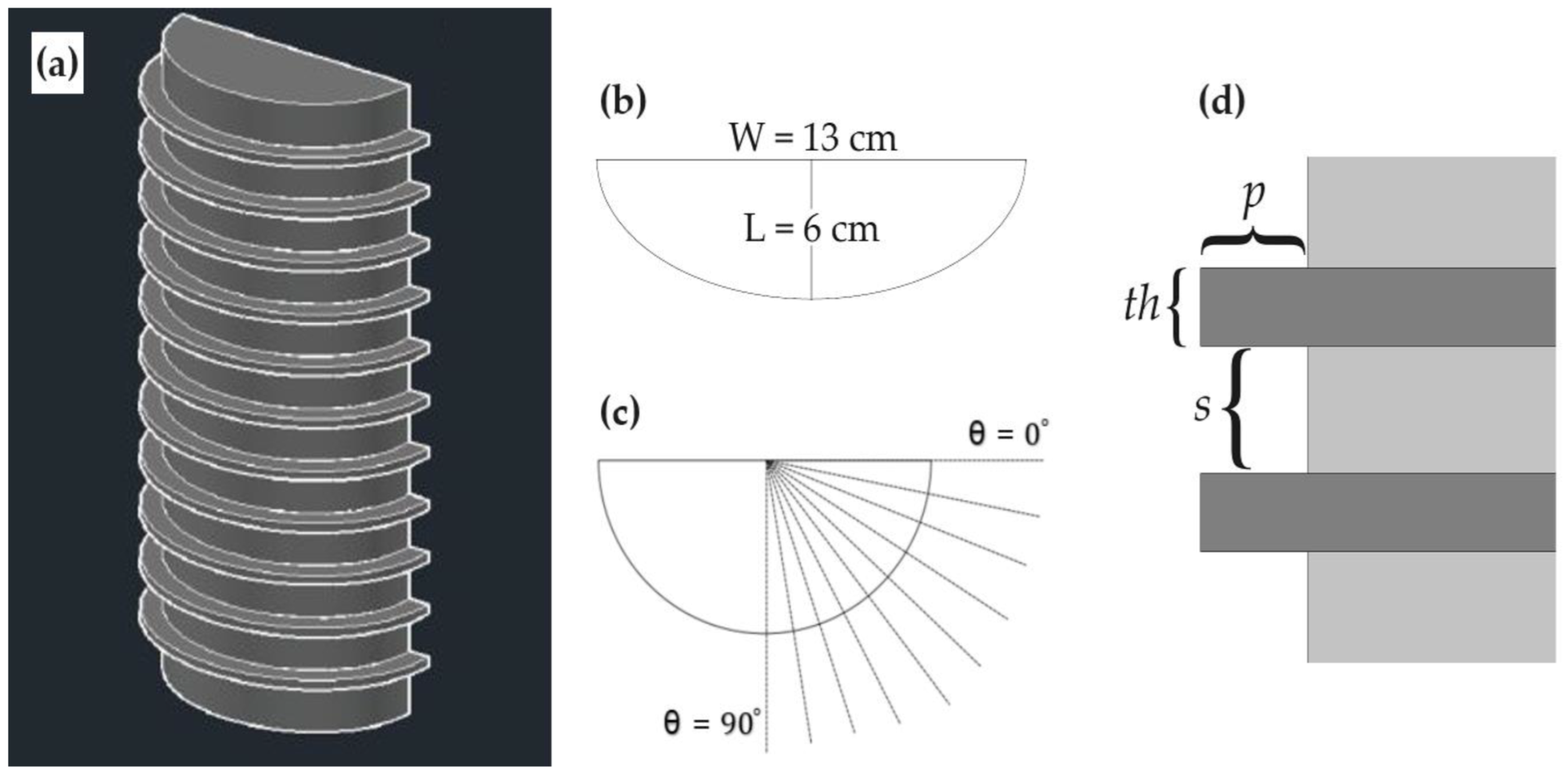
2. Materials and Methods
3. Results and Discussion
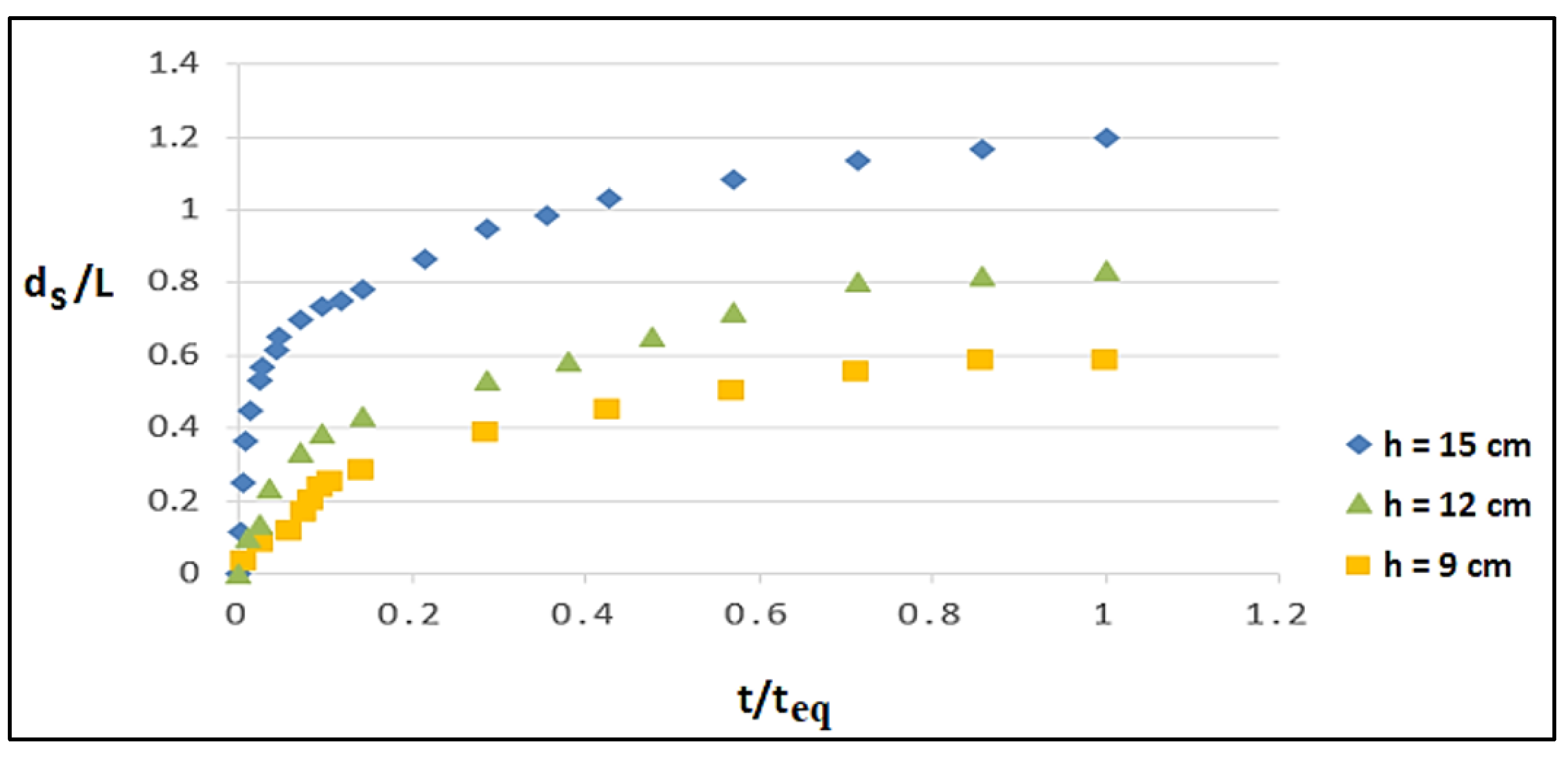
3.1. Temporal Development of Scour in the Abutment without Roughness Elements
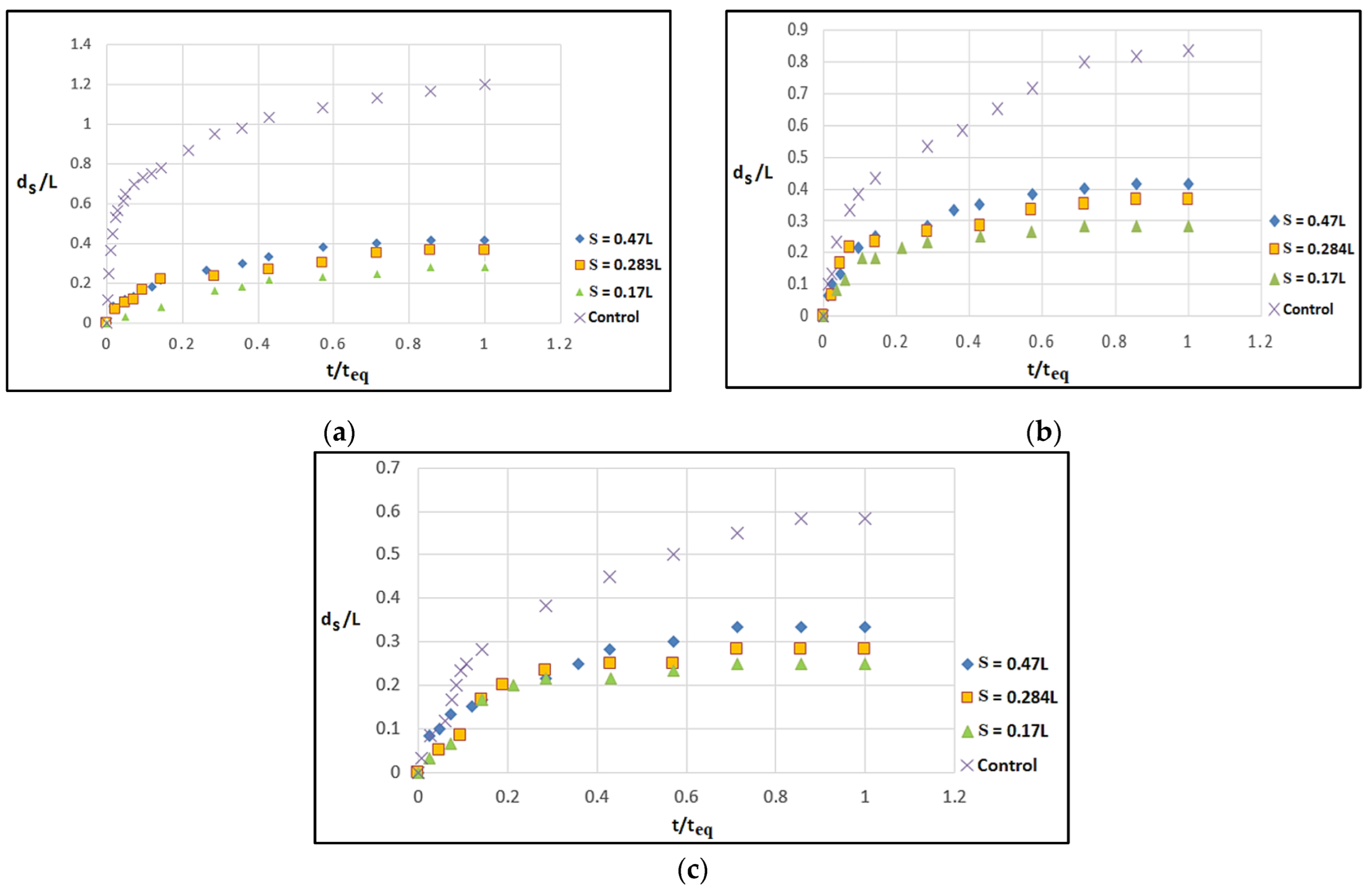
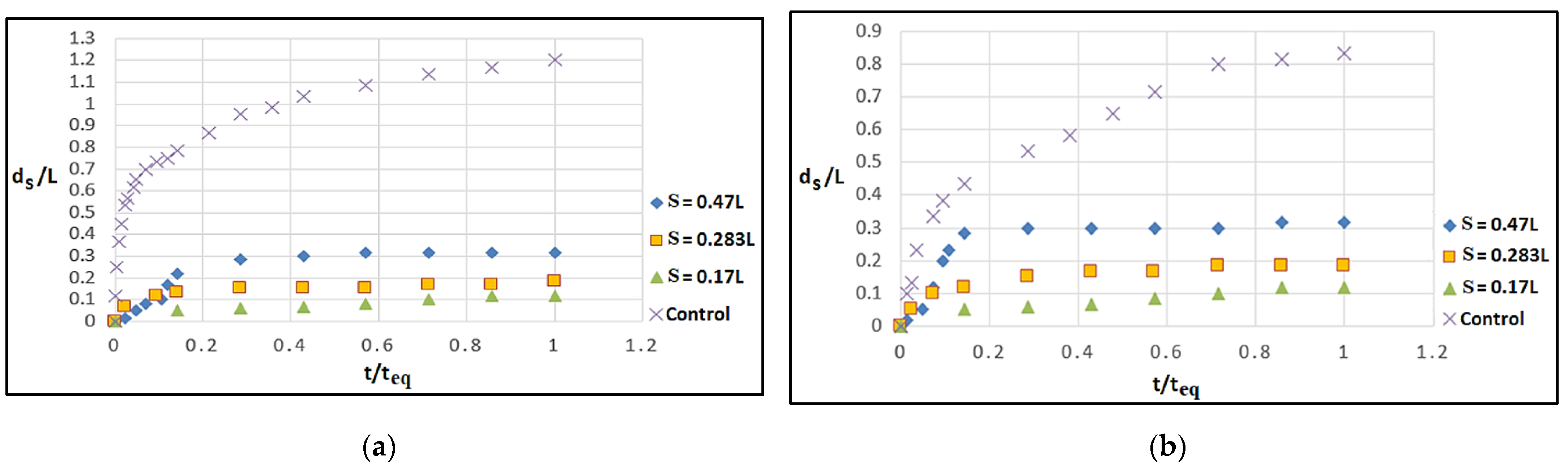
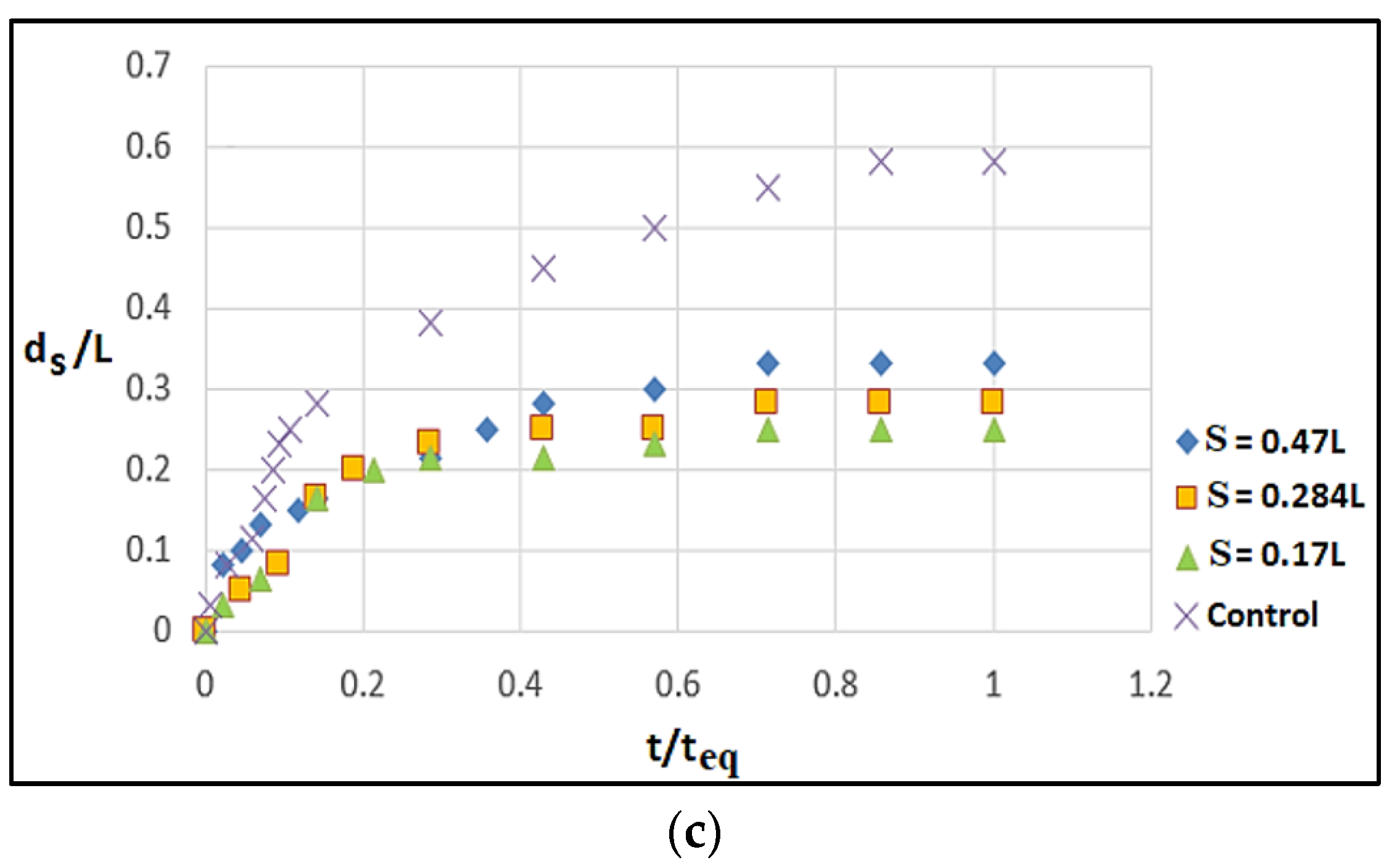
3.2. Effect of Spacing between Roughness Elements in Reducing Scour
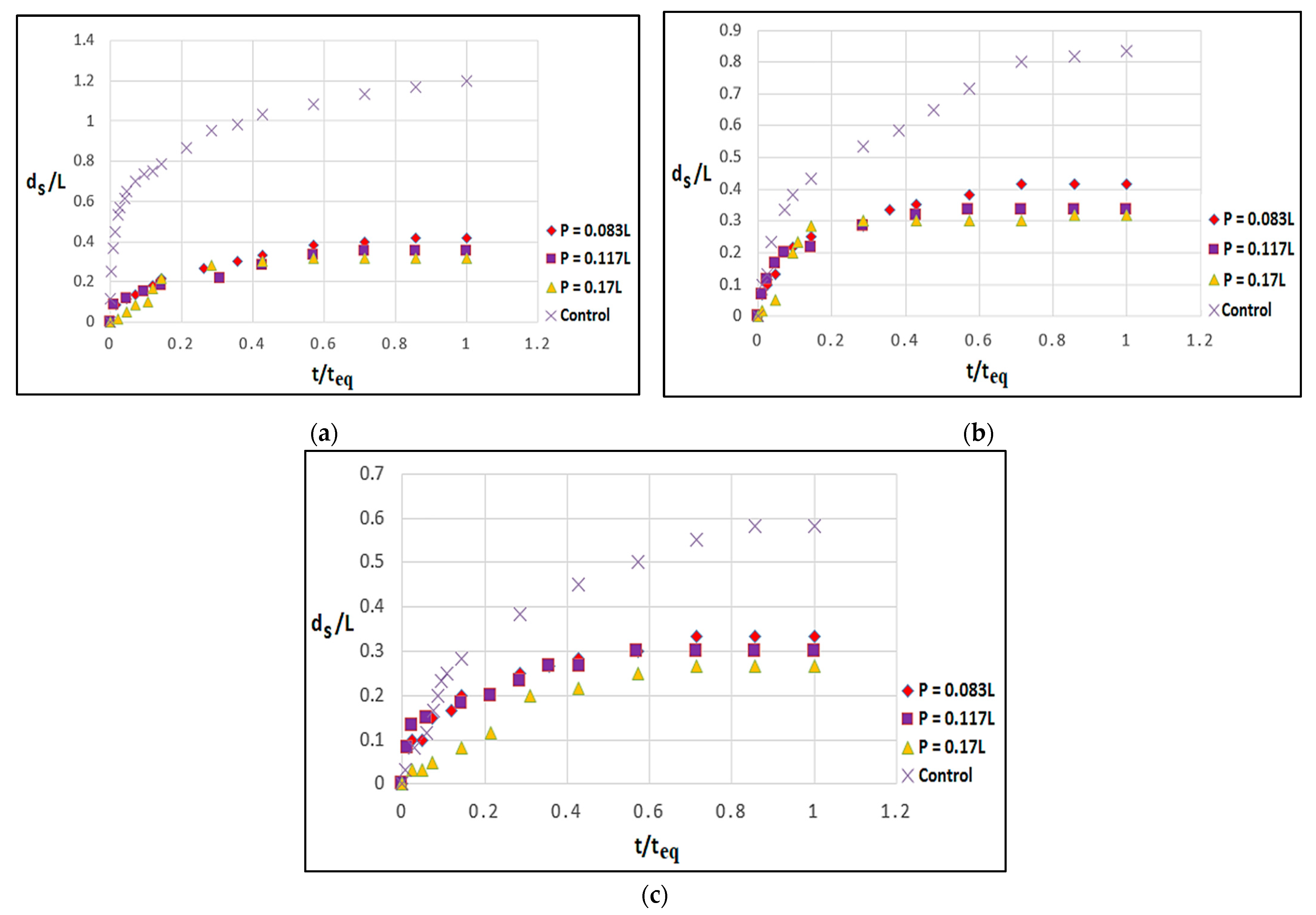
3.3. Effect of the Protrusion of Roughness Elements in Reducing Local Scour
3.4. Investigating the Effect of Roughness on the Upstream Slope of the Scour
4. Conclusions
- In bridge abutments that lacked a rough surface, the study observed an increase in scour depth as the flow depth increased. However, when roughness elements were present on the abutment surface, they contributed to a decrease in downflow, resulting in less scour around the structure. This reduction in scour was attributed to the weakening of adverse pressure and the primary vortices caused by the roughness elements.
- It was observed that a small spacing between the roughness elements hindered the power of the downflow. By increasing the size of the roughness elements for shorter spacings, the downflow was deflected, thereby preventing a direct and significant impact of the flow on the bed and scour hole. As a result, the flow strength around the abutment was reduced.
- The study revealed a notable correlation between the presence of roughness elements on the abutment surface and the spacing between them in relation to the scour around the bridge abutments. An observation was made that as the ratio of the spacing between roughness elements (s) to the size of the protrusion of elements (p) increased, there was a noticeable reduction in the impact of roughness on the scour. Specifically, at a given depth of flow and protrusion of roughness elements (p), when the spacing between roughness elements (s) approached a value closer to the ratio of the protrusion of roughness elements, a decrease in scour depth was observed.
- In the presence of roughness, the slope of the scour hole exhibited a distinctive pattern, as observed in the study. Initially, it commenced at a 0-degree angle and gradually increased, reaching angles ranging between 50 and 70 degrees. This range corresponded to the peak scour depth, indicating the most significant scour and this progressing in the slope of the scour hole causes the steeper slope at these angle ranges. Once the peak was reached, the slope of the scour hole began to decrease as the angle approached 90 degrees.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pourmansouri, R. Controlling the Scouring Occurrence of the Bridge by Implanting the Submerged Plates with Different Angles. Master’s Thesis, Chamran University of Ahwaz, Khuzestan, Iran, 2017. [Google Scholar]
- Shirole, A.M.; Holt, R.C. Planning for a comprehensive bridge safety assurance program. Transp. Res. Rec. 1991, 1290, 39–50. [Google Scholar]
- Ahmed, F.; Nallamuthu, R. Flow around bridge piers. J. Hydraul. Eng. 1998, 124, 288–300. [Google Scholar] [CrossRef]
- Ettema, R. Scour at Bridge Piers—Report No 216; School of Engineering, University of Auckland: Auckland, New Zealand, 1980. [Google Scholar]
- Chiew, Y.M. Local Scour at Bridge Piers. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 1984. [Google Scholar]
- Kwan, T.F. Study of Abutment Scour; No. 328; School of Engineering Report; University of Auckland: Auckland, New Zealand, 1984. [Google Scholar]
- Chiew, Y.M. Scour protection at bridge piers. J. Hydraul. Eng. 1992, 118, 1260–1269. [Google Scholar] [CrossRef]
- Melville, B.W. Local scour at bridge abutments. J. Hydraul. Eng. 1992, 118, 615–631. [Google Scholar] [CrossRef]
- Afzal, M.S.; Bihs, H.; Kumar, L. Computational fluid dynamics modeling of abutment scour under steady current using the level set method. Int. J. Sediment Res. 2020, 35, 355–364. [Google Scholar] [CrossRef]
- Dey, S.; Sumer, B.M.; Fredsøe, J. Control of scour at vertical circular piles under waves and current. J. Hydraul. Eng. 2006, 132, 270–279. [Google Scholar] [CrossRef]
- Radice, A.; Oskars, L. On flow-altering countermeasures for scour at vertical-wall abutment. Arch. Hydro-Eng. Environ. Mech. 2012, 59, 137–153. [Google Scholar]
- Daneshfaraz, R.; Norouzi, R.; Ebadzadeh, P.; Kuriqi, A. Influence of sill integration in labyrinth sluice gate hydraulic performance. Innov. Infrastruct. Solut. 2023, 8, 118. [Google Scholar] [CrossRef]
- Radice, A.; Vahid, D. Roughening elements as abutment scour countermeasures. J. Hydraul. Eng. 2014, 140, 06014014. [Google Scholar] [CrossRef]
- Shahsavari, H.; Manouchehr, H.; Mohammad, M. Simultaneous Effect of Collar and Roughness on Reducing and Controlling the Local Scour around Bridge Abutment. Acta Univ. Agric. Et Silvic. Mendel. Brun. 2017, 65, 52. [Google Scholar] [CrossRef]
- Shahsavari, H. Investigation of the Effect of Local Roughness in Controlling and Reducing the Local Scouring of the Bridge Abutment. Master’s Thesis, Isfahan University of Technology, Khomeyni Shahr, Iran, 2014. [Google Scholar]
- Raudkivi, A.J.; Ettema, R. Clear-water scour at cylindrical piers. J. Hydraul. Eng. 1983, 109, 338–350. [Google Scholar] [CrossRef]
- Ettema, R.; Gokhan, K.; Marian, M. Similitude of large-scale turbulence in experiments on local scour at cylinders. J. Hydraul. Eng. 2006, 132, 33–40. [Google Scholar] [CrossRef]
- Henderson, F.M. Open Channel Flow; Professor of Civil Engineering, University of Canterbury: Christchurch, New Zealand; Macmillan Publishing Co., Inc.: New York, NY, USA, 1966. [Google Scholar]
- Arneson, L.A.; Zevenbergen, L.W.; Lagasse, P.F.; Clopper, P.E. Evaluating Scour at Bridges, 5th ed.; FHWA Report: FHWA-HIF-12-003 HEC-18; Federal Highway Administration. Office of Technology Applications: Washington, DC, USA, 1995. [Google Scholar]
- Graf, W.H.; Altinakar, M.S. Fluvial Hydraulics: Flow and Transport Processes in Channels of Simple Geometry; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Follett, E.M.; Nepf, H.M. Sediment patterns near a model patch of reedy emergent vegetation. Geomorphology 2012, 179, 141–151. [Google Scholar] [CrossRef]
- Gill, M.A. Erosion of sand beds around spur dikes. J. Hydraul. Div. 1972, 98, 1587–1602. [Google Scholar] [CrossRef]
- Kandasamy, J.K. Abutment Scour; Rep. No. 458; School of Engineering, University of Auckland: Auckland, New Zealand, 1989. [Google Scholar]
- Dongol, D.M.S. Local Scour at Bridge Abutments. Ph.D. Thesis, The University of Auckland, Auckland, New Zealand, 1993. [Google Scholar]
- Wong, W.H. Scour at Bridge Abutments; Rep. No. 275; School of Engineering, University of Auckland: Auckland, New Zealand, 1982. [Google Scholar]
- Laursen, E.M. 1952 Observations on the nature of scour. In Proceedings of the 5th Hydraulic Conference; University of Iowa: Iowa City, IA, USA, 1952; pp. 179–197. [Google Scholar]
- Laursen, E.M.; Toch, A. Scour around Bridge Piers and Abutments; Iowa Highway Research Board: Ames, IA, USA, 1956; Volume 4. [Google Scholar]
- Melville, B.W.; Chiew, Y.M. Time scale for local scour at bridge piers. J. Hydraul. Eng. 1999, 125, 59–65. [Google Scholar] [CrossRef]



| Year | Number of Failed Bridges |
|---|---|
| 1952–1960 | 78 |
| 1972–1980 | 648 |
| 1982–1990 | 97 |
| 1992–2000 | 5724 |
| 2002–2006 | 9392 |
| Experiment Number | Roughness Thickness (th, cm) | Roughness Protrusion (p, cm) | Roughness Spacing (s, cm) |
|---|---|---|---|
| 1 | - | - | - |
| 2 | 0.3 | 0.5 | 1 |
| 3 | 0.3 | 0.7 | 1 |
| 4 | 0.3 | 1 | 1 |
| 5 | 0.3 | 0.5 | 1.7 |
| 6 | 0.3 | 0.7 | 1.7 |
| 7 | 0.3 | 1 | 1.7 |
| 8 | 0.3 | 0.5 | 2.8 |
| 9 | 0.3 | 0.7 | 2.8 |
| 10 | 0.3 | 1 | 2.8 |
| h (cm) | U (m/s) | |||
| 9 | 0.011 | 0.264 | 0.0250 | 0.28 |
| 12 | 0.015 | 0.275 | 0.0255 | 0.26 |
| 15 | 0.019 | 0.289 | 0.0258 | 0.24 |
| p, s (cm) | s/p | h (cm) | θ = 50° | θ = 60° | θ = 70° |
|---|---|---|---|---|---|
| p = s = 0 | 15 | 0.6835 | 0.6835 | 0.6835 | |
| - | 12 | 0.6471 | 0.6471 | 0.6471 | |
| 9 | 0.5412 | 0.5412 | 0.5412 | ||
| p = 0.5, s = 2.8 | 15 | 0.5092 | 0.5092 | 0.5092 | |
| 5.6 | 12 | 0.5011 | 0.5011 | 0.5011 | |
| 9 | 0.4767 | 0.4767 | 0.4767 | ||
| p = 0.5, s = 1.7 | 15 | 0.4683 | 0.4683 | 0.4683 | |
| 3.4 | 12 | 0.4621 | 0.4621 | 0.4621 | |
| 9 | 0.4073 | 0.4073 | 0.4073 | ||
| p = 0.7, s = 2.8 | 15 | 0.4274 | 0.4274 | 0.4274 | |
| 4.0 | 12 | 0.4203 | 0.4203 | 0.4203 | |
| 9 | 0.4388 | 0.4388 | 0.4388 | ||
| p = s = 1 | 15 | 0.0 | 0.1161 | 0.1161 | |
| 1 | 12 | 0.0 | 0.1142 | 0.1142 | |
| 9 | 0.0 | 0.101 | 0.101 | ||
| p = 1, s = 2.8 | 15 | 0.3896 | 0.3896 | 0.3896 | |
| 2.8 | 12 | 0.3892 | 0.3892 | 0.3892 | |
| 9 | 0.413 | 0.413 | 0.413 | ||
| p = 1, s = 1.7 | 15 | 0.1997 | 0.1997 | 0.1997 | |
| 1.7 | 12 | 0.1997 | 0.1997 | 0.1997 | |
| 9 | 0.1593 | 0.1593 | 0.1593 | ||
| p = 0.7, s = 1.7 | 15 | 0.2457 | 0.2457 | 0.2457 | |
| 2.43 | 12 | 0.2401 | 0.2401 | 0.2401 | |
| 9 | 0.1614 | 0.1614 | 0.1614 | ||
| p = 0.7, s = 1 | 15 | 0.0 | 0.138 | 0.138 | |
| 1.43 | 12 | 0.0 | 0.136 | 0.136 | |
| 9 | 0.0 | 0.1302 | 0.1302 | ||
| p = 0.5, s = 1 | 15 | 0.3164 | 0.3164 | 0.3164 | |
| 2.0 | 12 | 0.3126 | 0.3126 | 0.3126 | |
| 9 | 0.2952 | 0.2952 | 0.2952 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezaie, A.; Afzalimehr, H.; Sohrabi, S.; Nazari-Sharabian, M.; Karakouzian, M.; Ahmadi, R. Reducing Scour around Semi-Elliptical Bridge Abutments: Application of Roughness Elements. Fluids 2023, 8, 306. https://doi.org/10.3390/fluids8120306
Rezaie A, Afzalimehr H, Sohrabi S, Nazari-Sharabian M, Karakouzian M, Ahmadi R. Reducing Scour around Semi-Elliptical Bridge Abutments: Application of Roughness Elements. Fluids. 2023; 8(12):306. https://doi.org/10.3390/fluids8120306
Chicago/Turabian StyleRezaie, Afsaneh, Hossein Afzalimehr, Sina Sohrabi, Mohammad Nazari-Sharabian, Moses Karakouzian, and Reza Ahmadi. 2023. "Reducing Scour around Semi-Elliptical Bridge Abutments: Application of Roughness Elements" Fluids 8, no. 12: 306. https://doi.org/10.3390/fluids8120306
APA StyleRezaie, A., Afzalimehr, H., Sohrabi, S., Nazari-Sharabian, M., Karakouzian, M., & Ahmadi, R. (2023). Reducing Scour around Semi-Elliptical Bridge Abutments: Application of Roughness Elements. Fluids, 8(12), 306. https://doi.org/10.3390/fluids8120306









