Fluid Flow in Helically Coiled Pipes
Abstract
:1. Introduction
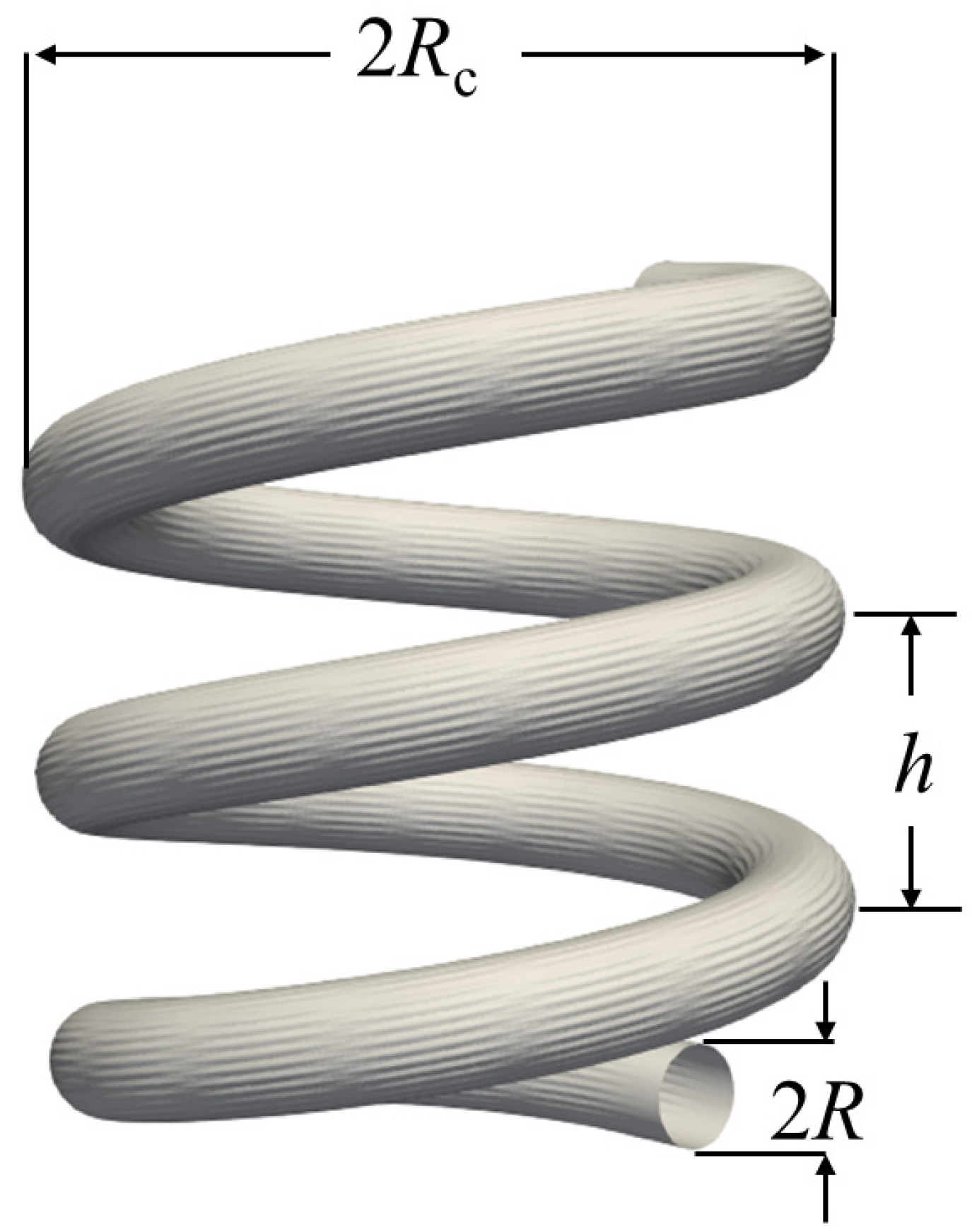
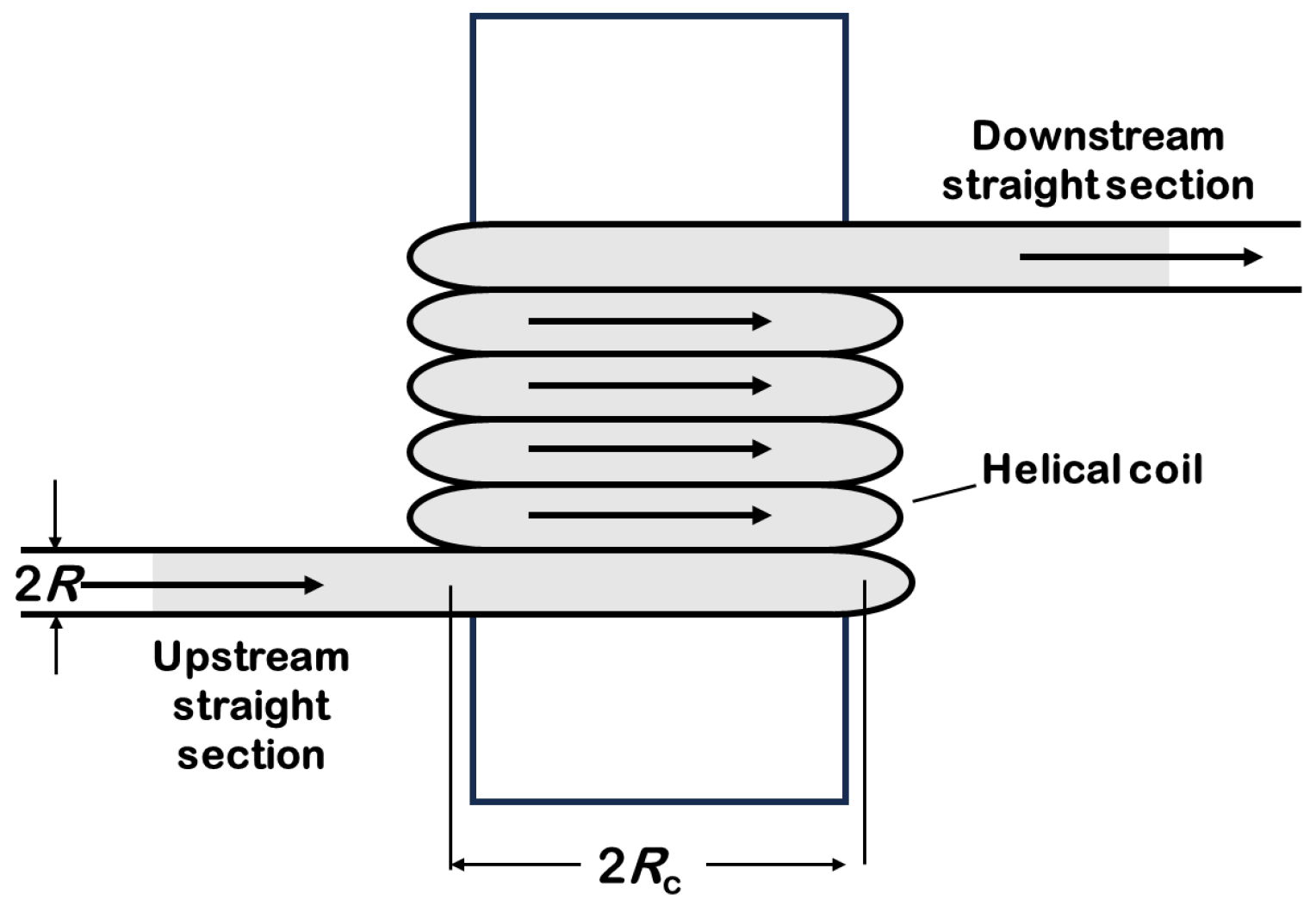
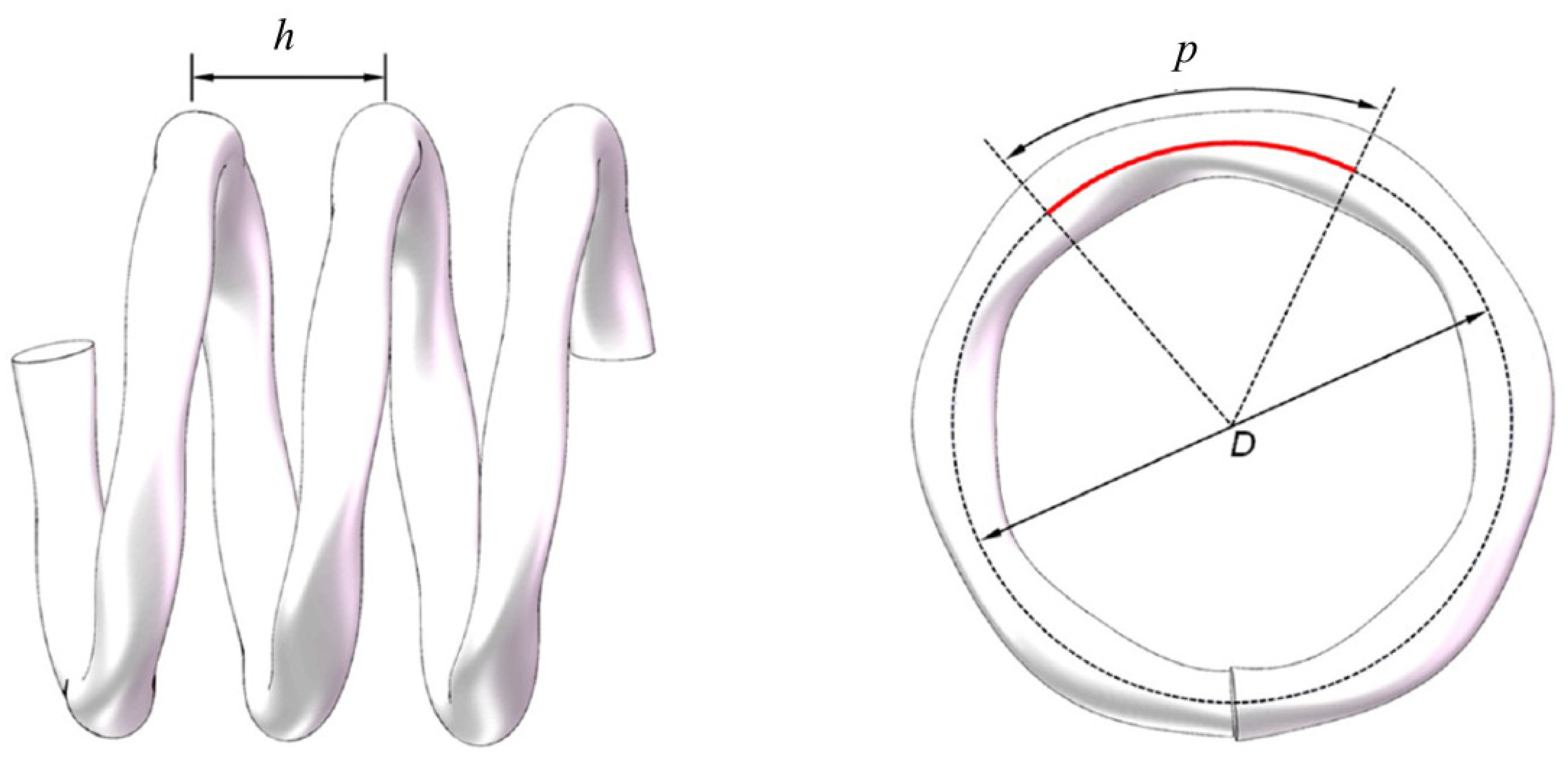
2. Geometrical Parameters of a Helically Coiled Pipe
3. Overview of Experimental Work
3.1. Earlier Observations
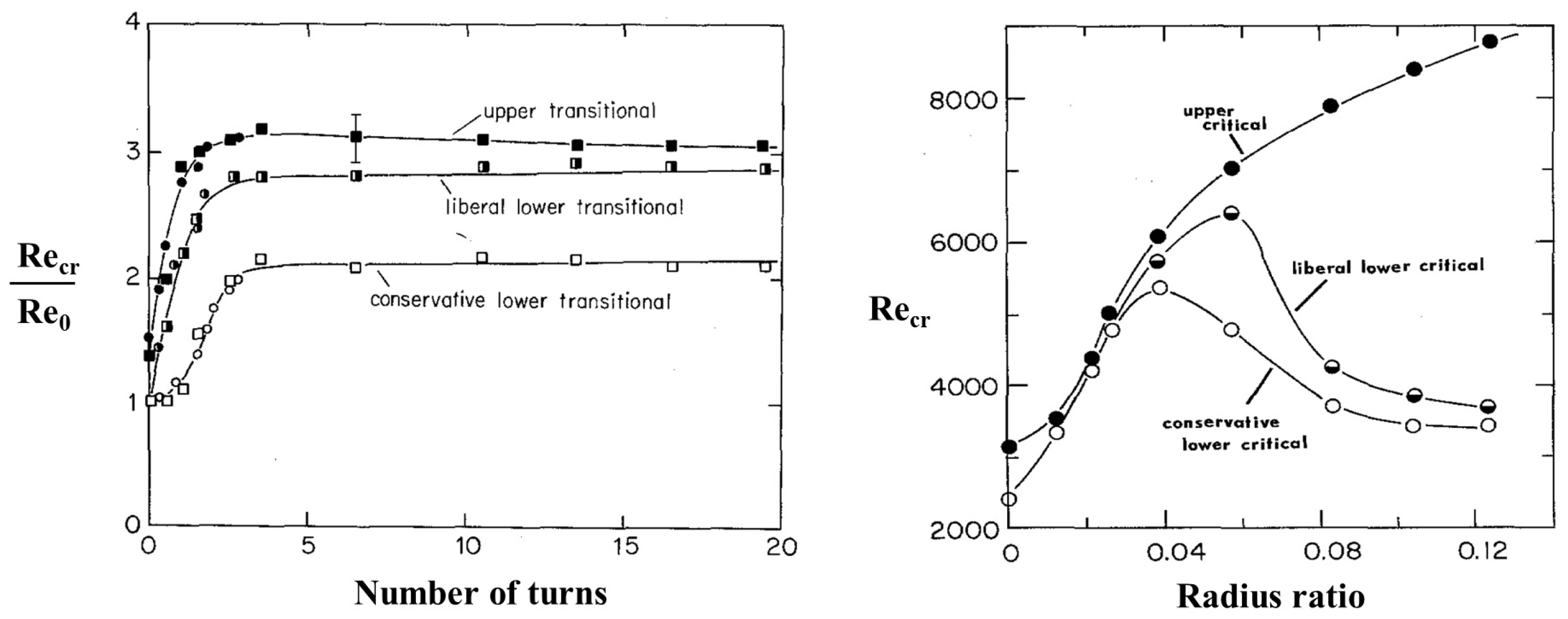
3.2. Flow Stabilization in Helical Pipes
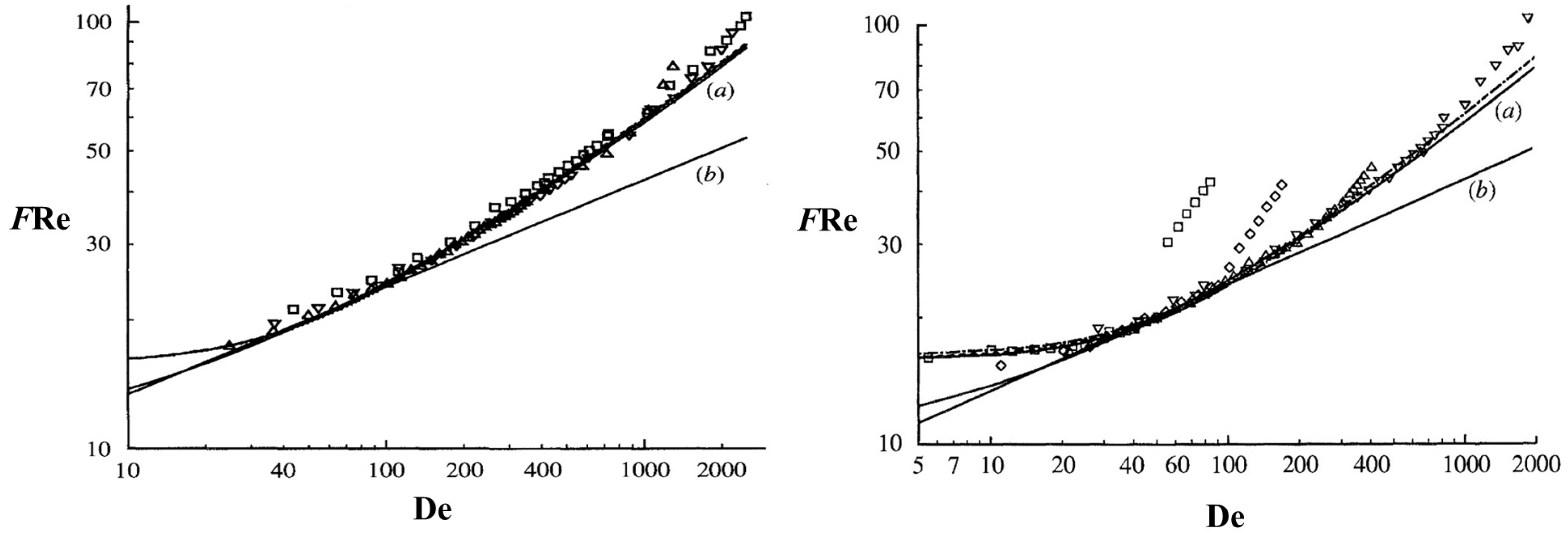
3.3. Pressure Drop
3.4. Heat Transfer
3.5. Non-Newtonian Fluid Flow
4. Overview of Theoretical Work
4.1. Analytical and Semi-Analytical Approaches
4.2. Numerical Simulations: Laminar Flow
4.3. Numerical Simulations: Turbulent Flow and Heat Transfer
4.4. Flow and Heat Transfer in Corrugated and Twisted Helical Pipes
5. Other Investigation Aspects of Helical Coiled Flows
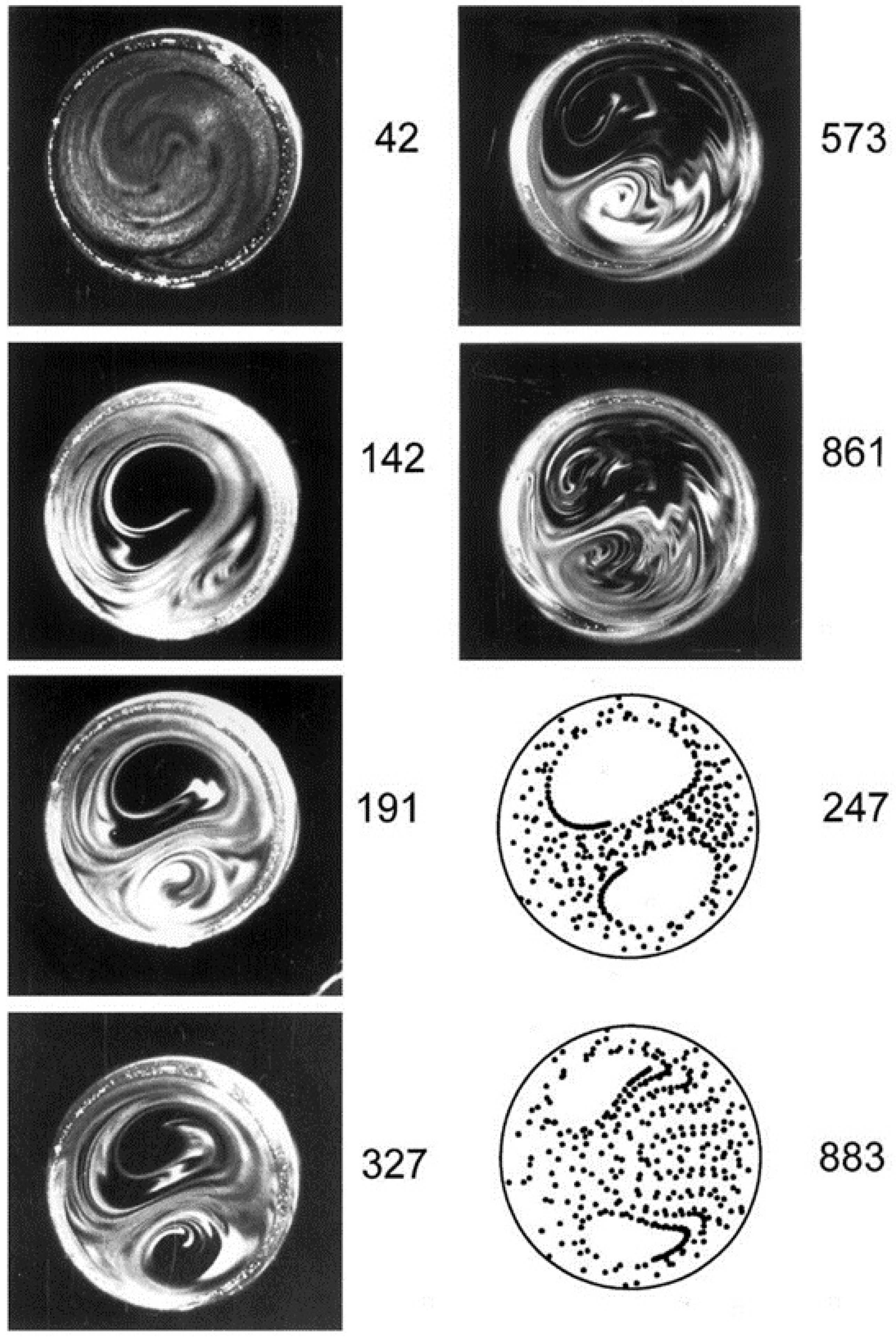
5.1. Visualization of Helical Pipe Flow
5.2. Entropy Generation of Helical Pipe Flow
6. Two-Phase Flow in Helically Coiled Pipes
7. Helical Flows in Magnetohydrodynamics (MHD)
8. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Constant factor |
| Semi-major axis of elliptical cross-section (m) | |
| b | Constant factor |
| Semi-minor axis of elliptical cross-section (m) | |
| Characteristic number (dimensionless) | |
| d | Diameter of circular cross-section (m) |
| D | Pipe inner diameter (m) |
| Coil diameter (m) | |
| De | Dean number (dimensionless) |
| Generalized Dean number (dimensionless) | |
| Equivalent coil diameter (m) | |
| e | Roughness height (mm) |
| Eu | Euler number (dimensionless) |
| Entropy flux vector (W m K) | |
| F | Fanning friction factor (dimensionless) |
| Darcy–Weisbach friction factor (dimensionless) | |
| FoM | Figure of merit |
| Friction factor for laminar flow (dimensionless) | |
| Gn | Germano number (dimensionless) |
| h | Coil pitch (m) |
| Pitch of spiral corrugation (mm) | |
| K | Behavior index |
| k | Thermal conductivity (W m K) |
| L | Straight pipe section (m) |
| Length of coil portion (m) | |
| n | Consistency index |
| Nu | Nusselt number (dimensionless) |
| p | Pressure (Pa) |
| Twist pitch (mm) | |
| Regression parameters | |
| Pumping power (W) | |
| Pr | Prandtl number (dimensionless) |
| q | Heat flux (W m) |
| Q | Volumetric flow rate (m s) |
| Total heat transfer rate (W) | |
| R | Pipe inner radius (m) |
| Helical coil radius (m) | |
| Re | Reynolds number (dimensionless) |
| Generalized Reynolds number (dimensionless) | |
| Critical Reynolds number (dimensionless) | |
| Frictional Reynolds number (dimensionless) | |
| S | Entropy generation rate per unit volume (W m K) |
| Viscous stress tensor (N m) | |
| Bulk temperature (K) | |
| Mean temperature (K) | |
| Inner wall temperature (K) | |
| v | Mean flow velocity (m s) |
| Velocity vector (m s) | |
| Friction velocity (m s) | |
| Differential pressure (Pa) | |
| Section length (m) | |
| Averaged wall shear stress (kg m s) | |
| Ratio of torsion to curvature ratio (dimensionless) | |
| Torsion parameter (dimensionless) | |
| ∇ | Nabla operator (m) |
| Greek letters | |
| Kinematic viscosity (m s) | |
| Curvature ratio (dimensionless) | |
| Helix angle, lift angle | |
| Ratio of pitch to length of one helical turn (dimensionless) | |
| Density (kg m) | |
| Generalized curvature ratio (dimensionless) | |
| Torsion of the helix (dimensionless) | |
| Flow pattern transition parameter (dimensionless) | |
| Constant | |
| Constant | |
| Concentration (dimensionless) | |
| Dimensionless curvature | |
| Dimensionless helix torsion | |
| Rotation angle | |
| Angle | |
| Dynamic viscosity (kg m s) | |
| Subscripts | |
| c | Curvature, coil |
| D | Darcy |
| cr | Critical |
| 0 | Initial, lower |
| eq | Equivalent |
| w | Wall |
| b | Bulk |
| i | Integer index |
| Shear stress | |
| ref | Reference |
| g | Gas, global |
| l | Liquid |
| tp | Two-phase |
| Viscous | |
| h | Heat transfer |
References
- Hagen, G. Über die Bewengung des Wassers in engen zylindrischen Röhr. Poggendorffs Ann. 1839, 46, 423–442. [Google Scholar]
- Poiseuille, J.L.M. Recherches expérimentales sur le mouvement del liquides dans les tubes de trés-petits diamètres. Comptes Rendus 1842, 11, 961–967. [Google Scholar]
- Darcy, H. Recherches Expérimentales Relatives au Mouvement de l’Eau dans les Tuyaux; Mallet-Bachelier: Paris, France, 1857. [Google Scholar]
- Reynolds, O. An experimental investigation of the circumstances which determine whether the motion of water should be direct or sinuous, and of the law of resistance in parallel channels. Proc. R. Soc. Lond. 1883, 11, 84–89. [Google Scholar]
- Boussinesq, M.J. Mémoire sur l’influence des frottements dans le mouvement réguliers des fluides. J. Math. Pures Appl. 1868, 13, 377–424. [Google Scholar]
- Thomson, J. On the origin of windings of rivers in alluvial plains with remarks on the flow of water round bends in pipes. Proc. R. Soc. Lond. 1876, 25, 5–8. [Google Scholar]
- Thomson, J. Experimental demonstration in respect to the origin of windings of rivers in alluvial plains, and to the mode of flow of water round bends of pipes. Proc. R. Soc. Lond. 1877, 26, 356–357. [Google Scholar]
- Williams, G.S.; Hubbell, C.W.; Fenkell, G.H. Experiments at Detroit, Mich.; on the effect of curvature upon the flow of water in pipes. Trans. Ofthe Am. Soc. Civ. Eng. 1902, 47, 1–196. [Google Scholar] [CrossRef]
- Eustice, J. Flow of water in curved pipes. Proc. R. Soc. A 1910, 84, 107–118. [Google Scholar]
- Eustice, J. Experiments on stream-line motion in curved pipes. Proc. R. Soc. A 1911, 85, 119–131. [Google Scholar]
- White, C.M. Streamline flow through curved pipes. Proc. R. Soc. A 1929, 123, 645–663. [Google Scholar]
- Kalpakli Vester, A.; Örlü, R.; Alfredsson, P.H. Turbulent flows in curved pipes: Recent advances in experiments and simulations. Appl. Mech. 2016, 68, 050802. [Google Scholar] [CrossRef]
- Dean, W.R. Note on the motion of fluid in a curved pipe. Philos. Mag. 1927, 4, 208–223. [Google Scholar] [CrossRef]
- Dean, W.R. The stream-line motion of fluid in a curved pipe. Philos. Mag. 1928, 5, 671–695. [Google Scholar] [CrossRef]
- Prabhanjan, G.S.V.; Raghavan, G.; Rennie, T.J. Comparison of heat transfer rates between a straight tube heat exchanger and a helically coiled heat exchanger. Int. Commun. Heat Mass Transf. 2002, 29, 185–191. [Google Scholar] [CrossRef]
- Carelli, M.D.; Conway, L.E.; Oriani, L.; Petrovič, B.; Lombardi, C.V.; Ricotti, M.E.; Barroso, A.C.O.; Collado, J.M.; Cinotti, L.; Todreas, N.E.; et al. The design and safety features of the IRIS reactor. Nucl. Des. 2004, 230, 151–167. [Google Scholar] [CrossRef]
- Di Piazza, I.; Ciofalo, M. Numerical prediction of turbulent flow and heat transfer in helically coiled pipes. Int. J. Therm. Sci. 2010, 49, 653–663. [Google Scholar] [CrossRef]
- Pioro, I.L. Handbook of Generation IV Nuclear Reactors; Woodhead Publishing Series in Energy: Thorston, UK, 2016. [Google Scholar]
- Gill, J.; Singh, J. Use of artificial neural network approach for depicting mass flow rate of R134a/LPG refrigerant through straight and helical coiled adiabatic capillary tubes of vapor compression refrigeration system. Int. Refrig. 2018, 86, 228–238. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Zhou, Y.; Wang, D.; Wang, Y.; Wang, D. Experimental research on the thermal performance of PEX helical coil pipes for heating the biogas digester. Appl. Therm. Eng. 2019, 147, 167–176. [Google Scholar] [CrossRef]
- Moll, R.; Veyret, D.; Charbit, F.; Moulin, P. Dean vortices applied to membrane process: Part I. Experimental approach. J. Membr. Sci. 2007, 288, 307–320. [Google Scholar] [CrossRef]
- Abdel-Aziz, M.H.; Mansour, L.A.S.; Sedahmed, G.H. Study of the rate of liquid-solid mass transfer controlled processes in helical tubes under turbulent flow conditions. Chem. Eng. Process. Process Intensif. 2010, 49, 643–648. [Google Scholar] [CrossRef]
- Mansour, M.; Liu, Z.; Janiga, G.; Nigam, K.D.; Sundmacher, K.; Thévenin, D.; Zähringer, K. Numerical study of liquid-liquid mixing in helical pipes. Chem. Eng. Sci. 2017, 172, 250–261. [Google Scholar] [CrossRef]
- Andhare, A.M.; Kriplani, V.M.; Modak, J.P. Heat transfer studies in helically coiled tube: A review. Int. J. Res. Mech. 2014, 2, 74–83. [Google Scholar]
- Pawar, Y.; Zare, A.; Sarode, A. Helically coiled tube with different geometry and curvature ratios on convective heat transfer: A review. Int. Innov. Res. Adv. Eng. 2016, 3, 19–23. [Google Scholar]
- Berger, S.A.; Talbot, L.; Yao, L.S. Flow in curved pipes. Annu. Rev. Fluid Mech. 1983, 15, 461–512. [Google Scholar] [CrossRef]
- Ito, H. Flow in curved pipes. Bull. JMSE 1987, 30, 543–552. [Google Scholar] [CrossRef]
- Naphon, P.; Wongwises, S. A review of flow and heat transfer characteristics in curved tubes. Renew. Sustain. Energy Rev. 2006, 10, 463–490. [Google Scholar] [CrossRef]
- Vashisth, S.; Kumar, V.; Nigam, K.D.P. A review on the potential applications of curved geometries in process industry. Ind. Eng. Chem. Res. 2008, 47, 3291–3337. [Google Scholar] [CrossRef]
- Taylor, G.I. The criterion for turbulence in curved pipes. Proc. R. Soc. Lond. A 1929, 124, 243–249. [Google Scholar]
- Viswanath, P.R.; Narasimha, R.; Prabhu, A. Visualization of relaminarizing flows. J. Indian Inst. Sci. 1978, 60, 159–165. [Google Scholar]
- Narasimha, R.; Sreenivasan, K.R. Relaminarization of fluid flows. Adv. Appl. Mech. 1979, 19, 221–309. [Google Scholar]
- Sreenivasan, K.R.; Strykowski, P.J. Stabilization effects in flow through helically coiled pipes. Exp. Fluids 1983, 1, 31–36. [Google Scholar] [CrossRef]
- Austen, D.S.; Soliman, H.M. Laminar flow and heat transfer in helically coiled tubes with substantial pitch. Exp. Therm. Fluid Sci. 1988, 1, 183–194. [Google Scholar] [CrossRef]
- Das, S.K. Water flow through helical coils in turbulent conditions. Can. J. Chem. Eng. 1993, 71, 971–973. [Google Scholar] [CrossRef]
- Liu, S.; Atacan, A.; Nasr-El-Din, H.A.; Masliyah, J.H. An experimental study of pressure drop in helical pipes. Proc. R. Soc. Lond. A 1994, 444, 307–316. [Google Scholar]
- De Amicis, J.; Cammi, A.; Colombo, L.P.M.; Colombo, M. Experimental and numerical study of the laminar flow in helically coiled pipes. Prog. Nucl. Energy 2014, 76, 206–215. [Google Scholar] [CrossRef]
- Rakhsha, M.; Akbaridoust, F.; Abbassi, A.; Saffar-Avval, M. Experimental and numerical investigations of turbulent forced convection flow of nano-fluid in helical coiled tubes at constant surface temperature. Powder Technol. 2015, 283, 178–189. [Google Scholar] [CrossRef]
- Abushammala, O.; Hreiz, R.; Lemaître, C.; Favre, É. Laminar flow friction factor in highly curved helical pipes: Numerical investigation, predictive correlation and experimental validation using a 3D-printed model. Chem. Sci. 2019, 207, 1030–1039. [Google Scholar] [CrossRef]
- Patankar, S.V.; Pratap, V.S.; Spalding, D.B. Prediction of laminar flow and heat transfer in helically coiled pipes. J. Fluid Mech. 1974, 62, 539–551. [Google Scholar] [CrossRef]
- Manlapaz, R.L.; Churchill, S.W. Fully developed laminar flow in a helically coiled tube of finite pitch. Chem. Eng. Commun. 1980, 7, 57–78. [Google Scholar] [CrossRef]
- Wang, J.-W.; Andrews, J.R.G. Numerical simulation of flow in helical ducts. AIChE J. 1995, 41, 1071–1080. [Google Scholar] [CrossRef]
- Jayakumar, J.S.; Mahajani, S.M.; Mandal, J.C.; Iyer, K.N.; Vijayan, P.K. CFD analysis of single-phase flows inside helically coiled tubes. Comput. Chem. Eng. 2010, 34, 430–446. [Google Scholar] [CrossRef]
- Ahmadloo, E.; Sobhanifar, N.; Hosseini, F.S. Computational fluid dynamics study on water flow in a hollow helical pipe. Open J. Fluid Dyn. 2014, 4, 133–139. [Google Scholar] [CrossRef]
- Colombo, M.; Cammi, A.; Ricotti, M.E. Assessment of different turbulence models in helically coiled pipes through comparison with experimental data. In Proceedings of the 2012 20th International Conference on Nuclear Energy Collocated with the ASME 2012 Power Conference, Anaheim, CA, USA, 30 July–3 August 2012; Paper No.: ICONE20-Power2012-54546. pp. 273–283. [Google Scholar]
- Faraj, A.F.; Azzawi, I.D.J.; Yahya, S.G. Pitch variations study on helically coiled pipe in turbulent flow region using CFD. Int. J. Heat Technol. 2020, 38, 775–784. [Google Scholar] [CrossRef]
- Kurnia, J.C.; Sasmito, A.P.; Shamim, T.; Mujumdar, A.S. Numerical investigation of heat transfer and entropy generation of laminar flow in helical tubes with various cross sections. Appl. Therm. Eng. 2016, 102, 849–860. [Google Scholar] [CrossRef]
- Adhikari, B.; Maharjan, S. Numerical simulation of helically coiled closed loop pulsating heat pipe. Int. J. Eng. Manag. 2019, 9, 206–212. [Google Scholar] [CrossRef]
- Tang, L.; Tang, Y.; Parameswaran, S. A numerical study of flow characteristcs in a helical pipe. Adv. Mech. Eng. 2016, 8, 1–8. [Google Scholar] [CrossRef]
- Demagh, Y.; Bitam, E.; Bordja, L. Comparative numerical study on pressure drop in helically coiled and longitudinally C-shaped pipes. SN Appl. Sci. 2020, 2, 1570. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Ding, R. Analysis of heat transfer and flow characteristics of a helically coiled tube with twisted elliptical in a low Reynolds number flow. Processes 2022, 10, 2229. [Google Scholar] [CrossRef]
- Colombo, M.; Cammi, A.; Guédon, G.R.; Inzoli, F.; Ricotti, M.E. CFD study of an air-water flow inside helically coiled pipes. Prog. Nucl. Energy 2015, 85, 462–472. [Google Scholar] [CrossRef]
- Murata, S.; Miyake, Y.; Inaba, T.; Ogata, H. Laminar flow in a helically coiled pipe. Bull. JSME 1981, 24, 355–362. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, B. Fluid flow in a helical pipe. Acta Mech. Sin. 1999, 15, 299–312. [Google Scholar]
- Marušić-Paloka, E.; Pažanin, I. Fluid flow through a helical pipe. Z. Angew. Math. Phys. 2007, 58, 81–99. [Google Scholar] [CrossRef]
- Prattipati, R.; Narla, V.K.; Pendyala, S. Effect of viscosity on entropy generation for laminar flow in helical pipes. J. Therm. 2021, 7, 1100–1109. [Google Scholar] [CrossRef]
- Kumar, A. Pressure-driven flows in helical pipes: Bounds on flow rate and friction factor. J. Fluid Mech. 2020, 904, A5. [Google Scholar] [CrossRef]
- Weisbach, J.L. Die Experimental-Hydraulik; Kessinger’s Legacy Reprints: Whitefish, MN, USA, 1855. [Google Scholar]
- Adler, M. Strömung in gekrümmten Rohren. Z. Angew. Math. Mech. 1934, 14, 257–275. [Google Scholar] [CrossRef]
- Wattendorf, F.L. A study of the effect of curvature on fully developed turbulent flow. Proc. R. Soc. A 1935, 148, 565–598. [Google Scholar]
- Kurokawa, M.; Cheng, K.C.; Shi, L. Flow visualization of relaminarization phenomena in curved pipes and related measurements. J. Vis. 1998, 1, 9–28. [Google Scholar] [CrossRef]
- Webster, D.R.; Humphrey, J.A.C. Experimental observations of flow instability in a helical coil (data bank contribution). J. Fluids Eng. 1993, 115, 436–443. [Google Scholar] [CrossRef]
- Webster, D.R.; Humphrey, J.A.C. Traveling wave instability in helical coil flow. Phys. Fluids 1997, 9, 407–418. [Google Scholar] [CrossRef]
- Dennis, S.C.R.; Ng, M. Dual solutions for steady laminar flow through a curved tube. Q. J. Mech. Appl. Math. 1982, 35, 305–324. [Google Scholar] [CrossRef]
- Ramshankar, R.; Sreenivasan, K.R. A paradox concerning the extended Stokes series solution for the pressure drop in coiled pipes. Phys. Fluids 1988, 31, 1339–1347. [Google Scholar] [CrossRef]
- Wang, C.Y. On the low-Reynolds-number flow in a helical pipe. J. Fluid Mech. 1981, 108, 185–194. [Google Scholar] [CrossRef]
- Germano, M. On the effect of the torsion in helical pipe flow. J. Fluid Mech. 1982, 125, 1–8. [Google Scholar] [CrossRef]
- Kao, H.C. Torsion effect on fully developed flow in a helical pipe. J. Fluid Mech. 1987, 184, 335–356. [Google Scholar] [CrossRef]
- Germano, M. The Dean equations extended to a helical pipe flow. J. Fluid Mech. 1989, 203, 289–305. [Google Scholar] [CrossRef]
- Tuttle, E.R. Laminar flow in twisted pipes. J. Fluid Mech. 1990, 219, 545–570. [Google Scholar] [CrossRef]
- Liu, S.; Masliyah, J.H. Axially-invariant laminar flow in helical pipes with a finite pitch. J. Fluid Mech. 1993, 251, 315–353. [Google Scholar] [CrossRef]
- Kubair, V.; Varrier, C.B.S. Pressure drop for liquid flow in helical coils. Trans. Indian Inst. Chem. Eng. 1961, 14, 93–97. [Google Scholar]
- Ito, H. Laminar flow in curved pipes. Z. Angew. Math. Mech. 1969, 11, 653–663. [Google Scholar] [CrossRef]
- Srinivasan, P.S.; Nandapurkar, S.S.; Holland, F.A. Pressure drop and heat transfer in coils. Chem. Eng. 1968, 218, 113–119. [Google Scholar]
- Ward-Smith, A.J. Internal Flow: The Fluid Dynamics of Flow in Pipes and Ducts; Clarendon Press: Oxford, UK, 1980. [Google Scholar]
- White, C.M. Fluid friction and its relation to heat transfer. Trans. Inst. Chem. Eng. 1932, 10, 66–86. [Google Scholar]
- McCabe, W.L.; Smith, C.J.; Harriott, P. Unit Operations of Chemical Engineering; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Prandtl, L. Führer durch die Strömungslehere: Grundlagen und Phänomene; F. Vieweg: Braunschweig, Germany, 1949. [Google Scholar]
- Hasson, D. Streamline flow resistance in coils. Res. Corresp. 1955, 1, S1. [Google Scholar]
- Topakoǧlu, H.C. Steady laminar flows of an incompressible viscous fluid in curved pipes. J. Math. Mech. 1967, 16, 1321–1337. [Google Scholar]
- Van Dyke, M. Extended Stokes series: Laminar flow through a loosely coiled pipe. J. Fluid Mech. 1978, 86, 129–145. [Google Scholar] [CrossRef]
- Barua, S.N. On secondary flow in stationary curved pipes. Q. J. Mech. Appl. Math. 1963, 16, 61–77. [Google Scholar] [CrossRef]
- Mori, Y.; Nakayama, W. Study on forced convective heat transfer in curved pipes: (1st report, laminar region). Int. J. Heat Mass Transf. 1965, 8, 67–82. [Google Scholar] [CrossRef]
- Liu, S. Laminar Flow and Heat Transfer in Helical Pipes with Finite Pitch. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 1992. [Google Scholar]
- Ali, S. Pressure drop correlations for flow through regular helical coil tubes. Fluid Dyn. Res. 2001, 28, 295–310. [Google Scholar] [CrossRef]
- Gupta, R.; Wanchoo, R.K.; Jafar Ali, T.R.M. Laminar flow in helical coils: A parametric study. Ind. Eng. Chem. Res. 2011, 50, 1150–1157. [Google Scholar] [CrossRef]
- Periasamy, G.; Mouleeswaran, S.; Venugopal, P.R.; Perumal, C. Investigation of hydrodynamic flow characteristics in helical coils with ovality and wrinkles. J. Mech. Eng. 2021, 67, 570–579. [Google Scholar] [CrossRef]
- Mishra, P.; Gupta, S.N. Momentum transfer in curved pipes. 1. Newtonian fluids. Ind. Eng. Chem. Process Des. Dev. 1979, 18, 130–137. [Google Scholar] [CrossRef]
- Jensen, M.K.; Bergles, A.E. Critical heat flux in helical coiled tubes. Trans. ASME 1981, 103, 660–666. [Google Scholar] [CrossRef]
- Manlapaz, R.L.; Churchill, S.W. Fully developed laminar convection from a helical coil. Chem. Eng. Commun. 1981, 9, 185–200. [Google Scholar] [CrossRef]
- Seban, R.A.; McLaughlin, E.F. Heat transfer in tube coils with laminar and turbulent flow. Int. J. Heat Mass Transf. 1963, 6, 387–395. [Google Scholar] [CrossRef]
- Dravid, A.N.; Smith, K.A.; Merrill, E.W.; Brian, P.L.T. Effect of secondary fluid motion on laminar flow heat transfer in helically coiled tubes. AIChE J. 1971, 17, 1114–1122. [Google Scholar] [CrossRef]
- Xin, R.C.; Ebadian, M.A. The effects of Prandtl numbers on local and average convective heat transfer characteristics in helical pipes. J. Heat Transf. 1997, 119, 467–473. [Google Scholar] [CrossRef]
- Cioncolini, A.; Santini, L. An experimental investigation regarding the laminar and turbulent flow transition in helically coiled pipes. Exp. Fluid Sci. 2006, 30, 367–380. [Google Scholar] [CrossRef]
- Zheng, X.; Lu, X.; Gao, Y.; Jin, D.; Hu, Y.; Hu, Y.; Mao, Y. Experimental study on friction pressure drop and circumferential heat transfer characteristics in helical tubes. Front. Energy Res. 2023, 11, 1204850. [Google Scholar] [CrossRef]
- Ito, H. Friction factors for turbulent flow in curved pipes. J. Basic Eng. 1959, 81, 123–132. [Google Scholar] [CrossRef]
- Ju, H.; Huang, Z.; Xu, Y.; Duan, B.; Yu, Y. Hydraulic performance of small bending radius helical coil-pipe. J. Nucl. Sci. Technol. 2001, 38, 826–831. [Google Scholar] [CrossRef]
- Hardik, B.K.; Prabhu, S.V. Boiling pressure drop and local heat transfer distribution of helical coils with water and low pressure. Int. Therm. Sci. 2017, 114, 44–63. [Google Scholar] [CrossRef]
- Xiao, Y.; Hu, Z.; Chen, S.; Gu, H. Experimental study of two-phase frictional pressure drop of steam-water in helically coiled tubes with small coil diameters and high pressure. Appl. Therm. Eng. 2018, 132, 18–29. [Google Scholar] [CrossRef]
- Rennie, T.J.; Raghavan, V.G.S. Experimental studies of a double-pipe helical heat exchanger. Exp. Therm. Fluid Sci. 2005, 29, 919–924. [Google Scholar] [CrossRef]
- Mandal, M.M.; Nigam, K.D.P. Experimental study on pressure drop and heat transfer of turbulent flow in tube helical heat exchanger. Ind. Eng. Res. 2009, 48, 9318–9324. [Google Scholar] [CrossRef]
- Ghorbani, N.; Taherian, H.; Gorji, M.; Mirgolbabaei, H. An experimental study of thermal performance of shell-and-coil heat exchangers. Int. Commun. Heat Mass Transf. 2010, 37, 775–781. [Google Scholar] [CrossRef]
- Pawar, S.S.; Sunnapwar, V.K. Studies of convective heat transfer through helical coils. Heat Mass Transf. 2013, 49, 1741–1754. [Google Scholar] [CrossRef]
- Pimenta, T.A.; Campos, L.M. Heat transfer coefficients from Newtonian and non-Newtonian fluids flowing in laminar regime in a helical coil. Int. J. Heat Mass Transf. 2013, 58, 676–690. [Google Scholar] [CrossRef]
- Hardik, B.K.; Baburajan, P.K.; Prabhu, S.V. Local heat transfer coefficient in helical coils with single phase flow. Int. J. Heat Mass Transf. 2015, 89, 522–538. [Google Scholar] [CrossRef]
- Kruthiventi, S.S.; Rasu, N.G.; Kruthiventi, S.S.; Rao, Y.V.H. Coiled tube heat exchangers—A review. Int. J. Mech. Eng. Technol. 2018, 9, 895–904. [Google Scholar]
- Zhao, H.; Li, X.; Wu, Y.; Wu, X. Friction factor and Nusselt number correlations for forced convection in helical tubes. Int. J. Heat Mass Transf. 2020, 155, 119759. [Google Scholar] [CrossRef]
- Ayuob, S.; Mahmood, M.; Ahmad, N.; Waqas, A.; Saeed, H. Development and validation of Nusselt number correlations for a helical coil based energy storage integrated with solar water heating systems. J. Energy Storage 2022, 55, 105777. [Google Scholar] [CrossRef]
- Aly, W.I.; Inaba, H.; Haruki, N.; Horibe, A. Drag and heat transfer reduction phenomena of drag-reducing surfactant solutions in straight and helical pipes. J. Heat Transf. 2006, 128, 800–810. [Google Scholar] [CrossRef]
- Jamshidi, N.; Farhadi, M.; Ganji, D.D.; Sedighi, K. Experimental analysis of heat transfer enhancement in shell and helical tube heat exchangers. Appl. Therm. Eng. 2013, 51, 644–652. [Google Scholar] [CrossRef]
- Hashemi, S.M.; Behabadi, M.A.A. An empirical study on heat transfer and pressure drop characteristics of CuO-base oil nanofluid flow in a horizontal helically coiled tube under constant heat flux. Int. Commun. Heat Mass Transf. 2012, 39, 144–151. [Google Scholar] [CrossRef]
- Pawar, S.S.; Sunnapwar, V.K. Experimental studies of heat transfer to Newtonian and non-Newtonian fluids in helical coils with laminar and turbulent flow. Exp. Therm. Fluid Sci. 2013, 44, 792–804. [Google Scholar] [CrossRef]
- Kumbhare, B.P.; Purandare, P.S.; Mali, K.V. Experimental analysis of square and circular coil for heat recovery system. Int. J. Sci. 2012, 2, 318–327. [Google Scholar]
- Jeschke, H. Wärmeübergang und Druckverlust in Rohrschlangen. VDI Z. 1925, 69, 24–28. [Google Scholar]
- Rogers, G.F.C.; Mayhew, Y.R. Heat transfer and pressure loss in helically coiled tube with turbulent flow. Int. J. Heat Mass Transf. 1964, 7, 1207–1216. [Google Scholar] [CrossRef]
- Mori, Y.; Nakayama, W. Study of forced convective heat transfer in curved pipes (3rd report, theoretical analysis under the condition of uniform wall temperature and practical formulae). Int. J. Heat Mass Transf. 1967, 10, 681–695. [Google Scholar] [CrossRef]
- Gnielinski, V. Heat transfer and pressure drop in helically coiled tubes. In International Heat Transfer Conference 8; Digital Library, Bergel House Inc.: Kington, UK, 1986; pp. 2847–2854. [Google Scholar]
- Bai, B.; Guo, L.; Feng, Z.; Chen, X. Turbulent heat transfer in a horizontal helically coiled tube. Heat Transf. 1999, 28, 395–403. [Google Scholar] [CrossRef]
- Schmidt, E.F. Wärmeübergang und Druckverlust in Rohrschlangen. Chem. Ing. Tech. 1967, 39, 781–789. [Google Scholar] [CrossRef]
- Jones, J.R. Flow of a non-Newtonian liquid in a curved pipe. Q. J. Mech. Appl. Math. 1960, 13, 428–443. [Google Scholar] [CrossRef]
- Thomas, R.H.; Walters, K. On the flow of an elastico-viscous liquid in a curved pipe under a pressure gradient. J. Fluid Mech. 1963, 16, 228–242. [Google Scholar] [CrossRef]
- Mashelkar, R.A.; Devarajan, G.V. Secondary flows of non-Newtonian fluids. Part I—Laminar boundary layer flow of a generalized non-Newtonian fluid in coiled tube. Trans. Inst. Chem. Eng. 1976, 54, 100–107. [Google Scholar]
- Mujawar, B.A.; Rao, M.R. Flow on non-Newtonian fluids through helical coils. Ind. Eng. Chem. Process Des. Dev. 1978, 17, 22–27. [Google Scholar] [CrossRef]
- Madlener, K.; Frey, B.; Ciezki, H.K. Generalized Reynolds number for non-Newtonian fluids. Prog. Propuls. Phys. 2009, 1, 237–250. [Google Scholar]
- Krishna, B.S.V.S.R. Prediction of pressure drop in helical coil with single phase flow of non-Newtonian fluid. Int. J. Appl. Res. Mech. Eng. 2012, 1, 6. [Google Scholar] [CrossRef]
- Gul, S.; Erge, O.; van Oort, E. Frictional pressure losses of non-Newtonian fluids in helical pipes: Applications for automated rheology measurements. J. Nat. Gas Sci. Eng. 2020, 73, 103042. [Google Scholar] [CrossRef]
- Hart, J.; Ellenberger, J.; Hamersma, P.J. Single- and two-phase flow through helically coiled tubes. Chem. Eng. Sci. 1988, 43, 775–783. [Google Scholar] [CrossRef]
- Pimenta, T.A.; Campos, J.B.I.M. Friction losses of Newtonian and non-Newtonian fluids flowing in laminar regime in a helical coil. Exp. Therm. Fluid Sci. 2012, 36, 194–204. [Google Scholar] [CrossRef]
- McConalogue, D.J.; Srivastava, R.S. Motion of a fluid in a curved tube. Proc. R. Soc. Lond. A 1968, 307, 37–53. [Google Scholar]
- Chen, W.H.; Jan, R. The characteristics of laminar flow in a helical circular pipe. J. Fluid Mech. 1992, 244, 241–256. [Google Scholar] [CrossRef]
- Xie, G.D. Torsion effect on secondary flow in helical pipe. Int. Heat Fluid Flow 1990, 11, 114–119. [Google Scholar] [CrossRef]
- Bolinder, C.J. First- and higher-order effects of curvature and torsion on the flow in a helical rectangular duct. J. Fluid Mech. 1996, 314, 113–138. [Google Scholar] [CrossRef]
- Marušić-Paloka, E. The effects of flexion and torsion for a fluid flow through a curved pipe. Appl. Math. Optim. 2001, 44, 245–272. [Google Scholar] [CrossRef]
- Austin, L.R.; Seader, J.D. Fully developed viscous flow in coiled circular pipes. AIChE J. 1973, 19, 85–94. [Google Scholar] [CrossRef]
- Tarbell, J.M.; Samuels, M.R. Momentum and heat transfer in helical coils. Chem. Eng. J. 1973, 5, 117–127. [Google Scholar] [CrossRef]
- Huang, W.; Gu, D. A study of secondary flow and fluid resistance in rectangular, helical coiled channel. Int. Chem. Eng. 1989, 29, 480–485. [Google Scholar]
- Choi, H.K.; Park, S.O. Laminar entrance flow in curved annular ducts. Int. J. Heat Fluid Flow 1992, 13, 41–49. [Google Scholar]
- Srinivasan, P.S.; Nandapurkar, S.S.; Holland, F.A. Friction factors for coils. Trans. Inst. Chem. Eng. 1970, 48, T156–T161. [Google Scholar]
- Janssen, L.A.M.; Hoogendoorn, C.J. Laminar convective heat transfer in helical coiled tubes. Int. J. Heat Mass Transf. 1978, 21, 1197–1206. [Google Scholar] [CrossRef]
- Mori, Y.; Nakayama, W. Study of forced convective heat transfer in curved pipes (2nd report, turbulent region). Int. J. Heat Mass Transf. 1967, 10, 37–59. [Google Scholar] [CrossRef]
- Yang, G.; Ebadian, M.A. Turbulent forced convection in a helicoidal pipe with substantial pitch. Int. J. Heat Mass Transf. 1996, 39, 2015–2022. [Google Scholar] [CrossRef]
- Lin, C.X.; Ebadian, M.A. Developing turbulent convective heat transfer in helical pipes. Int. J. Heat Mass Transf. 1997, 40, 3861–3873. [Google Scholar] [CrossRef]
- Li, L.J.; Lin, C.X.; Ebadian, M.A. Turbulent mixed convective heat transfer in the entrance region of a curved pipe with uniform-wall temperature. Int. J. Heat Mass Transf. 1998, 41, 3793–3805. [Google Scholar] [CrossRef]
- Chagny, C.; Castelain, C.; Peerhossaini, H. Chaotic heat transfer for heat exchanger design and comparison with a regular regime for a large range of Reynolds numbers. Appl. Therm. Eng. 2000, 20, 1615–1648. [Google Scholar] [CrossRef]
- Kumar, V.; Saini, S.; Sharma, M.; Nigam, K.D.P. Pressure drop and heat transfer in tube-in-tube helical heat exchanger. Chem. Eng. Sci. 2006, 61, 4403–4416. [Google Scholar] [CrossRef]
- Jayakumar, J.S.; Mahajani, S.M.; Mandal, J.C.; Vijayan, P.K.; Bhoi, R. Experimental and CFD estimation of heat transfer in helically coiled heat exchangers. Chem. Eng. Res. Des. 2008, 86, 221–232. [Google Scholar] [CrossRef]
- Ciofalo, M.; Di Liberto, M.; Marotta, G. On the influence of curvature and torsion on turbulence in helically coiled pipes. J. Phys. Conf. 2013, 501, 012025. [Google Scholar] [CrossRef]
- Li, Y.; Wu, J.; Wang, H.; Kou, L.; Tian, X. Fluid flow and heat transfer characteristics in helical tubes cooperating with spiral corrugation. Energy Procedia 2012, 17, 791–800. [Google Scholar] [CrossRef]
- Yildiz, C.; Biçer, Y.; Pehlivan, D. Heat transfer and pressure drop in a heat exchanger with a helical pipe containing inside springs. Energy Conserv. Manag. 1997, 38, 619–624. [Google Scholar] [CrossRef]
- Zachár, A. Analysis of coiled-tube heat exchangers to improve heat transfer rate with spirally corrugated wall. Int. J. Heat Mass Transf. 2010, 53, 3928–3939. [Google Scholar] [CrossRef]
- Salimpour, M.R. Heat transfer coefficients of shell and coiled tube heat exchangers. Exp. Therm. Fluid Sci. 2009, 33, 203–207. [Google Scholar] [CrossRef]
- Yanase, S.; Goto, N.; Yamamoto, K. Dual solutions of the flow through a curved tube. Fluid Dyn. Res. 1989, 5, 191–201. [Google Scholar] [CrossRef]
- Pachghare, P.R.; Mahalle, A.M. Thermo-hydrodynamics of close loop pulsating heat pipe: An experimental study. J. Mech. Sci. Technol. 2014, 28, 3387–3394. [Google Scholar] [CrossRef]
- Vijaya Kumar Reddy, K.; Sudheer Prem Kumar, B.; Ravi, G.; Kakaraparthi, A.; Vijaya Rao, P. CFD analysis of a helically coiled tube in tube heat exchanger. Mater. Today Proc. 2017, 4, 2341–2349. [Google Scholar] [CrossRef]
- Islami, S.B.; Wesolowski, M.; Revell, W.; Chen, X. Virtual reality visualization of CFD simulated blood flow in cerebral aneurysms treated with flow diverter stents. Appl. Sci. 2021, 11, 8082. [Google Scholar] [CrossRef]
- Liou, T.M. Flow visualization and LDV measurement of fully developed laminar flow in helically coiled tubes. Exp. Fluids 1992, 13, 332–338. [Google Scholar] [CrossRef]
- Chen, W.H.; Fan, C.N. Finite element analysis of incompressible viscous flow in helical pipe. Comput. Mech. 1986, 1, 281–292. [Google Scholar] [CrossRef]
- Yamamoto, K.; Aribowo, A.; Hayamizu, Y.; Hirose, T.; Kawahara, K. Visualization of the flow in a helical pipe. Fluid Dyn. Res. 2002, 30, 251–267. [Google Scholar] [CrossRef]
- Şahin, A.Z. A second law comparison for optimum shape of duct subjected to constant wall temperature and laminar flow. Heat Mass Transf. 1998, 33, 425–430. [Google Scholar] [CrossRef]
- Ko, T.H. A numerical study on entropy generation and optimization for laminar forced convection in a rectangular curved duct with longitudinal ribs. Int. J. Therm. Sci. 2006, 45, 1113–1125. [Google Scholar] [CrossRef]
- Sanchez, M.; Henderson, A.W.; Papavassiliou, D.V.; Lemley, E.C. Entropy generation in laminar flow junctions. In Proceedings of the ASME 2012 Fluids Engineering Division Summer Meeting Collocated with the ASME 2012 Heat Transfer Summer Conference and ASME 2012 10th International Conference on Nanochannels, Microchannels, and Minichannels, Rio Grande, Puerto Rico, 8–12 July 2012; pp. 325–330. [Google Scholar]
- Skokouhmand, H.; Salimpour, M.R. Entropy generation analysis of fully developed laminar forced convection in a helical tube with uniform wall temperature. Heat Mass Transf. 2007, 44, 213–220. [Google Scholar] [CrossRef]
- Satapathy, A.K. Thermodynamic optimization of a coiled tube heat exchanger under constant wall heat flux condition. Energy 2009, 34, 1122–1126. [Google Scholar] [CrossRef]
- Bahiraei, F.; Saray, R.K.; Salehzadeh, A. Investigation of potential of improvement of helical coils based on avoidable and unavoidable exergy destruction concepts. Energy 2011, 36, 3113–3119. [Google Scholar] [CrossRef]
- Ahadi, M.; Abbassi, A. Entropy generation analysis of laminar forced convection through uniformly heated helical coils considering effects of high length and heat flux and temperature dependence of thermophysical properties. Energy 2015, 82, 322–332. [Google Scholar] [CrossRef]
- Dizaji, H.S.; Jafarmadar, S.; Hashemian, M. The effect of flow, thermodynamic and geometrical characteristics on exergy loss in shell and coiled tube heat exchangers. Energy 2015, 91, 678–684. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Heat transfer and entropy generation analyses of nanofluids in helically coiled tube-in-tube heat exchangers. Int. Commun. Heat Mass Transf. 2016, 71, 118–125. [Google Scholar] [CrossRef]
- Pendyala, S.; Narla, V.K.; Prattipati, R. Second law analysis for turbulent flow in helical pipes subject to variable viscosity. AIP Conf. Proc. 2020, 2246, 020038. [Google Scholar]
- Sciacovelli, A.; Verda, V.; Sciubba, E. Entropy generation analysis as a design tool—A review. Renew. Sustain. Energy Rev. 2015, 43, 1167–1181. [Google Scholar] [CrossRef]
- Rippel, G.R.; Eidt, C.M.; Jordan, H.B. Two-phase flow in a coiled tube. Ind. Eng. Chem. Process Des. Dev. 1965, 5, 32–39. [Google Scholar] [CrossRef]
- Lockhart, R.W.; Martinelli, R.C. Proposed correlation of data for isothermal two-phase, two-component flow in pipes. Chem. Eng. Prog. 1949, 45, 38–48. [Google Scholar]
- Owhadi, A.; Bell, K.J.; Crain, B., Jr. Forced convection boiling inside helically-coiled tubes. Int. J. Heat Mass Transf. 1968, 11, 1779–1793. [Google Scholar] [CrossRef]
- Akagawa, B.K.; Sakaguchi, T.; Ueda, M. Study on gas-liquid two-phase flow in helically coiled tubes. Bull. JSME 1971, 14, 564–571. [Google Scholar] [CrossRef]
- Unal, H.C. Determination of void fraction, incipient point of boiling, and initial point of net vapor generation in sodium-heated helically coiled steam generator tubes. J. Heat Mass Transf. 1978, 100, 268–274. [Google Scholar]
- Czop, V.; Barbier, D.; Dong, S. Pressure drop, void fraction and shear stress measurements in an adiabatic two-phase flow in a coiled tube. Nucl. Des. 1994, 149, 323–333. [Google Scholar] [CrossRef]
- Xin, R.C.; Awwad, A.; Dong, Z.F.; Ebadian, M.A. An experimental study of single-phase and two-phase flow pressure drop in annular helicoidal pipes. Int. J. Heat Fluid Flow 1997, 18, 482–488. [Google Scholar] [CrossRef]
- Zhao, L.; Guo, L.; Bai, B.; Hou, Y.; Zhang, X. Convective boiling heat transfer and two-phase flow characteristics inside a small horizontal helically coiled tubing once through a steam generator. Int. J. Heat Mass Transf. 2003, 46, 4779–4788. [Google Scholar] [CrossRef]
- Santini, L.; Cioncolini, A.; Lombardi, C.; Ricotti, M.E. Two-phase pressure drops in a helically coiled steam generator. Int. J. Heat Mass Transf. 2008, 51, 4926–4939. [Google Scholar] [CrossRef]
- Chung, Y.-J.; Kim, H.J.; Chung, B.-D.; Lee, W.-J.; Kim, M.-H. Thermo-hydraulic characteristics of the helically coiled tube and the condesate heat exchanger for SMART. Ann. Nucl. Energy 2013, 55, 49–54. [Google Scholar] [CrossRef]
- Chung, Y.-J.; Bae, K.-H.; Kim, K.K.; Lee, W.-J. Boiling heat transfer and dryout in helically coiled tubes under different pressure conditions. Ann. Nucl. Energy 2014, 71, 298–303. [Google Scholar] [CrossRef]
- Zhou, C.; Song, M.; Xiao, S.; Zhou, X. Two-phase simulation of the pressure loss in helical channel. Vibroeng. Procedia 2018, 19, 259–263. [Google Scholar] [CrossRef]
- Sun, S.; Liu, J.; Zhang, W.; Yi, T. Frictional pressure drop for gas-liquid two-phase flow in coiled tubing. Energies 2022, 15, 8969. [Google Scholar] [CrossRef]
- Guo, L.; Feng, Z.; Chen, X. An experimental investigation of the frictional pressure drop of steam–water two–phase flow in helical coils. Int. J. Heat Mass Transf. 2001, 44, 2601–2610. [Google Scholar] [CrossRef]
- Zhao, H.; Li, X.; Wu, X. New friction factor equations developed for turbulent flows in rough helical tubes. Int. J. Heat Mass Transf. 2016, 95, 525–534. [Google Scholar] [CrossRef]
- Pouquet, A.; Yokoi, N. Helical fluid and (Hall)-MHD turbulence: A brief review. Philos. Trans. R. Soc. A 2022, 380, 20210087. [Google Scholar] [CrossRef] [PubMed]
- Berger, M.A.; Field, G.B. The topological properties of magnetic helicity. J. Fluid Mech. 1984, 147, 133–148. [Google Scholar] [CrossRef]
- Moffat, H.K.; Tsinober, A. Helicity in laminar and turbulent flows. Annu. Fluid Mech. 1992, 24, 281–312. [Google Scholar] [CrossRef]
- Howard, L.N.; Gupta, A.S. On the hydrodynamic and hydromagnetic stability of swirling flows. J. Fluid Mech. 1962, 14, 463–476. [Google Scholar] [CrossRef]
- Agrawal, G.S. Rayleigh-Taylor instability with Hall-currents. J. Phys. Soc. Jpn. 1969, 26, 561–565. [Google Scholar] [CrossRef]
- Ganguly, K.; Gupta, A.S. On the hydromagnetic stability of helical flows. J. Math. Anal. Appl. 1985, 106, 26–40. [Google Scholar] [CrossRef]
- Brunetti, D.; Graves, J.P.; Lazzaro, E.; Mariani, A.; Nowak, S.; Cooper, W.A.; Wahlberg, C. Helical equilibrium magnetohydrodynamic flow effects on the stability properties of low-n ideal external-infernal modes in weak shear tokamak configurations. Plasma Phys. Control. Fusion 2019, 61, 064003. [Google Scholar] [CrossRef]
- Brandenburg, A.; Subramanian, K. Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 2005, 417, 1–209. [Google Scholar] [CrossRef]
- Tobias, S.M. The turbulent dynamo. J. Fluid Mech. 2021, 912, 1–76. [Google Scholar] [CrossRef] [PubMed]
- Gailitis, A.; Freibergs, Y. Nonuniform model of a helical dynamo. Magnetohydrodynamics 1980, 16, 116–121. [Google Scholar]
- Gailitis, A.; Lielausis, O.; Dement’ev, S.; Platacis, E.; Cifersons, A.; Gerbeth, G.; Gundrum, T.; Stefani, F.; Christen, M.; Hänel, H.; et al. Detection of a flow induced magnetic field eigenmode in the Riga dynamo facility. Phys. Rev. 2000, 84, 4365–4368. [Google Scholar]
- Gailitis, A.; Gerbeth, G.; Gundrum, T.; Lielausis, O.; Lipsbergs, G.; Platacis, E.; Stefani, F. Self-excitation in a helical liquid metal flow: The Riga dynamo experiments. J. Plasma Phys. 2018, 84, 735840301. [Google Scholar] [CrossRef]
- Stefani, F.; Gundrum, T.; Gerbeth, G.; Rüdiger, G.; Schultz, M.; Szklarski, J.; Hollerbach, R. Experimental evidence for magnetorotational instability in a Taylor-Couette flow under the influence of a helical magnetic field. Phys. Lett. 2006, 97, 184502. [Google Scholar] [CrossRef]
- Seilmayer, M.; Stefani, F.; Gundrum, T.; Weier, T.; Gerbeth, G.; Gellert, M.; Rüdiger, G. Experimental evidence for a transient Taylor instability in a cylindrical liquid-metal column. Phys. Rev. Lett. 2012, 108, 244501. [Google Scholar] [CrossRef]
- Gilbert, A.D.; Frisch, U.; Pouquet, A. Helicity is unnecessary for alpha effect dynamos, but it helps. Geophys. Astrophys. Fluid Dyn. 1988, 42, 151–161. [Google Scholar] [CrossRef]
- Andrievsky, A.; Chertovskih, R.; Zheligovsky, V. Pointwise vanishing velocity helicity of a flow does not preclude magnetic field generation. Phys. Rev. E 2019, 99, 033204. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sigalotti, L.D.G.; Alvarado-Rodríguez, C.E.; Rendón, O. Fluid Flow in Helically Coiled Pipes. Fluids 2023, 8, 308. https://doi.org/10.3390/fluids8120308
Sigalotti LDG, Alvarado-Rodríguez CE, Rendón O. Fluid Flow in Helically Coiled Pipes. Fluids. 2023; 8(12):308. https://doi.org/10.3390/fluids8120308
Chicago/Turabian StyleSigalotti, Leonardo Di G., Carlos E. Alvarado-Rodríguez, and Otto Rendón. 2023. "Fluid Flow in Helically Coiled Pipes" Fluids 8, no. 12: 308. https://doi.org/10.3390/fluids8120308
APA StyleSigalotti, L. D. G., Alvarado-Rodríguez, C. E., & Rendón, O. (2023). Fluid Flow in Helically Coiled Pipes. Fluids, 8(12), 308. https://doi.org/10.3390/fluids8120308







