The Use of Uncertainty Quantification and Numerical Optimization to Support the Design and Operation Management of Air-Staging Gas Recirculation Strategies in Glass Furnaces
Abstract
1. Introduction
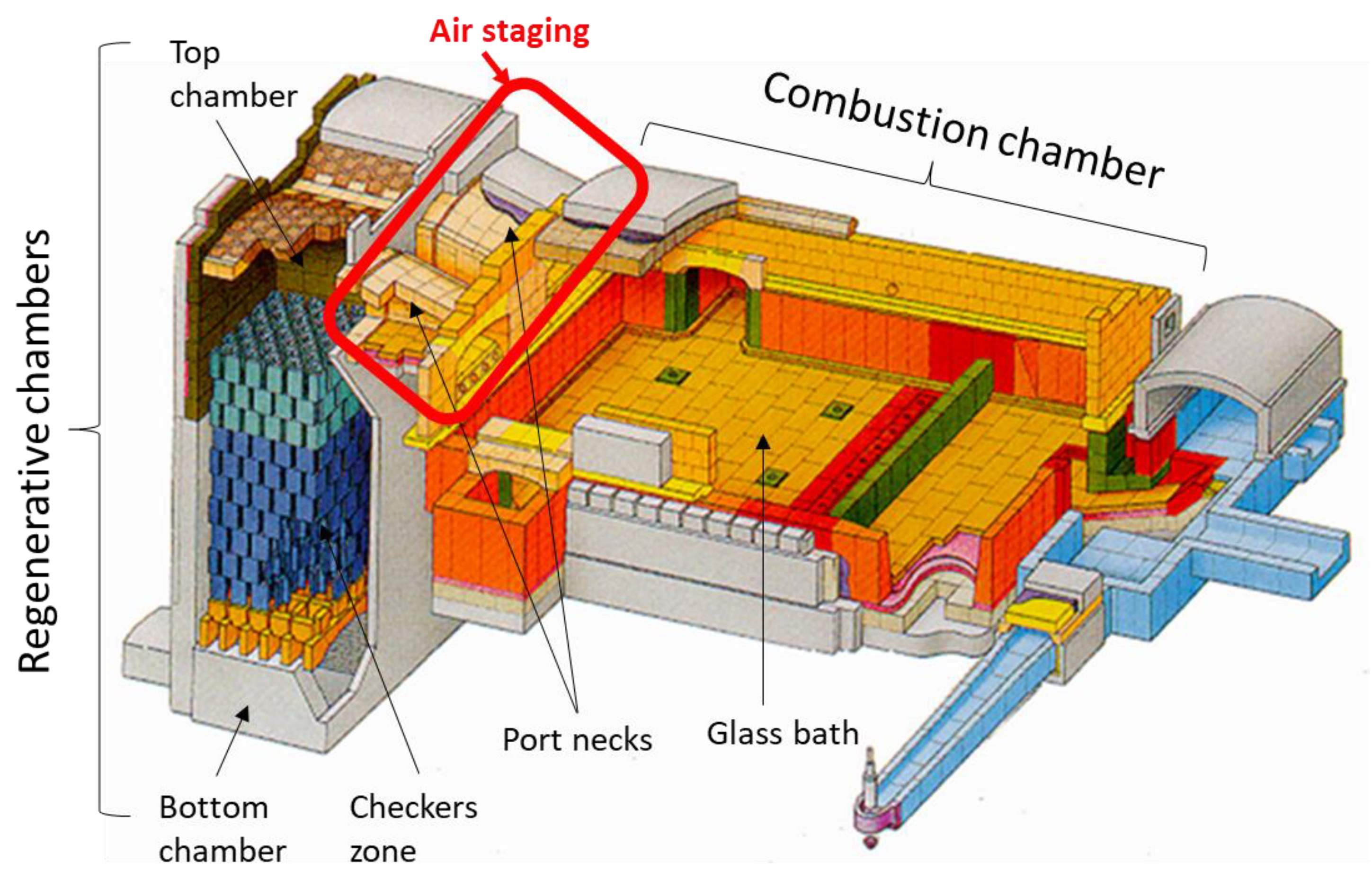
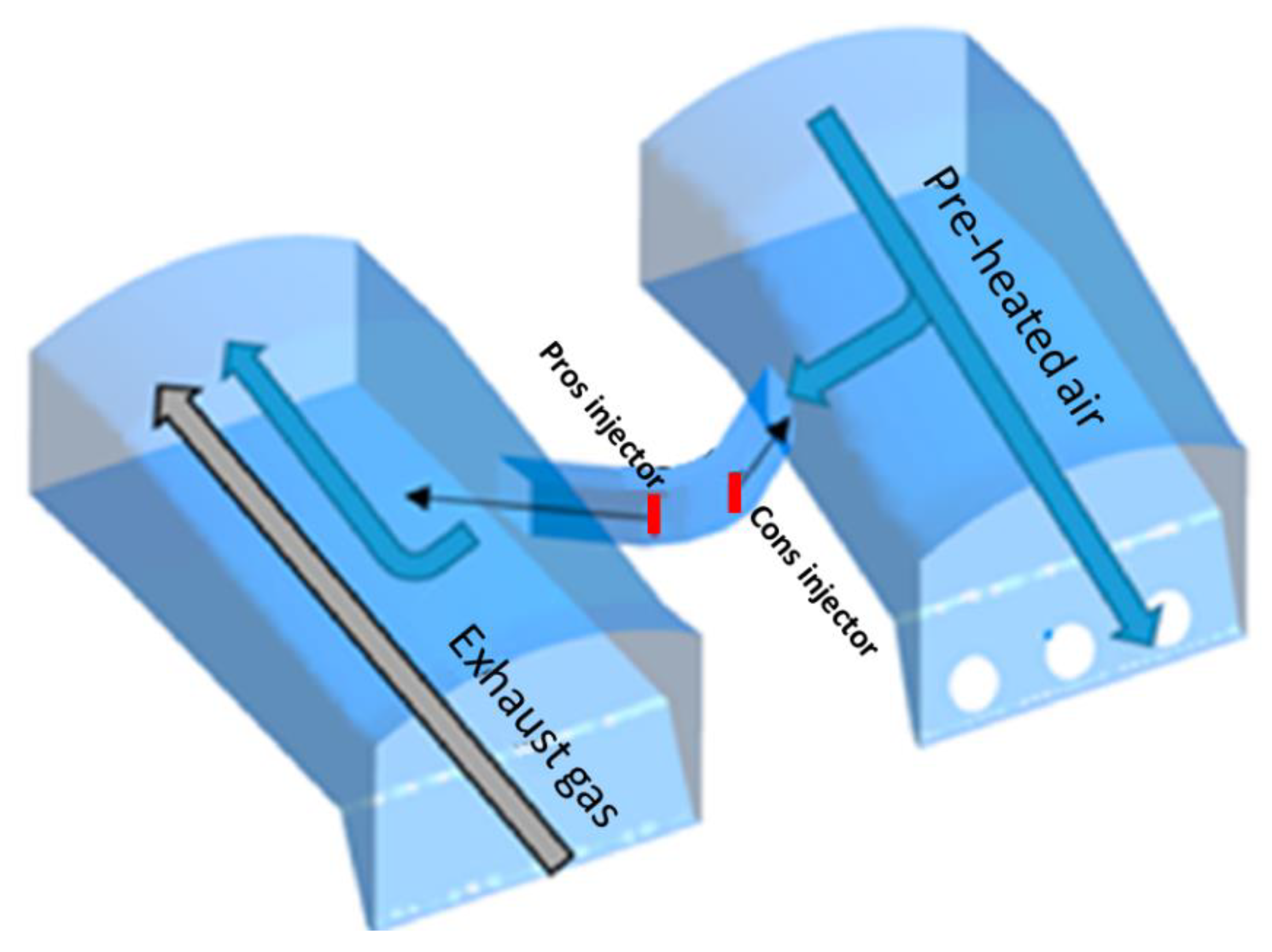
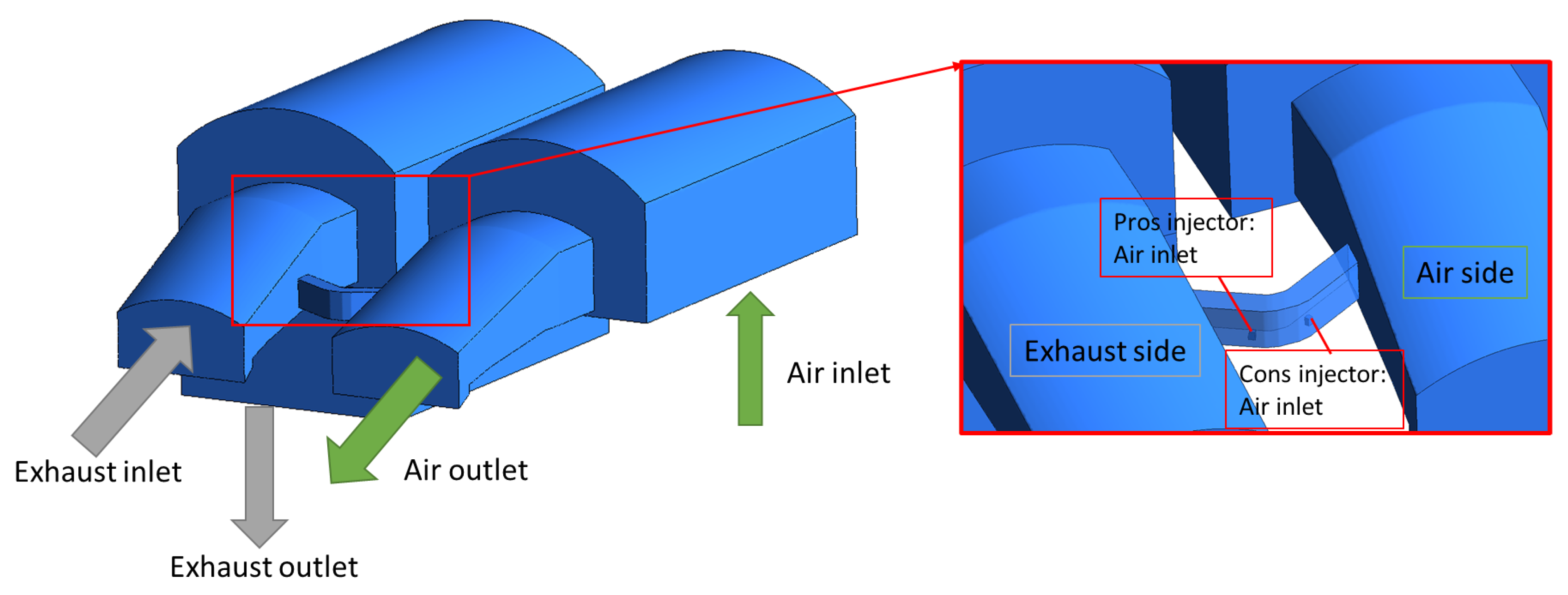
2. Layout of the Glass Production Plant with Regenerative Chamber and the Hybrid Air Staging
3. Numerical Model
3.1. Governing Equations
3.2. CFD Model
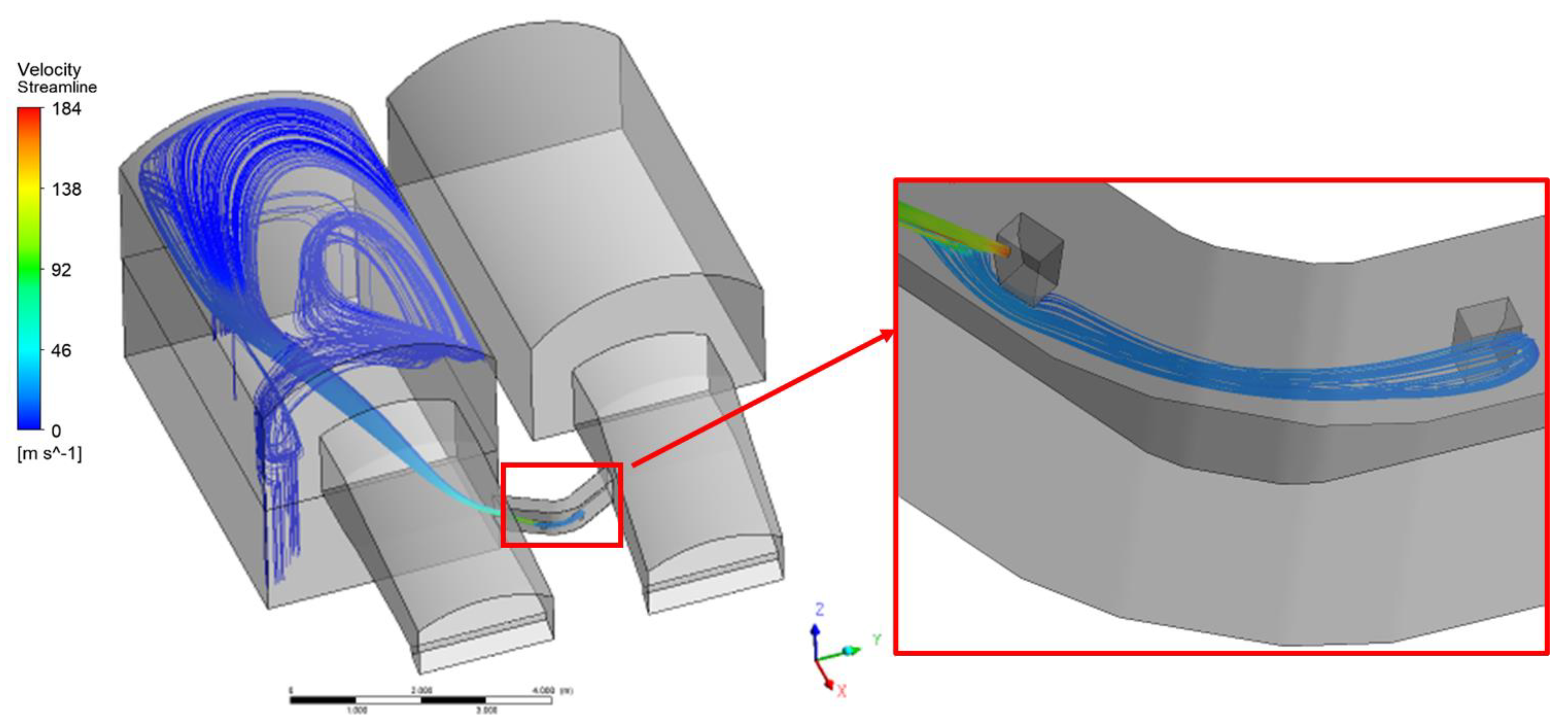
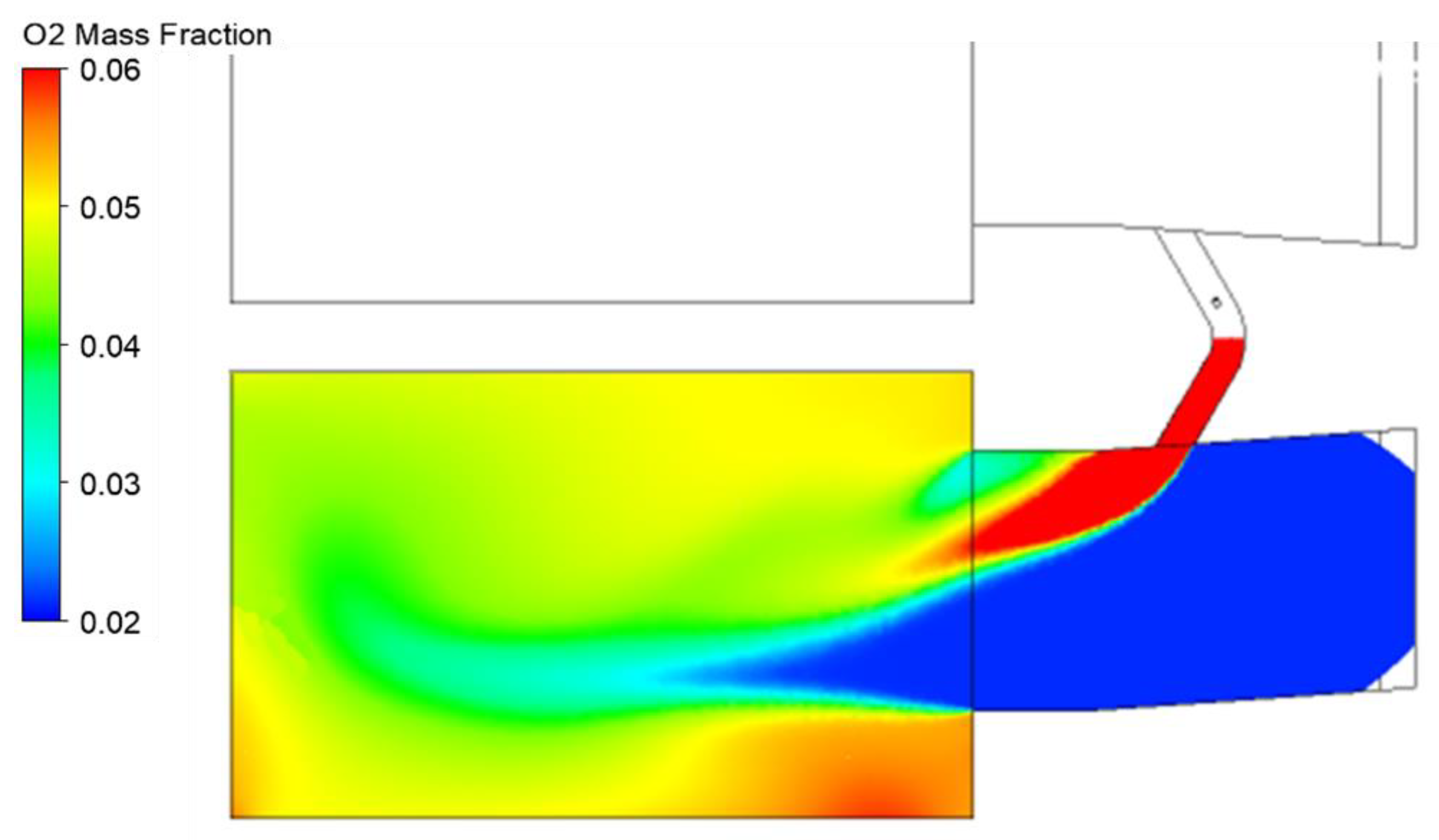
4. Flow Analysis—Baseline Case
5. Surrogate Models
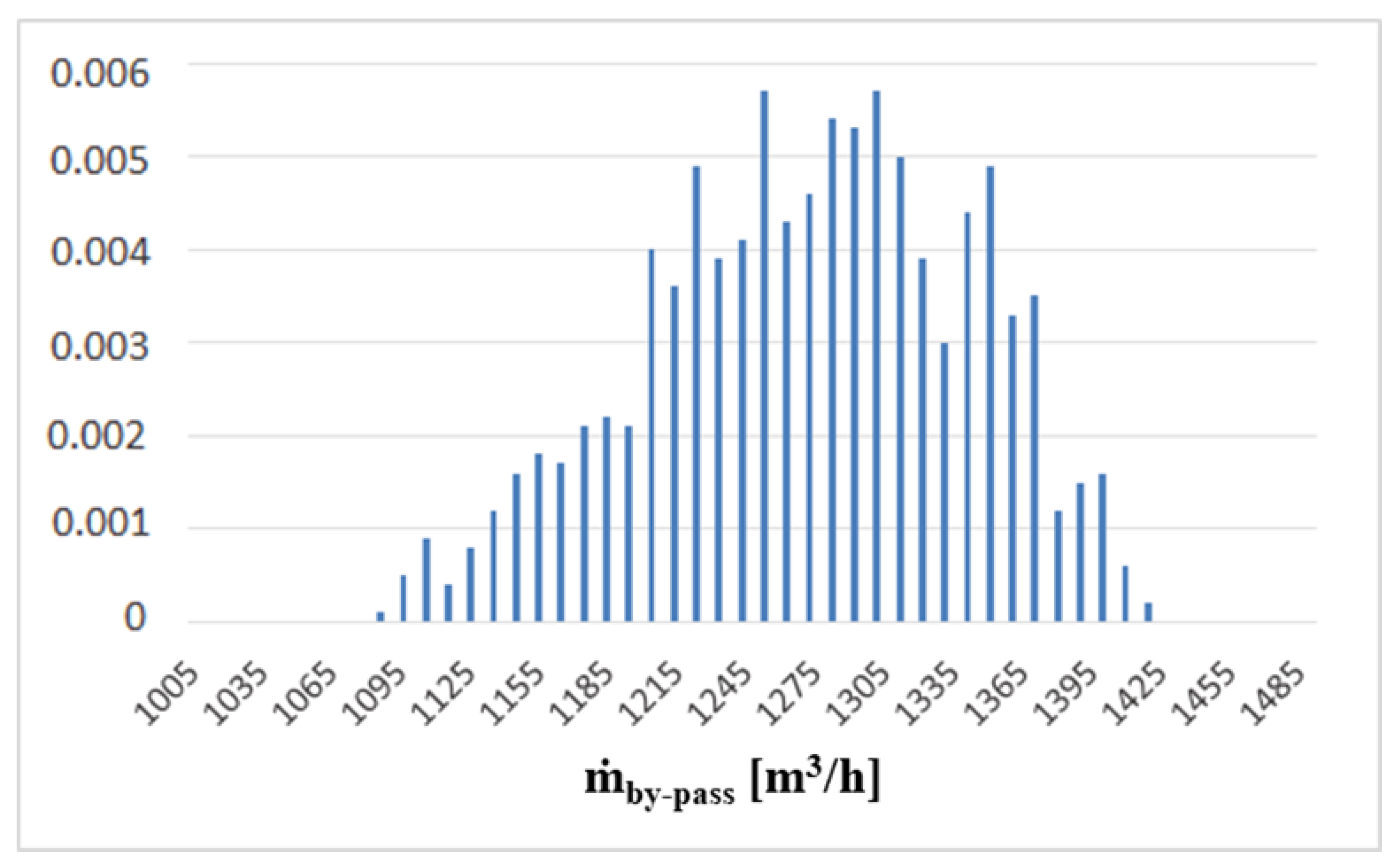
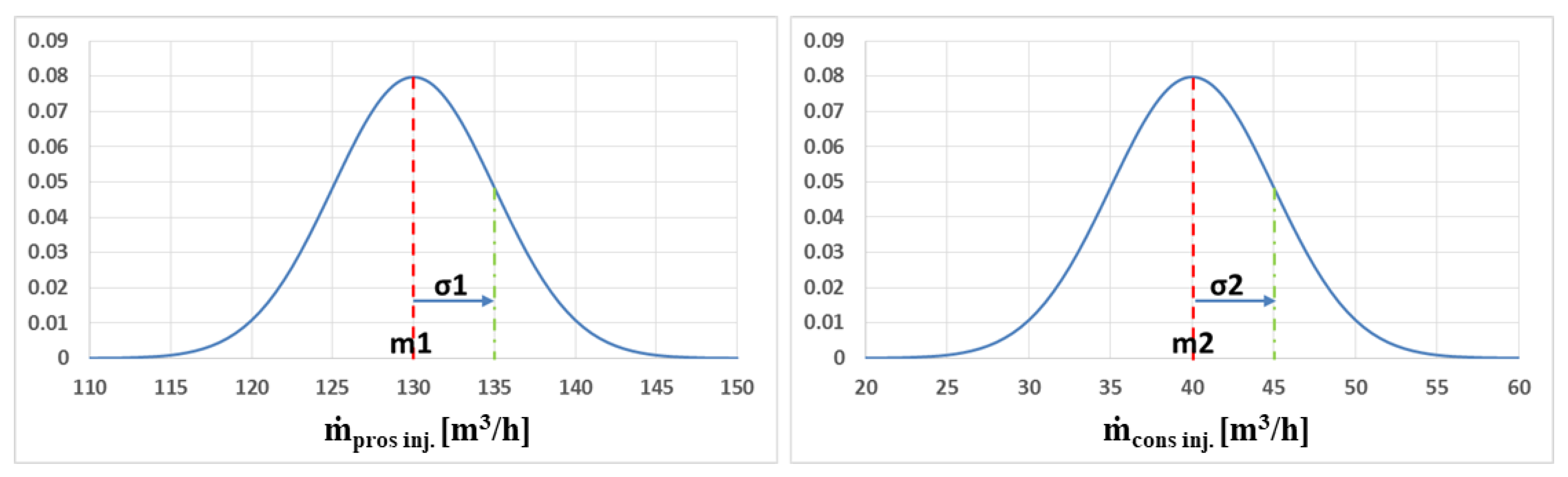
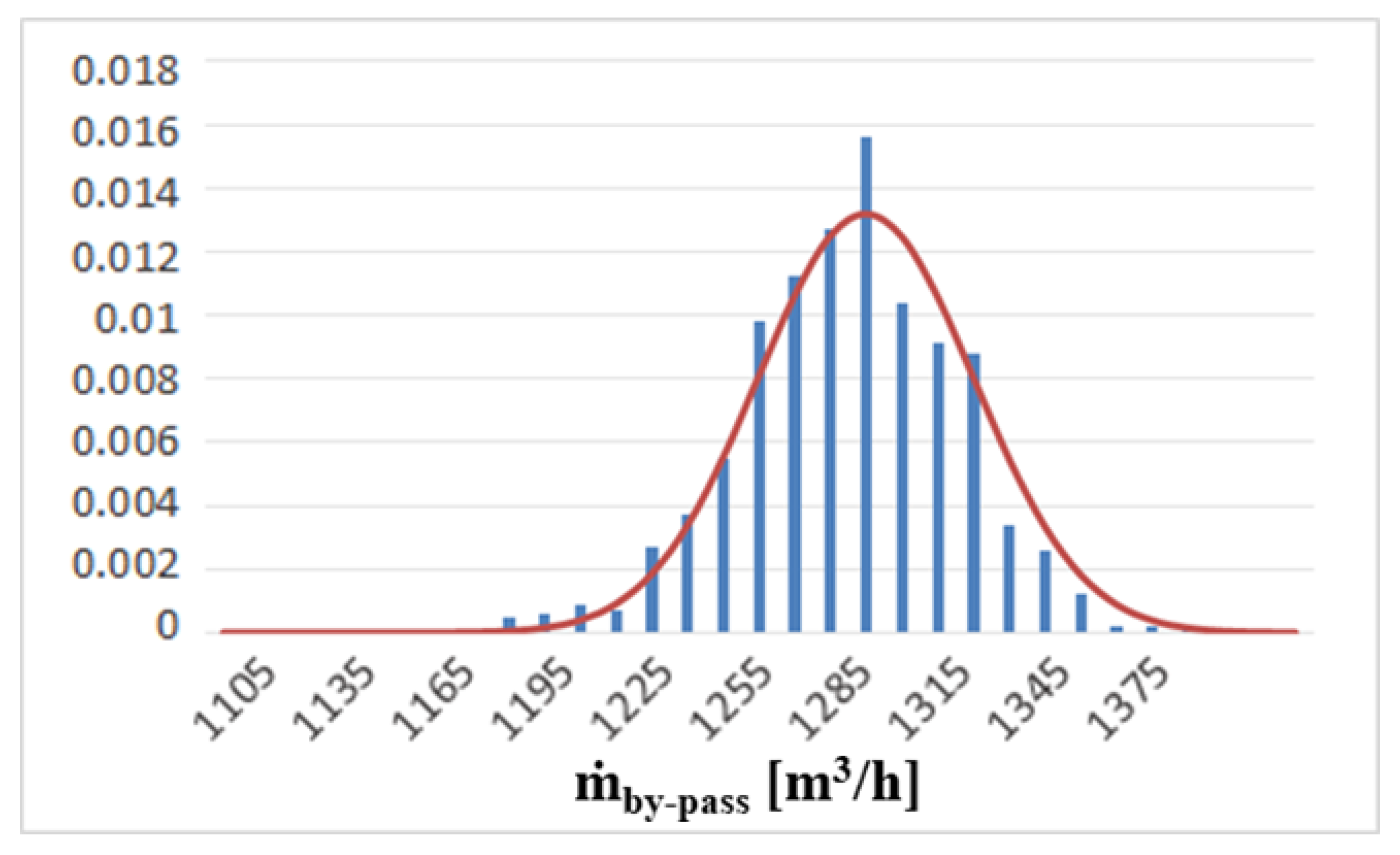
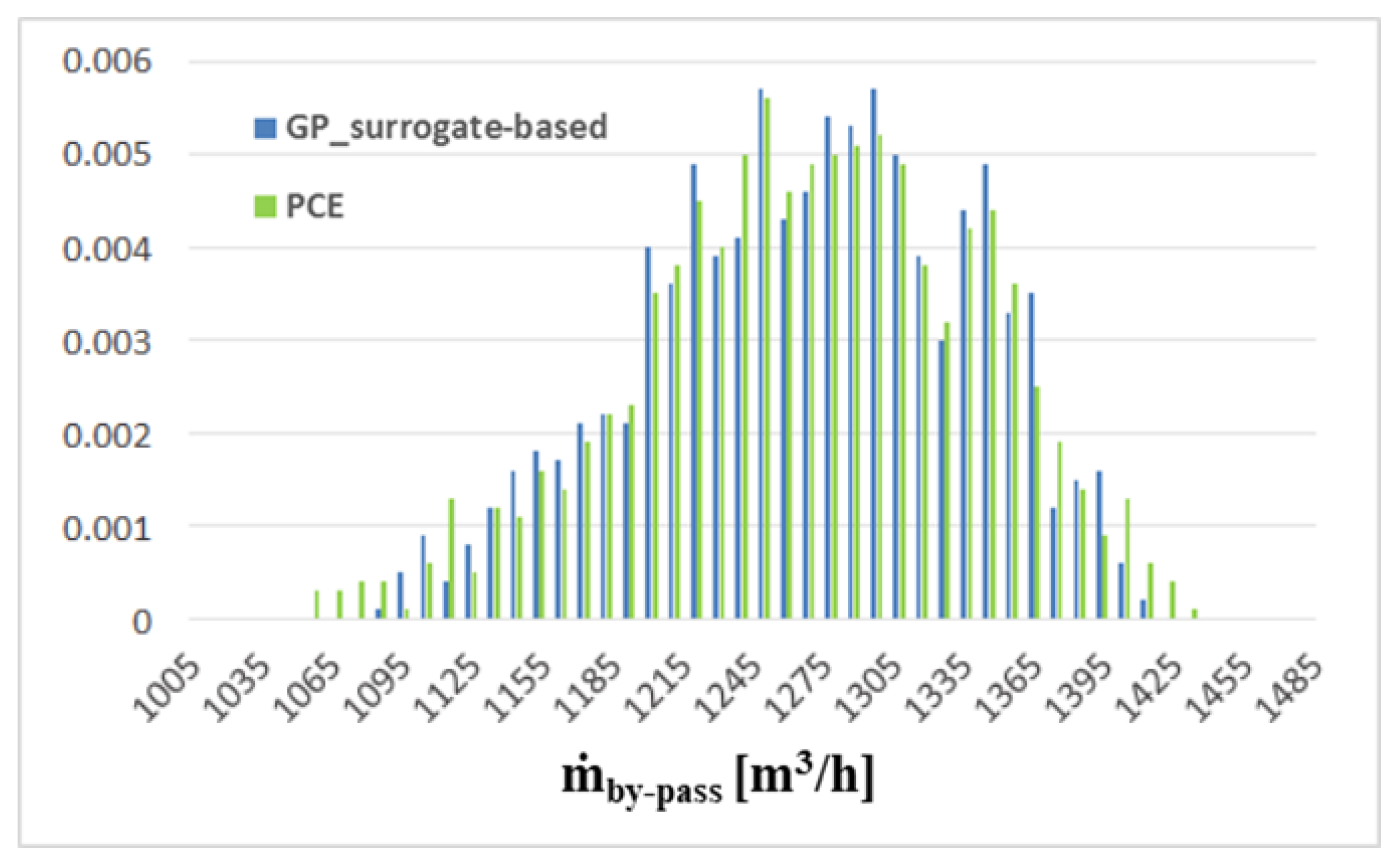
6. Uncertainty Quantification Analysis—UQ
6.1. Uniform Distribution
6.2. Normal Distribution
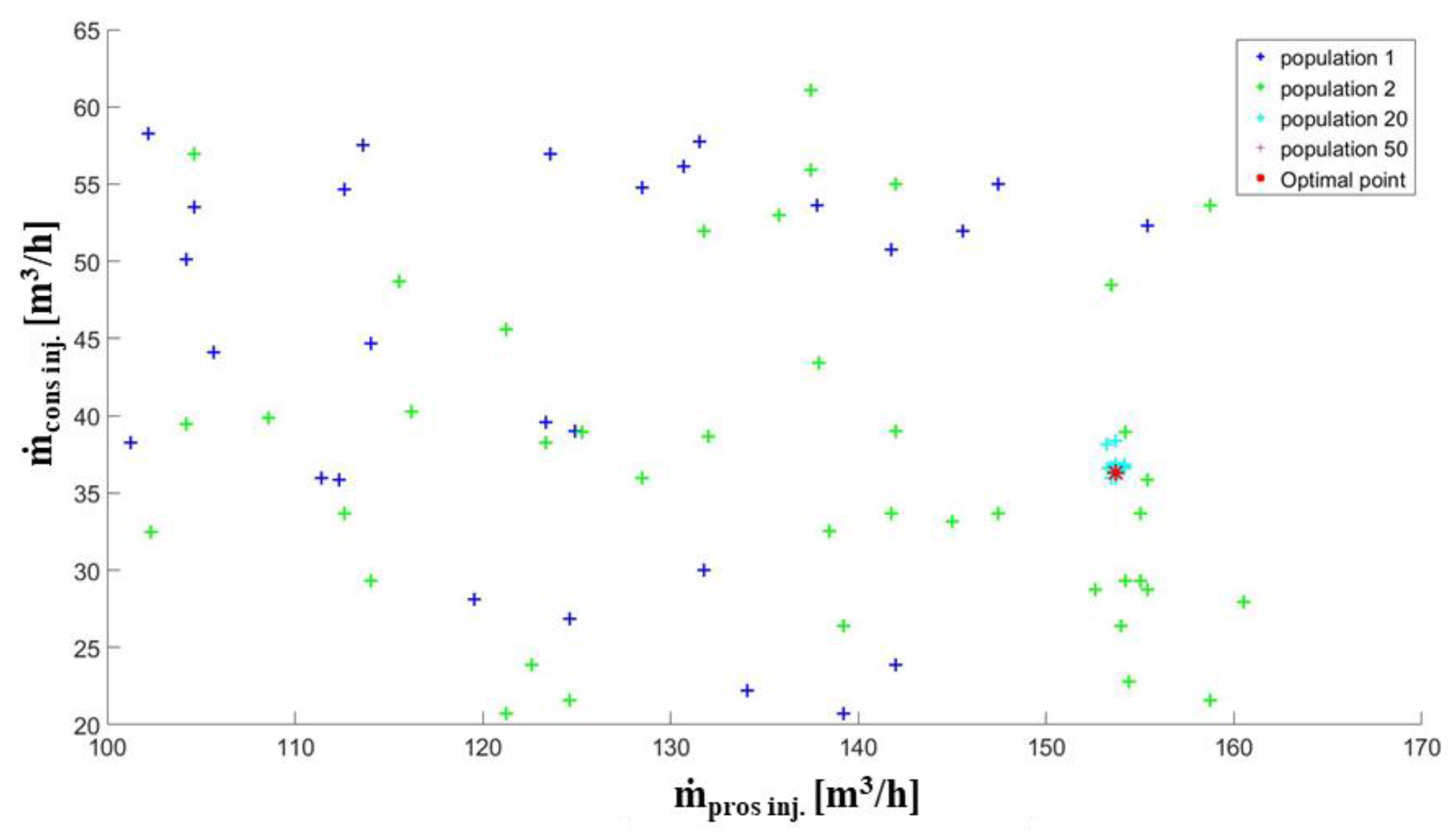
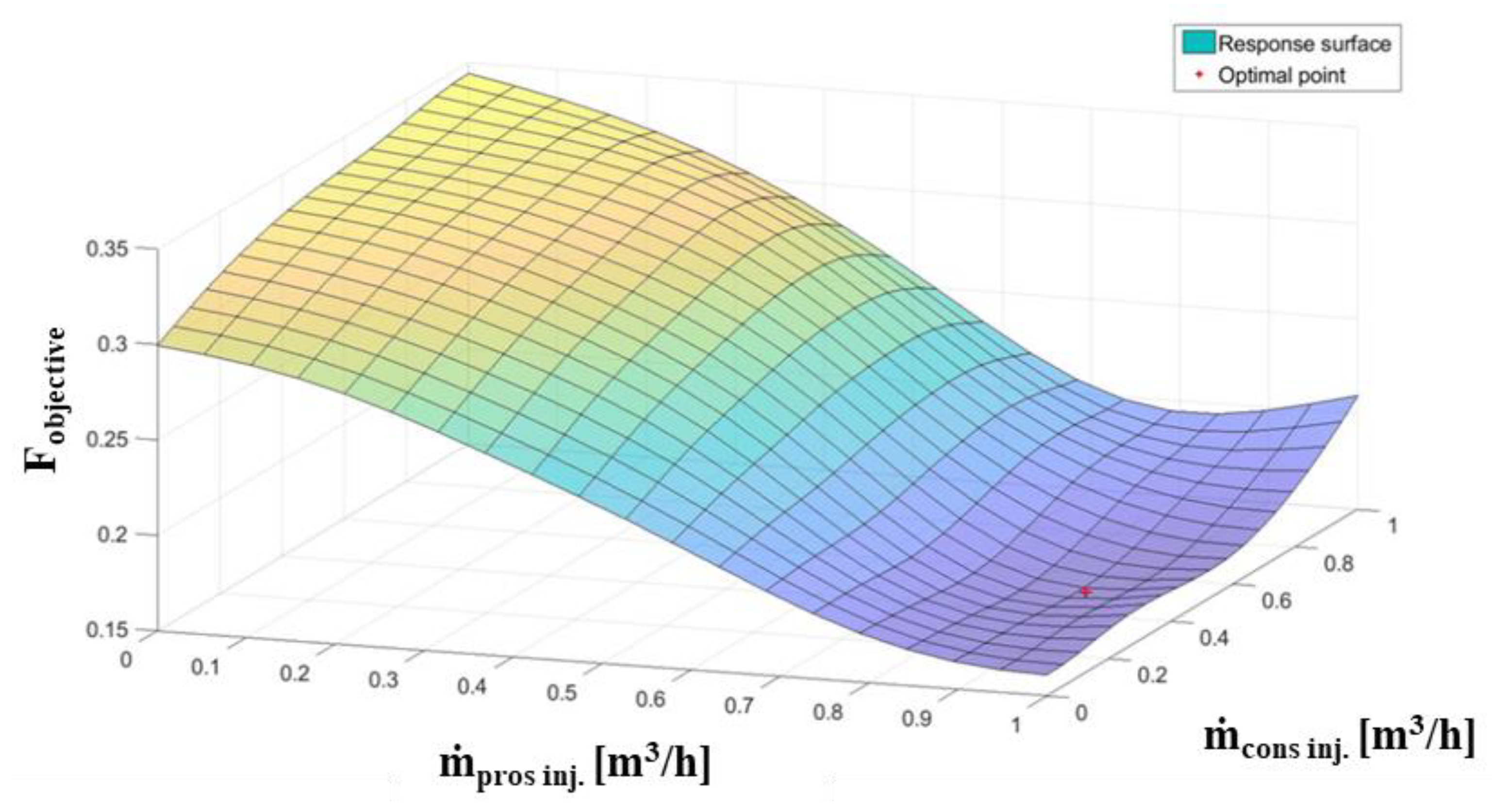
7. Optimization Process to Support System Operation Management
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Surface area |
| AR | Aspect ratio: Length × height |
| k | Turbulent kinetic energy |
| ṁ | Mass flow rate |
| P | Static pressure |
| t | Time |
| T | Temperature |
| u | Velocity |
| y+ | Non dimensional boundary layer distance from wall |
| γ | Uniform index |
| ε | Rate of dissipation of turbulent kinetic energy |
| ρ | Density |
| τ | Tensor of tangential and normal stress |
References
- Galitsky, C.; Worrell, E.; Masanet, E.; Graus, W. Energy Efficiency Improvement and Cost Saving Opportunities for the Glass Industry. In Energy Star Guide for Energy and Plant Managers; No. LBNL-57335-Revision; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2008. [Google Scholar]
- Schmitz, A.; Kaminski, J.; Scalet, B.M.; Soria, A. Energy consumption and CO2 emissions of the European glass industry. Energy Policy 2011, 39, 142–155. [Google Scholar] [CrossRef]
- Dogan, E.; Chishti, M.Z.; Alavijeh, N.K.; Tzeremes, P. The roles of technology and Kyoto Protocol in energy transition towards COP26 targets: Evidence from the novel GMM-PVAR approach for G-7 countries. Technol. Forecast. Soc. Chang. 2022, 181, 121756. [Google Scholar] [CrossRef]
- Aziz, G.; Sarwar, S.; Waheed, R.; Khan, M.S. Significance of hydrogen energy to control the environmental gasses in light of COP26: A case of European Countries. Resour. Policy 2023, 80, 103240. [Google Scholar] [CrossRef]
- Reboussin, Y.; Fourmigué, J.F.; Marthy, J.F.; Citti, O. A numerical approach for the study of glass furnace regenerators. Appl. Therm. Eng. 2005, 25, 2299–2320. [Google Scholar] [CrossRef]
- Yakinthos, K.; Missirlis, D.; Sideridis, A.; Vlahostergios, Z.; Seite, O.; Goulas, A. Modelling operation of system of recuperative heat exchangers for aero engine with combined use of porosity model and thermos-mechanical model. Eng. Appl. Comput. Fluid Mech. 2012, 6, 608–621. [Google Scholar] [CrossRef]
- Sardeshpande, V.; Anthony, R.; Gaitonde, U.N.; Banerjee, R. Performance analysis for glass furnace regenerator. Appl. Energy 2011, 88, 4451–4458. [Google Scholar] [CrossRef]
- Verheijen, O.; Habraken, A.; Gramberg, H. Modeling of Heat Transfer and Gas Flows in Glass Furnace Regenerators. In Proceedings of the 75th Conference on Glass Problems, Columbus, OH, USA, 3–6 November 2014; Greater Columbus Convention Center: Columbus, OH, USA, 2014; Volume 36, p. 1. [Google Scholar]
- Cravero, C.; Marsano, D. Numerical simulation of regenerative chambers for glass production plants with a non-equilibrium heat transfer model. WSEAS Trans. Heat Mass Transf. 2017, 12, 21–29. [Google Scholar]
- Selvaray, J.; Varun, V.S.; Vishwam, V. Waste heat recovery from metal casting and scrap preheating using recovered heat. Procedia Eng. 2014, 97, 267–276. [Google Scholar] [CrossRef][Green Version]
- Cravero, C.; De Domenico, D.; Leutcha, P.J.; Marsano, D. Strategies for the numerical modelling of regenerative pre-heating systems for recycled glass raw material. Math. Model. Eng. Probl. IIETA 2019, 6, 324–332. [Google Scholar] [CrossRef][Green Version]
- Scalet, B.M.; Garcia Muñoz, M.; Sissa, A.Q.; Roudier, S.; Delgado Sancho, L. Best Available Tecniques (BAT) Reference Document for The Manufacture of Glass. In Industrial Emission Directive 2010/75/EU; Integrated Pollution Prevention and Control; Joint Research Centre (JRC): Seville, Spain, 2013. [Google Scholar]
- Zeldovich, Y.B. The oxidation of nitrogen in combustion explosions. Acta Physiochim. 1946, 21, 577–628. [Google Scholar]
- Hayhurst, A.N.; Vince, I.M. Nitric oxide formation from N2 in flames: The importance of “prompt” NO. Prog. Energy Combust. Sci. 1980, 6, 35–51. [Google Scholar] [CrossRef]
- Bowman, C.T. Chapter 4: Chemistry of Gaseous Pollutant Formation and Destruction. In Fossil Fuel Combustion: A Source Book; John Wiley & Sons Inc.: New York, NY, USA, 1991. [Google Scholar]
- Skalska, K.; Miller, J.S.; Ledakowicz, S. Trends in NOx abatement: A review. Sci. Total Environ. 2010, 408, 3976–3989. [Google Scholar] [CrossRef] [PubMed]
- LIFE Project “LIFE 12ENV/IT/001020”. Available online: http://ec.europa.eu/environment/life/project/Projects (accessed on 1 January 2023).
- PRIMEGLASS LIFE Project. Available online: http://www.primeglass.it/ (accessed on 1 January 2023).
- Fathi, M.; Saray, R.K.; Checkel, M.D. The influence of Exhaust Gas Recirculation (EGR) on combustion and emissions of n-heptane/natural gas fueled Homogeneous Charge Compression Ignition (HCCI) engines. Appl. Energy 2011, 88, 4719–4724. [Google Scholar] [CrossRef]
- Agarwal, D.; Singh, S.K.; Agarwal, A.K. Effect of Exhaust Gas Recirculation (EGR) on performance, emission, deposits and durability of a constant speed compression ignition engine. Appl. Energy 2011, 88, 2900–2907. [Google Scholar] [CrossRef]
- Ghazikhani, M.; Feyz, M.E.; Joharchi, A. Experimental investigation of the exhaust gas recirculation effects on irreversibility and brake specific fuel consumption of indirect injection diesel engines. Appl. Therm. Eng. 2010, 30, 1711–1718. [Google Scholar] [CrossRef]
- Cravero, C.; Spoladore, A. Transient Numerical Simulation of Regenerative Systems with Waste Gas Recirculation Strategies in Glass Production Plant. Appl. Sci. 2019, 9, 1496. [Google Scholar] [CrossRef]
- Cravero, C.; De Domenico, D. The Use of CFD for the Design and Development of Innovative Configurations in Regenerative Glass Production Furnaces. Energies 2019, 12, 2455. [Google Scholar] [CrossRef]
- Cravero, C.; Mola, A.; Rollini, M.; Spinelli, L.; Battaglia, W.; Cattaneo, E. Designing and implementing a high efficiency furnace system. Glass Int. 2021, 44, 41–46. [Google Scholar]
- Spliethoff, H.; Greul, U.; Rüdiger, H.; Hein, K.R. Basic effects on NOx emissions in air staging and reburning at a bench-scale test facility. Fuel 1996, 75, 560–564. [Google Scholar] [CrossRef]
- Staiger, B.; Unterberger, S.; Berger, R.; Hein, K.R. Development of an air staging technology to reduce NOx emissions in grate fired boilers. Energy 2005, 30, 1429–1438. [Google Scholar] [CrossRef]
- Fan, W.; Lin, Z.; Kuang, J.; Li, Y. Impact of air staging along furnace height on NOx emissions from pulverized coal combustion. Fuel Process. Technol. 2010, 91, 625–634. [Google Scholar] [CrossRef]
- Houshfar, E.; Lovas, T.; Skreiberg, O. Experimental investigation on NOx reduction by primary measures in biomass combustion: Straw, peat, sewage sludge, forest residues and wood pellets. Energies 2012, 5, 270–290. [Google Scholar] [CrossRef]
- Biedermann, F.; Brunner, T.; Obernberger, I.; Sippula, O.; Boman, C.; Öhman, M. Summary and evaluation of existing strategies on air staging strategies. In Report Produced as Part of the ERANET Futurebiotec Project; BIOENERGY 2020+ GmbH: Graz, Austria, 2010. [Google Scholar]
- Carroll, J.P.; Finnan, J.M.; Biedermann, F.; Brunner, T.; Obernberger, I. Air staging to reduce emissions from energy crop combustion in small scale applications. Fuel 2015, 155, 37–43. [Google Scholar] [CrossRef]
- Zha, Q.; Li, D.; Che, D. Numerical evaluation of heat transfer and NOx emissions under deep-air-staging conditions within a 600 MWe tangentially fired pulverized-coal boiler. Appl. Therm. Eng. 2017, 116, 170–181. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, Y.; Jin, Q.; Chen, Q.; Zhou, Y. Mechanism analysis on the pulverized coal combustion flame stability and NOx emission in a swirl burner with deep air staging. J. Energy Inst. 2019, 92, 298–310. [Google Scholar] [CrossRef]
- Zadravec, T.; Rajh, B.; Kokalj, F.; Samec, N. CFD modelling of air staged combustion in a wood pellet boiler using the coupled modelling approach. Therm. Sci. Eng. Prog. 2020, 20, 100715. [Google Scholar] [CrossRef]
- Campora, U.; Capelli, M.; Cravero, C.; Zaccone, R. Metamodels of a Gas Turbine Powered Marine Propulsion system for Simulation and Diagnostic Purposes. J. Nav. Arch. Mar. Eng. 2015, 12, 1–14. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Rodi, W. Turbulence Models and Their Application in Hydraulics. A State-of-the-Art Review, 3rd ed.; IAHR Monograph Series; Routledge: Rotterdam, The Netherlands, 2017. [Google Scholar]
- Baake, E.; Mühlbauer, A.; Jakowitsch, A.; Andree, W. Extension of the k-ε model for the numerical simulation of the melt flow in induction crucible furnaces. Metall. Mater. Trans. B 1995, 26, 529–536. [Google Scholar] [CrossRef]
- Cellek, M.S. Flameless combustion investigation of CH4/H2 in the laboratory-scaled furnace. Int. J. Hydrog. Energy 2020, 45, 35208–35222. [Google Scholar] [CrossRef]
- ANSYS Inc. Ansys Fluent Theory Guide v.17; ANSYS Inc.: Canonsburg, PA, USA, 2016. [Google Scholar]
- Cademartori, S.; Cravero, C.; Marini, M.; Marsano, D. CFD Simulation of the Slot Jet Impingement Heat Transfer Process and Application to a Temperature Control System for Galvanizing Line of Metal Band. Appl. Sci. 2021, 11, 1149. [Google Scholar] [CrossRef]
- Adams, B.M.; Bohnhoff, W.J.; Dalbey, K.R.; Eddy, J.P.; Ebeida, M.S.; Eldred, M.S.; Frye, J.R.; Gerarci, G.; Hooper, R.W.; Hough, P.D.; et al. Dakota, a Multilevel Parallel Object-Oriented Framework for Design Optimization, Parameter Estimation, Uncertainty Quantification and Sensitivity Analysis; Version 6.11 User’s Manual; Sandia National Laboratories: Albuquerque, NM, USA, 2019.
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Helton, J.C.; Johnson, J.D.; Sallaberry, C.J.; Storlie, C.B. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Cravero, C.; De Domenico, D.; Ottonello, A. Uncertainty Quantification Approach on Numerical Simulation for Supersonic Jets Performance. Algorithms 2020, 13, 130. [Google Scholar] [CrossRef]
- Om Ariara Guhan, C.P.; Arthanareeswaran, G.; Varadarajan, K.N.; Krishnan, S. Numerical optimization of flow uniformity inside an under body- oval substrate to improve emissions of IC engines. J. Comput. Des. Eng. 2016, 3, 198–214. [Google Scholar] [CrossRef]








| Geometrical Parameters | Value |
|---|---|
| Aexhaust/Aair | 0.05 |
| Aexhaust/Aexit | 0.1 |
| Bottom chamber AR | 3.9 |
| Top chamber AR | 1.5 |
| Metrics | ṁbypass [m3/h] |
|---|---|
| Means quare error | 1.37 |
| Average error | 0.61 |
| Maximum error | 8.16 |
| Geometrical Parameters | ṁpros [m3/h] | ṁcons [m3/h] |
|---|---|---|
| Mean | 130 | 40 |
| Standard Deviation | 5 | 5 |
| Standard Deviation/Mean | 3.8% | 12.5% |
| Geometrical Parameters | ṁbypass [m3/h] |
|---|---|
| Mean | 1279 |
| Standard Deviation | 30.2 |
| Standard Deviation/Mean | 2.4% |
| Pros Mass Flow Rate Non-Dimensional/Dimensional | Cons Mass Flow Rate Non-Dimensional/Dimensional | Objective Function |
|---|---|---|
| 0.9036/155.05 [m3/h] | 0.3999/36.90 [m3/h] | 0.1618 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cravero, C.; De Domenico, D.; Marsano, D. The Use of Uncertainty Quantification and Numerical Optimization to Support the Design and Operation Management of Air-Staging Gas Recirculation Strategies in Glass Furnaces. Fluids 2023, 8, 76. https://doi.org/10.3390/fluids8020076
Cravero C, De Domenico D, Marsano D. The Use of Uncertainty Quantification and Numerical Optimization to Support the Design and Operation Management of Air-Staging Gas Recirculation Strategies in Glass Furnaces. Fluids. 2023; 8(2):76. https://doi.org/10.3390/fluids8020076
Chicago/Turabian StyleCravero, Carlo, Davide De Domenico, and Davide Marsano. 2023. "The Use of Uncertainty Quantification and Numerical Optimization to Support the Design and Operation Management of Air-Staging Gas Recirculation Strategies in Glass Furnaces" Fluids 8, no. 2: 76. https://doi.org/10.3390/fluids8020076
APA StyleCravero, C., De Domenico, D., & Marsano, D. (2023). The Use of Uncertainty Quantification and Numerical Optimization to Support the Design and Operation Management of Air-Staging Gas Recirculation Strategies in Glass Furnaces. Fluids, 8(2), 76. https://doi.org/10.3390/fluids8020076








