A Review of Preconditioning and Artificial Compressibility Dual-Time Navier–Stokes Solvers for Multiphase Flows
Abstract
:1. Introduction
2. Incompressible Multiphase Flows
2.1. Preconditioning Dual-Time Stepping Method
2.2. Numerical Method and Body-Fitted Curvilinear Coordinate System
2.3. Coupling Artificial Density-Based Dual-Time Method and Sharp Interface Methods
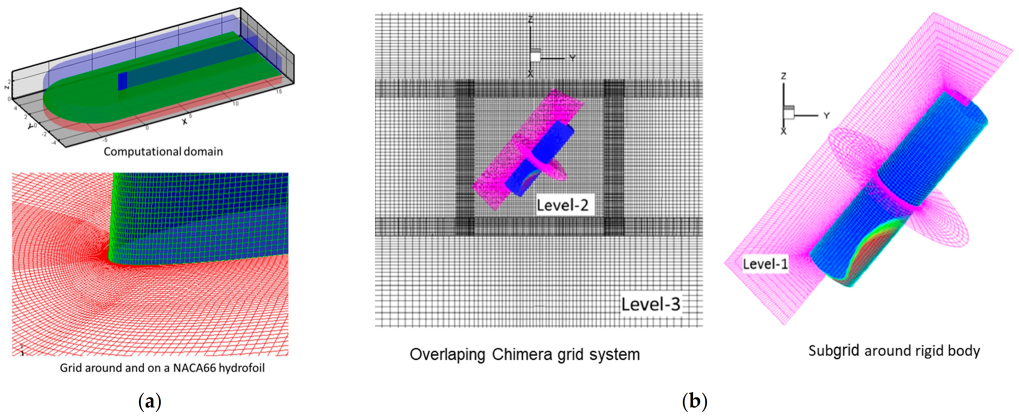
2.4. Simulations of Incompressible Multiphase Flows
2.4.1. Modeling Two-Phase Flows with Sharp Interface
2.4.2. Modeling Cavitating Flows
3. Compressible Multiphase Flows
3.1. Dual-Time Preconditioning Method for Compressible NS Equation System
3.2. Numerical Solution Procedures
3.3. Simulations of Compressible Multiphase Flows
4. Conclusions
- (i)
- Incorporating more accurate and efficient numerical schemes for solving dual-time, pseudo-compressibility NS equations.
- (ii)
- Considering the effects of turbulence by implementing various accurate turbulence models and other physical phenomena that may affect the multiphase flow behaviors.
- (iii)
- Additionally, the method can be extended to handle more complex and realistic boundary conditions and geometries. Accordingly, efforts should be focused on reducing the computational cost of the method while preserving its accuracy and robustness.
Funding
Conflicts of Interest
Nomenclature
| Phasic volume fraction | |
| Phasic mass fraction | |
| Preconditioning parameter | |
| Density | |
| Exponential factor of mixture density | |
| Preconditioning matrix | |
| Jacobian of physical time derivatives | |
| Molecular viscosity | |
| Pseudo time | |
| Pseudo time step | |
| Physical time step | |
| Cavitation number | |
| Gravity | |
| Pressure | |
| Physical time | |
| Transformation matrix | |
| x-direction velocity of fluid | |
| Contravariant velocity in x-direction | |
| Parameter reference to velocity | |
| Free-stream velocity | |
| y-direction velocity of fluid | |
| Contravariant velocity in y-direction | |
| z-direction velocity of fluid | |
| Contravariant velocity in z-direction | |
| computational space in the general curvilinear coordinate system | |
| Mass transfer rate | |
| Artificial density | |
| Reference to free stream |
References
- Nguyen, V.-T.; Park, W.-G. Enhancement of Navier–Stokes solver based on an improved volume-of-fluid method for complex interfacial-flow simulations. Appl. Ocean. Res. 2018, 72, 92–109. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Vu, D.-T.; Park, W.-G.; Jung, C.-M. Navier–Stokes solver for water entry bodies with moving Chimera grid method in 6DOF motions. Comput. Fluids 2016, 140, 19–38. [Google Scholar] [CrossRef]
- Palomino Solis, D.A.; Piscaglia, F. Toward the Simulation of Flashing Cryogenic Liquids by a Fully Compressible Volume of Fluid Solver. Fluids 2022, 7, 289. [Google Scholar] [CrossRef]
- Yao, J.; Yao, Y. Transient CFD Modelling of Air–Water Two-Phase Annular Flow Characteristics in a Small Horizontal Circular Pipe. Fluids 2022, 7, 191. [Google Scholar] [CrossRef]
- Fayed, H.; Bukhari, M.; Ragab, S. Large-Eddy Simulation of a Hydrocyclone with an Air Core Using Two-Fluid and Volume-of-Fluid Models. Fluids 2021, 6, 364. [Google Scholar] [CrossRef]
- Harlow, F.H.; Welch, J.E. Numerical Calculation of Time-Dependent Viscous Incompressible Flow of Fluid with Free Surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Puckett, E.G.; Almgren, A.S.; Bell, J.B.; Marcus, D.L.; Rider, W.J. A High-Order Projection Method for Tracking Fluid Interfaces in Variable Density Incompressible Flows. J. Comput. Phys. 1997, 130, 269–282. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.D.; Sakai, S.; Sethian, J.A. A coupled level set projection method applied to ink jet simulation. Interface Free. Bound. 2003, 5, 459–482. [Google Scholar] [CrossRef] [Green Version]
- Merkle, C. Time-accurate unsteady incompressible flow algorithms based on artificial compressibility. In Proceedings of the 8th Computational Fluid Dynamics Conference, Honolulu, HI, USA, 9–11 June 1987. [Google Scholar]
- Chorin, A.J. A Numerical Method for Solving Incompressible Viscous Flow Problems. J. Comput. Phys. 1997, 135, 118–125. [Google Scholar] [CrossRef]
- Štrubelj, L.; Tiselj, I. Modeling of Rayleigh-Taylor instability with conservative level set method. In Proceedings of the ICMF 2007, 6th International Conference on Multiphase Flow, Leipzig, Germany, 9–13 July 2007. [Google Scholar]
- Elmahi, I.; Gloth, O.; Hänel, D.; Vilsmeier, R. A preconditioned dual time-stepping method for combustion problems. Int. J. Comput. Fluid Dyn. 2008, 22, 169–181. [Google Scholar] [CrossRef]
- Lin, H.; Jiang, C.; Hu, S.; Gao, Z.; Lee, C.-H. Disturbance region update method with preconditioning for steady compressible and incompressible flows. Comput. Phys. Commun. 2023, 285, 108635. [Google Scholar] [CrossRef]
- Li, X.-s.; Gu, C.-w.; Xu, J.-z. Development of Roe-type scheme for all-speed flows based on preconditioning method. Comput. Fluids 2009, 38, 810–817. [Google Scholar] [CrossRef]
- Muradoglu, M.; Gokaltun, S. Implicit Multigrid Computations of Buoyant Drops Through Sinusoidal Constrictions. J. Appl. Mech. 2005, 71, 857–865. [Google Scholar] [CrossRef]
- Kinzel, M.P. Computational Techniques and Analysis of Cavitating-Fluid Flows; A Dissertation in Aerospace Engineering; The Pennsylvania State University: State College, PA, USA, 2008. [Google Scholar]
- Maia, A.A.G.; Kapat, J.S.; Tomita, J.T.; Silva, J.F.; Bringhenti, C.; Cavalca, D.F. Preconditioning methods for compressible flow CFD codes: Revisited. Int. J. Mech. Sci. 2020, 186, 105898. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics. A Practical Introduction; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Nguyen, V.-T.; Phan, T.-H.; Duy, T.-N.; Kim, D.-H.; Park, W.-G. Fully compressible multiphase model for computation of compressible fluid flows with large density ratio and the presence of shock waves. Comput. Fluids 2022, 237, 105325. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Phan, T.-H.; Duy, T.-N.; Park, W.-G. Unsteady cavitation around submerged and water-exit projectiles under the effect of the free surface: A numerical study. Ocean. Eng. 2022, 263, 112368. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Park, W.-G. A free surface flow solver for complex three-dimensional water impact problems based on the VOF method. Int. J. Numer. Methods Fluids 2016, 82, 3–34. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Park, W.-G. A volume-of-fluid (VOF) interface-sharpening method for two-phase incompressible flows. Comput. Fluids 2017, 152, 104–119. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Thang, V.-D.; Park, W.-G. A novel sharp interface capturing method for two- and three-phase incompressible flows. Comput. Fluids 2018, 172, 147–161. [Google Scholar] [CrossRef]
- Ansari, M.R.; Nimvari, M.E. Bubble viscosity effect on internal circulation within the bubble rising due to buoyancy using the level set method. Ann. Nucl. Energy 2011, 38, 2770–2778. [Google Scholar] [CrossRef]
- Komrakova, A.E.; Eskin, D.; Derksen, J.J. Lattice Boltzmann simulations of a single n-butanol drop rising in water. Phys. Fluids 2013, 25, 042102. [Google Scholar] [CrossRef] [Green Version]
- Magnini, M.; Pulvirenti, B.; Thome, J.R. Numerical investigation of the influence of leading and sequential bubbles on slug flow boiling within a microchannel. Int. J. Therm. Sci. 2013, 71, 36–52. [Google Scholar] [CrossRef]
- Tomar, G.; Biswas, G.; Sharma, A.; Agrawal, A. Numerical simulation of bubble growth in film boiling using a coupled level-set and volume-of-fluid method. Phys. Fluids 2005, 17, 112103. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Park, W.-G. Numerical study of the thermodynamics and supercavitating flow around an underwater high-speed projectile using a fully compressible multiphase flow model. Ocean. Eng. 2022, 257, 111686. [Google Scholar] [CrossRef]
- Ding, H.; Zhang, Y.; Yang, Y.; Wen, C. A modified Euler-Lagrange-Euler approach for modelling homogeneous and heterogeneous condensing droplets and films in supersonic flows. Int. J. Heat Mass. Tran. 2023, 200, 123537. [Google Scholar] [CrossRef]
- Chen, J.; Huang, Z.; Li, A.; Gao, R.; Jiang, W.; Xi, G. Numerical simulation of carbon separation with shock waves and phase change in supersonic separators. Process. Saf. Environ. 2023, 170, 277–285. [Google Scholar] [CrossRef]
- Heydar Rajaee Shooshtari, S.; Honoré Walther, J.; Wen, C. Combination of genetic algorithm and CFD modelling to develop a new model for reliable prediction of normal shock wave in supersonic flows contributing to carbon capture. Sep. Purif. Technol. 2022, 309, 122878. [Google Scholar] [CrossRef]
- Munz, C.D.; Roller, S.; Klein, R.; Geratz, K.J. The extension of incompressible flow solvers to the weakly compressible regime. Comput. Fluids 2003, 32, 173–196. [Google Scholar] [CrossRef]
- Kajzer, A.; Pozorski, J. A weakly Compressible, Diffuse-Interface Model for Two-Phase Flows. Flow Turbul. Combust. 2020, 105, 299–333. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Nguyen, N.T.; Phan, T.-H.; Park, W.-G. Efficient three-equation two-phase model for free surface and water impact flows on a general curvilinear body-fitted grid. Comput. Fluids 2019, 196, 104324. [Google Scholar] [CrossRef]
- Phan, T.-H.; Shin, J.-G.; Nguyen, V.-T.; Duy, T.-N.; Park, W.-G. Numerical analysis of an unsteady natural cavitating flow around an axisymmetric projectile under various free-stream temperature conditions. Int. J. Heat Mass. Tran. 2021, 164, 120484. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Ha, C.-T.; Park, W.-G. Multiphase Flow Simulation of Water-entry and -exit of axisymmetric bodies. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Diego, CA, USA, 15–21 November 2013. [Google Scholar]
- Phan, T.-H.; Kadivar, E.; Nguyen, V.-T.; el Moctar, O.; Park, W.-G. Thermodynamic effects on single cavitation bubble dynamics under various ambient temperature conditions. Phys. Fluids 2022, 34, 023318. [Google Scholar] [CrossRef]
- Phan, T.-H.; Nguyen, V.-T.; Duy, T.-N.; Kim, D.-H.; Park, W.-G. Numerical study on simultaneous thermodynamic and hydrodynamic mechanisms of underwater explosion. Int. J. Heat Mass. Tran. 2021, 178, 121581. [Google Scholar] [CrossRef]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T.R. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Kunz, R.F.; Boger, D.A.; Chyczewski, T.S.; Stinebring, D.; Gibeling, H.; Govindan, T. Multi-phase CFD analysis of natural and ventilated cavitation about submerged bodies. In Proceedings of the 3rd ASME-JSME Joint Fluids Engineering Conference, San Francisco, CA, USA, 18–23 July 1999; Volume 99. [Google Scholar]
- Owis, F.M.; Nayfeh, A.H. Numerical simulation of 3-D incompressible, multi-phase flows over cavitating projectiles. Eur. J. Mech. B-Fluid. 2004, 23, 339–351. [Google Scholar] [CrossRef]
- de Jouëtte, C.; Laget, O.; Le Gouez, J.M.; Viviand, H. A dual time stepping method for fluid–structure interaction problems. Comput. Fluids 2002, 31, 509–537. [Google Scholar] [CrossRef]
- Helluy, P.; Golay, F.; Caltagirone, J.-P.; Lubin, P.; Vincent, S.; Drevard, D.; Marcer, R.; Fraunié, P.; Seguin, N.; Grilli, S.; et al. Numerical simulations of wave breaking. ESAIM Math. Model. Numer. Anal. Model. Math. Anal. Numer. 2005, 39, 591–607. [Google Scholar] [CrossRef]
- Nourgaliev, R.R.; Dinh, T.N.; Theofanous, T.G. A pseudocompressibility method for the numerical simulation of incompressible multifluid flows. Int. J. Multiphas Flow. 2004, 30, 901–937. [Google Scholar] [CrossRef]
- Ha, C.-T.; Lee, J.H. A modified monotonicity-preserving high-order scheme with application to computation of multi-phase flows. Comput. Fluids 2020, 197, 104345. [Google Scholar] [CrossRef]
- Metcalf, B.; Longo, J.; Ghosh, S.; Stern, F. Unsteady free-surface wave-induced boundary-layer separation for a surface-piercing NACA 0024 foil: Towing tank experiments. J. Fluid. Struct. 2006, 22, 77–98. [Google Scholar] [CrossRef]
- GeolLee, C.; YoubLee, S.; Ha, C.-T.; HwaLee, J. Bursting jet in two tandem bubbles at the free surface. Phys. Fluids 2022, 34, 083309. [Google Scholar]
- Alotaibi, H.; Abeykoon, C.; Soutis, C.; Jabbari, M. Numerical Simulation of Two-Phase Flow in Liquid Composite Moulding Using VOF-Based Implicit Time-Stepping Scheme. J. Compos. Sci. 2022, 6, 330. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Phan, T.-H.; Duy, T.-N.; Park, W.-G. Numerical simulation of supercavitating flow around a submerged projectile near a free surface. In Proceedings of the 11th International Symposium on Cavitation, Daejon, Korea, 10–13 May 2021. [Google Scholar]
- Merkle, C.L.; Feng, J.; Buelow, P. Computational modeling of the dynamics of sheet cavitation. In Proceedings of the Third International Symposium on Cavitation, Grenoble, France, 7–10 April 1998. [Google Scholar]
- Schnerr, G.H.; Sauer, J. Physical and numerical modeling of unsteady cavitation dynamics. In Proceedings of the Fourth International Conference on Multiphase Flow, New Orleans, LA, USA, 27 May–1 June 2001. [Google Scholar]
- Ullas, P.K.; Chatterjee, D.; Vengadesan, S. Prediction of unsteady, internal turbulent cavitating flow using dynamic cavitation model. Int. J. Numer. Methods Heat 2022, 32, 3210–3232. [Google Scholar] [CrossRef]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical Basis and Validation of the Full Cavitation Model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the Fifth International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004. [Google Scholar]
- Tauviqirrahman, M.; Jamari, J.; Susilowati, S.; Pujiastuti, C.; Setiyana, B.; Pasaribu, A.H.; Ammarullah, M.I. Performance Comparison of Newtonian and Non-Newtonian Fluid on a Heterogeneous Slip/No-Slip Journal Bearing System Based on CFD-FSI Method. Fluids 2022, 7, 225. [Google Scholar] [CrossRef]
- Hejranfar, K.; Ezzatneshan, E.; Fattah-Hesari, K. A comparative study of two cavitation modeling strategies for simulation of inviscid cavitating flows. Ocean. Eng. 2015, 108, 257–275. [Google Scholar] [CrossRef]
- Lindau, J.W.; Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Gibeling, H.J. High Reynolds number, unsteady, multiphase CFD modeling of cavitating flows. J. Fluid. Eng. 2002, 124, 607–616. [Google Scholar] [CrossRef]
- Lindau, J.W.; Kunz, R.F.; Mulherin, J.M.; Dreyer, J.J.; Stinebring, D.R. Fully coupled, 6-DOF to URANS, modeling of cavitating flows around a supercavitating vehicle. In Proceedings of the Fifth International Symposium on Cavitation (CAV2003), Osaka, Japan, 1–4 November 2003. [Google Scholar]
- Vrionis, Y.-P.G.; Samouchos, K.D.; Giannakoglou, K.C. Implementation of a conservative cut-cell method for the simulation of two-phase cavitating flows. In Proceedings of the 10th International Conference on Computational Methods (ICCM2019), Singapore, 9–13 July 2019; pp. 440–452. [Google Scholar]
- Coutier-Delgosha, O.; Fortes-Patella, R.; Reboud, J.L.; Hakimi, N.; Hirsch, C. Stability of preconditioned Navier–Stokes equations associated with a cavitation model. Comput. Fluids 2005, 34, 319–349. [Google Scholar] [CrossRef]
- Hejranfar, K.; Fattah-Hesary, K. Assessment of a central difference finite volume scheme for modeling of cavitating flows using preconditioned multiphase Euler equations. J. Hydrodyn. Ser. B. 2011, 23, 302–313. [Google Scholar] [CrossRef] [Green Version]
- Hajihassanpour, M.; Hejranfar, K. A high-order nodal discontinuous Galerkin method to solve preconditioned multiphase Euler/Navier-Stokes equations for inviscid/viscous cavitating flows. Int. J. Numer. Methods Fluids 2020, 92, 478–508. [Google Scholar] [CrossRef]
- Tian, B.; Chen, J.; Zhao, X.; Zhang, M.; Huang, B. Numerical analysis of interaction between turbulent structures and transient sheet/cloud cavitation. Phys. Fluids 2022, 34, 047116. [Google Scholar] [CrossRef]
- Kinzel, M.P.; Lindau, J.W.; Kunz, R.F. Gas entrainment from gaseous supercavities: Insight based on numerical simulation. Ocean. Eng. 2021, 221, 108544. [Google Scholar] [CrossRef]
- Saurel, R.; Pantano, C. Diffuse-Interface Capturing Methods for Compressible Two-Phase Flows. Annu. Rev. Fluid. Mech. 2018, 50, 105–130. [Google Scholar] [CrossRef] [Green Version]
- Weiss, J.M.; Smith, W.A. Preconditioning applied to variable and constant density flows. AIAA J. 1995, 33, 2050–2057. [Google Scholar] [CrossRef]
- Venkateswaran, S.; Lindau, J.W.; Kunz, R.F.; Merkle, C.L. Computation of multiphase mixture flows with compressibility effects. J. Comput. Phys. 2002, 180, 54–77. [Google Scholar] [CrossRef]
- Lindau, J.; Kunz, R.; Venkateswaran, S.; Merkle, C. Development of a fully-compressible multi-phase Reynolds-averaged Navier-Stokes model. In Proceedings of the 15th AIAA Computational Fluid, Dynamics Conference, Anaheim, CA, USA, 11–14 June 2001. [Google Scholar]
- Braconnier, B.; Nkonga, B. An all-speed relaxation scheme for interface flows with surface tension. J. Comput. Phys. 2009, 228, 5722–5739. [Google Scholar] [CrossRef]
- Pelanti, M. Low Mach number preconditioning techniques for Roe-type and HLLC-type methods for a two-phase compressible flow model. Appl. Math. Comput. 2017, 310, 112–133. [Google Scholar] [CrossRef]
- Murrone, A.; Guillard, H. Behavior of upwind scheme in the low Mach number limit: III. Preconditioned dissipation for a five equation two phase model. Comput. Fluids 2008, 37, 1209–1224. [Google Scholar] [CrossRef] [Green Version]
- Gupta, A. Preconditioning Methods for Ideal and Multiphase Fluid Flows. Ph.D. Thesis, The University of Tennessee at Chattanooga, Chattanooga, TN, USA, 2013. [Google Scholar]
- Yoon, S.; Jameson, A. Lower-upper Symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations. AIAA J. 1988, 26, 1025–1026. [Google Scholar] [CrossRef] [Green Version]
- Housman, J.A.; Kiris, C.C.; Hafez, M.M. Time-Derivative Preconditioning Methods for Multicomponent Flows—Part I: Riemann Problems. J. Appl. Mech. 2009, 76, 021210. [Google Scholar] [CrossRef]
- Ha, C.-T.; Park, W.-G. Evaluation of a new scaling term in preconditioning schemes for computations of compressible cavitating and ventilated flows. Ocean. Eng. 2016, 126, 432–466. [Google Scholar] [CrossRef]
- Kim, H.; Kim, C. A physics-based cavitation model ranging from inertial to thermal regimes. Int. J. Heat Mass. Tran. 2021, 181, 121991. [Google Scholar] [CrossRef]
- Yoo, Y.-L.; Sung, H.-G. A hybrid AUSM scheme (HAUS) for multi-phase flows with all Mach numbers. Comput. Fluids 2021, 227, 105050. [Google Scholar] [CrossRef]
- Kadioglu, S.Y.; Sussman, M.; Osher, S.; Wright, J.P.; Kang, M. A second order primitive preconditioner for solving all speed multi-phase flows. J. Comput. Phys. 2005, 209, 477–503. [Google Scholar] [CrossRef]
- Shin, B.R.; Yamamoto, S.; Yuan, X. Application of Preconditioning Method to Gas-Liquid Two-Phase Flow Computations. J. Fluids Eng. 2004, 126, 605–612. [Google Scholar] [CrossRef]
- Goncalves, E.; Patella, R.F. Numerical simulation of cavitating flows with homogeneous models. Comput. Fluids 2009, 38, 1682–1696. [Google Scholar] [CrossRef] [Green Version]
- Phan, T.-H.; Nguyen, V.-T.; Duy, T.-N.; Kim, D.-H.; Park, W.-G. Influence of phase-change on the collapse and rebound stages of a single spark-generated cavitation bubble. Int. J. Heat Mass. Tran. 2022, 184, 122270. [Google Scholar] [CrossRef]
- Kinzel, M.P.; Lindau, J.W.; Kunz, R.F. A multiphase level-set approach for all-Mach numbers. Comput. Fluids 2018, 167, 1–16. [Google Scholar] [CrossRef]
- Cassidy, D.A.; Edwards, J.R.; Tian, M. An investigation of interface-sharpening schemes for multi-phase mixture flows. J. Comput. Phys. 2009, 228, 5628–5649. [Google Scholar] [CrossRef]
- Kakumanu, N.; Edwards, J.R.; Choi, J.-I. Numerical Simulation of Underwater Burst Events Using Sharp Interface Capturing Methods. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2019. [Google Scholar]
- Gouin, C.; Junqueira-Junior, C.; Goncalves Da Silva, E.; Robinet, J.-C. Numerical investigation of three-dimensional partial cavitation in a Venturi geometry. Phys. Fluids 2021, 33, 063312. [Google Scholar] [CrossRef]
- Yoo, Y.-L.; Kim, J.-C.; Sung, H.-G. Homogeneous mixture model simulation of compressible multi-phase flows at all Mach number. Int. J. Multiphas Flow. 2021, 143, 103745. [Google Scholar] [CrossRef]
- Huber, G.; Tanguy, S.; Béra, J.-C.; Gilles, B. A time splitting projection scheme for compressible two-phase flows. Application to the interaction of bubbles with ultrasound waves. J. Comput. Phys. 2015, 302, 439–468. [Google Scholar] [CrossRef] [Green Version]
- LeMartelot, S.; Nkonga, B.; Saurel, R. Liquid and liquid–gas flows at all speeds. J. Comput. Phys. 2013, 255, 53–82. [Google Scholar] [CrossRef]
- Meng, H.; Yang, V. A unified treatment of general fluid thermodynamics and its application to a preconditioning scheme. J. Comput. Phys. 2003, 189, 277–304. [Google Scholar] [CrossRef]
- Huang, D.; Wang, Q.; Meng, H. Modeling of supercritical-pressure turbulent combustion of hydrocarbon fuels using a modified flamelet-progress-variable approach. Appl. Therm. Eng. 2017, 119, 472–480. [Google Scholar] [CrossRef]
- Neaves, M.D.; Edwards, J.R. All-Speed Time-Accurate Underwater Projectile Calculations Using a Preconditioning Algorithm. J. Fluids Eng. 2005, 128, 284–296. [Google Scholar] [CrossRef]
- De Wilde, J.; Heynderickx, G.J.; Vierendeels, J.; Dick, E.; Marin, G.B. An extension of the preconditioned advection upstream splitting method for 3D two-phase flow calculations in circulating fluidized beds. Comput. Chem. Eng. 2002, 26, 1677–1702. [Google Scholar] [CrossRef]
- De Wilde, J.; Vierendeels, J.; Heynderickx, G.J.; Marin, G.B. Simultaneous solution algorithms for Eulerian–Eulerian gas–solid flow models: Stability analysis and convergence behaviour of a point and a plane solver. J. Comput. Phys. 2005, 207, 309–353. [Google Scholar] [CrossRef]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, V.-T.; Park, W.-G. A Review of Preconditioning and Artificial Compressibility Dual-Time Navier–Stokes Solvers for Multiphase Flows. Fluids 2023, 8, 100. https://doi.org/10.3390/fluids8030100
Nguyen V-T, Park W-G. A Review of Preconditioning and Artificial Compressibility Dual-Time Navier–Stokes Solvers for Multiphase Flows. Fluids. 2023; 8(3):100. https://doi.org/10.3390/fluids8030100
Chicago/Turabian StyleNguyen, Van-Tu, and Warn-Gyu Park. 2023. "A Review of Preconditioning and Artificial Compressibility Dual-Time Navier–Stokes Solvers for Multiphase Flows" Fluids 8, no. 3: 100. https://doi.org/10.3390/fluids8030100
APA StyleNguyen, V.-T., & Park, W.-G. (2023). A Review of Preconditioning and Artificial Compressibility Dual-Time Navier–Stokes Solvers for Multiphase Flows. Fluids, 8(3), 100. https://doi.org/10.3390/fluids8030100






