Prediction of Critical Heat Flux of Mixtures Flowing in Channels
Abstract
:1. Introduction
2. Previous Work
2.1. Pool Boiling CHF
2.2. Mixture CHF in Annuli
2.3. Mixture CHF in Tubes
3. Present Data Analysis
3.1. Choice of Correlations for Evaluation
3.2. Selection of Test Data
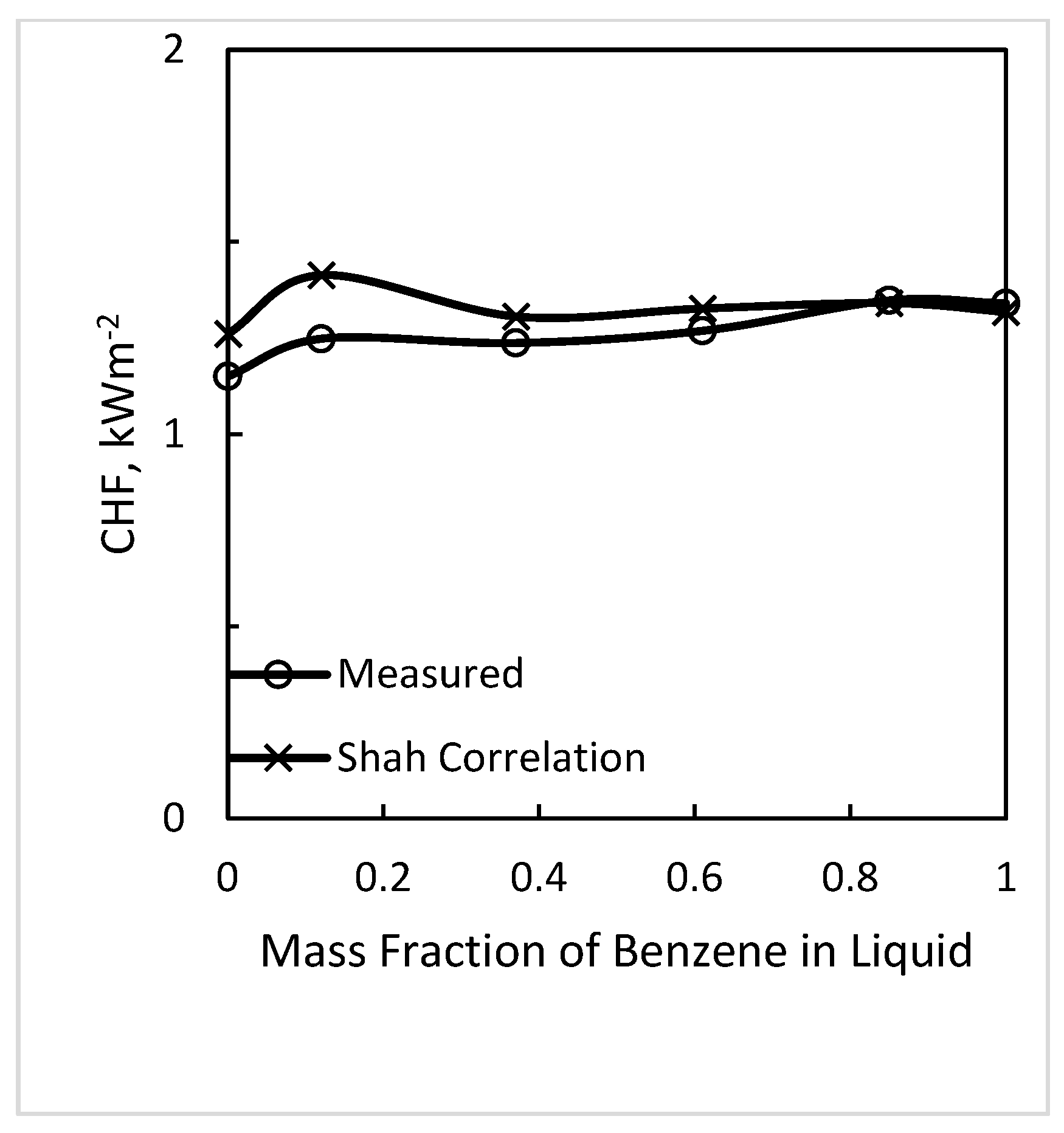
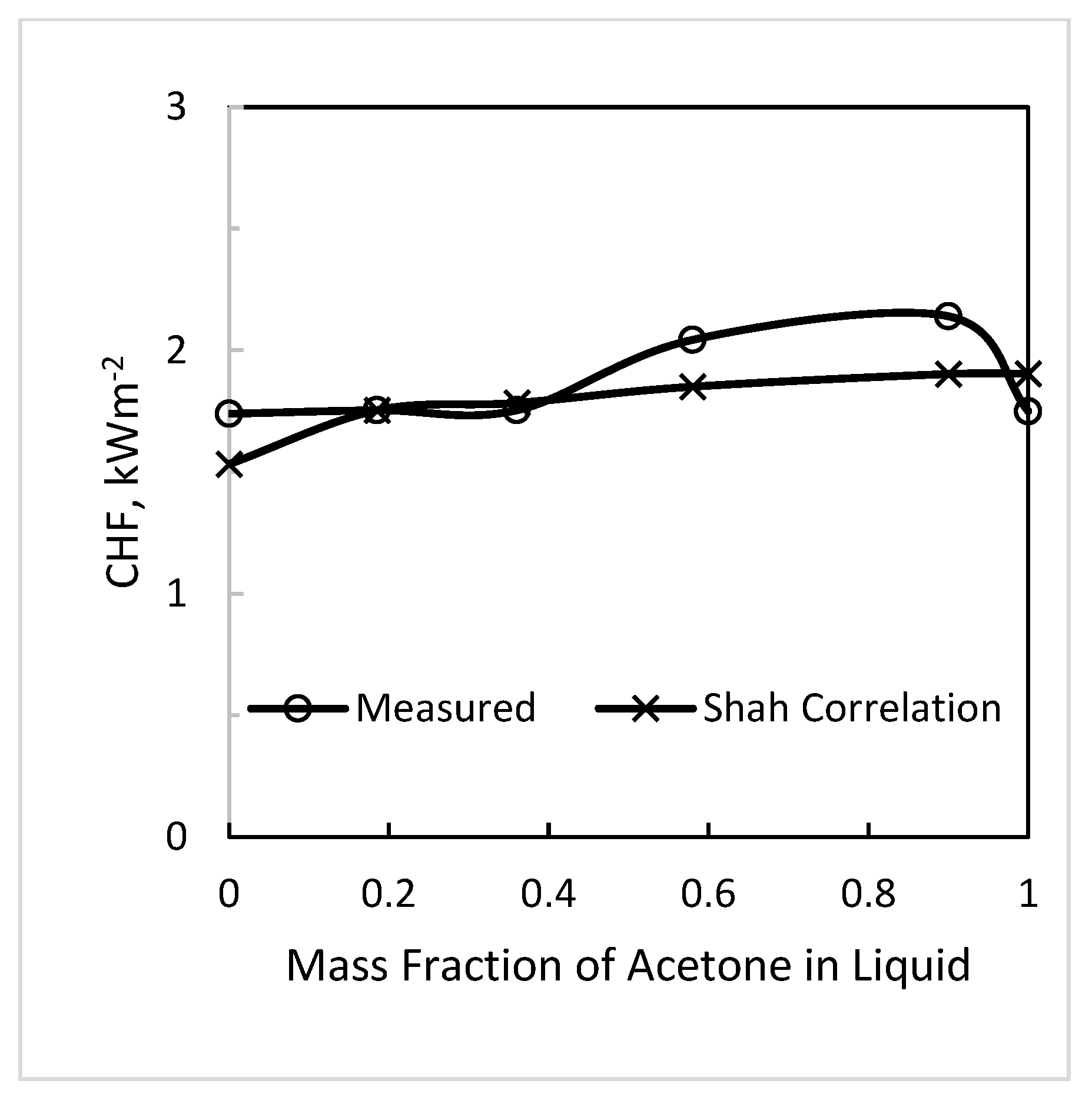
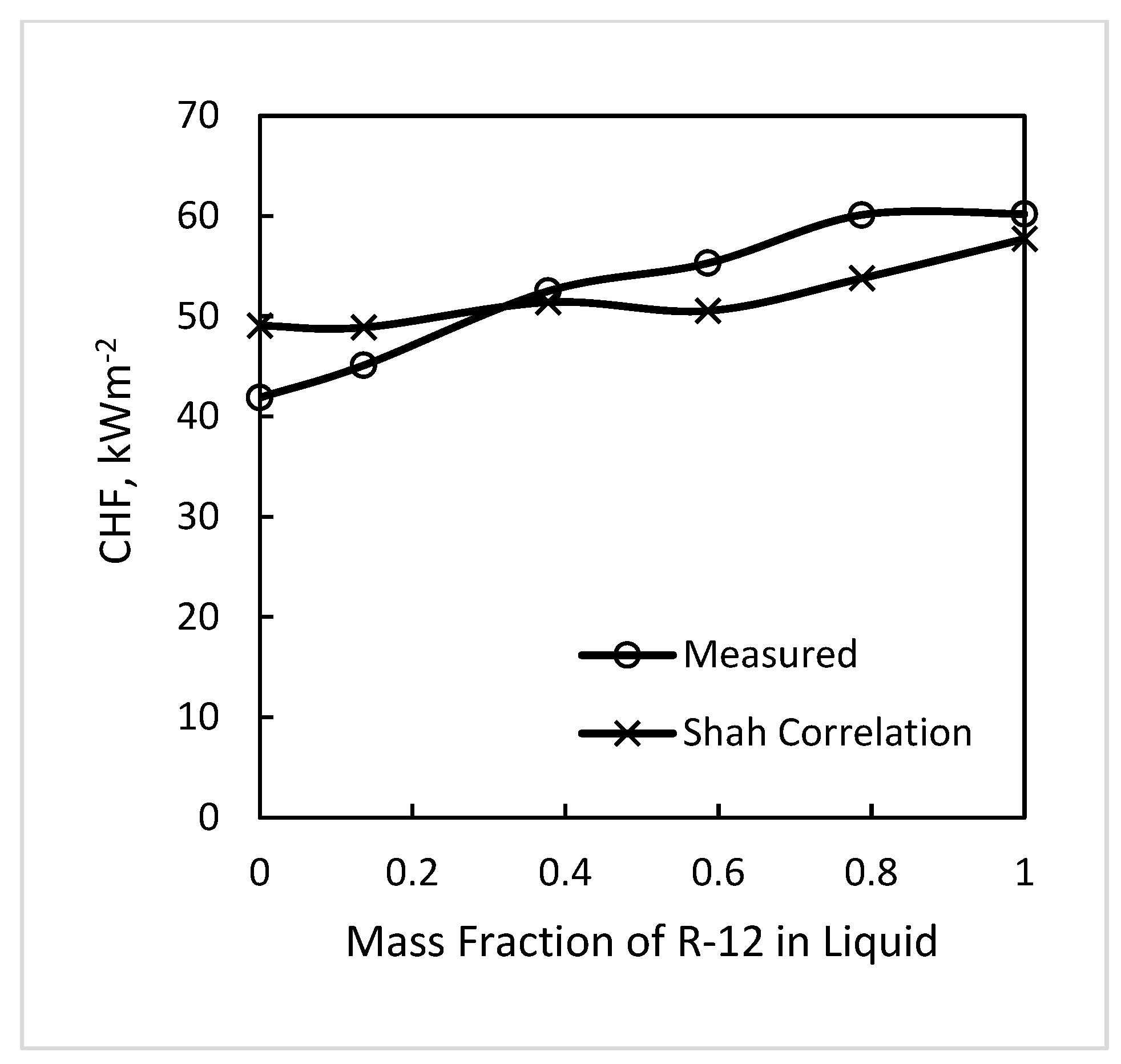
3.3. Results of Data Analysis
4. Discussion
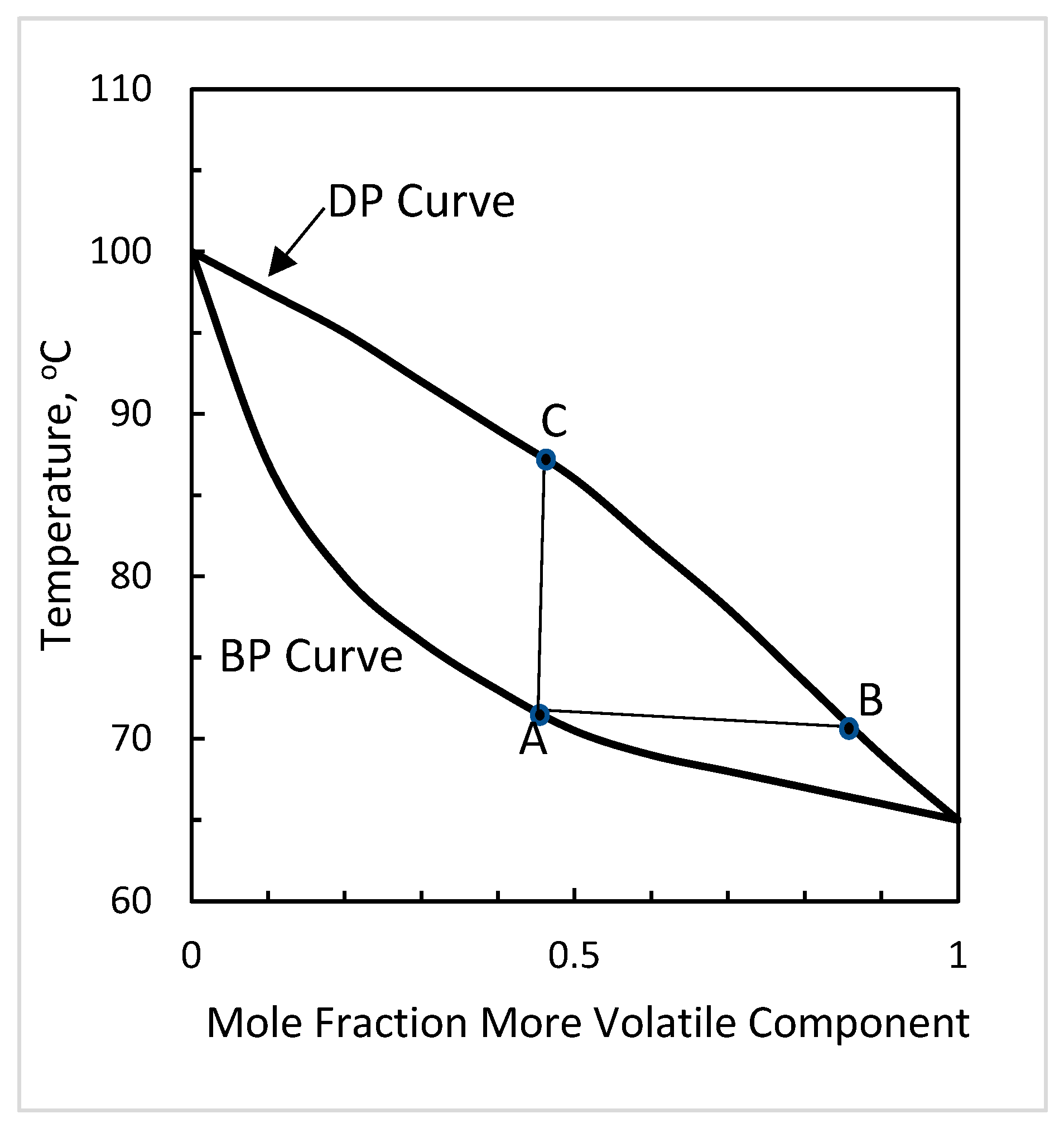
4.1. Variation of CHF with Mixture Composition
4.2. Effect of Surface Tension Difference
4.3. Effect of Glide
4.4. Mass Flux
4.5. Reduced Pressure
4.6. Inlet and Critical Qualities
4.7. Orientations Other Than Vertical Upflow
4.8. Correlations for Mixture CHF
5. Conclusions
- Data for CHF mixtures of halocarbon refrigerants (R-407C, R-12, R-114) and mixtures of chemicals (benzene, acetone, toluene) in annuli and tubes were compared to well-verified general correlations for pure fluids. The data included subcooled CHF as well as at high qualities. The range of flow rates and reduced pressures was very wide.
- Based on the results of this data analysis and results of pool boiling CHF, the best recommendation is that correlations for pure fluids can be used without any correction to predict CHF of mixtures provided that Δσ is the range −2.4 to +2.8 mN/m. Δσ is the difference between surface tension of the mixture at a vapor phase composition and that at a liquid phase composition, both at the same liquid phase temperature. The data analyzed were in this range and were in good agreement with the correlations of Shah (1987) for tubes and Shah (2015a) for annuli, both well verified for pure fluids.
- Most refrigerant mixtures have Δσ in the range stated above, and hence, this result will be particularly useful in the design of refrigerant evaporators.
- There is no verified method for calculation of CHF when Δσ is outside the range −2.4 to +2.8 mN/m.
- A number of available data sets for mixture CHF could not be analyzed due to the unavailability of software for calculating their properties. There is a need to develop software to predict properties of such fluids and mixtures.
- There is a great need for more experimental studies on the CHF of mixtures so that reliable methods to calculate the CHF of all types of fluid mixtures could be developed.
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature | |
| D | diameter, m |
| DHP | equivalent diameter of annulus based on heated perimeter, m |
| G | mass flux, kgm−2s−1 |
| L | length of channel from entrance to CHF location, m |
| N | number of data points, (-) |
| pr | reduced pressure = (actual pressure)/(critical pressure) (-) |
| qc | critical heat flux, kWm−2 |
| TSAT | saturation temperature, K |
| x’ | mole fraction of more volatile component in liquid phase at bubble point temperature, (-) |
| xc | quality at CHF location (called critical quality), (-) |
| xin | inlet quality, (-) |
| y’ | mole fraction of more volatile component in vapor phase at bubble point temperature, (-) |
| Greek | |
| β | parameter in Equation (2), (-) |
| σ | surface tension, Nm−1 |
| Δσ | σ at liquid phase composition minus σ at vapor phase composition both at bubble point temperature, Nm−1 |
| μ | dynamic viscosity, Pa.s |
| Subscripts | |
| I | ideal pure fluid with properties of mixture |
| mix | mixture |
Appendix A. Shah Correlation (1987) for CHF in Vertical Tubes
Appendix B. Shah (2015a) Correlation for CHF in Vertical Annuli
References
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Reference Fluid Thermodynamic and Transport Properties, REFPROP Version 9.1; NIST: Gaithersburg, MD, USA, 2013.
- Collier, J.G.; Thome, J.R. Convective Boiling & Condensation, 2nd ed.; Chapter 4; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Celata, G.P.; Cumo, M.; Setaro, T. A Review of Pool and Forced Convective Boiling of Binary Mixtures. Exp. Therm. Fluid Sci. 1994, 9, 367–381. [Google Scholar] [CrossRef]
- Shah, M.M. Two-Phase Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Fujita, Y.; Bai, Q. Critical heat flux of binary mixtures in pool boiling and its correlation in terms of Marangoni number. Int. J. Refrig. 1997, 20, 616–622. [Google Scholar] [CrossRef]
- Zuber, N. Hydrodynamic Aspects of Boiling Heat Transfer, AECU-4439; University of California: Los Angeles, CA, USA, 1959. [Google Scholar]
- Van Stralen, S.J.D.; Sluyter, W.M. Investigations on the critical heat flux of pure liquids and mixtures under various conditions. Int. J. Heat Mass Transf. 1969, 12, 1353–1384. [Google Scholar] [CrossRef]
- Reddy, R.P.; Lienhard, J.H. The peak boiling heat flux in saturated ethanol-water mixtures. J. Heat Transf. 1989, 111, 480–486. [Google Scholar] [CrossRef]
- Yagov, V.V. Critical heat flux prediction for pool boiling of binary mixtures. Chem. Eng. Res. Des. 2004, 82, 457–461. [Google Scholar] [CrossRef]
- Sterman, L.A.; Abramov, A.; Checheta, G. Investigation of boiling crisis at forced motion of high temperature organic heat carriers and mixtures. In International Symposium on Research into Co-Current Gas-Liquid Flow; Paper E2, Quoted in Collier and Thome (1994); University of Waterloo: Waterloo, ON, Canada, 1968. [Google Scholar]
- Carne, M. Studies of the Critical Heat Flux for some Binary Mixtures and their Components. Can. J. Chem. Eng. 1963, 41, 235–240. [Google Scholar] [CrossRef]
- Andrews, D.G.; Hooper, F.C.; Butt, P. Velocity, Subcooling and Surface Effects in the Departure from Nucleate Boiling of Organic Binaries. Can. J. Chem. Eng. 1968, 46, 194–199. [Google Scholar] [CrossRef]
- Naboichenko, K.V.; Kiryutin, A.A.; Gribov, B.S. A study of critical heat flux with forced flow of monoisopropyldiphenyl- benzene mixture. Teploenergetika 1965, 12, 81–86, Quoted in Collier & Thome (1994). [Google Scholar]
- Tolubinsky, V.I.; Matorin, P.S. Forced Convection Boiling Heat Transfer Crisis with Binary Mixtures. Heat Transf.—Sov. Res. 1973, 5, 98–101. [Google Scholar]
- Celata, G.P.; Cumo, M.; Setaro, T. Critical heat flux in upflow convective boiling of refrigerant binary mixtures. Int. J. Heat Mass Transf. 1994, 37, 1143–1153. [Google Scholar] [CrossRef]
- Katto, Y.; Ohno, H. An improved version of the generalized correlation of critical heat flux for the forced convection boiling in uniformly heated vertical tubes. Int. J. Heat Mass Transf. 1984, 27, 1641–1648. [Google Scholar] [CrossRef]
- Sindhuja, R.; Balakrishnan, A.R.; Murthy, S.S. Critical heat flux of R-407C in upflow boiling in a vertical pipe. Appl. Therm. Eng. 2008, 28, 1058–1065. [Google Scholar] [CrossRef]
- Groeneveld, D.C.; Leung, L.K.H.; Erbacher, F.J.; Zeggel, W. An improved table look-up method for predicting critical heat flux. In Proceedings of the NURETH-6, Sixth International Topical Meeting on Nuclear Reactor Thermal Hydraulics, Grenoble, France, 5–8 October 1993; Volume 1, pp. 223–230. [Google Scholar]
- Vijayarangan, B.R.; Jayanti, S.; Balakrishnan, A.R. Studies on critical heat flux in flow boiling under near critical pressures. Int. J. Heat Mass Transf. 2006, 49, 259–268. [Google Scholar] [CrossRef]
- Mori, H.; Yoshida, S.; Ohno, M.; Kusumoto, K.; Itoh, T. Critical heat flux for non-azeotropic binary mixtures at high pressure. Proc. JSME 1990, 908, 210–214, Quoted in Auracher and Marroquin (1995). [Google Scholar]
- Auracher, H.; Marroquin, A. Forced Convection Critical Heat Flux and Transition Boiling of Mixtures Flowing Upward in a Vertical Tube. In Convective Flow Boiling; Chen, J., Ed.; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Robinson, J.M.; Lurie, H. Critical heat flux of some polyphenyl coolants. In Proceedings of the Symposium on Boiling Phenomena in Nuclear Heat Transfer, Fifty-fifth Annual Meeting of AIChE, Chicago, IL, USA, 2–6 December 1962. Preprint 156. [Google Scholar]
- Shah, M.M. Improved general correlation for critical heat flux in uniformly heated vertical tubes. Int. J. Heat Fluid Flow 1987, 8, 326–335. [Google Scholar] [CrossRef]
- Shah, M.M. Applicability of general correlations for CHF in conventional tubes to mini/macro channels. Heat Transf. Eng. 2017, 38, 1–10. [Google Scholar] [CrossRef]
- Zhang, W.; Hibiki, T.; Mishima, K.; Mi, Y. Correlation of critical heat flux for flow boiling of water in mini-channels. Int. J. Heat Mass Transf. 2006, 49, 1058–1072. [Google Scholar] [CrossRef]
- Wojtan, L.; Revellin, R.; Thome, J.R. Investigation of saturated critical heat flux in a single uniformly heated microchannel. Exp. Therm. Fluid Sci. 2006, 30, 765–774. [Google Scholar] [CrossRef]
- Shah, M.M. Improved general correlation for CHF in vertical annuli with upflow. Heat Transf. Eng. 2015, 37, 557–570. [Google Scholar] [CrossRef]
- Katto, Y. Generalized Correlation of Critical Heat Flux for the Forced Convection Boiling in Vertical Uniformly Heated Annuli. Int. J. Heat Mass Transf. 1979, 22, 575–584. [Google Scholar] [CrossRef]
- Doerffer, S.; Groeneveld, D.C.; Cheng, S.C.; Rudzinski, K.F. A Comparison of Critical Heat Flux in Tubes and Annuli. Nucl. Eng. Des. 1994, 149, 167–175. [Google Scholar] [CrossRef]
- Hung, Y.H.; Yao, S.C. Critical Heat Flux of Convective R-113 in Very Narrow Annuli; ASME Paper 83-HT-10; ASME: New York, NY, USA, 1983. [Google Scholar]
- Huber, M.L.; National Bureau of Standards, Washington, DC, USA. Personal communication, 21 November 2022.
- Bell, K.J.; Ghaly, M.A. An approximate generalized method for multicomponent partial condenser. Am. Inst. Chem. Eng. Symp. Ser. 1973, 69, 72–79. [Google Scholar]
- Shah, M.M. A general correlation for CHF in horizontal channels. Int. J. Refrig. 2015, 59, 37–52. [Google Scholar] [CrossRef]
- Gong, S.; Dong, S.; Mei, Y.; Zhang, B.; Yuan, Y.; Zhang, Z. Separate factors’ effects on CHF for flow boiling in an inclined rectangular channel under low mass flux. Appl. Therm. Eng. 2022, 207, 118207. [Google Scholar] [CrossRef]




| Source | D, mm | L/D | Fluid (Mol Fractions) | pr | Glide, K | Δσ, mNm−1 | G | xin | xc | N | Deviation, % MAD (Above)/AD (Below) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shah [23] | Katto and Ohno [16] | Zhang et al. [25] | |||||||||||
| Sindhuja et al. (2008) [25] | 12.7 | 205 | R-407C | 0.6632 | 3.5 | 0.248 | 200 | −0.06 | 0.99 | 1 | 7.4 −7.4 | 4.3 4.3 | 11.7 11.7 |
| Celata et al. (1994) [4] | 7.57 | 277 | R-12/R-114 (0.136/0.864) | 0.3500 0.6770 | 2.1 | 0.081 | 393 1684 | −0.6 −0.2 | 0.24 0.84 | 14 | 27.7 23.3 | 47.2 46.9 | 45.4 44.9 |
| R-12/R-114 (0.377/0.623) | 0.3298 0.6770 | 5.5 | 0.374 | 431 1634 | −0.48 −0.23 | 0.26 0.67 | 14 | 19.4 10.0 | 32.2 31.3 | 34.1 33.0 | |||
| R-12/R-114 (0.586/0.414) | 0.3164 0.6770 | 6.9 | 0.498 | 402 1607 | −0.41 −0.22 | 0.30 0.86 | 14 | 14.0 2.0 | 21.0 20.2 | 24.5 23.4 | |||
| R-12/R-114 (0.787/0.213) | 0.3006 0.6770 | 6.5 | 0.503 | 421 1578 | −0.38 −0.20 | 0.30 0.98 | 14 | 6.9 −3.2 | 15.7 13.7 | 21.1 19.0 | |||
| R-12 | 0.2910 0.6770 | NA | NA | 384 1571 | −0.36 −0.22 | 0.29 0.95 | 14 | 7.0 1.2 | 18.8 17.8 | 25.5 24.2 | |||
| R-114 | 0.3684 0.8597 | NA | NA | 414 1773 | −0.72 −0.26 | 0.01 0.73 | 14 | 9.0 7.8 | 22.1 22.1 | 24.4 16.9 | |||
| All data | 0.2910 0.8597 | 2.1 6.5 | 0.081 0.503 | 200 1773 | −0.48 −0.06 | 0.01 0.99 | 85 | 13.9 6.7 | 25.9 25.1 | 29.0 26.7 | |||
| Source | Din, mm | Gap, mm | L/DHP | Fluid | pr | Glide, K | Δσ, mNm−1 | G Kgm−2s−1 | xin | xc | N | Deviation MAD (Above)/AD (Below) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Andrews et al. (1968) [1] | 6.3 | 7.2 | 1.2 | Benzene–Toluene | 0.021 0.024 | 3.0 6.1 | −0.018 0.109 | 912 3723 | −0.26 −0.19 | −0.19 −0.17 | 16 | 10.1 9.7 |
| Acetone–Toluene | 0.021 0.022 | 4.1 21.0 | 0.445 2.764 | 1705 3583 | −0.15 −0.04 | −0.14 −0.03 | 12 | 26.9 25.7 | ||||
| Acetone | 0.021 | NA | NA | 2450 | −0.13 −0.04 | −0.13 −0.04 | 3 | 30.2 30.2 | ||||
| Toluene | 0.024 | NA | NA | 850 3400 | −0.22 −0.11 | −0.21 −0.05 | 10 | 9.7 9.7 | ||||
| Benzene | 0.020 | NA | NA | 407 3549 | −0.39 −0.20 | −0.39 −0.18 | 9 | 9.6 5.1 | ||||
| Carne (1963) [3] | 6.3 | 6.4 | 1.5 | Acetone–Toluene | 0.046 0.048 | 3.4 21.9 | 0.396 2.680 | 1633 3588 | −0.28 −0.09 | −0.25 −0.08 | 41 | 10.2 5.6 |
| Benzene–Toluene | 0.047 0.053 | 2.8 5.8 | 0.007 0.034 | 1759 3770 | −0.43 −0.21 | −0.43 −0.21 | 46 | 9.3 5.7 | ||||
| Acetone | 0.047 | NA | NA | 1620 3440 | −0.27 −0.10 | −0.27 −0.09 | 16 | 23.7 23.7 | ||||
| Toluene | 0.054 | NA | NA | 1720 3640 | −0.48 −0.13 | −0.46 −0.12 | 13 | 15.6 10.7 | ||||
| Benzene | 0.045 | NA | NA | 1803 3798 | −0.40 −0.21 | −0.39 −0.20 | 16 | 9.6 −0.8 | ||||
| All | 6.3 | 6.4 7.2 | 1.2 1.5 | 0.021 0.053 | 2.8 21.9 | −0.018 2.764 | 407 3798 | −0.48 −0.04 | −0.46 −0.3 | 181 | 13.4 9.8 |
| Parameter | Range |
|---|---|
| Fluids | R-407C; mixtures R-12/R-114, acetone/benzene, acetone/toluene, benzene/toluene (mol fraction of components 0 to 1) |
| Flow channels | Vertical tubes and annuli with upflow |
| Tube diameter, mm | 7.57 to 12.7 |
| Annuli | Internally heated, tube diameter 6.3 mm, gap between tubes 6.4 to 7.2 mm |
| L/DHP | 1.2 to 277 |
| Reduced pressure | 0.021 to 0.677 for mixtures. 0.02 to 0.86 for pure fluids. |
| Mass flux, kgm−2s−1 | 200 to 3798 |
| Glide, K | 2.1 to 21.9 |
| Δσ, mNm−1 | −0.02 to 2.8 |
| Inlet quality | −0.78 to −0.03 |
| Critical quality | −0.46 to 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, M.M. Prediction of Critical Heat Flux of Mixtures Flowing in Channels. Fluids 2023, 8, 90. https://doi.org/10.3390/fluids8030090
Shah MM. Prediction of Critical Heat Flux of Mixtures Flowing in Channels. Fluids. 2023; 8(3):90. https://doi.org/10.3390/fluids8030090
Chicago/Turabian StyleShah, Mirza M. 2023. "Prediction of Critical Heat Flux of Mixtures Flowing in Channels" Fluids 8, no. 3: 90. https://doi.org/10.3390/fluids8030090
APA StyleShah, M. M. (2023). Prediction of Critical Heat Flux of Mixtures Flowing in Channels. Fluids, 8(3), 90. https://doi.org/10.3390/fluids8030090





