Abstract
The aim of this work is to describe an efficient implementation of cubic and multiparameter real gas models in an existing discontinuous Galerkin solver to extend its capabilities to the simulation of turbulent real gas flows. The adopted thermodynamic models are van der Waals, Peng–Robinson, and Span–Wagner, which differ from each other in terms of accuracy and computational cost. Convective numerical fluxes across elements interfaces are calculated with a thermodynamic consistent linearized Riemann solver, whereas for boundary conditions, a linearized expression of the generalized Riemann invariants is employed. Transport properties are treated as temperature- and density-dependent quantities through multiparameter correlations. An implicit time integration is adopted; Jacobian matrix and thermodynamic derivatives are obtained with the automatic differentiation tool Tapenade. The solver accuracy is assessed by computing both steady and unsteady real gas test cases available in the literature, and the effect of the mesh size and polynomial degree of approximation on the solution accuracy is investigated. A good agreement with experimental and numerical reference data is observed and specific non-classical phenomena are well reproduced by the solver.
1. Introduction
Nowadays, the increasing interest of industries towards highly accurate simulation tools motivates the implementation of complex physical models and numerical schemes to reproduce specific phenomena. In this context, non ideal compressible fluid dynamics (NICFD) is still quite a challenging task, mainly because the determination of correct thermophysical properties is crucial to obtain accurate and robust solvers, but also because non-classical behaviors may arise in these flows. Examples can be found in turbomachinery for organic Rankine cycles (ORC), carbon capture and storage (CCS), and refrigeration systems.
During the last decades, many real gas models have been proposed to overcome the limits of the perfect gas law. Actually, the most accurate models are the multi-parameter Helmholtz energy equations of state (MEoSs). Simpler models are available, generally written in terms of cubic polynomials of the density. These cubic equations of state (CEoSs) are widely used, and, sometimes, preferred to MEoSs for the easiness of implementation and use. CEoSs have simpler formulations, require a very limited number of fluid parameters, and their computational cost is an order of magnitude lower than MEoSs. However, for some particular problems or with highly accurate solvers, the adoption of ad hoc models is desirable to obtain accurate predictions.
The aim of the present work is the development of a highly accurate discontinuous Galerkin (dG) solver for the simulation of turbulent real gas flows, where the higher accuracy guaranteed by dG methods is coupled with reliable methods for the calculation of thermodynamic properties. In particular, different thermal EoSs are implemented: (i) the pressure-explicit van der Waals (vdW) [1] and Peng–Robinson (PR) [2] CEoSs, and (ii) the Helmholtz-explicit MEoS of Span–Wagner (SW) [3].
The test cases chosen to asses the new solver performances are (i) an unsteady shock tube problem [4], (ii) a stationary supersonic wedge-shaped channel [5], and (iii) an ORC turbine blade nozzle [6]. Chung et al. model [7] is adopted to compute transport properties.
The implementation of a non ideal EoS in a dG solver requires also the modification of the algorithm to compute the convective numerical flux and the boundary conditions. The dG finite element method (FEM) provides by definition a solution that is discontinuous across elements interfaces in the grid, so a unique value for the convective flux must be determined to guarantee the conservation and the stability of the numerical scheme, just as in finite volume methods (FVM). Many procedures for the computation of the convective numerical flux are available, based on the exact or approximate solution of a Riemann problem, but they assume an ideal behavior of the flow. As a consequence, a thermodynamic generalization is required, and the extension to real gas flows of the Roe’s linearization for the Riemann problem [8] proposed by Vinokur and Montagné [9] is adopted (the average speed of sound at the interfaces is computed according to Glaister [10]). Moreover, a generalized set of boundary conditions has to be determined, especially for inflow/outflow boundaries, which are normally based on the theory of the Riemann invariants. The extension of the Riemann invariants to real gas models is quite complex, and, for this reason, the linearization proposed by Colonna et al. [11] is employed in this work to solve the boundary problem in a consistent and generalized way.
The proposed implementation has been used to extend the prediction capability of the dG-FEM solver MIGALE [12,13,14], whose performance has been already assessed for turbulent flows with ideal behavior. The solver adopts an implicit time integration strategy, and, as a consequence, at each iteration the Jacobian matrix must be computed. In this work, the automatic differentiation (AD) tool Tapenade [15] is used to derive the exact Jacobian matrix to keep the solver able to reach the quadratic convergence speed on stationary problems, which is proper of the Newton-type method. AD has been also employed to derive some complex thermodynamic derivatives.
This paper is organized as follows. First, a brief description of the dG-FEM solver MIGALE is presented from the spatial and temporal points of view (Section 2). Then, all the details of implementation of the real gas models are discussed with a focus on the implementation of the auxiliary procedures (Section 3). After that, the results obtained from the validation test cases are discussed (Section 4) and, in the end, some conclusions are presented (Section 5).
2. Discontinuous Galerkin Solver
In this section, the main features of the dG-solver MIGALE [12,13,14] are outlined. In particular, the governing equations are presented in Section 2.1 and the discretization methods, in space (Section 2.2) and time (Section 2.3), are discussed, with a particular emphasis on the aspect that will be crucial for the implementation of the new thermodynamic models.
2.1. Governing Equations
The set of conservation laws to be solved for inviscid flows is given by the Euler equations, whereas for turbulent flows by the Reynolds-averaged Navier–Stokes (RANS) equations, here supplemented by the turbulence model [12,13,14]. The RANS and model equations can be written using Einstein’s notation as
where is the flow velocity, p the pressure, the density, and
are the total mass-specific internal energy and enthalpy, the turbulent and the overall shear stress tensors, and the overall Fourier’s conductive heat flux, calculated using both a molecular and a turbulent thermal conductivity and , where is the turbulent Prandtl number. The remaining quantities are the mean strain–rate tensor, i.e.,
the turbulent dynamic viscosity , the limited mass-specific turbulent kinetic energy and the logarithm of the specific dissipation rate . , , , , , are the closure parameters [16]. The production term of the energy equation and the destruction term of the k and equations are computed with the value , which satisfies the realizability condition for the turbulent stresses [12]. In this work, no additional terms are added in the turbulence model equations to account for compressibility effects. In fact, this treatment should be considered just for hypersonic flows, i.e., , with cold walls, which are not present in the proposed testcases. A brief review of the possible pressure corrections can be found in [17].
Equations (1)–(5) can then be written in the following compact form as
where is the vector of the unknown variables, and are, respectively, the convective and the viscous flux, and is the vector of the source terms. The matrix takes into account the change of variables from the conservative to the primitive set , where , , and are used to enhance the solver’s robustness [12].
2.2. Spatial Discretization
The weak formulation of the problem is obtained by multiplying Equation (10) by an arbitrary smooth test function and integrating by parts over a physical domain , with m being the total number of unknowns. Once a proper triangulation of the approximated domain in arbitrary shaped non-overlapping elements having the set of faces is given, the discrete weak problem is obtained by substituting the continuous solution and the continuous test function with their discrete finite element approximations and , each one belonging to the discrete polynomial space expressed in physical coordinates.
The set of test and shape functions in every element is chosen here as the set of orthonormal and hierarchical basis functions having compact support over K, defined from its principal inertial axes and with being the total number of degrees of freedom of the solution in K. Each component of the discrete elemental solutions , with , can then be expressed as the linear combination , with and . The direct sum of all the discrete elemental solutions over represents the global discrete solution, which is the objective of the solver. The dG-FEM spatial discretization of the governing equations consists therefore in seek, at every time instant, the elements of the degrees of freedom’s vector with being the total number of elements, such that for and , they represent the solution of the semi-discrete weak problem
As the functional approximation is discontinuous, the sum of the convective and viscous flux functions is not uniquely defined at each element’s interface, so a numerical flux vector is adopted. The convective part is based on the local solution of linearized Riemann problems, using the Roe solver [8] generalized to the case of an arbitrary gas model with the Vinokur-Montagné approach [9] and Glaister’s [10] generalized average speed of sound. The viscous part is instead centered and discretized with the BR2 scheme [18], by employing either local and global lifting operators and on the solution’s componentwise jump across mesh interfaces. In this sense, denotes the outward or inward pointing unit vector normal to the interface, whereas is the stability parameter of Brezzi et al. [19].
To avoid spurious oscillations of the solution, an artificial diffusion contribution is introduced inside each element using a shock sensor to detect discontinuities. The shock-capturing term is added to the left-hand side of Equation (11), and, as reported in [14,20], is given by
where is a unit vector representing the direction along which the dissipation is acting. In this work, is given by the logarithmic pressure gradient,
where is a small value proportional to the machine precision. In Equation (12), is the artificial diffusion coefficient defined in each element as
where C is a user-defined constant, is a characteristic dimension of the element K, and is a pressure-based shock sensor defined through the global lifting operator as
is always active in every element, but the numerical viscosity is introduced only in regions where unphysical oscillations are present. The remaining terms and in Equation (14) introduce also the dependence of the numerical viscosity from the magnitude of the divergence of the convective flux and from the polynomial degree of discretization, respectively.
2.3. Temporal Discretization
Assembling the elemental contribution of Equation (11), the following system of ordinary differential Equations (ODEs) in time is obtained
where is the vector of the global residuals and is the global block diagonal mass matrix arising from the calculation of the first integral in Equation (11). The Linearized Backward Euler (LBE) scheme with a pseudo-transient continuation strategy for stationary problems is adopted to solve Equation (16) [21], which can be written as
When the final solution is steady, an exponential CFL law, the function of the residuals norms, enables the usage of progressively higher values of that reduce Equation (17) to a Newton–Rhapson method, which guarantees quadratic convergence rates, once an exact Jacobian matrix is provided at every timestep n. The algebraic system described by Equation (17) is nonlinear, and an iterative solver is required . In this work, a restarted version of the generalized minimal residual (GMRES) Krylov’s subspace-type method is used, as available in the PETSc library [22]. These kinds of methods have been extensively used and developed during the last decades [23] for their generality and robustness. They are still the subject of intense research activity to improve their convergence speeds through techniques such as globalization [24], efficient preconditioning [25], and Jacobian approximation [26]. Here, the GMRES convergence is enhanced by system preconditioning; MIGALE allows us to choose the block Jacobi method with one block per process, each of which is solved with ILU(0), or the additive Schwarz method (ASM), as available in the PETSc library. The ASM [27] is used for the simulation presented in this work.
Devising an effective and robust strategy to increase the CFL number as the residual decreases is far from trivial, especially for transitional or turbulent simulations, an empirically determined “CFL law” is here used to speed up convergence. It is based on the and norms of the residual and depends on three user-defined parameters. The first and second ones are and to set the minimum and maximum limits of the CFL number during the simulation. The third one is an exponent governing the growth rate of the CFL number, where typically . The “CFL law” is
where is the minimum value between the maximum CFL number proper of an explicit scheme and the user-defined minimum value, with q being the polynomial degree of discretization of the solution. The remaining terms are and , which is defined as
where and are the and norms of the residual vector of the i-th equation of the system and is the corresponding residual at the first iteration.
3. Thermodynamic Models
The MIGALE solver’s predicting capabilities are extended with three real gas models: the pressure-explicit CEoSs of van der Waals [1] and Peng–Robinson [2] (Section 3.1) and the Helmholtz-explicit MEoS of Span–Wagner [3] (Section 3.2). MEoSs generally require more coefficients with respect to CEoSs and their computational cost is, therefore, much higher. On the other hand, they also guarantee superior accuracy for thermodynamic quantities whose values are crucial during a fluid dynamic simulation, such as the speed of sound. The implementation of all models is discussed, also describing modifications needed by other algorithms of the solver, such as the numerical flux computation and boundary conditions (Section 3.3 and Section 3.4).
3.1. Peng–Robinson and van der Waals Models
The pressure-explicit CEoSs of van der Waals [1] and Peng–Robinson [2] can be obtained from the general formulation [28] as
where p is the fluid pressure, the density, T the temperature, the mass-specific gas constant, the universal gas constant, and the fluid’s molecular weight. Equation (20) shows also the term , which accounts for intermolecular attractions, and the terms B, C, and D that account for molecular volume. The term A is usually written as , where the function (if not null) contains the dependence of from the molecular shape, whereas a is a constant. For all models that can be obtained from Equation (20), A, B, C, and D assume different values, depending on the working fluid. In fact, they depend from some input parameters, which are the critical pressure and temperature , the molecular weight, and the acentric factor , which is an estimation of the non-sphericity of the molecules defined as , where , , and is the saturation pressure. Table 1 summarizes the expressions that must be used for A, B, C, and D to obtain the van der Waals and the Peng–Robinson gas models, which are given by

Table 1.
Expressions for all the quantities involved in Equation (20).
If the ideal gas law is recovered.
Starting from these equations, a complete characterization of a pure single-phase substance comes from the determination of at least one caloric EoS for each model [29]. A general procedure for any thermal pressure-explicit EoS like the one in Equation (20) is given by Reynolds [30]. The expression for the mass-specific internal energy takes the form
whereas the mass-specific entropy is
where and are used as symbolic substitutes of and T in the integral functions and identifies an arbitrary reference state. The last terms in both Equations (22) and (23) represent departure functions from the non-polytropic ideal gas behavior since they vanish for sufficiently rarefied thermodynamic states, i.e., . The remaining two integrals require instead an expression for the ideal gas contribution to the isochoric specific heat , which is by definition the limit of as . In this work, a polynomial function of the absolute temperature in the form is employed for each considered fluid, where is the ideal gas contribution to the isobaric specific heat. Coefficients for can be determined theoretically from chemical group contribution methods such as the one in [31], or from given polynomial fittings of experimental data available in the literature.
Once the expressions for and are known, all the other relevant thermodynamic properties can be determined using a combination of them and of their derivatives. For example, by definition the mass-specific enthalpy and real gas isochoric specific heat are obtained as
As reported in [32], the real gas isobaric specific heat and the speed of sound are obtained from
Another important quantity that must be determined is the fundamental derivative of gas dynamics , that following the work of Cramer [33] can be again expressed as a function of temperature and density only, as
This derivative is crucial in real gas dynamics, since with negative values of some non-classical phenomena may arise, such as expansion shocks or compression fans [34].
Lastly, since the solver works with p and T as independent variables, the computation of the inverse problem is needed, as
The fluid density is determined from the equation for the pressure. When the models are derived by Equation (20), the thermal EoS can be reformulated as a third-degree polynomial in the density, whose coefficients are a function of temperature and pressure, i.e., , with for . The analytical resolution method of Cardano is employed in this work, whereas the physical meaning and validity of each root have been determined using the considerations in [35]. For temperature, some Newton’s iterations are employed on the functions and , since their derivatives are known and the resulting formulation is more complicated. Initial guesses are calculated using the polytropic ideal gas model with .
3.2. Span–Wagner Model
The Helmholtz-explicit MEoS of Span–Wagner [3] is formulated in terms of an optimized functional fit of experimental measurements, which can be derived for any fluid having a sufficiently wide and precise range of data [36]. The derived EoS is formulated for the free Helmholtz energy state function , described in a non-dimensional form with the summation of an ideal gas contribution and a real gas residual as
where is the reduced density and is the inverse of the reduced temperature. In Equation (28), the dimensional ideal gas part is defined as
since for the ideal gas . So, once a suitable approximation of is provided, can be completely determined by computing two integrals. In this work, four different functional forms can be activated by the user, since is implemented as
where each term represents an approximation of a statistical mechanical behavior of the ideal gas heat capacity as suggested by Aly and Lee [37]. In Equation (30), coefficients are considered as user parameter, since many functional fittings can be found in the literature. The non-dimensional residual part of Equation (28) is similarly provided as a summation of various activatable terms as
with and where the last Gaussian bell-shaped sums are generally used to improve the fluid description near the critical point [36].
Thanks to the Helmholtz energy definition, all the other relevant thermodynamic properties can be computed with Maxwell’s relations, such as
whereas Equations (24)–(26) still hold for the calculation of the enthalpy, specific heats, speed of sound, and fundamental derivative. The inverse problem of Equation (27) is here treated with Newton’s iterations also for the density, but since the number of roots may be higher than the CEoS case, some efficient initial guesses are chosen as suggested by Span [36]. In particular, the initial guess for the density is provided by the Peng–Robinson model, whose coefficients are calculated and stored once. For the temperature, a simplified version of the van der Waals model with a power law ideal gas-specific heat is analytically inverted. The adopted expression is , where and as suggested by [33]. Furthermore, the van der Waals coefficients are calculated and stored before computations.
3.3. Derivatives
The first and second derivatives of the thermodynamic properties are needed for the Jacobian matrix of the implicit time integration scheme, the shock-capturing term, the permutation matrix, and the convective fluxes. In particular, the following derivatives must be provided:
where can represent e, h, c, s, , . Since all the properties are formulated as functions of and T, the exact expressions of their first and second derivatives with respect to these variables are obtained with the AD tool Tapenade [15]. Then, using the relations from [38], which involve just the derivatives of , the values of
are calculated. Thanks to the chain rule on , and considering that , where y can be either p or T, the last five derivatives in Equation (33) can be rewritten as
The first two derivatives in Equation (33) are determined as suggested by Cinnella [39]. However, despite Equations (35)–(39) being valid for all the chosen EoSs, the Span–Wagner model requires a further step, i.e., the computation of all the pure and mixed derivatives, from the first to the third order of the non-dimensional Helmholtz energy state function. This task is here performed with the AD tool Tapenade [15].
3.4. Numerical Fluxes and Boundary Conditions
The first thermodynamic generalization required by the solver is the adoption of a consistent numerical flux for real gas computations. In this work, the generalization of the approximate Riemann solver of Roe [8] proposed by Vinokur-Montagné [9] is used for the convective part. This procedure differs from the original Roe version since in the real gas regime the description of the Roe averaged state must be enriched with the definition of averaged values of the pressure derivatives and between the two sides of every mesh interface. These values are here obtained following the procedure proposed by Glaister [10] and then used to generalize the Roe averaged a speed of sound for the determination of convective eigenvalues.
For the viscous part, the generalized multiparameter correlation of Chung et al. [7] for the determination of transport properties in real gas regime is applied. In particular, the procedure allows for estimating reliable values of the molecular dynamic viscosity and thermal conductivity of polar and non-polar fluids as functions of and T. The required additional input data are the critical density , the dipole moment of the fluid molecules, and the equilibrium dissociation constant of the substance.
The contribution of the new flux to the global Jacobian matrix is computed with the AD tool Tapenade [15], an open source algorithm developed by the Institut National de Recherche en Sciences et Technologies du Numérique (INRIA). AD guarantees that every derivative will be mathematically exact and will not suffer any truncation error, which is typical of the finite differences (FD) approach [40]. In fact, every derivative is obtained with a symbolic optimized differentiation of all the lines of a source code, to generate a new program that will contain the calculations for both the original outputs and their derivatives. This is made possible by an iterative application of the chain rule of differentiation since the whole source code is interpreted as a composite function of all its lines. The chain can be traveled from top to bottom with the tangent (or direct) differentiation mode or from bottom to top with the adjoint (or reverse) mode (see [15] for further details). In this work, the tangent mode has been used, since it is best suited for large amounts of inputs and is easy to use. In particular, the focus is on the term in Equation (11), where and are the unknown variables at the inner and outer side of an element face. The Jacobian matrix of is generated column by column, differentiating one time in tangent mode for every component of and . Every column is then wrapped with the others to assemble the Jacobian matrix. This often results in an increment of the computational cost with respect to manually derived analytical procedures, which are often difficult to obtain. In this work, an ad hoc automated strategy for the use of Tapenade has been derived, that is able to scan and modify the generated routines to avoid or regroup redundant computations. The new Jacobian matrix is thus characterized by a lower computational cost with respect to FD, especially when the thermodynamic or physical complexity is high. Table 2 reports the time required to perform calls to the routines to build the Jacobian matrix of an inviscid two-dimensional convective flux and a three-dimensional turbulent diffusive flux. AD is always less expansive than the FD counterpart, and shows a maximum reduction in the computing time .

Table 2.
Time required for the evaluation of the Jacobian matrix of some routines through AD and FDs with ideal gas law.
The second generalization concerns inflow and outflow boundary conditions, which are implemented following the work of Colonna and Rebay [11]. The approach relies on the determination of a linearized form of the Riemann invariants, that allows the imposition of the proper set of physical quantities at every boundary face in both subsonic and supersonic regimes, for both incoming and outgoing flows. The contribution to the global Jacobian matrix of the residual is also here derived with Tapenade [15], following the same approach described for the convective and viscous fluxes.
4. Results
In this section, the results obtained with the new solver are discussed and the predicted solutions are compared with available experimental and numerical reference data.
4.1. Unsteady Shock Tube
The first case consists of the Euler solution of a one-dimensional Riemann problem proposed by Guardone et al. [4] for the fluid PP10 (). The aim of the original setup is to reproduce and capture a non-classical expansion shock at a precise time instant and spatial location. The length of the tube is 5 m, which is divided into 400 uniform elements. At m, a diaphragm separates two regions, where the fluid is at different densities and pressure, as reported in Table 3. At time s the diaphragm is removed and a right-running compression shock wave, a contact discontinuity, and a left-running rarefaction shock wave start to travel along the tube. Peng–Robinson EoS is used against the Martin–Hou (MH) model employed by Guardone et al. [4] and a second-order approximation is adopted for the spatial discretization.

Table 3.
Shock tube. Setup for shock tube case [4]. Temperatures are computed with Peng–Robinson EoS.
The simulation is stopped at s and Figure 1 shows the density and pressure profiles. The initial condition resulted in an almost isothermal domain and one-dimensional wave propagation is well captured by the solver. In particular, a rarefaction shock is observed, as expected, and oscillations of the solution in the neighborhood of discontinuities are kept small thanks to the shock-capturing term. In this case, the polynomial degrees and the number of mesh elements do not influence the predicted result, whereas a sufficiently low value for the maximum “CFL” number is mandatory to achieve a satisfactory accuracy in time, since the adopted time integration scheme, i.e., the LBE scheme, has a higher truncation error.
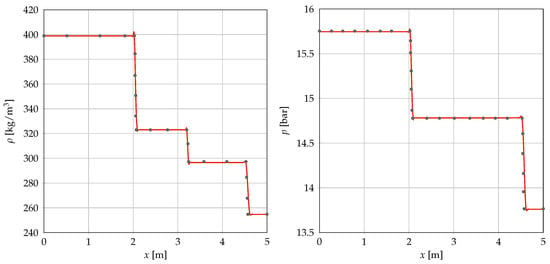
Figure 1.
Shock tube. Density and pressure profiles at time s.  Guardone MH EoS [4],
Guardone MH EoS [4],  PR EoS.
PR EoS.
 Guardone MH EoS [4],
Guardone MH EoS [4],  PR EoS.
PR EoS.
4.2. Supersonic Wedge
The second case consists of a supersonic inviscid flow of supercritical gaseous MDM () in a wedge-shaped channel. The free stream Mach number at the entry of the domain is , whereas pressure and density are 15 bar and kg/m3, respectively. The temperature is K, calculated in this condition from Equation (21). The original problem is used by Pini et al. [5] to assess the performances of the code SU2 using the van der Waals EoS, which allows for predicting a negative zone for MDM where non-classical phenomena are possible. Different simulations have been performed for different polynomial degrees and a number of mesh elements: (i) 42,000 elements and solution approximation, (ii) 2650 elements and solution approximation, and (iii) 42,000 elements and solution approximation. The total number of degrees of freedom for every solution can be calculated in this case as
where q is the polynomial degree of the discretization, m the number of unknowns, and the number of elements.
The angle formed by the rarefaction shock is reported together with the solution parameters in Table 4, whereas the value of the same angle from the theoretical relation reported by Pini et al. [5] is
where subscripts u and d refer to the quantities upstream and downstream from the shock, respectively. Furthermore, Figure 2 shows the Mach number contours obtained for each solution. As expected, a reasonable accuracy is obtained even on very coarse grids, thanks to the high-order dG spatial discretization. Figure 2 shows as increasing the spatial resolution, both in terms of mesh density and polynomial approximation, the discontinuity given by the shock can be confined in a narrower stripe of elements. Furthermore, for this case, the non-classical behavior is well captured.

Table 4.
Wedge. Angles for the rarefaction shock in the wedge-shaped channel case.
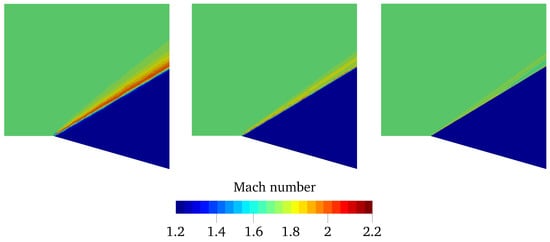
Figure 2.
Wedge. Mach number contours predicted with the following set of mesh elements and polynomial order: 42,400 and (left), 2650 and (center), and 42,400 and (right).
4.3. ORC Turbine Nozzle
The last problem investigated is the turbulent flow through an ORC turbine nozzle (the geometry has been provided by Turboden) with the Siloxane MDM as working fluid. The operating condition is characterized by a total inlet pressure of 8 bar, a total inlet temperature of °C, and a total to static pressure ratio of 6. An inviscid two-dimensional solver was used by Colonna et al. [6], with a Span–Wagner-type MEoS given in the form of Equation (28), whose coefficients are given in [41]. The same thermodynamic model is used in this work, but the RANS equation coupled with the k- turbulence model are solved on a quasi 3D domain, as the mesh is two-dimensional and it is extruded on one element in the third direction. The grid is unstructured with 5305 elements, as shown in Figure 3. At the inflow, the total temperature, the total pressure, the flow angle , and the turbulence intensity are prescribed, whereas at the outflow, the static pressure is set. Blade wall is considered adiabatic.

Figure 3.
ORC nozzle. Mesh of the blade channel, 5305 hybrid elements (hexahedral in the boundary layer and prisms outside). The geometry is distorted because the blade design is confidential property of the manufacturer.
All computations are performed for a solution approximation and a convergence tolerance of on the residuals norm is reached for every equation. All the computations have been run in parallel, initialising the solution from the uniform flow at outflow conditions and the higher order solutions from the lower order ones. Figure 4 shows the convergence history of the simulation with PR EoS.
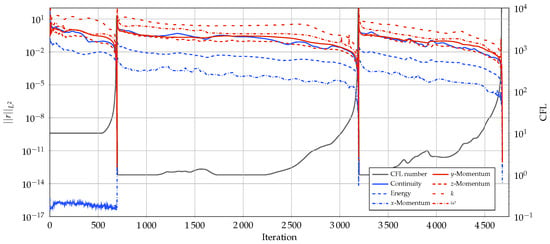
Figure 4.
ORC nozzle. Convergence history of the simulation with PR EoS.
Figure 5 shows the Mach number and compressibility factor contours of a mesh section for the solution employing SW model. Some spurious reflections appear at the outflow boundary and pollute a bit the solution for the lack of non-reflective boundary conditions. However, the main structures of the flow field are captured and well-represented by the solver. Figure 6 (left) compares the predicted pressure coefficient distribution along the blade with the reference numerical data by Colonna et al. [6]. Curves obtained with Peng–Robinson and ideal gas EoS are also added to highlight the effect of different thermodynamic models. The matching with the available reference data is satisfactory and the small differences can be ascribed to the different set of Equations (Euler for reference and RANS for present computations). Figure 6 (right) shows also the value of the non-dimensional wall shear stress along the blade for the three models. Both figures demonstrate an almost perfect matching between PR and SW curves, whereas some differences are evident when using the ideal gas law. More differences between SW/PR models and ideal gas EoS can be seen from the pitch-wise distribution at the outflow section for the flow angle, the Mach number, and the total pressure loss coefficient , as shown in Figure 7. The computations reveal a very similar behavior between Peng–Robinson and Span–Wagner models, whereas the ideal gas EoS shows a very different distribution for the Mach number and the total pressure loss coefficient distributions. In particular, the ideal gas EoS predicts higher peaks in the Mach number distribution, whereas the loss coefficient is lower. These trends are confirmed also by the mixed-out quantities, as reported in Table 5. The mixed-out values for these quantities are calculated for the generic property x with the mass flow average , where A is the outflow section.
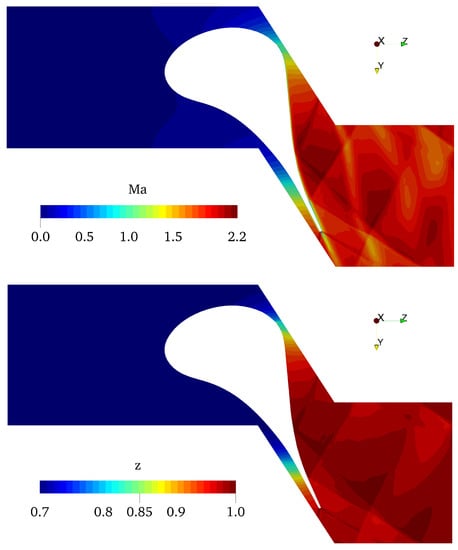
Figure 5.
ORC nozzle. Mach number (top) and compressibility factor (bottom) contours, solution. Distorted geometries are depicted because the blade design is confidential property of the manufacturer.
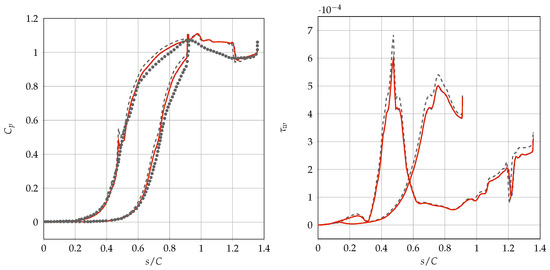
Figure 6.
ORC nozzle. Pressure coefficient (left) and non-dimensional wall shear stress (right) distributions along the blade profile.  Colonna et al. [6] 2D Euler,
Colonna et al. [6] 2D Euler,  RANS IG EoS,
RANS IG EoS,  RANS PR EoS,
RANS PR EoS,  RANS SW EoS.
RANS SW EoS.
 Colonna et al. [6] 2D Euler,
Colonna et al. [6] 2D Euler,  RANS IG EoS,
RANS IG EoS,  RANS PR EoS,
RANS PR EoS,  RANS SW EoS.
RANS SW EoS.
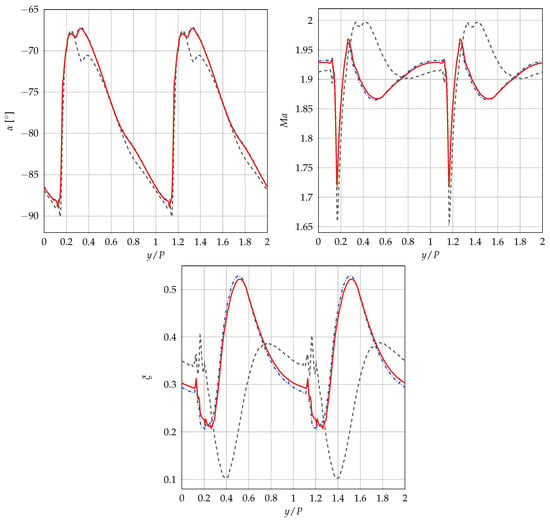
Figure 7.
ORC nozzle. Outlet flow angle (top left), Mach number (top right), and total pressure loss coefficient (bottom) pitch-wise distribution.  RANS IG EoS,
RANS IG EoS,  RANS PR EoS,
RANS PR EoS,  RANS SW EoS.
RANS SW EoS.
 RANS IG EoS,
RANS IG EoS,  RANS PR EoS,
RANS PR EoS,  RANS SW EoS.
RANS SW EoS.

Table 5.
ORC nozzle. Mixed-out values of the flow angle, Mach number, and total pressure loss coefficient with various thermodynamic models, solution approximation.
5. Conclusions and Future Works
A dG-FEM solver with complex thermodynamic models is developed and assessed with reference literature problems characterized by classical and non-classical gas dynamics phenomena. Cubic and multiparameter equations of state are implemented to achieve the best possible accuracy in the determination of thermophysical and transport properties in a RANS framework. A good agreement of results with respect to the reference is obtained and non-classical real gas dynamic phenomena are well captured by the solver.
Future works will cover the implementation of ad hoc numerical procedures, with the aim of achieving a systematical use of the solver for the design process of ORC turbomachinery, e.g., non-reflective boundary conditions and mixing-planes. The generation and use of efficient look up tables to speed up computations with heavy gas models will also be evaluated.
Author Contributions
Conceptualization, A.C. and A.G.; methodology, E.M.; software, A.C. and A.G.; validation, E.M.; formal analysis, E.M.; investigation, E.M.; resources, S.R.; data curation, E.M. and G.N.; writing—original draft preparation, E.M. and G.N.; writing—review and editing, E.M. and G.N.; visualization, E.M.; supervision, A.C., A.G., and D.P.; project administration, A.C. and A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request due to restrictions, e.g., privacy or ethical.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NICFD | Non ideal compressible fluid dynamics |
| ORC | Organic Rankine cycle |
| CCS | Carbon capture and storage |
| EoS | Equation of state |
| CEoS | Cubic equation of state |
| MEoS | Multiparameter equation of state |
| dG | Discontinuous Galerkin |
| vdW | van der Waals |
| PR | Peng–Robinson |
| SW | Span–Wagner |
| MH | Martin–Hou |
| FEM | Finite element method |
| FVM | Finite volume method |
| dG-FEM | Discontinuous Galerkin finite element method |
| LBE | Linearized backward Euler |
| AD | Automatic differentiation |
| GMRES | Generalized minimal residual |
| ASM | Additive Schwarz method |
| FD | Finite differences |
| RANS | Reynolds-averaged Navier–Stokes |
| ODE | Ordinary differential equation |
References
- Van der Waals, J. The equation of state for gases and liquids. Nobel Lect. Phys. 1910, 1, 254–265. [Google Scholar]
- Peng, D.; Robinson, D. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Span, R.; Wagner, W. A New Equation of State for Carbon Dioxide Covering the Fluid Region from the Triple-Point Temperature to 1100 K at Pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. [Google Scholar] [CrossRef]
- Guardone, A.; Vigevano, L.; Argrow, B.M. Assessment of thermodynamic models for dense gas dynamics. Phys. Fluids 2004, 16, 3878–3887. [Google Scholar] [CrossRef]
- Pini, M.; Vitale, S.; Colonna, P.; Gori, G.; Guardone, A.; Economon, T.; Alonso, J.; Palacios, F. SU2: The Open-Source Software for Non-ideal Compressible Flows. J. Phys. Conf. Ser. 2017, 821, 012013. [Google Scholar] [CrossRef]
- Colonna, P.; Harinck, J.; Rebay, S.; Guardone, A. Real-Gas Effects in Organic Rankine Cycle Turbine Nozzles. J. Propuls. Power 2008, 24, 282–294. [Google Scholar] [CrossRef]
- Chung, T.H.; Ajlan, M.; Lee, L.L.; Starling, K.E. Generalized multiparameter correlation for nonpolar and polar fluid transport properties. Ind. Eng. Chem. Res. 1988, 27, 671–679. [Google Scholar] [CrossRef]
- Roe, P. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Vinokur, M.; Montagné, J. Generalized flux-vector splitting and Roe average for an equilibrium real gas. J. Comput. Phys. 1990, 89, 276–300. [Google Scholar] [CrossRef]
- Glaister, P. An approximate linearised riemann solver for the Euler equations for real gases. J. Comput. Phys. 1988, 74, 382–408. [Google Scholar] [CrossRef]
- Colonna, P.; Rebay, S. Numerical simulation of dense gas flows on unstructured grids with an implicit high resolution upwind Euler solver. Int. J. Numer. Methods Fluids 2004, 46, 735–765. [Google Scholar] [CrossRef]
- Bassi, F.; Botti, L.; Colombo, A.; Crivellini, A.; Ghidoni, A.; Nigro, A.; Rebay, S. Time Integration in the Discontinuous Galerkin Code MIGALE—Unsteady Problems. In IDIHOM: Industrialization of High-Order Methods—A Top-Down Approach: Results of a Collaborative Research Project Funded by the European Union, 2010–2014; Springer International Publishing: Cham, Switzerland, 2015; pp. 205–230. [Google Scholar] [CrossRef]
- Bassi, F.; Botti, L.; Colombo, A.; Crivellini, A.; De Bartolo, C.; Franchina, N.; Ghidoni, A.; Rebay, S. Time Integration in the Discontinuous Galerkin Code MIGALE—Steady Problems. In IDIHOM: Industrialization of High-Order Methods—A Top-Down Approach: Results of a Collaborative Research Project Funded by the European Union, 2010–2014; Springer International Publishing: Cham, Switzerland, 2015; pp. 179–204. [Google Scholar] [CrossRef]
- Bassi, F.; Botti, L.; Colombo, A.; Crivellini, A.; Franchina, N.; Ghidoni, A. Assessment of a high-order accurate Discontinuous Galerkin method for turbomachinery flows. Int. J. Comput. Fluid Dyn. 2016, 30, 307–328. [Google Scholar] [CrossRef]
- Hascoet, L.; Pascual, V. The Tapenade Automatic Differentiation Tool: Principles, Model, and Specification. ACM Trans. Math. Softw. 2013, 39, 20. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modelling for CFD; DCW Industries Inc.: La Cañada, CA, USA, 2006. [Google Scholar]
- Rumsey, C.L. Compressibility Considerations for k-w Turbulence Models in Hypersonic Boundary-Layer Applications. J. Spacecr. Rocket. 2010, 47, 11–20. [Google Scholar] [CrossRef]
- Bassi, F.; Rebay, S.; Mariotti, G.; Pedinotti, S.; Savini, M. A high-order accurate discontinuous finite element method for inviscid and viscous turbomachinery flows. In Proceedings of the 2nd European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Antwerpen, Belgium, 5–7 March 1997; pp. 99–109. [Google Scholar]
- Arnold, D.N.; Brezzi, F.; Cockburn, B.; Marini, L.D. Unified Analysis of Discontinuous Galerkin Methods for Elliptic Problems. SIAM J. Numer. Anal. 2002, 39, 1749–1779. [Google Scholar] [CrossRef]
- Bassi, F.; Botti, L.; Colombo, A.; Crivellini, A.; Franchina, N.; Ghidoni, A.; Rebay, S. Very High-Order Accurate Discontinuous Galerkin Computation of Transonic Turbulent Flows on Aeronautical Configurations. In ADIGMA—A European Initiative on the Development of Adaptive Higher-Order Variational Methods for Aerospace Applications; Springer: Berlin/Heidelberg, Germany, 2010; pp. 25–38. [Google Scholar]
- Bassi, F.; Ghidoni, A.; Perbellini, A.; Rebay, S.; Crivellini, A.; Franchina, N.; Savini, M. A high-order Discontinuous Galerkin solver for the incompressible RANS and k–ω turbulence model equations. Comput. Fluids 2014, 98, 54–68. [Google Scholar] [CrossRef]
- PETSc Web Page. 2018. Available online: https://petsc.org (accessed on 2 January 2023).
- Zou, Q. GMRES algorithms over 35 years. Appl. Math. Comput. 2023, 445, 127869. [Google Scholar] [CrossRef]
- Pawlowski, R.P.; Shadid, J.N.; Simonis, J.P.; Walker, H.F. Globalization Techniques for Newton–Krylov Methods and Applications to the Fully Coupled Solution of the Navier–Stokes Equations. SIAM Rev. 2006, 48, 700–721. [Google Scholar] [CrossRef]
- Pearson, J.W.; Pestana, J. Preconditioners for Krylov subspace methods: An overview. GAMM-Mitteilungen 2020, 43, e202000015. [Google Scholar] [CrossRef]
- Yildirim, A.; Kenway, G.K.; Mader, C.A.; Martins, J.R. A Jacobian-free approximate Newton–Krylov startup strategy for RANS simulations. J. Comput. Phys. 2019, 397, 108741. [Google Scholar] [CrossRef]
- Cai, X.C.; Sarkis, M. A Restricted Additive Schwarz Preconditioner for General Sparse Linear Systems. SIAM J. Sci. Comput. 1999, 21, 792–797. [Google Scholar] [CrossRef]
- Martin, J.J. Cubic Equations of State-Which? Ind. Eng. Chem. Fundam. 1979, 18, 81–97. [Google Scholar] [CrossRef]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics, 2nd ed.; Wiley: Hoboken, NJ, USA, 1985. [Google Scholar]
- Reynolds, W. Thermodynamic Properties in SI: Graphs, Tables, and Computational Equations for Forty Substances; Stanford University, Department of Mechanical Engineering: Stanford, CA, USA, 1979. [Google Scholar]
- Poling, B.; Prausnitz, J.; O’Connell, J. The Properties of Gases and Liquids 5E; McGraw-Hill Education: Columbus, OH, USA, 2000. [Google Scholar]
- Hanimann, L.; Mangani, L.; Casartelli, E.; Vogt, D.M.; Darwish, M. Real Gas Models in Coupled Algorithms Numerical Recipes and Thermophysical Relations. Int. J. Turbomach. Propuls. Power 2020, 5, 20. [Google Scholar] [CrossRef]
- Cramer, M. Negative nonlinearity in selected fluorocarbons. Phys. Fluids A Fluid Dyn. 1989, 1, 1894–1897. [Google Scholar] [CrossRef]
- Argrow, B.M. Computational analysis of dense gas shock tube flow. Shock Waves 1996, 6, 241–248. [Google Scholar] [CrossRef]
- Lawal, A.S. A consistent rule for selecting roots in cubic equations of state. Ind. Eng. Chem. Res. 1987, 26, 857–859. [Google Scholar] [CrossRef]
- Span, R. Multiparameter Equations of State; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Aly, F.A.; Lee, L.L. Self-consistent equations for calculating the ideal gas heat capacity, enthalpy, and entropy. Fluid Phase Equilibria 1981, 6, 169–179. [Google Scholar] [CrossRef]
- Thorade, M.; Saadat, A. Partial derivatives of thermodynamic state properties for dynamic simulation. Environ. Earth Sci. 2013, 70, 3497–3503. [Google Scholar] [CrossRef]
- Cinnella, P. Roe-type schemes for dense gas flow computations. Comput. Fluids 2006, 35, 1264–1281. [Google Scholar] [CrossRef]
- Liu, B.; Wu, Y.; Guo, J.; Zhang, H.; Niu, J.; Li, F. Finite difference Jacobian based Newton–Krylov coupling method for solving multi-physics nonlinear system of nuclear reactor. Ann. Nucl. Energy 2020, 148, 107670. [Google Scholar] [CrossRef]
- Colonna, P.; Nannan, N.; Guardone, A. Multiparameter equations of state for siloxanes: [(CH3)3-Si-O1/2]2-[O-Si-(CH3)2]i=1,...,3, and [O-Si-(CH3)2]6. Fluid Phase Equilibria 2008, 263, 115–130. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).