Comparison of Vortex Cut and Vortex Ring Models for Toroidal Bubble Dynamics in Underwater Explosions
Abstract
1. Introduction
2. Theories and Numerical Methods
2.1. Boundary Integral Method
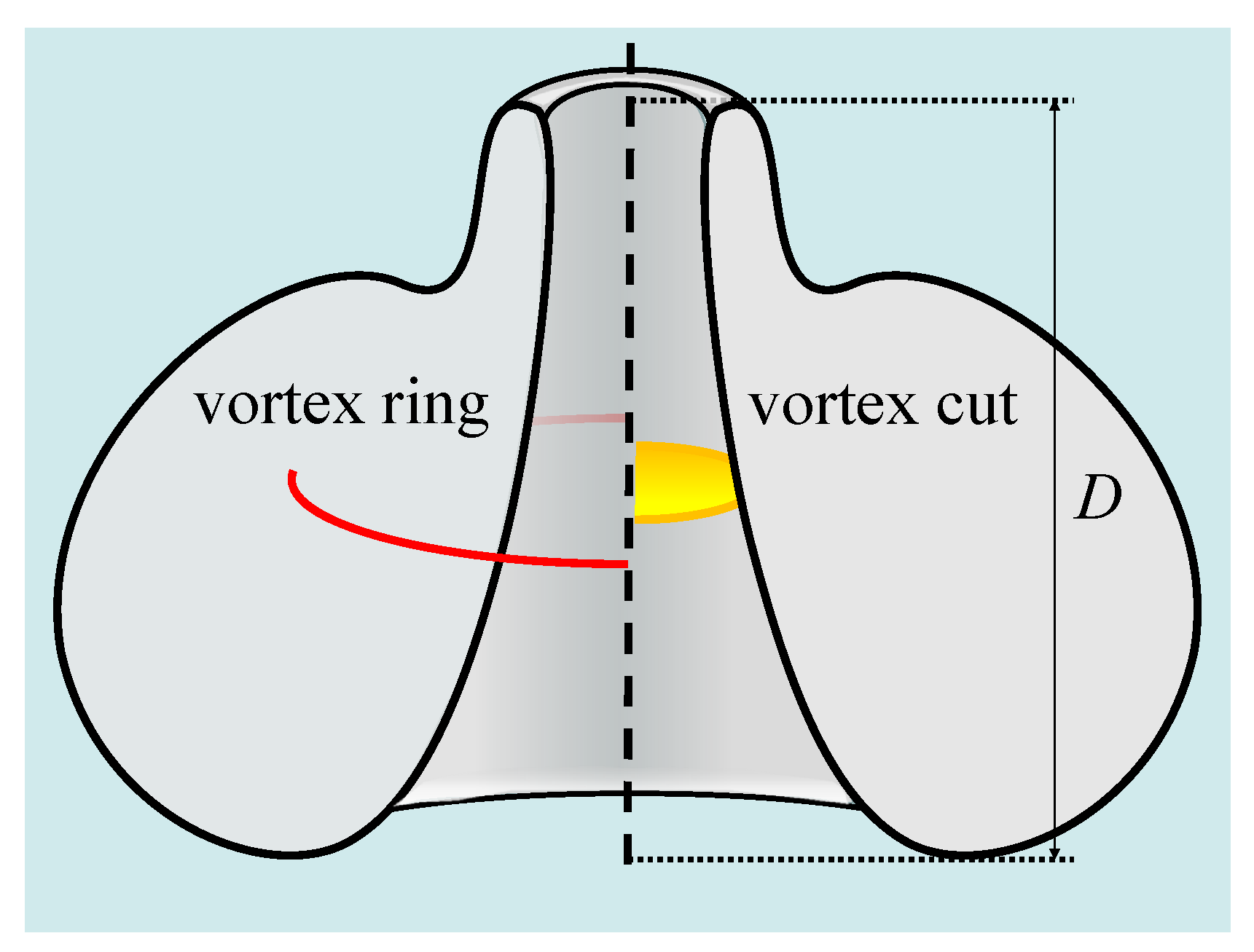
2.2. Vortex Cut Model
2.3. Vortex Ring Model
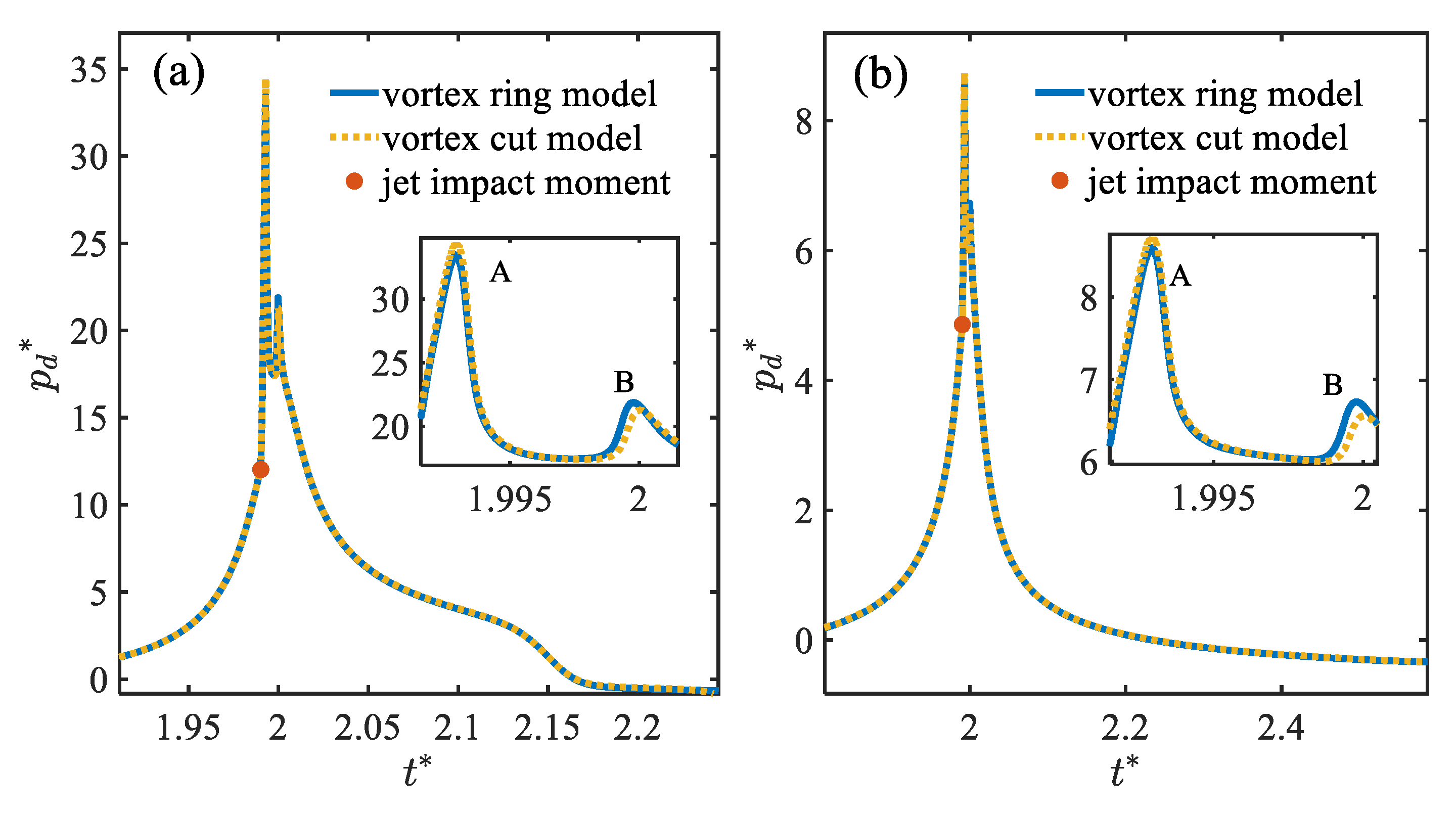
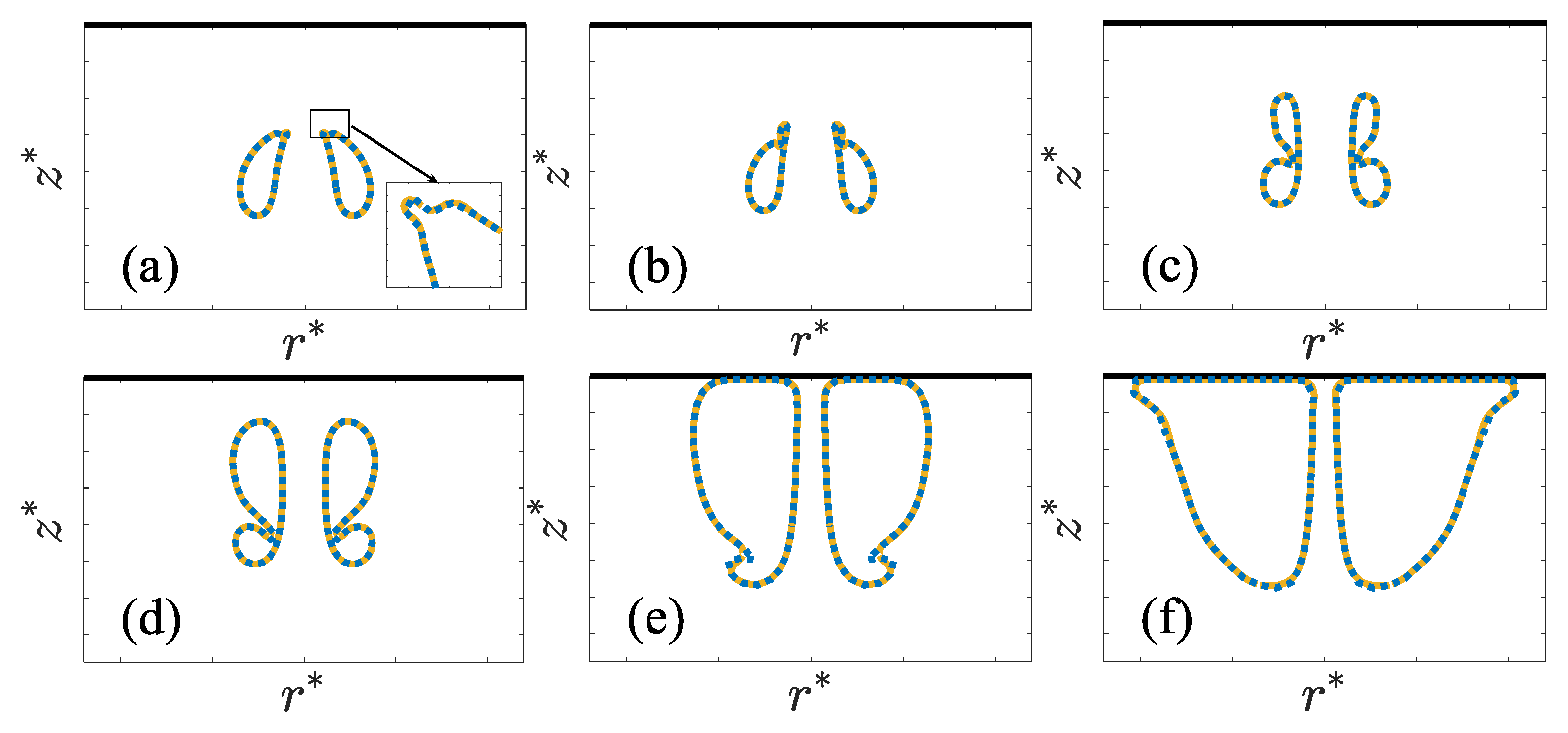
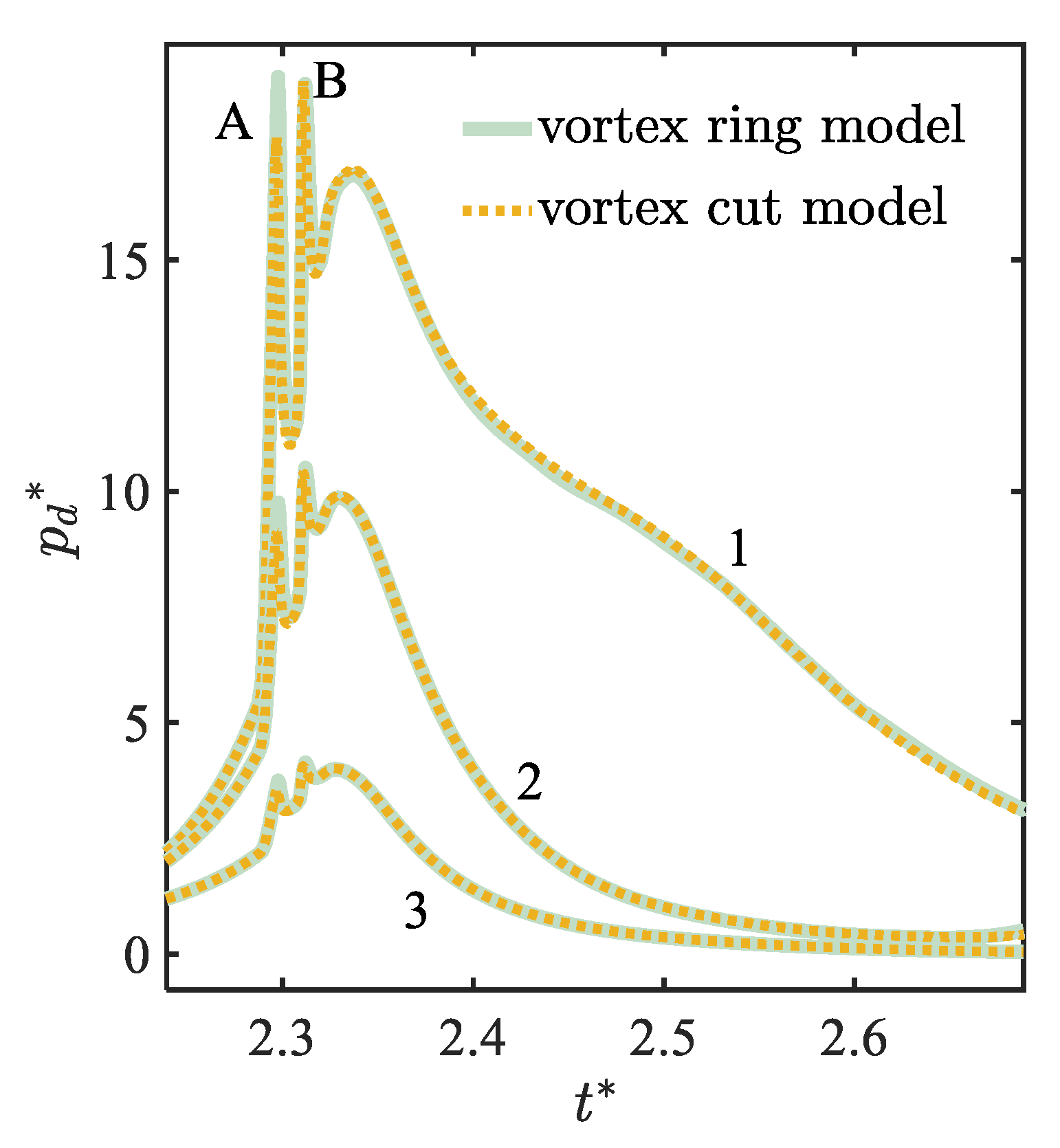
3. Results
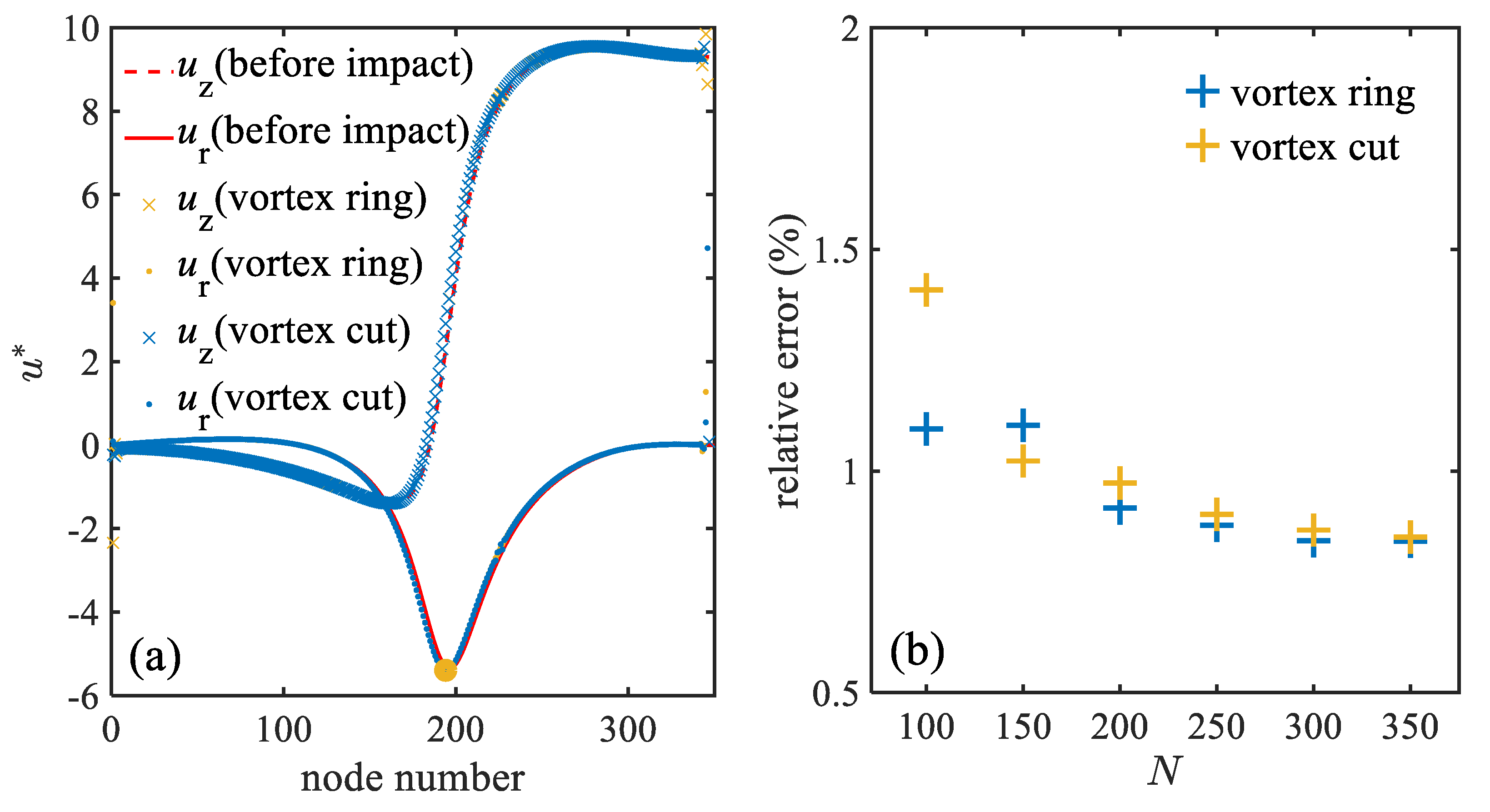
3.1. Verification Analysis
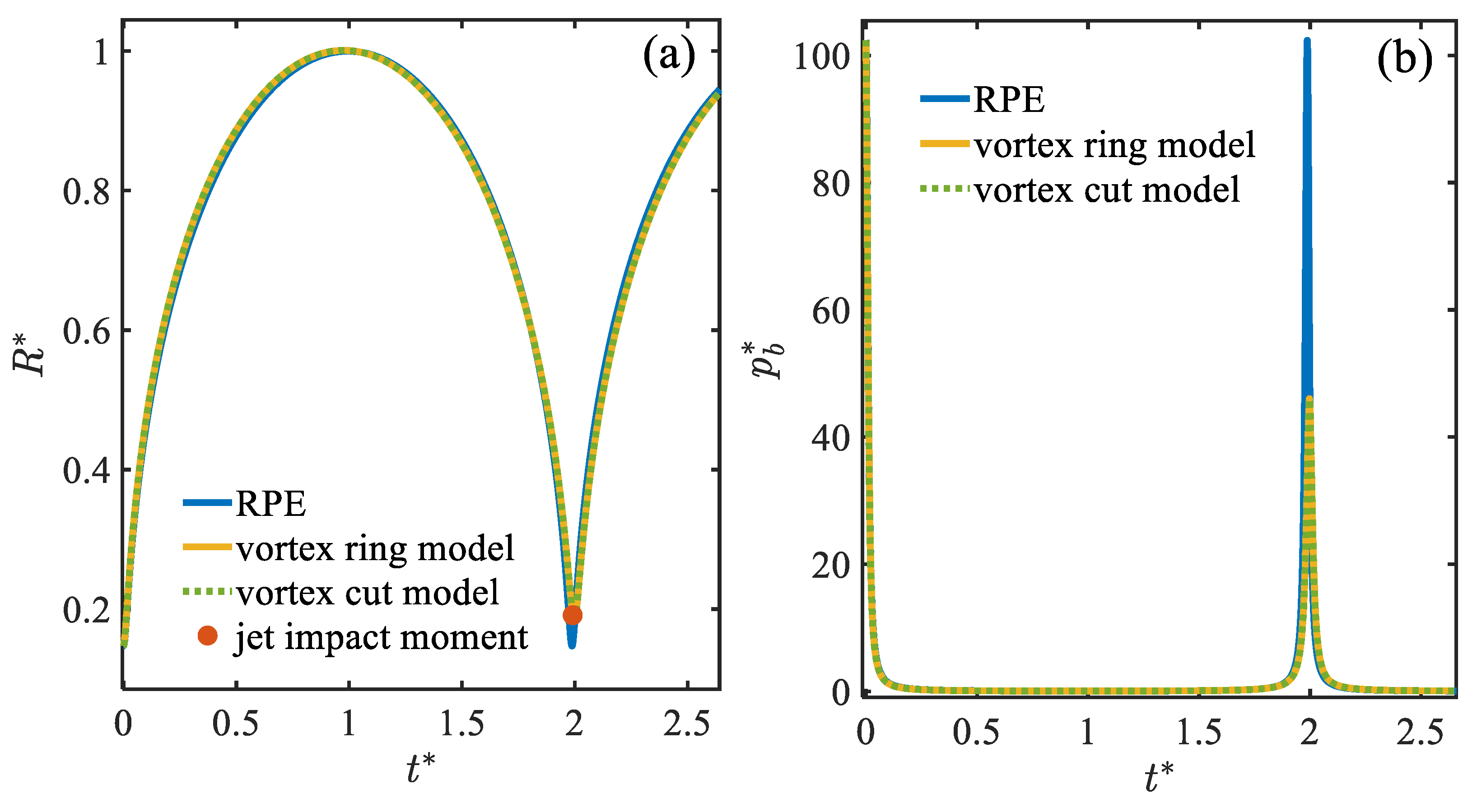
3.2. Toroidal Bubble in a Free Field
3.3. Toroidal Bubble near a Rigid Wall
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Versluis, M.; Schmitz, B.; von der Heydt, A.; Lohse, D. How snapping shrimp snap: Through cavitating bubbles. Science 2000, 289, 2114–2117. [Google Scholar] [CrossRef] [PubMed]
- Lohse, D.; Schmitz, B.; Versluis, M. Snapping shrimp make flashing bubbles. Nature 2001, 413, 477–478. [Google Scholar] [CrossRef]
- Lindau, J.W.; Boger, D.A.; Medvitz, R.B.; Kunz, R.F. Propeller cavitation breakdown analysis. J. Fluids Eng. 2005, 127, 995–1002. [Google Scholar] [CrossRef]
- Liu, Y.L.; Zhang, A.M.; Tian, Z.L.; Wang, S.P. Investigation of free-field underwater explosion with Eulerian finite element method. Ocean Eng. 2018, 166, 182–190. [Google Scholar] [CrossRef]
- Ghoshal, R.; Mitra, N. Underwater explosion induced shock loading of structures: Influence of water depth, salinity and temperature. Ocean Eng. 2016, 126, 22–28. [Google Scholar] [CrossRef]
- Tian, Z.L.; Liu, Y.L.; Zhang, A.M.; Tao, L.B.; Chen, L. Jet development and impact load of underwater explosion bubble on solid wall. Appl. Ocean Res. 2020, 95, 102013. [Google Scholar] [CrossRef]
- Li, S.; Prosperetti, A.; van der Meer, D. Dynamics of a toroidal bubble on a cylinder surface with an application to geophysical exploration. Int. J. Multiph. Flow 2020, 129, 103335. [Google Scholar] [CrossRef]
- Li, S.; van der Meer, D.; Zhang, A.M.; Prosperetti, A.; Lohse, D. Modelling large scale airgun-bubble dynamics with highly non-spherical features. Int. J. Multiph. Flow 2020, 122, 103143. [Google Scholar] [CrossRef]
- Plesset, M.S. The dynamics of cavitation bubbles. J. Appl. Mech. 1949, 16, 277–282. [Google Scholar] [CrossRef]
- Brenner, M.P.; Hilgenfeldt, S.; Lohse, D. Single-bubble sonoluminescence. Rev. Mod. Phys. 2002, 74, 425. [Google Scholar] [CrossRef]
- Rayleigh, L. On the pressure developed in a liquid during the collapse of a spherical cavity. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1917, 34, 94–98. [Google Scholar] [CrossRef]
- Keller, J.B.; Kolodner, I.I. Damping of underwater explosion bubble oscillations. J. Appl. Phys. 1956, 27, 1152–1161. [Google Scholar] [CrossRef]
- Prosperetti, A.; Lezzi, A. Bubble dynamics in a compressible liquid. Part 1. First-order theory. J. Fluid Mech. 1986, 168, 457–478. [Google Scholar] [CrossRef]
- Lezzi, A.; Prosperetti, A. Bubble dynamics in a compressible liquid. Part 2. Second-order theory. J. Fluid Mech. 1987, 185, 289–321. [Google Scholar] [CrossRef]
- Zhang, A.M.; Li, S.M.; Cui, P.; Li, S.; Liu, Y.L. A unified theory for bubble dynamics. Phys. Fluids 2023, 35, 033323. [Google Scholar] [CrossRef]
- Pearson, A.; Blake, J.R.; Otto, S.R. Jets in bubbles. J. Eng. Math. 2004, 48, 391–412. [Google Scholar] [CrossRef]
- Blake, J.R.; Taib, B.B.; Doherty, G. Transient cavities near boundaries. Part 1. Rigid boundary. J. Fluid Mech. 1986, 170, 479–497. [Google Scholar] [CrossRef]
- Blake, J.R.; Gibson, D.C. Cavitation bubbles near boundaries. Annu. Rev. Fluid Mech. 1987, 19, 99–123. [Google Scholar] [CrossRef]
- Kalumuck, K.M.; Duraiswami, R.; Chahine, G.L. Bubble dynamics fluid-structure interaction simulation by coupling fluid BEM and structural FEM codes. J. Fluids Struct. 1995, 9, 861–883. [Google Scholar] [CrossRef]
- Wang, C.; Khoo, B.C. An indirect boundary element method for three-dimensional explosion bubbles. J. Comput. Phys. 2004, 194, 451–480. [Google Scholar] [CrossRef]
- Klaseboer, E.; Hung, K.C.; Wang, C.; Wang, C.W.; Khoo, B.C.; Boyce, P.; Debono, S.; Charlier, H. Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure. J. Fluid Mech. 2005, 537, 387–413. [Google Scholar] [CrossRef]
- Li, S.; Zhang, A.M.; Han, R.; Ma, Q. 3D full coupling model for strong interaction between a pulsating bubble and a movable sphere. J. Comput. Phys. 2019, 392, 713–731. [Google Scholar] [CrossRef]
- Zhang, A.M.; Wu, W.B.; Liu, Y.L.; Wang, Q.X. Nonlinear interaction between underwater explosion bubble and structure based on fully coupled model. Phys. Fluids 2017, 29, 082111. [Google Scholar] [CrossRef]
- Han, R.; Zhang, A.M.; Tan, S.C.; Li, S. Interaction of cavitation bubbles with the interface of two immiscible fluids on multiple time scales. J. Fluid Mech. 2021, 932, A8. [Google Scholar] [CrossRef]
- Manmi, K.M.A.; Aziz, I.A.; Arjunan, A.; Saeed, R.K.; Dadvand, A. Three-dimensional oscillation of an acoustic microbubble between two rigid curved plates. J. Hydrodyn. 2021, 33, 1019–1034. [Google Scholar] [CrossRef]
- Dadvand, A.; Manmi, K.M.A.; Aziz, I.A. Three-dimensional bubble jetting inside a corner formed by rigid curved plates: Boundary integral analysis. Int. J. Multiph. Flow 2023, 158, 104308. [Google Scholar] [CrossRef]
- Curtiss, G.A.; Leppinen, D.M.; Wang, Q.X.; Blake, J.R. Ultrasonic cavitation near a tissue layer. J. Fluid Mech. 2013, 730, 245–272. [Google Scholar] [CrossRef]
- Wang, Q.X. Non-spherical bubble dynamics of underwater explosions in a compressible fluid. Phys. Fluids 2013, 25. [Google Scholar] [CrossRef]
- Li, S.; Saade, Y.; van der Meer, D.; Lohse, D. Comparison of Boundary Integral and Volume-of-Fluid methods for compressible bubble dynamics. Int. J. Multiph. Flow 2021, 145, 103834. [Google Scholar] [CrossRef]
- Wang, Q.X.; Blake, J.R. Non-spherical bubble dynamics in a compressible liquid. Part 1. Travelling acoustic wave. J. Fluid Mech. 2010, 659, 191–224. [Google Scholar] [CrossRef]
- Lundgern, T.S.; Mansour, N.N. Vortex ring bubbles. J. Mech. 1991, 224, 177–196. [Google Scholar]
- Best, J.P. The Dynamics of Underwater Explosions. Ph.D. Thesis, The University of Wollongong, Wollongong, Australia, 1991. [Google Scholar]
- Best, J.P. The Rebound of Toroidal Bubbles; Bubble Dynamics and Interface Phenomena; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Zhang, S.; Duncan, J.H.; Chahine, G.L. The final stage of the collapse of a cavitation bubble near a rigid wall. J. Fluid Mech. 1993, 257, 147–181. [Google Scholar] [CrossRef]
- Wang, Q.X.; Yeo, K.S.; Khoo, B.C.; Lam, K.Y. Nonlinear interaction between gas bubble and free surface. Comput. Fluids 1996, 25, 607–628. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Yeo, K.S.; Khoo, B.C.; Wang, C. 3D jet impact and toroidal bubbles. J. Comput. Phys. 2001, 166, 336–360. [Google Scholar] [CrossRef]
- Wang, Q.X. Multi-oscillations of a bubble in a compressible liquid near a rigid boundary. J. Fluid Mech. 2014, 745, 509–536. [Google Scholar] [CrossRef]
- Wang, Q.X.; Yeo, K.S.; Khoo, B.C.; Lam, K.Y. Vortex ring modelling of toroidal bubbles. Theor. Comput. Fluid Dyn. 2005, 19, 303–317. [Google Scholar] [CrossRef]
- Lauterborn, W.; Lechner, C.; Koch, M.; Mettin, R. Bubble models and real bubbles: Rayleigh and energy-deposit cases in a Tait-compressible liquid. IMA J. Appl. Math. 2018, 83, 556–589. [Google Scholar] [CrossRef]
- Li, T.; Wang, S.; Li, S.; Zhang, A.M. Numerical investigation of an underwater explosion bubble based on FVM and VOF. Appl. Ocean Res. 2018, 74, 49–58. [Google Scholar] [CrossRef]
- Li, T.; Zhang, A.M.; Wang, S.; Li, S.; Liu, W. Bubble interactions and bursting behaviors near a free surface. Phys. Fluids 2019, 31, 042104. [Google Scholar]
- Zeng, Q.; Cai, J. Three-dimension simulation of bubble behavior under nonlinear oscillation. Ann. Nucl. Energy 2014, 63, 680–690. [Google Scholar] [CrossRef]
- Tian, Z.L.; Liu, Y.L.; Zhang, A.M.; Tao, L.B. Energy dissipation of pulsating bubbles in compressible fluids using the Eulerian finite-element method. Ocean Eng. 2020, 196, 106714. [Google Scholar] [CrossRef]
- Liu, N.N.; Zhang, A.M.; Liu, Y.L.; Li, T. Numerical analysis of the interaction of two underwater explosion bubbles using the compressible Eulerian finite-element method. Phys. Fluids 2020, 32, 046107. [Google Scholar]
- He, M.; Liu, Y.L.; Zhang, S.; Zhang, A.M. Research on characteristics of deep-sea implosion based on Eulerian finite element method. Ocean Eng. 2022, 244, 110270. [Google Scholar] [CrossRef]
- Sun, P.; Le Touzé, D.; Oger, G.; Zhang, A.M. An accurate SPH Volume Adaptive Scheme for modeling strongly-compressible multiphase flows. Part 2: Extension of the scheme to cylindrical coordinates and simulations of 3D axisymmetric problems with experimental validations. J. Comput. Phys. 2021, 426, 109936. [Google Scholar] [CrossRef]
- Sun, P.N.; Pilloton, C.; Antuono, M.; Colagrossi, A. Inclusion of an acoustic damper term in weakly-compressible SPH models. J. Comput. Phys. 2023, 483, 112056. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, A.M.; Fang, X.; Khayyer, A.; Meng, Z. Axisymmetric Riemann–smoothed particle hydrodynamics modeling of high-pressure bubble dynamics with a simple shifting scheme. Phys. Fluids 2022, 34, 112122. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Phan, T.H.; Duy, T.N.; Kim, D.H.; Park, W.G. Modeling of the bubble collapse with water jets and pressure loads using a geometrical volume of fluid based simulation method. Int. J. Multiph. Flow 2022, 152, 104103. [Google Scholar] [CrossRef]
- Nguyen, Q.T.; Nguyen, V.T.; Phan, T.H.; Duy, T.N.; Park, S.H.; Park, W.G. Numerical study of dynamics of cavitation bubble collapse near oscillating walls. Phys. Fluids 2023, 35, 013306. [Google Scholar] [CrossRef]
- Ni, B.Y.; Zhang, A.M.; Wu, G.X. Numerical and experimental study of bubble impact on a solid wall. J. Fluids Eng. 2015, 137, 031206. [Google Scholar] [CrossRef]
- Li, S.; Li, Y.B.; Zhang, A.M. Numerical analysis of the bubble jet impact on a rigid wall. Appl. Ocean Res. 2015, 50, 227–236. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Zhang, A.M.; Silberschmidt, V.V.; Wang, L. SPH-BEM simulation of underwater explosion and bubble dynamics near rigid wall. Sci. China Technol. Sci. 2019, 62, 1082–1093. [Google Scholar] [CrossRef]
- Wang, J.X.; Zong, Z.; Sun, L.; Li, Z.R.; Jiang, M.Z. Numerical study of spike characteristics due to the motions of a non-spherical rebounding bubble. J. Hydrodyn. 2016, 28, 52–65. [Google Scholar] [CrossRef]
- Wang, Q.X.; Yang, Y.X.; Tan, D.S.; Su, J.; Tan, S.K. Non-spherical multi-oscillations of a bubble in a compressible liquid. J. Hydrodyn. 2014, 26, 848–855. [Google Scholar] [CrossRef]
- Klaseboer, E.; Khoo, B.C.; Hung, K.C. Dynamics of an oscillating bubble near a floating structure. J. Fluids Struct. 2005, 21, 395–412. [Google Scholar] [CrossRef]
- Cole, R.H. Underwater Explosions; Princeton University Press: Princeton, NJ, USA, 1948. [Google Scholar]
- Pearson, A.; Cox, E.; Blake, J.R. Bubble interactions near a free surface. Eng. Anal. Bound. Elem. 2004, 28, 295–313. [Google Scholar] [CrossRef]
- Zhang, S.; Duncan, J.H. On the nonspherical collapse and rebound of a cavitation bubble. Phys. Fluids 1994, 6, 2352–2362. [Google Scholar] [CrossRef]
- Tong, R.P.; Schiffers, W.P.; Shaw, S.J.; Blake, J.R.; Emmony, D.C. The role of ‘splashing’ in the collapse of a laser-generated cavity near a rigid boundary. J. Fluid Mech. 1999, 380, 339–361. [Google Scholar] [CrossRef]
- Li, S.; Han, R.; Zhang, A.M.; Wang, Q.X. Analysis of pressure field generated by a collapsing bubble. Ocean Eng. 2016, 117, 22–38. [Google Scholar] [CrossRef]
- Zhang, A.M.; Liu, Y.L. Improved three-dimensional bubble dynamics model based on boundary element method. J. Comput. Phys. 2015, 294, 208–223. [Google Scholar] [CrossRef]

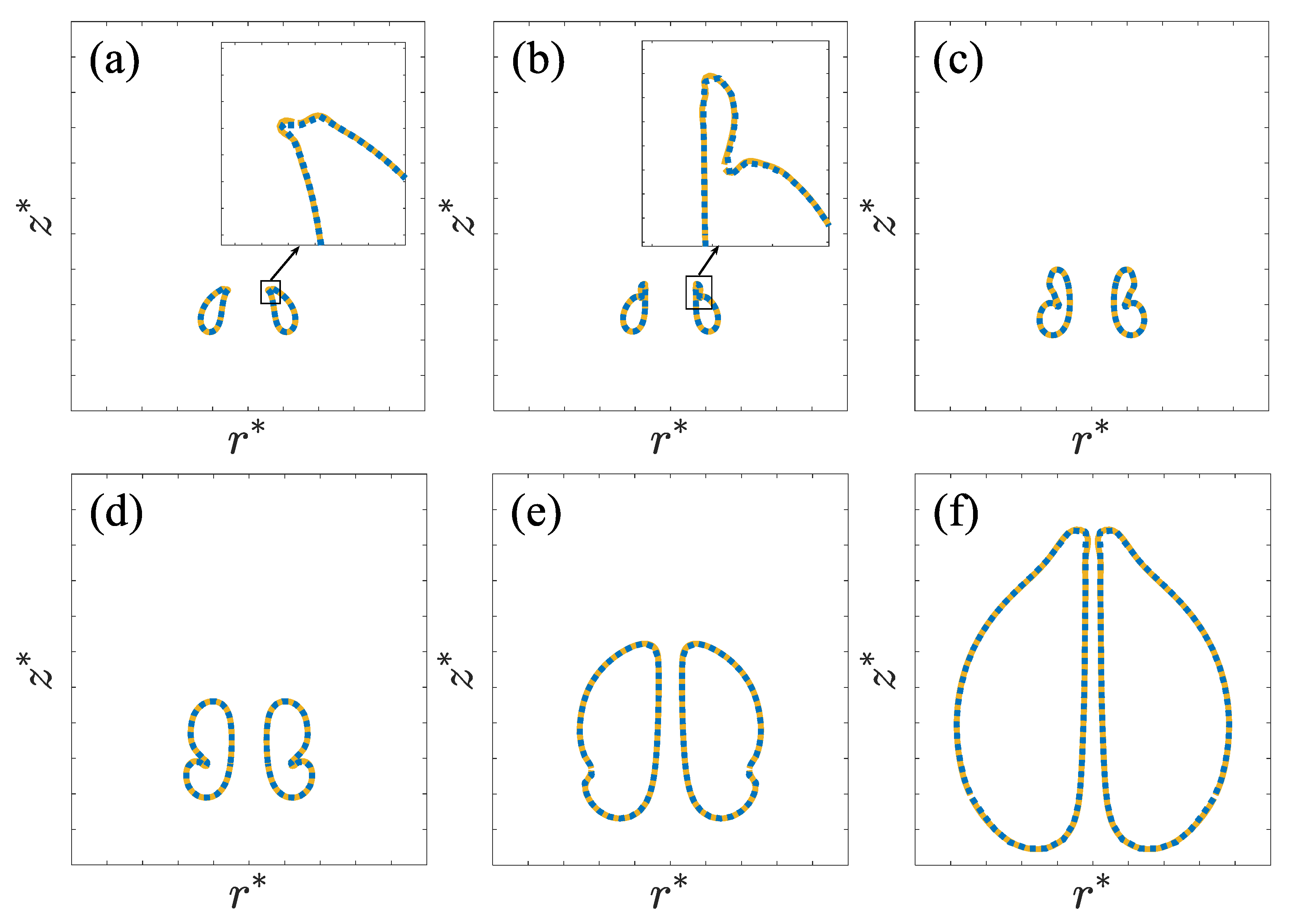

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, L.; Zhang, T.; Yang, D.; Han, R.; Li, S. Comparison of Vortex Cut and Vortex Ring Models for Toroidal Bubble Dynamics in Underwater Explosions. Fluids 2023, 8, 131. https://doi.org/10.3390/fluids8040131
Han L, Zhang T, Yang D, Han R, Li S. Comparison of Vortex Cut and Vortex Ring Models for Toroidal Bubble Dynamics in Underwater Explosions. Fluids. 2023; 8(4):131. https://doi.org/10.3390/fluids8040131
Chicago/Turabian StyleHan, Lingxi, Tianyuan Zhang, Di Yang, Rui Han, and Shuai Li. 2023. "Comparison of Vortex Cut and Vortex Ring Models for Toroidal Bubble Dynamics in Underwater Explosions" Fluids 8, no. 4: 131. https://doi.org/10.3390/fluids8040131
APA StyleHan, L., Zhang, T., Yang, D., Han, R., & Li, S. (2023). Comparison of Vortex Cut and Vortex Ring Models for Toroidal Bubble Dynamics in Underwater Explosions. Fluids, 8(4), 131. https://doi.org/10.3390/fluids8040131






