Numerical Study of a Small Horizontal-Axis Wind Turbine Aerodynamics Operating at Low Wind Speed
Abstract
:1. Introduction
2. Mathematical Model
2.1. Wind Turbine Geometry
2.2. Mesh Generation
2.3. Computational Analysis
2.4. Numerical Solution
3. Results and Discussion
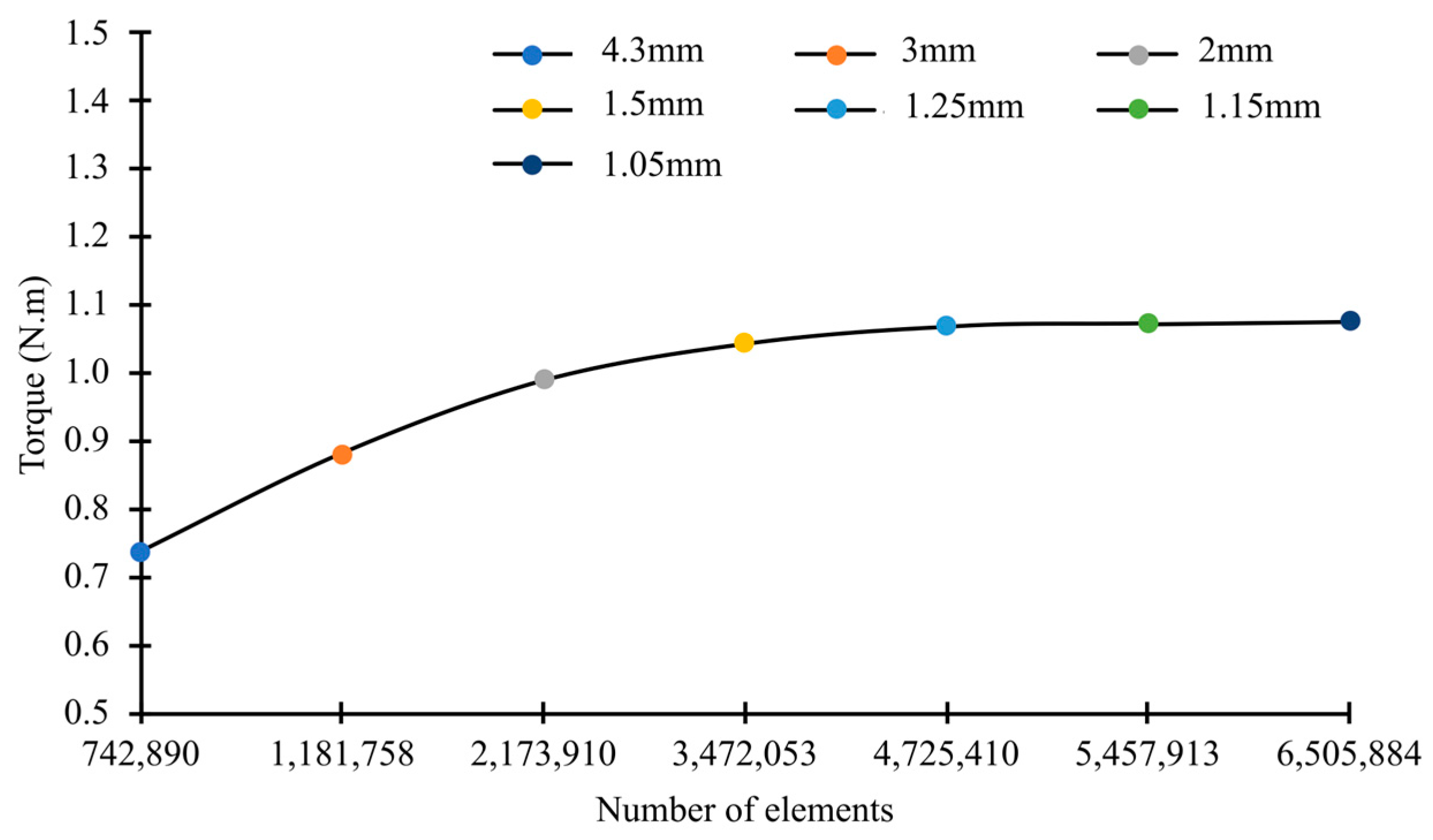
3.1. Grid Convergence Study
| Blade Element Size (mm) | Number of Elements | Average Orthogonal | Average Skewness | Aerodynamic Torque (N.m) |
|---|---|---|---|---|
| 4.3 mm | 742,890 | 0.717 | 0.245 | 0.738 |
| 3 mm | 1,181,758 | 0.743 | 0.229 | 0.881 |
| 2 mm | 2,173,910 | 0.789 | 0.197 | 0.989 |
| 1.5 mm | 3,472,053 | 0.814 | 0.179 | 1.044 |
| 1.25 mm | 4,725,410 | 0.824 | 0.17 | 1.069 |
| 1.15 mm | 5,457,913 | 0.827 | 0.168 | 1.072 |
| 1.05 mm | 6,505,884 | 0.833 | 0.163 | 1.076 |
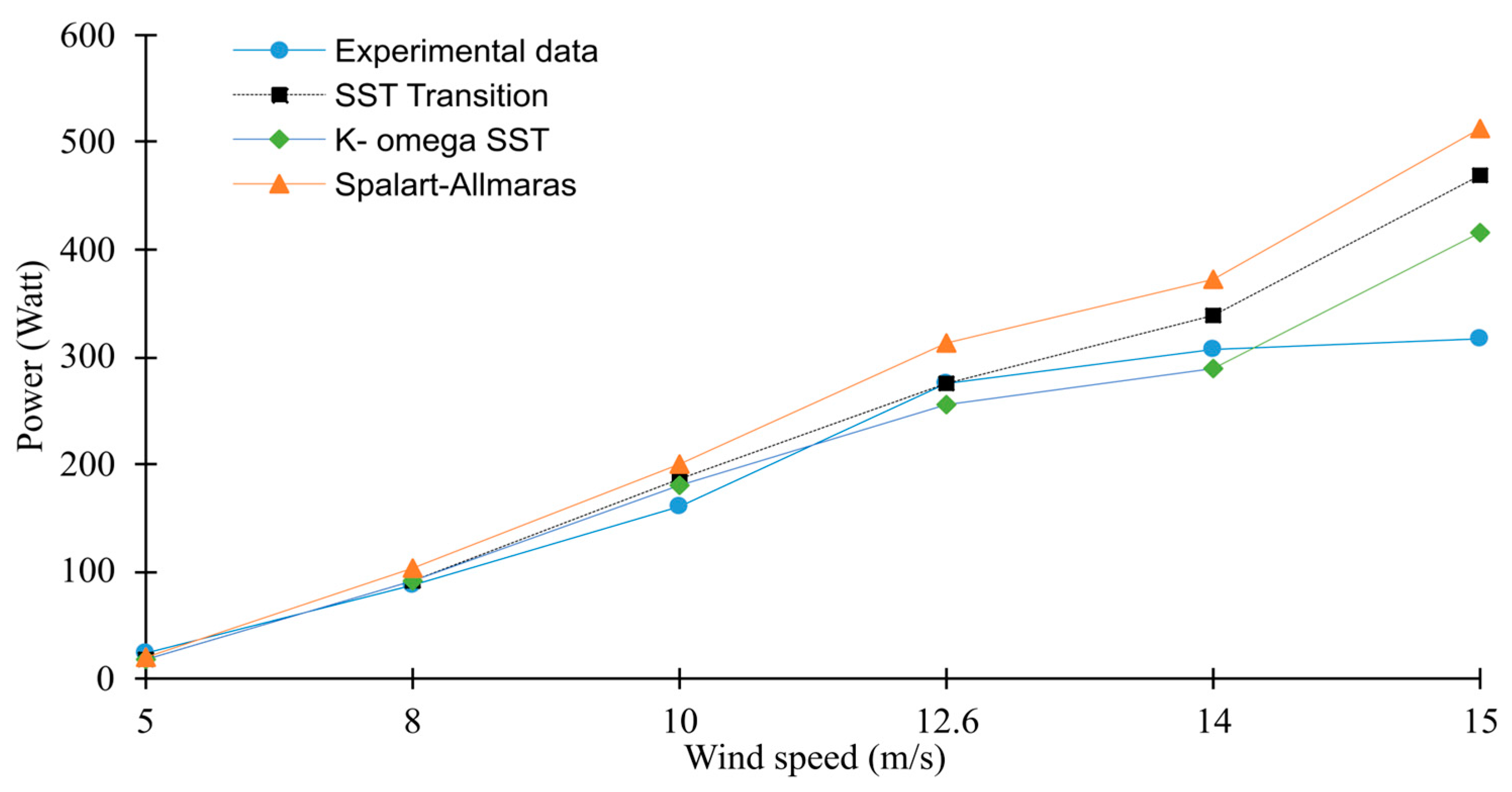
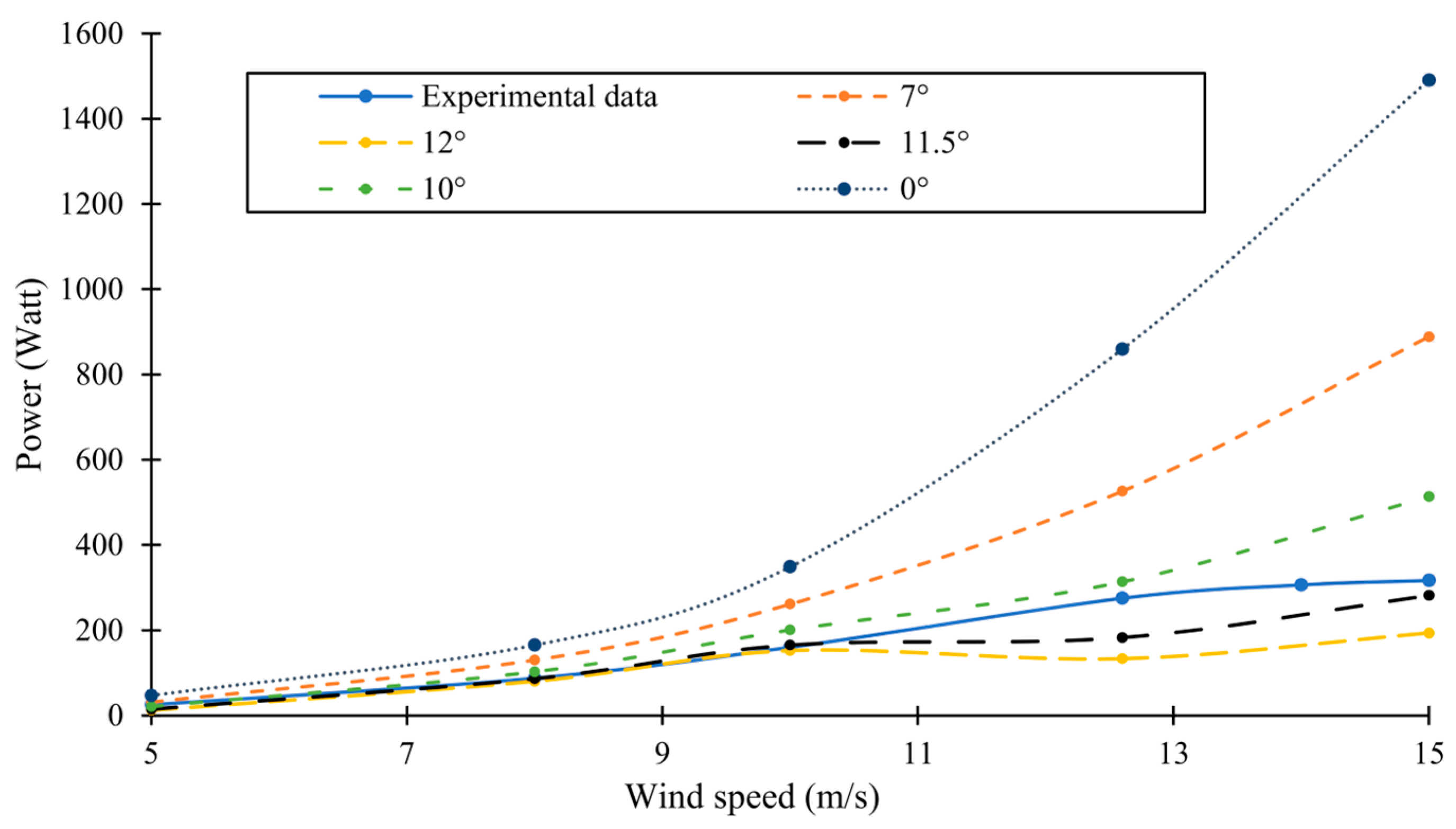
3.2. Model Validation
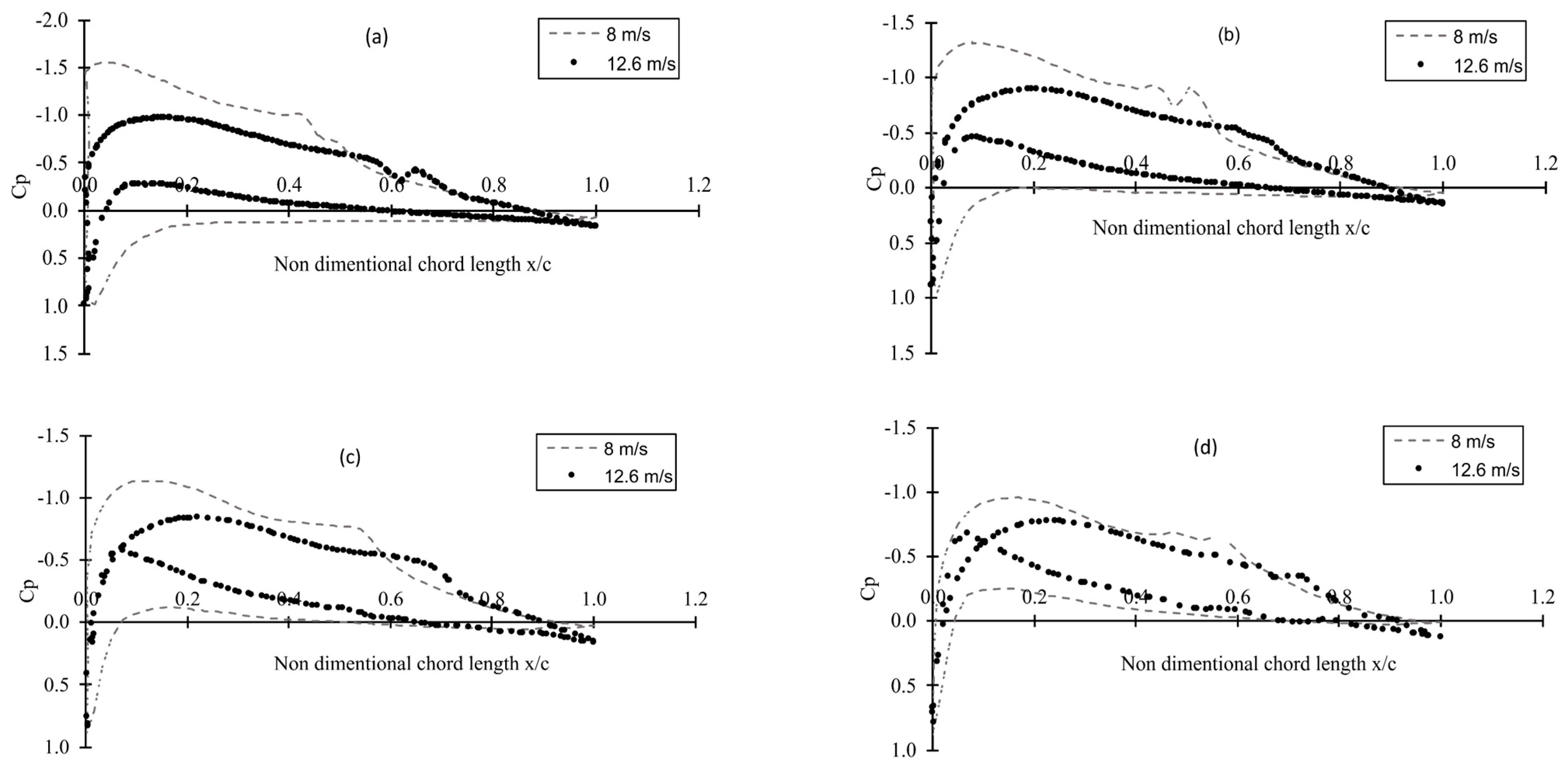
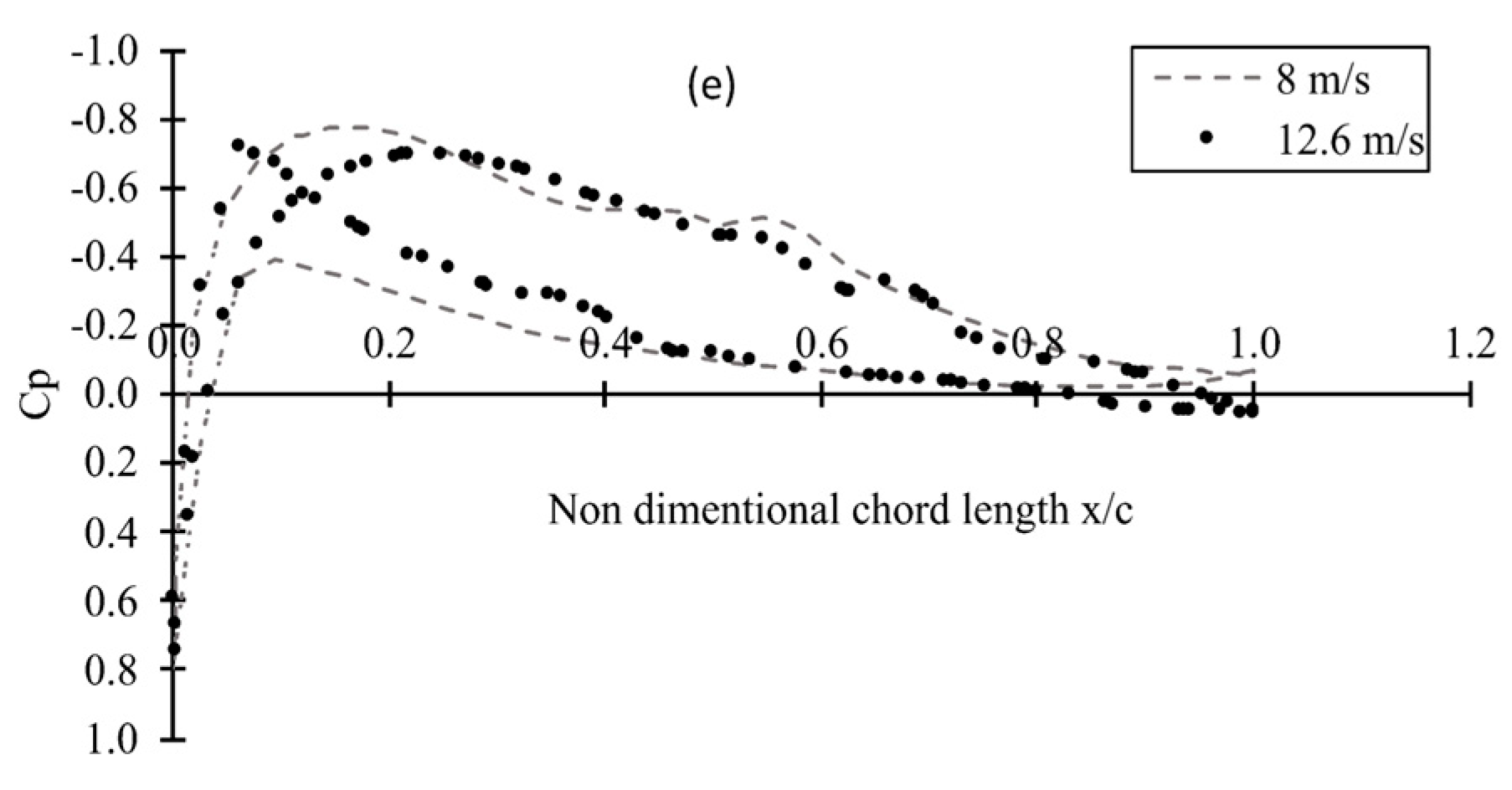
3.3. Pressure Coefficient
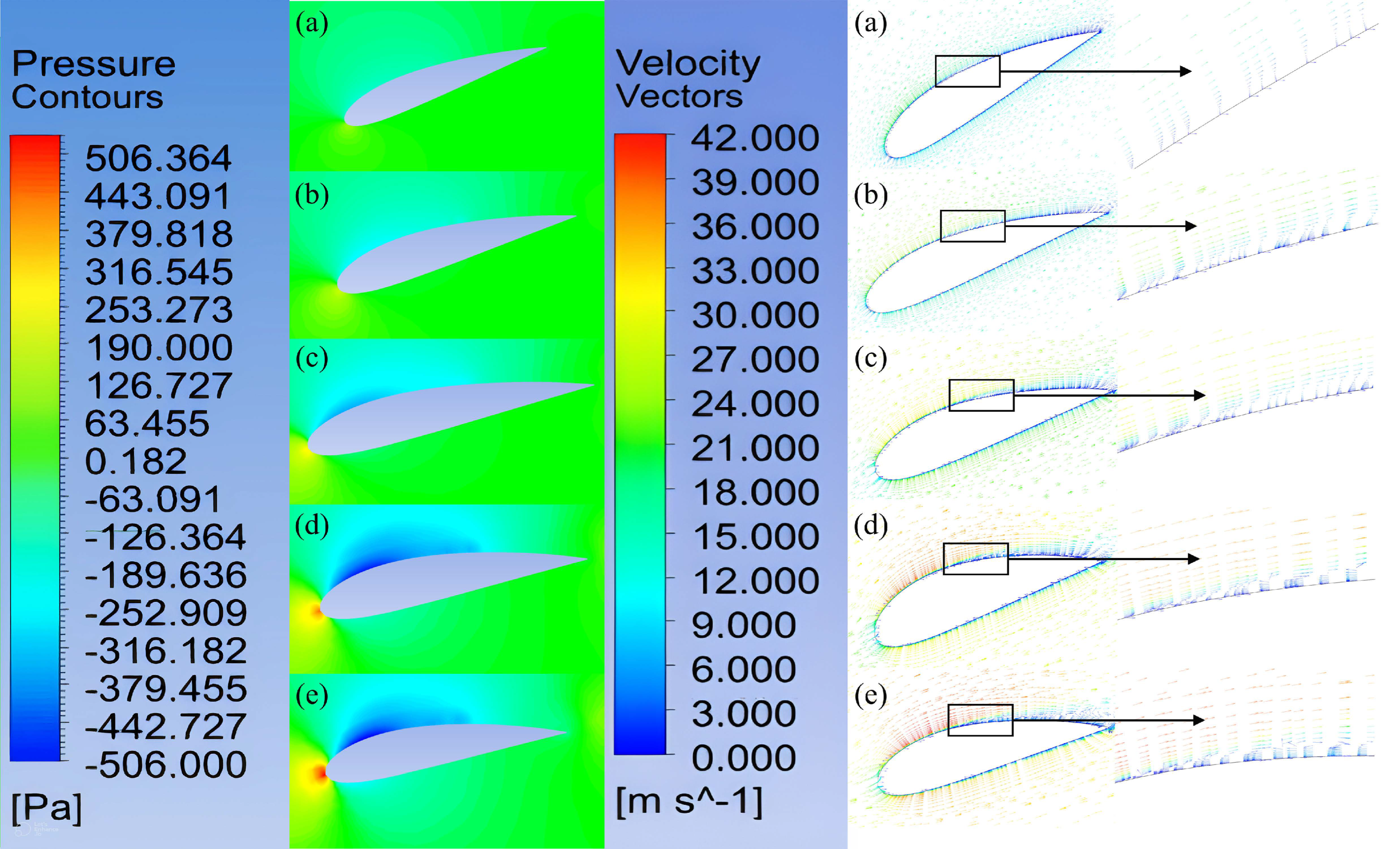
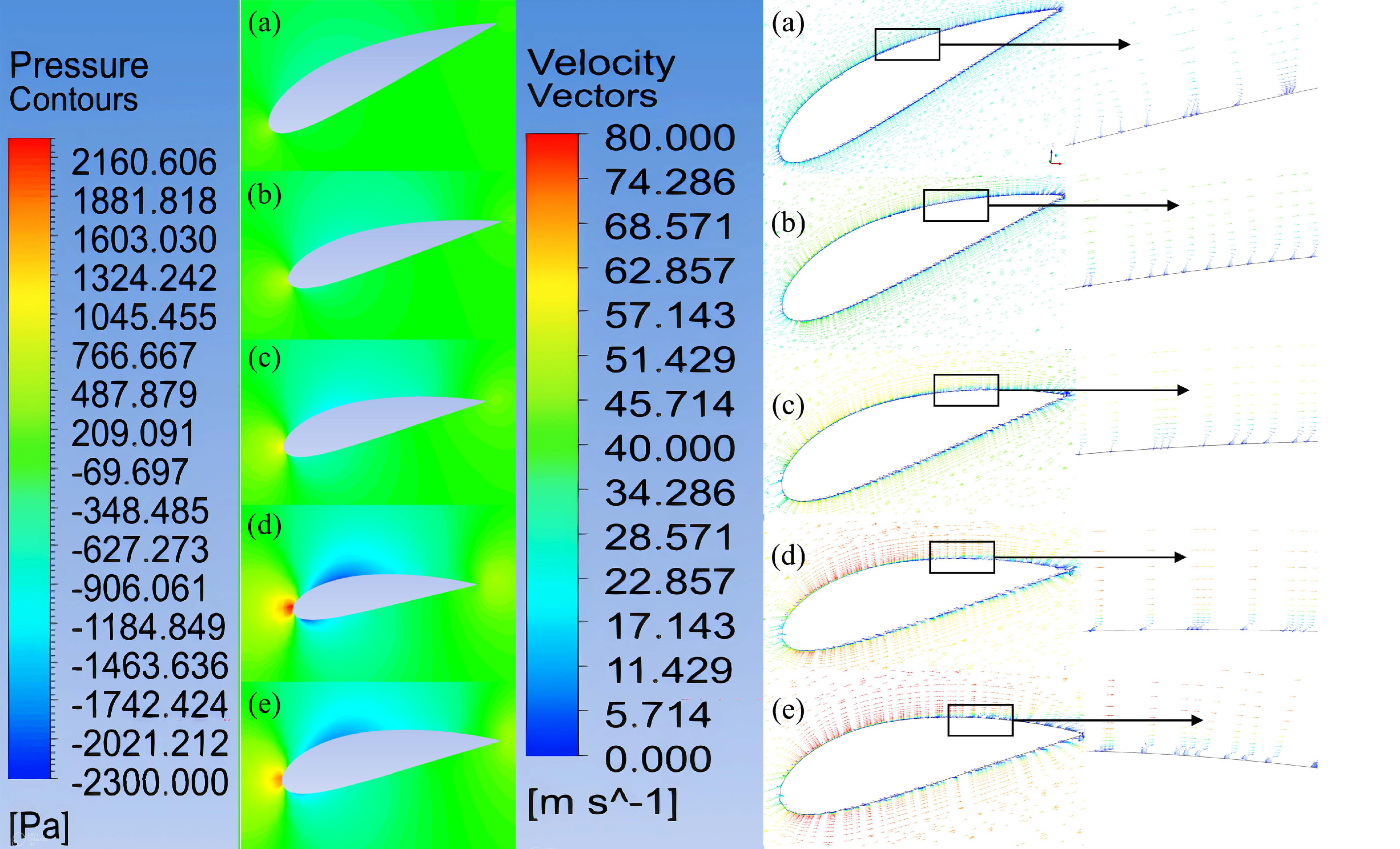
3.4. Flow Field around the Blade
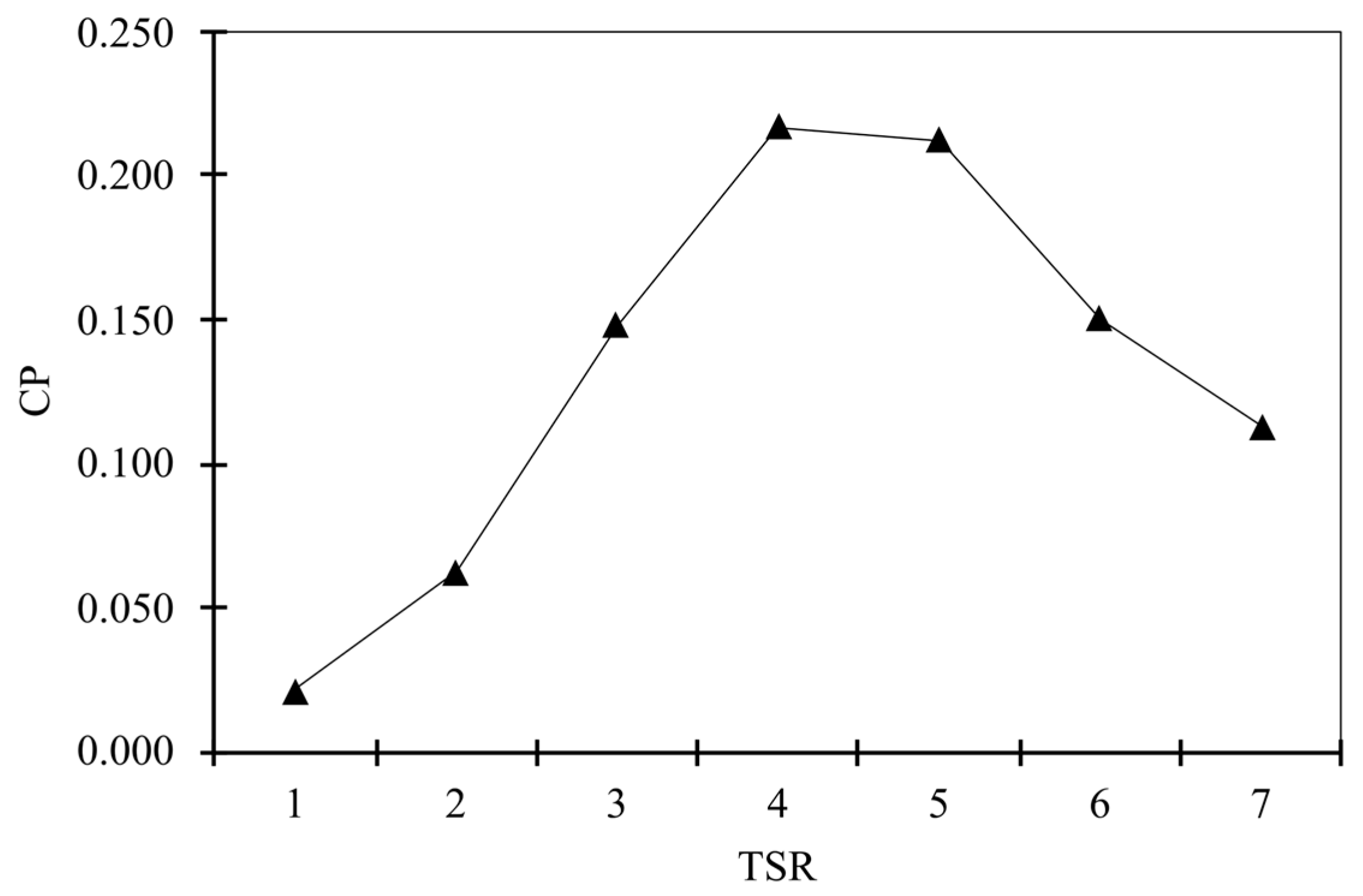
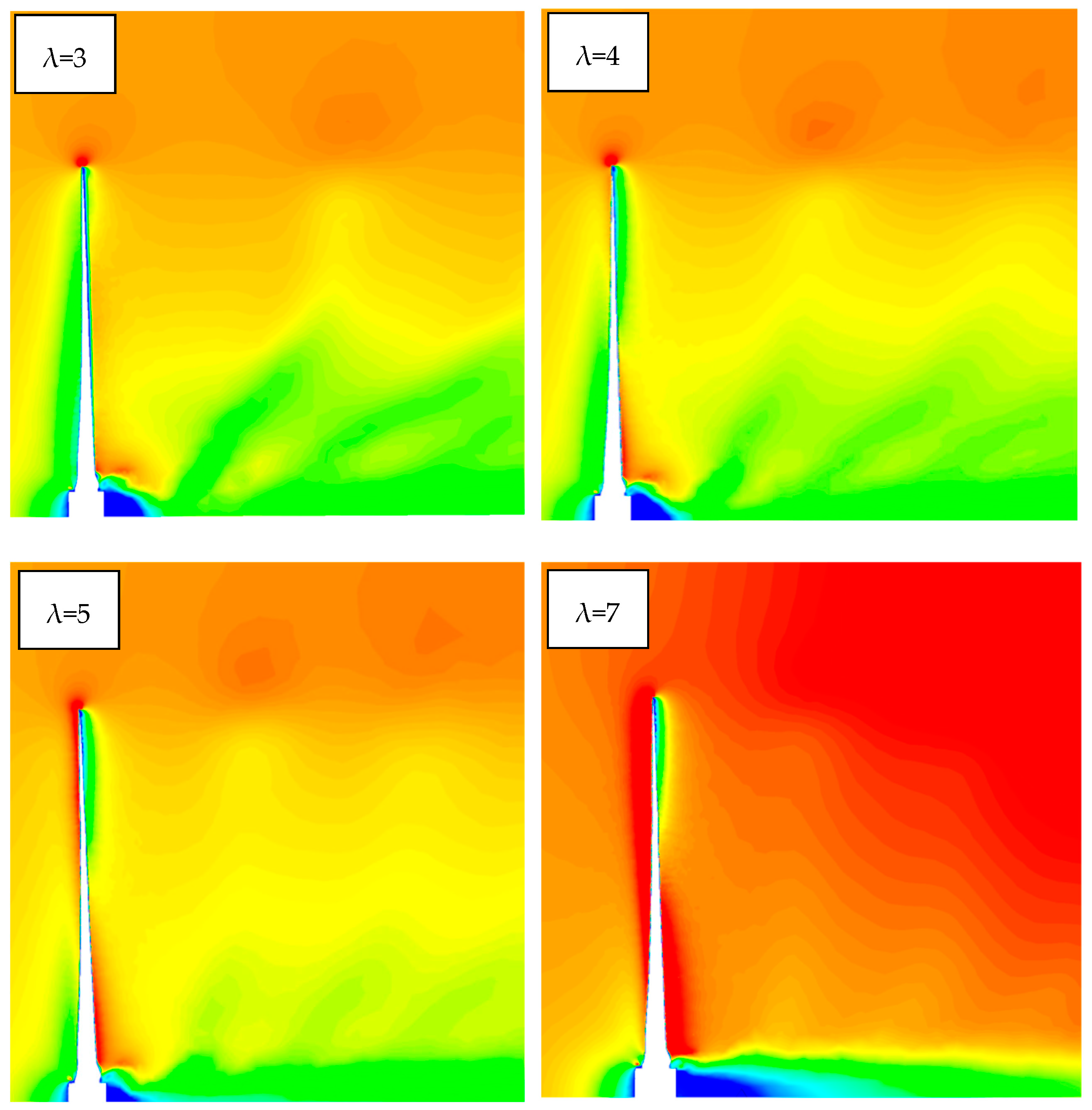
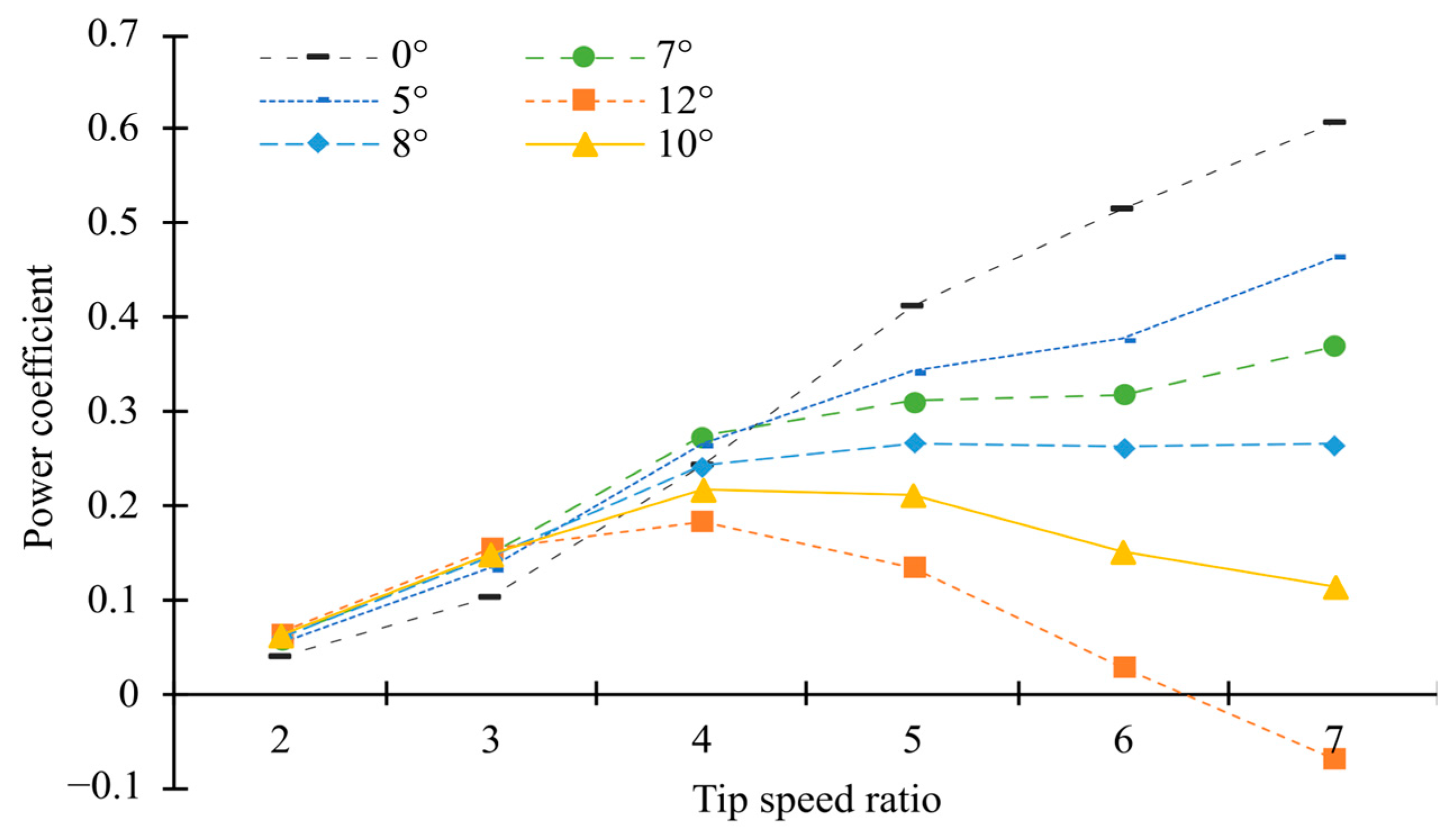
3.5. TSR Effects
3.6. Pitch Angle Effects
4. Conclusions
- The transition SST turbulence model was found to be the most appropriate turbulence model for predicting the performance and flow behavior.
- The laminar–turbulent transition phenomenon was found to be important in the blade’s root region at different rotational and wind speeds. The length of the Laminar Separation Bubble (LSB) increases with the span-wise direction, whereas the height of the LSB decreases with the increase in the wind speed.
- At 8 m/s wind speed, the maximum power coefficient of 0.22 was recorded at a TSR of 4. The increase in the TSR leads to a delay in the transition and separation phenomena. On the blade surface, the areas of separated flow zones decrease with the rise in TSR.
- At 8 m/s, the decrease in the pitch angle reduced the blade efficiency at low TSRs. This result was reversed at high TSRs, and the maximum power coefficient of 0.6 was obtained at a pitch angle of 0° when operating at a TSR of 7. At the medium value of TSR (λ = 4), the variation in the efficiency was found to be non-linear with the pitch angles.
- At 8 m/s, the newly designed wind turbine with a pitch angle of 0° operates more efficiently than Ampair300 at TSRs greater than 4.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Short-Term Energy Outlook—U.S. Energy Information Administration (EIA). Available online: https://www.eia.gov/outlooks/steo/report/global_oil.php (accessed on 15 June 2022).
- U.S. Energy Information Administration. International Energy Outlook 2016; Office of Energy Analysis U.S. Department of Energy: Washington, DC, USA, 2016.
- Gökmen, A.; Temiz, D. The Importance and Impact of Fossil and Renewable Energy Sources in Turkey on Business and the Economy. Energy Sources Part B Econ. Plan. Policy 2015, 10, 14–20. [Google Scholar] [CrossRef]
- The Socioeconomic Impacts of Wind Energy in the Context of the Energy Transition I Siemens Gamesa I KPMG. Available online: https://www.siemensgamesa.com/explore/journal/socioeconomic-report-wind-energy-2019 (accessed on 8 July 2022).
- International Renewable Energy Agency. Wind Energy. Available online: https://www.irena.org/Energy-Transition/Technology/Wind-energy (accessed on 22 July 2022).
- GWEC. Global Wind Report 2022; Global Wind Energy Council: Brussels, Belgium, 2022. [Google Scholar]
- Runchal, A. Brian Spalding: CFD & Reality A Personal Recollection. J. Frankl. Inst. 2014, 351, 65–87. [Google Scholar] [CrossRef]
- Iranzo, A. CFD Applications in Energy Engineering Research and Simulation: An Introduction to Published Reviews. Processes 2019, 7, 883. [Google Scholar] [CrossRef]
- Jonathon, S.; Sibuet Watters, C.; Masson, C. CFD in Wind Energy: The Virtual, Multiscale Wind Tunnel. Energies 2010, 3, 989–1013. [Google Scholar] [CrossRef] [Green Version]
- Kumar Gupta, R.; Warudkar, V.; Purohit, R.; Singh Rajpurohit, S. Modeling and Aerodynamic Analysis of Small Scale, Mixed Airfoil Horizontal Axis Wind Turbine Blade. Mater. Today Proc. 2017, 4, 5370–5384. [Google Scholar] [CrossRef]
- Hasan, M.; El-Shahat, A.; Rahman, M. Performance Investigation of Three Combined Airfoils Bladed Small Scale Horizontal Axis Wind Turbine by BEM and CFD Analysis. J. Power Energy Eng. 2017, 5, 14–27. [Google Scholar] [CrossRef] [Green Version]
- Muhsen, H.; Al-Kouz, W.; Khan, W. Small Wind Turbine Blade Design and Optimization. Symmetry 2020, 12, 18. [Google Scholar] [CrossRef] [Green Version]
- Yang, K. Geometry Design Optimization of a Wind Turbine Blade Considering Effects on Aerodynamic Performance by Linearization. Energies 2020, 13, 2320. [Google Scholar] [CrossRef]
- Plaza, B.; Bardera, R.; Visiedo, S. Comparison of BEM and CFD Results for MEXICO Rotor Aerodynamics. J. Wind. Eng. Ind. Aerodyn. 2015, 145, 115–122. [Google Scholar] [CrossRef]
- Bangga, G. Comparison of Blade Element Method and CFD Simulations of a 10 MW Wind Turbine. Fluids 2018, 3, 73. [Google Scholar] [CrossRef] [Green Version]
- Keerthana, M.; Sriramkrishnan, M.; Velayutham, T.; Abraham, A.; Rajan, S.S.; Parammasivam, K.M. Aerodynamic analysis of a small horizontal axis wind turbine using CFD. J. Wind. Eng. 2012, 9, 14–28. [Google Scholar]
- Khlaifat, N.; Altaee, A.; Zhou, J.; Huang, Y.; Braytee, A. Optimization of a Small Wind Turbine for a Rural Area: A Case Study of Deniliquin, New South Wales, Australia. Energies 2020, 13, 2292. [Google Scholar] [CrossRef]
- Ampair_300_Manual.Pdf. Available online: https://www.energymatters.com.au/images/ampair/Ampair_300_manual.pdf (accessed on 28 January 2022).
- Younoussi, S.; Ettaouil, A. Design and Optimization of a Small Horizontal Axis Wind Turbine Using BEM Theory and Tip Loss Corrections. E3S Web Conf. 2021, 294, 01003. [Google Scholar] [CrossRef]
- Ahmad, T.; Plee, S.L.; Myers, J.P. Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Luo, J.; Gosman, A. Prediction of impeller induced flows in mixing vessels using multiple frames of reference. I. Chem. E. Symp. Ser. 1994, 136, 549–556. [Google Scholar]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992; American Institute of Aeronautics and Astronautics: Reno, NV, USA, 1992. [Google Scholar]
- Menter, F.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Langtry, R.B.; Menter, F.R. Correlation-Based Transition Modeling for Unstructured Parallelized Computational Fluid Dynamics Codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow, 1st ed.; CRC Press: Boca Raton, FL, USA, 1980; ISBN 978-0-89116-522-4. [Google Scholar] [CrossRef]
- Sudhamshu, A.R.; Pandey, M.C.; Sunil, N.; Satish, N.S.; Mugundhan, V.; Velamati, R.K. Numerical Study of Effect of Pitch Angle on Performance Characteristics of a HAWT. Eng. Sci. Technol. Int. J. 2016, 1, 632–641. [Google Scholar] [CrossRef] [Green Version]
- Huo, Q. Structural Response Analysis of Wind Turbine under Different Wind Speeds. IOP Conf. Ser. Earth Environ. Sci. 2021, 791, 012099. [Google Scholar] [CrossRef]
- Shi, F.; Wang, Z.; Zhang, J.; Gong, Z.; Guo, L. Influences of Wind and Rotating Speed on the Fluid-Structure Interaction Vibration for the Offshore Wind Turbine Blade. J. Vibroengineering 2019, 21, 483–497. [Google Scholar] [CrossRef] [Green Version]
- Genç, M.S.; Karasu, İ.; Açıkel, H.H.; Akpolat, M.T. Low Reynolds Number Flows and Transition; IntechOpen: London, UK, 2012; ISBN 978-953-51-0492-6. [Google Scholar]
- Shen, W.Z.; Soerensen, N. Quasi-3D Navier-Stokes Model for Rotating Airfoil. J. Comput. Phys. 1998, 150, 518–548. [Google Scholar] [CrossRef]
- Koca, K.; Genç, M.S.; Açıkel, H.H.; Çağdaş, M.; Bodur, T.M. Identification of Flow Phenomena over NACA 4412 Wind Turbine Airfoil at Low Reynolds Numbers and Role of Laminar Separation Bubble on Flow Evolution. Energy 2018, 144, 750–764. [Google Scholar] [CrossRef]
- Kang, H.; Altman, A. Generalized Empirical Airfoil Stagnation Point Location Prediction. J. Aircr. 2007, 44, 698–701. [Google Scholar] [CrossRef]
- Meseguer, J.; Alonso, G.; Sanz-Andrés, A.; Pérez-Grande, I. On the Circulation and the Position of the Forward Stagnation Point on Airfoils. Int. J. Mech. Eng. Educ. 2007, 35, 65–75. [Google Scholar] [CrossRef] [Green Version]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; McGraw-Hill: New York, NY, USA, 2017. [Google Scholar]
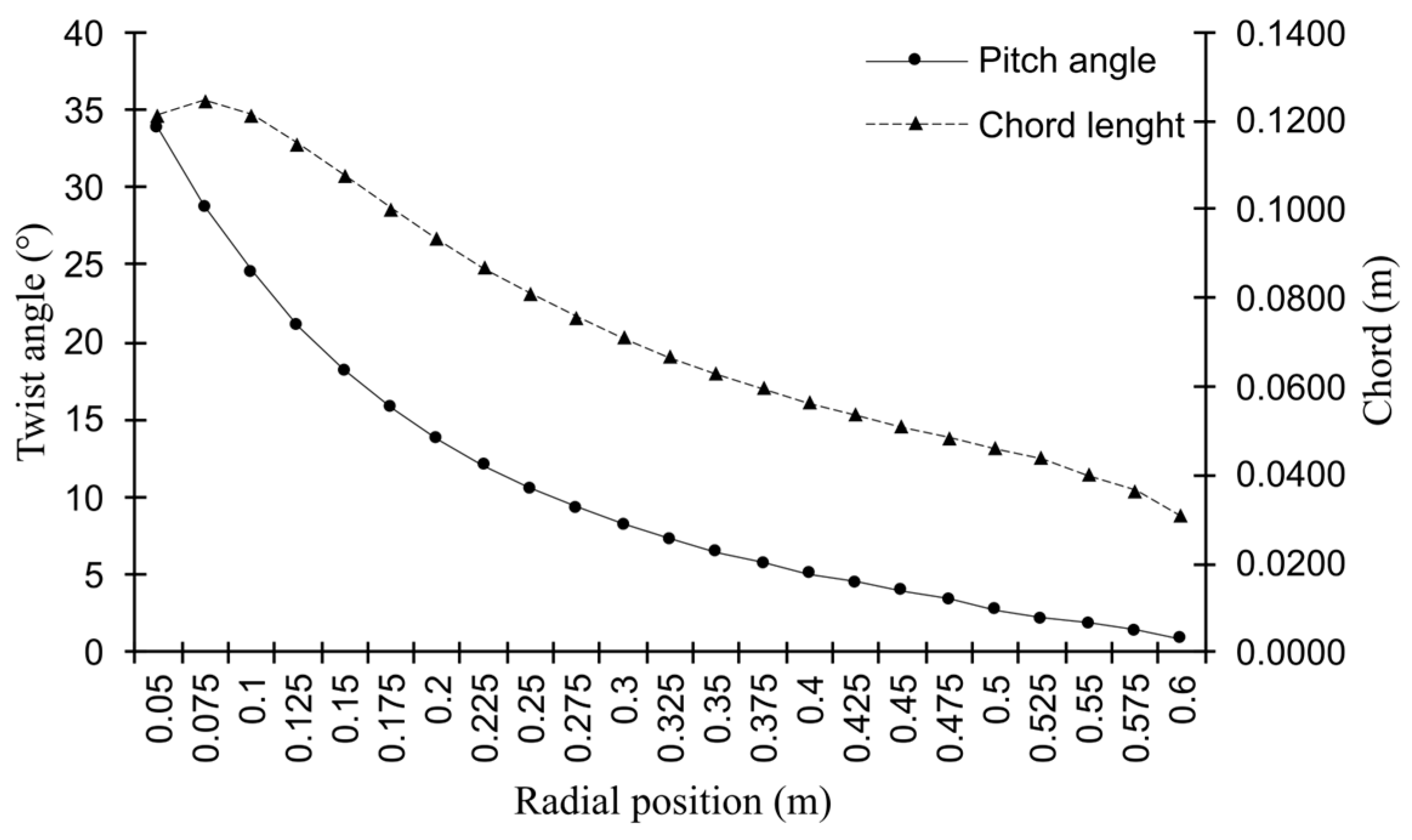
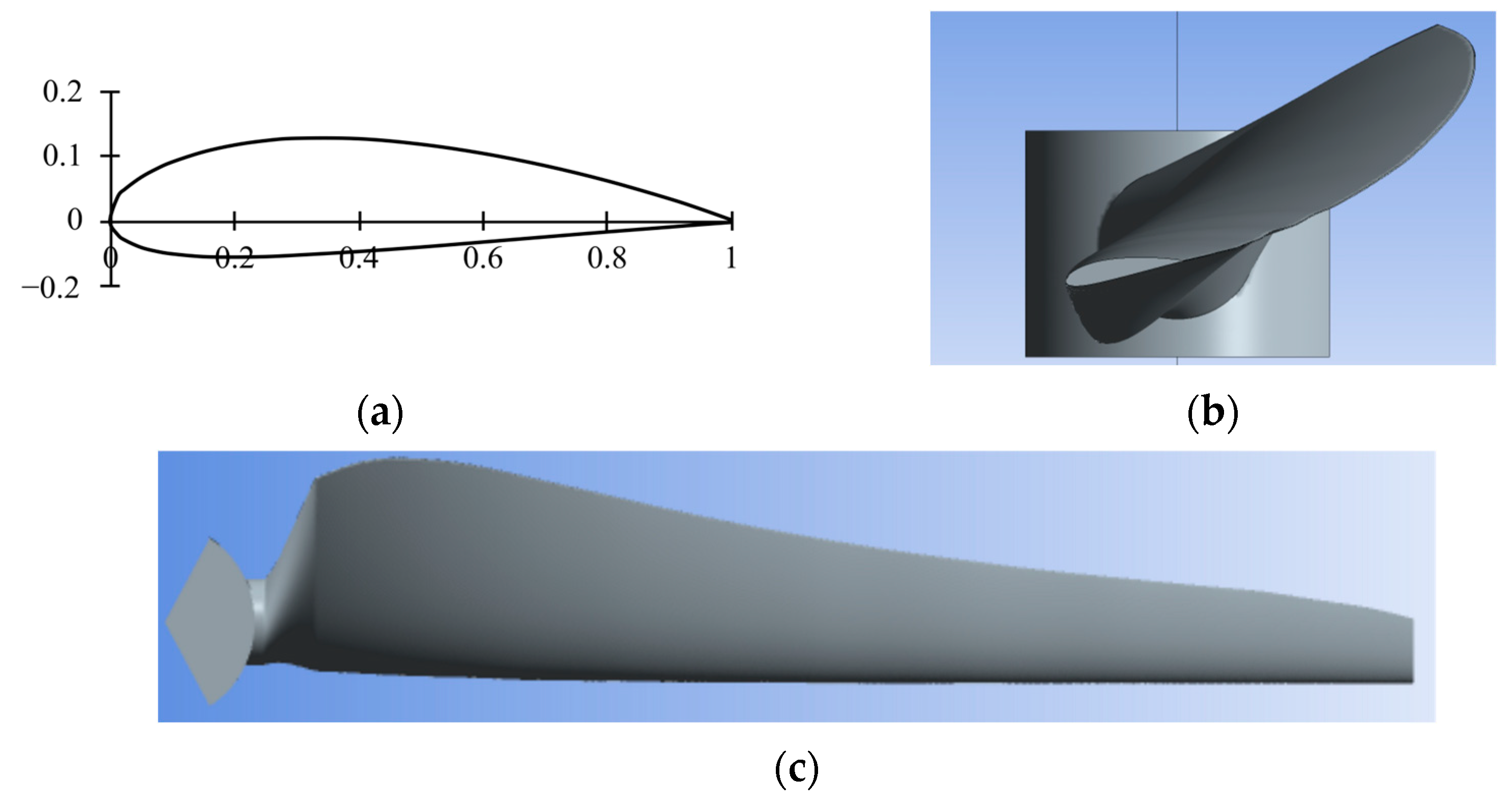
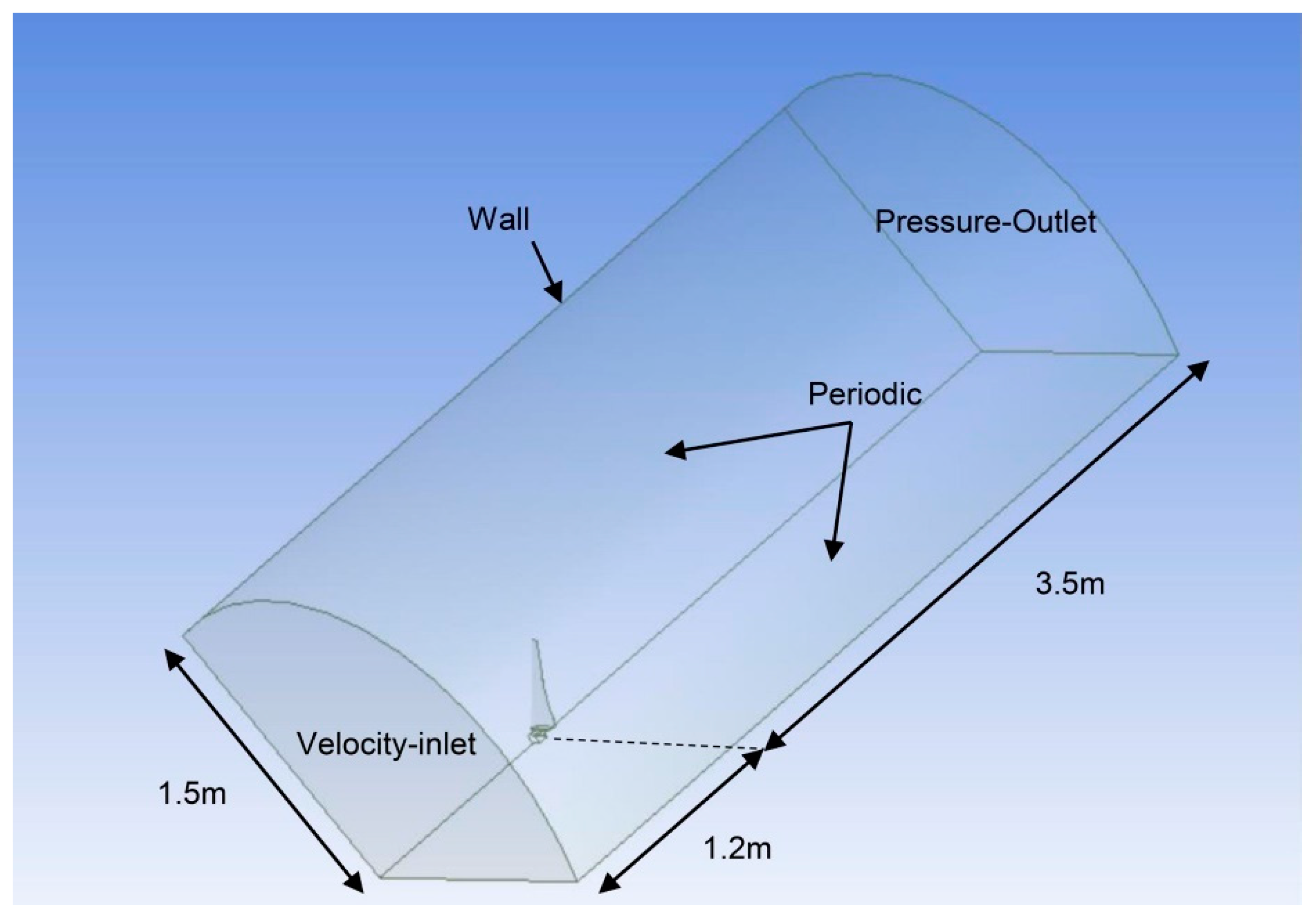
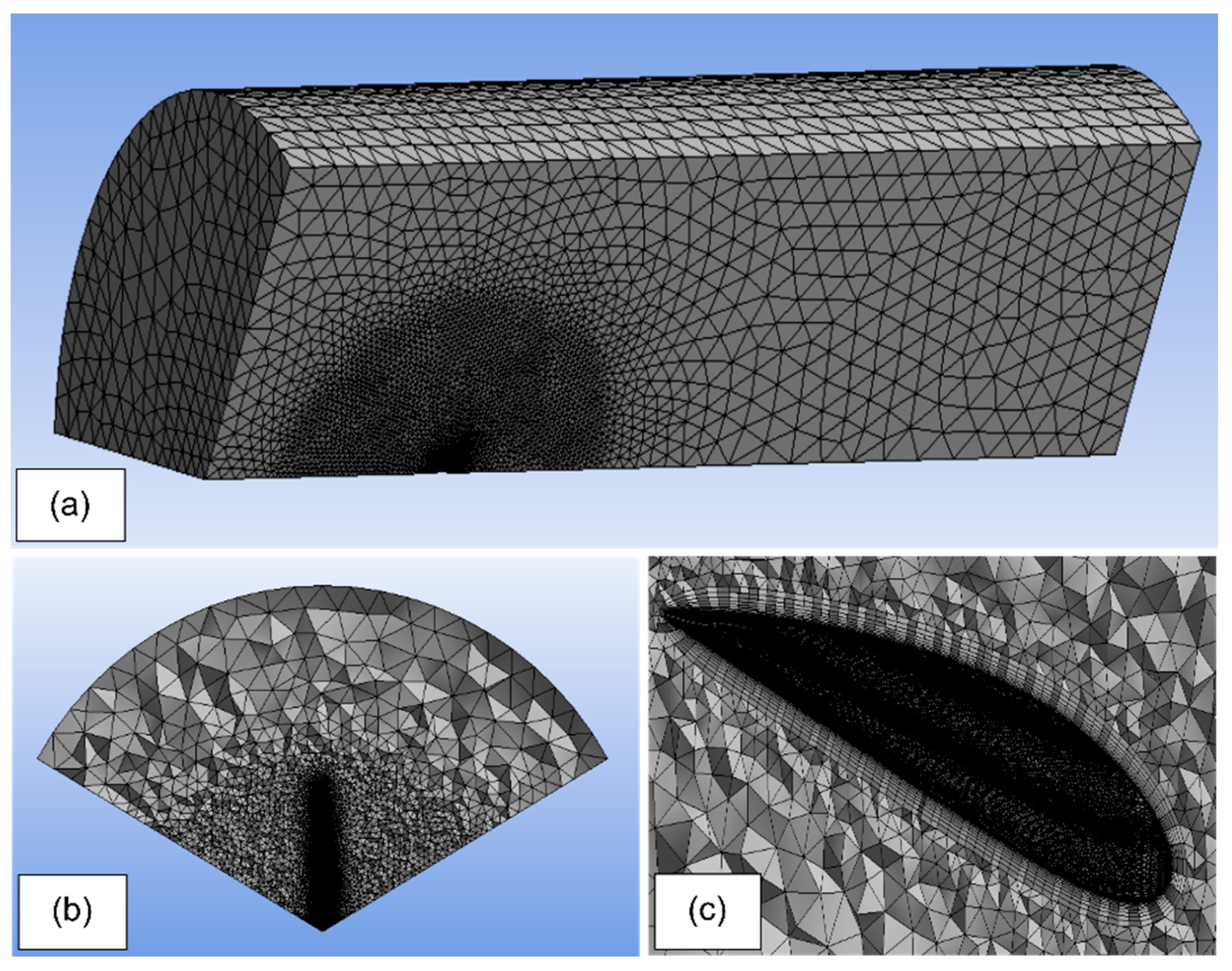

| Parameters | Values |
|---|---|
| Airfoil profile | NACA4418 |
| Designed wind speed | 8 m/s |
| Designed tip speed ratio | 5 |
| αopt | 6.5° |
| R | 0.65 m |
| B | 3 |
| r | 0.05 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Younoussi, S.; Ettaouil, A. Numerical Study of a Small Horizontal-Axis Wind Turbine Aerodynamics Operating at Low Wind Speed. Fluids 2023, 8, 192. https://doi.org/10.3390/fluids8070192
Younoussi S, Ettaouil A. Numerical Study of a Small Horizontal-Axis Wind Turbine Aerodynamics Operating at Low Wind Speed. Fluids. 2023; 8(7):192. https://doi.org/10.3390/fluids8070192
Chicago/Turabian StyleYounoussi, Somaya, and Abdeslem Ettaouil. 2023. "Numerical Study of a Small Horizontal-Axis Wind Turbine Aerodynamics Operating at Low Wind Speed" Fluids 8, no. 7: 192. https://doi.org/10.3390/fluids8070192
APA StyleYounoussi, S., & Ettaouil, A. (2023). Numerical Study of a Small Horizontal-Axis Wind Turbine Aerodynamics Operating at Low Wind Speed. Fluids, 8(7), 192. https://doi.org/10.3390/fluids8070192






