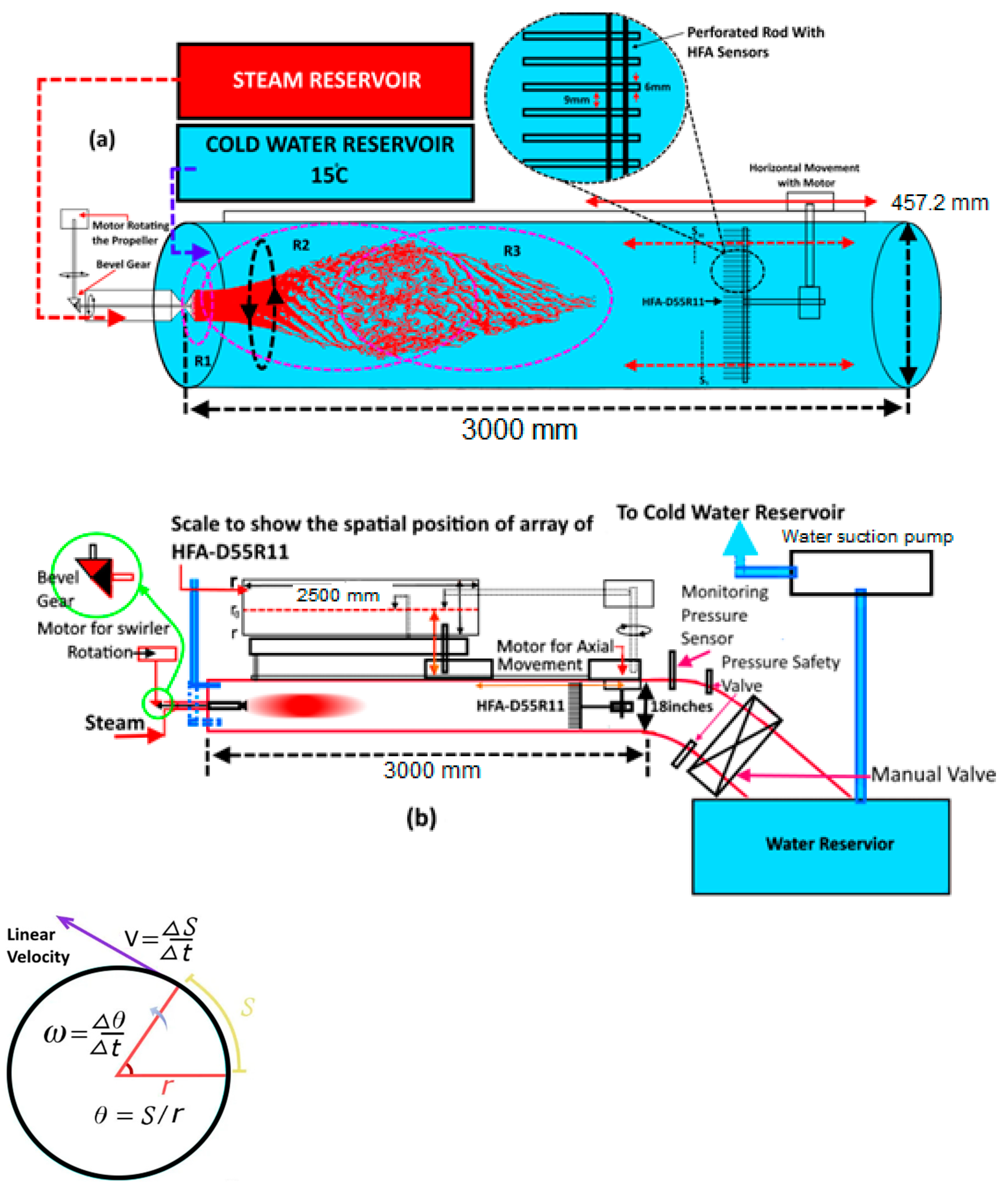
Both steam and water were injected at varying inlet gauge pressures of 1–2 bars, whereas the propeller was used to generate the swirling steam, which was rotated at rotational speeds of n = 60 and n = 300 rpm.
3.1. Ensembled Nature of the Normalized Amplitudes of the Velocity Fluctuations
In the current experimental setup, steam is injected in a swirling configuration into the water, which flows concurrently. The concurrently flowing water acts to impart shear force on the swirling steam body of the steam–water mixture, which leads to velocity fluctuations at the interface between the swirling steam and water flowing concurrently as a mixture, and this can be found from the attenuation of the normalized amplitudes of the velocity fluctuations. However, before looking into the results that were drawn from the observations, it is useful to briefly discuss the methodology that was used for the processing of the data. As outlined before, the data were acquired at a sampling rate of 5 kHz over 0.5 cm of the axial distance for 5 min across regions R1, R2, and R3. Therefore, a total of 15 million data points were recorded within R1, 45 million within region R2, and 60 million within region R3. The data were processed from each sensor based on the respective mean in each region (i.e., R1, R2, and R3) separately. The velocity fluctuations measured by each of the HFA sensors and their respective amplitudes were normalized by the respective mean amplitude of each HFA sensor in each region separately. The normalized amplitudes of these velocity fluctuations were found to decrease along the axial direction. This decrease was observed up to a certain point, corresponding to the vicinity of the most swollen portion of the steam–water swirling body along the axial axis, afterwards which point the trend changed and the velocity started increasing and then decreasing up to the end of the body of the swirling steam–water flow. This may have either been due to the contribution of the concurrently flowing water or due to the loss of strength (pressure drop along the axial direction) of the swirling steam–water volume inside the flow rig. Along the radial direction, these fluctuations increased, as measured by each of the HFA sensors with respect to their positions along the radial direction. This increase in the normalized velocity amplitudes shifted to large-scale fluctuations, which depicted that the sensors showing this trend were located across the steam–water swirling fluid’s interface with the concurrently flowing water. Thus, these measurements from the HFA sensors consolidate the idea that the velocity fluctuations and their respective normalized amplitudes exist inside a layer between the volumes of the two co-axial ellipsoidal areas, with one lying inside the other. The first (small) ellipsoidal volume is defined by the approximate proportionality or linearity of the variations in the velocity fluctuations along the radial direction inside the core ellipsoidal volume, while the second (larger) ellipsoidal volume is defined by the higher amplitude velocity fluctuations in the respective positions, thereby defining the layer in terms of the difference between their volumes. The thickness of this layer under the action of shear force by the concurrently flowing water decreases, which shows the attenuation of the normalized amplitudes under various operating conditions (as shown in
Table 1). The attenuation of the velocity fluctuations is due to the decrease in thickness of the inhibiting layer across all regions in the absence and in the presence of the concurrently acting shear force at a maximum of 300 rpm, as can be seen in
Figure 2a–c. Under the action of shear force, the thickness of the layer inhibiting flow instabilities cannot be decreased if the density of the fluid within the layer along the vertical axis is constant. In the present case, the density varies, so the thickness of the layer will also vary. These results are summarized further in terms of the variations in the volumes and surface areas of the respective ellipsoidal volumes, as shown by
Figure 3. The first and fourth bar chart in
Figure 3 support the conditions of no shear, whereas the rest of the bar charts depict the effects of the operating hydrodynamic conditions induced by shearing on the thickness of this layer, as well as the volume and surface areas.
It has been observed that across some length scales, the shear force from the concurrently flowing water imparts a similar effect on these amplitudes, decreasing their values uniformly. Alternatively, the normalized amplitudes corresponding to the velocity fluctuations behave in an ensembled manner to the shear force, acting on the co-current swirling steam–water body across the length scale, where their originating velocity fluctuations are recorded. A possible reason for the observation of this behavior across some spatial positions, across which the uniform attenuation of the velocity fluctuations by the concurrently flowing water and shear force occurs, is presented as follows. A mixing layer between the two fluids that interact with each other in any orientation can be regarded as a Rayleigh layer [
21,
22,
23], in which the velocity of the injected fluid itself sometimes becomes a source of filamentation of small scales at the outer surface of the injected fluid [
24]. This concept helps us to understand the dynamics of the cascading turbulence. The inner core velocities are connected to the outer core mixing layer velocities linearly, wherein the mixing Rayleigh layer is composed of small unstable coherent structures with a fine filamentary nature [
25]. Thus, if we consider the boundaries of the fluid layer exerting shear forces as static boundaries, the mixing Rayleigh layer interaction with the outer flowing fluid layers can be defined by the Rossby waves [
26,
27,
28].
According to the picture portrayed by Bains and Mitsudra [
29], the interaction of the mixing layers with the outer layers occurs in counter-propagation, which presents the possibility of enhanced constructive interaction and a phase-locking between these layers; on a contrary basis, any other flow orientation differing from the counter-propagation could inhibit the possibility of the non-constructive interaction, whereby the propagation due to the enhanced constructive interaction could be attenuated in an ensemble manner across a control plane. Thus, we can say that in such control planes under the length scale as defined previously, the rotational effects of the swirling fluids can perform a vital role to an extent, as contributed by the buoyancy and gravity waves, which impart a dominant influence on the evolution of the flow under certain shear forces [
30]. The uniform attenuation effect imparted by the shear force from the concurrently flowing water has been shown in a similar manner before [
24,
30], as the shearing affects the stability of the flow in the vicinity of the rotating volume of fluids on a large scale; the filaments rapidly become aligned; and when constantly applying shear force, the instabilities are suppressed on a uniform basis.
The shear force acts to suppress the growth rate and reduce the range of unstable wave numbers. Such behavior sheds light on the cascading turbulence in terms of local interactions, thereby bringing down the shearing from the global scale to the small filament scale. The initial stretching of the length scale along the radial direction can lead into a control plan; however, when this scale is traversed to a certain length along the axial direction, ensembled normalized amplitudes of the velocity fluctuations occur. The effect of the non-dimensional swirl intensity
(where
is the horizontal distance from the nozzle outlet and
is the diameter of the rig) against the initial swirl intensity
(given by Equations (3) and (4)) [
31] on the location of the control plane is shown in
Figure 4:
where
is the radius of the swirl and
is the density of the fluid; in this case, we calculate the approximate density of the fluid at the respective spatial position with the help of the temperature of the fluid, i.e., either steam or water, using the LM35 temperature sensor [
17]. Here,
is the tangential velocity, which is determined using Equation (4), and
is the axial velocity. It should be noted that the velocity fluctuations are measured across the flow rig, whereas
Ux is the axial velocity, which is merely confined to the axial measurements. It should be noted that not only was the existence of the control plane confirmed by the repetition of the experiments. Changing the rpm of the propeller as well as replacing the base plate for the cold water injection with the new base plate, which had a different orientation of the water injection ports on the left-hand side of the rig, led to the value for the non-dimensionalized swirl intensity being equal to the value of the initial swirl intensity at the spatial location within the control plane. This point is referred to as the critical point where both swirl intensities are equal. The possible reasons for this critical point where the values of the
are approximately equal to the
S0 are illustrated in the following paragraph.
The Brunt–Väisälä frequency or buoyancy frequency is a measure of the stability of the fluid to the vertical displacements. In the present case, the swirl intensity
S0 is measured at the position in the proximity of the steam nozzle and
is measured along the axial axis, so this can be attributed to the frequency of the steam bubble’s inception and collapse inside the water domain. If this frequency is weak as compared to the rotational frequency, this will permit large amplitudes of the flow fluctuations. On a contrary basis, when the frequency of the buoyancy is more rapid than the frequency of the rotation, the amplitudes of the disturbances are not so significant [
32,
33] and the fluid layers can become stratified. In the present case, across all three regions, R1, R2, and R3, the equality of these two frequencies may be due to the delay in the propagation of the velocity fluctuations until those spatial positions at which
,
S0 ≈ 0.07. This equality condition exists within the uniform attenuation control plane length scale, so the role being played by the equality of these two frequencies in the uniform attenuation cannot be ignored in view of equating the effects of stabilizing and non-stabilizing factors.
3.2. Hydrodynamics of the Swirling Steam–Water Two-Phase Flow
The existence of spatial positions across which the swirling steam–water two-phase flow-induced velocity-fluctuation-based normalized amplitudes behave in an ensembled way was observed at varying inlet gauge pressure levels of the steam and water, i.e., 1–2 bars, and at varying rpm values of 60–300. The normalized amplitudes of the velocity fluctuations were investigated under three conditions, i.e., under the effect of shearing, which was investigated by varying the inlet pressures of the steam and concurrently flowing water; swirling, which was investigated by varying the rpm rates of the swirler; and discrete large-scale changes in the operating conditions. The details of these applied conditions and their outcomes are presented and discussed in the following paragraphs.
3.2.1. Hydrodynamic Nature of the Normalized Velocity Amplitudes under Shearing
The normalized velocity amplitudes were estimated based on the velocity fluctuations across the three regions, namely R1, R2, and R3. As mentioned before, during the analysis of the normalized amplitudes of velocity fluctuations, the amplitudes were measured against the normalized velocity fluctuations under the shear force acting on the swirling steam–water flow in an ensemble way.
It was observed that along a radial line segment, we could define a length using certain spatial points by traversing the HFA sensor array along the axial direction away from the exit of the nozzle. Under varying conditions of the inlet pressure and a fixed rotational speed, i.e., 300 rpm (higher swirl intensity S0 at the exit of the nozzle), it was observed that the normalized amplitudes of the velocity fluctuations at these spatial positions showed varying behaviors under the effects of the shear force acting on this region from the concurrently flowing water.
First, it should be noted that the spatial resolution for the observation of this behavior was 0.1 cm, i.e., the vertically mounted HFA sensors were traversed at a discrete spatial step of 0.1 cm. Thus, the measurements being collected over the increased spatial resolution of the fluid region totaled about 600 million data points across all regions, i.e., R1, R2, and R3, at the maximum rotation speed of 300 rpm. Further, it was observed in the first case that after the onset of a steam and water injection at 1 bar of gauge pressure, the velocity fluctuations showed an ensembled nature over an area with a length of ~2.1 cm, with ~6.3% of the total data points showing ensembled normalized behavior in view of the normalized amplitudes of the velocity fluctuations. When the shear was increased in the second case, corresponding to 2 bars of the gauge pressure for the water, the values of the normalized amplitudes of the velocity fluctuations were reduced and the area at which these normalized velocity fluctuation amplitudes prevailed was stretched, with a total increase of ~1.2% as compared to the total area where these amplitudes prevailed at 1 bar of gauge pressure.
Thus, it was observed that in the first two cases, i.e., Ps and Pw = 1 bar and Ps and Pw = 2 bars, the spatial distance across which the ensemble normalized amplitudes of the velocity fluctuations were found increased by ~1.2%. In the third and fourth cases, i.e., Ps = 2 bars and Pw = 1 bar and Ps = 2 bars and Pw = 2 bars, the number of these ensembled normalized amplitudes of the velocity fluctuations increased, with a total of 4.7% of the fluctuations showing an ensembled nature. These ensembled amplitudes of the velocity fluctuations in case 4 prevailed at a length that was 2.7% longer than the length at which the amplitudes prevailed in case 3.
Thus, we can safely say that under the action of the shear-induced stretching exerted by the concurrently flowing water, as well as by keeping in mind the unstable fluctuating nature of the steam inside the water and the relative error in the HFA measurements (3–3.2%), the swirling steam–water two-phase flows showed a nearly proportional varying nature in view of the ensembled normalized velocity amplitudes across the spatial length scale.
3.2.2. Normalized Velocity Amplitudes under the Action of Shearing
The hydrodynamic characteristics of the swirling steam–water two-phase flows were investigated under the action of the operating conditions. It was observed that the effect of the stretching was imparted on the ensembled normalized amplitudes of the velocity fluctuations in view of an increase in the number of their occurrences as well as stretching in an area on a proportional basis. Here, the effect of the swirl intensity was investigated on the swirling steam–water two-phase flows. The propeller’s non-dimensionalized swirl intensity rates S0 at the exit of the steam nozzle varied from 0 to 0.15, with the maximum values used for the rest of the hydrodynamic conditions, i.e., Ps and Pw = 2 bars. Further, it was found that by segregating the values of the swirling intensity into three blocks, i.e., (0–0.05), (0.05–0.10), and (0.10–0.15), the effect of the increase in non-dimensionalized swirling intensity on the area under the influence of the ensembled normalized amplitudes of the velocity fluctuations was imparted on a proportional basis. Initially, with an increase in the values of the non-dimensionalized swirling intensity S0 from 0 to 0.05, the thickness of the layer, i.e., the radial distance across which the amplitudes travelled increased to around 0.7%. The length scale under the influence of the ensembled normalized amplitudes of the velocity fluctuations was increased to a length of 1.81 cm, with the total number of ensembled normalized amplitudes of the velocity fluctuations being approximately equal to 0.18% of the total number of velocity fluctuation amplitudes across this length. Further, with an increase in the values of the non-dimensionalized swirling intensity from 0.05 to 0.10, the thickness of the layer was increased by around 0.82% and the length under the influence of the ensembled normalized amplitudes of the velocity fluctuations was increased to 1.7%. With a further increase in the values of the non-dimensionalized swirling intensity S0 from 0.10 to 0.15, the thickness of the layer was increased to around 1%, with the length under the influence of these ensembled normalized amplitudes of the velocity fluctuations increasing to 2.1%. Thus, we can safely say that under the action of the swirling exerted by the propeller, while also keeping in mind the unstable fluctuating nature of the steam inside the water and the relative errors in the HFA measurements (3–3.2%), the swirling steam–water two-phase flows showed a nearly proportional nature under the action of swirling in terms of the ensembled normalized velocity amplitudes across the length scale.
3.2.3. Normalized Velocity Amplitudes under Large Discrete Variations in Inlet Hydrodynamic Conditions
The steam–water two-phase flows were investigated under the action of stretching as well as swirling. It was observed that the two-phase fluid flow exhibited a nearly proportional nature in terms of the number of ensemble average velocity fluctuation magnitudes under the action of the mentioned conditions. Here, in order to confirm the nature of these flows under discrete large-scale variations of the hydrodynamic conditions, we used two sets of operating conditions. In the first set, both the steam and water were injected at the same 1 bar of gauge pressure at 60 rpm. In the second set of operating conditions, both the steam and water were injected at the same pressure of 2 bars of gauge pressure at
S0 = 0.15. For this purpose, the steam and water concurrent injection was controlled by a solenoid valve, which was controlled electronically with a delay time of 0.001 s. The speed of the motor was controlled by another DC motor, which was regulated for a step increase of
n = 300 rpm, with a delay time of 0.01 s. The difference in these delays could play a significant role if the length scale for the ensemble velocity fluctuates within the vicinity of the steam nozzle exit. However, these delays were ignored, as the propagation of these effects by the steam and water imparted respective variations in the inlet injection pressures, as well as variations in rpm, while
S0 was measured approximately at a distance greater than ~20 cm away from the nozzle exit (
Figure 4). It was observed that in the first case, i.e., at Ps and Pw = 1 bar at rpm = 60, the length scale was equal to a length of ~1.91 cm, with 0.9% of the total length along the radial direction showing these ensembled amplitudes of the velocity fluctuations.
In the second case, i.e., at Ps and Pw = 2 bar at n = 300 rpm, the length scale increased to around ~4.9%, where the ensembled normalized amplitudes of the velocity fluctuations were observed. Thus, if we consider the number of these ensembled normalized amplitudes of the velocity fluctuations/cm as the response of the steam–water two-phase flow system to the discrete variation of the hydrodynamic conditions, along with the variations in the length scale across which these ensembled normalized amplitudes of the velocity fluctuations were recorded, we can say that the steam–water two-phase flow system responded to the discrete large-scale variations of the hydrodynamic operating conditions on a proportionally varying basis. Thus, we can safely say that by keeping in mind the unstable fluctuating nature of the steam inside the water and the relative errors in the HFA measurements (3–3.2%), the swirling steam–water two-phase flows showed a nearly varying proportional nature in terms of the ensembled normalized velocity amplitudes across the length scale under the action of discrete large-scale changes in the hydrodynamical conditions.