Simulation of Dynamic Rearrangement Events in Wall-Flow Filters Applying Lattice Boltzmann Methods
Abstract
1. Introduction
2. Mathematical Modelling and Numerical Methods
2.1. Discrete Contact Modelling
3. Application to a Wall-Flow Filter
- Fluid velocity ramp-up and convergence with static fragmented layer;
- Detachment of fragments;
- Transport of fragments;
- Plug formation.
- Areas of complete detachment;
- Areas of incomplete detachment and re-deposition;
- Volume occupied by the plug;
- Local compactness inside the plug.
4. Results and Discussion
4.1. Rearrangement in Base Configuration
4.1.1. Fragmented Layer State
4.1.2. Transient Behaviour
4.1.3. Plug State
4.2. Influence of Fragmented Layer Topology
4.2.1. Influence of Layer Height
4.2.2. Influence of Fragment Dimensions
4.2.3. Influence of Layer Structure
4.3. Influence of PM Properties and Operating Conditions
4.3.1. Influence of PM Density
4.3.2. Influence of Mechanical Properties
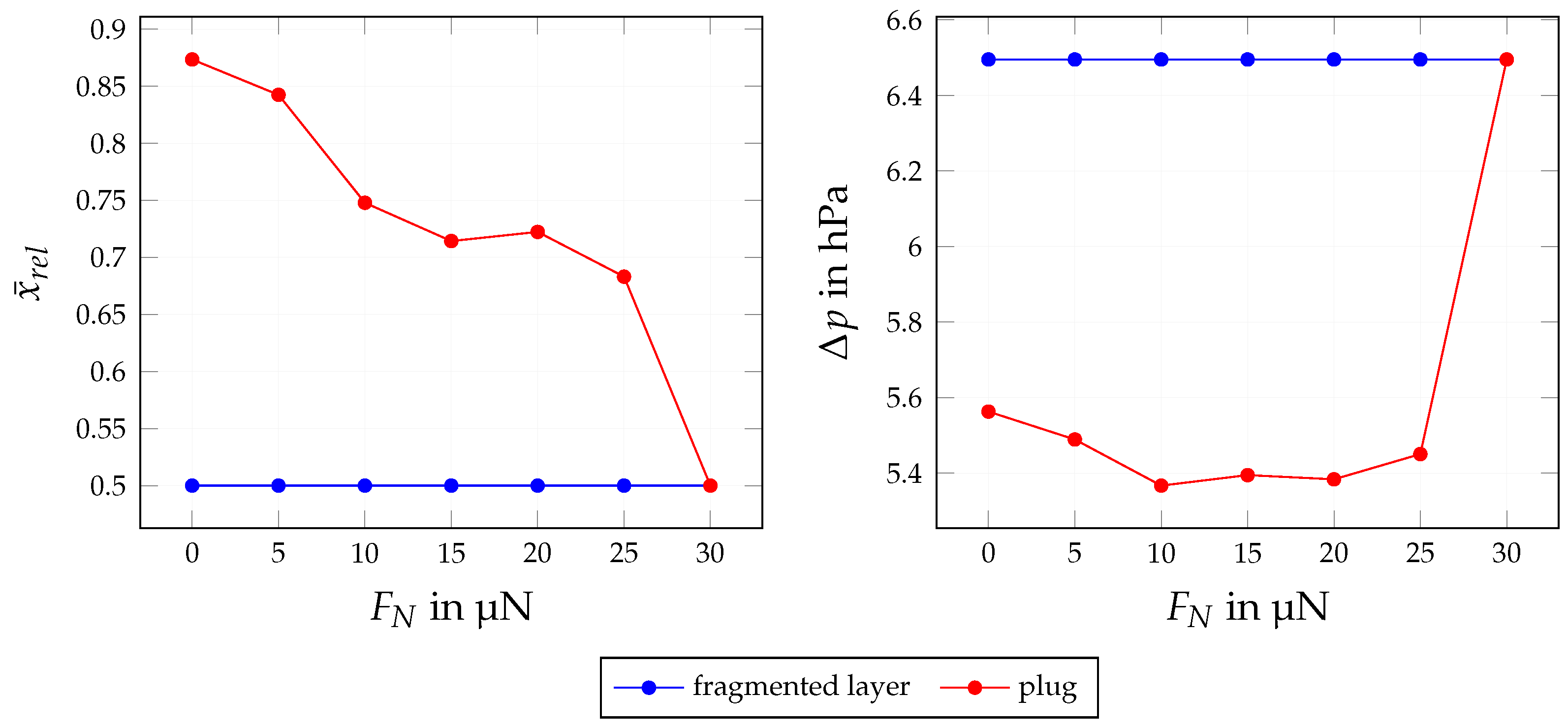
4.3.3. Influence of Adhesive Forces
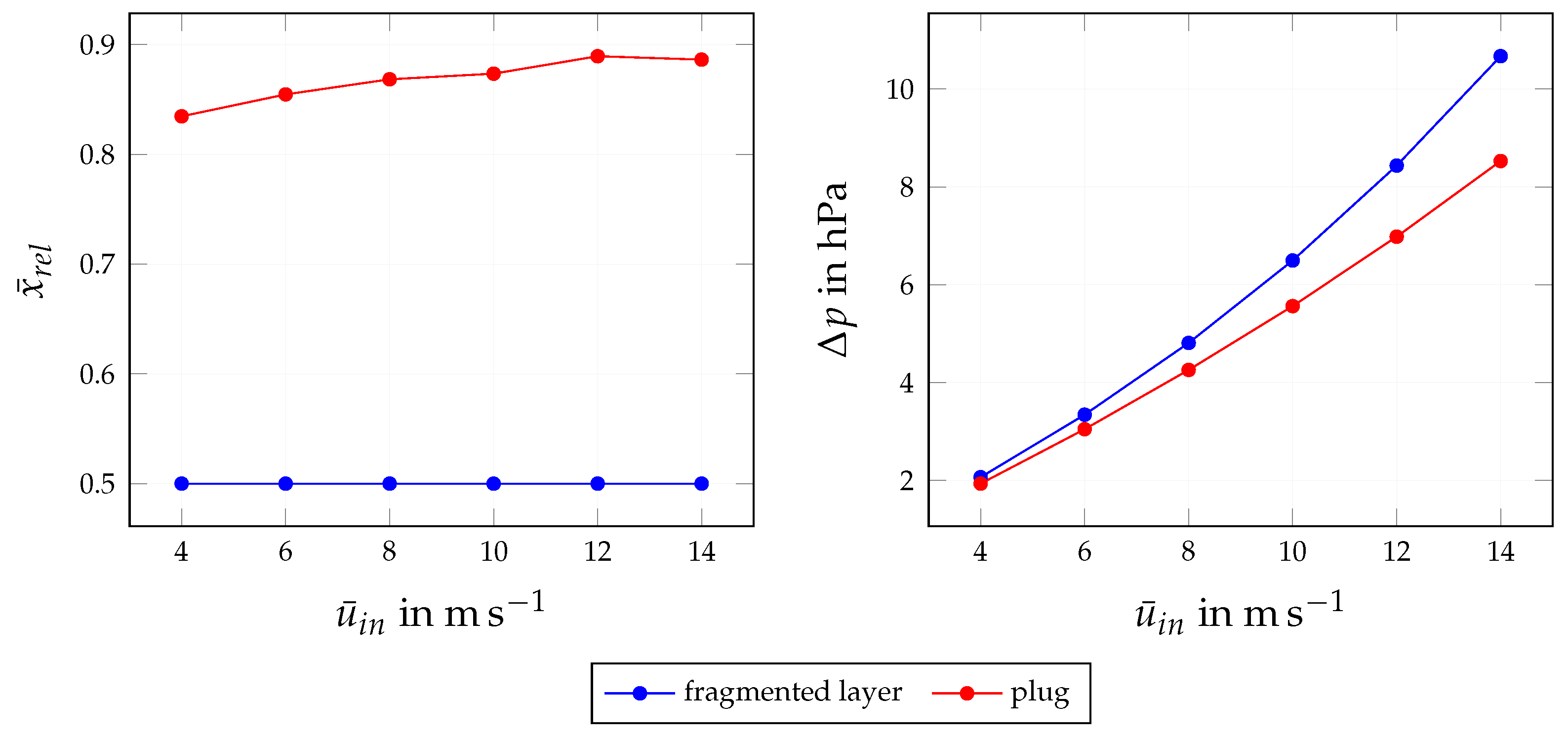
4.3.4. Influence of Inflow Velocity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | computational fluid dynamics |
| LBM | lattice Boltzmann method |
| NSE | Navier–Stokes equation |
| PM | particulate matter |
Nomenclature
| fluid velocity | |
| p | fluid pressure |
| position | |
| t | time |
| N | resolution of voxel mesh |
| particle velocity | |
| particle angular velocity | |
| particle mass | |
| particle’s momentum of inertia | |
| particle’s kinetic energy | |
| channel length | |
| channel width | |
| scaled channel length | |
| average inflow velocity | |
| particle density | |
| mean density (along layer and plug) | |
| fragment’s x-dimension | |
| fragment’s equilateral width | |
| hydrodynamic normal force | |
| number of fragment rows over channel length | |
| time at converged fragmented layer state | |
| time at final plug state | |
| Inlet channel domain | |
| Outlet channel domain | |
| normal contact force | |
| effective modulus of elasticity | |
| k | contact type constant |
| contact overlap volume | |
| contact indentation depth | |
| c | damping factor |
| relative velocity between objects | |
| modulus of elasticity of object A | |
| Poisson’s ratio of object A | |
| e | coefficient of restitution |
| domain of central inlet channel | |
| domain of representative outlet channel |
References
- Wang, Y.; Kamp, C.J.; Wang, Y.; Toops, T.J.; Su, C.; Wang, R.; Gong, J.; Wong, V.W. The origin, transport and evolution of ash in engine particulate filters. Appl. Energy 2020, 263, 114631. [Google Scholar] [CrossRef]
- Gaiser, G. Berechnung von Druckverlust, Ruß- und Ascheverteilung in Partikelfiltern. MTZ-Mot. Z. 2005, 66, 92–102. [Google Scholar] [CrossRef]
- Sappok, A.; Govani, I.; Kamp, C.; Wang, Y.; Wong, V. In-Situ Optical Analysis of Ash Formation and Transport in Diesel Particulate Filters during Active and Passive DPF Regeneration Processes. SAE Int. J. Fuels Lubr. 2013, 6, 336–349. [Google Scholar] [CrossRef]
- Ishizawa, T.; Yamane, H.; Satoh, H.; Sekiguchi, K.; Arai, M.; Yoshimoto, N.; Inoue, T. Investigation into Ash Loading and Its Relationship to DPF Regeneration Method. SAE Int. J. Commer. Veh. 2009, 2, 164–175. [Google Scholar] [CrossRef]
- Aravelli, K.; Heibel, A. Improved Lifetime Pressure Drop Management for Robust Cordierite (RC) Filters with Asymmetric Cell Technology (ACT). In Proceedings of the SAE World Congress & Exhibition; SAE International: Warrendale, PA, USA, 2007. [Google Scholar] [CrossRef]
- Dittler, A. Ash Transport in Diesel Particle Filters. In Proceedings of the SAE 2012 International Powertrains, Fuels & Lubricants Meeting; SAE International: Warrendale, PA, USA, 2012. [Google Scholar] [CrossRef]
- Dittler, A. Abgasnachbehandlung mit Partikelfiltersystemen in Nutzfahrzeugen, 1st ed.; Wuppertaler Reihe zur Umweltsicherheit; Shaker: Herzogenrath, Germany, 2014. [Google Scholar]
- Wang, Y.; Kamp, C. The Effects of Mid-Channel Ash Plug on DPF Pressure Drop. In Proceedings of the SAE 2016 World Congress and Exhibition; SAE International: Warrendale, PA, USA, 2016. [Google Scholar] [CrossRef]
- Hafen, N.; Dittler, A.; Krause, M.J. Simulation of particulate matter structure detachment from surfaces of wall-flow filters applying lattice Boltzmann methods. Comput. Fluids 2022, 239, 105381. [Google Scholar] [CrossRef]
- Hafen, N.; Thieringer, J.R.; Meyer, J.; Krause, M.J.; Dittler, A. Numerical investigation of detachment and transport of particulate structures in wall-flow filters using lattice Boltzmann methods. J. Fluid Mech. 2023, 956, A30. [Google Scholar] [CrossRef]
- Hafen, N.; Marquardt, J.E.; Dittler, A.; Krause, M.J. Simulation of Particulate Matter Structure Detachment from Surfaces of Wall-Flow Filters for Elevated Velocities Applying Lattice Boltzmann Methods. Fluids 2023, 8, 99. [Google Scholar] [CrossRef]
- Krause, M.J.; Kummerländer, A.; Avis, S.J.; Kusumaatmaja, H.; Dapelo, D.; Klemens, F.; Gaedtke, M.; Hafen, N.; Mink, A.; Trunk, R.; et al. OpenLB—Open source lattice Boltzmann code. Comput. Math. Appl. 2021, 81, 258–288. [Google Scholar] [CrossRef]
- Kummerländer, A.; Avis, S.; Kusumaatmaja, H.; Bukreev, F.; Crocoll, M.; Dapelo, D.; Hafen, N.; Ito, S.; Jeßberger, J.; Marquardt, J.E.; et al. OpenLB Release 1.6: Open Source Lattice Boltzmann Code. 2023. Available online: https://doi.org/10.5281/zenodo.7773497 (accessed on 18 June 2023).
- Konstandopoulos, A.G.; Skaperdas, E.; Warren, J.; Allansson, R. Optimized Filter Design and Selection Criteria for Continuously Regenerating Diesel Particulate Traps. In Proceedings of the International Congress & Exposition; SAE International: Warrendale, PA, USA, 1999. [Google Scholar] [CrossRef]
- Thieringer, J.R.D.; Hafen, N.; Meyer, J.; Krause, M.J.; Dittler, A. Investigation of the Rearrangement of Reactive ash; Inert Particulate Structures in a Single Channel of a Wall-Flow Filter. Separations 2022, 9, 195. [Google Scholar] [CrossRef]
- Kimura, K.; Lynskey, M.; Corrigan, E.R.; Hickman, D.L.; Wang, J.; Fang, H.L.; Chatterjee, S. Real World Study of Diesel Particulate Filter Ash Accumulation in Heavy-Duty Diesel Trucks. In Proceedings of the Powertrain & Fluid Systems Conference and Exhibition; SAE International: Warrendale, PA, USA, 2006. [Google Scholar] [CrossRef]
- Sappok, A.; Santiago, M.; Vianna, T.; Wong, V.W. Controlled Experiments on the Effects of Lubricant/Additive (Low-Ash, Ashless) Characteristics on DPF Degradation. In Proceedings of the Diesel Engine-Efficiency and Emissions Research (DEER) Conference, Dearborn, MI, USA, 4–7 August 2008. [Google Scholar]
- Hafen, N.; Krause, M.J.; Dittler, A. Simulation of Particle-Agglomerate Transport in a Particle Filter using Lattice Boltzmann Methods. In 22. Internationales Stuttgarter Symposium; Bargende, M., Reuss, H.C., Wagner, A., Eds.; Springer: Wiesbaden, Germany, 2022; pp. 292–303. [Google Scholar]
- Marquardt, J.E.; Römer, U.J.; Nirschl, H.; Krause, M.J. A discrete contact model for complex arbitrary-shaped convex geometries. Particuology 2023, 80, 180–191. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M. Numerische Strömungsmechanik; Springer eBook Collection; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Nassauer, B.; Kuna, M. Contact forces of polyhedral particles in discrete element method. Granul. Matter 2013, 15, 349–355. [Google Scholar] [CrossRef]
- Carvalho, A.S.; Martins, J.M. Exact restitution and generalizations for the Hunt–Crossley contact model. Mech. Mach. Theory 2019, 139, 174–194. [Google Scholar] [CrossRef]
- Ladd, A.J.C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 1994, 271, 285–309. [Google Scholar] [CrossRef]
- Latt, J.; Chopard, B.; Malaspinas, O.; Deville, M.; Michler, A. Straight velocity boundaries in the lattice Boltzmann method. Phys. Rev. E 2008, 77, 056703. [Google Scholar] [CrossRef] [PubMed]
- Skordos, P.A. Initial and boundary conditions for the lattice Boltzmann method. Phys. Rev. E 1993, 48, 4823–4842. [Google Scholar] [CrossRef]
- Cooper, R.C.; Bruno, G.; Onel, Y.; Lange, A.; Watkins, T.R.; Shyam, A. Young’s modulus and Poisson’s ratio changes due to machining in porous microcracked cordierite. J. Mater. Sci. 2016, 51, 9749–9760. [Google Scholar] [CrossRef]
- Pandey, A.; Shyam, A.; Watkins, T.R.; Lara-Curzio, E.; Stafford, R.J.; Hemker, K.J. The Uniaxial Tensile Response of Porous and Microcracked Ceramic Materials. J. Am. Ceram. Soc. 2014, 97, 899–906. [Google Scholar] [CrossRef]
- Thota, S.K.; Cao, T.D.; Vahedifard, F. Poissons Ratio Characteristic Curve of Unsaturated Soils. J. Geotech. Geoenviron. Eng. 2021, 147, 04020149. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]

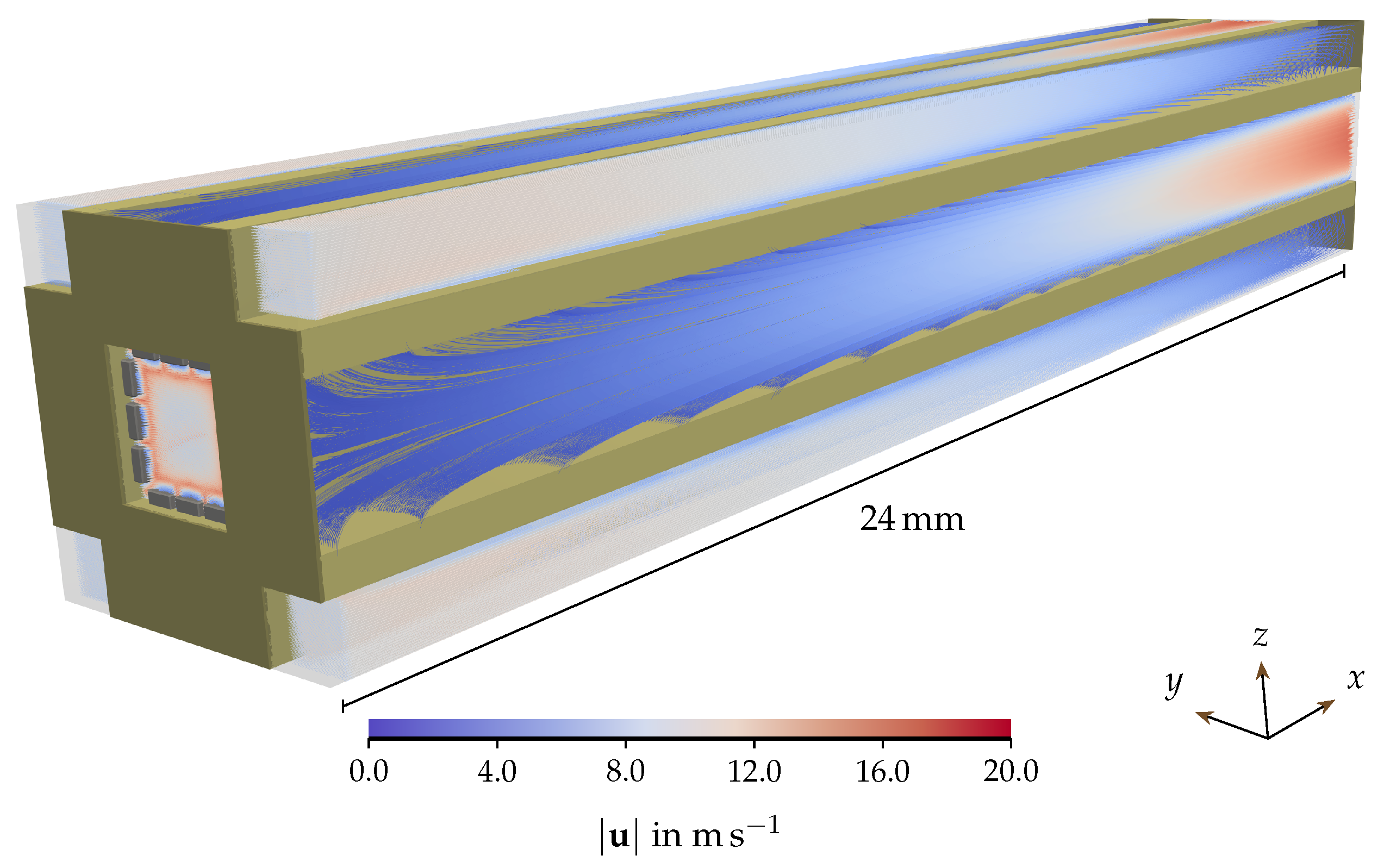

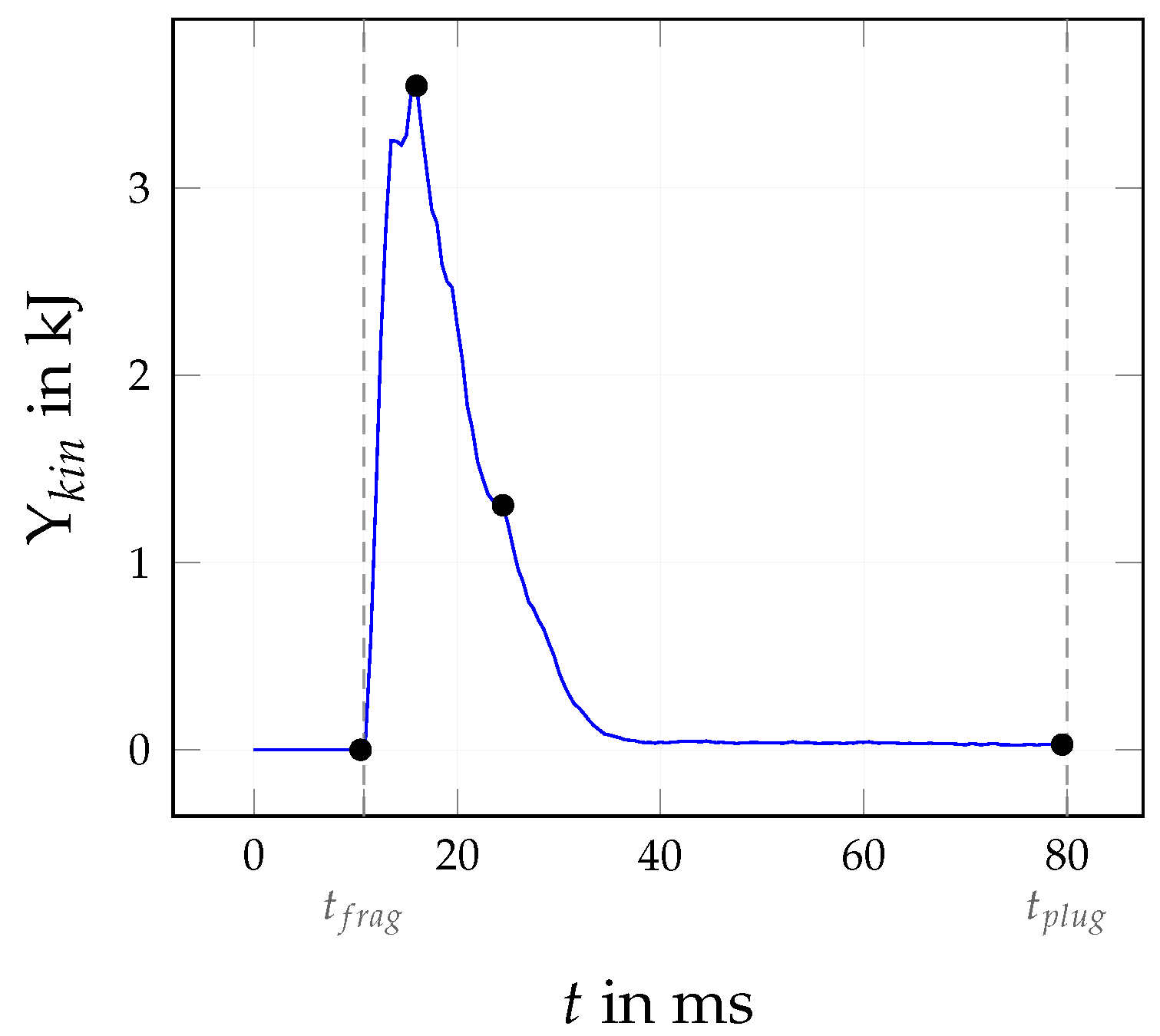
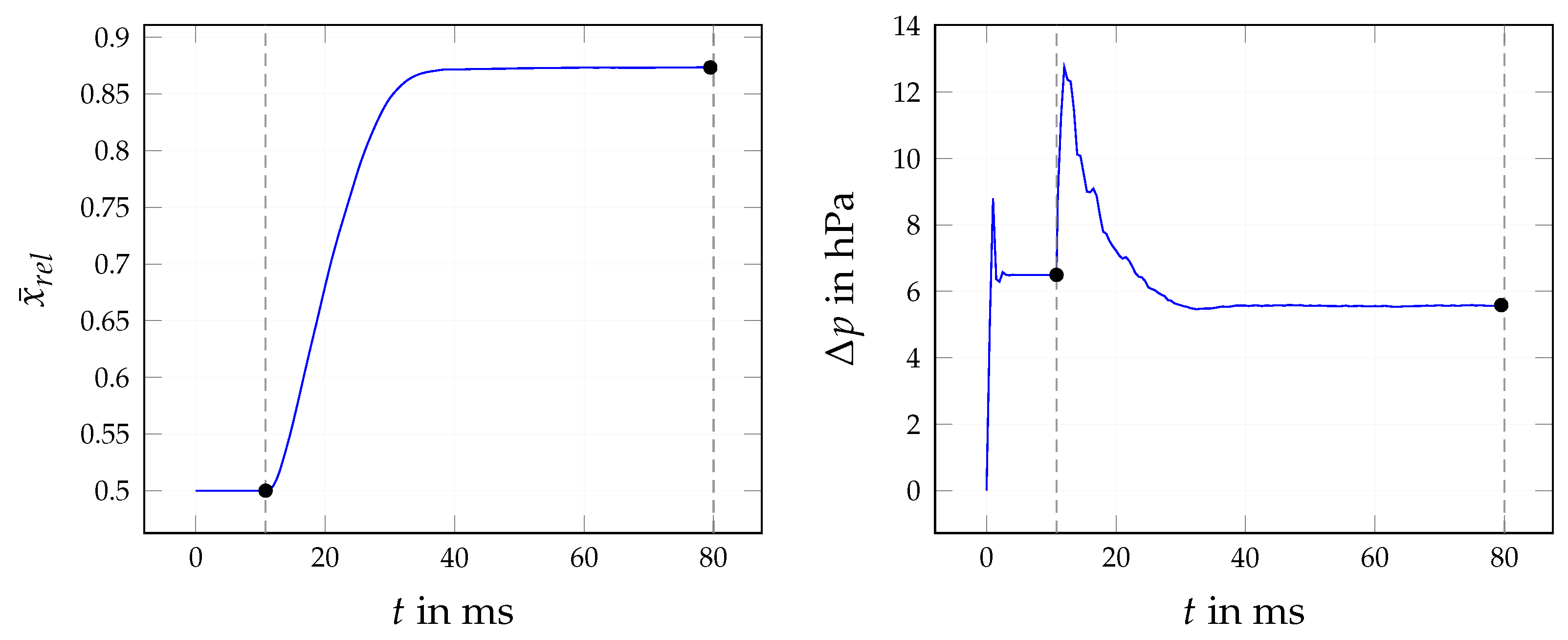

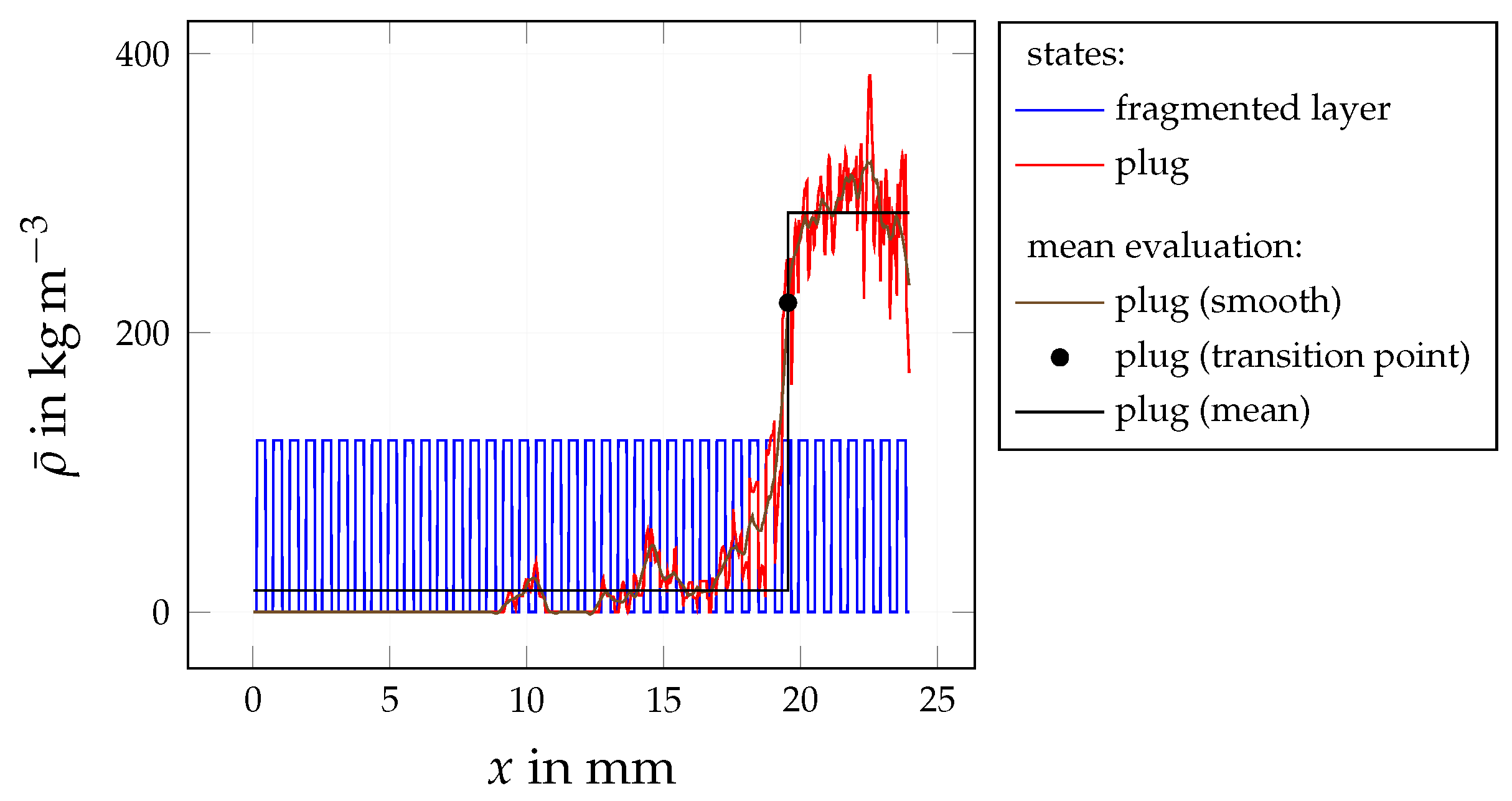
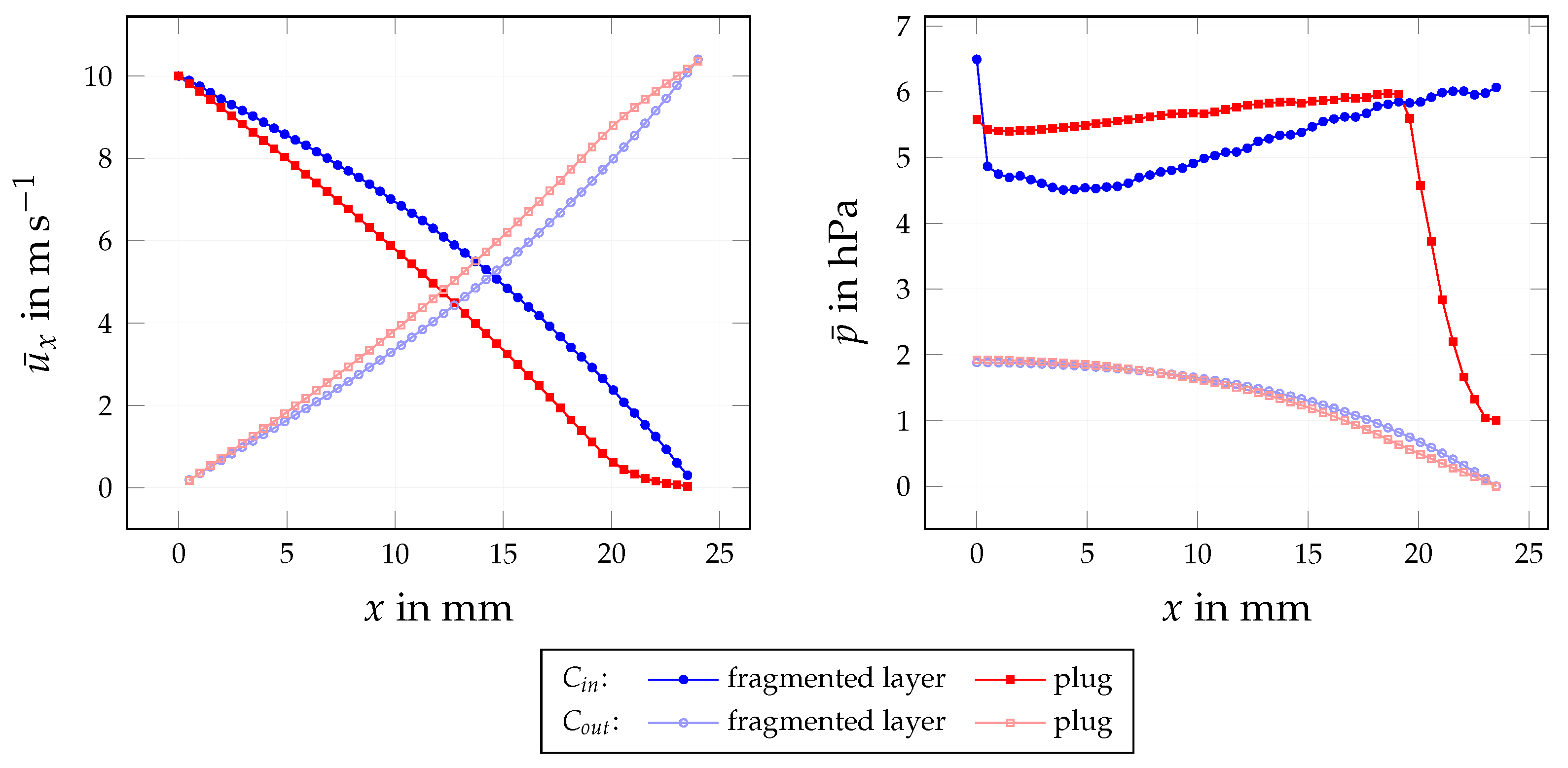
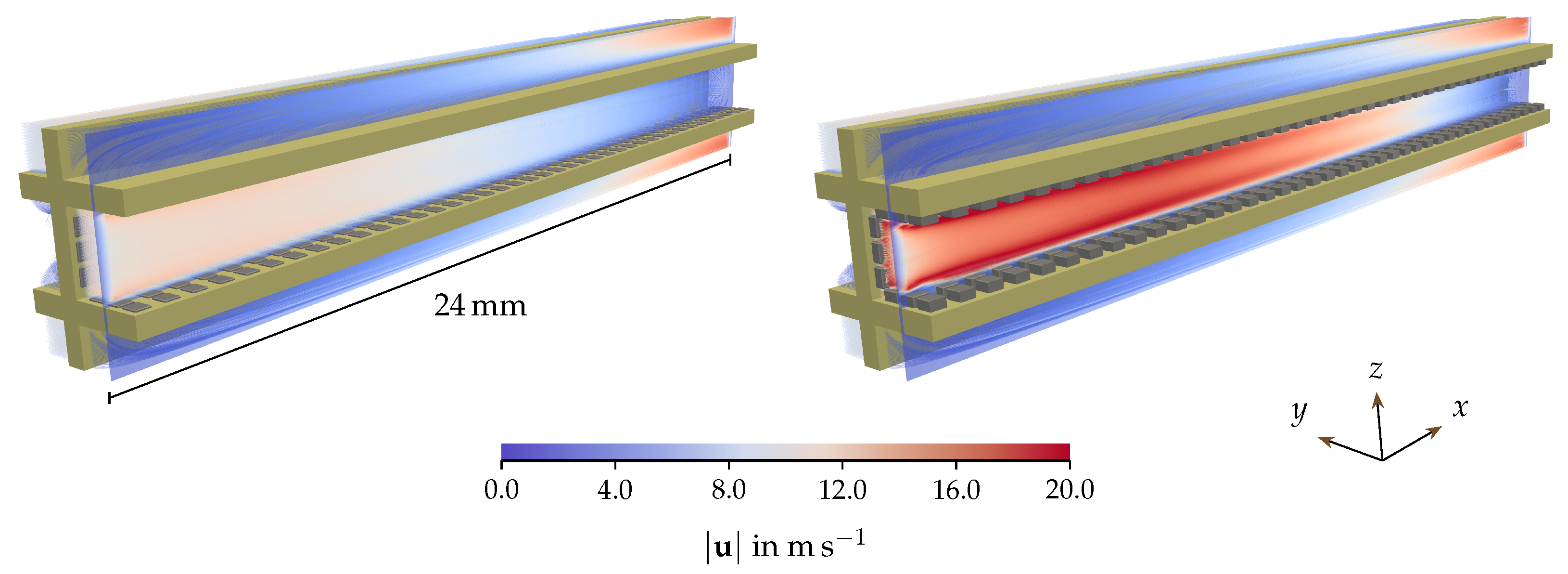
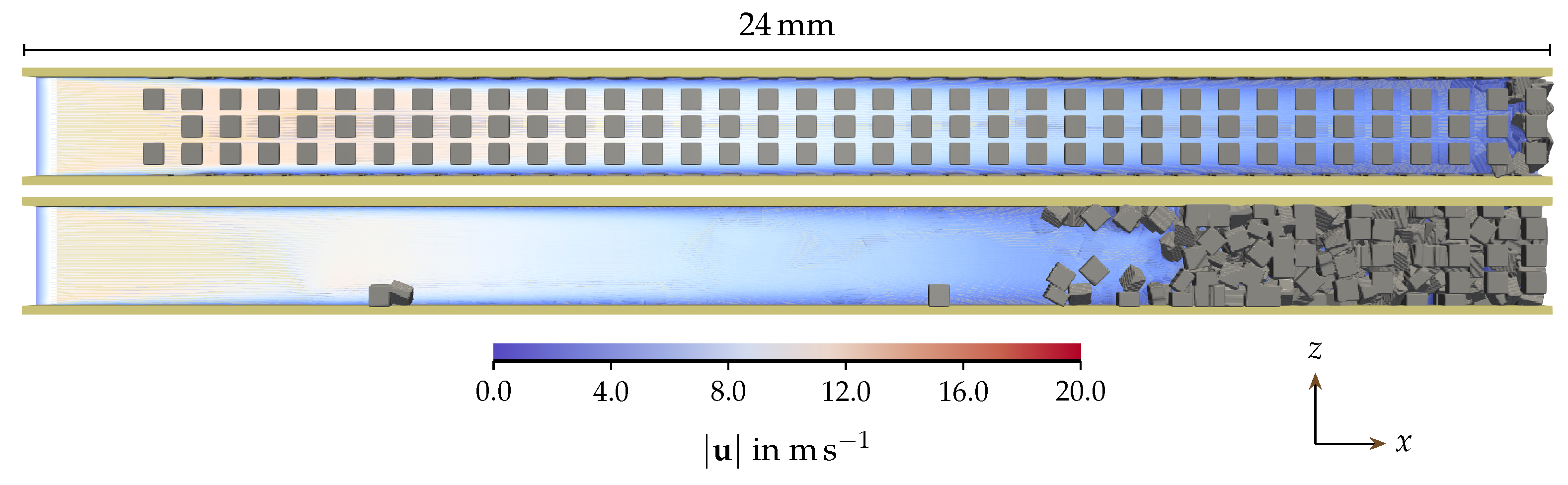
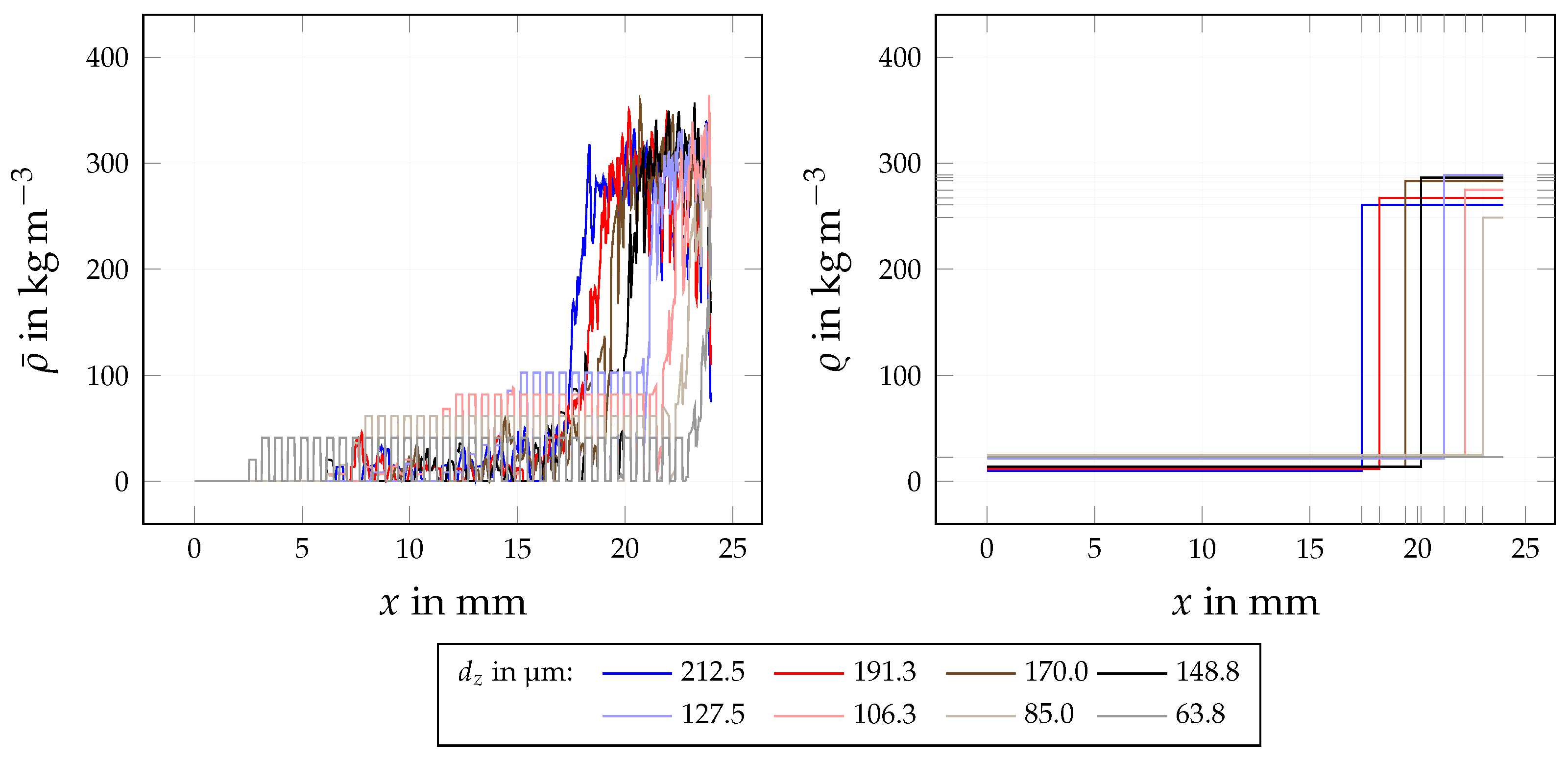

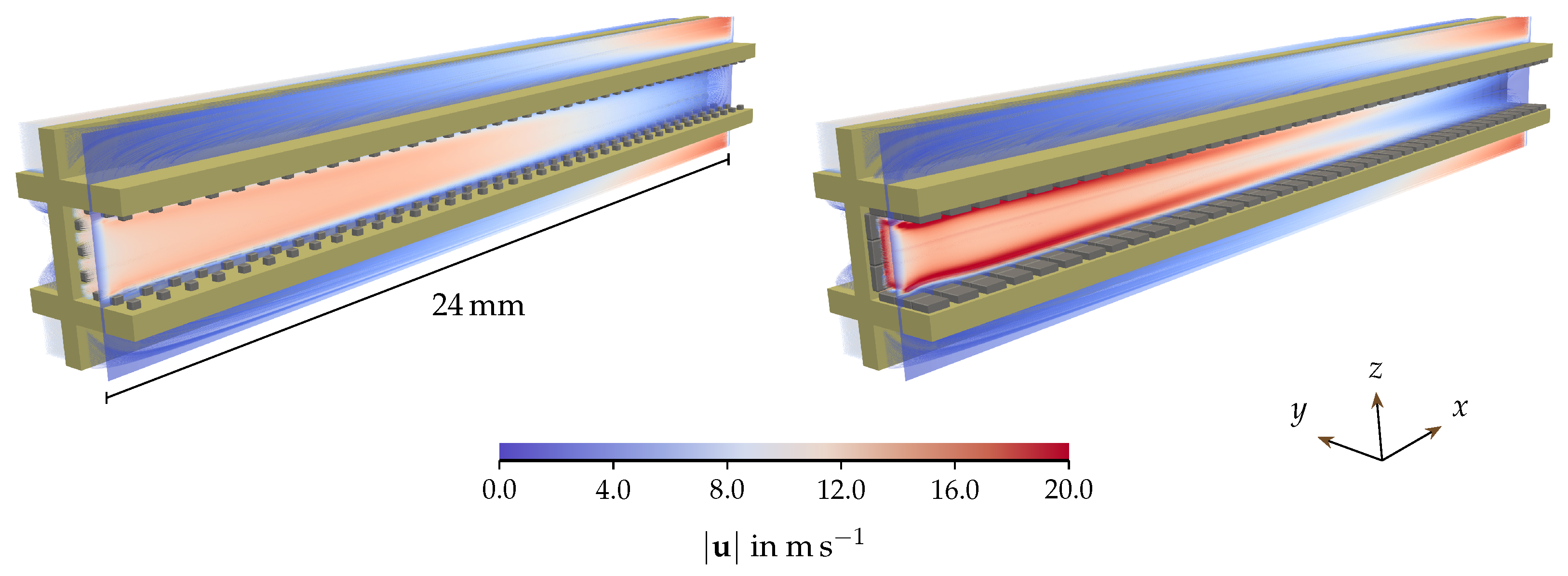



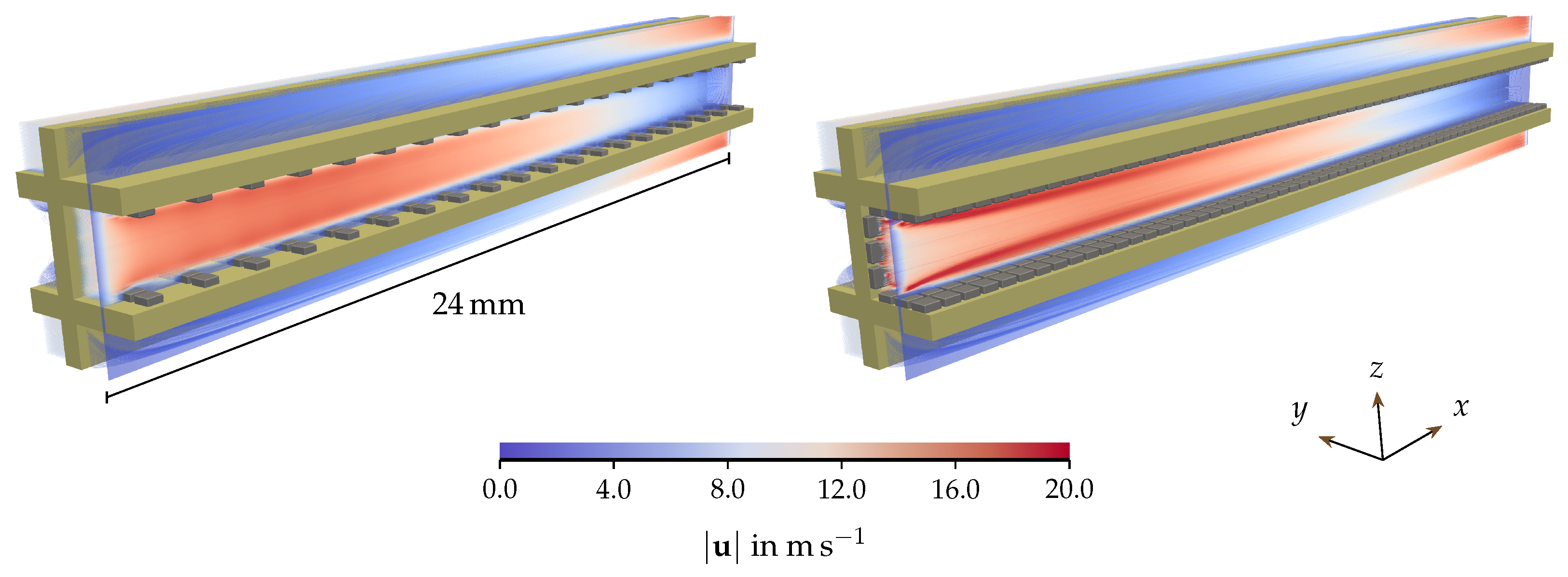


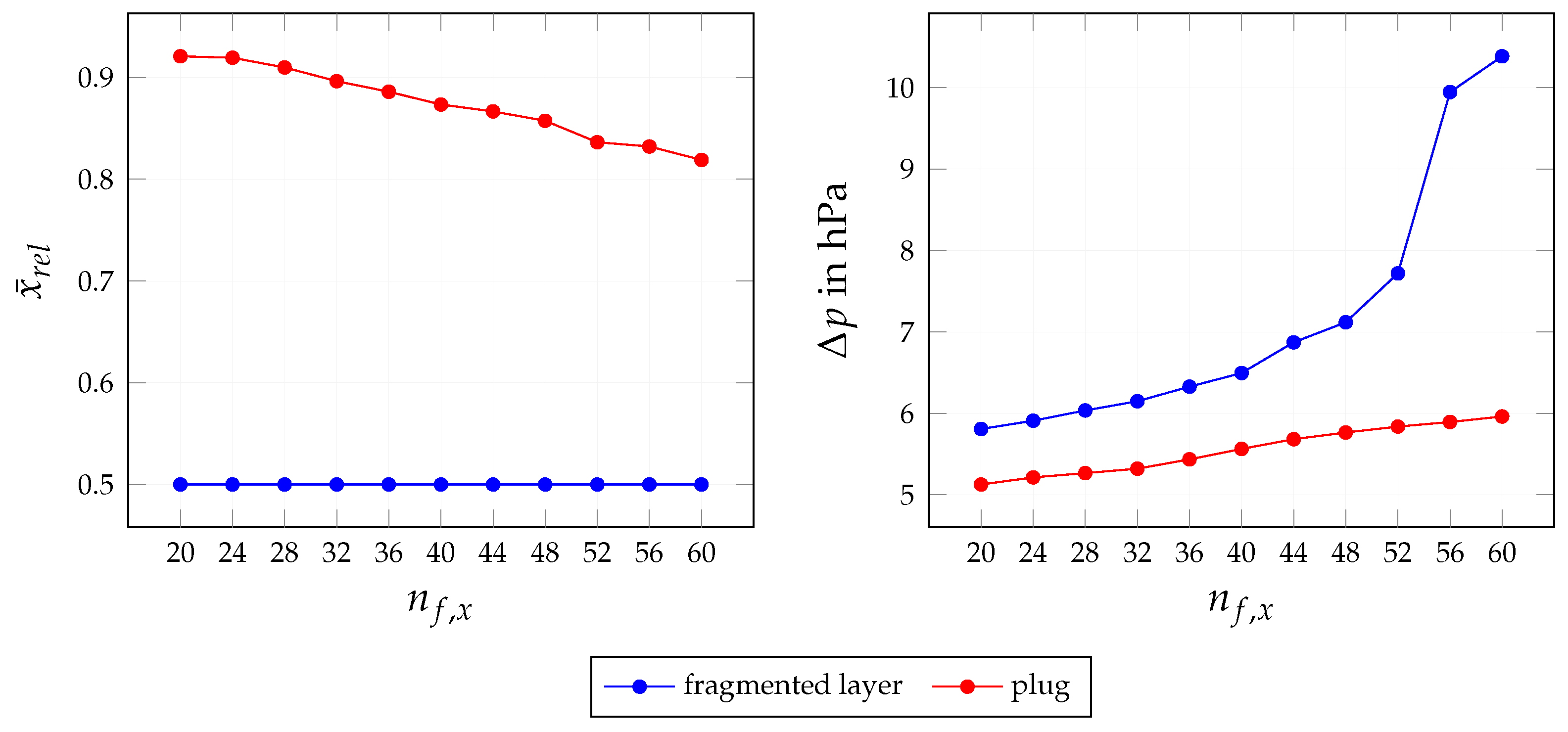
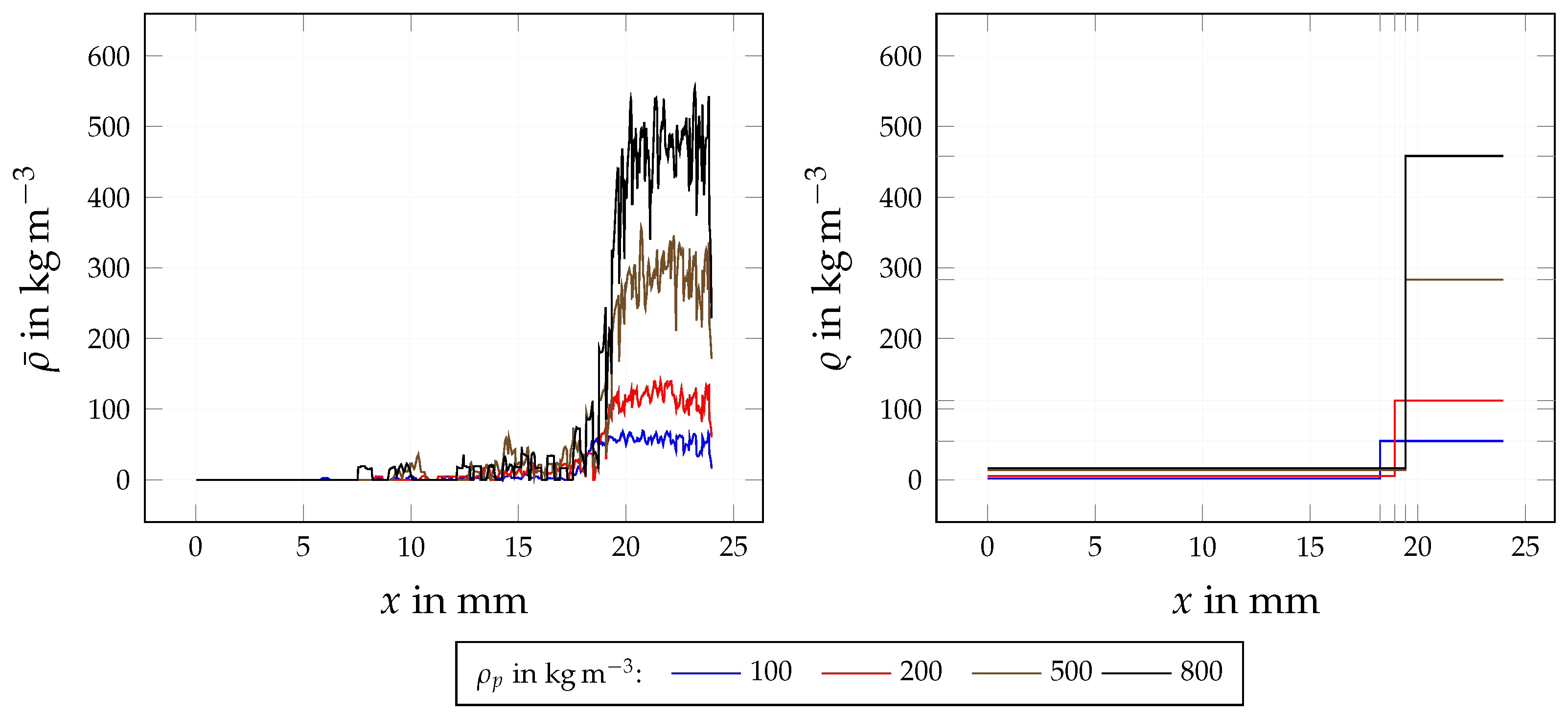
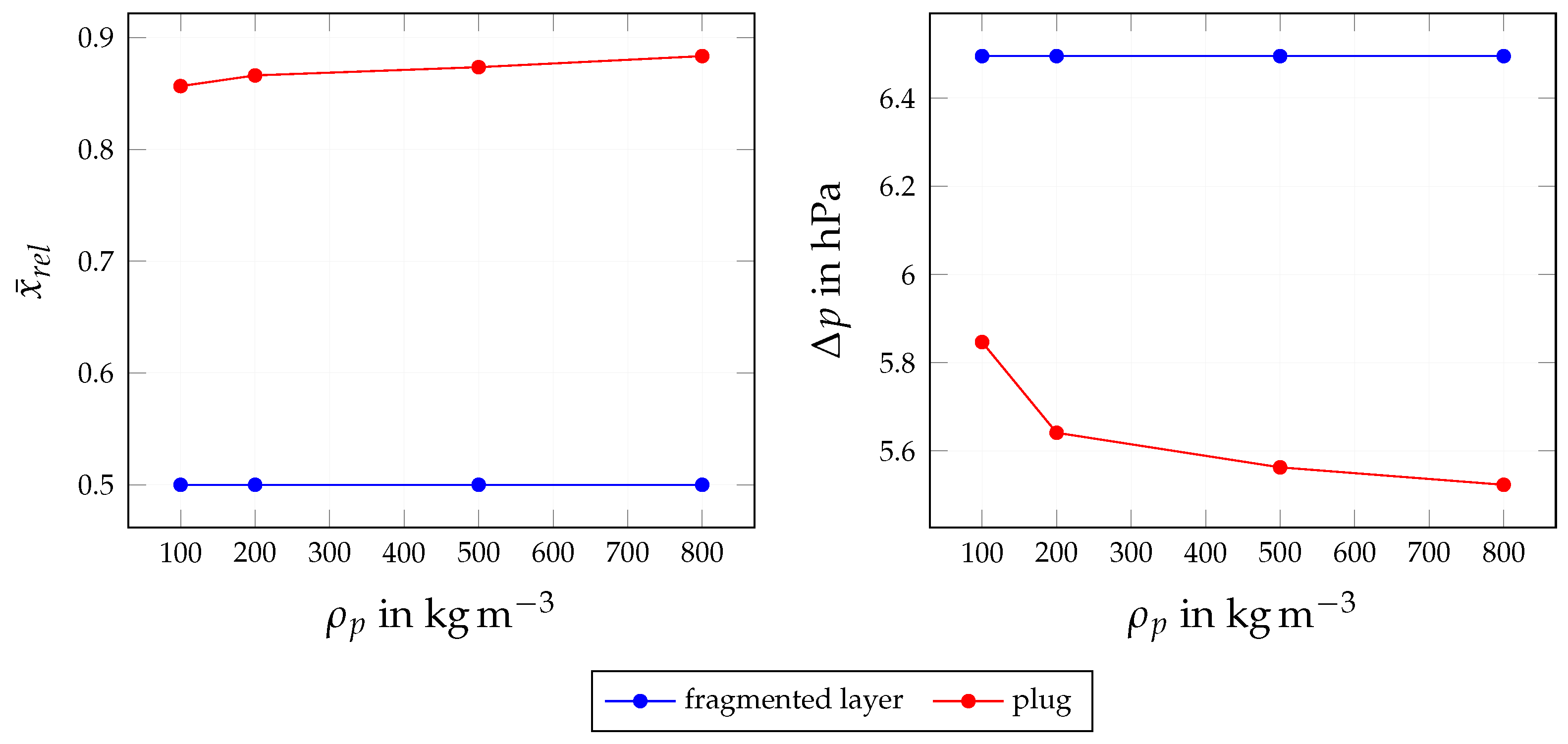
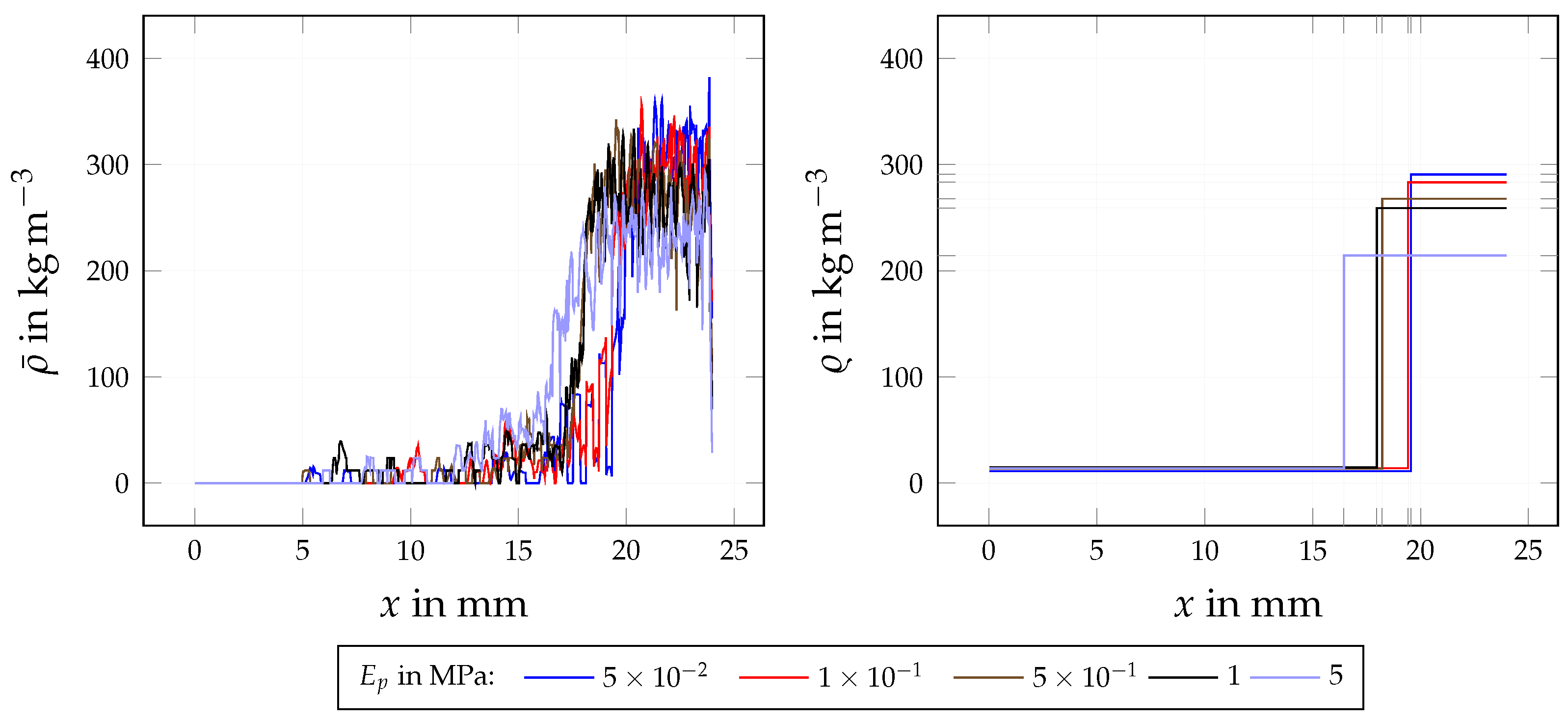
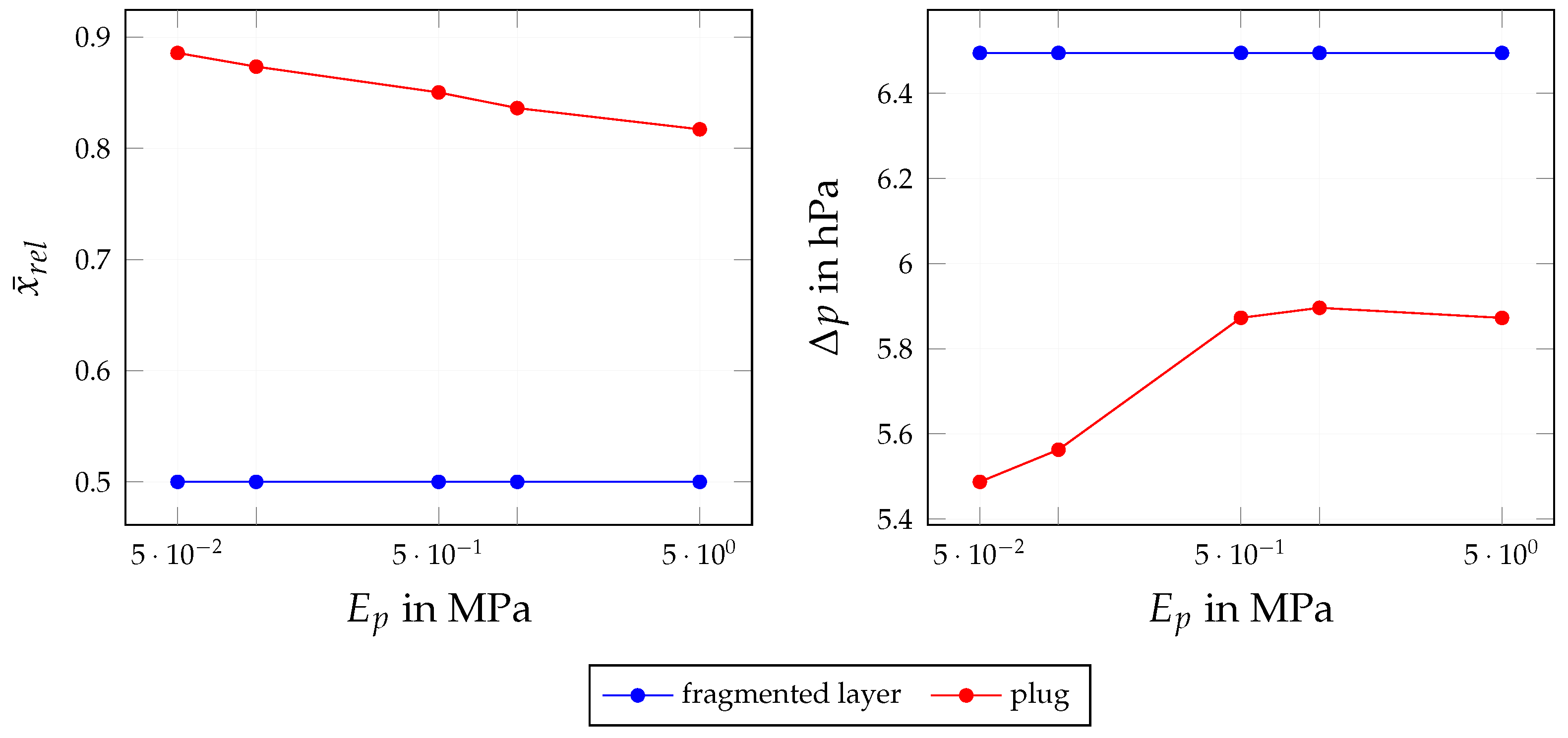
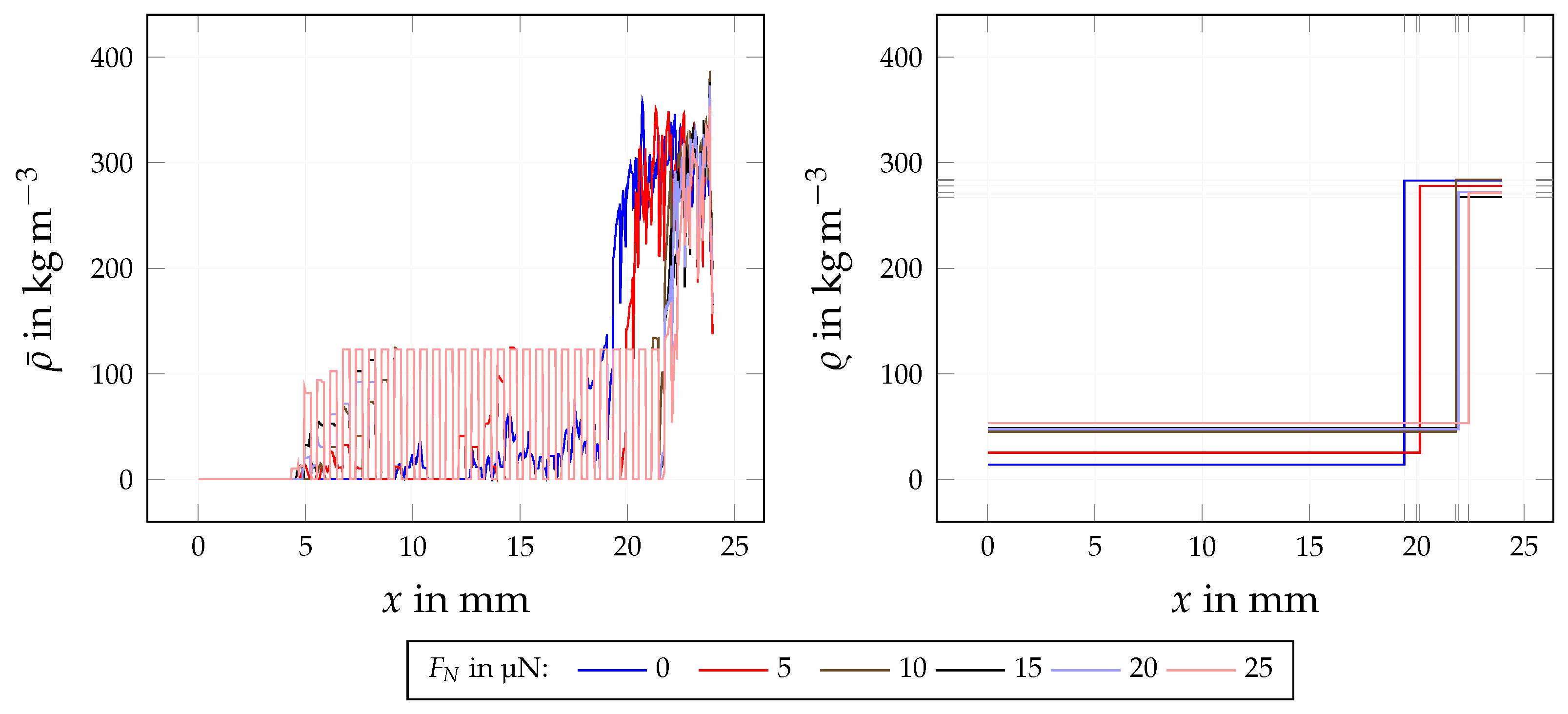

| Quantity | Symbol | Base Value | Variation Range (min, max) | Investigation |
|---|---|---|---|---|
| Fragment height | , | Layer height | ||
| Equilateral fragment width | , | Fragment dimensions | ||
| Fragment rows along channel | 40 | 20, 60 | Layer structure | |
| Fragment density | , | PM density | ||
| Fragment’s modulus of elasticity | , | Contact properties | ||
| Adhesion in normal direction | , | Adhesive forces | ||
| Inflow velocity | , | Inflow velocity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hafen, N.; Marquardt, J.E.; Dittler, A.; Krause, M.J. Simulation of Dynamic Rearrangement Events in Wall-Flow Filters Applying Lattice Boltzmann Methods. Fluids 2023, 8, 213. https://doi.org/10.3390/fluids8070213
Hafen N, Marquardt JE, Dittler A, Krause MJ. Simulation of Dynamic Rearrangement Events in Wall-Flow Filters Applying Lattice Boltzmann Methods. Fluids. 2023; 8(7):213. https://doi.org/10.3390/fluids8070213
Chicago/Turabian StyleHafen, Nicolas, Jan E. Marquardt, Achim Dittler, and Mathias J. Krause. 2023. "Simulation of Dynamic Rearrangement Events in Wall-Flow Filters Applying Lattice Boltzmann Methods" Fluids 8, no. 7: 213. https://doi.org/10.3390/fluids8070213
APA StyleHafen, N., Marquardt, J. E., Dittler, A., & Krause, M. J. (2023). Simulation of Dynamic Rearrangement Events in Wall-Flow Filters Applying Lattice Boltzmann Methods. Fluids, 8(7), 213. https://doi.org/10.3390/fluids8070213







