CFD Thermo-Hydraulic Evaluation of a Liquid Hydrogen Storage Tank with Different Insulation Thickness in a Small-Scale Hydrogen Liquefier
Abstract
:1. Introduction
2. Numerical Modeling
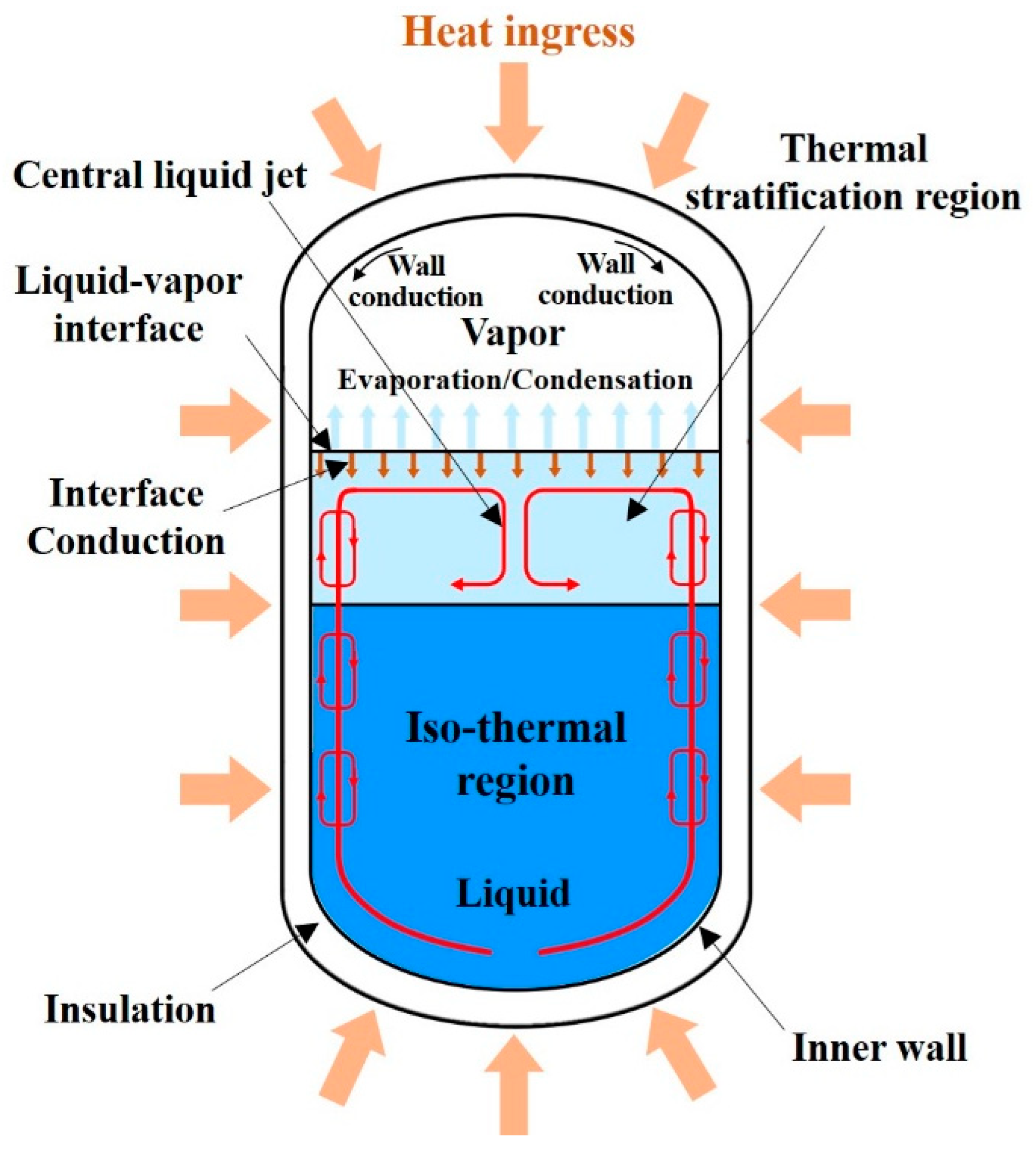
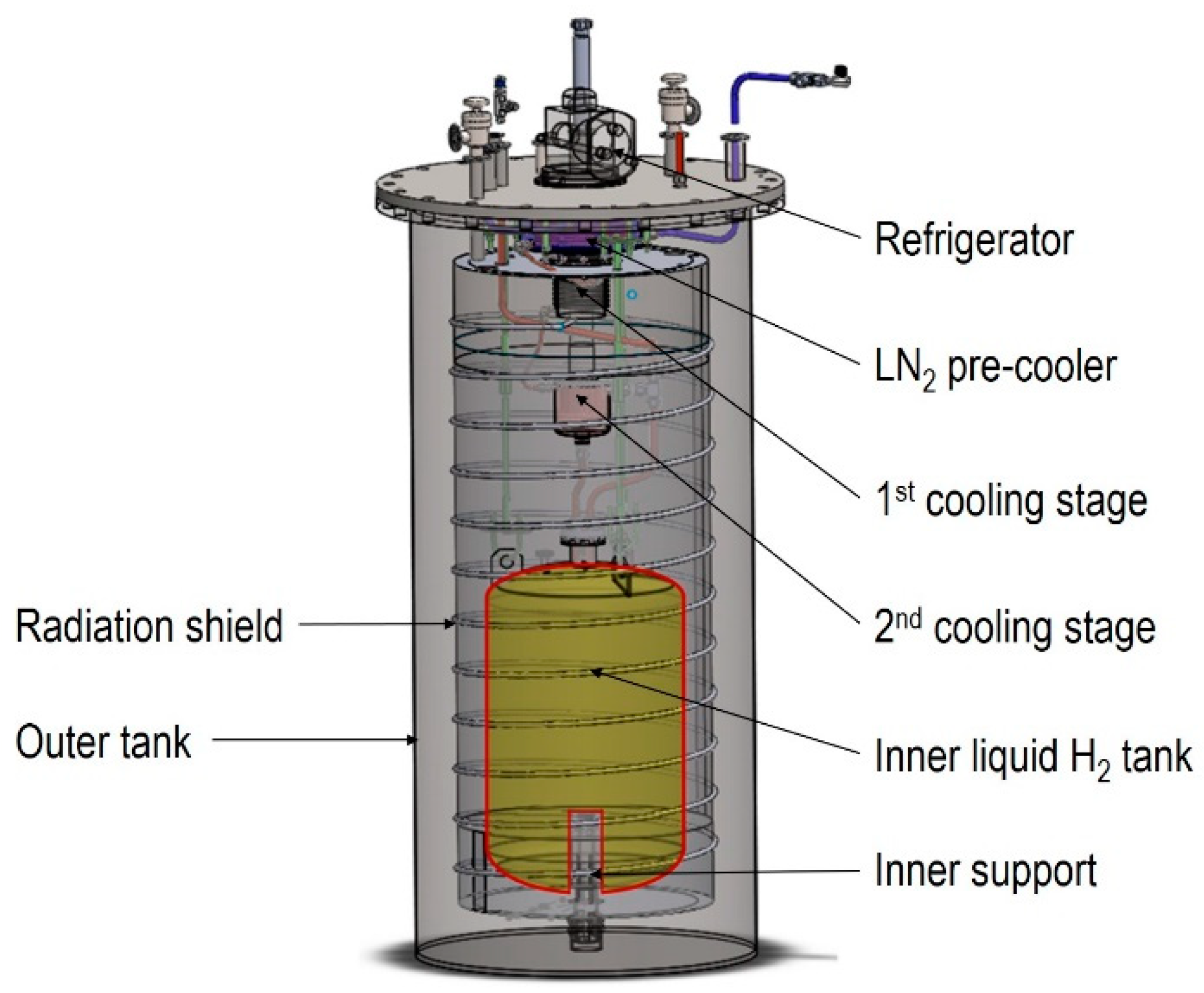
2.1. Modeling Description
2.2. Governing Equations and Numerical Modeling
2.3. Initial and Boundary Conditions
2.4. Turbulence Model
2.5. Numerical Implementation
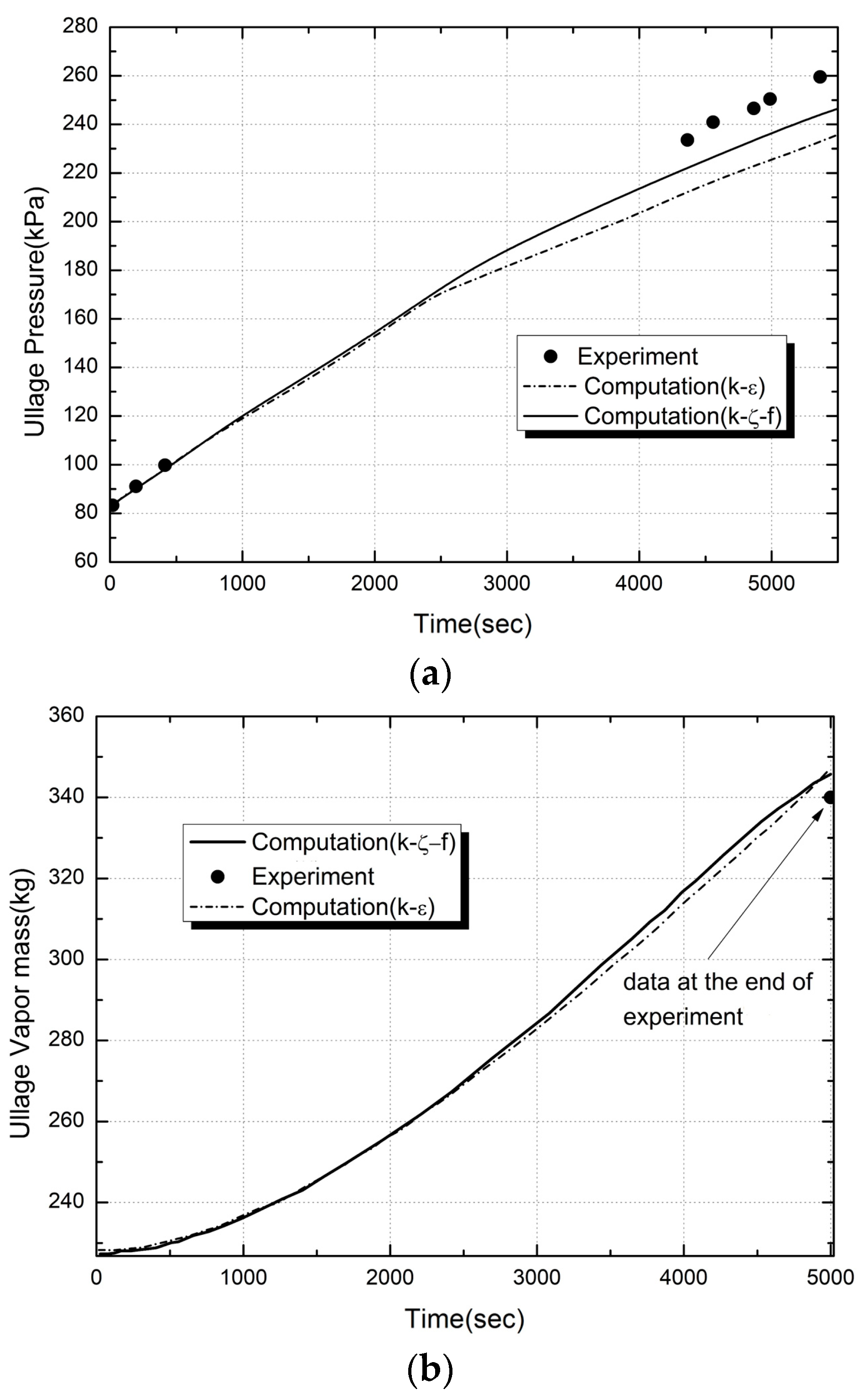
2.6. Model Validation
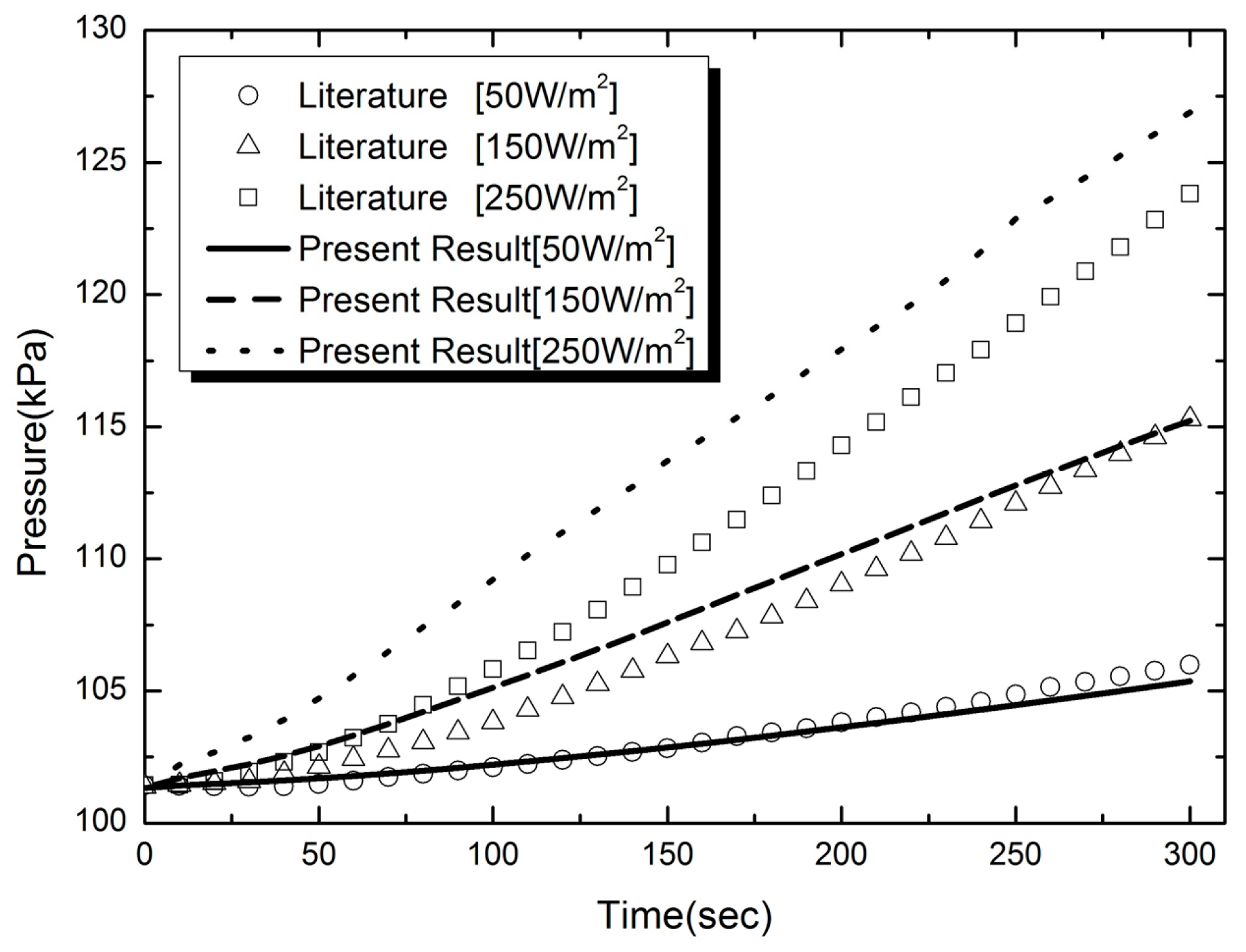
2.6.1. Numerical Validation
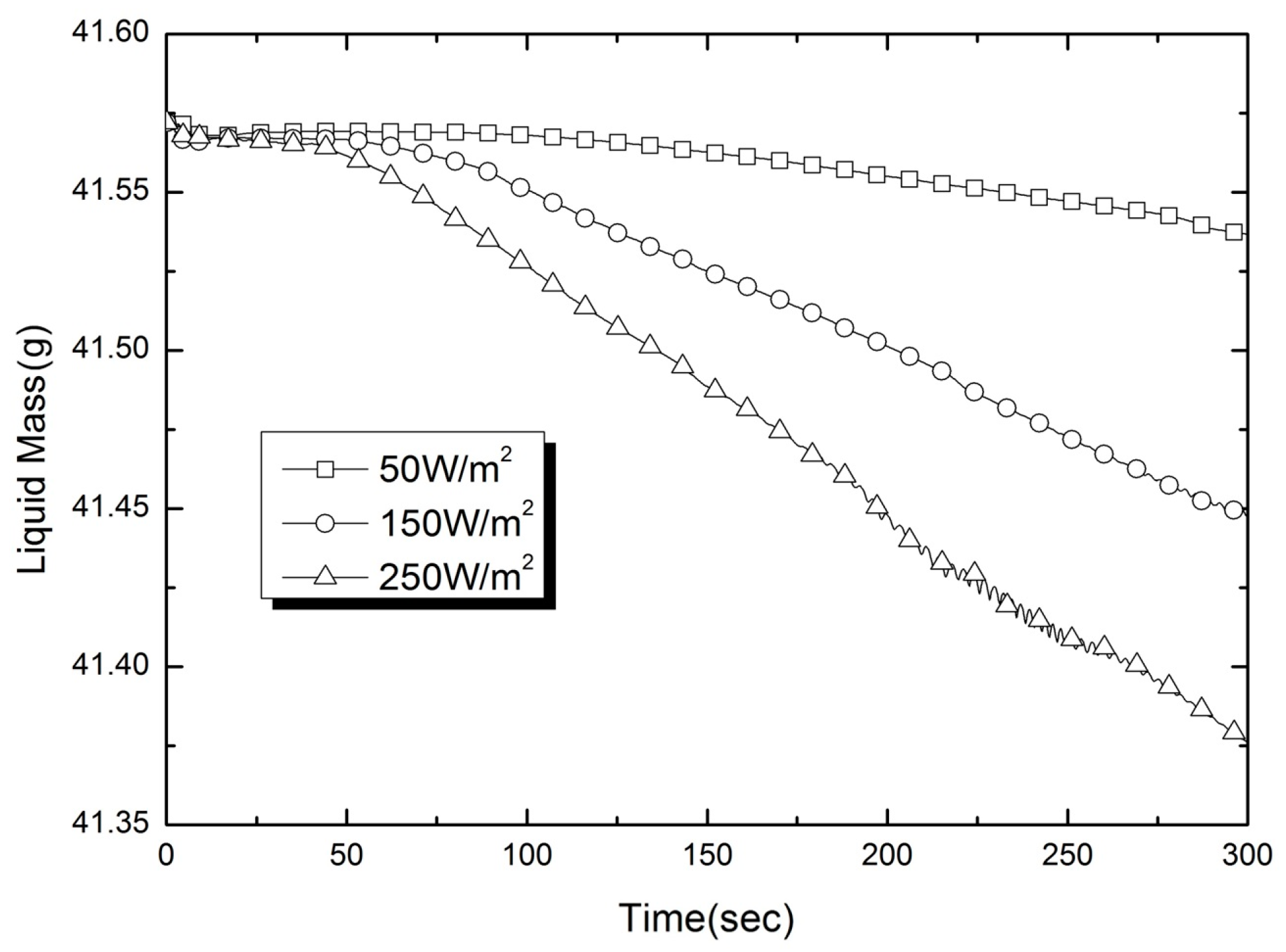
2.6.2. Experimental Validation
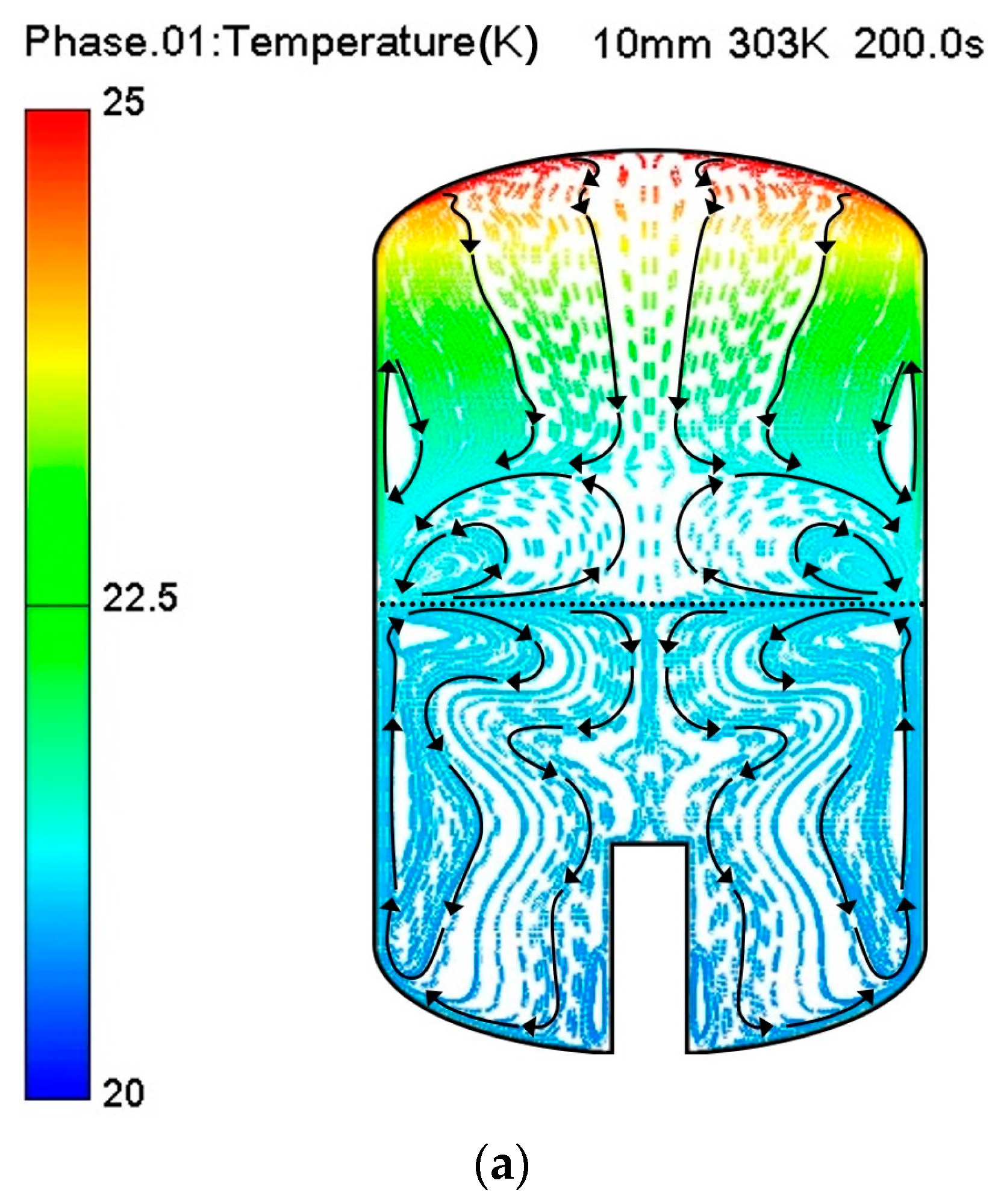
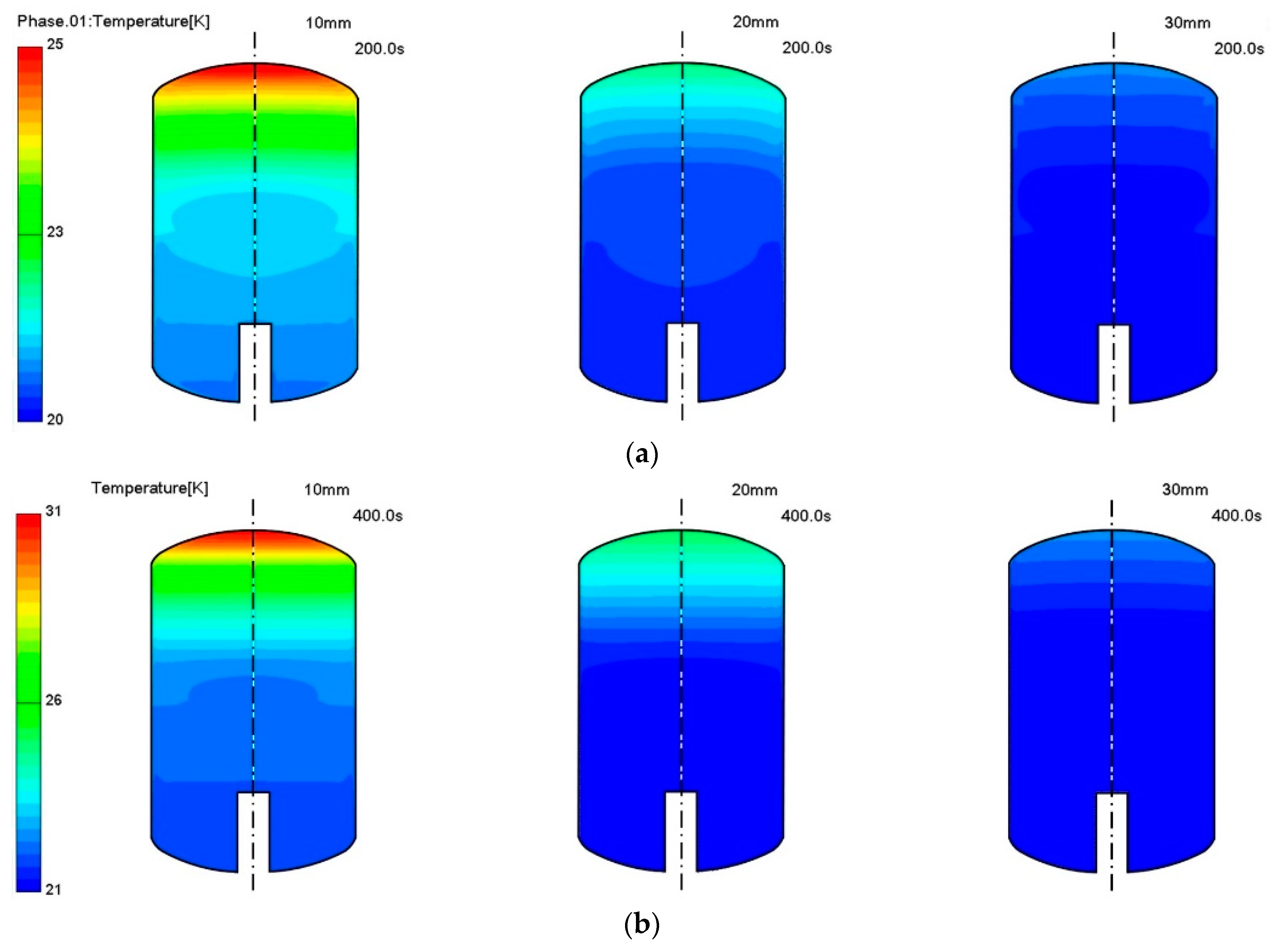
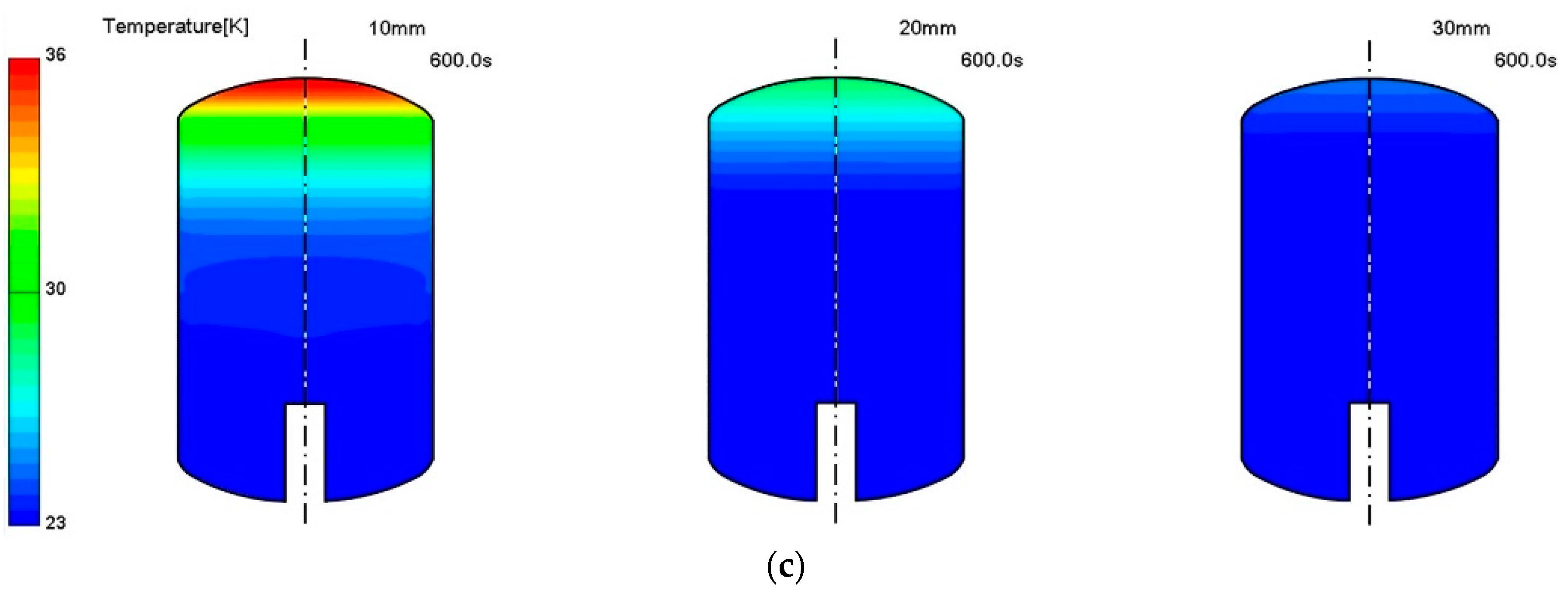
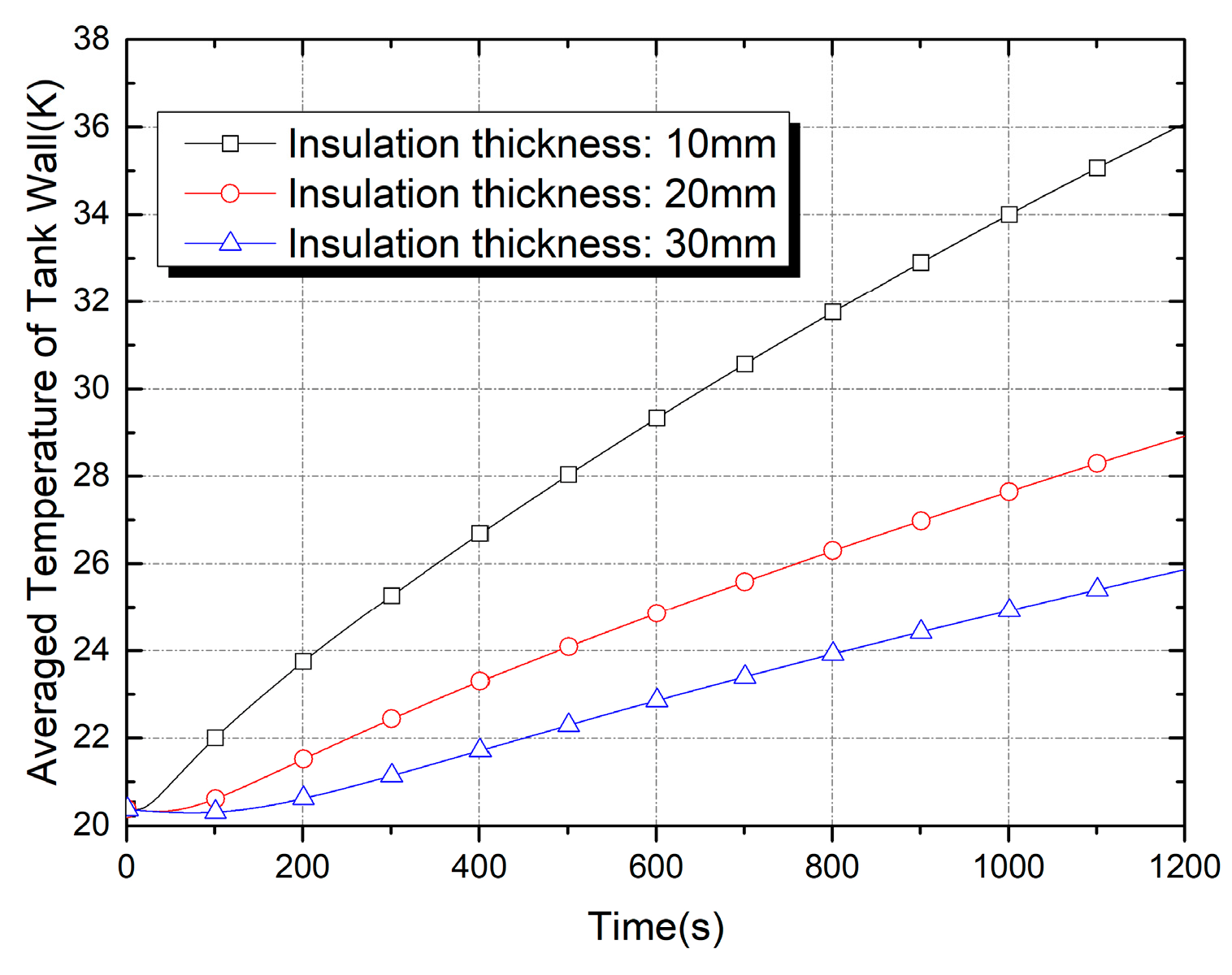
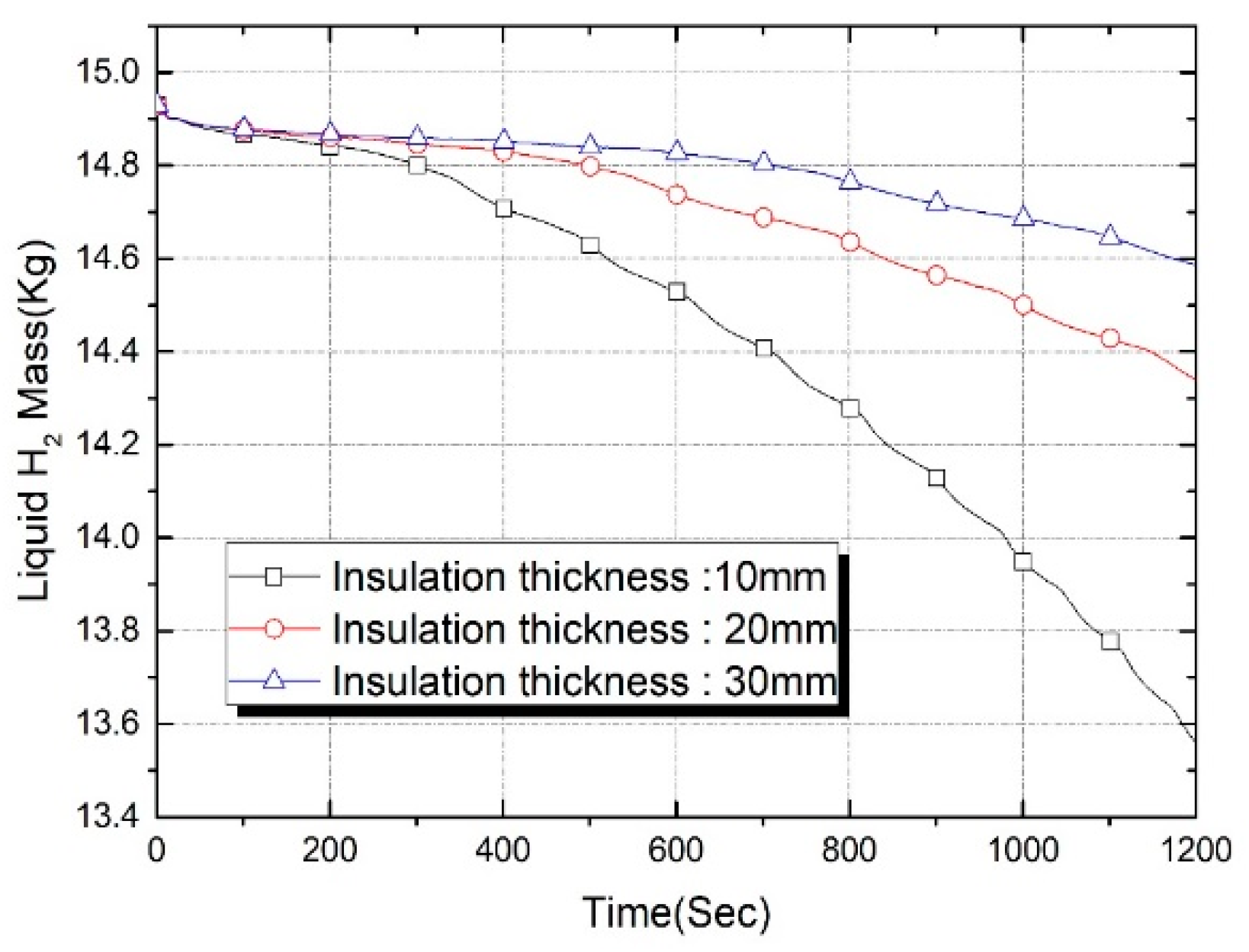
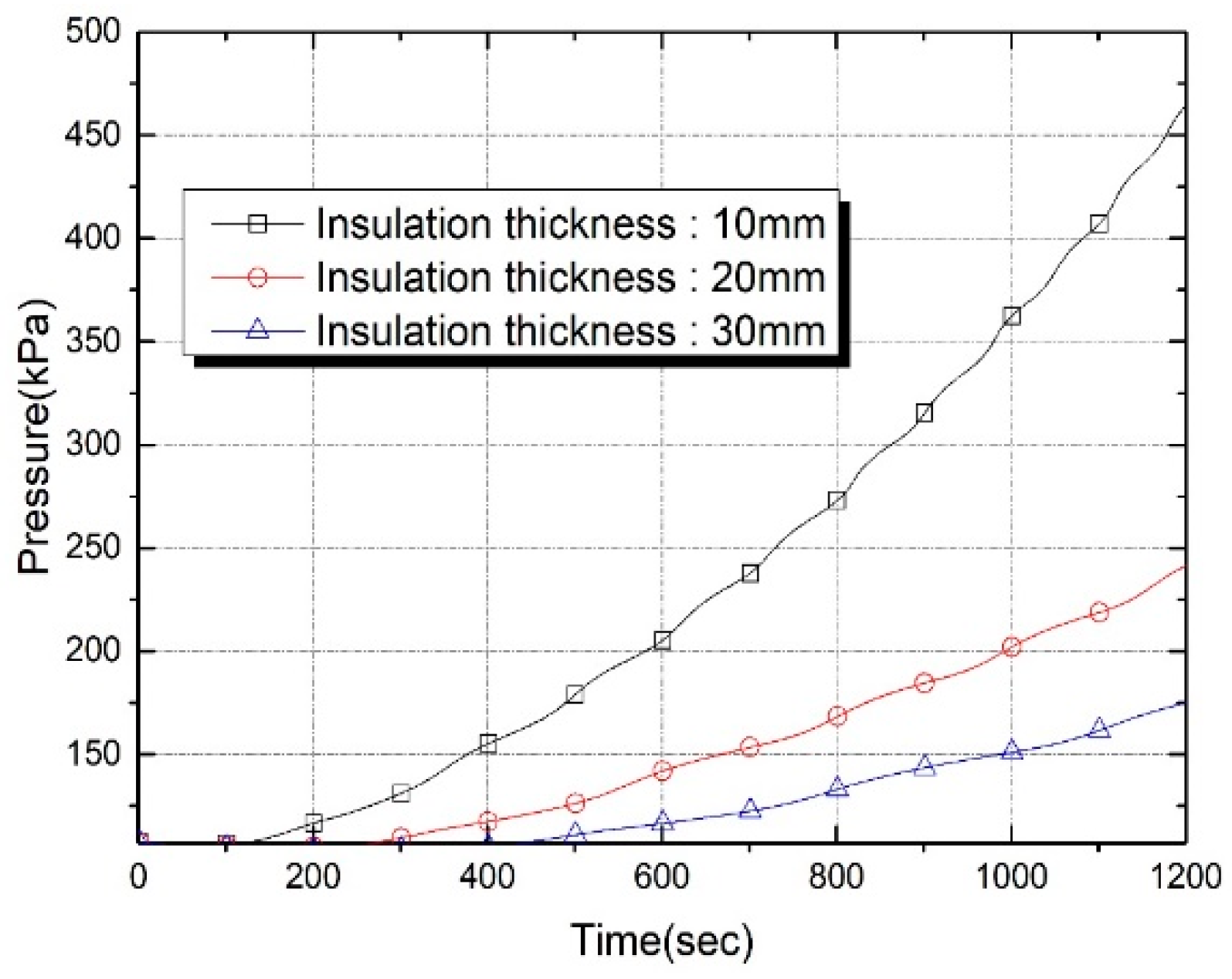
3. Results and Discussion
Thermo-Fluid Characteristics in the Tank
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| g | Gravitational acceleration (m2/s) |
| h | Heat transfer coefficient (W/m2K) |
| k | Conductivity (W/mK) |
| Wall normal fluctuations | |
| D | Diameter of tank or diffusivity (m, m2/s) |
| H | Height of tank (m) |
| n | Normal direction |
| α | Volume fraction |
| ρ | Density |
| μ | Viscosity |
| δ | Insulation thickness |
| ν | Kinematic viscosity |
| χ | Species mass fraction |
| Subscripts | |
| air | Air |
| Amb | Ambient |
| c | condensation |
| Effective | |
| e | Evaporation |
| g | Gas |
| i, j | Coordinate |
| ℓ | Liquid |
| m | mass concentration |
| s | Tank outer surface |
| sat | Saturation |
| v | Vapor |
| o | Surface |
| s | Surface |
| w | Wall |
References
- White, C.; Steeper, R.; Lutz, A. The hydrogen-fueled internal combustion engine: A technical review. Int. J. Hydrogen Energy 2006, 31, 1292–1305. [Google Scholar] [CrossRef]
- Gruz, M.; Baltacioglu, E.; Hames, Y.; Kaya, K. The meeting of hydrogen and automotive: A review. Int. J. Hydrogen Energy 2017, 42, 23334–23346. [Google Scholar] [CrossRef]
- Verstraete, D.; Hendrick, P.; Pilidis, P.; Ramsden, K. Hydrogen fuel for subsonic transport aircraft. Int. J. Hydrogen Energy 2010, 35, 11085–11098. [Google Scholar] [CrossRef]
- Kang, M.; Kim, J.; You, H.; Chang, D. Experimental investigation of thermal stratification in cryogenic tanks. Exp. Therm. Fluid Sci. 2018, 96, 371–382. [Google Scholar] [CrossRef]
- Kang, H.; Kim, S.Y. Thermal design analysis of a 1 L cryogenic liquid hydrogen tank for an unmanned aerial vehicle. Int. J. Hydrogen Energy 2018, 39, 20009–20016. [Google Scholar] [CrossRef]
- Jeong, S.-J.; Moon, S.-J.; Park, K.W.; Moon, S.-J. Development of the three-dimensional numerical model for predicting thermal physical performance in liquified hydrogen tank for hydrogen fueled vehicle. Trans. Korean Soc. Automot. Eng. 2020, 28, 203–210. [Google Scholar] [CrossRef]
- Saif, Z.S.; Stephanie, M.; Umberto, C.; Eric, F.M. Hydrogen liquefaction: A review of the fundamental physics, engineering practice and future opportunities. Energy Environ. Sci. 2022, 15, 2690–2731. [Google Scholar]
- Masters, P.A. Computer Programs for Pressurization (RAMP) and Pressurized Expulsion from a Cryogenic Liquid Propellant Tank; NASA TN D-7504; NASA: Greenbelt, MD, USA, 1974. [Google Scholar]
- Panzarella, C.; Kassemi, M. On the validity of purely thermodynamic descriptions of two-phase cryogenic fluid storage. J. Fluid Mech. 2003, 484, 41–68. [Google Scholar] [CrossRef]
- Panzarella, C.; Plachta, D.; Kassemi, M. Pressure control of large cryogenic tanks in microgravity. Cryogenics 2004, 44, 475–483. [Google Scholar] [CrossRef]
- Karimi, H.; Nassirharand, A.; Mohseni, M. Modeling and simulation of a class of liquid propellant engine pressurization systems. Acta Astrongautica 2010, 66, 539–549. [Google Scholar] [CrossRef]
- Barsi, S.; Kassemi, M. Numerical and experimental comparison of the self-pressurization behavior of an LH2 tank in normal gravity. Cryogenics 2008, 48, 122–129. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, Y.; Lei, G.; Li, Y. Sloshing hydrodynamic performance in cryogenic liquid oxygen tanks under different amplitudes. Appl. Therm. Eng. 2019, 150, 359–371. [Google Scholar] [CrossRef]
- Joseph, J.; Agrawal, G.; Agarwal, D.K.; Pisharady, J.C.; Kumar, S.S. Effect of insulation thickness on pressure evolution and thermal stratification in a cryogenic tank. Appl. Therm. Eng. 2017, 111, 1629–1639. [Google Scholar] [CrossRef]
- Adnani, P.; Jennings, R.W. Pressurization analysis of cryogenic propulsion systems. In Proceedings of the 36th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Las Vegas, NV, USA, 24–28 July 2000. AIAA-2000-3788. [Google Scholar]
- Roh, S.; Son, G. Numerical study of natural convection in a liquefied natural gas tank. J. Mech. Sci. Technol. 2012, 26, 3133–3140. [Google Scholar] [CrossRef]
- Kassemi, M.; Kartuzova, O. Effect of interfacial turbulence and accommodation coefficient on CFD predictions of pressurization and pressure control in cryogenic storage tank. Cryogenics 2016, 74, 138–153. [Google Scholar] [CrossRef]
- Liu, Z.; Li, C. Influence of slosh baffles on thermodynamic performance in liquid hydrogen tank. J. Hazard. Mater. 2018, 346, 253–262. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Liang, G.Z. Simulation research of vaporization and pressure variation in a cryogenic propellant tank at the launch site. Microgravity Sci. Technol. 2013, 25, 203–211. [Google Scholar] [CrossRef]
- Fu, J.; Sunden, B.; Chen, X. Influence of wall ribs on the thermal stratification and self-pressurization in a cryogenic liquid tank. Appl. Therm. Eng. 2014, 73, 1421–1431. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Jin, Y.; Li, C. Thermodynamic performance of pre-pressurization in a cryogenic tank. Appl. Therm. Eng. 2017, 112, 801–810. [Google Scholar] [CrossRef]
- Wang, L.; Ye, S.; Ma, Y.; Wang, J.; Li, Y. CFD investigation on helium pressurization behaviors in liquid hydrogen tank. J. Hydrog. Energy 2017, 42, 30792–30803. [Google Scholar] [CrossRef]
- Schrage, R.W. A Theoretical Study of Interphase Mass Transfer; Columbia University Press: New York, NY, USA, 1953. [Google Scholar]
- Liu, Z.; Li, Y. Thermal physical performance in liquid hydrogen tank under constant wall temperature. Renew. Energy 2019, 130, 601–612. [Google Scholar] [CrossRef]
- Duan, Z.; Zhu, Y.; Wang, C.; Yuan, Y.; Xue, H.; Tang, W. Numerical and Theoretical Prediction of the Thermodynamic Response in Marine LNG Fuel Tanks under Sloshing Conditions. Energy 2023, 270, 126935–126949. [Google Scholar] [CrossRef]
- Wang, H.; Wang, B.; Li, R.; Shen, X.; Wu, Y.; Pan, Q.; He, Y.; Zhou, W.; Gan, Z. Theoretical Investigation on Heat Leakage Distribution between Vapor and Liquid in Liquid Hydrogen Tanks. Int. J. Hydrogen Energy 2023, 48, 17187–17201. [Google Scholar]
- Zuo, Z.; Jiang, W.; Qin, X.; Huang, Y. A numerical model for liquid-vapor transition in self-pressurized cyogenic containers. Appl. Therm. Eng. 2021, 193, 117005–117015. [Google Scholar] [CrossRef]
- Le, T.-L.; Chen, J.-C.; Nguyen, H.-B. Numerical investigation of the forward and backward thermocapillary motion of a water droplet in a microchannel by two periodically activated heat sources. Numer. Transf. Part A Appl. 2021, 79, 146–162. [Google Scholar] [CrossRef]
- Sun, P.; Wu, J.Y.; Zhang, P.; Xu, L.; Jiang, M. Experimental study of the influences of degraded vacuum on multilayer insulation blankets. Cryogenics 2009, 49, 719–726. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Xie, F.; Zhou, K. Thermal performance of foam/MLI for cryogenic liquid hydrogen tank during the ascent and on orbit period. Appl. Therm. Eng. 2016, 98, 430–439. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Jin, Y. Pressurization performance and temperature stratification in cryogenic final stage propellant tank. Appl. Therm. Eng. 2016, 106, 211–220. [Google Scholar] [CrossRef]
- Li, X.; Xie, G.; Wang, R. Experimental and numerical investigations of fluid flow and heat transfer in a cryogenic tank at loss of vacuum. Heat Mass Transf. 2010, 46, 395–404. [Google Scholar] [CrossRef]
- Lemmon, E.W.; McLinden, M.O.; Friend, D.G.; Linstrom, P.; Mallard, W. NIST Chemistry WebBook; NIST Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2011. [Google Scholar] [CrossRef]
- Hardt, S.; Wondra, F. Evaporation model for interfacial flows based on a continuum-field representation of the source terms. J. Comput. Phys. 2008, 227, 5871–5895. [Google Scholar] [CrossRef]
- Ranz, W.; Marshall, W.R. Modeling the interaction between a thermal flow and a liquid: Review and future eulerian-lagrangian approaches. Chem. Eng. Prog. 1952, 48, 141–146. [Google Scholar]
- Chu, X.; Chen, W.; Shang, Y.; Hao, J.; Zhang, D. CFD investigation on reverse flow characteristics in U-tubes under two-phase natural circulation. Prog. Nucl. Energy 2019, 114, 145–154. [Google Scholar] [CrossRef]
- FIRE ver. 2019 R2 Main Program User Manual. Available online: https://www.avl.com/en (accessed on 10 December 2022).
- Churchill, S.W.; Bernstein, M. A Correlating Equation for Forced Convection from Gases and Liquids to a Circular Cylinder in Crossflow. J. Heat Transf. 1977, 99, 300–306. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer, 8th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2018; ISBN 978-1-119-35388-1. [Google Scholar]
- Whitaker, S. Forced convection heat transfer correlations for flow in pipes, past flat plates, single cylinders, single spheres, and for flow in packed beds and tube bundles. AIChE J. 1972, 18, 361–371. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Li, C.; Zhao, Z. CFD investigation of thermal and pressurization performance in LH2 tank during discharge. Cryogenics 2013, 57, 63–73. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Zhu, K.; Jin, Y. Comparison of three computational models for predicting pressurization characteristics of cryogenic tank during discharge. Cryogenics 2015, 65, 16–25. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed.; DCW Industries Inc.: La Cañada Flintridge, CA, USA, 1998. [Google Scholar]
- Hanjalić, K.; Popovac, M.; Hadžiabdić, M. A robust near-wall elliptic-relaxation eddy-viscosity turbulence model for CFD. Int. J. Heat Fluid Flow 2004, 25, 1047–1051. [Google Scholar] [CrossRef]
- Durbin, P.A. Near-wall turbulence closure modeling without “damping functions”. Theor. Comput. Fluid Dyn. 1991, 3, 1–13. [Google Scholar] [CrossRef]
- Nzebuka, G.G.; Waheed, M.A. Thermal evolution in the direct chill casting of an Al-4 pct Cu alloy using the low-Reynolds number turbulence model. Int. J. Therm. Sci. 2020, 147, 106152. [Google Scholar] [CrossRef]
- Wu, X.; Durbin, P.A. Numerical simulation of heat transfer in a transitional boundary layer with passing wakes. J. Heat Transf. 1991, 122, 248–257. [Google Scholar] [CrossRef]
- Sundén, B.; Fu, J. Heat Transfer in Aerospace Applications; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Altac, Z.; Ugurlubilek, N. Assessment of turbulence models in natural convection from two- and three-dimensional rectangular enclosures. Int. J. Therm. Sci. 2016, 107, 237–246. [Google Scholar] [CrossRef]
- Spall, E.; Richards, A.; McEligot, D.M. An assessment of k-w and v2-f turbulence models for strongly heated internal gas flows. Numer. Heat Transf. 2004, 46, 831–849. [Google Scholar] [CrossRef]
- Ward, W.D. Evaluation of AS-203 low-gravity orbital experiment. NASA CR 1967, 94045, 13. [Google Scholar]
- Van Dresar, N.; Lin, C.; Hasan, M. Self-pressurization of a flight weight liquid hydrogen tank: Effects of fill level at low wall heat flux. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. NASA TM-105411. [Google Scholar]


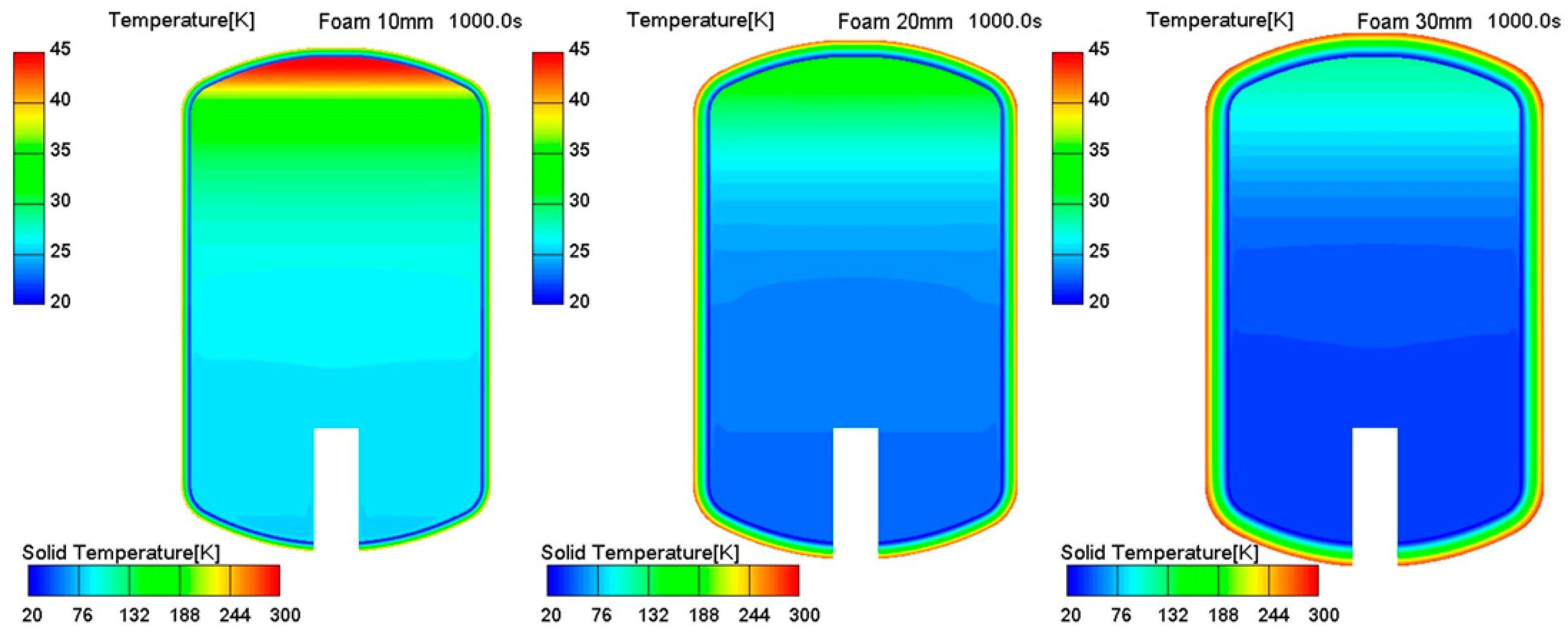
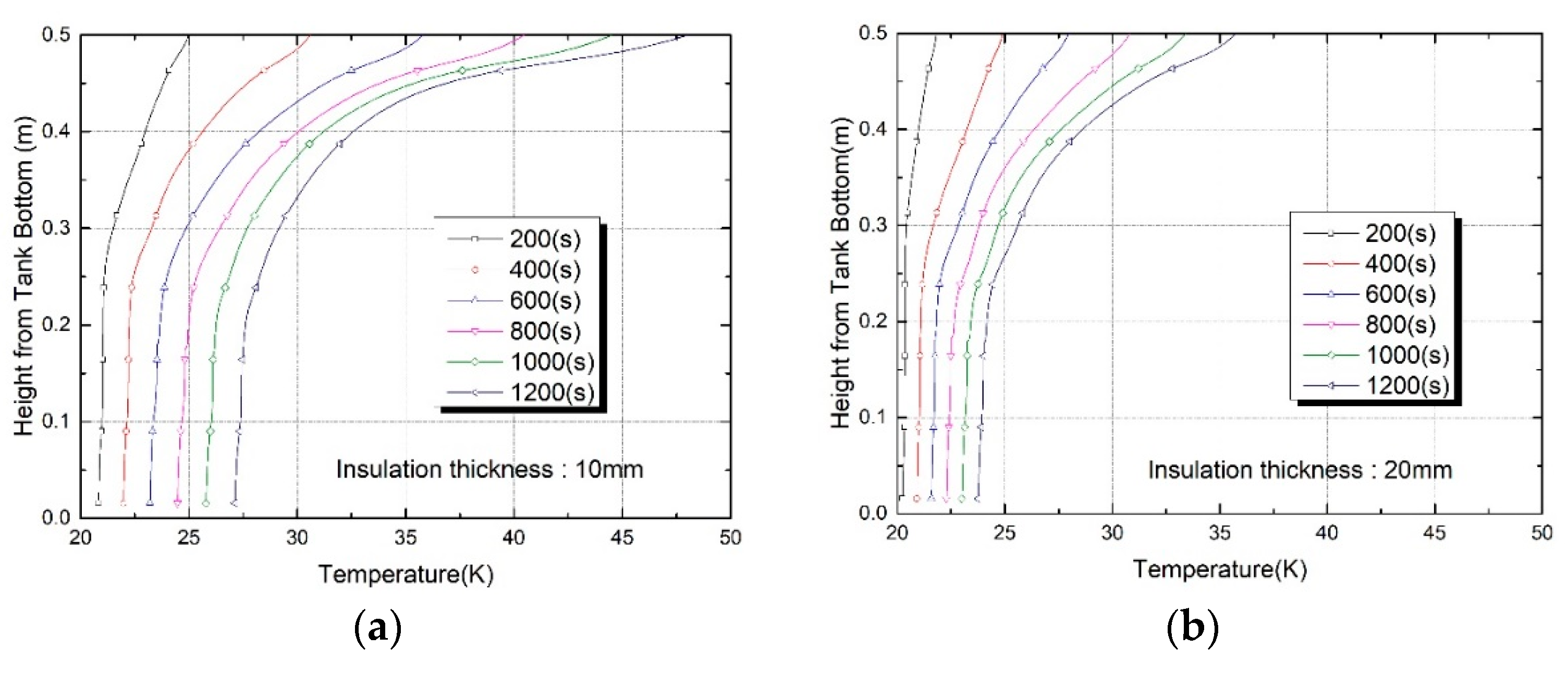
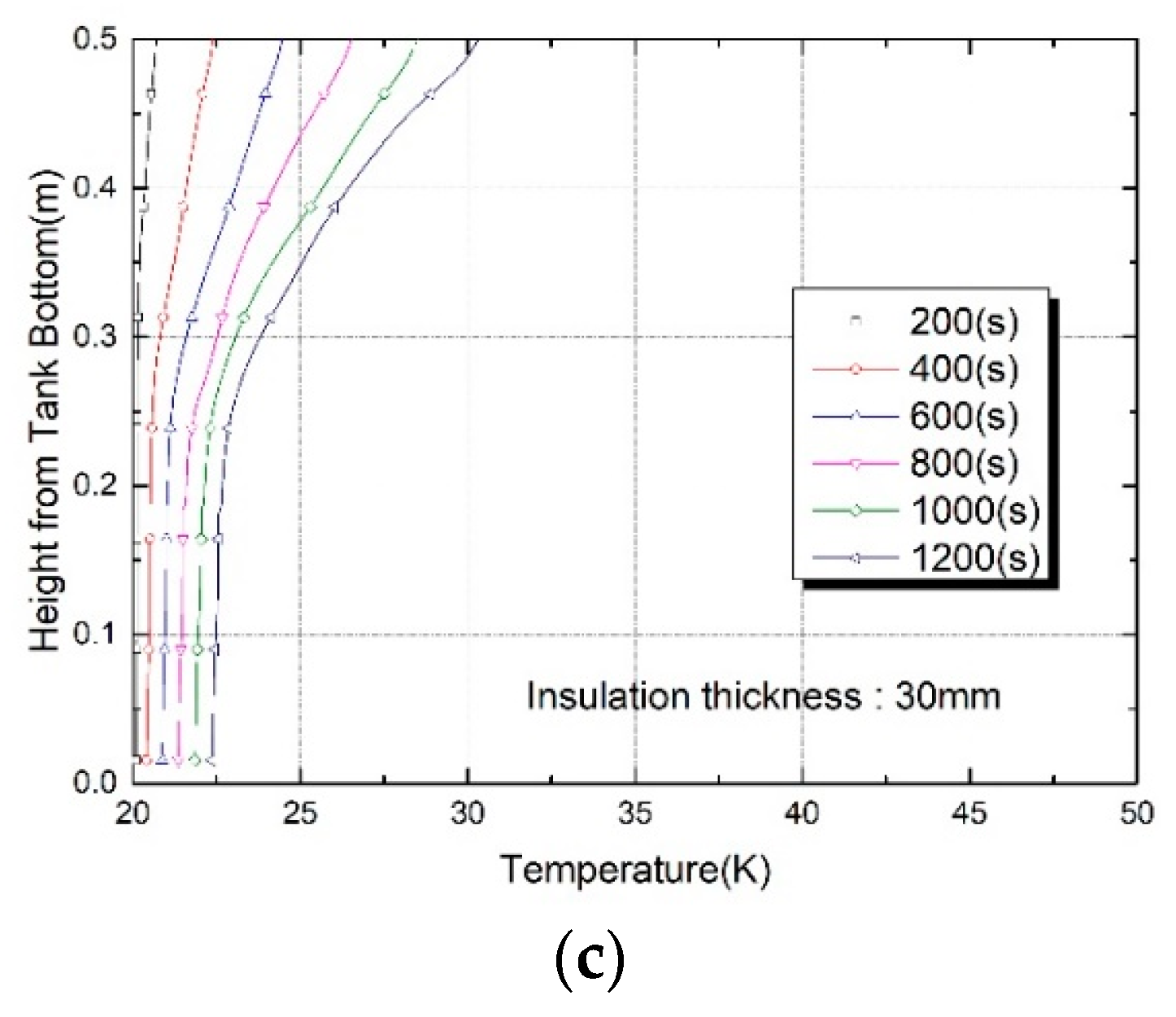
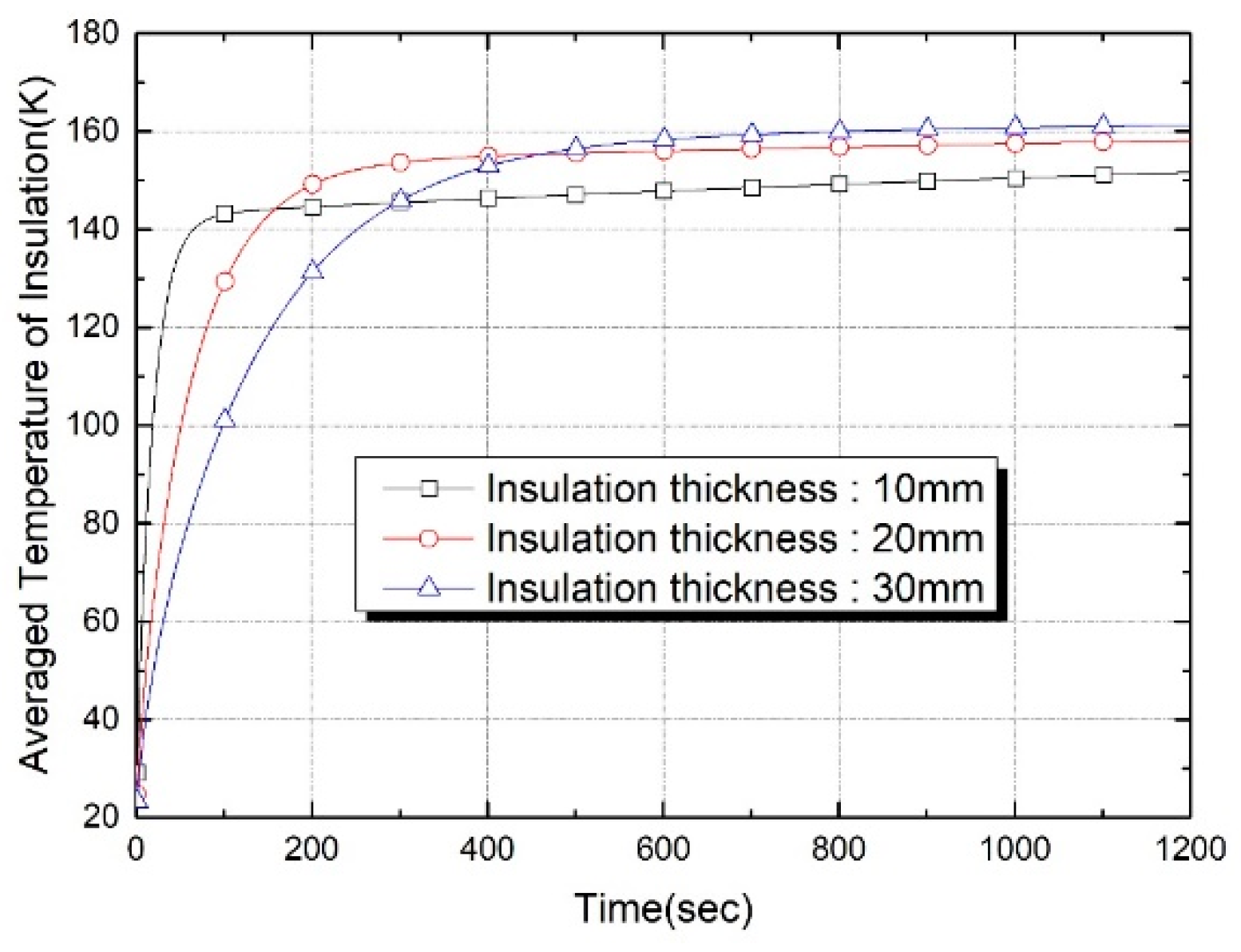
| Properties | Tank Wall (2219 Al Alloy) | Insulation Foam |
|---|---|---|
| Thickness (mm) | 3 | 10~30 |
| Density (kg/m2) | 2840 | 35 |
| Specific heat (J/(kgK)) | 864 | 1674 |
| Thermal conductivity (W/(m·k)) | 143 | 0.02 |
| Insulation Thickness (mm) | Thermal Capacitance (J/K) | Evaporation Loss (g) at t = 600 s | Evaporation Loss (g) at t = 1200 s |
|---|---|---|---|
| 10 | 174.2 | 0.398 | 1.360 |
| 20 | 366.3 | 0.190 | 0.588 |
| 30 | 577.4 | 0.101 | 0.341 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, S.-J.; Lee, S.-J.; Moon, S.-J. CFD Thermo-Hydraulic Evaluation of a Liquid Hydrogen Storage Tank with Different Insulation Thickness in a Small-Scale Hydrogen Liquefier. Fluids 2023, 8, 239. https://doi.org/10.3390/fluids8090239
Jeong S-J, Lee S-J, Moon S-J. CFD Thermo-Hydraulic Evaluation of a Liquid Hydrogen Storage Tank with Different Insulation Thickness in a Small-Scale Hydrogen Liquefier. Fluids. 2023; 8(9):239. https://doi.org/10.3390/fluids8090239
Chicago/Turabian StyleJeong, Soo-Jin, Sang-Jin Lee, and Seong-Joon Moon. 2023. "CFD Thermo-Hydraulic Evaluation of a Liquid Hydrogen Storage Tank with Different Insulation Thickness in a Small-Scale Hydrogen Liquefier" Fluids 8, no. 9: 239. https://doi.org/10.3390/fluids8090239
APA StyleJeong, S.-J., Lee, S.-J., & Moon, S.-J. (2023). CFD Thermo-Hydraulic Evaluation of a Liquid Hydrogen Storage Tank with Different Insulation Thickness in a Small-Scale Hydrogen Liquefier. Fluids, 8(9), 239. https://doi.org/10.3390/fluids8090239








