Thermal Transpiration Flow: Molecular Dynamics Study from Dense to Dilute Gas
Abstract
:1. Introduction
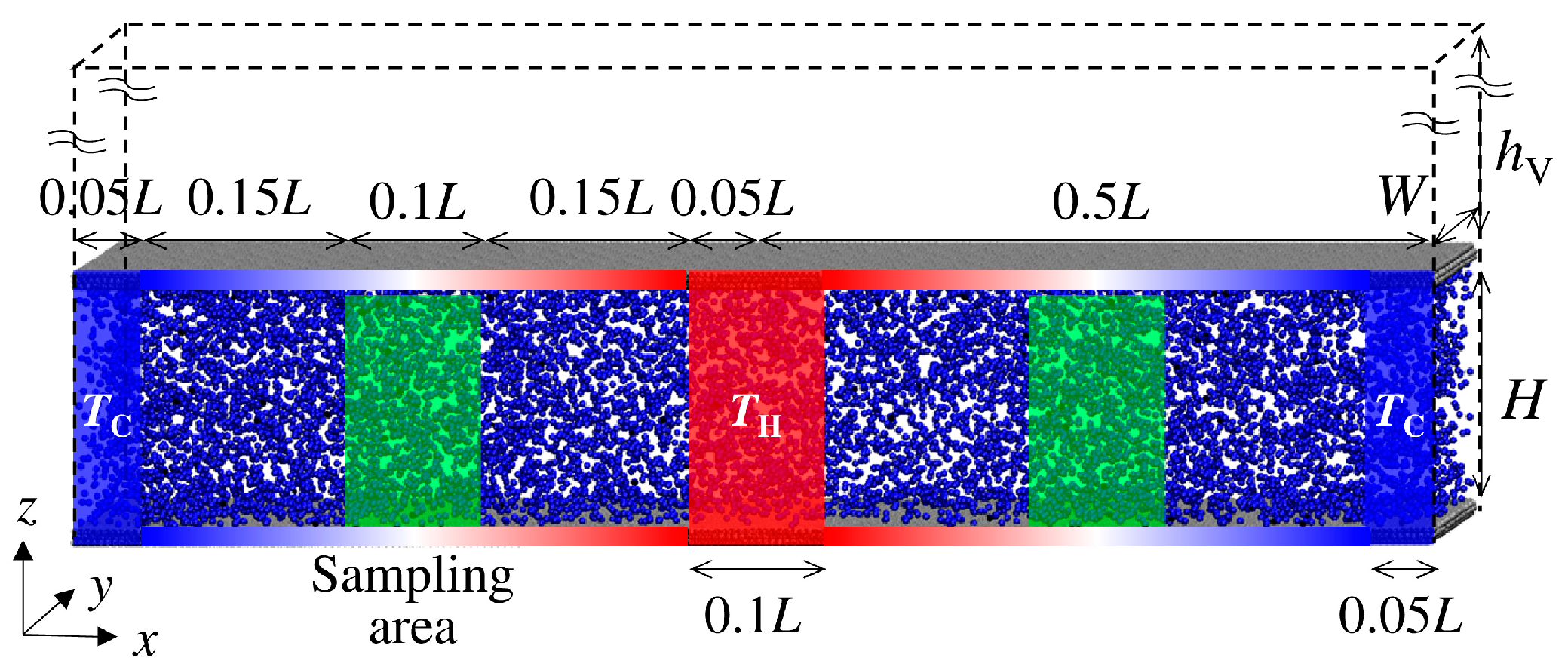
2. Numerical Methods
3. Results and Discussion
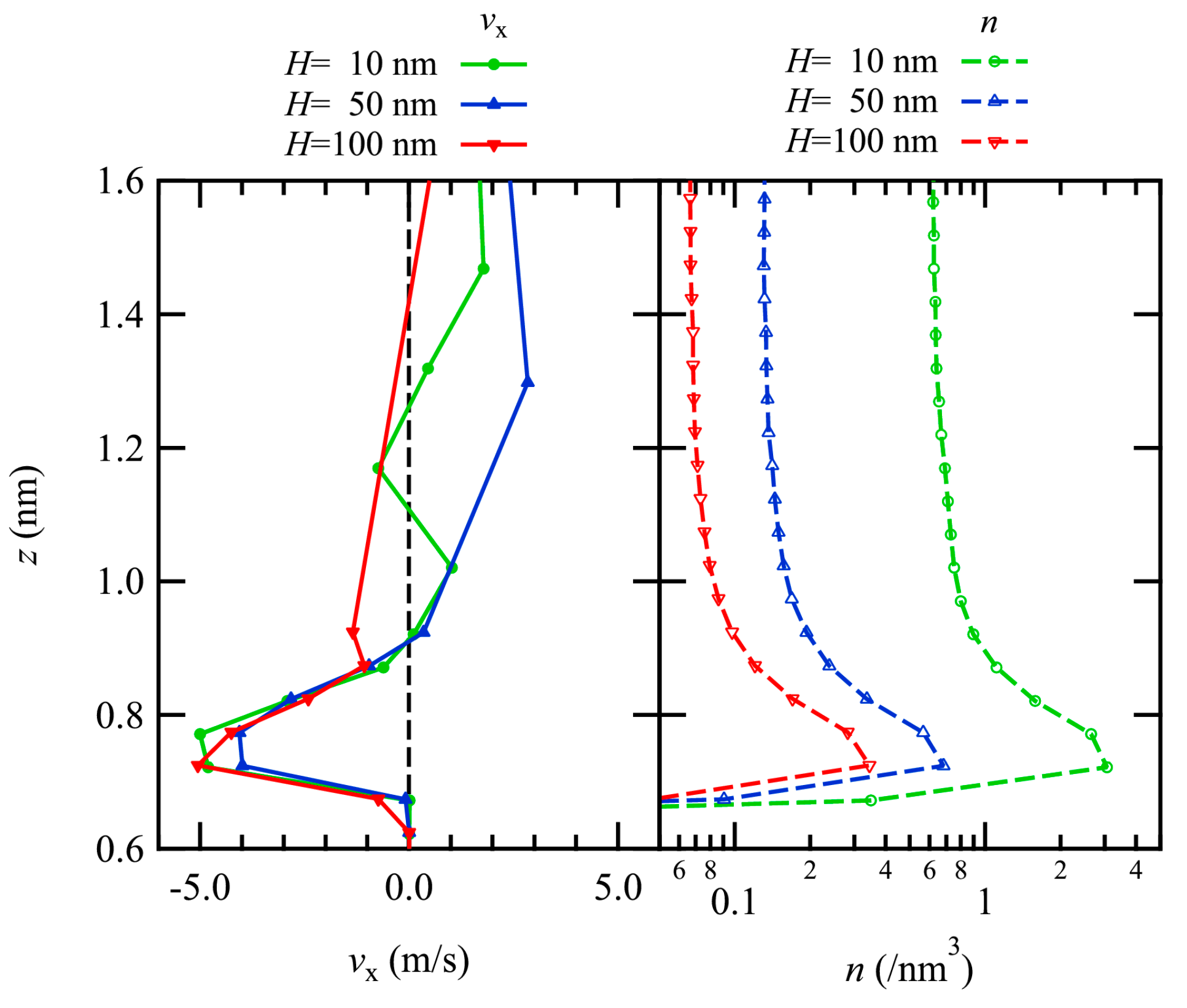
3.1. Bulk Flow Velocity Profile
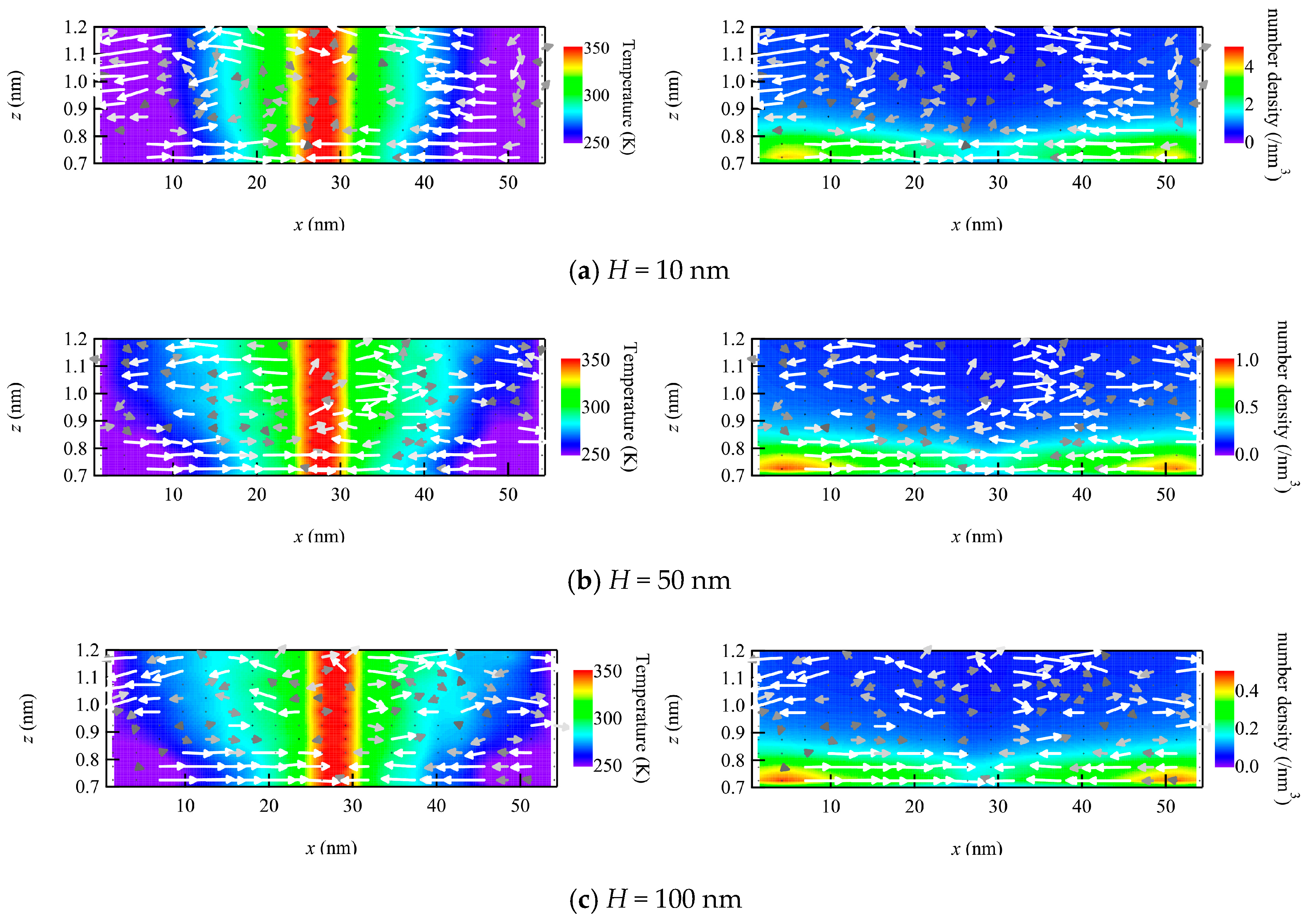
3.2. Profiles near the Wall
3.3. Molecular Motions near the Wall
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sone, Y. Molecular Gas Dynamics: Theory, Techniques, and Applications; Birkhäuser: Boston, MA, USA, 2007. [Google Scholar]
- Sharipov, F. Rarefied Gas Dynamics: Fundamentals for Research and Practice; Wiley-VCH: Weinheim, Germany, 2016. [Google Scholar]
- Akhlaghi, H.; Roohi, E.; Stefanov, S. A comprehensive review on micro- and nano-scale gas flow effects: Slip-jump phenomena, Knudsen paradox, thermally-driven flows, and Knudsen pumps. Phys. Rep. 2023, 997, 1–60. [Google Scholar] [CrossRef]
- Wang, X.; Su, T.; Zhang, W.; Zhang, S. Knudsen pumps: A review. Microsyst. Nanoeng. 2020, 26, 2–28. [Google Scholar] [CrossRef]
- Vargo, S.E.; Muntz, E.P. Initial results from the first MEMS fabricated thermal transpiration-driven vacuum pump. AIP Conf. Proc. 2001, 585, 502–509. [Google Scholar] [CrossRef]
- McNamara, S.; Gianchandani, Y.B. On-chip vacuum generated by a micromachined Knudsen pump. J. MEMS 2005, 14, 741–746. [Google Scholar] [CrossRef]
- An, S.; Gupta, N.K.; Gianchandani, Y.B. A Si-micromachined 162-stage two-part knudsen pump for on-chip vacuum. J. MEMS 2014, 23, 406–416. [Google Scholar] [CrossRef]
- Liu, J.; Gupta, N.K.; Wise, K.D.; Gianchandani, Y.B.; Fan, X. Demonstration of motionless Knudsen pump based micro-gas chromatography featuring micro-fabricated columns and on-column detectors. Lab Chip 2011, 11, 3487–3492. [Google Scholar] [CrossRef] [PubMed]
- Nakaye, S.; Sugimoto, H. Demonstration of a gas separator composed of Knudsen pumps. Vacuum 2016, 125, 154–164. [Google Scholar] [CrossRef]
- Kugimoto, K.; Hirota, Y.; Yamauchi, T.; Yamaguchi, H.; Niimi, T. Design and demonstration of Knudsen heat pump without moving parts free from electricity. Appl. Energy 2019, 250, 1260–1269. [Google Scholar] [CrossRef]
- Porodnov, B.T.; Kulev, A.N.; Tuchevetov, F.T. Thermal transpiration in a circular capillary with a small temperature difference. J. Fluid Mech. 1978, 88, 609–622. [Google Scholar] [CrossRef]
- Rojas-Cárdenas, M.; Graur, I.; Perrier, P.; Méolans, J.G. Thermal transpiration flow: A circular cross-section microtube submitted to a temperature gradient. Phys. Fluids 2011, 23, 031702. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Rojas-Cárdenas, M.; Perrier, P.; Graur, I.; Niimi, T. Thermal transpiration flow through a single rectangular channel. J. Fluid Mech. 2014, 744, 169–182. [Google Scholar] [CrossRef]
- Rojas-Cárdenas, M.; Graur, I.; Perrier, P.; Méolans, J.G. Time-dependent experimental analysis of a thermal transpiration rarefied gas flow. Phys. Fluids 2013, 25, 072001. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Perrier, P.; Ho, M.T.; Méolans, J.G.; Niimi, T.; Graur, I. Mass flow rate measurement of thermal creep flow from transitional to slip flow regime. J. Fluid Mech. 2016, 795, 690–707. [Google Scholar] [CrossRef]
- Sharipov, F.; Seleznev, V. Data on Internal Rarefied Gas Flows. J. Phys. Chem. Ref. Data 1998, 27, 657–706. [Google Scholar] [CrossRef]
- Sharipov, F.; Bertoldo, G. Poiseuille flow and thermal creep based on the Boltzmann equation with the Lennard-Jones potential over a wide range of the Knudsen number. Phys. Fluids 2009, 21, 067101. [Google Scholar] [CrossRef]
- Babac, G.; Dongari, N.; Zhang, Y.; Reese, J.M. Thermal transpiration of nanoscale gas flow. AIP Conf. Proc. 2012, 1501, 946–953. [Google Scholar] [CrossRef]
- Francis, J.T.; Sathian, S.P. Thermal transpiration: A molecular dynamics study. AIP Conf. Proc. 2014, 1628, 901–908. [Google Scholar] [CrossRef]
- Akhlaghi, H.; Roohi, E. Mass flow rate prediction of pressure-temperature-driven gas flows through micro/nanoscale channels. Contin. Mech. Thermodyn. 2014, 26, 67–78. [Google Scholar] [CrossRef]
- Lockerby, D.A.; Patronis, A.; Borg, M.K.; Reese, J.M. Asynchronous coupling of hybrid models for efficient simulation of multiscale systems. J. Comput. Phys. 2015, 284, 261–272. [Google Scholar] [CrossRef]
- Wang, P.; Su, W.; Wu, L. Thermal transpiration in molecular gas. Phys. Fluids 2020, 32, 082005. [Google Scholar] [CrossRef]
- Akhlaghi, H.; Balaj, M.; Roohi, E. Hydrodynamic behaviour of micro/nanoscale Poiseuille flow under thermal creep condition. Appl. Phys. Lett. 2013, 103, 073108. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Kikugawa, G. Molecular dynamics study on flow structure inside a thermal transpiration flow field. Phys. Fluids 2021, 33, 012005. [Google Scholar] [CrossRef]
- Chapman, S.; Cowling, T.G. The Mathematical Theory of Non-Uniform Gases; Cambridge University Press: London, UK, 1970. [Google Scholar]
- Sahebi, M.; Azimian, A.R. A molecular dynamics study about the mechanisms of liquid thermal transpiration flow in nanotubes. Int. J. Therm. Sci. 2019, 136, 9–14. [Google Scholar] [CrossRef]
- Humphrey, T.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graphics Modell. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Bird, G. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Kikugawa, G.; Ando, S.; Suzuki, J.; Naruke, Y.; Nakano, T.; Ohara, T. Effect of the computational domain size and shape on the self-diffusion coefficient in a Lennard-Jones liquid. J. Chem. Phys. 2015, 142, 024503. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Prabha, S.K.; Sathian, S.P. Molecular-dynamics study of Poiseuille flow in a nanochannel and calculation of energy and momentum accommodation coefficients. Phys. Rev. E 2012, 85, 041201. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamaguchi, H.; Kikugawa, G. Thermal Transpiration Flow: Molecular Dynamics Study from Dense to Dilute Gas. Fluids 2024, 9, 12. https://doi.org/10.3390/fluids9010012
Yamaguchi H, Kikugawa G. Thermal Transpiration Flow: Molecular Dynamics Study from Dense to Dilute Gas. Fluids. 2024; 9(1):12. https://doi.org/10.3390/fluids9010012
Chicago/Turabian StyleYamaguchi, Hiroki, and Gota Kikugawa. 2024. "Thermal Transpiration Flow: Molecular Dynamics Study from Dense to Dilute Gas" Fluids 9, no. 1: 12. https://doi.org/10.3390/fluids9010012
APA StyleYamaguchi, H., & Kikugawa, G. (2024). Thermal Transpiration Flow: Molecular Dynamics Study from Dense to Dilute Gas. Fluids, 9(1), 12. https://doi.org/10.3390/fluids9010012






