Thermophysical Properties of Silicon Oxide Nanoparticles in Water and Ethylene Glycol–Water Dispersions
Abstract
1. Introduction
2. Experimental Section
2.1. Investigated Fluids and Sample Preparation
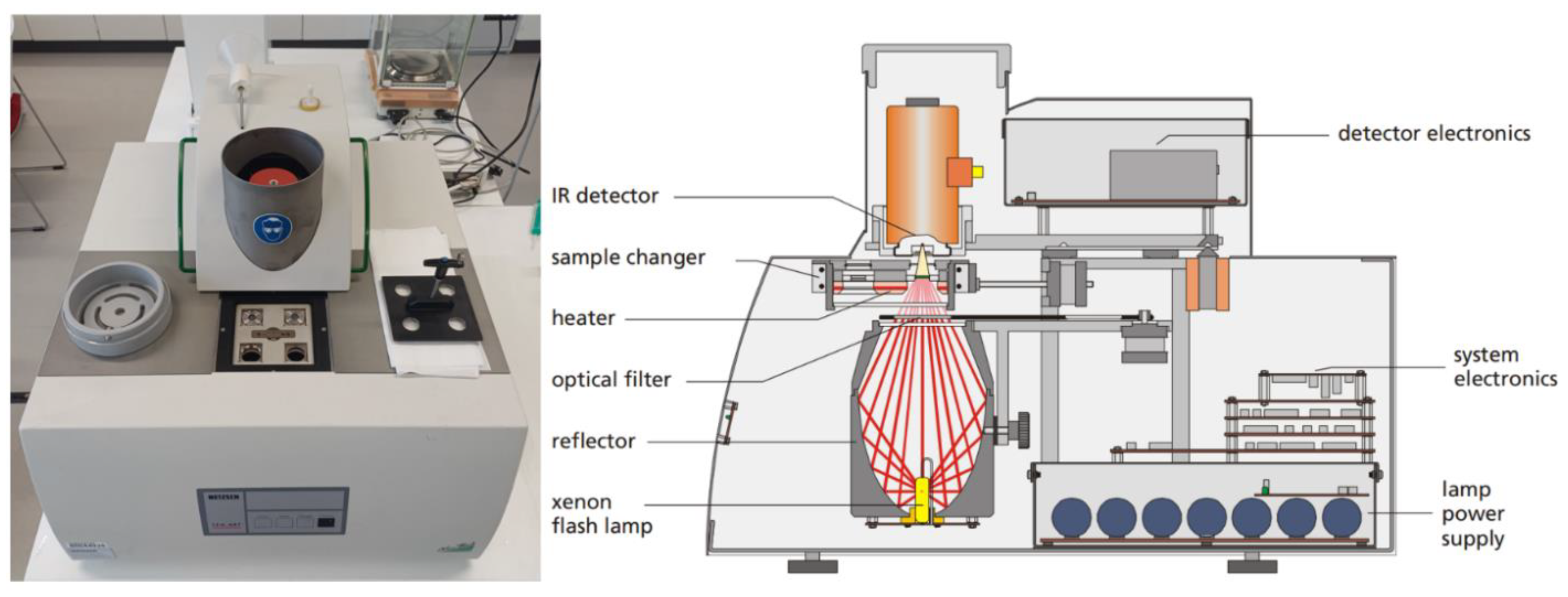
2.2. Apparatus and Procedure
2.2.1. Transmission
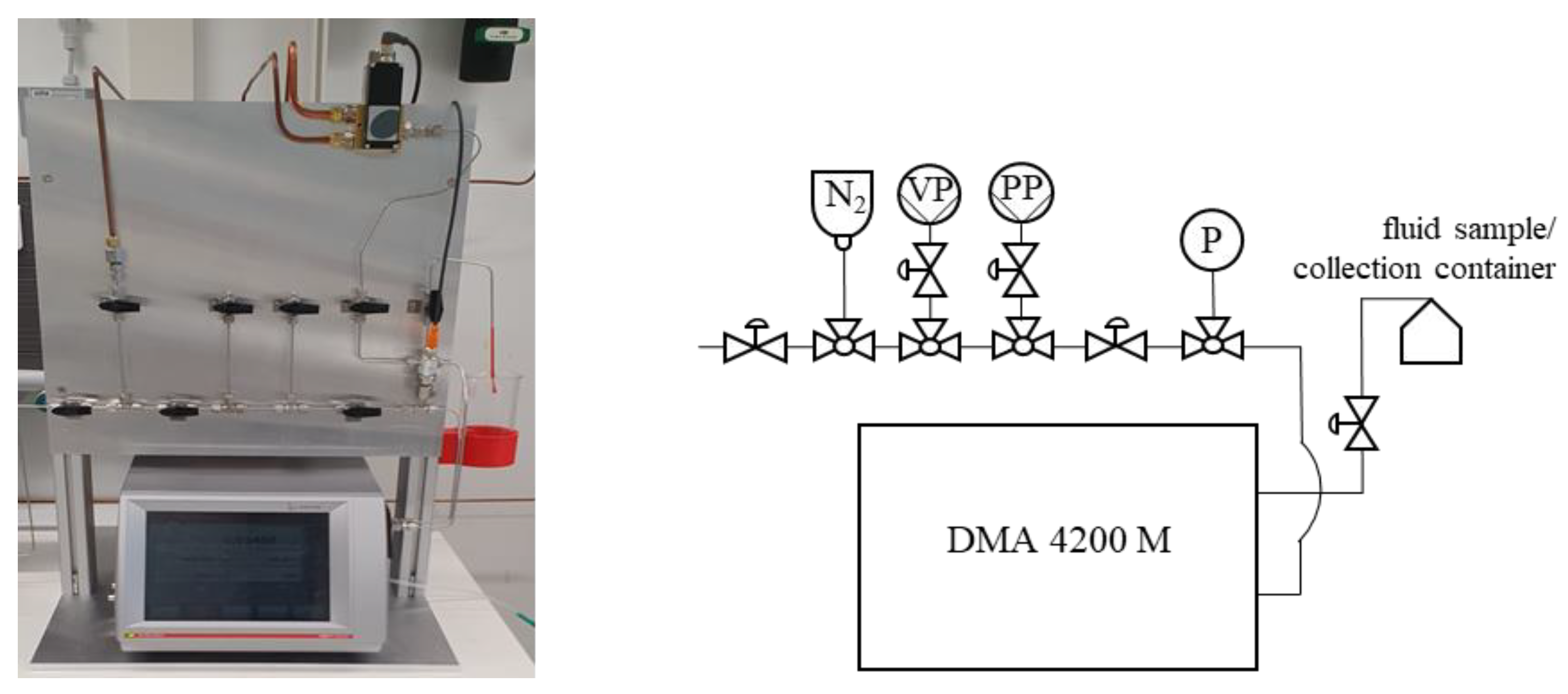
2.2.2. Density
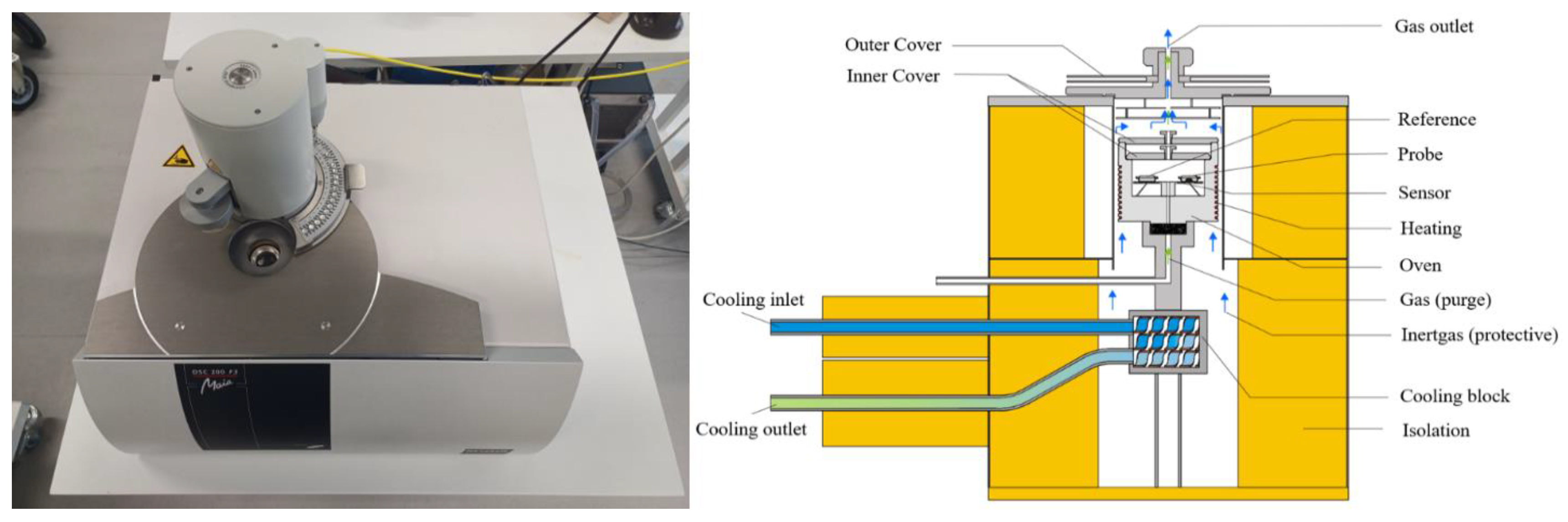
2.2.3. Differential Scanning Calorimetry
2.2.4. Laser Flash Analysis
3. Correlations
3.1. Density
3.2. Specific Heat Capacity
3.3. Thermal Conductivity
3.4. New Empirical Correlation for Density, Specific Heat Capacity, and Thermal Diffusivity
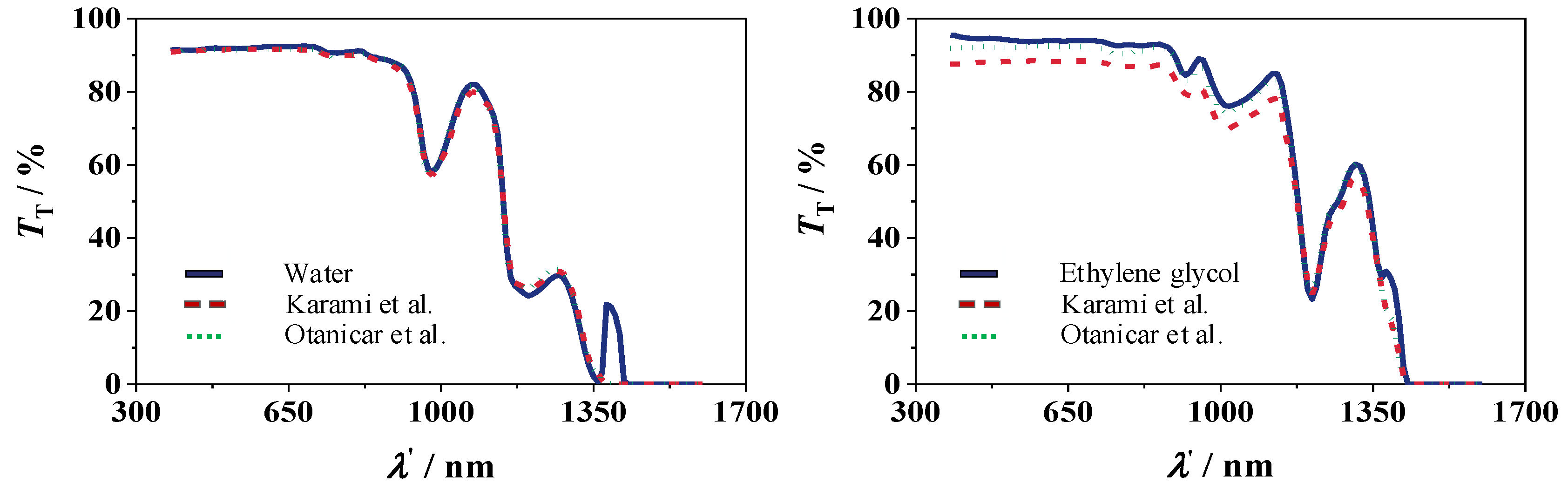
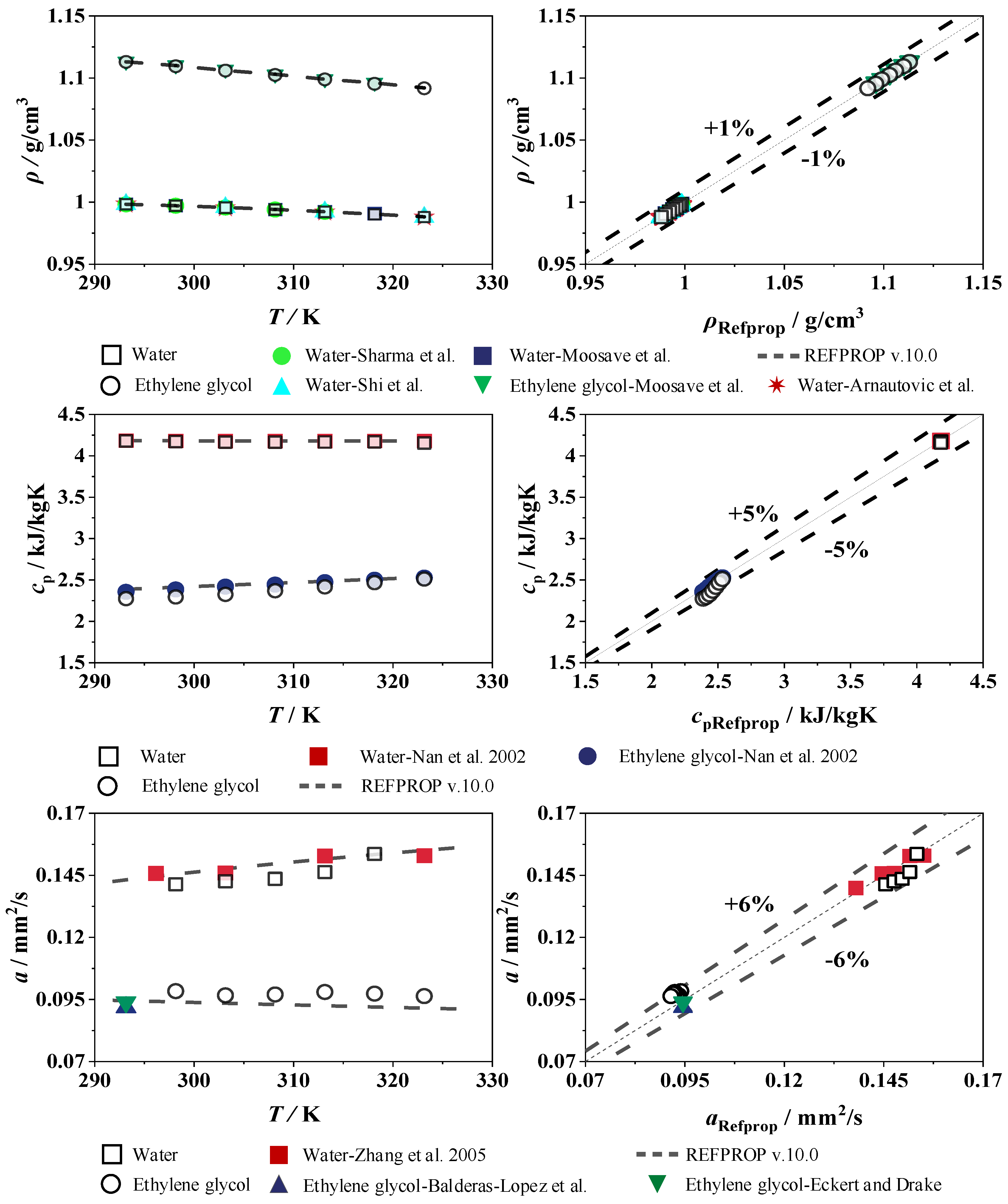
3.5. Validation
4. Results
4.1. Pure Components
4.2. Nanofluid
4.2.1. Sample Stability
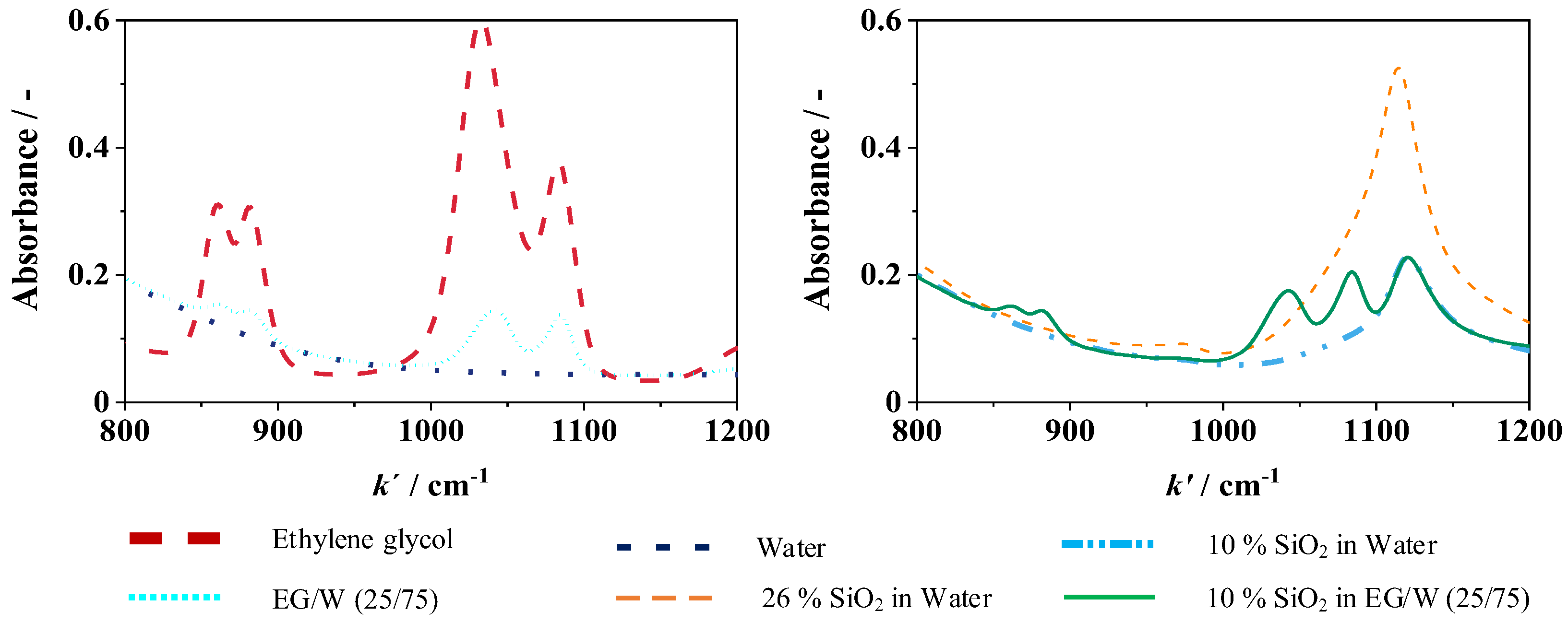
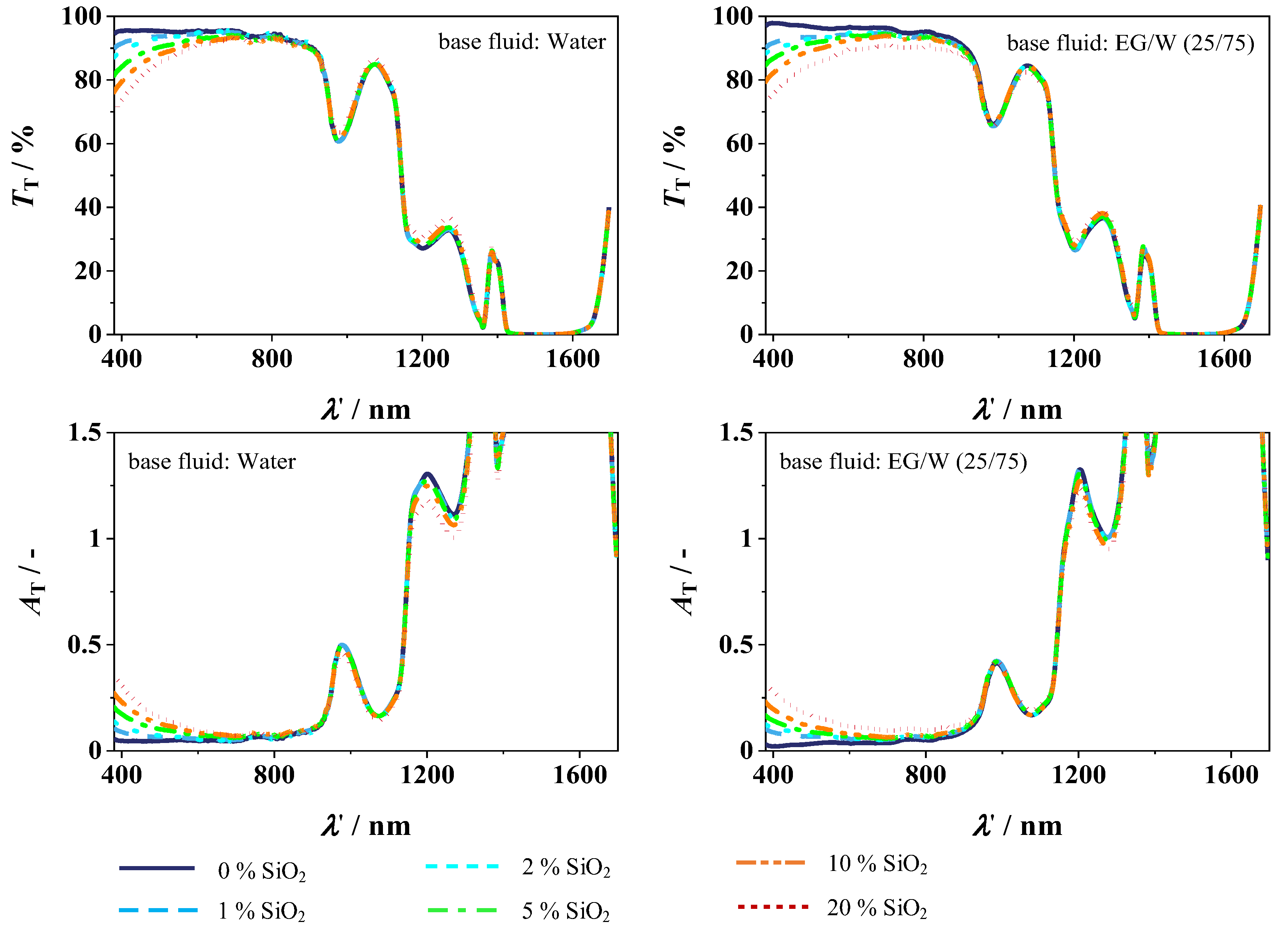
4.2.2. Transmission
4.2.3. Density
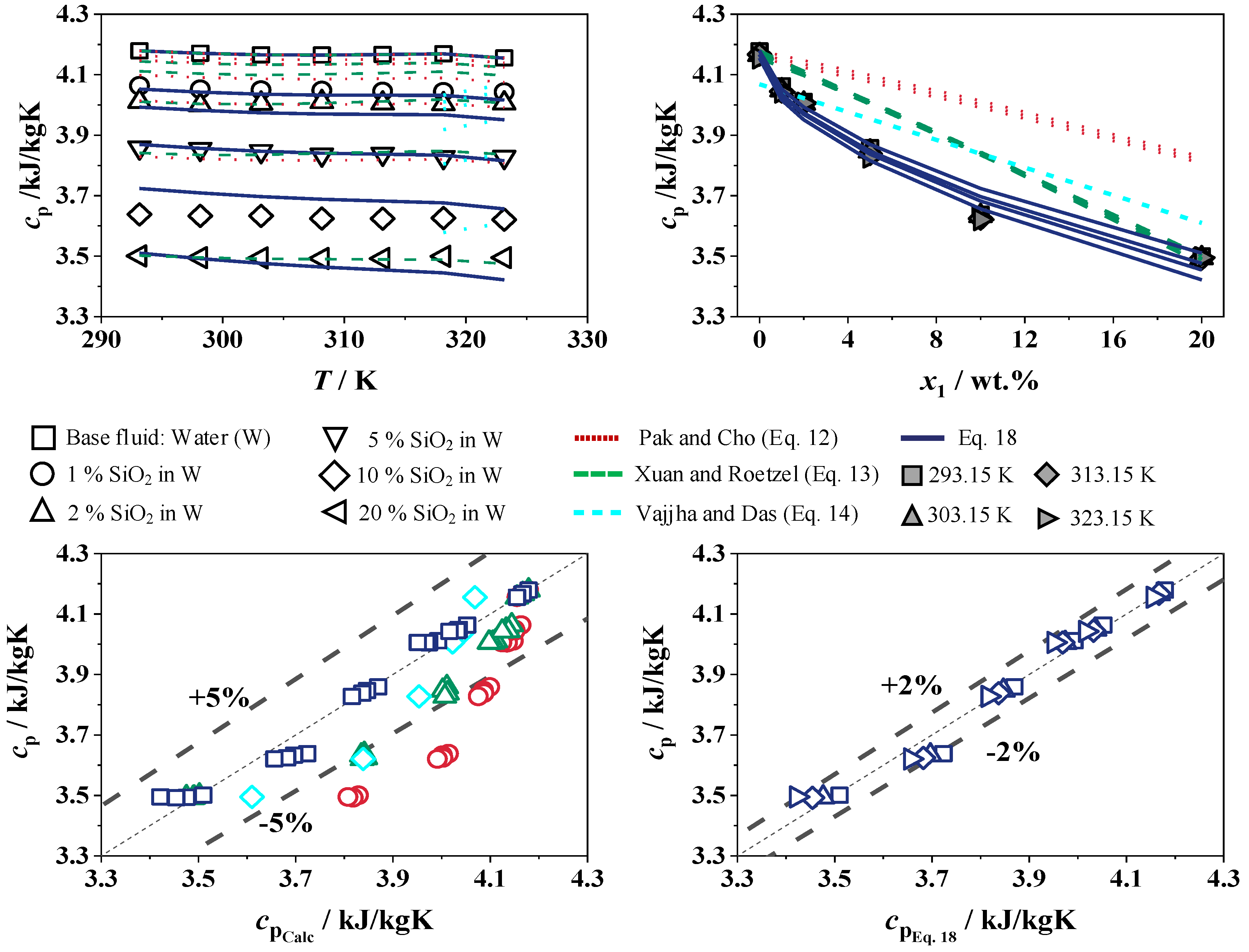
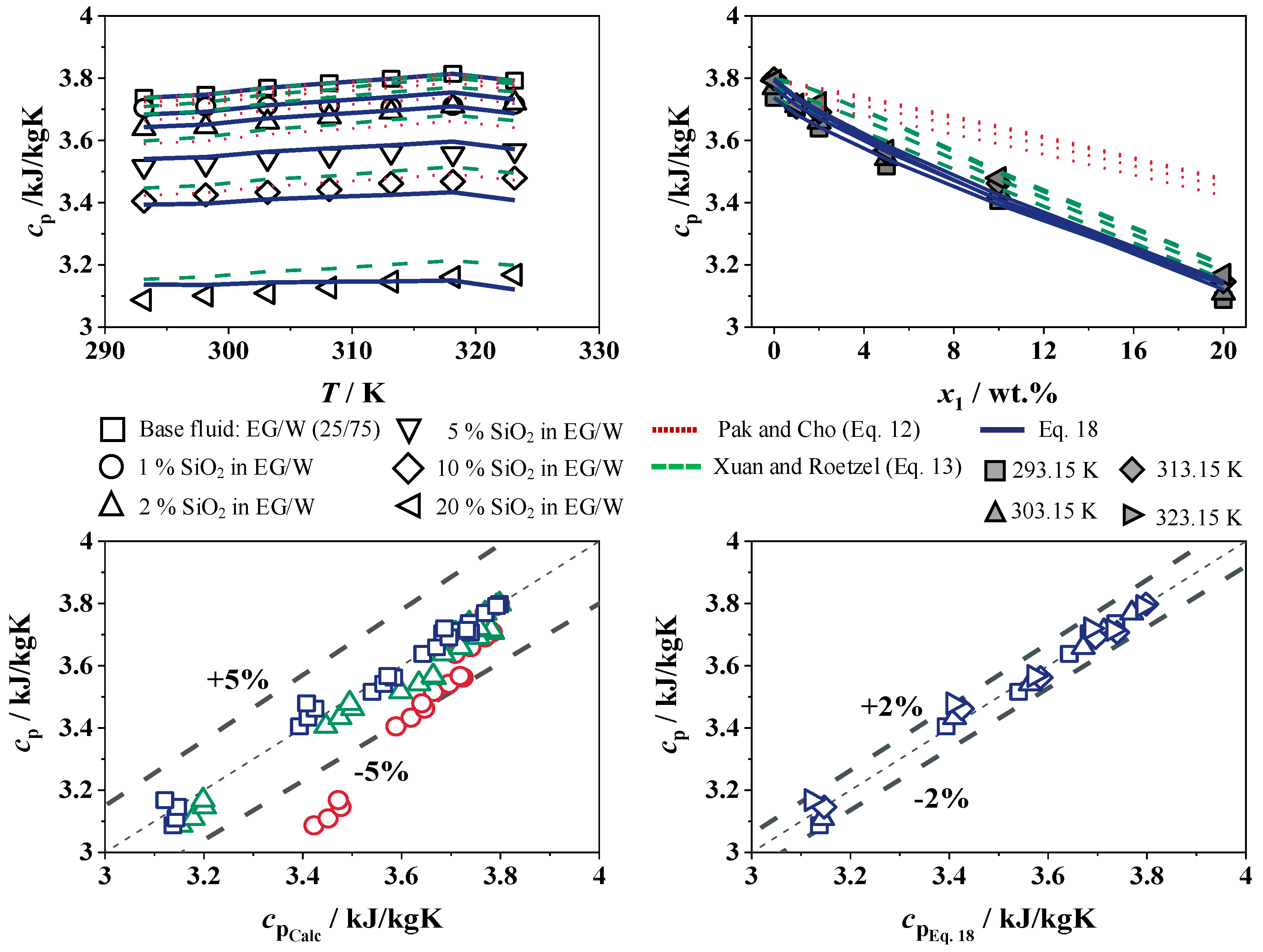
4.2.4. Specific Heat Capacity
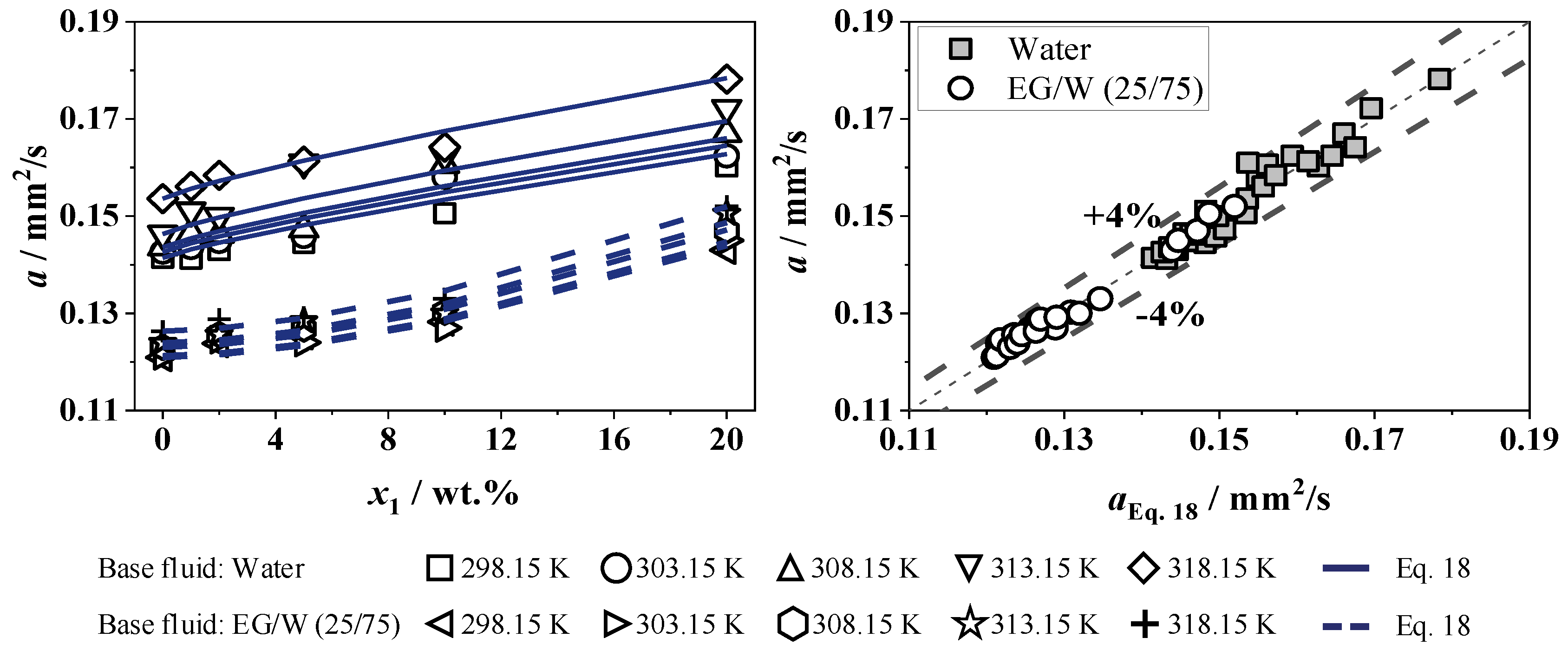
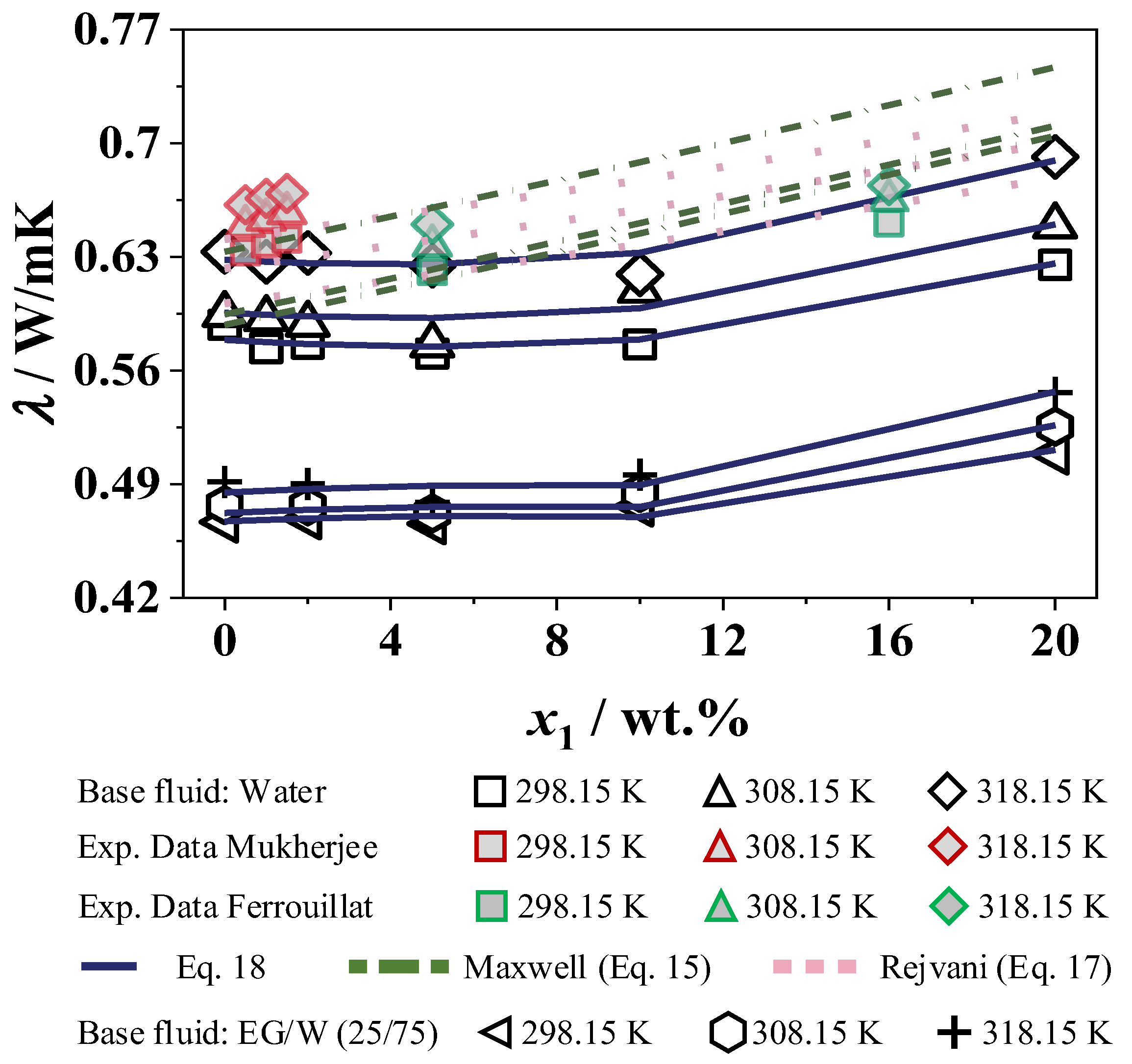
4.2.5. Thermal Diffusivity and Conductivity
5. Conclusions
- At a constant concentration, the density decreases with increasing temperature, while, at constant temperature, the density increases linearly with an increasing SiO2 concentration of up to 12.3% and 11.3% compared to the base fluids W and EG/W (25/75), respectively.
- At a constant temperature and with an increasing concentration of SiO2 in W, the specific heat capacity decreases strongly by up to 7.7% at 5 wt.% SiO2, after which the decrease flattens out to a 15.9% lower specific heat capacity at 20 wt.% compared to pure W. For SiO2 in EG/W (25/75), the specific heat capacity decreases with an increasing nanoparticle concentration at a constant temperature by up to 17.3%. The correlations of Pak and Cho [15] as well as Xuan and Roetzel [41] predict high specific heat capacities that are too high, resulting in relative deviations greater than 5%. With a decreasing nanoparticle size, the specific heat capacity of nanofluids decreases [55,59]. This is because the number of vibrational sources increases with decreasing particle size for the same volume concentration. The surface area per unit volume of small particles is greater than that of large particles. Therefore, Brownian motion and heat transfer are more active for small particles than for large particles, leading to an acceleration of heat transfer [55].
- The measured thermal diffusivity of W rises with increasing temperature by up to 8.6% at 318 K, while EG/W has a rise of 4.5%. Adding SiO2 nanoparticles, the thermal diffusivity increases for 318 K and 20 wt.% SiO2 to a maximum of 16.4% in W and 20.4% in EG/W, respectively.
- Equation (18) provides a maximum relative deviation of less than 1, 4, and 5% for the density, specific heat capacity, and thermal diffusivity, respectively.
- The calculated thermal conductivity shows a slight decrease of 3% in W and 1% in EG/W (25/75) at 5 wt.% SiO2. With a higher concentration, it increases to a maximum at 20 wt.% SiO2 with a rise of 9% for the base fluid W and 12% for the base fluid EG/W (25/75).
- The thermal conductivity is measured by various measuring devices. In this study, it is calculated by measuring the density, specific heat capacity, and thermal diffusivity. The decrease in the heat capacity in the low concentration range has a corresponding effect on the result for the thermal conductivity. With different geometries of the nanoparticles, the sphericity could also influence the thermal conductivity, which is shown in Equation (16). However, a more detailed analysis of sphericity with SEM images of different geometries would be necessary to examine this. In terms of the particle size, smaller particles lead to increased thermal conductivity due to increased Brownian motion.
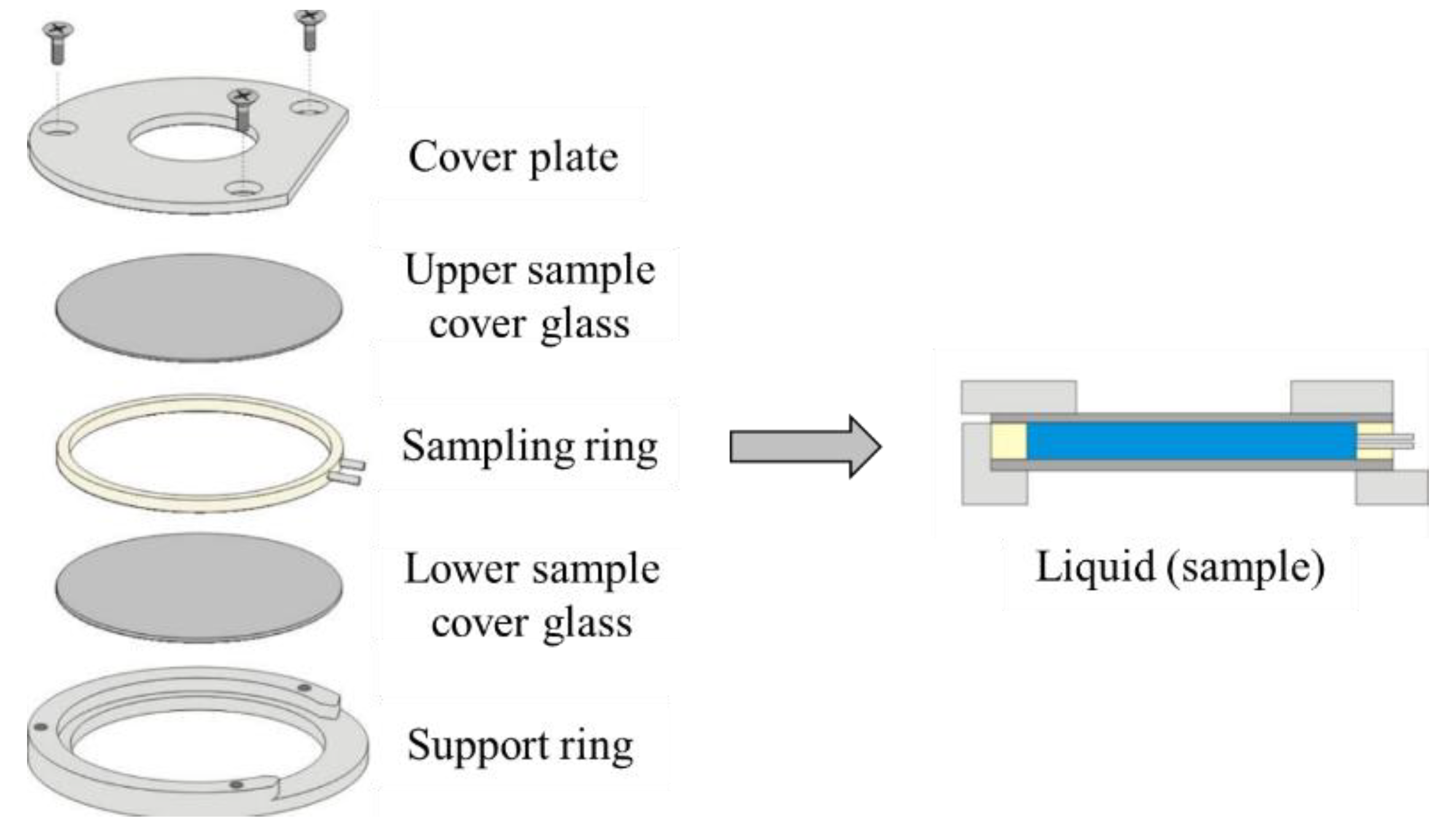
- In comparison with other measuring devices, it has been found that the thermal conductivity values with the LFA are often lower than with the transient hot wire (THW) or hot disk method, for example [60,61,62,63]. Due to the low filling height of the sample of 0.5 mm (see Figure 6), the Brownian motion is inhibited, which is largely responsible for the increase in thermal conductivity in nanofluids [64,65]. As a result, the thermal conductivities differ depending on the application and are lower for heat transfer in a thin gap.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Roman letters | |
| a | thermal diffusivity, (mm2/s) |
| A, B | adjustable parameter in Equation (18) |
| AV, BV, CV | adjustable parameter in Equation (14) |
| cp | specific heat capacity (kJ/kgK) |
| I0 | initial radiation |
| IT | radiation transmitted |
| k | thermal conductivity, (W/mK) |
| wavenumber, (cm−1) | |
| calibration function | |
| lABS | length of the absorption path, (cm) |
| m | mass, (kg) |
| n | number of data points |
| T | temperature, (K) |
| TT | transmission, (-) |
| half-time of the temperature rise | |
| u | uncertainties, (-) |
| V | volume, (m3) |
| xi | mass fraction liquid phase, (wt.%) |
| z | values, (-) |
| Greek letters | |
| αext | absorption coefficient, (cm−1) |
| β | shape factor, (-) |
| heat rate | |
| heat flow rate, (W) | |
| wavelength (nm) | |
| ρ | density, (g/cm3) |
| τ | oscillation period, (s) |
| φ | concentration |
| ψ | particle sphericity, (-) |
| Subscripts | |
| 0 | baseline |
| bf | base fluid |
| Calc | calculated |
| Exp | experimental |
| i | component index |
| nf | nanofluid |
| Np | nanoparticle |
| Ref | reference |
| S | sample |
| Abbreviations | |
| Ag/CoSO4 | silver nanoparticle in cobalt sulphate |
| Al2O3 | aluminum oxide |
| Au | gold |
| Cu | copper |
| CuO | copper oxide |
| DMA | density meter |
| DSC | differential scanning calorimetry |
| EG | ethylene glycol |
| eq | equation |
| FT-IR | Fourier-transform infrared spectroscopy |
| LFA | laser flash analysis |
| PP | pressure pump |
| RD | relative deviation |
| RMSE | root mean square error |
| SiO2 | silicon dioxide |
| TiO2 | titanium dioxide |
| TPP | thermo-physical properties |
| VP | vacuum pump |
| W | water |
| ZnO | zinc oxide |
| ZrO2 | zirconium dioxide |
References
- Kabir, E.; Kumar, P.; Kumar, S.; Adelodun, A.; Kim, K.-H. Solar energy: Potential and future prospects. Renew. Sustain. Energy Rev. 2018, 82, 894–900. [Google Scholar] [CrossRef]
- Gorji, T.B.; Ranjbar, A.A. A review on optical properties and application of nanofluids in direct absorption solar collectors (DASCs). Renew. Sustain. Energy Rev. 2017, 72, 10–32. [Google Scholar] [CrossRef]
- Arthur, O.; Karim, M.A. An investigation into the thermophysical and rheological properties of nanofluids for solar thermal applications. Renew. Sustain. Energy Rev. 2016, 55, 739–755. [Google Scholar] [CrossRef]
- Tembhare, S.P.; Barai, D.P.; Bhanvase, B.A. Performance evaluation of nanofluids in solar thermal and solar photovoltaic systems: A comprehensive review. Renew. Sustain. Energy Rev. 2022, 153, 111738. [Google Scholar] [CrossRef]
- Okonkwo, E.C.; Wole-Osho, I.; Almanassra, I.W.; Abdullatif, Y.M.; Al-Ansari, T. An updated review of nanofluids in various heat transfer devices. J. Therm. Anal. Calorim. 2021, 145, 2817–2872. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In ASME International Mechanical Engineering Congress & Exposition; Argonne National Lab: Argonne, IL, USA, 1995; Volume 29. [Google Scholar]
- Mokhtarpour, M.; Homayoon-far, S.; Shekaari, H.; Zafarani-Moattar, M.T. Effect of Some Imidazolium-Based Ionic Liquids on the Stability, Volumetric, and Transport Properties of ZnO Nanofluids. J. Chem. Eng. Data 2020, 65, 5369–5383. [Google Scholar] [CrossRef]
- Dey, D.; Kumar, P.; Samantaray, S. A review of nanofluid preparation, stability, and thermo-physical properties. Heat Transf. Asian Res. 2017, 46, 1413–1442. [Google Scholar] [CrossRef]
- Zahmatkesh, I.; Sheremet, M.; Yang, L.; Heris, S.Z.; Sharifpur, M.; Meyer, J.P.; Ghalambaz, M.; Wongwises, S.; Jing, D.; Mahian, O. Effect of nanoparticle shape on the performance of thermal systems utilizing nanofluids: A critical review. J. Mol. Liq. 2021, 321, 114430. [Google Scholar] [CrossRef]
- Zhong-Yong, Y.; Bao-Lian, S. Titanium oxide nanotubes, nanofibers and nanowires. Colloids Surf. A Physicochem. Eng. Asp. 2004, 241, 173–183. [Google Scholar] [CrossRef]
- Vandrangi, S.K.; Hassan, S.; Sharma, K.V.; Akilu, S.; Emani, S.; Nabipour, N. Effect of base fluids on thermo-physical properties of SiO2 nanofluids and development of new correlations. In Mathematical Methods in the Applied Science; Special Issue Paper; Wiley: Hoboken, NJ, USA, 2020; pp. 1–19. [Google Scholar] [CrossRef]
- Wong, K.V.; De Leon, O. Applications of Nanofluids: Current and Future. Adv. Mech. Eng. 2010, 2, 519659. [Google Scholar] [CrossRef]
- Talib, S.; Azmi, W.H.; Zakaria, I.; Mohamed, W.; Mamat, A.; Ismail, H.; Daud, W. Thermophysical Properties of Silicon Dioxide (SiO2) in Ethylene Glycol/Water Mixture for Proton Exchange Membrane Fuel Cell Cooling Application. Energy Procedia 2015, 79, 366–371. [Google Scholar] [CrossRef]
- Hashimoto, S.; Harada, M.; Higuchi, Y.; Matsunaga, T. Enhancement mechanism of convective heat transfer via nanofluid: An analysis by means of synchrotron radiation imaging. Int. J. Heat Mass Transf. 2020, 159, 120081. [Google Scholar] [CrossRef]
- Pak, B.C.; Cho, Y.I. Hydrodynamic and Heat Transfer Study of Dispersed Fluids with Submicron Metallic Oxide Particle. Exp. Heat Transf. 1998, 11, 151–170. [Google Scholar] [CrossRef]
- Ali, A.R.I.; Salam, B. A review on nanofluid: Preparation, stability, thermophysical properties, heat transfer characteristics and application. SN Appl. Sci. 2020, 2, 280. [Google Scholar] [CrossRef]
- O’Hanley, H.; Buongiorno, J.; McKrell, T.; Hu, L. Measurement and Model Validation of Nanofluid Specific Heat Capacity with Differential Scanning Calorimetry. Adv. Mech. Eng. 2012, 4, 181079. [Google Scholar] [CrossRef]
- Gupta, M.; Singh, V.; Kumar, R.; Said, Z. A review on thermophysical properties of nanofluids and heat transfer applications. Renew. Sustain. Energy Rev. 2017, 74, 638–670. [Google Scholar] [CrossRef]
- Namburu, P.K.; Kulkarni, D.P.; Dandekar, A.; Das, D.K. Experimental investigation of viscosity and specific heat of silicon dioxide nanofluids. Micro Nano Lett. 2007, 2, 67–71. [Google Scholar] [CrossRef]
- Vajjha, R.S.; Das, D.K. Specific heat measurement of three nanofluids and development of new correlation. J. Heat Transf. 2009, 131, 071601. [Google Scholar] [CrossRef]
- Kwek, D.; Crivoi, A.; Duan, F. Effects of Temperature and Particle Size on the Thermal Property Measurements of Al2O3—Water Nanofluids. J. Chem. Eng. Data 2010, 55, 5690–5695. [Google Scholar] [CrossRef]
- Tertsinidou, G.J.; Tsolakidou, C.M.; Pantzali, M.; Assael, M.J. New Measurements of the Apparent Thermal Conductivity of Nanofluids and Investigation of Their Heat Transfer Capabilities. J. Chem. Eng. Data 2016, 62, 491–507. [Google Scholar] [CrossRef]
- Xie, H.; Chen, L. Review on the Preparation and Thermal Performances of Carbon Nanotube Contained Nanofluids. J. Chem. Eng. Data 2011, 56, 1030–1041. [Google Scholar] [CrossRef]
- Bhandari, S.S.; Muralidhar, K.; Joshi, Y.M. Thermal Diffusivity and Viscosity of Suspensions of Disk-Shaped Nanoparticles. Ind. Eng. Chem. Res. 2013, 52, 15114–15123. [Google Scholar] [CrossRef][Green Version]
- Sahoo, B.C.; Das, D.K.; Vajjha, R.S.; Satti, J.R. Measurement of the Thermal Conductivity of Silicon Dioxide Nanofluid and Development of Correlations. J. Nanotechnol. Eng. Med. 2012, 3, 041006. [Google Scholar] [CrossRef]
- Ferrouillat, S.; Bontemps, A.; Ribeiro, J.-P.; Gruss, J.-A.; Soriano, O. Hydraulic and heat transfer study of SiO2/water nanofluids in horizontal tubes with imposed wall temperature boundary conditions. Int. J. Heat Fluid Flow 2011, 32, 424–439. [Google Scholar] [CrossRef]
- Dong, J.; Zheng, Q.; Xiong, C.; Sun, E.; Chen, J. Experimental investigation and application of stability and thermal characteristics of SiO2-ethylene-glycol/water nanofluids. Int. J. Therm. Sci. 2022, 176, 107533. [Google Scholar] [CrossRef]
- Rejvani, M.; Alipour, A.; Vahedi, S.M.; Chamkha, A.J.; Wongwises, S. Optimal characteristics and heat transfer efficiency of SiO2/water nanofluid for application of energy devices: A comprehensive study. Int. J. Energy Res. 2019, 43, 8548–8571. [Google Scholar] [CrossRef]
- Mukherjee, S.; Panda, S.R.; Mishra, P.C.; Sen, S.; Chaudhuri, P. Thermophysical and transient heat transfer characteristics of aqueous SiO2 nanofluid in energy management applications. J. Process Mech. Eng. 2022, 237, 1100–1111. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, T.; Zhang, D.; Wang, Q. Experimental investigation of thermal and electrical conductivity of silicon oxide nanofluids in ethylene glycol/water mixture. Int. J. Heat Mass Transf. 2018, 117, 280–286. [Google Scholar] [CrossRef]
- Otanicar, P.T.; Phelan, P.E.; Golden, J.S. Optical properties of liquids for direct absorption solar thermal energy systems. Sol. Energy 2009, 83, 969–977. [Google Scholar] [CrossRef]
- Taylor, R.A.; Otanicar, P.T.; Rosengarten, G. Nanofluid-based optical filter optimization for PV/T systems. Light Sci. Appl. 2012, 1, e34. [Google Scholar] [CrossRef]
- Han, X.; Chen, X.; Wang, Q.; Alelyani, S.M.; Qu, J. Investigation of CoSO4-based Ag nanofluids as spectral beam splitters for hybrid PV/T applications. Sol. Energy 2019, 177, 387–394. [Google Scholar] [CrossRef]
- Khullar, V.; Bhalla, V.; Tyagi, H. Potential Heat Transfer Fluids (Nanofluids) for Direct Volumetric Absorption-Based Solar Thermal Systems. J. Therm. Sci. Eng. Appl. 2018, 10, 011009. [Google Scholar] [CrossRef]
- Huber, M.; Harvey, A.; Lemmon, E.; Hardin, G.; Bell, I.; McLinden, M. Reference Fluid Thermodynamic and Transport Properties Database (REFPROP) Version 10-SRD 23. NIST2018. Available online: https://data.nist.gov/od/id/725039AC054648F9E0532457068156CB1948 (accessed on 8 October 2024).
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Anton Paar GmbH. Operating Instructions Density Meter 4200 M; Anton Paar GmbH: Tokyo, Japan, 2017. [Google Scholar]
- Netzsch Gerätebau GmbH. Operating Instructions DSC Apparatus DSC 200 F3 Maia; Netzsch Gerätebau GmbH: Selb, Germany, 2012. [Google Scholar]
- Höhne, G.W.H.; Hemminger, W.F.; Flammersheim, H.-J. Differential Scanning Calorimetry, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Netzsch Gerätebau GmbH. Operating Instructions Nano-Flash-Apparatus LFA 447; Netzsch Gerätebau GmbH: Selb, Germany, 2012. [Google Scholar]
- Xuan, Y.; Roetzel, W. Conceptions for heat transfer correlation of nanofluid. Int. J. Heat Mass Transf. 2000, 43, 3701–3707. [Google Scholar] [CrossRef]
- Esfe, M.H.; Afrand, M. An updated review on the nanofluids characteristics. J. Therm. Anal. Calorim. 2019, 138, 4091–4101. [Google Scholar] [CrossRef]
- Pietrak, K.; Wisniewski, T.S. A review of models for effective thermal conductivity of composite material. J. Power Technol. 2015, 95, 14–24. [Google Scholar]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Macmillan & Co. Ltd.: New York, NY, USA, 1881. [Google Scholar]
- Hamilton, R.L.; Crosser, O.K. Thermal Conductivity of Heterogeneous Two-Component Systems. Div. Ind. Eng. Chem. 1962, 1, 3. [Google Scholar] [CrossRef]
- Karami, M.; Raisee, M.; Delfani, S.; Akhavan Bahabadi, M.A.; Rashidi, A.M. Sunlight Absorbing Potential of Carbon Nanoball Water and Ethylene Glycol-Based Nanofluids. Opt. Spectrosc. 2013, 3, 400–405. [Google Scholar] [CrossRef]
- Sharma, T.; Rani, R.; Kumar, A.; Bamezai, R.K. Solution properties of an antidiabetic drug metformin hydrochloride in aqueous urea and thiourea solutions: A physicochemical study. J. Mol. Liq. 2020, 300, 111985. [Google Scholar] [CrossRef]
- Shi, Y.; Zhu, C.; Fu, T.; Gao, X.; Ma, Y. Volumetric and Viscometric Properties of Maltitol in Glycylglycine Aqueous Solutions at T = 293.15–333.15 K. J. Chem. Eng. Data 2021, 66, 360–367. [Google Scholar] [CrossRef]
- Moosavi, M.; Rostami, A.A. Densities, Viscosities, Refractive Indices, and Excess Properties of Aqueous 1,2-Etanediol, 1,3-Propanediol, 1,4-Butanediol, and 1,5-Pentanediol Binary Mixtures. J. Chem. Eng. Data 2017, 62, 156–168. [Google Scholar] [CrossRef]
- Arnautovic, Z.; Kutzner, S.; Weith, T.; Heberle, F.; Brüggemann, D. Density and Viscosity of Linear Siloxanes and Their Mixtures. J. Chem. Eng. Data 2023, 68, 314–329. [Google Scholar] [CrossRef]
- Nan, Z.; Liu, B.; Tan, Z. Calorimetric investigation of excess molar heat capacities for water + ethylene glycol from T = 273.15 to T = 373.15 K. J. Chem. Thermodyn. 2002, 34, 915–926. [Google Scholar] [CrossRef]
- Zhang, X.; Gu, H.; Fujii, M. Experimental study on the effective thermal conductivity and thermal diffusivity of nanofluids. Int. J. Thermophys. 2006, 27, 569–580. [Google Scholar] [CrossRef]
- Balderas-Lopez, J.A.; Mandelis, A.; Garcia, J.A. Measurements of the Thermal Diffusivity of Liquids with a Thermal-Wave Resonator Cavity. Anal. Sci./Suppl. 2001, 17, s519–s522. [Google Scholar] [CrossRef]
- Eckert, E.R.; Drake, R.M.J.R. Analysis of Heat and Mass Transfer. 1987. Available online: https://www.osti.gov/biblio/7142648 (accessed on 8 October 2024).
- Zhang, L.; Zhang, A.; Jing, Y.; Qu, P.; Wu, Z. Effect of Particle Size on the Heat Transfer Performance of SiO2—Water Nanofluids. J. Phys. Chem. C 2021, 125, 13590–13600. [Google Scholar] [CrossRef]
- Pantzali, M.M.; Kanaris, A.G.; Antoniadis, K.D.; Mouza, A.A.; Paras, S.V. Effect of nanofluids on the performance of a miniature plate heat exchanger with modulated surface. Int. J. Heat Fluid Flow 2009, 30, 691–699. [Google Scholar] [CrossRef]
- Kotia, A.; Borkakoti, S.; Deval, P.; Ghosh, S.K. Review of interfacial layer’s effect on thermal conductivity in nanofluid. Heat Mass Transf. 2017, 53, 2199–2209. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Shahrul, I.M.; Mahbubul, I.M.; Khaleduzzaman, S.S.; Saidur, R.; Sabri, M. A comparative review on the specific heat of nanofluids for energy perspective. Renew. Sustain. Energy Rev. 2014, 38, 88–98. [Google Scholar] [CrossRef]
- Buonomo, B.; Colla, L.; Fedele, L. A comparison of nanofluid thermal conductivity measurements by flash and hot disk techniques. In Proceedings of the 32nd UIT Heat Transfer Conference, Pisa, Italy, 23–25 June 2014; Volume 547, p. 012046. [Google Scholar] [CrossRef]
- Zagabathuni, A.; Ghosh, S.; Pabi, S.K. The difference in the thermal conductivity of nanofluids measured by different methods and its rationalization. Beilstein J. Nanotechnol. 2016, 7, 2037–2044. [Google Scholar] [CrossRef]
- Aparna, Z.; Michael, M.M.; Pabi, S.K.; Ghosh, S. Diversity in thermal conductivity of aqueous Al2O3- and Ag-nanofluids measured by transient hot-wire and laser flash methods. Exp. Therm. Fluid Sci. 2018, 94, 231–245. [Google Scholar] [CrossRef]
- Palacios, A.; Cong, L.; Navarro, M.E.; Ding, Y.; Barreneche, C. Thermal conductivity measurement techniques for characterizing thermal energy storage materials—A review. Renew. Sustain. Energy Rev. 2019, 108, 32–52. [Google Scholar] [CrossRef]
- Krishnamurthy, S.; Bhattacharya, P.; Phelan, P.E.; Prasher, R.S. Enhanced Mass Transport in Nanofluids. Nano Lett. 2006, 6, 419–423. [Google Scholar] [CrossRef] [PubMed]
- Jang, S.P.; Choi, S.U.S. Role of Brownian motion in the enhanced thermal conductivity of nanofluids. Appl. Phys. Lett. 2004, 84, 4316–4318. [Google Scholar] [CrossRef]





| Chemical Name | CAS Number | Purity (%) | Particle Size (nm) | Density at 25 °C (g/cm3) | Specific Heat Capacity at 25 °C (kJ/kgK) | Thermal Conductivity at 25 °C (W/mK) |
|---|---|---|---|---|---|---|
| Water (H2O) | 7732-18-5 | >99.95 | - | 0.997 a | 4.181 a | 0.607 a |
| Ethylene glycol (C2H6O2) | 107-21-1 | 99.5 | - | 1.110 a | 2.412 a | 0.252 a |
| Silicon dioxide (SiO2) | 7631-86-9 | 99.5 | 28 | 2.650 b | 0.680 b | 1.400 b |
| Nanofluid | Base Fluid | AV | BV | CV |
|---|---|---|---|---|
| Al2O3 | EG/W (60/40) | 0.0008911 | 0.5179 | 0.4250 |
| ZnO | EG/W (60/40) | 0.0004604 | 0.9855 | 0.2990 |
| SiO2 | W | 0.0017690 | 1.1937 | 0.8021 |
| Density | |||
|---|---|---|---|
| A | B | RSME | |
| base fluid water | 0.002432 | 1.137 | 0.002297 |
| base fluid EG/W (25/75) | 0.002346 | 1.143 | 0.002361 |
| Base Fluid | Water | |||||
|---|---|---|---|---|---|---|
| SiO2 (wt.%) | 0 | 1 | 2 | 5 | 10 | 20 |
| Temperature | Density | |||||
| K | g/cm3 | g/cm3 | g/cm3 | g/cm3 | g/cm3 | g/cm3 |
| 293.15 | 0.99827 | 1.00388 | 1.00898 | 1.02541 | 1.05442 | 1.11754 |
| 298.15 | 0.99710 | 1.00267 | 1.00783 | 1.02415 | 1.05297 | 1.11633 |
| 303.15 | 0.99569 | 1.00093 | 1.00638 | 1.02178 | 1.05018 | 1.11488 |
| 308.15 | 0.99408 | 0.99867 | 1.00389 | 1.01900 | 1.04691 | 1.11320 |
| 313.15 | 0.99143 | 0.99580 | 1.00073 | 1.01523 | 1.04349 | 1.11126 |
| 318.15 | 0.98875 | 0.99313 | 0.99734 | 1.01147 | 1.04028 | 1.10909 |
| 323.15 | 0.98602 | 0.99058 | 0.99436 | 1.00822 | 1.03710 | 1.10681 |
| Base fluid | EG/W (25/75) | |||||
| SiO2 (wt.%) | 0 | 1 | 2 | 5 | 10 | 20 |
| Temperature | Density | |||||
| K | g/cm3 | g/cm3 | g/cm3 | g/cm3 | g/cm3 | g/cm3 |
| 293.15 | 1.03170 | 1.03652 | 1.04126 | 1.05747 | 1.08731 | 1.14934 |
| 298.15 | 1.02974 | 1.03391 | 1.03855 | 1.05403 | 1.08530 | 1.14733 |
| 303.15 | 1.02763 | 1.03093 | 1.03551 | 1.05115 | 1.08313 | 1.14509 |
| 308.15 | 1.02534 | 1.02754 | 1.03200 | 1.04824 | 1.08076 | 1.14250 |
| 313.15 | 1.02275 | 1.02431 | 1.02897 | 1.04517 | 1.07803 | 1.13970 |
| 318.15 | 1.02001 | 1.02111 | 1.02568 | 1.04209 | 1.07527 | 1.13694 |
| 323.15 | 1.01762 | 1.01805 | 1.02239 | 1.03927 | 1.07252 | 1.13416 |
| Specific Heat Capacity | |||
|---|---|---|---|
| A | B | RMSE | |
| base fluid water | −0.00134 | 0.5558 | 0.008291 |
| base fluid EG/W (25/75) | −0.00200 | 0.8043 | 0.006693 |
| Base Fluid | Water | |||||
|---|---|---|---|---|---|---|
| SiO2 (wt.%) | 0 | 1 | 2 | 5 | 10 | 20 |
| Temperature | Specific heat capacity | |||||
| K | kJ/kgK | kJ/kgK | kJ/kgK | kJ/kgK | kJ/kgK | kJ/kgK |
| 293.15 | 4.179 | 4.064 | 4.011 | 3.859 | 3.638 | 3.501 |
| 298.15 | 4.171 | 4.052 | 4.000 | 3.854 | 3.633 | 3.495 |
| 303.15 | 4.166 | 4.049 | 4.005 | 3.847 | 3.633 | 3.494 |
| 308.15 | 4.165 | 4.048 | 4.010 | 3.835 | 3.625 | 3.492 |
| 313.15 | 4.167 | 4.045 | 4.006 | 3.838 | 3.624 | 3.492 |
| 318.15 | 4.169 | 4.043 | 4.003 | 3.827 | 3.626 | 3.499 |
| 323.15 | 4.155 | 4.043 | 4.006 | 3.828 | 3.621 | 3.495 |
| Base fluid | EG/W (25/75) | |||||
| SiO2 (wt.%) | 0 | 1 | 2 | 5 | 10 | 20 |
| Temperature | Specific heat capacity | |||||
| K | kJ/kgK | kJ/kgK | kJ/kgK | kJ/kgK | kJ/kgK | kJ/kgK |
| 293.15 | 3.737 | 3.704 | 3.638 | 3.516 | 3.405 | 3.087 |
| 298.15 | 3.747 | 3.709 | 3.644 | 3.523 | 3.425 | 3.101 |
| 303.15 | 3.769 | 3.712 | 3.659 | 3.542 | 3.433 | 3.109 |
| 308.15 | 3.784 | 3.712 | 3.676 | 3.552 | 3.442 | 3.127 |
| 313.15 | 3.798 | 3.707 | 3.691 | 3.562 | 3.462 | 3.146 |
| 318.15 | 3.814 | 3.711 | 3.710 | 3.557 | 3.468 | 3.161 |
| 323.15 | 3.792 | 3.715 | 3.721 | 3.567 | 3.479 | 3.168 |
| Thermal Diffusivity | |||
|---|---|---|---|
| A | B | RMSE | |
| base fluid water | 0.001936 | 0.8322 | 0.01725 |
| base fluid EG/W (25/75) | 0.008746 | 1.6270 | 0.011038 |
| Base Fluid | Water | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SiO2 (wt.%) | 0 | 1 | 2 | 5 | 10 | 20 | ||||
| Temperature | Thermal Diffusivity | |||||||||
| K | mm2/s | mm2/s | mm2/s | mm2/s | mm2/s | mm2/s | ||||
| 298.15 | 0.1414 | 0.1412 | 0.1431 | 0.1445 | 0.1506 | 0.1602 | ||||
| 303.15 | 0.1427 | 0.1436 | 0.1448 | 0.1458 | 0.1580 | 0.1624 | ||||
| 308.15 | 0.1436 | 0.1464 | 0.1462 | 0.1473 | 0.1606 | 0.1670 | ||||
| 313.15 | 0.1463 | 0.1511 | 0.1500 | 0.1610 | 0.1624 | 0.1722 | ||||
| 318.15 | 0.1536 | 0.1561 | 0.1584 | 0.1613 | 0.1642 | 0.1782 | ||||
| Base fluid | Ethylene glycol/Water (25/75) | |||||||||
| SiO2 (wt.%) | 0 | 2 | 5 | 10 | 20 | |||||
| Temperature | Thermal Diffusivity | |||||||||
| K | mm2/s | mm2/s | mm2/s | mm2/s | mm2/s | |||||
| 298.15 | 0.1209 | 0.1238 | 0.1254 | 0.1283 | 0.1433 | |||||
| 303.15 | 0.1213 | 0.1246 | 0.1240 | 0.1271 | 0.1452 | |||||
| 308.15 | 0.1230 | 0.1256 | 0.1268 | 0.1303 | 0.1469 | |||||
| 313.15 | 0.1239 | 0.1256 | 0.1284 | 0.1324 | 0.1505 | |||||
| 318.15 | 0.1263 | 0.1288 | 0.1292 | 0.1330 | 0.1521 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wittmann, F.; Arnautovic, Z.; Heberle, F.; Brüggemann, D. Thermophysical Properties of Silicon Oxide Nanoparticles in Water and Ethylene Glycol–Water Dispersions. Fluids 2024, 9, 261. https://doi.org/10.3390/fluids9110261
Wittmann F, Arnautovic Z, Heberle F, Brüggemann D. Thermophysical Properties of Silicon Oxide Nanoparticles in Water and Ethylene Glycol–Water Dispersions. Fluids. 2024; 9(11):261. https://doi.org/10.3390/fluids9110261
Chicago/Turabian StyleWittmann, Franz, Zlatan Arnautovic, Florian Heberle, and Dieter Brüggemann. 2024. "Thermophysical Properties of Silicon Oxide Nanoparticles in Water and Ethylene Glycol–Water Dispersions" Fluids 9, no. 11: 261. https://doi.org/10.3390/fluids9110261
APA StyleWittmann, F., Arnautovic, Z., Heberle, F., & Brüggemann, D. (2024). Thermophysical Properties of Silicon Oxide Nanoparticles in Water and Ethylene Glycol–Water Dispersions. Fluids, 9(11), 261. https://doi.org/10.3390/fluids9110261







