Large Eddy Simulation (LES) of Hydrogen Jet Flames and Finite Element Analysis of Thermal Barrier Coating
Abstract
1. Introduction
1.1. Literature Review of CFD Modeling of Hydrogen Jet Flames
1.2. Scope and Novelty of This Study
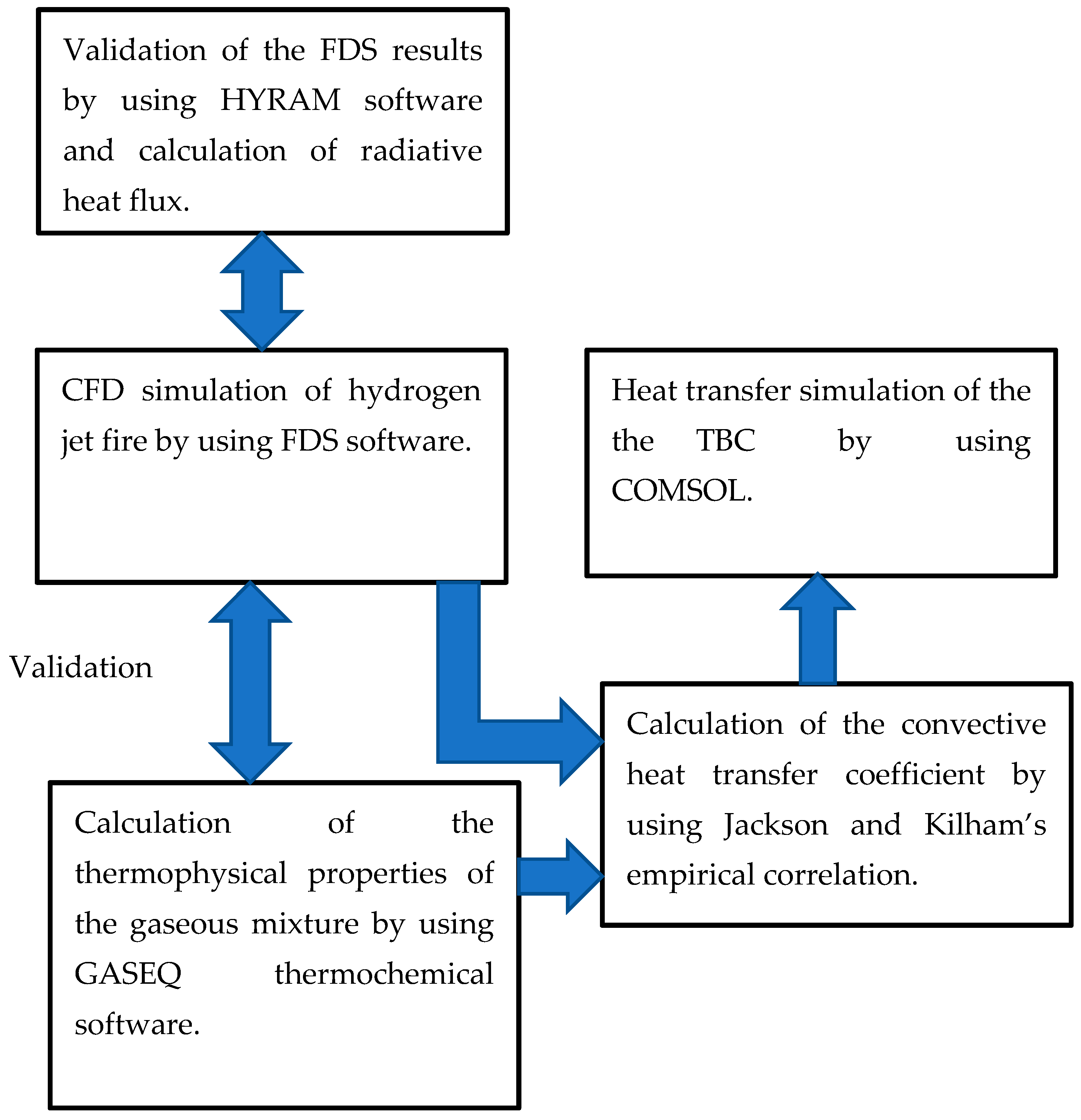
2. Materials and Methods
2.1. Fire Dynamics Simulator (FDS) Overview
2.2. Governing Equations of FDS Software
2.2.1. Mass and Species Transport
2.2.2. Momentum Transport
2.2.3. Large Eddy Simulation (LES)
2.2.4. Energy Transport
2.2.5. Equation of State
2.3. FDS Modeling of the Hydrogen Jet Flame
Boundary and Initial Conditions
2.4. Hydrogen Risk Assessment Model Overview
2.5. Thermal Barrier Coatings Types
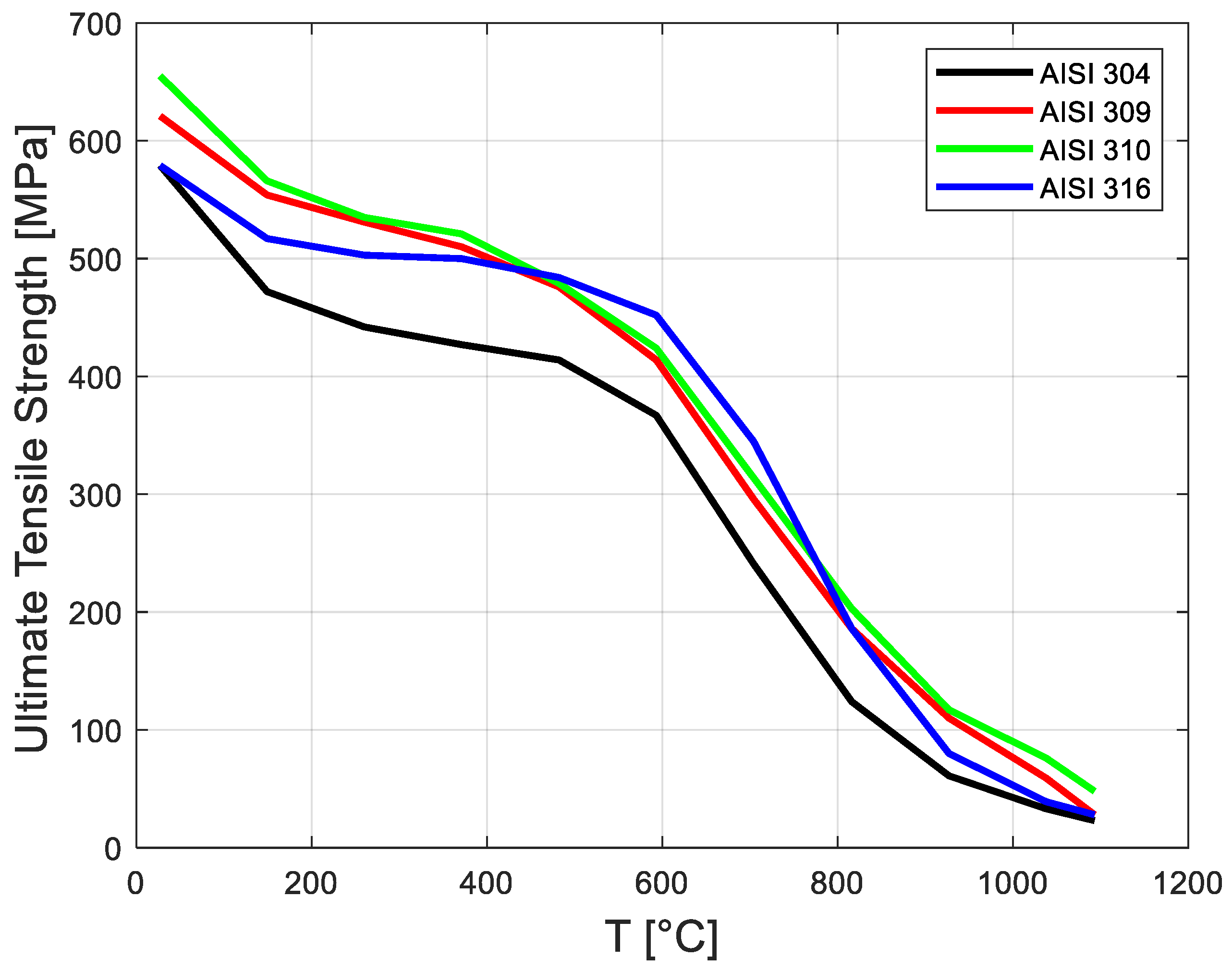
Thermo-Physical Properties of the Ceramic Thermal Barrier Coating and Stainless Steel 304 L
3. Results
3.1. Grid Sensitivity Study Results
3.2. FDS Hydrogen Jet Fire Numerical Results
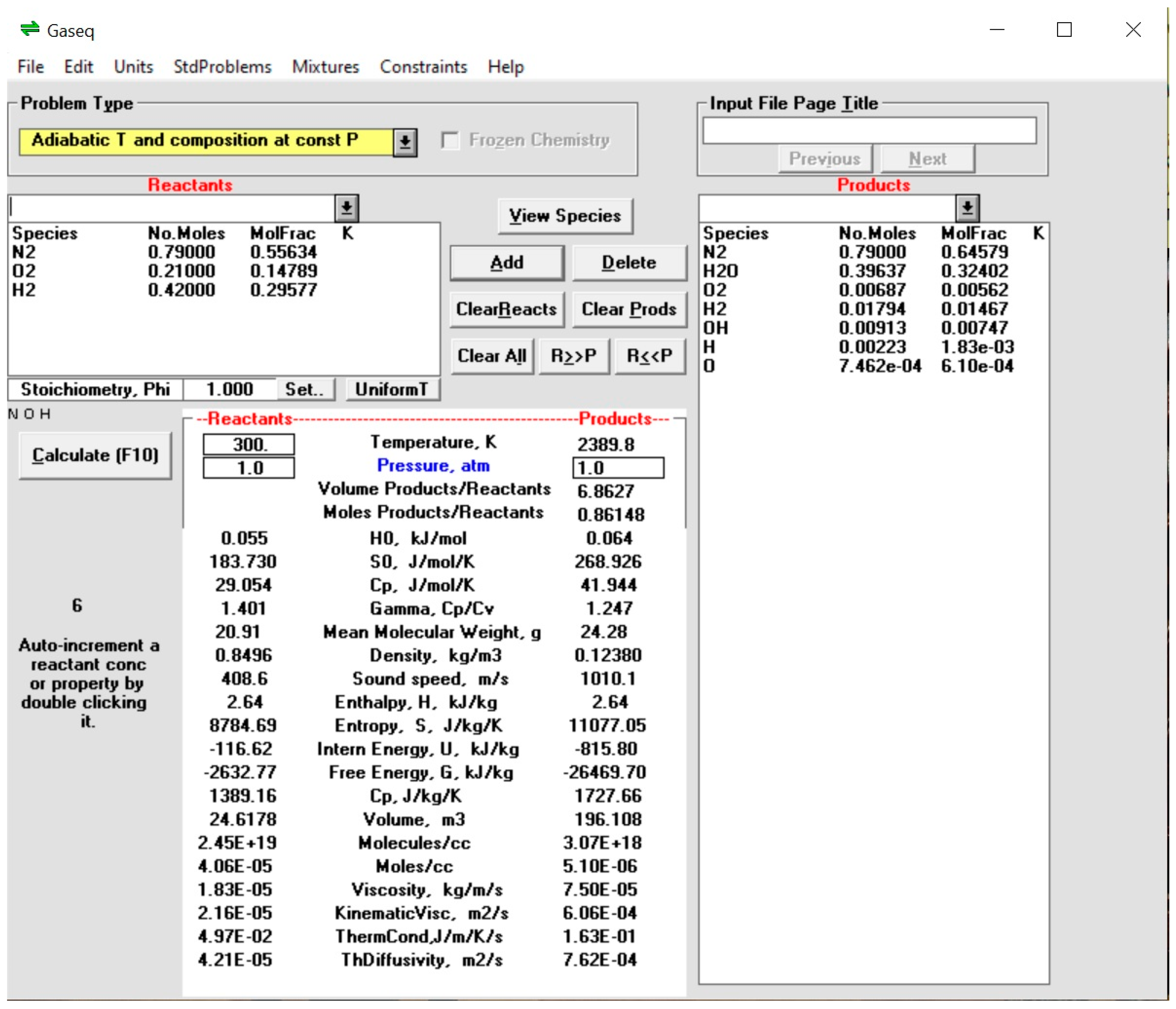
3.3. GASEQ Thermochemical Code Results
3.4. Calculation of Thermal Loads Acting on the TBC’s External Surface
3.5. HyRAM Numerical Results for Hydrogen Jet Flame Radiative Heat Transfer
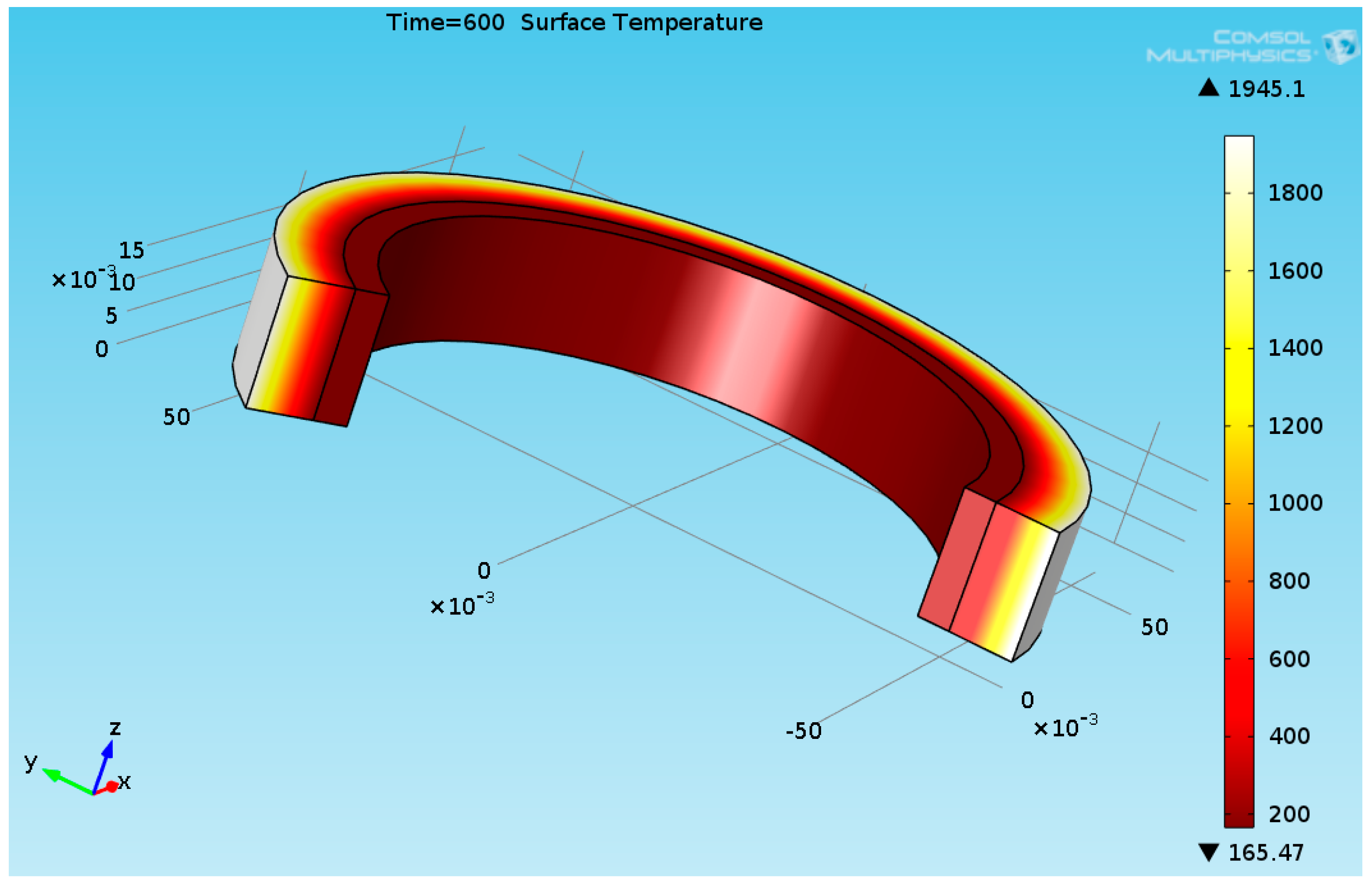
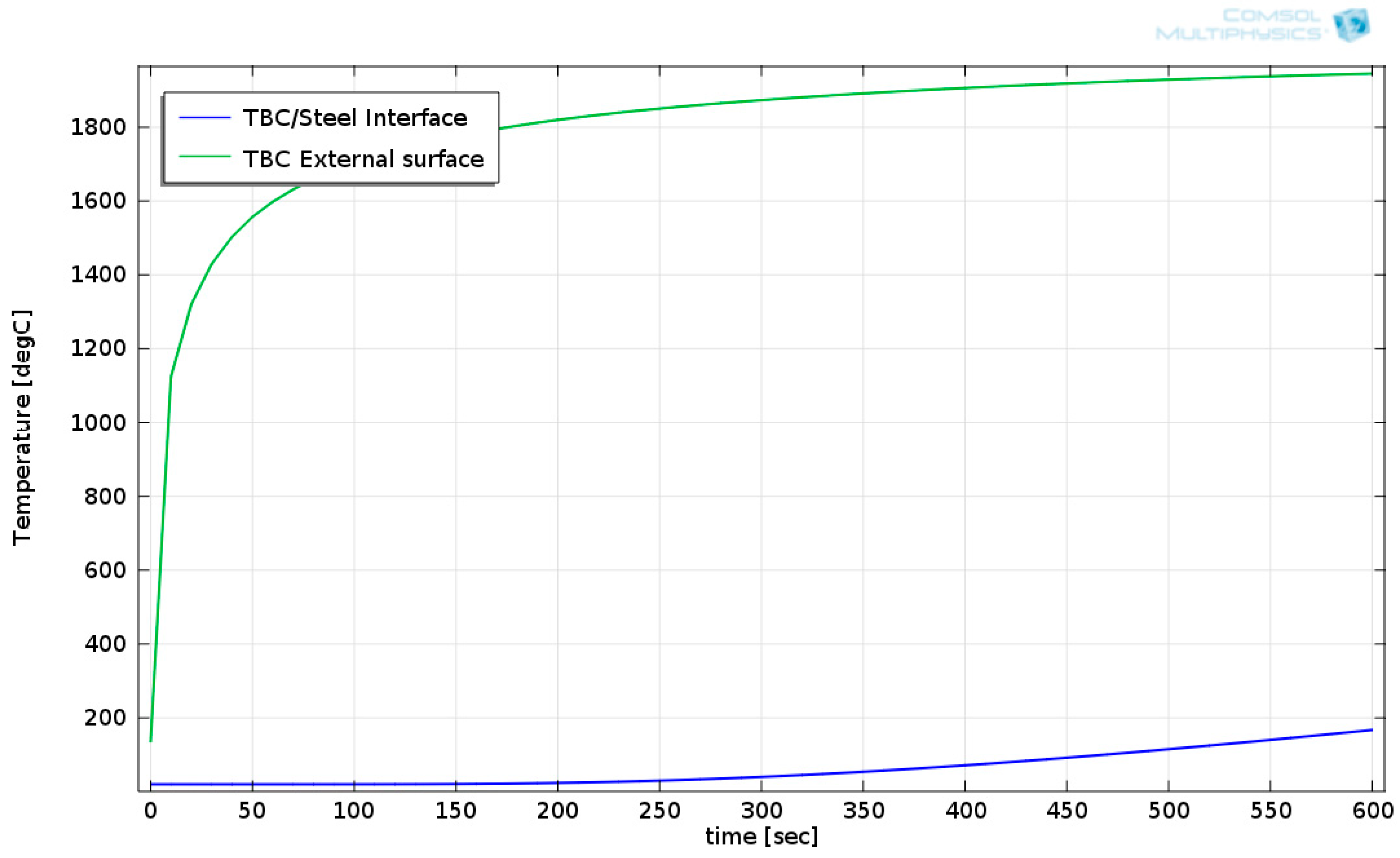
3.6. Temperature Calculation Results for the Ceramic Blanket
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BLEVE | Boiling Liquid Expanding Vapor Explosion; |
| CFD | Computational Fluid Dynamics; |
| FDS | Fire Dynamic Simulator; |
| FRP | Fiber-reinforced Polymer; |
| FVM | Finite Volume Method; |
| LES | Large Eddy Simulation; |
| Probability Density Function; | |
| TBC | Thermal Barrier Coatings; |
| UTS | Ultimate Tensile Strength. |
| Nomenclature | |
| c | Concentration; |
| D | Diffusion coefficient in [m2/s]; |
| h | Enthalpy in [J/kg]; convective coefficient in Equation (15) in [W/(m2*K)]; |
| p | Pressure in [Pa]; |
| Pr | Prantl number; |
| Prt | Turbulent Prandtl number; |
| Gas constant (8.3143 J/(mole·K)); | |
| Re | Reynolds number; |
| T | Temperature in [K]; |
| t | Time in [s]; |
| Velocity vector in [m/s]; | |
| v | Velocity of the impinging hydrogen jet [m/s]; |
| Greek letters | |
| γ | Ratio of the specific heats of the gasous products; |
| ρ | Density in [kg/m3]; |
| ν | Kinematic viscosity of in [m2/s]. |
References
- Fischer, S.; Markus, D.; Maas, U. Numerical investigation of the ignition of diethyl ether/air and propane/air mixtures by hot jets. J. Loss Prev. Process Ind. 2017, 49 Pt B, 832–838. [Google Scholar] [CrossRef]
- Cermelli, D.; Curro, F.; Vairo, T.; Fabiano, B. Hydrogen Jet-Fire: Accident Investigation and Implementation of Safety Measures for the Design of a Downstream Oil Plant. Chem. Eng. Trans. 2018, 67, 415–420. [Google Scholar] [CrossRef]
- Vallejo-Molina, L.F. Educational Program for the Prevention of Fires and Explosions through Emerging Technologies. Doctoral Dissertation, Chemical Engineering, National University of Colombia Medellin Campus Faculty of Mines, Department of Processes and Energy, Medellín, Colombia, 2023. [Google Scholar]
- Lewis, B.; Von Elbe, G. Combustion Flames and Explosion of Gases, 2nd ed.; Academic Press Inc.: New York, NY, USA; London, UK, 1961. [Google Scholar]
- Molkov, V.; Saffers, J.B. Hydrogen jet flames. Int. J. Hydrogen Energy 2013, 38, 8141–8158. [Google Scholar] [CrossRef]
- Rowinski, D.H.; Pope, S.B. PDF calculations of piloted premixed jet flames. Combust. Theory Model. 2011, 15, 245–266. [Google Scholar] [CrossRef]
- Davidy, A. CFD Simulation and Mitigation with Boiling Liquid Expanding Vapor Explosion (BLEVE) Caused by Jet Fire. ChemEngineering 2019, 3, 1. [Google Scholar] [CrossRef]
- Jang, C.B.; Choi, S.W.; Baek, J.B. CFD modeling and fire damage analysis of jet fire on hydrogen pipeline in a pipe rack structure. Int. J. Hydrogen Energy 2015, 40, 15760–15772. [Google Scholar] [CrossRef]
- McGrattan, K. Fire Dynamics Simulator (Version 5)—Technical Reference Guide Volume 1: Mathematical Model; NIST Special Publication 1018; National Institute of Standards and Technology U.S. Department of Commerce: Washington, DC, USA, 2010. [Google Scholar]
- McGrattan, K.; Forney, G.P. Fire Dynamics Simulator (Version 5)—User’s Guide; NIST Special Publication 1019; National Institute of Standards and Technology U.S. Department of Commerce: Washington, DC, USA, 2010. [Google Scholar]
- McGrattan, K. Numerical Simulation of the Caldecott Tunnel Fire, April 1982; NISTIR 7231; National Institute of Standards and Technology U.S. Department of Commerce: Washington, DC, USA, 2005. [Google Scholar]
- Ingason, H.; Zhen Li, Y.; Lönnermark, A. Tunnel Fire Dynamics; Springer: Berlin, Germany, 2024. [Google Scholar] [CrossRef]
- Van Hees, P.; Wahlqvist, J.; Hostikka, S.; Sikanen, T.; Husted, B.; Magnusson, T.; Jörud, F. Prediction and Validation of Pool Fire Development in Enclosures by Means of CFD Models for Risk Assessment of Nuclear Power Plants (Pool fire)—Report Year 1; Department of Fire Safety Engineering and System Safety Lund University: Lund, Sweden, 2012. [Google Scholar]
- Davidy, A. Multiphysics Design of Pet-Coke Burner and Hydrogen Production by Applying Methane Steam Reforming System. Clean Technol. 2021, 3, 260–287. [Google Scholar] [CrossRef]
- Ehrhart Brian, D.; Hecht Ethan, S. Hydrogen Plus Other Alternative Fuels Risk Assessment Models (HyRAM+) Version 5.0 Technical Reference Manual; SAND2022-16425; Sandia National Lab.(SNL-NM): Albuquerque, NM, USA, 2022. [Google Scholar]
- Available online: https://flameseal.com/2023/11/08/types-of-thermal-barrier-coatings-used-in-fire-prevention/ (accessed on 1 June 2024).
- Abdul Karim, M.; Abdullah, M.Z.; Deifalla, A.F.; Azab, M.; Waqar, A. An assessment of the processing parameters and application of fibre-reinforced polymers (FRPs) in the petroleum and natural gas industries: A review. Results Eng. 2023, 18, 101091. [Google Scholar] [CrossRef]
- Gravit, M.; Klementev, B.; Shabunina, D. Fire Protection of Steel Structures with Epoxy Coatings under Cryogenic Exposure. Buildings 2021, 11, 537. [Google Scholar] [CrossRef]
- Wang, X.; Weinell, C.E.; Ring, L.; Kiil, S. Proof of concept investigation of alternative and less harmful boron compounds for epoxy-based hydrocarbon intumescent coatings. Fire Saf. J. 2021, 125, 103437. [Google Scholar] [CrossRef]
- HILTEX, ALF the Ultimate Solution. Available online: https://www.hiltex.com (accessed on 1 June 2024).
- Gravit, M.; Korolchenko, D.; Nedviga, E.; Portnov, F.; Diachenko, S. Impact of Jet Fires on Steel Structures: Application of Passive Fire Protection Materials. Fire 2024, 7, 281. [Google Scholar] [CrossRef]
- Karadimas, G.; Salonitis, K. Ceramic Matrix Composites for Aero Engine Applications—A Review. Appl. Sci. 2023, 13, 3017. [Google Scholar] [CrossRef]
- Steel, A.K. Product Data Bulletin; 304L Stainless Steel; Scientific Research Publishing Inc.: Irvine, CA, USA, 2007. [Google Scholar]
- Li, M.; Wang, Z.; Jiang, J.; Lin, W.; Ni, L.; Pan, Y.; Wang, G. Numerical Simulation and Consequence Analysis of Full-Scale Jet Fires for Pipelines Transporting Pure Hydrogen or Hydrogen Blended with Natural Gas. Fire 2024, 7, 180. [Google Scholar] [CrossRef]
- Available online: http://www.gaseq.co.uk/ (accessed on 12 June 2024).
- Baukal, C.E. Heat Transfer in Industrial Combustion; CRC Press LLC: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Lee, J.H.W.; Chu, V.H. Turbulent Jets. In Turbulent Jets and Plumes; Springer: Boston, MA, USA, 2003. [Google Scholar] [CrossRef]
- American Iron and Steel Institute. High Temperature Characteristics of Stainless Steels, A Designer’s Handbook Series, No. 9004; American Iron and Steel Institute: Washington, DC, USA, 1979. [Google Scholar]
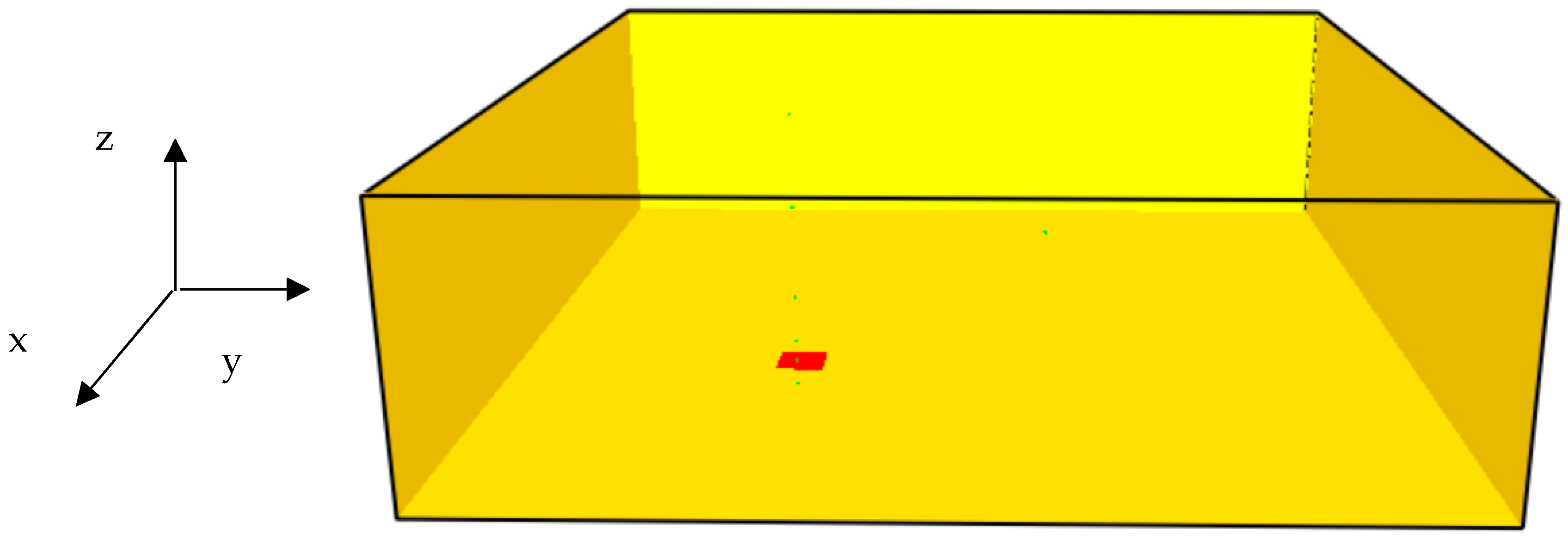

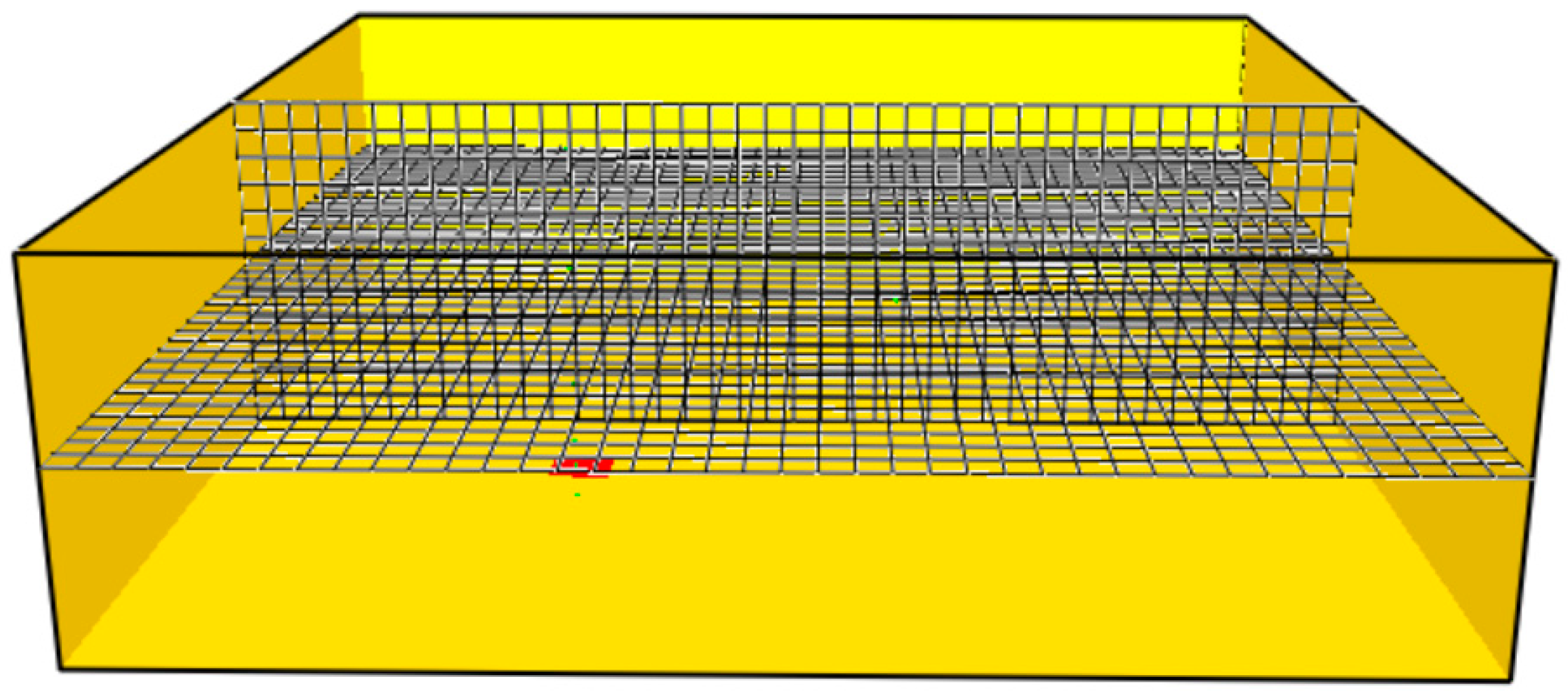
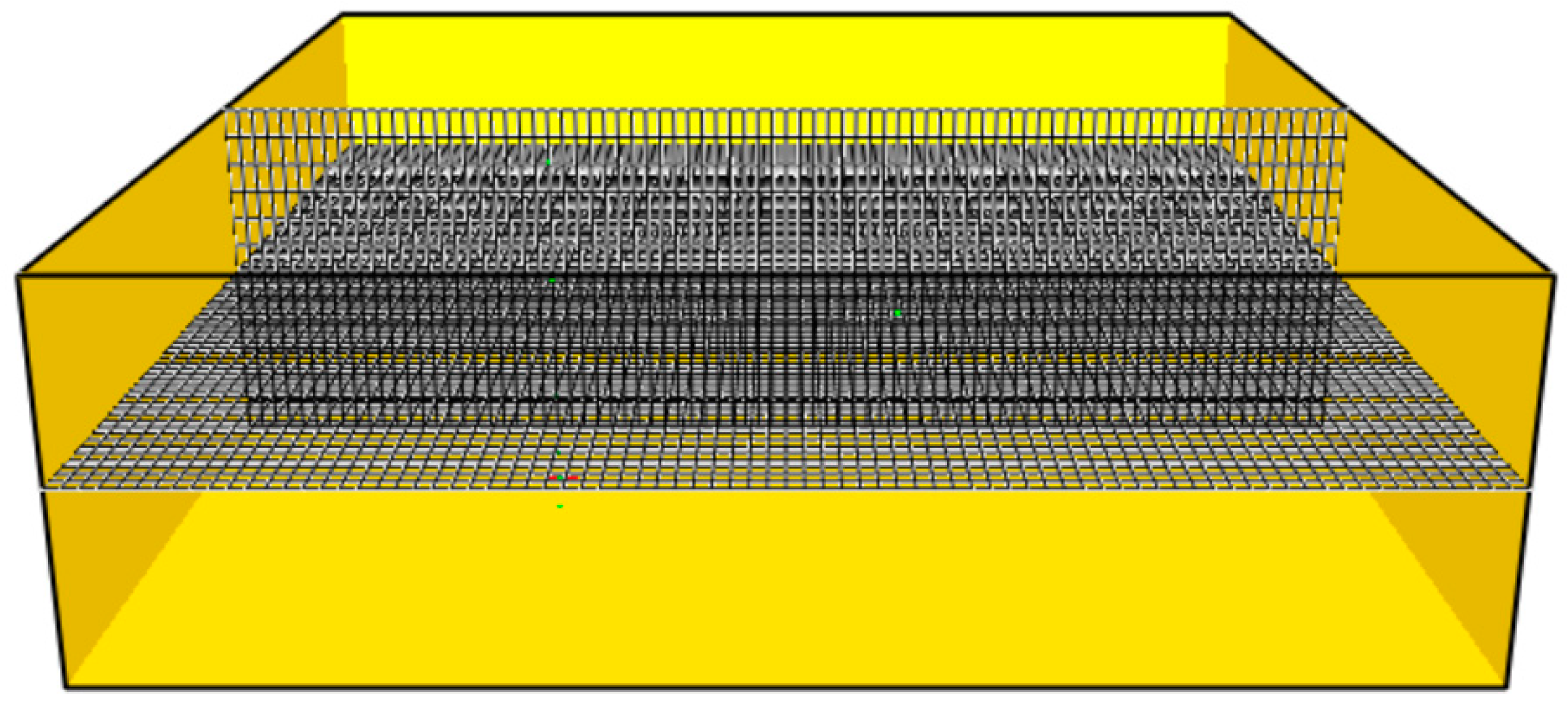
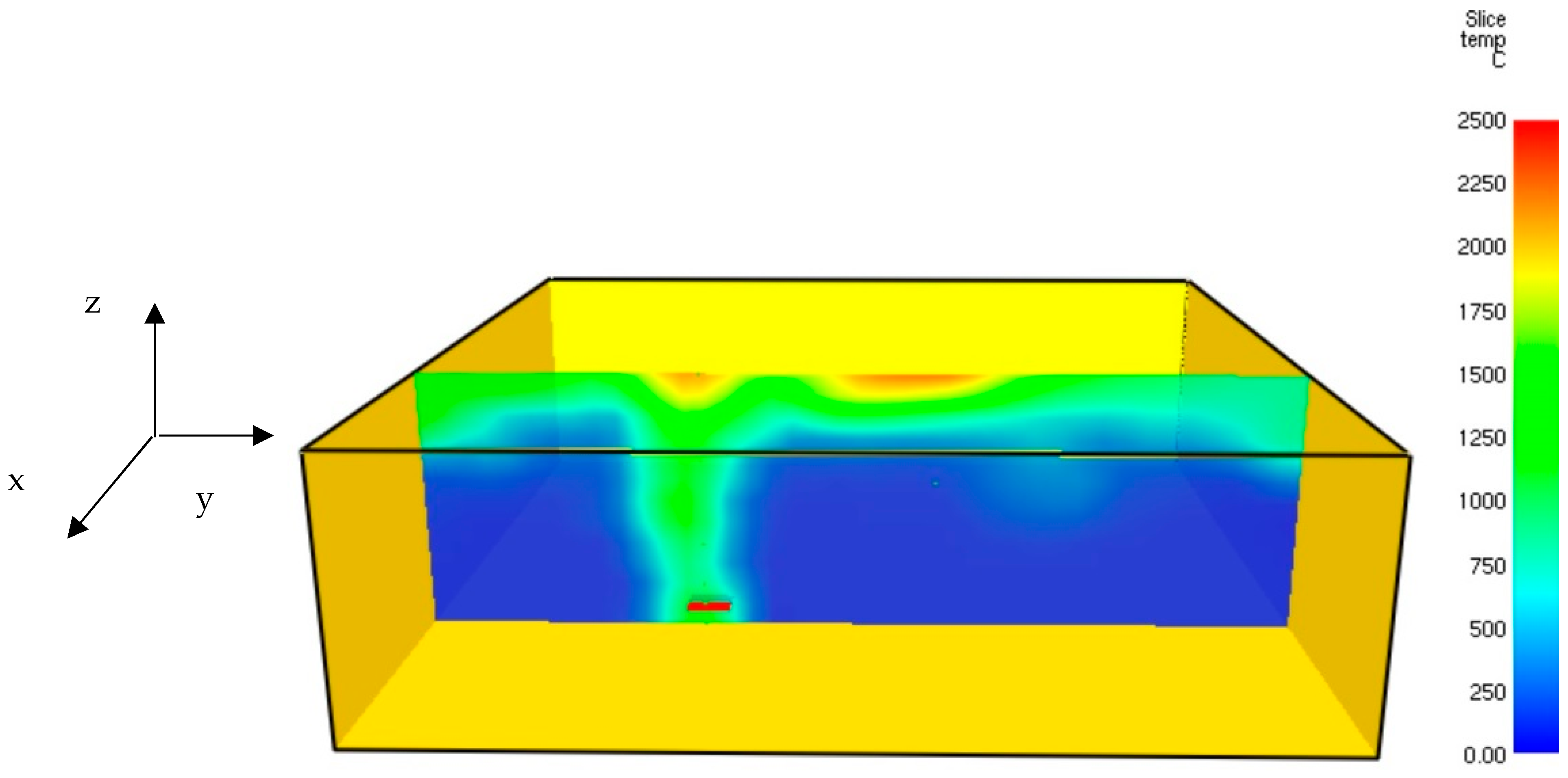
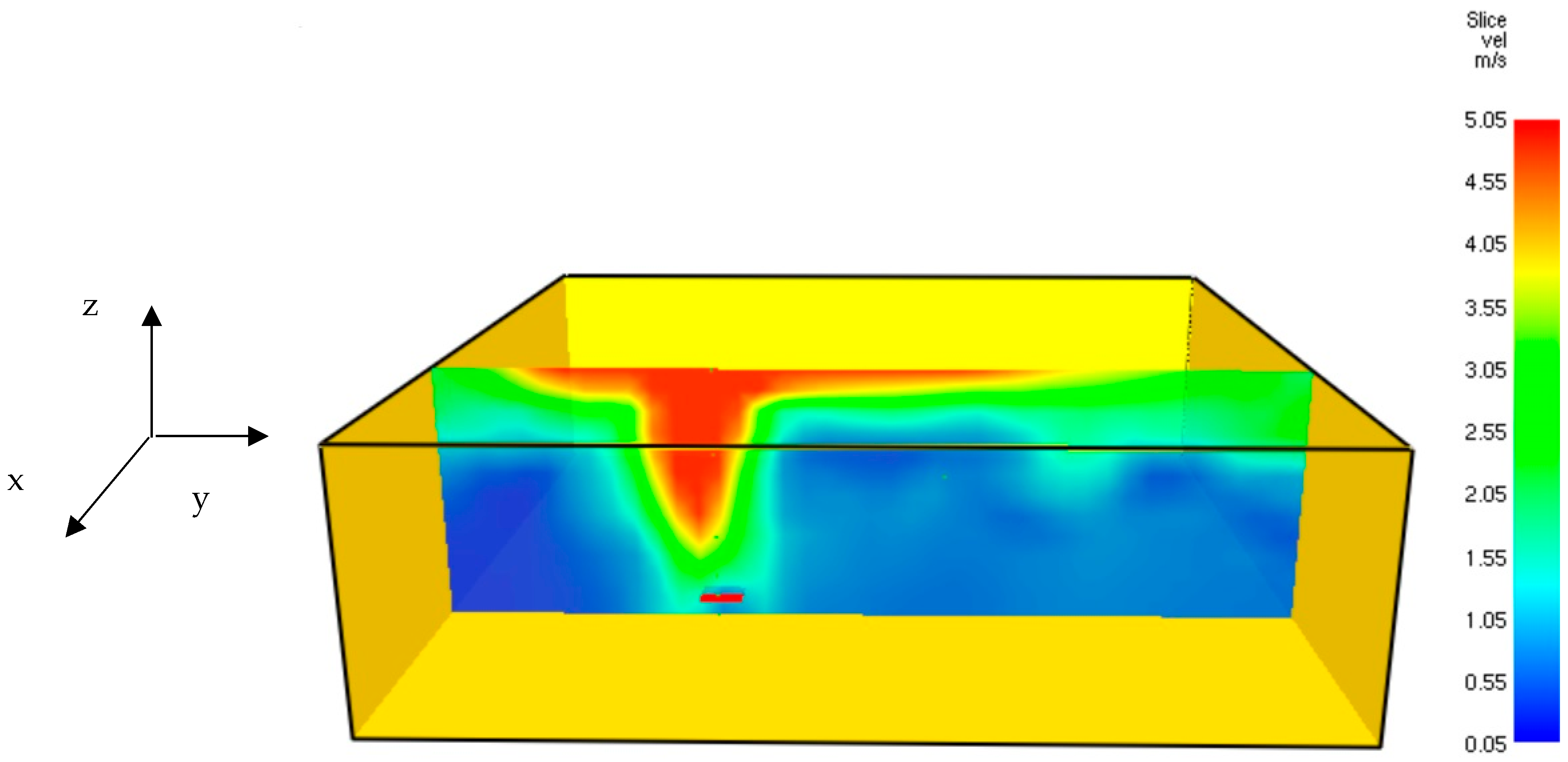
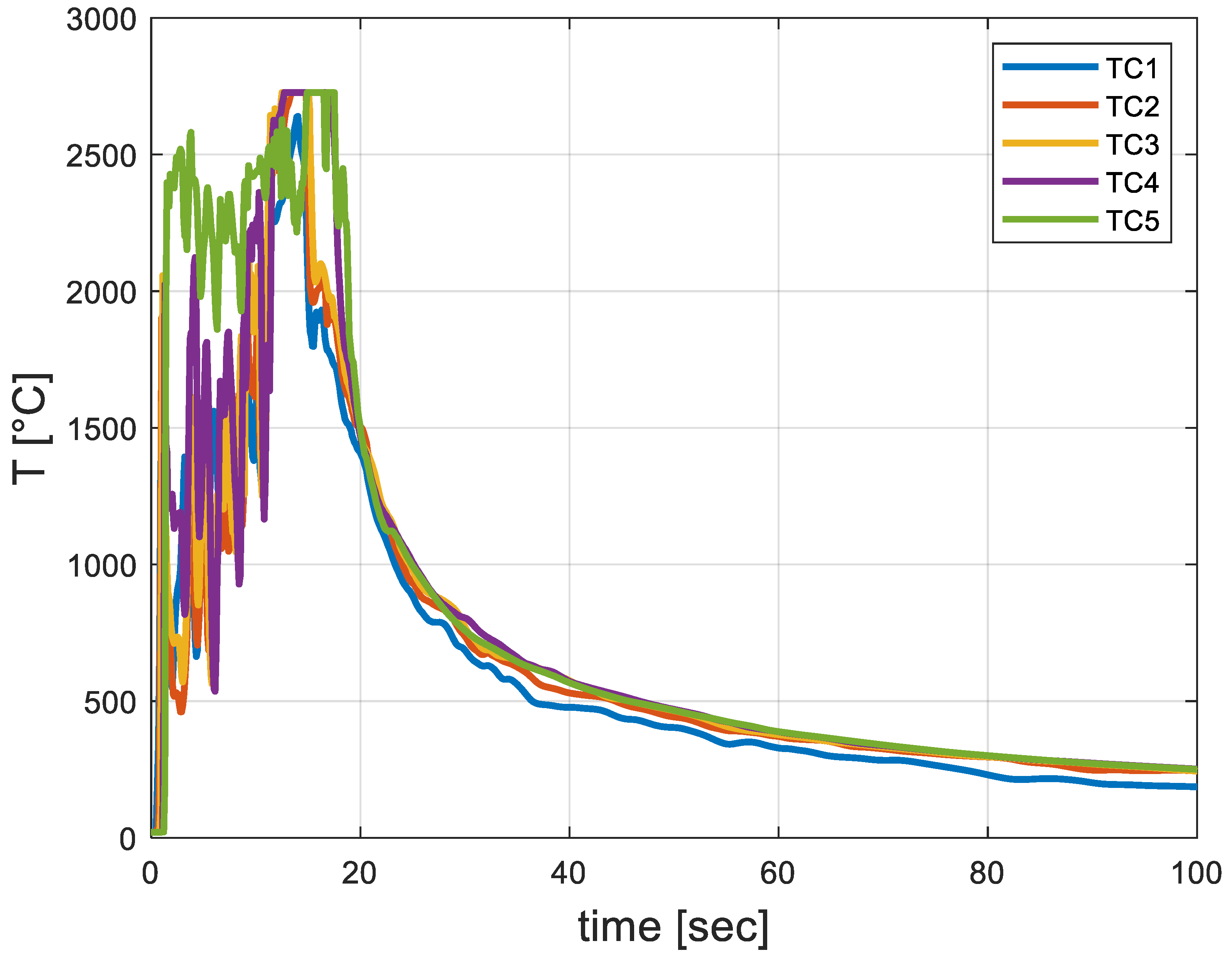

| Sensor | Position [m] |
| TC1 | x = 3.2, y = 3.2, z = 0.27 |
| TC2 | x = 3.2, y = 3.2, z = 0.50 |
| TC3 | x = 3.2, y = 3.2, z = 1.0 |
| TC4 | x = 3.2, y = 3.2, z = 2.0 |
| TC5 | x = 3.2, y = 3.2, z = 3.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davidy, A. Large Eddy Simulation (LES) of Hydrogen Jet Flames and Finite Element Analysis of Thermal Barrier Coating. Fluids 2024, 9, 287. https://doi.org/10.3390/fluids9120287
Davidy A. Large Eddy Simulation (LES) of Hydrogen Jet Flames and Finite Element Analysis of Thermal Barrier Coating. Fluids. 2024; 9(12):287. https://doi.org/10.3390/fluids9120287
Chicago/Turabian StyleDavidy, Alon. 2024. "Large Eddy Simulation (LES) of Hydrogen Jet Flames and Finite Element Analysis of Thermal Barrier Coating" Fluids 9, no. 12: 287. https://doi.org/10.3390/fluids9120287
APA StyleDavidy, A. (2024). Large Eddy Simulation (LES) of Hydrogen Jet Flames and Finite Element Analysis of Thermal Barrier Coating. Fluids, 9(12), 287. https://doi.org/10.3390/fluids9120287






