Numerical Analysis of Non-Newtonian Fluid Effects on the Equilibrium Position of a Suspended Particle and Relative Viscosity in Two-Dimensional Flow
Abstract
:1. Introduction
2. Methods
2.1. Computational Model
2.2. Governing Equation for Fluids
2.3. Herschel–Bulkley Model
2.4. Governing Equation for a Suspended Particle
2.5. Relative Viscosity
3. Results and Discussion
3.1. Validation for Velocity Profile and Apparent Viscosity without Particles
3.2. Validation for Particle Migration in Power-Law Fluid
3.3. Inertial Migration of a Suspended Particle Using Herschel–Bulkley Model
3.3.1. Dependence on Solvents
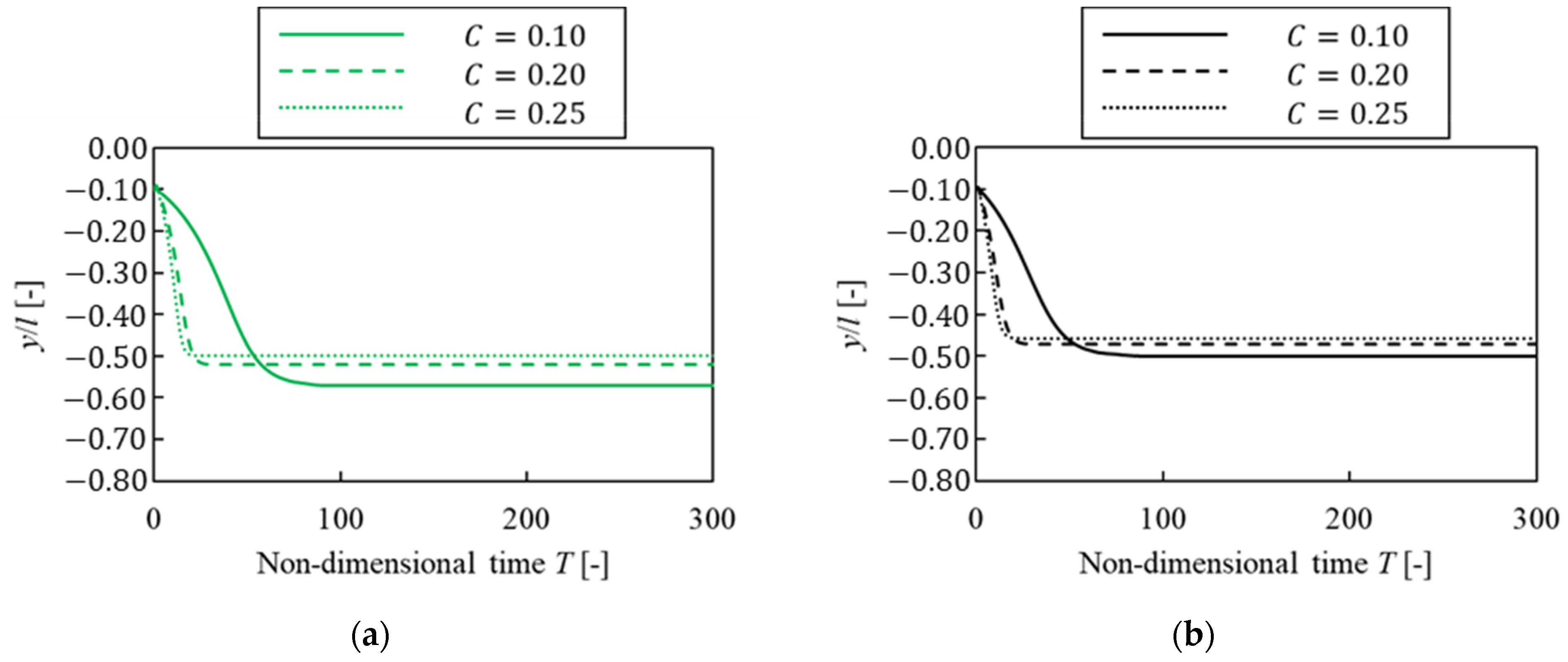
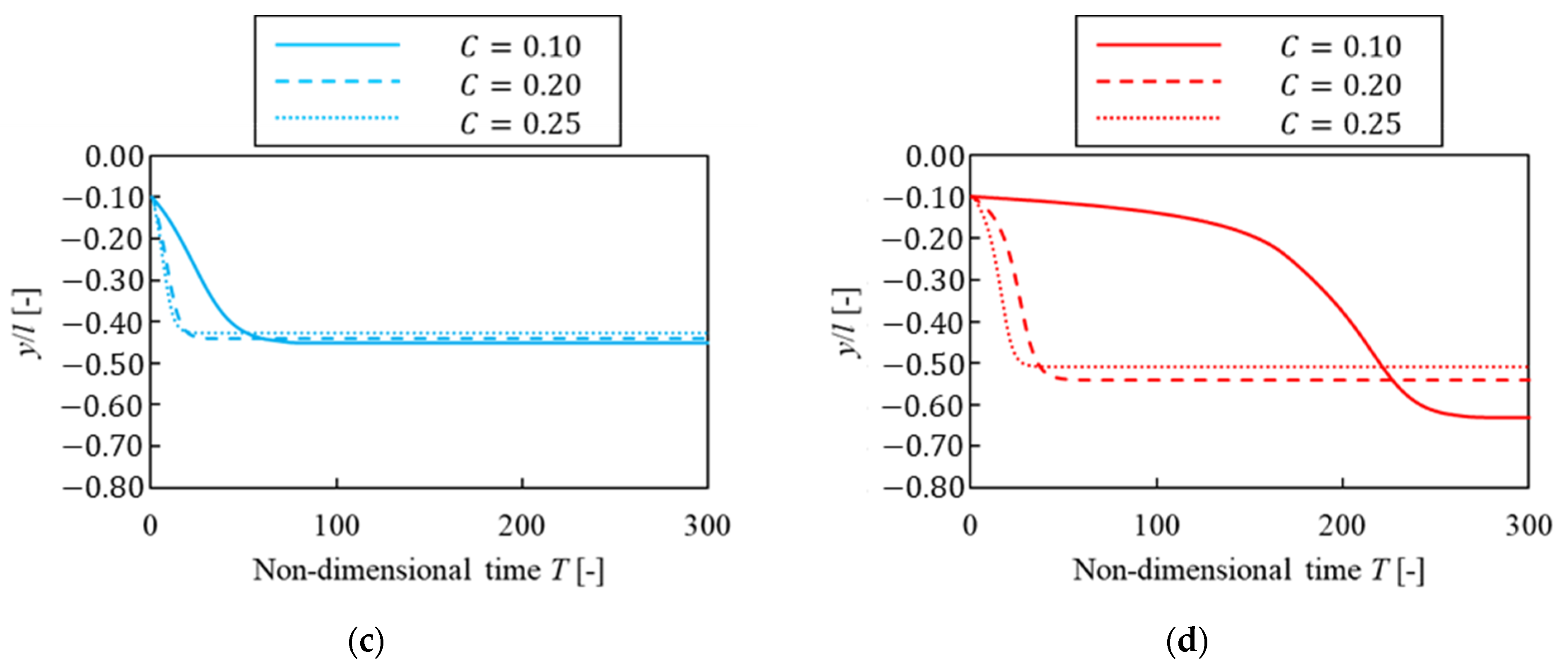
3.3.2. Dependence on Confinements
3.4. Lift Force Acting on a Particle
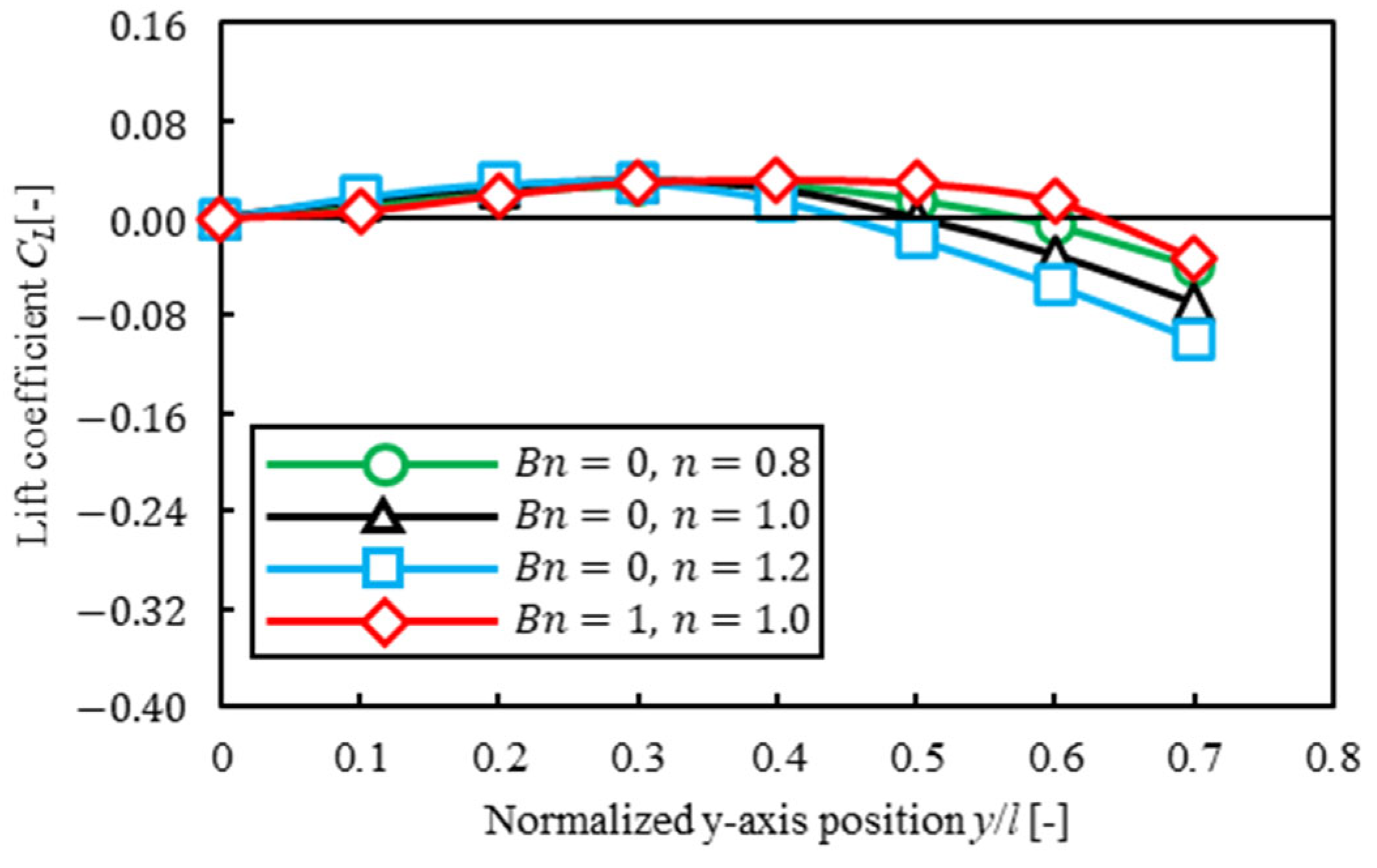
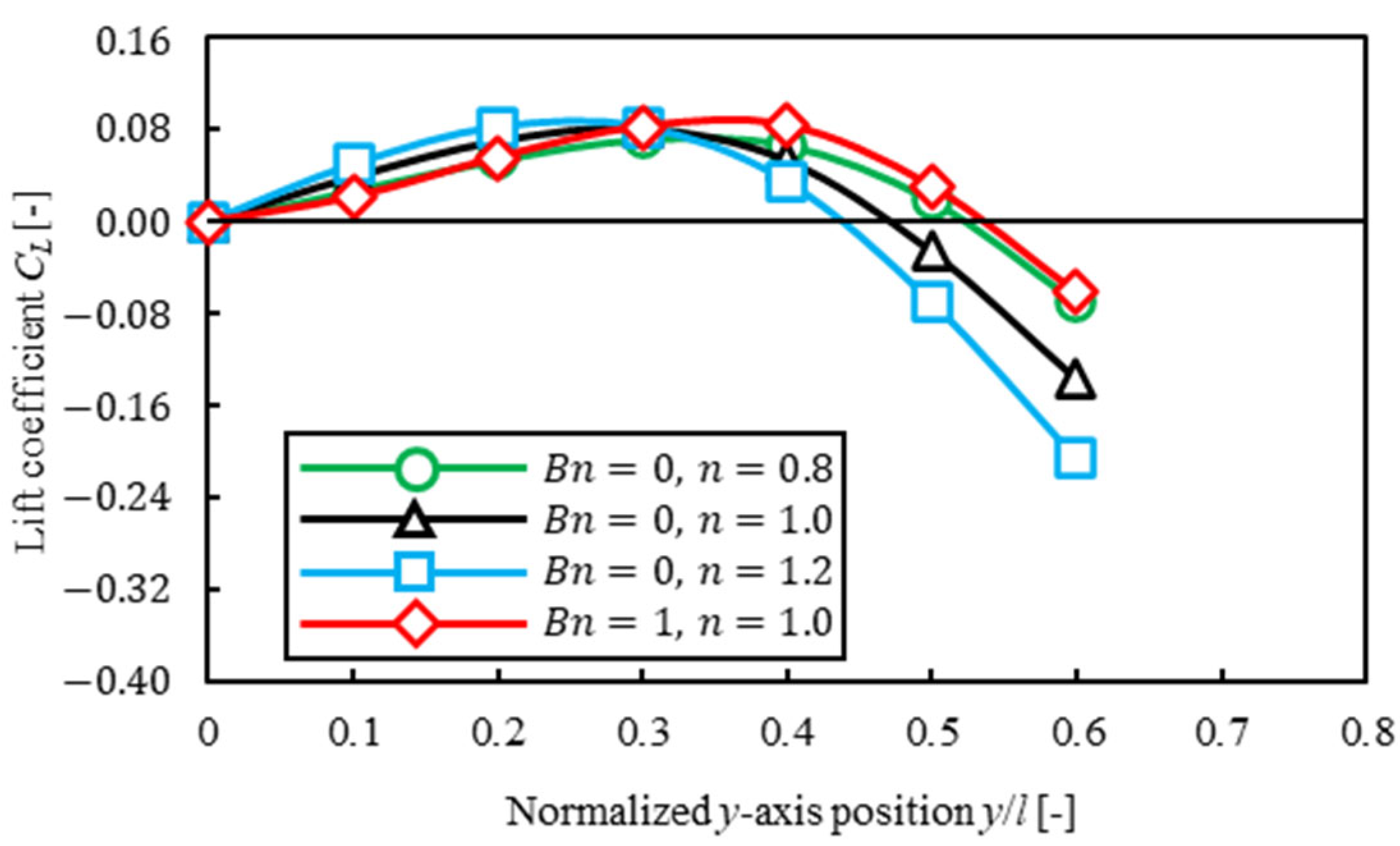
3.4.1. Dependence on Solvents
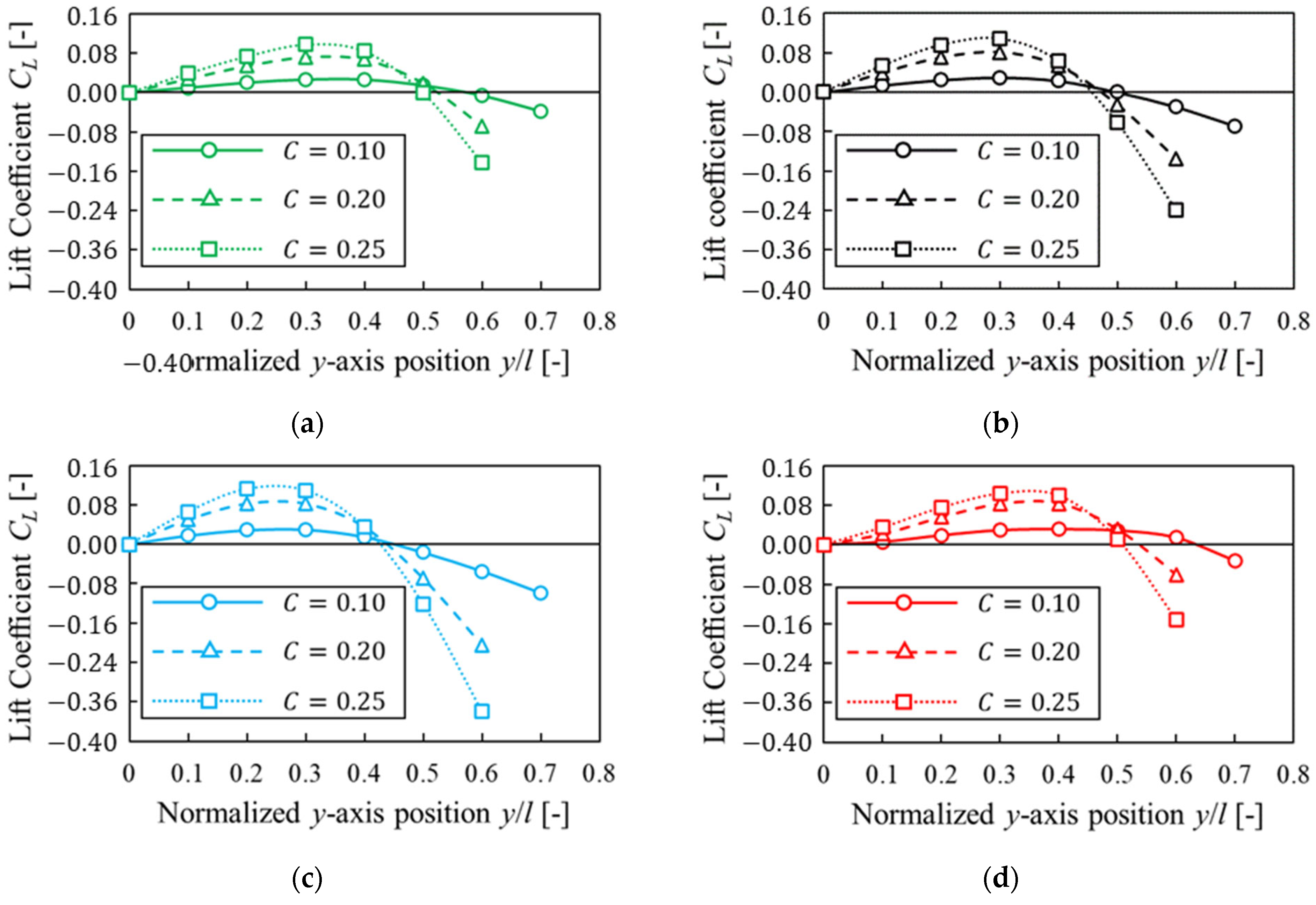
3.4.2. Dependence on Confinements
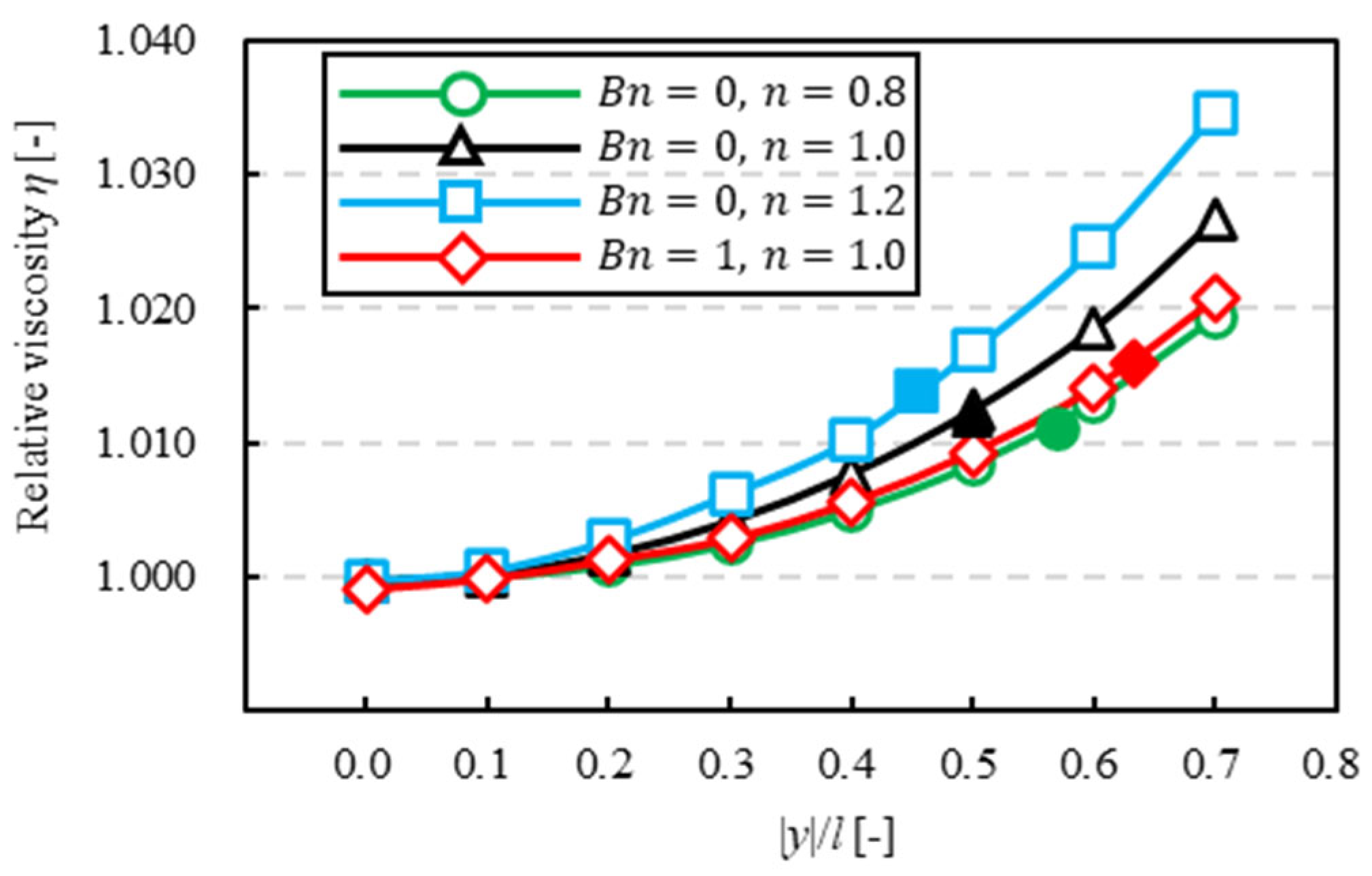
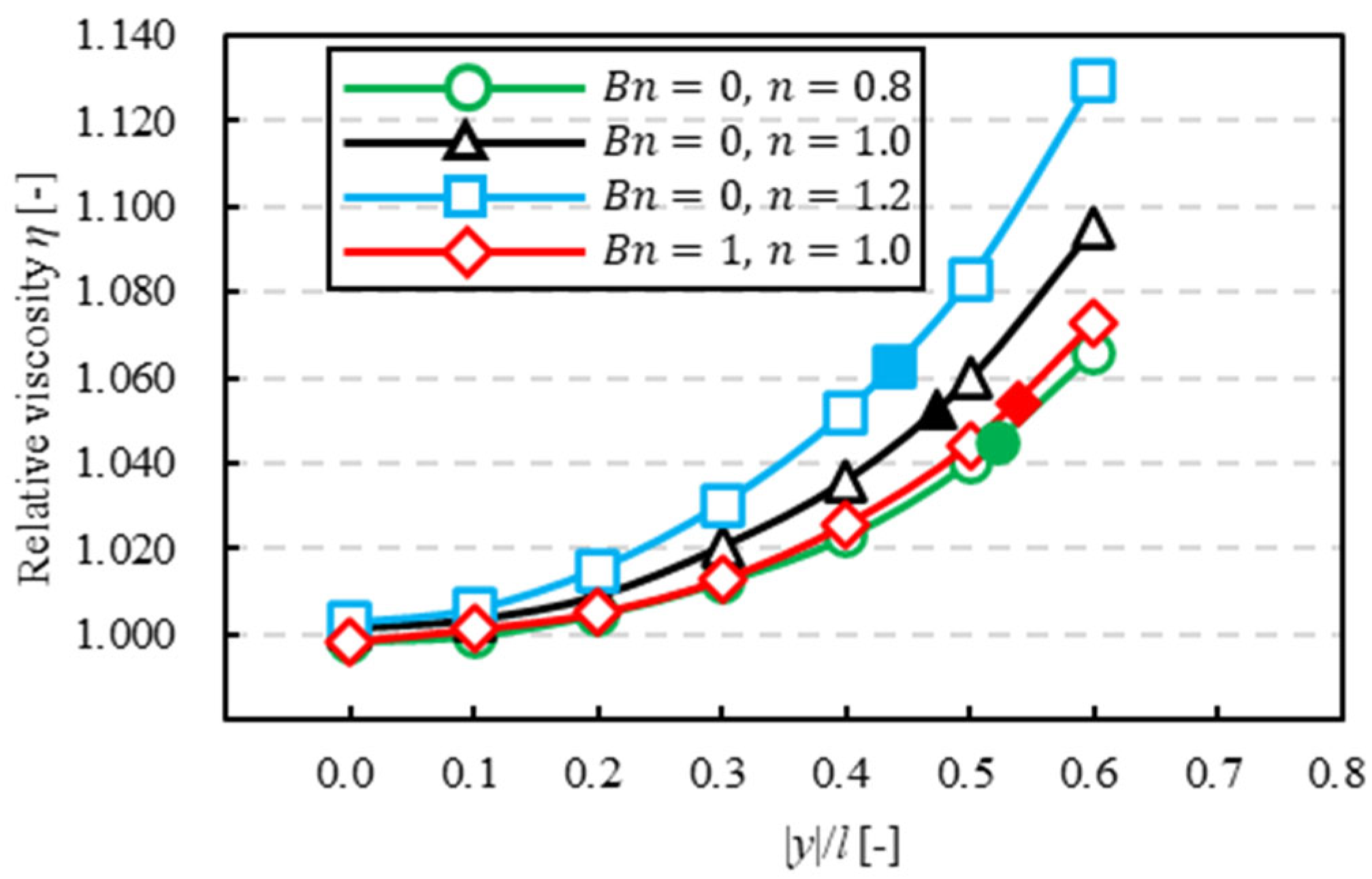
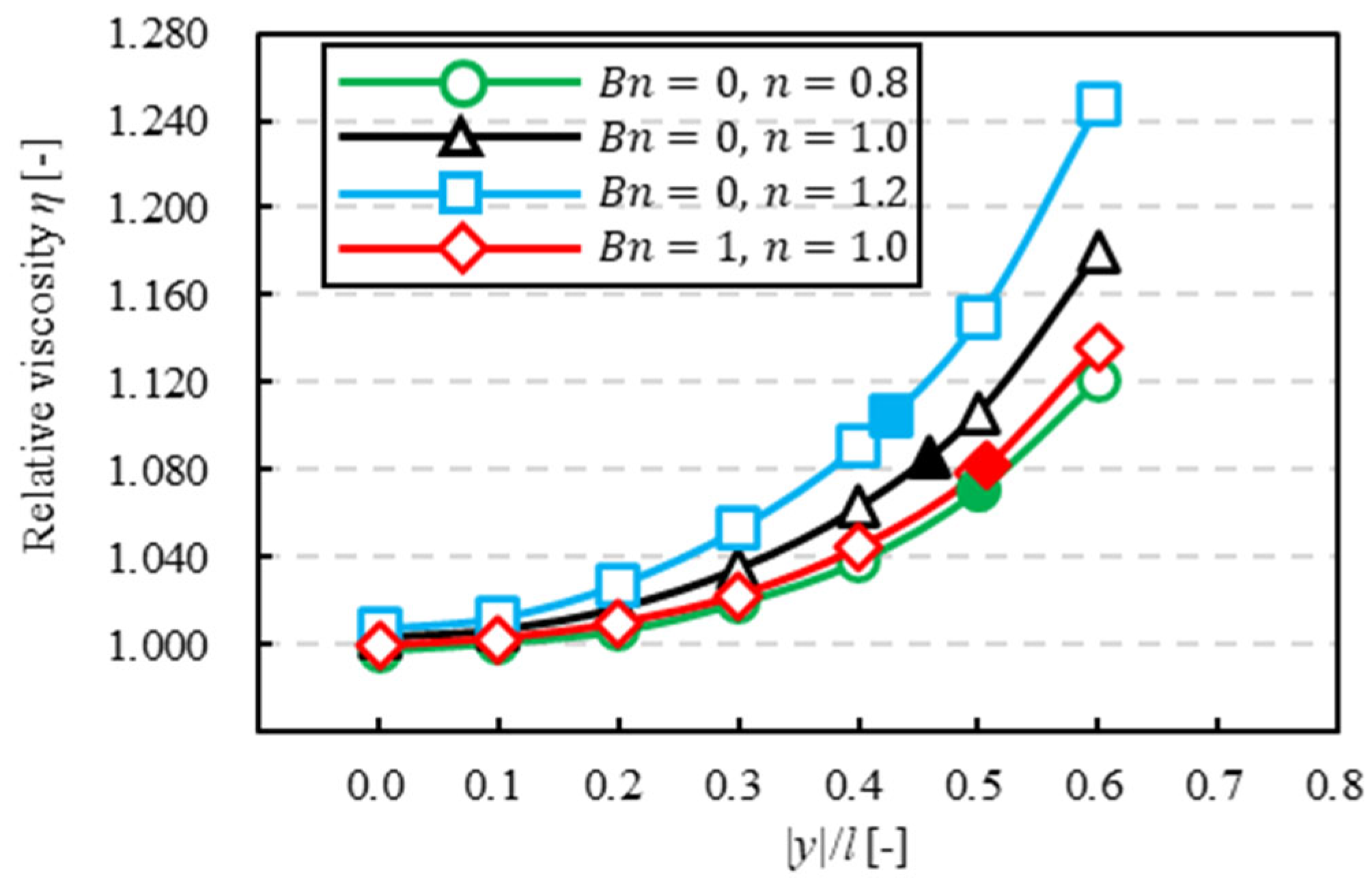
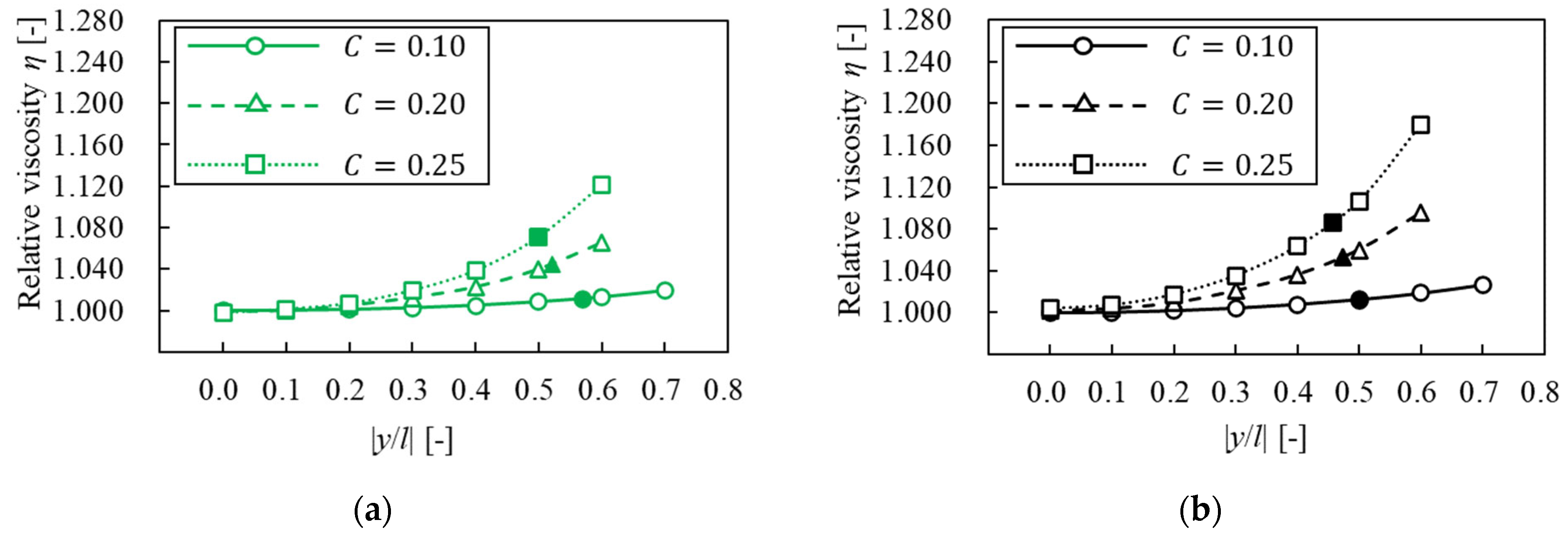
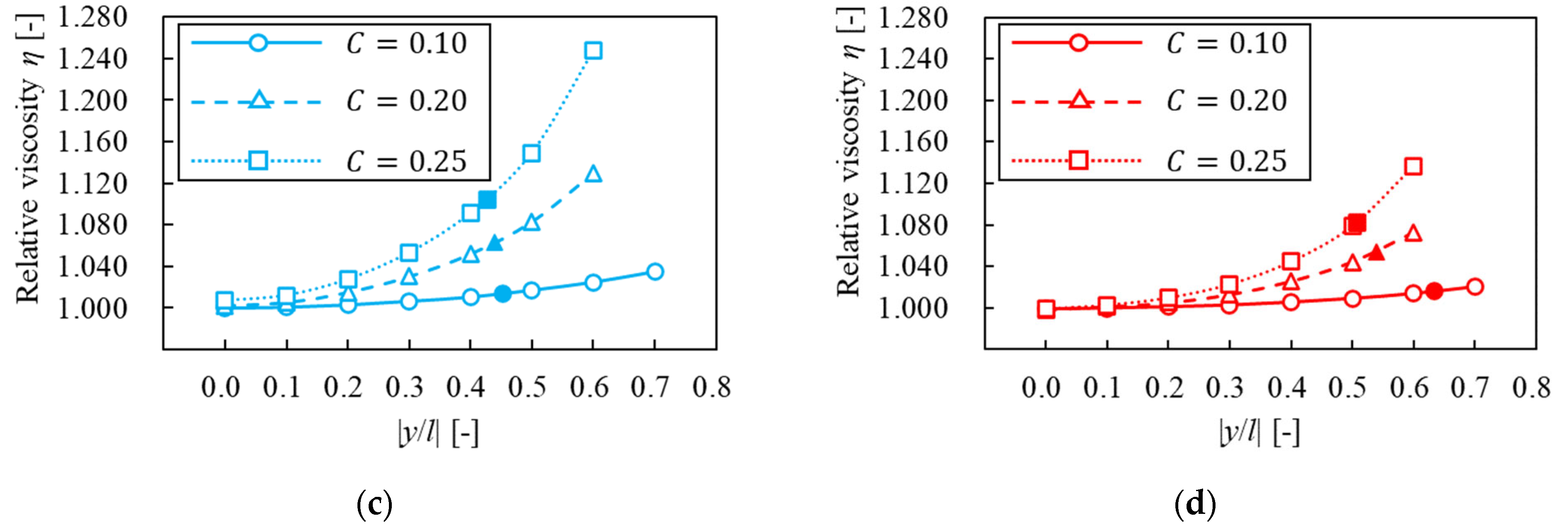
3.5. Relative Viscosity
3.5.1. Dependence on Solvents
3.5.2. Dependence on Confinements
4. Conclusions
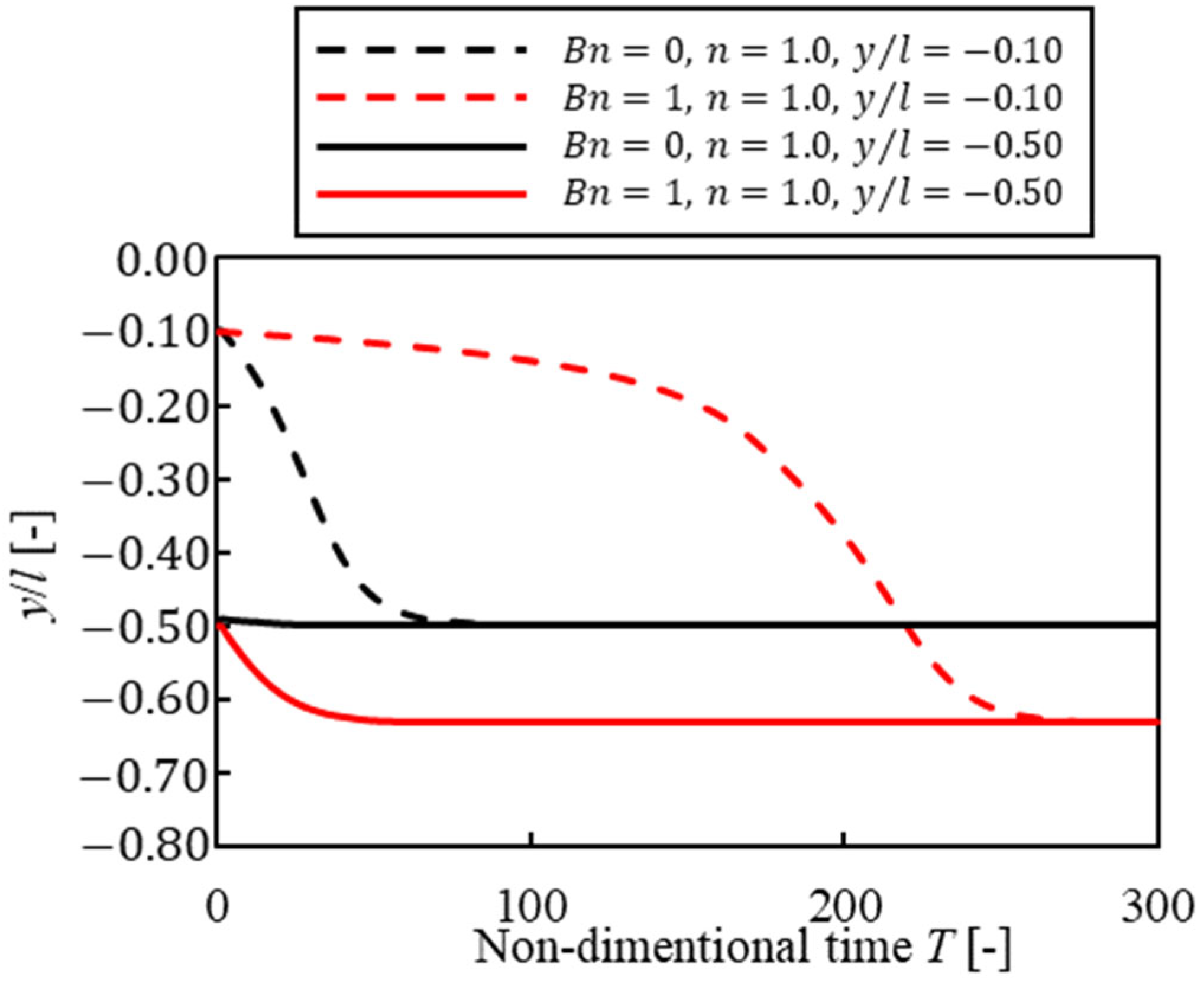
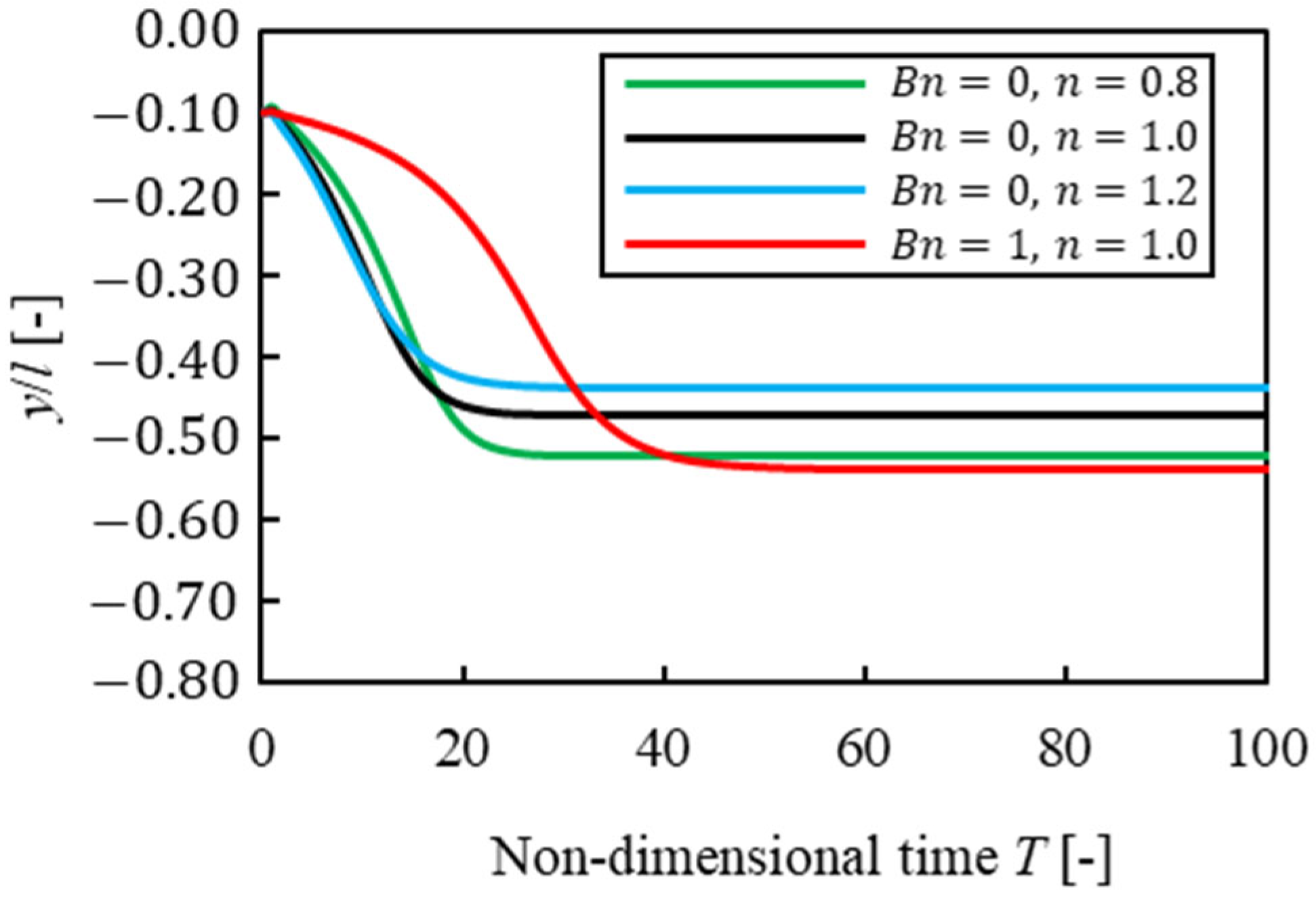
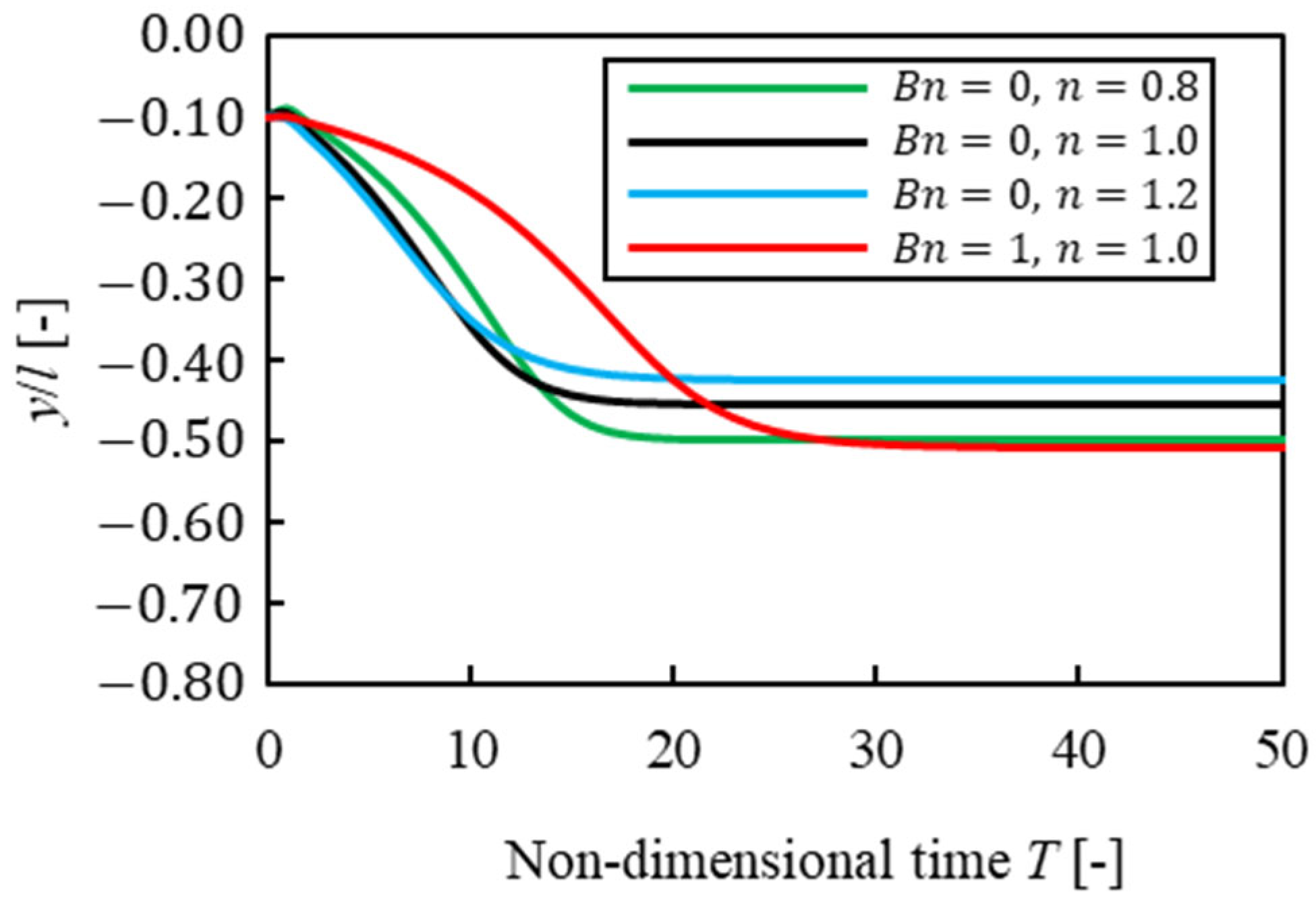
- We confirmed that the equilibrium position in Bingham fluid was closer to the wall than that in power-law fluid. Moreover, when a particle started to flow near the channel center, it was difficult for a particle in Bingham fluid to migrate in the direction and it spend more time reaching the equilibrium position than that in power-law fluid. These results were mainly caused by the velocity profile of a particle-free fluid, which indicates that shear rate near the wall and plug flow at the center of the channel strongly affected particle migration.
- When a particle was near the center, trajectories of migration in Bingham fluid were different from that in power-law fluid because of the different lift coefficient profile for each solvent.
- The tendency of relative viscosity, including that of a suspended particle in Bingham fluid was similar to that in pseudoplastic fluid. However, when the particle was at the equilibrium position, relative viscosity in Bingham fluid was different from that in pseudoplastic fluid.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gamonpilas, C.; Morris, J.F.; Denn, M.M. Shear and normal stress measurements in non-Brownian monodisperse and bidisperse suspensions. J. Rheol. 2016, 60, 289–296. [Google Scholar] [CrossRef]
- Stickel, J.J.; Powell, R.L. Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 2005, 37, 129–149. [Google Scholar] [CrossRef]
- Picano, F.; Breugem, W.-P.; Brandt, L. Turbulent channel flow of dense suspensions of neutrally-buoyant spheres. J. Fluid Mech. 2015, 764, 463–487. [Google Scholar] [CrossRef]
- Einstein, A. Eine neue Bestimmung der Moleküldimensionen. Ann. Der Physik 1906, 324, 289–306. [Google Scholar] [CrossRef]
- Brady, J.F. The Einstein viscosity correction in n dimensions. Int. J. Multiph. Flow 1983, 10, 113–114. [Google Scholar] [CrossRef]
- Segré, G.; Silberberg, A. Radial particle displacements in Poiseuille flow of suspensions. Nature 1961, 189, 209–210. [Google Scholar] [CrossRef]
- Okamura, N.; Fukui, T.; Kawaguchi, M.; Morinishi, K. Influence of each cylinder’s contribution on the total effective viscosity of a two-dimensional suspension by a two-way coupling scheme. J. Fluid Sci. Technol. 2021, 16, JFST0020. [Google Scholar] [CrossRef]
- Chen, D.; Lin, J. Steady State of Motion of Two Particles in Poiseuille Flow of Power-Law Fluid. Polymers 2022, 14, 2368. [Google Scholar] [CrossRef] [PubMed]
- Mueller, S.; Llewellin, E.W.; Mader, H.M. The rheology of suspensions of solid particles. Proc. Math. Phys. 2010, 466, 1201–1228. [Google Scholar] [CrossRef]
- Hu, X.; Lin, J.; Ku, X. Inertial migration of circular particles in Poiseuille flow of a power-law fluid. Phys. Fluids 2019, 31, 073306. [Google Scholar] [CrossRef]
- Tanaka, M.; Fukui, T.; Kawaguchi, M.; Morinishi, K. Numerical simulation on the effects of power-law fluidic properties on the suspension rheology. J. Fluid Sci. Technol. 2021, 16, JFST0022. [Google Scholar] [CrossRef]
- Masuyama, N.; Fukui, T. Numerical simulation of the effects of non-Newtonian property of the solvent on particle suspension rheology. Adv. Mech. Eng. 2023, 15, 16878132231198338. [Google Scholar] [CrossRef]
- Sobhani, S.M.J.; Bazargan, S.; Sadeghy, K. Sedimentation of an elliptic rigid particle in a yield-stress fluid: A Lattice-Boltzmann simulation. Phys. Fluids 2019, 31, 081902. [Google Scholar] [CrossRef]
- Chaparian, E.; Ardekani, M.N.; Brandt, L.; Tammisola, O. Particle migration in channel flow of an elastoviscoplastic fluid. J. Non-Newton. Fluid Mech. 2020, 284, 104376. [Google Scholar] [CrossRef]
- Siqueira, I.R.; De Souza Mendes, P.R. On the pressure-driven flow of suspensions: Particle migration in apparent yield-stress fluids. J. Non-Newton. Fluid Mech. 2019, 265, 92–98. [Google Scholar] [CrossRef]
- Herschel, W.H.; Bulkley, R. Konsistenzmessungen von Gummi-Benzollösungen. Kolloid-Z. 1926, 39, 291–300. [Google Scholar] [CrossRef]
- Fukui, T.; Kawaguchi, M.; Morinishi, K. A two-way coupling scheme to model the effects of particle rotation on the rheological properties of a semidilute suspension. Comput. Fluids 2018, 173, 6–16. [Google Scholar] [CrossRef]
- Miura, K.; Itano, T.; Sugihara-Seki, M. Inertial migration of neutrally buoyant spheres in a pressure-driven flow through square channels. J. Fluid Mech. 2014, 749, 320–330. [Google Scholar] [CrossRef]
- Tanno, I.; Morinishi, K.; Matsuno, K.; Nishida, H. Validation of virtual flux method for forced convection flow. JSME Int. J. Ser. B 2006, 49, 1141–1148. [Google Scholar] [CrossRef]
- Morinishi, K.; Fukui, T. An Eulerian approach for fluid -structure interaction problems. Comput. Fluids 2012, 65, 92–98. [Google Scholar] [CrossRef]
- Kawaguchi, M.; Fukui, T.; Morinishi, K. Comparative study of the virtual flux method and immersed boundary method coupled with regularized lattice Boltzmann method for suspension flow method. Comput. Fluids 2022, 246, 105615. [Google Scholar] [CrossRef]
- Izham, M.; Fukui, T.; Morinshi, K. Application of regularized lattice Boltzmann method incompressible flow simulation at high Reynolds number and flow with curved boundary. J. Fluid Sci. Technol. 2011, 6, 812–822. [Google Scholar] [CrossRef]
- Morinishi, K.; Fukui, T. Parallel computation of turbulent flows using moment base lattice Boltzmann method. Int. J. Comput. Fluid Dyn. 2016, 30, 363–369. [Google Scholar] [CrossRef]
- Gsell, S.; D’Ortona, U.; Favier, J. Lattice-Boltzmann simulation of creeping generalized Newtonian flows: Theory and guidelines. J. Comput. Phys. 2021, 173, 6–16. [Google Scholar] [CrossRef]
- Papanastasiou, T.C. Flows of viscoplastic materials: Models and Computations. Comput. Struct. 1997, 64, 677–694. [Google Scholar] [CrossRef]
- Chatzimina, M.; Georgiou, G.C.; Argyropaidas, I.; Mitsoulis, E.; Huilgo, R.R. Cessation of annular Poiseuille flows of Bingham plastics. J. Nonnewton. Fluid Mech. 2005, 129, 117–127. [Google Scholar] [CrossRef]
- Sewell, G. The Numerical Solution of Ordinary and Partial Differential Equations; Academic Press: Cambridge, MA, USA, 1988; pp. 43–50. [Google Scholar]
- Boyd, J.; Buick, J.; Green, S. A Second-Order Accurate Lattice Boltzmann Non-Newtonian Flow Model. J. Phys. A Math. Gen. 2006, 39, 14241–14247. [Google Scholar] [CrossRef]
- Mahmood, R.; Kousar, N.; Usman, K.; Mahmood, A. Finite element simulations for stationary Bingham fluid flow past a circular cylinder. J. Braz. Soc. Mech. Sci. 2018, 40, 459. [Google Scholar] [CrossRef]
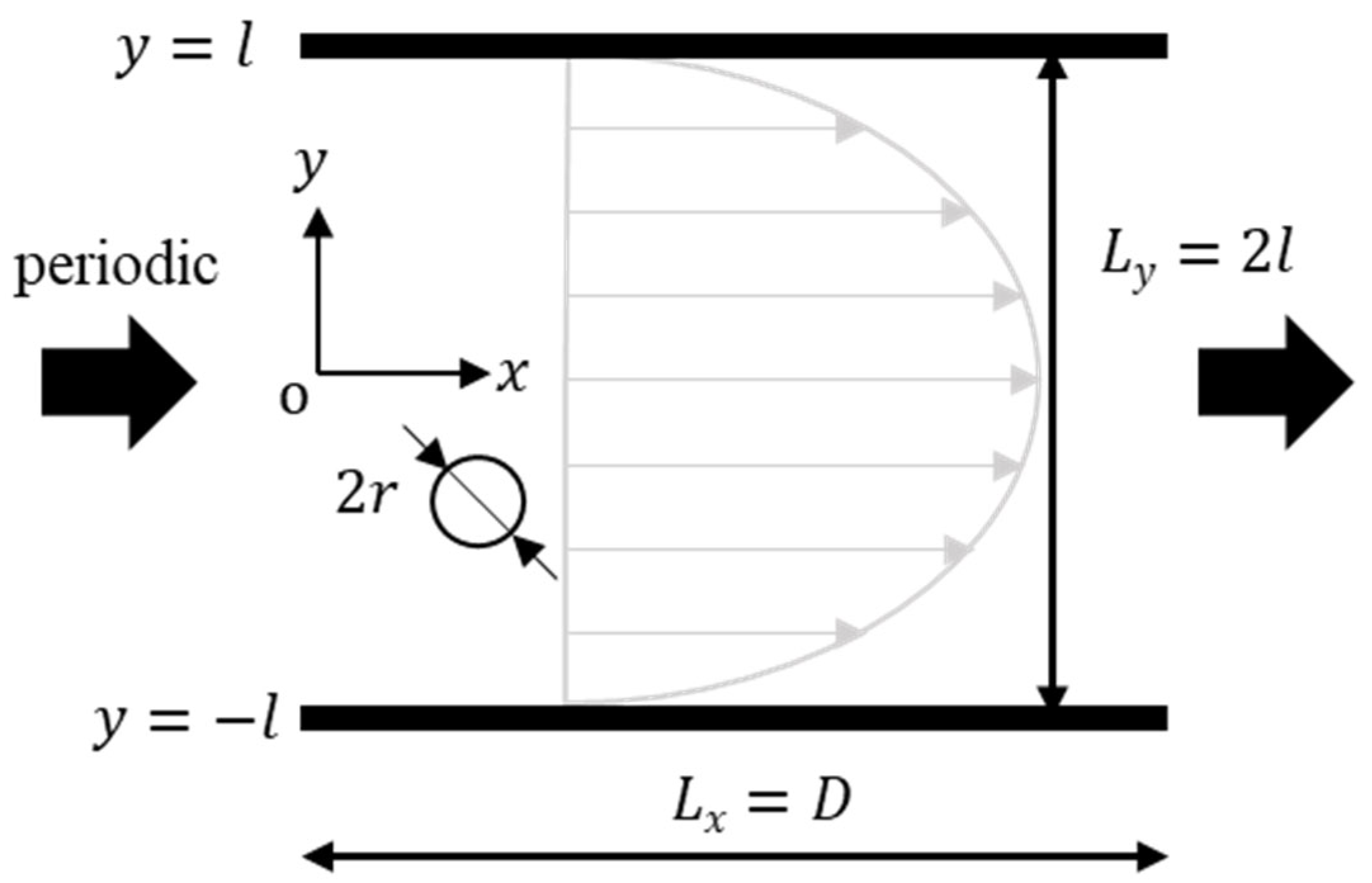
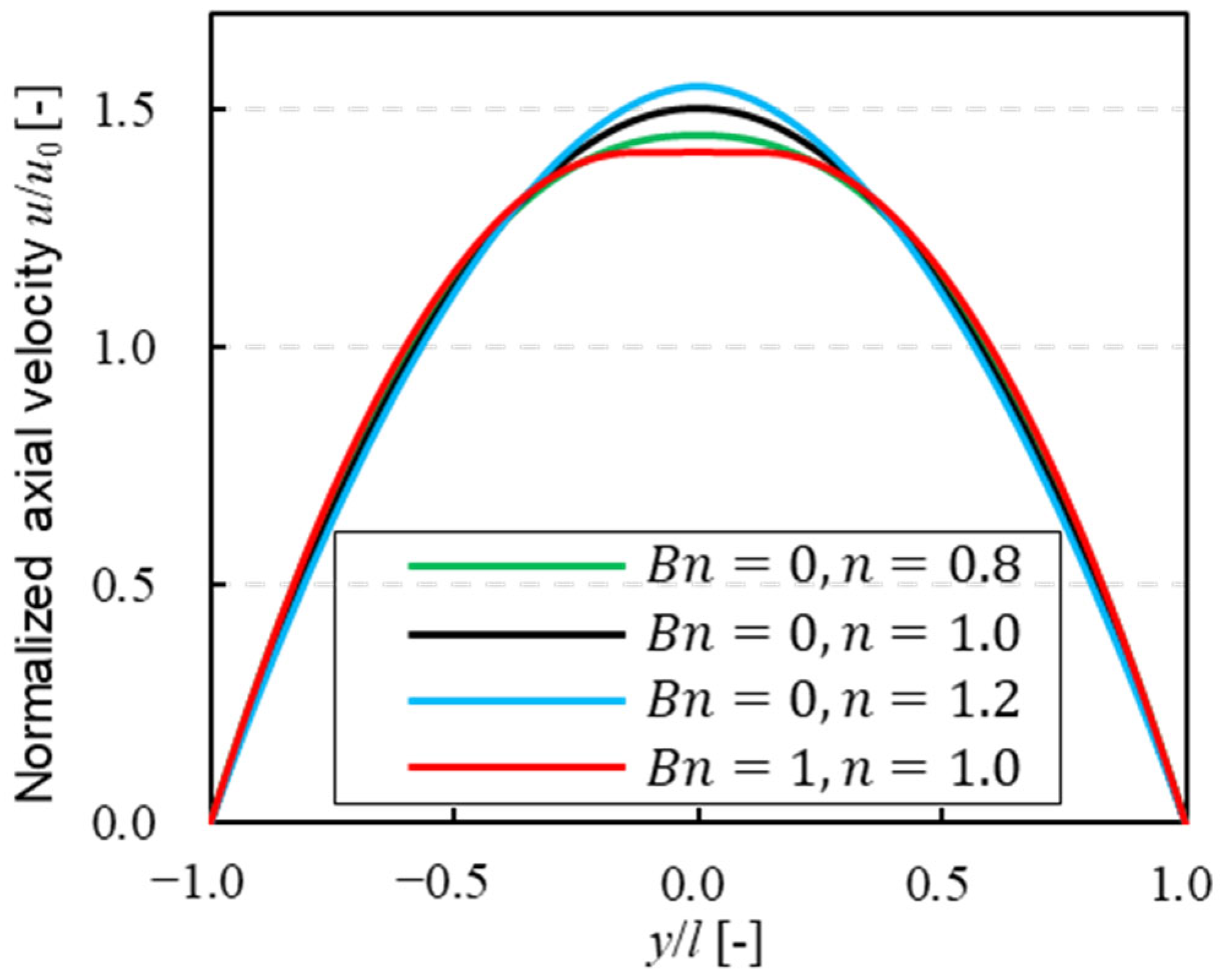
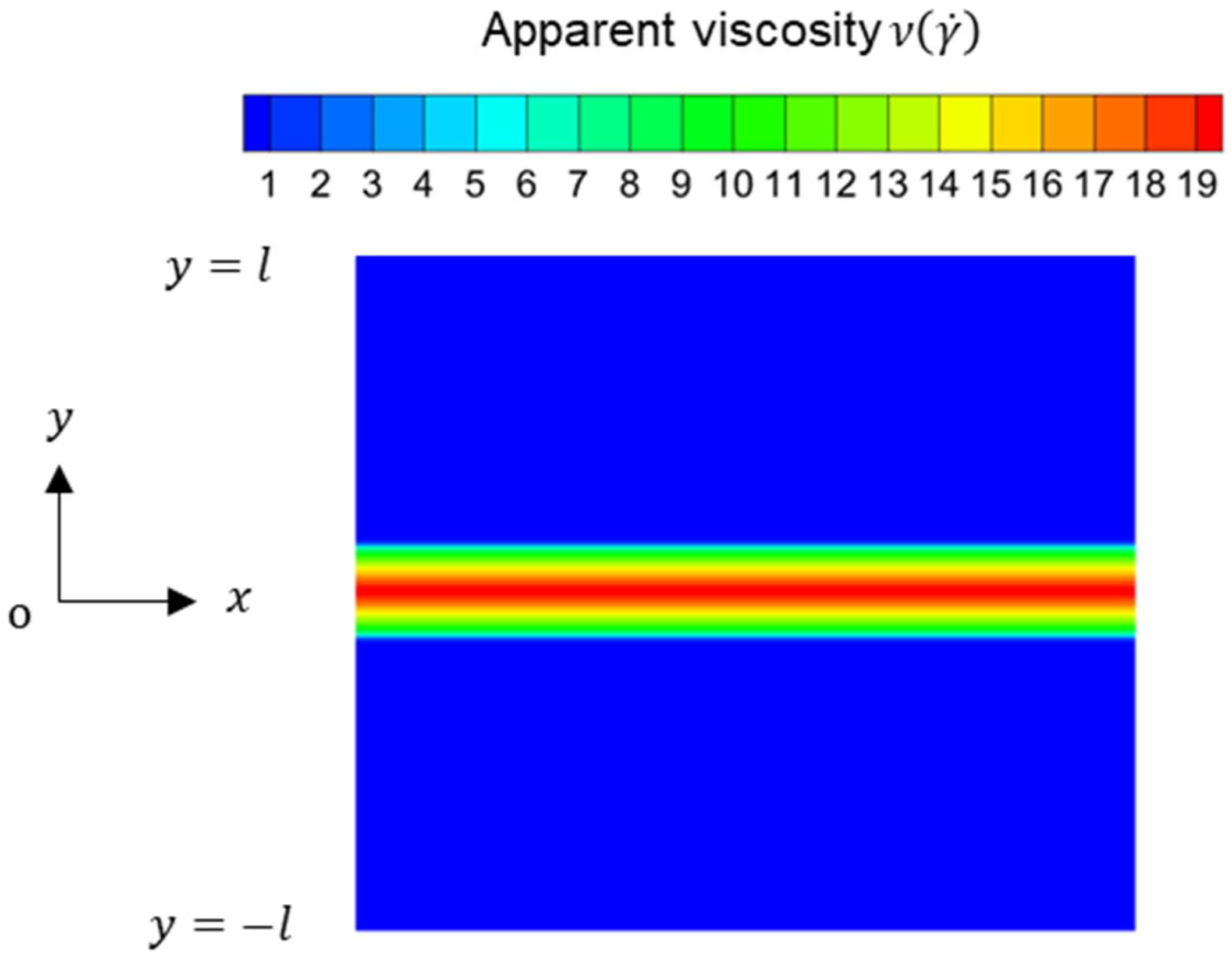

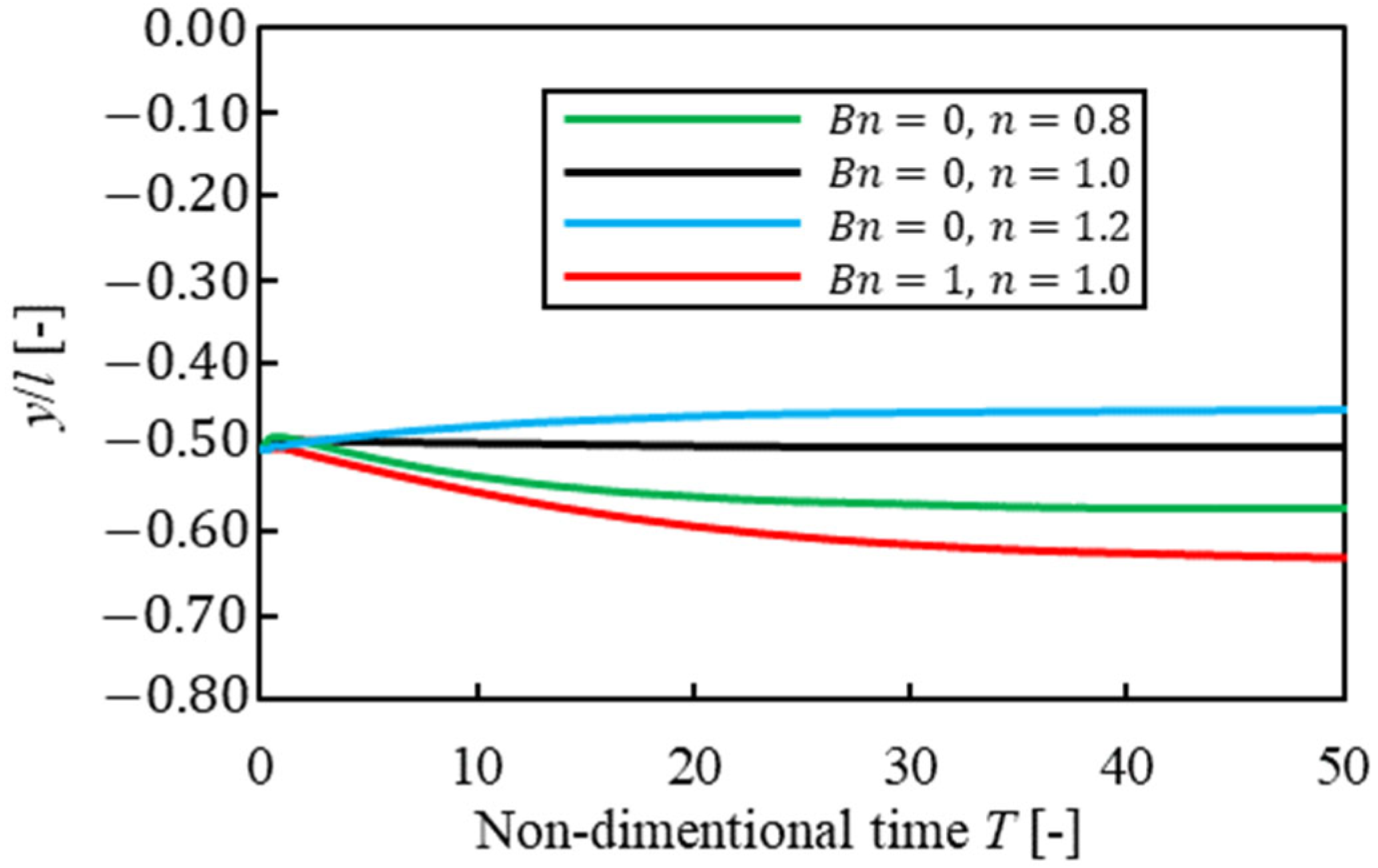

| Power-Law Index n | 0.6 | 0.8 | 1.0 | 1.2 |
|---|---|---|---|---|
| Present | −0.515 | −0.464 | −0.429 | −0.402 |
| Hu et al. [10] | −0.50 | −0.45 | −0.42 | −0.40 |
| Difference [%] | 3.0 | 3.1 | 2.1 | 0.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomioka, K.; Fukui, T. Numerical Analysis of Non-Newtonian Fluid Effects on the Equilibrium Position of a Suspended Particle and Relative Viscosity in Two-Dimensional Flow. Fluids 2024, 9, 37. https://doi.org/10.3390/fluids9020037
Tomioka K, Fukui T. Numerical Analysis of Non-Newtonian Fluid Effects on the Equilibrium Position of a Suspended Particle and Relative Viscosity in Two-Dimensional Flow. Fluids. 2024; 9(2):37. https://doi.org/10.3390/fluids9020037
Chicago/Turabian StyleTomioka, Keiya, and Tomohiro Fukui. 2024. "Numerical Analysis of Non-Newtonian Fluid Effects on the Equilibrium Position of a Suspended Particle and Relative Viscosity in Two-Dimensional Flow" Fluids 9, no. 2: 37. https://doi.org/10.3390/fluids9020037
APA StyleTomioka, K., & Fukui, T. (2024). Numerical Analysis of Non-Newtonian Fluid Effects on the Equilibrium Position of a Suspended Particle and Relative Viscosity in Two-Dimensional Flow. Fluids, 9(2), 37. https://doi.org/10.3390/fluids9020037






