Hemodynamic Insights into Abdominal Aortic Aneurysms: Bridging the Knowledge Gap for Improved Patient Care
Abstract
1. Introduction
2. Key Hemodynamic Parameters in Abdominal Aortic Aneurysms
3. Modeling
3.1. Anatomical Representation of Aortic Aneurysm and Surrounding Vessels
3.2. Fluid Dynamics
3.2.1. Mesh Configuration and Grid Independence Analysis
3.2.2. Physiological Blood Entry Control and Cardiac Cycle Phases
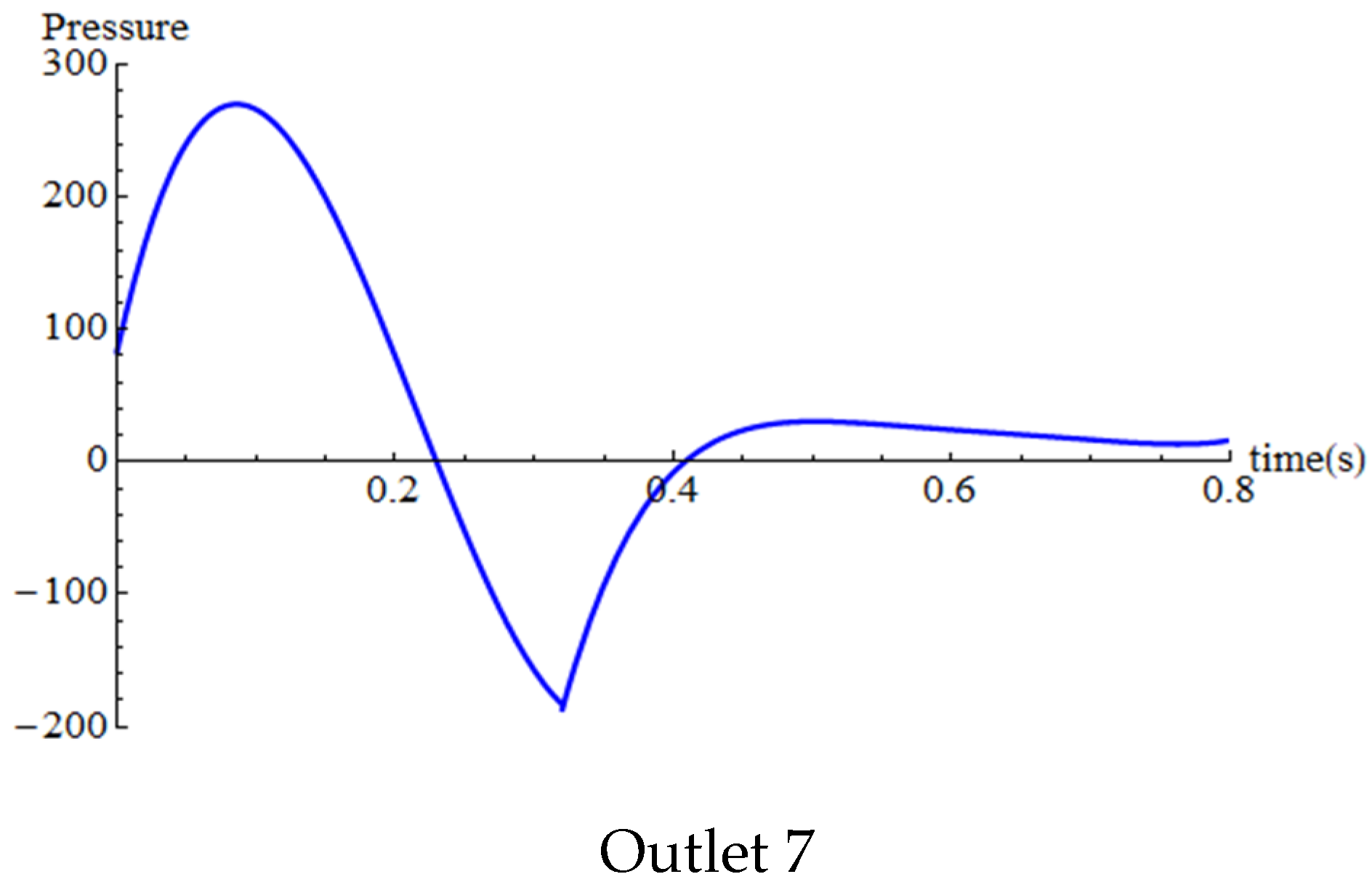
3.2.3. Integrating the Windkessel Model with Outlet Boundary Conditions
4. Results
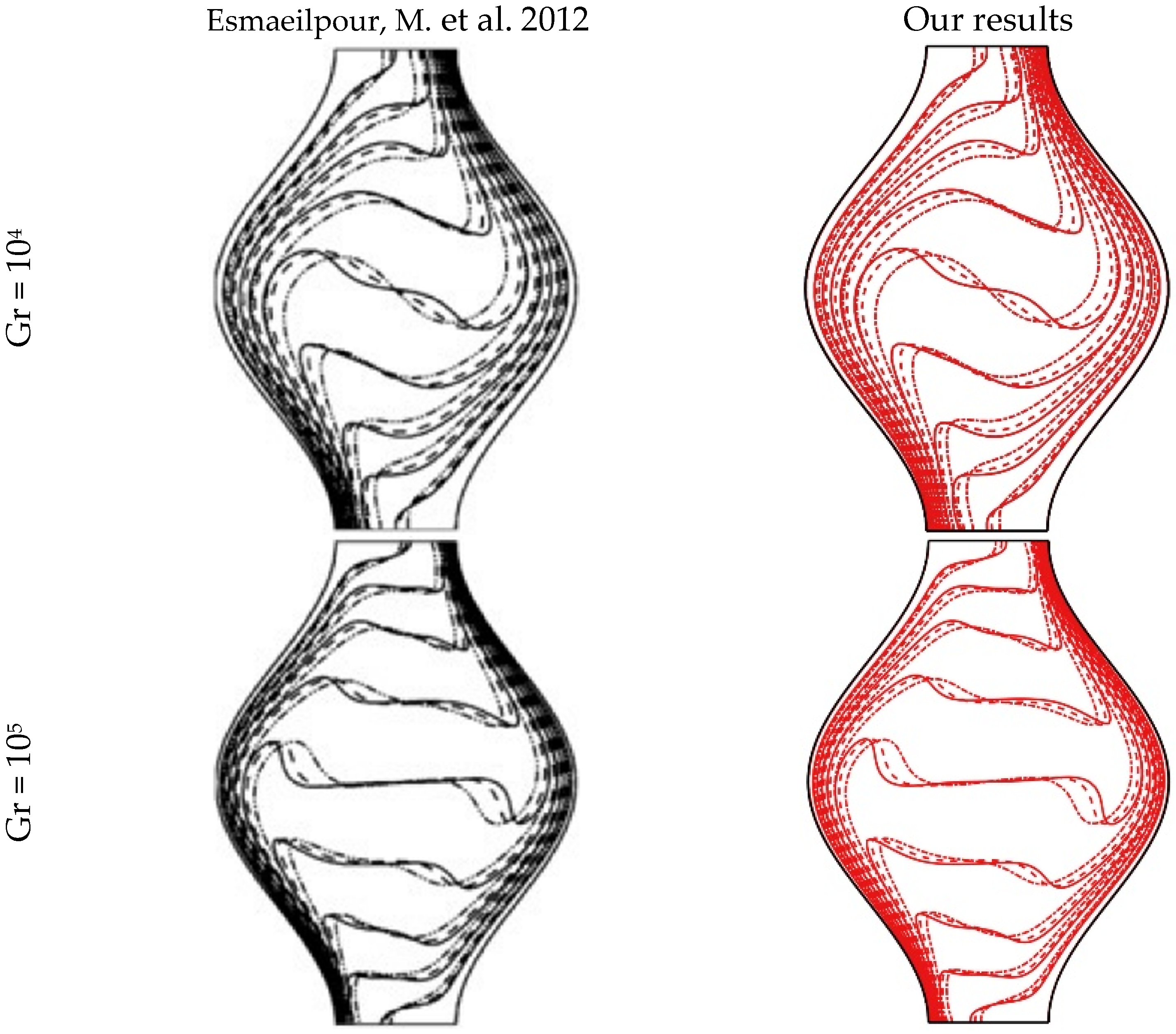
4.1. Validation
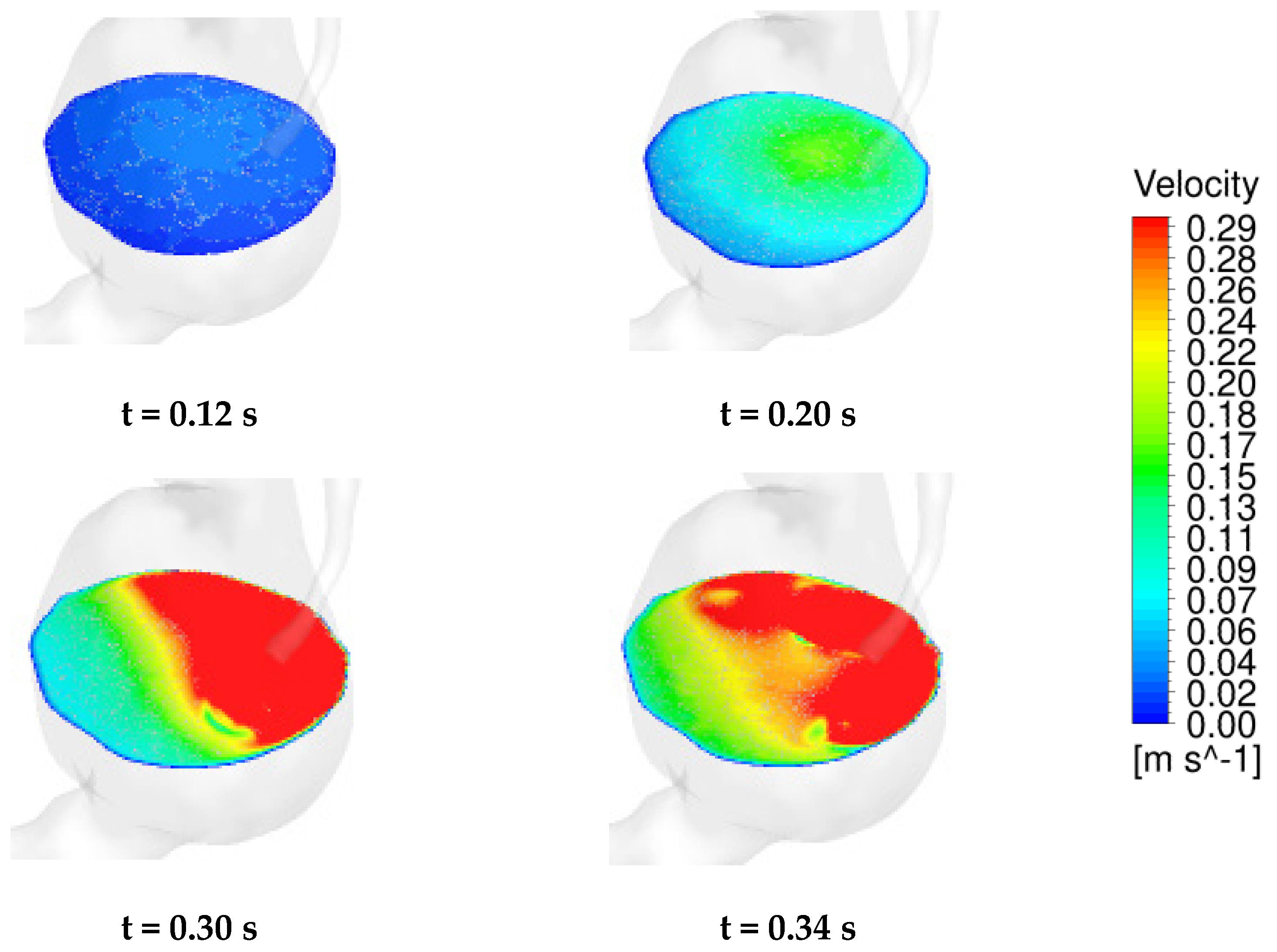
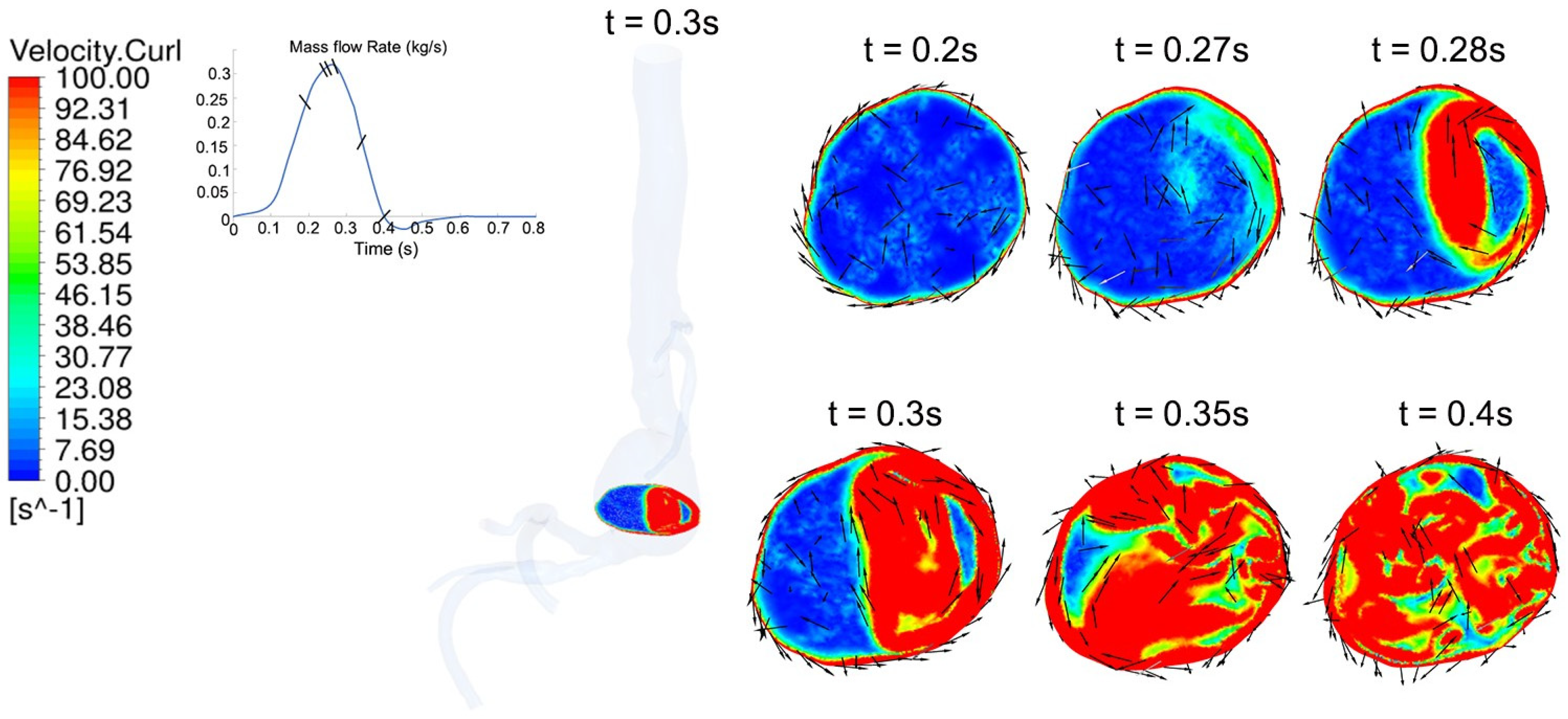
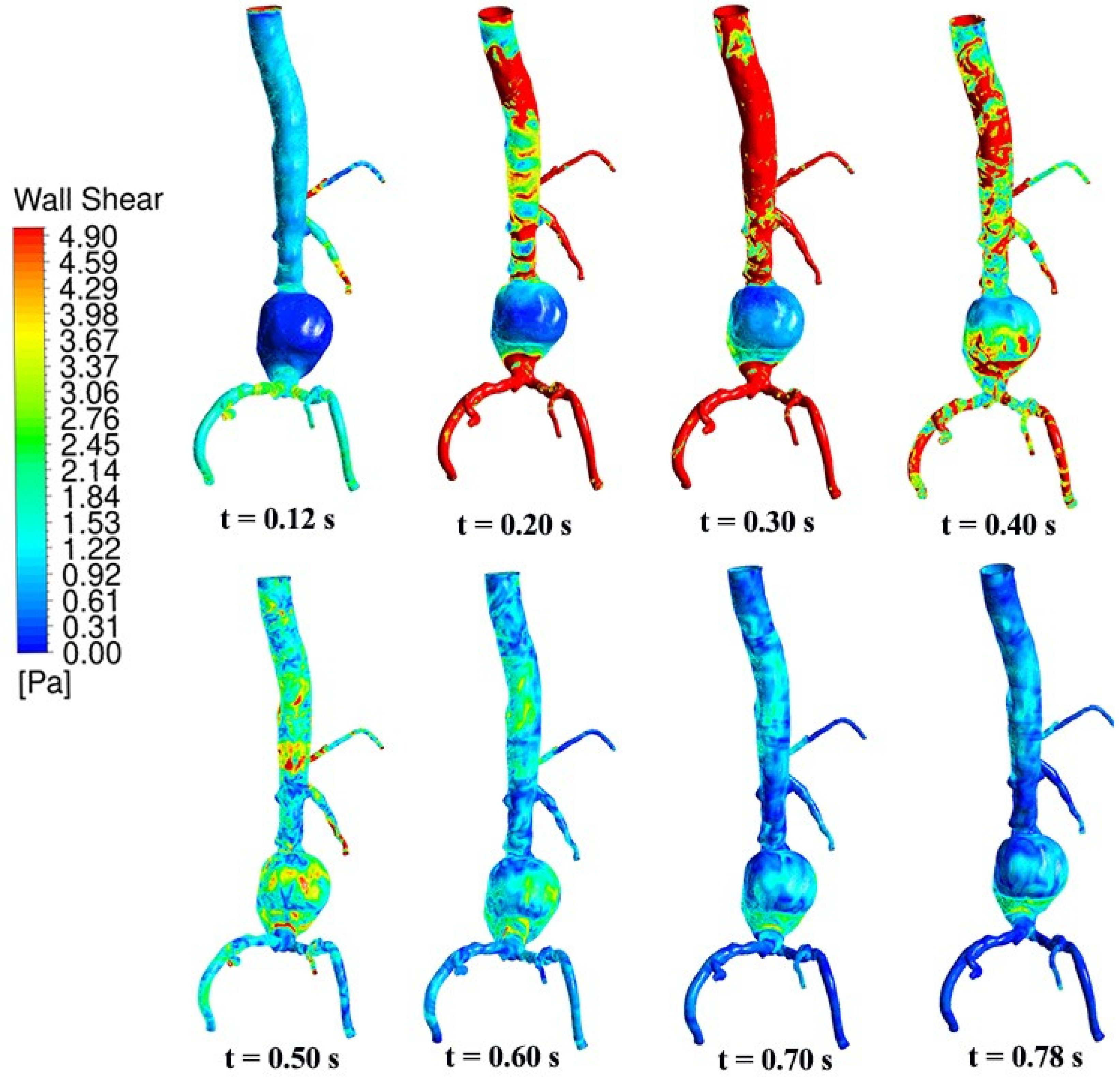
4.2. Temporal Hemodynamic Analysis in a Non-Newtonian Vascular Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Ethics Statement
Abbreviations
| d | Aortic vessel diameter |
| FEM | Finite element method |
| FVM | Finite volume method |
| Gr | Grashof number |
| HLPT | Hybrid Lagrangian particle tracking |
| L | Total length of the aorta |
| La | Total length of the aneurysm |
| PIMPLE | Combination of SIMPLE and PISO |
| PISO | Pressure-Implicit with Splitting of Operators |
| Pr | Prandtl number |
| Q | Flow rate |
| Remax | Maximum Reynolds number |
| Reavg | Average Reynolds number |
| SEM | Spectral element method |
| SIMPLE | Semi-Implicit Method for Pressure-Linked Equations |
| We | Weissenberg number |
| W0 | Womersley number |
| Y | Young’s modulus |
References
- Francis, I.; Saha, S.C. Surface tension effects on flow dynamics and alveolar mechanics in the acinar region of human lung. Heliyon 2022, 8, e11026. [Google Scholar] [CrossRef]
- Francis, I.; Saha, S.C. Computational fluid dynamics and machine learning algorithms analysis of striking particle velocity magnitude, particle diameter, and impact time inside an acinar region of the human lung. Phys. Fluids 2022, 34, 101904. [Google Scholar] [CrossRef]
- Ali, D.; Ozalp, M.; Blanquer, S.B.; Onel, S. Permeability and fluid flow-induced wall shear stress in bone scaffolds with TPMS and lattice architectures: A CFD analysis. Eur. J. Mech. B/Fluids 2020, 79, 376–385. [Google Scholar] [CrossRef]
- Derycke, L.; Avril, S.; Vermunt, J.; Perrin, D.; El Batti, S.; Alsac, J.M.; Millon, A.; Albertini, J.N. Computational prediction of proximal sealing in endovascular abdominal aortic aneurysm repair with unfavorable necks. Comput. Methods Programs Biomed. 2024, 244, 107993. [Google Scholar] [CrossRef]
- Mutlu, O.; Salman, H.E.; Al-Thani, H.; El-Menyar, A.; Qidwai, U.A.; Yalcin, H.C. How does hemodynamics affect rupture tissue mechanics in abdominal aortic aneurysm: Focus on wall shear stress derived parameters, time-averaged wall shear stress, oscillatory shear index, endothelial cell activation potential, and relative residence time. Comput. Biol. Med. 2023, 154, 106609. [Google Scholar] [CrossRef]
- Qiu, Y.; Wang, J.; Zhao, J.; Wang, T.; Zheng, T.; Yuan, D. Association between flow pattern and rupture risk of abdominal aortic aneurysm based on computational fluid dynamics. Eur. J. Vasc. Endovasc. Surg. 2022, 64, 155–164. [Google Scholar] [CrossRef]
- Taylor, T.; Yamaguchi, T. Three-Dimensional Simulation of Blood Flow in an Abdominal Aortic Aneurysm using Steady and Unsteady Computational Methods. ASME Adv. Bioeng. 1992, 22, 229–232. [Google Scholar]
- Taylor, T.; Yamaguchi, T. Three-Dimensional Simulation of Blood Flow in an Abdominal Aortic Aneurysm—Steady and Unsteady Flow Cases. ASME J. Biomech. Eng. 1994, 116, 89–97. [Google Scholar] [CrossRef]
- Vorp, D.A.; Raghavan, M.L.; Webster, M.W. Mechanical wall stress in abdominal aortic aneurysm: Influence of diameter and asymmetry. J. Vasc. Surg. 1998, 27, 632–639. [Google Scholar] [CrossRef]
- Finol, E.A.; Amon, C.H. Blood flow in abdominal aortic aneurysms: Pulsatile flow hemodynamics. J. Biomech. Eng. 2001, 123, 474–484. [Google Scholar] [CrossRef]
- Finol, E.A.; Amon, C.H. Flow-induced wall shear stress in abdominal aortic aneurysms: Part II—Pulsatile flow hemodynamics. Comput. Methods Biomech. Biomed. Eng. 2002, 5, 319–328. [Google Scholar] [CrossRef] [PubMed]
- Guzman, A.; Moraga, N.; Amon, C.H. Pulsatile Non-Newtonian Flow in a Double Aneurysm. ASME Adv. Bioeng. 1997, 36, 87–88. [Google Scholar]
- Finol, E.A.; Amon, C.H. Momentum Transfer in Abdominal Aortic Aneurysms: The Effect of Aneurysm Size in Steady Flow Hemodynamics. In Proceedings of the 34th ASME National Heat Transfer Conference—NHTC 2000, Pittsburgh, PA, USA, 21 August 2000. No. NHTC2000-12205. [Google Scholar]
- Finol, E.A.; Keyhani, K.; Amon, C.H. The effect of asymmetry in abdominal aortic aneurysms under physiologically realistic pulsatile flow conditions. J. Biomech. Eng. 2003, 125, 207. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Kleinstreuer, C. Blood flow and structure interactions in a stented abdominal aortic aneurysm model. Med. Eng. Phys. 2005, 27, 369–382. [Google Scholar] [CrossRef] [PubMed]
- Frauenfelder, T.; Lotfey, M.; Boehm, T.; Wildermuth, S. Computational fluid dynamics: Hemodynamic changes in abdominal aortic aneurysm after stent-graft implantation. Cardio Vasc. Interv. Radiol. 2006, 29, 613–623. [Google Scholar] [CrossRef]
- Hardman, D.; Doyle, B.J.; Semple, S.I.K.; Richards, J.M.J.; Newby, D.E.; Easson, W.J.; Hoskins, P.R. On the prediction of monocyte deposition in abdominal aortic aneurysms using computational fluid dynamics. Proc. IMechE Part H J. Eng. Med. 2013, 227, 1114–1124. [Google Scholar] [CrossRef]
- Deplano, V.; Knapp, Y.; Bailly, L.; Bertrand, E. Flow of a blood analogue fluid in a compliant abdominal aortic aneurysm model: Experimental modeling. J. Biomech. 2014, 47, 1262–1269. [Google Scholar] [CrossRef]
- Rana, M.S.; Rubby, M.F.; Hasan, A.B.M.T. Study of physiological flow through an abdominal aortic aneurysm (AAA). Procedia Eng. 2015, 105, 885–892. [Google Scholar] [CrossRef][Green Version]
- Vergara, C.; Van, D.L.; Quadrio, M.; Formaggia, L.; Domanin, M. Large eddy simulations of blood dynamics in abdominal aortic aneurysms. Med. Eng. Phys. 2017, 47, 38–46. [Google Scholar] [CrossRef]
- Shit, G.C.; Majee, S. Magnetic field interaction with blood flow and heat transfer through diseased artery having Abdominal Aortic Aneurysm. Eur. J. Mech.-B/Fluids 2018, 71, 1–14. [Google Scholar] [CrossRef]
- Joly, F.; Soulez, G.; Garcia, D.; Lessard, S.; Kauffmann, C. Flow stagnation volume and abdominal aortic aneurysm growth: Insights from patient-specific computational flow dynamics of Lagrangian-coherent structures. Comput. Biol. Med. 2018, 92, 98–109. [Google Scholar] [CrossRef]
- Elhanafy, A.; Guaily, A.; Elsaid, A. Numerical simulation of blood flow in abdominal aortic aneurysms: Effects of blood shear-thinning and viscoelastic properties. Math. Comput. Simul. 2019, 160, 55–71. [Google Scholar] [CrossRef]
- Espa, S.; Moroni, M.; Boniforti, M.A. In-vitro simulation of the blood flow in an axisymmetric abdominal aortic aneurysm. Appl. Sci. 2019, 9, 4560. [Google Scholar] [CrossRef]
- Jafarzadeh, S.; Sadr, A.N.; Kaffash, E.; Goudarzi, S.; Golab, E.; Karimipour, A. The Effect of Hematocrit and Nanoparticles Diameter on Hemodynamic Parameters and Drug Delivery in Abdominal Aortic Aneurysm with Consideration of Blood Pulsatile Flow. Comput. Methods Programs Biomed. 2020, 195, 105545. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Ismael, M.A.; Al-Hadraawy, S.K.; Ghalambaz, M.; Hashim, I.; Chamkha, A.J. Fluid-structure interaction model of blood flow in abdominal aortic aneurysms with thermic treatment. Alex. Eng. J. 2023, 64, 81–95. [Google Scholar] [CrossRef]
- Hussain, A.; Dar, M.N.R.; Alrasheedi, N.H.; Hajlaoui, K.; Hamida, M.B.B. Assessment of heat transfer and the consequences of iron oxide (Fe3O4) nanoparticles on flow of blood in an abdominal aortic aneurysm. Heliyon 2023, 9, e17660. [Google Scholar] [CrossRef] [PubMed]
- Gallo, D.; De Santis, G.; Negri, F.; Tresoldi, D.; Ponzini, R.; Massai, D.; Deriu, M.A.; Segers, P.; Verhegghe, B.; Rizzo, G.; et al. On the use of in vivo measured flow rates as boundary conditions for image-based hemodynamic models of the human aorta: Implications for indicators of abnormal flow. Ann. Biomed. Eng. 2012, 40, 729–741. [Google Scholar] [CrossRef] [PubMed]
- Afrouzi, H.H.; Ahmadian, M.; Hosseini, M.; Arasteh, H.; Toghraie, D.; Rostami, S. Simulation of blood flow in arteries with aneurysm: Lattice Boltzmann Approach (LBM). Comput. Methods Programs Biomed. 2020, 187, 105312. [Google Scholar] [CrossRef]
- Boccadifuoco, A.; Mariotti, A.; Celi, S.; Martini, N.; Salvetti, M.V. Uncertainty quantification in numerical simulations of the flow in thoracic aortic aneurysms. In Proceedings of the ECCOMAS Congress 2016, VII European Congress on Computational Methods in Applied Sciences and Engineering, Crete Island, Greece, 5–10 June 2016. [Google Scholar]
- Westerhof, N.; Lankhaar, J.-W.; Westerhof, B.E. The arterial windkessel. Med. Biol. Eng. Comput. 2009, 47, 131–141. [Google Scholar] [CrossRef]
- Wang, X.; Ghayesh, M.H.; Kotousov, A.; Zander, A.C.; Amabili, M.; Dawson, J.A.; Psaltis, P.J. Biomechanics of abdominal aortic aneurysm in the framework of Windkessel effect and fully-developed inflow velocity via two-way non-linear FSI. Int. J. Non-Linear Mech. 2023, 157, 104517. [Google Scholar] [CrossRef]
- Esmaeilpour, M.; Abdollahzadeh, M. Free convection and entropy generation of nanofluid inside an enclosure with different patterns of vertical wavy walls. Int. J. Therm. Sci. 2012, 52, 127–136. [Google Scholar] [CrossRef]
- Omodaka, S.; Sugiyama, S.I.; Inoue, T.; Funamoto, K.; Fujimura, M.; Shimizu, H.; Hayase, T.; Takahashi, A.; Tominaga, T. Local hemodynamics at the rupture point of cerebral aneurysms determined by computational fluid dynamics analysis. Cerebrovasc. Dis. 2012, 34, 121–129. [Google Scholar] [CrossRef] [PubMed]
- Nagargoje, M.S.; Valeti, C.; Manjunath, N.; Akhade, B.; Sudhir, B.J.; Patnaik, B.S.V.; Kannath, S.K. Influence of morphological parameters on hemodynamics in internal carotid artery bifurcation aneurysms. Phys. Fluids 2022, 34, 101901. [Google Scholar] [CrossRef]
- Lu, G.; Huang, L.; Zhang, X.L.; Wang, S.Z.; Hong, Y.; Hu, Z.; Geng, D.Y. Influence of hemodynamic factors on rupture of intracranial aneurysms: Patient-specific 3D mirror aneurysms model computational fluid dynamics simulation. Am. J. Neuroradiol. 2011, 32, 1255–1261. [Google Scholar] [CrossRef]
- Xiang, J.; Natarajan, S.K.; Tremmel, M.; Ma, D.; Mocco, J.; Hopkins, L.N.; Siddiqui, A.H.; Levy, E.I.; Meng, H. Hemodynamic-morphologic discriminants for intracranial aneurysm rupture. Stroke 2011, 42, 144–152. [Google Scholar] [CrossRef]
- Ku, D.N. Blood flow in arteries. Annu. Rev. Fluid Mech. 1997, 29, 399–434. [Google Scholar] [CrossRef]
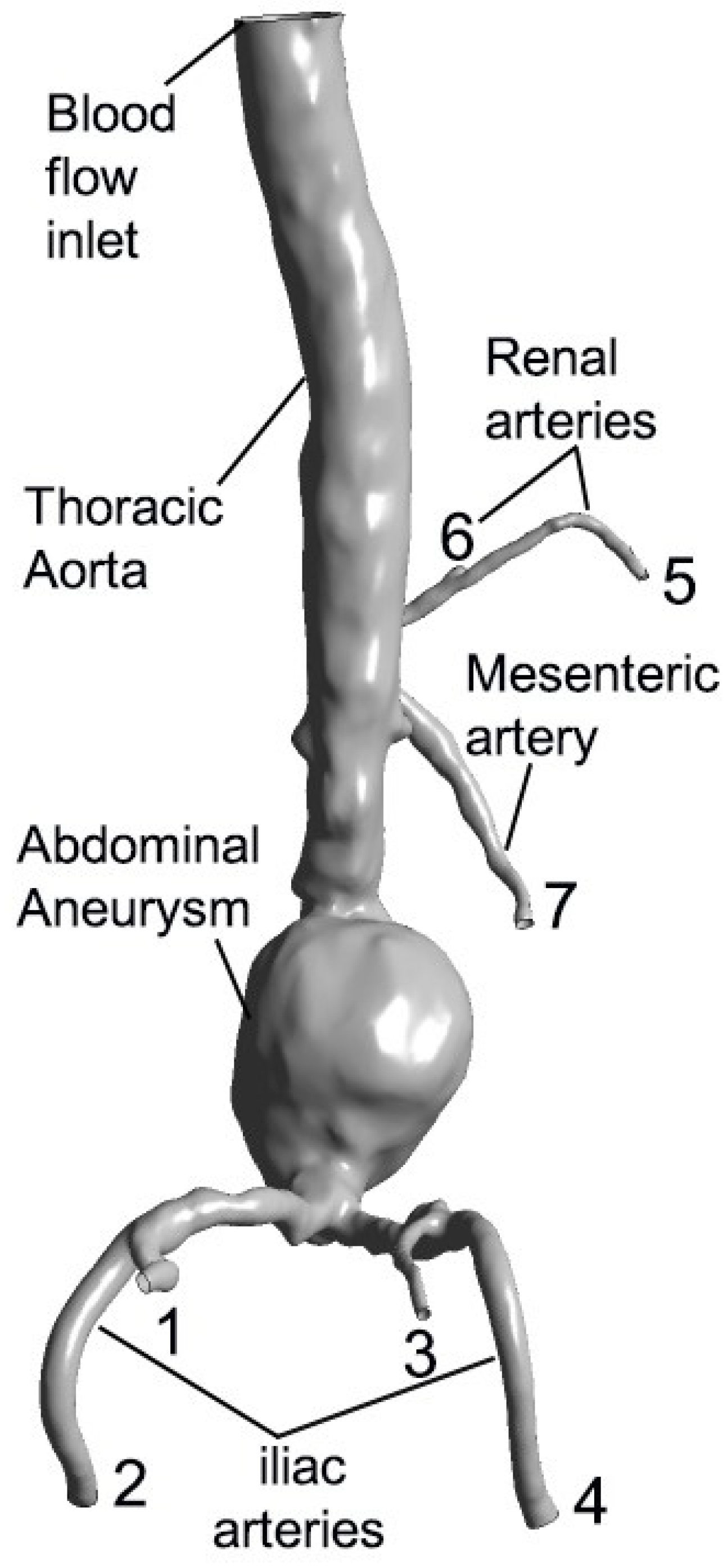
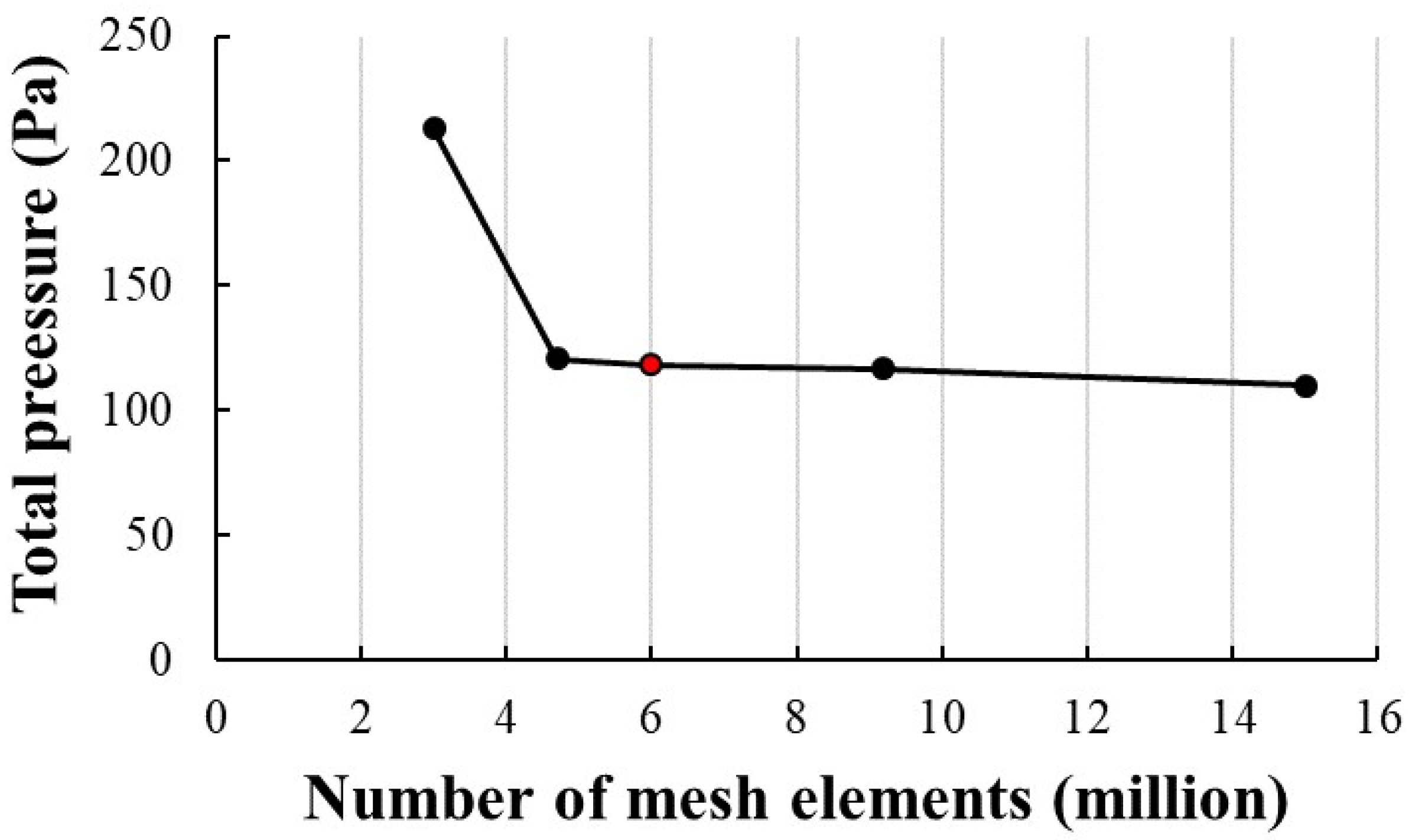
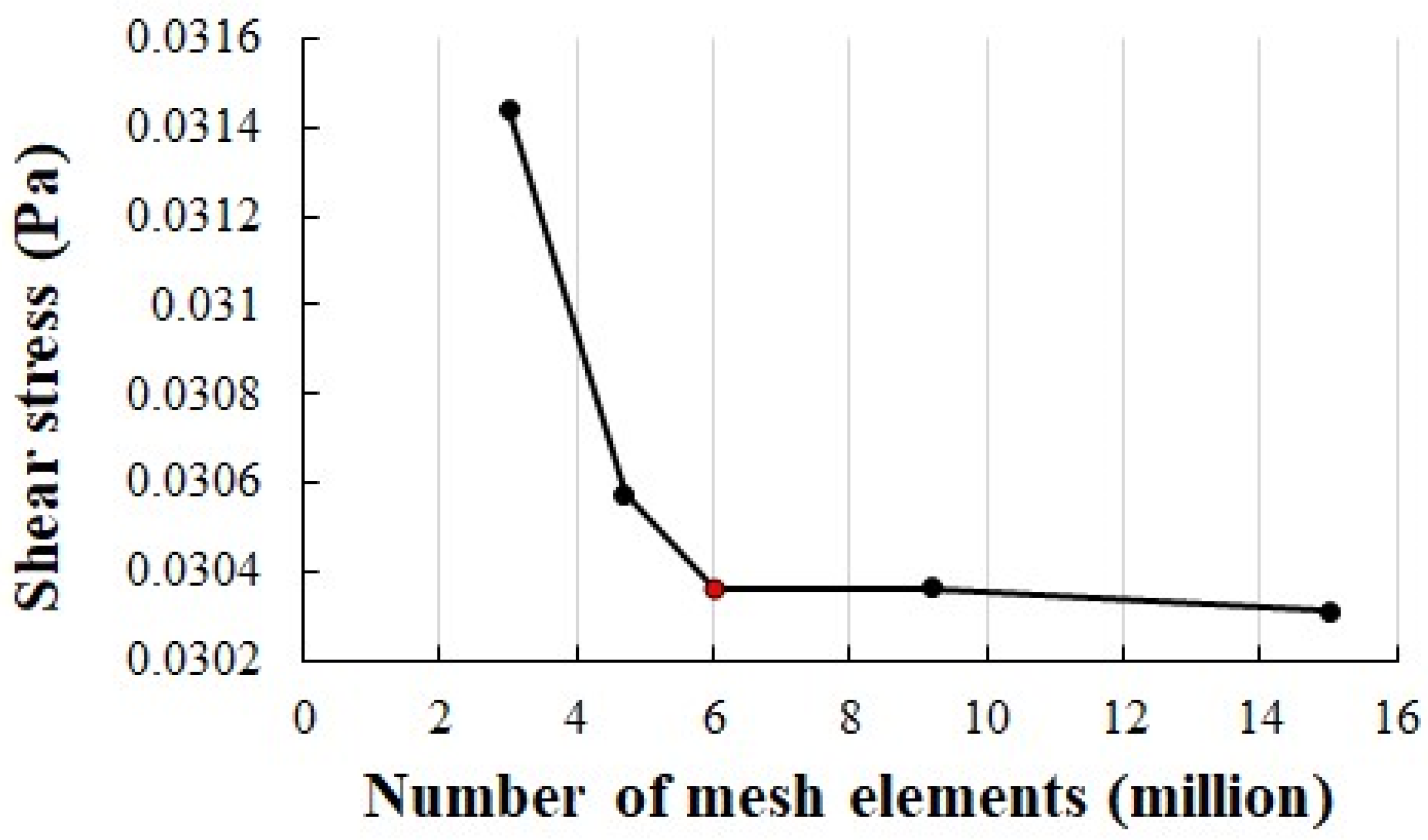





| Ref. | Methods | Dimension, Type of Flow | Fluid, Type of Wall, Parameters, and/or Particles | Grid Type and Size |
|---|---|---|---|---|
| [8] | SCRYU Code, FVM, SIMPLE | 3D, steady, unsteady, Newtonian, incompressible | Blood, Re = 350, 700 (steady), Re = 350, 700, 1400 (unsteady), L = 8 cm, d = 1 cm, La = 4 cm | 24,000 grid points |
| [10] | SEM | 2D, axisymmetric, Newtonian, unsteady, incompressible | Blood, 50 Remax 300 | 228 quadrilateral macro elements |
| [15] | Ansys, FEM, ALE, FSI | 3D, asymmetric, unsteady, laminar, incompressible, non-Newtonian | Blood, Y = 4.66 MPa, Remax = 1950, Reavg = 330 | Structural 76,730 elements |
| [18] | Experiment | 2D, Newtonian | Mixture of sodium salt and distilled aqueous solution of glycerine, Q = 7.09 L/min, Re = 1941 | - |
| [20] | LES | 3D, Newtonian, transition to turbulent | Blood, Re = 1277, 1220, 1186, Re > 2250, d = 2 cm, Q = 120 cm3/s | - |
| [21] | FDM, SOR, ADI | 2D, laminar, unsteady, Newtonian, incompressible | Blood, Re = 100, 300, 500, Pr = 21, 25, Ec = 0.002, 0 Ha 10 | Uniform grid |
| [22] | Experiment, OpenFOAM, FVM, PIMPLE | 3D, laminar, non-Newtonian | Blood, rigid wall, 1634 Re 1954, 10 W0 14.97 | 463,000 polyhedral elements |
| [23] | FEM | 2D, unsteady, laminar, incompressible | Blood, 2.14 Re 535.61, 0.1 Q (cm3/s) 25, 0.001865 We 0.4662 | 5120 quadrilateral elements |
| [24] | Experiment, HLPT | 2D, Newtonian, laminar to turbulent | Water, 410 Re 2650, d = 1.8 cm, L = 140 cm, La = 6.6 cm | - |
| [25] | OpenFOAM, FVM, PIMPLE | 2D, non-Newtonian, unsteady, laminar, incompressible | Blood, Fe3O4 nanoparticles, rigid wall, d = 1.7 cm, Re = 264, Q = 0.8 lit/min, W0 = 12 | 680 × 72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, S.C.; Francis, I.; Saha, G.; Huang, X.; Molla, M.M. Hemodynamic Insights into Abdominal Aortic Aneurysms: Bridging the Knowledge Gap for Improved Patient Care. Fluids 2024, 9, 50. https://doi.org/10.3390/fluids9020050
Saha SC, Francis I, Saha G, Huang X, Molla MM. Hemodynamic Insights into Abdominal Aortic Aneurysms: Bridging the Knowledge Gap for Improved Patient Care. Fluids. 2024; 9(2):50. https://doi.org/10.3390/fluids9020050
Chicago/Turabian StyleSaha, Suvash C., Isabella Francis, Goutam Saha, Xinlei Huang, and Md. Mamun Molla. 2024. "Hemodynamic Insights into Abdominal Aortic Aneurysms: Bridging the Knowledge Gap for Improved Patient Care" Fluids 9, no. 2: 50. https://doi.org/10.3390/fluids9020050
APA StyleSaha, S. C., Francis, I., Saha, G., Huang, X., & Molla, M. M. (2024). Hemodynamic Insights into Abdominal Aortic Aneurysms: Bridging the Knowledge Gap for Improved Patient Care. Fluids, 9(2), 50. https://doi.org/10.3390/fluids9020050











