Application of Deep Learning in Predicting Particle Concentration of Gas–Solid Two-Phase Flow
Abstract
:1. Introduction
2. Materials and Methods
2.1. BPNN
2.1.1. Forward Propagation
2.1.2. Backward Propagation
2.1.3. Advantages and Disadvantages of BPNNs
2.2. RNNs and LSTMs
2.2.1. RNNs
2.2.2. LSTM
- 1.
- Forget gate.
- 2.
- Input gate.
- 3.
- Updating memory state (cell state).
- 4.
- Output gate.
2.2.3. Advantages and Disadvantages of RNNs and LSTM
3. Data Collection and Processing
3.1. Data Collection
- 1.
- KZWSRS485 temperature and humidity transmitter.
- 2.
- KZY-808BGA pressure difference sensor.
- 3.
- Electrostatic sensor.
- 4.
- APS3005S-3D power supply unit.
- 5.
- GDM-842 digital multimeter.
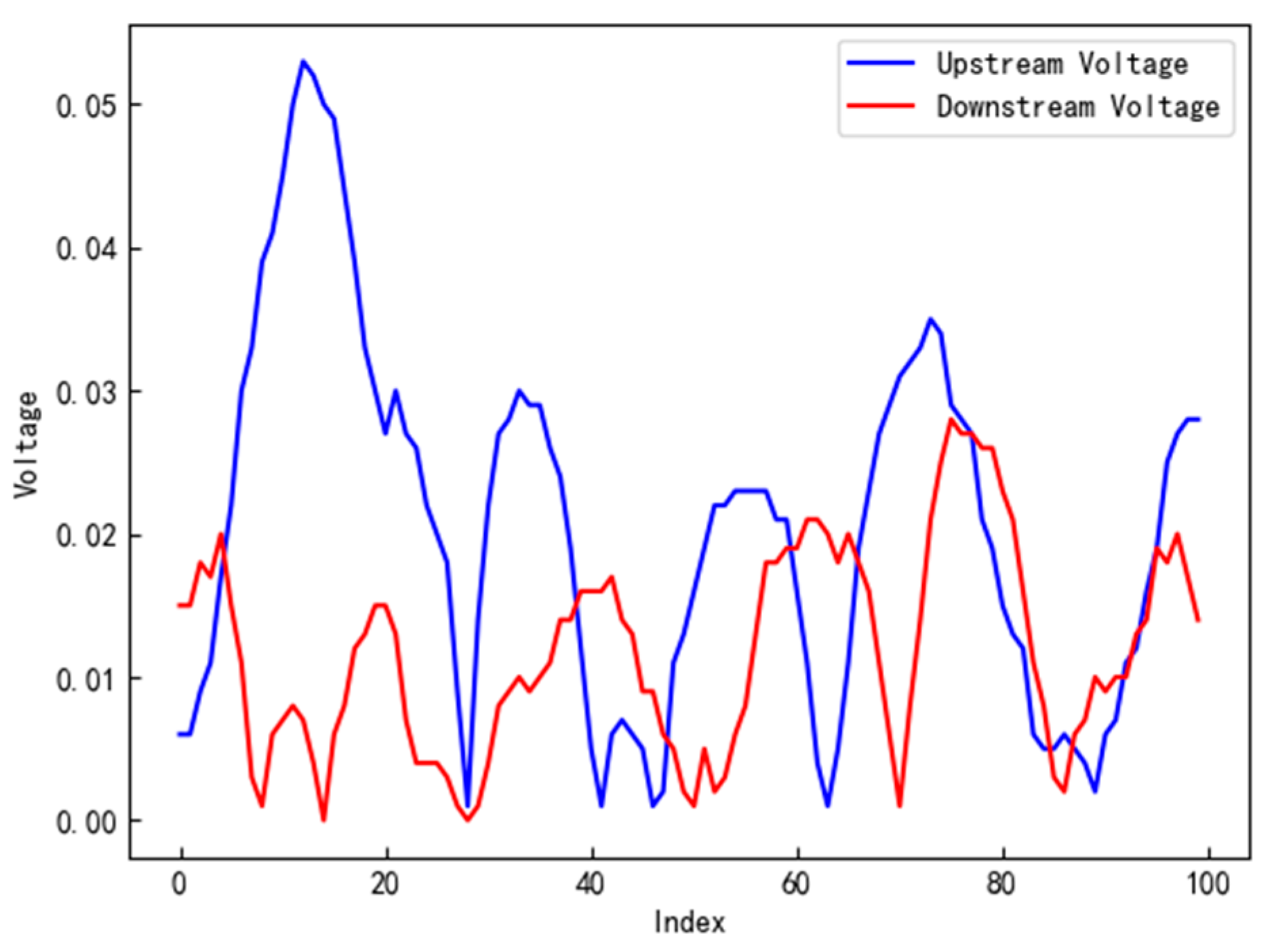
3.2. Calculation of Particle Velocity and Particle Concentration
3.3. Normalization of Model Data
4. Results
4.1. Experimental Preparation and Environment Configuration
4.2. Model Evaluation Metrics
4.3. Model Construction and Parameter Determination
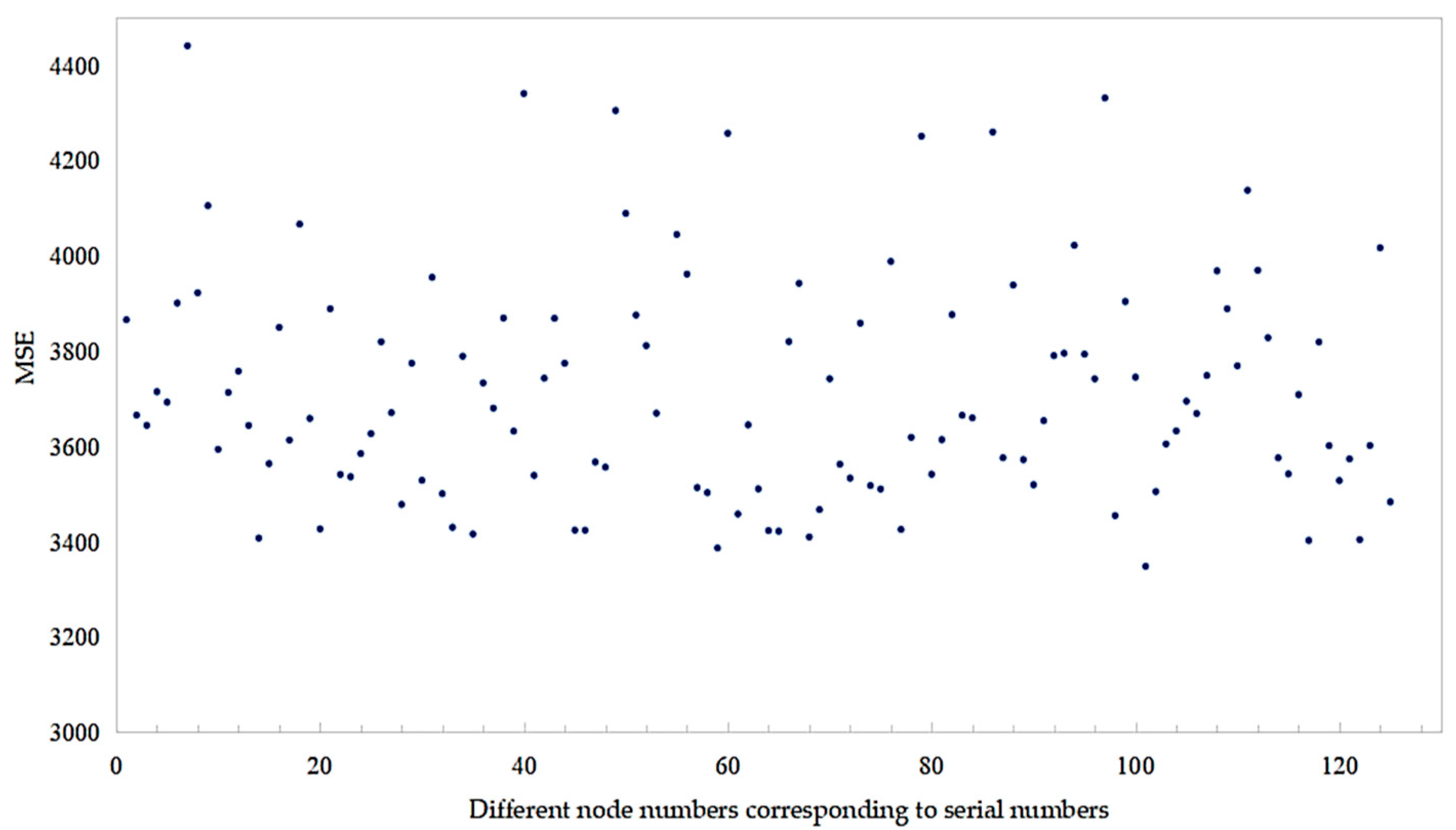
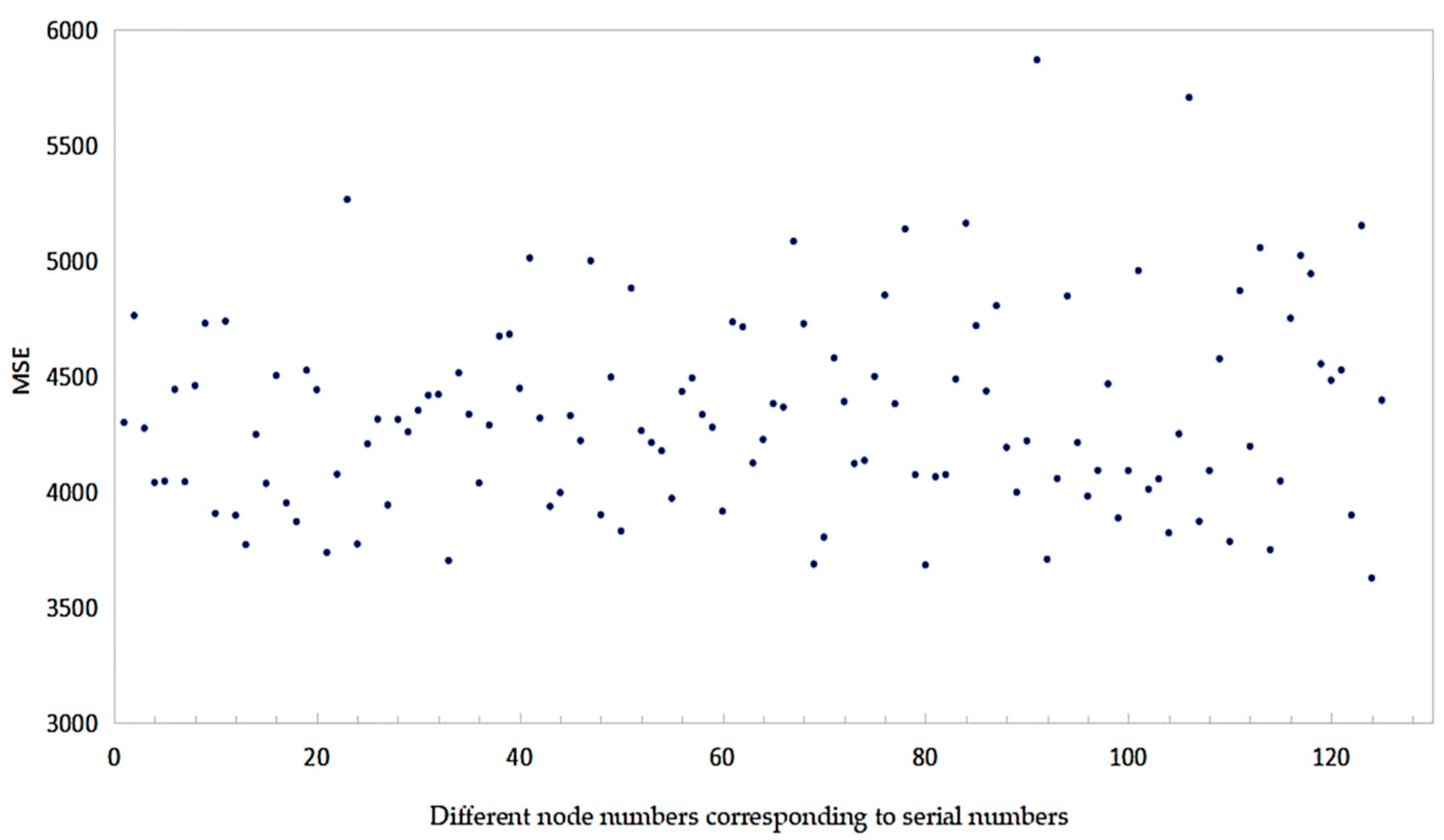
4.4. Results
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Lyu, X.; Li, W.; Yao, G.; Bai, J.; Bao, A. Investigation on Measurement of Size and Concentration of Solid Phase Particles in Gas-Solid Two Phase Flow. Chin. J. Electron. 2018, 27, 381–385. [Google Scholar] [CrossRef]
- Datta, U.; Dyakowski, T.; Mylvaganam, S. Estimation of Particulate Velocity Components in Pneumatic Transport Using Pixel Based Correlation with Dual Plane ECT. Chem. Eng. J. 2007, 130, 87–99. [Google Scholar] [CrossRef]
- Coghill, P.J. Particle Size of Pneumatically Conveyed Powders Measured Using Impact Duration. Part. Part. Syst. Charact. 2007, 24, 464–469. [Google Scholar] [CrossRef]
- Yan, F.; Rinoshika, A. Application of High-Speed PIV and Image Processing to Measuring Particle Velocity and Concentration in a Horizontal Pneumatic Conveying with Dune Model. Powder Technol. 2011, 208, 158–165. [Google Scholar] [CrossRef]
- Baer, C.; Jaeschke, T.; Mertmann, P.; Pohl, N.; Musch, T. A mmWave Measuring Procedure for Mass Flow Monitoring of Pneumatic Conveyed Bulk Materials. IEEE Sens. J. 2014, 14, 3201–3209. [Google Scholar] [CrossRef]
- Qian, X.; Huang, X.; Yonghui, H.; Yan, Y. Pulverized Coal Flow Metering on a Full-Scale Power Plant Using Electrostatic Sensor Arrays. Flow Meas. Instrum. 2014, 40, 185–191. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J.; Zheng, W.; Gao, W.; Jia, L. Signal Decoupling and Analysis from Inner Flush-Mounted Electrostatic Sensor for Detecting Pneumatic Conveying Particles. Powder Technol. 2017, 305, 197–205. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, C.; Wang, H. Hilbert–Huang Transform-Based Electrostatic Signal Analysis of Ring-Shape Electrodes With Different Widths. IEEE Trans. Instrum. Meas. 2012, 61, 1209–1217. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, R.; Yan, B.; Abdalla, M. Improvement of Spatial Sensitivity of an Electrostatic Sensor for Particle Flow Measurement. Flow Meas. Instrum. 2020, 72, 101713. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, R.; Yan, B.; Abdalla, M. Reweighting Signal Spectra to Improve Spatial Sensitivity for an Electrostatic Sensor. Sensors 2019, 19, 4963. [Google Scholar] [CrossRef] [PubMed]
- Shao, J.; Yan, Y.; Lv, Z. On-Line Non-Intrusive Measurements of the Velocity and Particle Size Distribution of Pulverised Fuel on a Full Scale Power Plant. In Proceedings of the 2011 IEEE International Instrumentation and Measurement Technology Conference, Hangzhou, China, 10–12 May 2011; pp. 1–5. [Google Scholar]
- Wang, C.; Zhan, N.; Zhang, J. Induced and Transferred Charge Signals Decoupling Based on Discrete Wavelet Transform for Dilute Gas-Solid Two-Phase Flow Measurement. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; pp. 1–6. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G.E. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Yu, K.; Jin, K.; Deng, X. Review of Deep Reinforcement Learning. In Proceedings of the 2022 IEEE 5th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 16–18 December 2022; Volume 5, pp. 41–48. [Google Scholar]
- Kawaguchi, K.; Kaelbling, L.P.; Bengio, Y. Generalization in Deep Learning; Cambridge University Press: Cambridge, UK, 2022; pp. 112–148. [Google Scholar]
- Yan, B.; Zhang, J.; Cheng, R.; Liu, C. Modelling of A Flow Meter through Machine Learning. In Proceedings of the 2020 IEEE SENSORS, Rotterdam, The Netherlands, 25–28 October 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Basheer, I.A.; Hajmeer, M. Artificial Neural Networks: Fundamentals, Computing, Design, and Application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, N.; Wu, L.; Wang, Y. Wind Speed Forecasting Based on the Hybrid Ensemble Empirical Mode Decomposition and GA-BP Neural Network Method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems 27: Annual Conference on Neural Information Processing Systems 2014, Montreal, QC, Canada, 8–13 December 2014; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2014; pp. 3104–3112. [Google Scholar]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. In Proceedings of the 1999 Ninth International Conference on Artificial Neural Networks ICANN 99. (Conf. Publ. No. 470), Edinburgh, UK, 7–10 September 1999; Volume 2, pp. 850–855. [Google Scholar]
- Zhang, Y.; Tang, J.; Liao, R.; Zhang, M.; Zhang, Y.; Wang, X.; Su, Z. Application of an Enhanced BP Neural Network Model with Water Cycle Algorithm on Landslide Prediction. Stoch. Environ. Res. Risk Assess. 2021, 35, 1273–1291. [Google Scholar] [CrossRef]





| Parameter | BPNN | RNN | LSTM |
|---|---|---|---|
| Number of Hidden Layers | 3 | 3 | 3 |
| Number of Units per Layer | 80, 60, 50 | 80, 40, 40 | 80, 80, 70 |
| Maximum Number of Iterations | 500 | 500 | 500 |
| Training Batch Size | 32 | 32 | 32 |
| Prediction Model | AF | RMSE | RMAE |
|---|---|---|---|
| BPNN | 92.5 | 52.22 | 37.45 |
| RNN | 92.4 | 53.19 | 38.88 |
| LSTM | 92.7 | 53.43 | 38.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yan, B.; Wang, H. Application of Deep Learning in Predicting Particle Concentration of Gas–Solid Two-Phase Flow. Fluids 2024, 9, 59. https://doi.org/10.3390/fluids9030059
Wang Z, Yan B, Wang H. Application of Deep Learning in Predicting Particle Concentration of Gas–Solid Two-Phase Flow. Fluids. 2024; 9(3):59. https://doi.org/10.3390/fluids9030059
Chicago/Turabian StyleWang, Zhiyong, Bing Yan, and Haoquan Wang. 2024. "Application of Deep Learning in Predicting Particle Concentration of Gas–Solid Two-Phase Flow" Fluids 9, no. 3: 59. https://doi.org/10.3390/fluids9030059
APA StyleWang, Z., Yan, B., & Wang, H. (2024). Application of Deep Learning in Predicting Particle Concentration of Gas–Solid Two-Phase Flow. Fluids, 9(3), 59. https://doi.org/10.3390/fluids9030059






