Numerical Study of Rarefied Gas Flow in Diverging Channels of Finite Length at Various Pressure Ratios
Abstract
1. Introduction
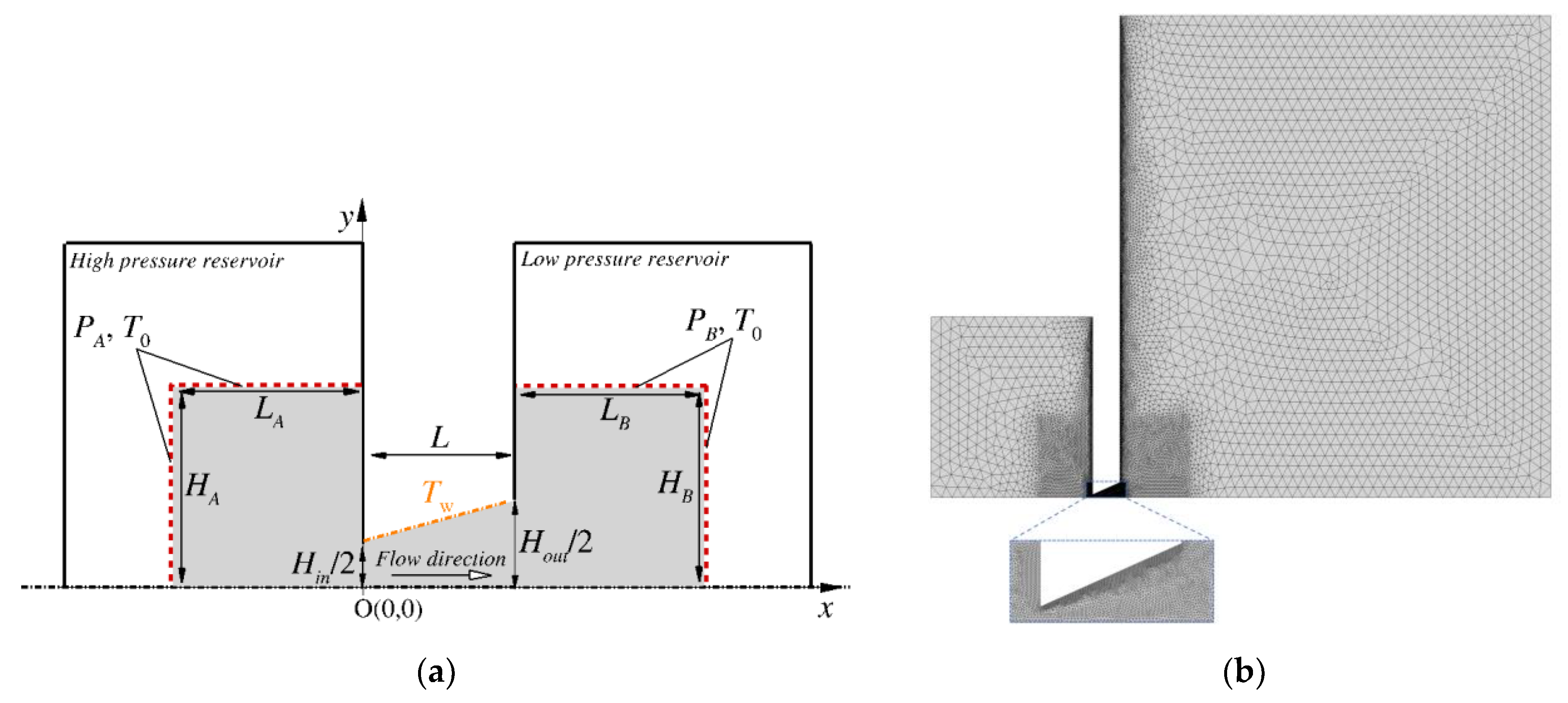
2. Flow Configuration
- The reference rarefaction parameter , defined aswhere is the gas viscosity at the reference temperature . The rarefaction parameter is proportional to the inverse Knudsen number;
- The dimensionless channel length ;
- The ratio of channel height at the two channel ends ;
- The pressure ratio ;
- The temperature ratio .
3. Kinetic Approaches
3.1. Complete 4D Kinetic Solution
3.2. Approximate Kinetic Approach
4. Results and Discussion
4.1. Isothermal Case
4.2. Non-Isothermal Case—Effect of the Wall Temperature
5. Conclusions
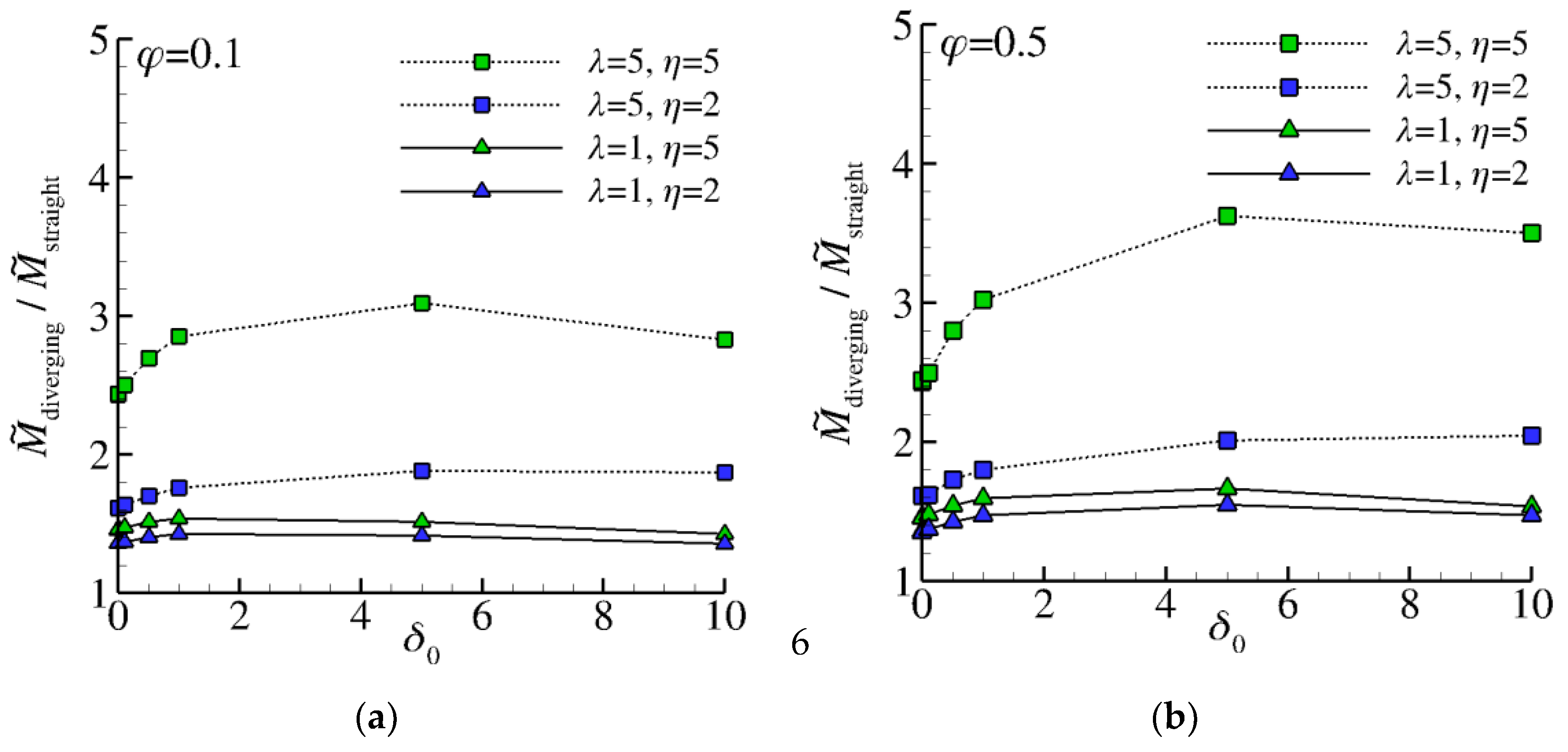
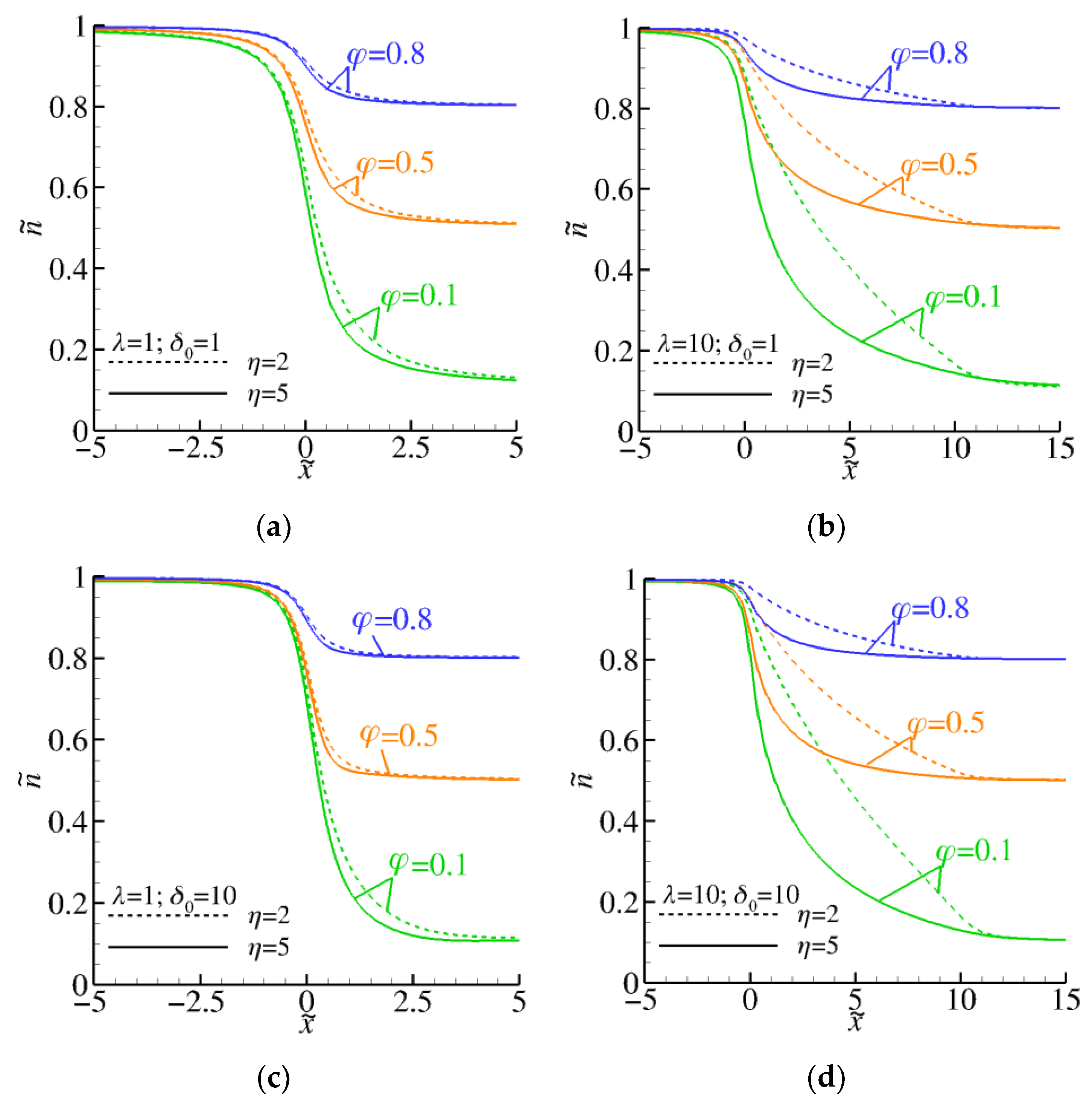
- The effect of the geometry parameters, namely dimensionless length and the aspect ratio on , remains quantitatively significant over the entire range of the pressure ratio .
- The values of the dimensionless mass flow rates in the diverging channel flows are significantly higher compared to the corresponding ones in the straight channel flows, not only for large pressure drops but also for small pressure drops. For channels with and , at least an increase between 1.5 and 3 times can be expected in the transition flow regime.
- This study confirms the existence of a shallow Knudsen minimum for all values of the pressure ratio in the case of long channels () with small values of the aspect ratio . No Knudsen minimum is observed for , even for the longest examined channel case with
- Attention should be paid to the use of the approximate kinetic approach (Section 3.2), which makes use of the fully developed flow data when flows through diverging channels are considered. Although the accuracy of the approximate kinetic approach improves as the pressure drop decreases, the deviations compared to the complete flow solution (Section 3.1) remain high even for relatively long channels with . However, the present analysis shows that by applying the end-effect correction lengths of the straight channel flow, the validity range of the approximate kinetic approach is improved significantly. More specifically, the application of the approximate kinetic approach coupled with the end-effect correction approach results in a maximum deviation of less than 10% when and .
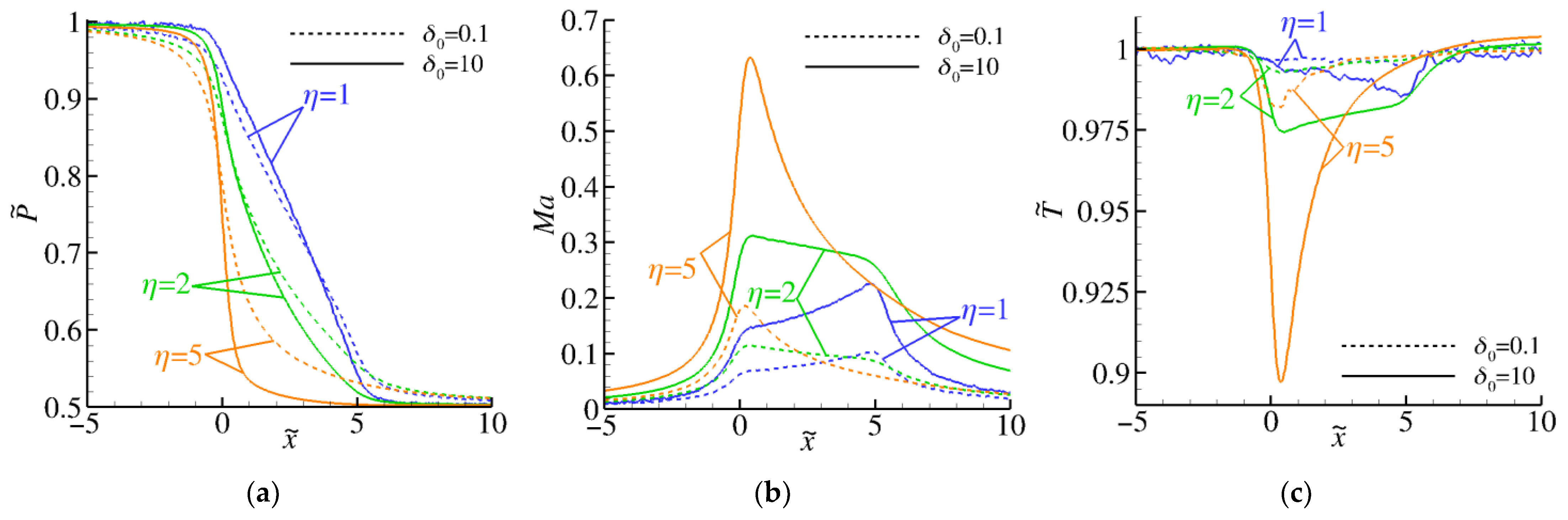
- The diverging channel geometry has a significant effect on the distributions of the macroscopic quantities. The analysis shows that an increase in the aspect ratio of the channel causes a drop of the pressure (and density) in the channel not only for flows under large pressure drops but also for small ones. In addition, depending on the pressure ratio, the velocity distributions may differ, not only quantitatively but also qualitatively, compared to the corresponding ones reported in the literature for straight channel flows.
- The influence of the wall temperature on the mass flow rate is observed to be strong in less-rarefied cases, with the mass flow rate being a decreasing function of the temperature ratio , while this influence is reduced as the channel aspect ratio increases. In the highly rarefied cases, the influence was noticeably smaller.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cercignani, C. The Boltzmann Equation: Some Mathematical Aspects. In Kinetic Theory and Gas Dynamics; Cercignani, C., Ed.; International Centre for Mechanical Sciences; Springer: Vienna, Austria, 1988; pp. 1–36. ISBN 978-3-7091-2762-9. [Google Scholar]
- Bird, G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Oxford Engineering Science Series; Clarendon Press: Oxford, UK; Oxford University Press: Oxford, NY, USA, 1994; ISBN 978-0-19-856195-8. [Google Scholar]
- Sharipov, F. Rarefied Gas Dynamics: Fundamentals for Research and Practice; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2016; ISBN 978-3-527-68553-0. [Google Scholar]
- Varoutis, S.; Hauer, V.; Day, C.; Pantazis, S.; Valougeorgis, D. Experimental and Numerical Investigation in Flow Configurations Related to the Vacuum Systems of Fusion Reactors. Fusion Eng. Des. 2010, 85, 1798–1802. [Google Scholar] [CrossRef]
- Varoutis, S.; Valougeorgis, D.; Sazhin, O.; Sharipov, F. Rarefied Gas Flow through Short Tubes into Vacuum. J. Vac. Sci. Technol. A 2008, 26, 228–238. [Google Scholar] [CrossRef]
- Sharipov, F.; Kozak, D.V. Rarefied Gas Flow through a Thin Slit into Vacuum Simulated by the Monte Carlo Method over the Whole Range of the Knudsen Number. J. Vac. Sci. Technol. Vac. Surf. Films 2009, 27, 479–484. [Google Scholar] [CrossRef]
- Graur, I.; Polikarpov, A.P.; Sharipov, F. Numerical Modeling of Rarefied Gas Flow through a Slit into Vacuum Based on the Kinetic Equation. Comput. Fluids 2011, 49, 87–92. [Google Scholar] [CrossRef]
- Sharipov, F.; Seleznev, V. Data on Internal Rarefied Gas Flows. J. Phys. Chem. Ref. Data 1998, 27, 657–706. [Google Scholar] [CrossRef]
- Graur, I.; Sharipov, F. Gas Flow through an Elliptical Tube over the Whole Range of the Gas Rarefaction. Eur. J. Mech.-B/Fluids 2008, 27, 335–345. [Google Scholar] [CrossRef]
- Breyiannis, G.; Varoutis, S.; Valougeorgis, D. Rarefied Gas Flow in Concentric Annular Tube: Estimation of the Poiseuille Number and the Exact Hydraulic Diameter. Eur. J. Mech.-B/Fluids 2008, 27, 609–622. [Google Scholar] [CrossRef]
- Varoutis, S.; Naris, S.; Hauer, V.; Day, C.; Valougeorgis, D. Computational and Experimental Study of Gas Flows through Long Channels of Various Cross Sections in the Whole Range of the Knudsen Number. J. Vac. Sci. Technol. Vac. Surf. Films 2009, 27, 89–100. [Google Scholar] [CrossRef]
- Cervone, A.; Mancas, A.; Zandbergen, B. Conceptual Design of a Low-Pressure Micro-Resistojet Based on a Sublimating Solid Propellant. Acta Acta Astronaut. 2015, 108, 30–39. [Google Scholar] [CrossRef]
- Alexeenko, A.A.; Fedosov, D.A.; Gimelshein, S.F.; Levin, D.A.; Collins, R.J. Transient Heat Transfer and Gas Flow in a MEMS-Based Thruster. J. Microelectromech. Syst. 2006, 15, 181–194. [Google Scholar] [CrossRef]
- Markelov, G.N. Numerical Study of 2D/3D Micronozzle Flows. AIP Conf. Proc. 2001, 585, 539–546. [Google Scholar] [CrossRef]
- Zuppardi, G.; Esposito, A. Aerodynamic Characterization of the Jet of an Arc Wind Tunnel. AIP Conf. Proc. 2016, 1786, 190003. [Google Scholar] [CrossRef]
- Tatsios, G.; Lopez Quesada, G.; Rojas-Cardenas, M.; Baldas, L.; Colin, S.; Valougeorgis, D. Computational Investigation and Parametrization of the Pumping Effect in Temperature-Driven Flows through Long Tapered Channels. Microfluid. Nanofluid. 2017, 21, 99. [Google Scholar] [CrossRef]
- Wang, X.; Su, T.; Zhang, W.; Zhang, Z.; Zhang, S. Knudsen Pumps: A Review. Microsyst. Nanoeng. 2020, 6, 26. [Google Scholar] [CrossRef] [PubMed]
- Sazhin, O.; Sazhin, A. Rarefied Gas Flow into Vacuum through Linearly Diverging and Converging Channels. Int. J. Heat Mass Transf. 2023, 203, 123842. [Google Scholar] [CrossRef]
- Darbandi, M.; Roohi, E. Study of Subsonic–Supersonic Gas Flow through Micro/Nanoscale Nozzles Using Unstructured DSMC Solver. Microfluid. Nanofluid. 2011, 10, 321–335. [Google Scholar] [CrossRef]
- Saadati, S.A.; Roohi, E. Detailed Investigation of Flow and Thermal Field in Micro/Nano Nozzles Using Simplified Bernoulli Trial (SBT) Collision Scheme in DSMC. Aerosp. Sci. Technol. 2015, 46, 236–255. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Roohi, E. DSMC Investigation of Rarefied Gas Flow through Diverging Micro- and Nanochannels. Microfluid. Nanofluid. 2017, 21, 18. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Shahabi, V.; Roohi, E. Pressure-Driven Nitrogen Flow in Divergent Microchannels with Isothermal Walls. Appl. Sci. 2021, 11, 3602. [Google Scholar] [CrossRef]
- Tatsios, G.; Valougeorgis, D.; Stefanov, S.K. Reconsideration of the Implicit Boundary Conditions in Pressure Driven Rarefied Gas Flows through Capillaries. Vacuum 2019, 160, 114–122. [Google Scholar] [CrossRef]
- Titarev, V.A.; Shakhov, E.M.; Utyuzhnikov, S.V. Rarefied Gas Flow through a Diverging Conical Pipe into Vacuum. Vacuum 2014, 101, 10–17. [Google Scholar] [CrossRef]
- Yakunchikov, A.; Kosyanchuk, V. Application of Event-Driven Molecular Dynamics Approach to Rarefied Gas Dynamics Problems. Comput. Fluids 2018, 170, 121–127. [Google Scholar] [CrossRef]
- Graur, I.; Ho, M.T. Rarefied Gas Flow through a Long Rectangular Channel of Variable Cross Section. Vacuum 2014, 101, 328–332. [Google Scholar] [CrossRef]
- Zhang, M.; Day, C.; Varoutis, S.; Cai, G. Rarefied Gas Flow into Vacuum through Short Tubes at Variable Wall Temperatures. J. Vac. Sci. Technol. A 2017, 35, 021604. [Google Scholar] [CrossRef]
- Varoutis, S.; Day, C.; Sharipov, F. Rarefied Gas Flow through Channels of Finite Length at Various Pressure Ratios. Vacuum 2012, 86, 1952–1959. [Google Scholar] [CrossRef]
- Shakhov, E.M. Generalization of the Krook Kinetic Relaxation Equation. Fluid Dyn. 1968, 3, 95–96. [Google Scholar] [CrossRef]
- Titarev, V.A.; Shakhov, E.M. Kinetic Analysis of the Isothermal Flow in a Long Rectangular Microchannel. Comput. Math. Math. Phys. 2010, 50, 1221–1237. [Google Scholar] [CrossRef]
- Polikarpov, A.P.; Graur, I. Unsteady Rarefied Gas Flow through a Slit. Vacuum 2014, 101, 79–85. [Google Scholar] [CrossRef]
- Pan, D.; Zhong, C.; Zhuo, C. An Implicit Discrete Unified Gas-Kinetic Scheme for Simulations of Steady Flow in All Flow Regimes. Commun. Comput. Phys. 2019, 25, 1469–1495. [Google Scholar] [CrossRef]
- Tantos, C.; Teichmann, T.; Sarris, I.; Day, C. Extensive Analysis of the Applicability Range of the Linear Kinetic Approaches in the Case of the Pressure Driven Gas Mixture Flows. Phys. Fluids 2024, 36, 012009. [Google Scholar] [CrossRef]
- Sharipov, F. Rarefied Gas Flow through a Long Tube at Any Temperature Ratio. J. Vac. Sci. Technol. A 1996, 14, 2627–2635. [Google Scholar] [CrossRef]
- Sharipov, F. Non-Isothermal Rarefied Gas Flow through a Slit. Phys. Fluids 1997, 9, 1804–1810. [Google Scholar] [CrossRef]
- Titarev, V.A.; Shakhov, E.M. Nonisothermal Gas Flow in a Long Channel Analyzed on the Basis of the Kinetic S-Model. Comput. Math. Math. Phys. 2010, 50, 2131–2144. [Google Scholar] [CrossRef]
- Titarev, V.A.; Shakhov, E.M. Efficient Method for Computing Rarefied Gas Flow in a Long Finite Plane Channel. Comput. Math. Math. Phys. 2012, 52, 269–284. [Google Scholar] [CrossRef]
- Pantazis, S.; Naris, S.; Tantos, C.; Valougeorgis, D.; André, J.; Millet, F.; Perin, J.P. Nonlinear Vacuum Gas Flow through a Short Tube Due to Pressure and Temperature Gradients. Fusion Eng. Des. 2013, 88, 2384–2387. [Google Scholar] [CrossRef]
- Titarev, V.A.; Shakhov, E.M.; Frolova, A.A. Shock Wave Reflection from a Short Orifice Open to Vacuum. Vacuum 2019, 161, 232–241. [Google Scholar] [CrossRef]
- Zhu, L.; Guo, Z. Application of Discrete Unified Gas Kinetic Scheme to Thermally Induced Nonequilibrium Flows. Comput. Fluids 2019, 193, 103613. [Google Scholar] [CrossRef]
- Tantos, C. Polyatomic Thermal Creep Flows through Long Microchannels at Large Temperature Ratios. J. Vac. Sci. Technol. A 2019, 37, 051602. [Google Scholar] [CrossRef]
- Rojas-Cárdenas, M.; Graur, I.; Perrier, P.; Méolans, J.G. Time-Dependent Experimental Analysis of a Thermal Transpiration Rarefied Gas Flow. Phys. Fluids 2013, 25, 072001. [Google Scholar] [CrossRef]
- Sharipov, F.; Bertoldo, G. Heat Transfer through a Rarefied Gas Confined between Two Coaxial Cylinders with High Radius Ratio. J. Vac. Sci. Technol. A 2006, 24, 2087–2093. [Google Scholar] [CrossRef]
- Li, Z.-H.; Zhang, H.-X. Gas-Kinetic Description of Shock Wave Structures by Solving Boltzmann Model Equation. Int. J. Comput. Fluid Dyn. 2008, 22, 623–638. [Google Scholar] [CrossRef]
- Khan, M.A.; Jobic, Y.; Graur, I.; Hadj-Nacer, M.; Zampella, C.; Greiner, M. Experimentally-Benchmarked Kinetic Simulations of Heat Transfer through Rarefied Gas with Constant Heat Flux at the Boundary. Int. J. Heat Mass Transf. 2021, 176, 121378. [Google Scholar] [CrossRef]
- Bond, D.M.; Macrossan, M.N.; Wheatley, V. Comparison of Discrete BGK-Shakhov System with DSMC. AIP Conf. Proc. 2012, 1501, 350–357. [Google Scholar] [CrossRef]
- Aristov, V.V.; Shakhov, E.M.; Titarev, V.A.; Zabelok, S.A. Comparative Study for Rarefied Gas Flow into Vacuum through a Short Circular Pipe. Vacuum 2014, 103, 5–8. [Google Scholar] [CrossRef]
- Tatsios, G.; Vargas, M.H.; Stefanov, S.K.; Valougeorgis, D. Nonequilibrium Gas Flow and Heat Transfer in a Heated Square Microcavity. Heat Transf. Eng. 2016, 37, 1085–1095. [Google Scholar] [CrossRef]
- Titarev, V.A.; Frolova, A.A.; Rykov, V.A.; Vashchenkov, P.V.; Shevyrin, A.A.; Bondar, Y.A. Comparison of the Shakhov Kinetic Equation and DSMC Method as Applied to Space Vehicle Aerothermodynamics. J. Comput. Appl. Math. 2020, 364, 112354. [Google Scholar] [CrossRef]
- Misdanitis, S.; Pantazis, S.; Valougeorgis, D. Pressure Driven Rarefied Gas Flow through a Slit and an Orifice. Vacuum 2012, 86, 1701–1708. [Google Scholar] [CrossRef]
- Tantos, C.; Varoutis, S.; Day, C. Deterministic and Stochastic Modeling of Rarefied Gas Flows in Fusion Particle Exhaust Systems. J. Vac. Sci. Technol. B 2020, 38, 064201. [Google Scholar] [CrossRef]
- Tantos, C.; Valougeorgis, D. Conductive Heat Transfer in Rarefied Binary Gas Mixtures Confined between Parallel Plates Based on Kinetic Modeling. Int. J. Heat Mass Transf. 2018, 117, 846–860. [Google Scholar] [CrossRef]
- Tantos, C. Steady Planar Couette Flow of Rarefied Binary Gaseous Mixture Based on Kinetic Modeling. Eur. J. Mech.-B/Fluids 2019, 76, 375–389. [Google Scholar] [CrossRef]
- Yang, W.; Gu, X.-J.; Emerson, D.R.; Zhang, Y.; Tang, S. Modelling Thermally Induced Non-Equilibrium Gas Flows by Coupling Kinetic and Extended Thermodynamic Methods. Entropy 2019, 21, 816. [Google Scholar] [CrossRef]
- Ho, M.T.; Li, J.; Wu, L.; Reese, J.M.; Zhang, Y. A Comparative Study of the DSBGK and DVM Methods for Low-Speed Rarefied Gas Flows. Comput. Fluids 2019, 181, 143–159. [Google Scholar] [CrossRef]
- Li, J. Simulation Methods for Rarefied Gas Flows. In Multiscale and Multiphysics Flow Simulations of Using the Boltzmann Equation: Applications to Porous Media and MEMS; Li, J., Ed.; Springer International Publishing: Cham, Switzerland, 2020; pp. 67–117. ISBN 978-3-030-26466-6. [Google Scholar]
- Liu, Z.J.; Shu, C.; Chen, S.Y.; Yang, L.M.; Wan, M.P.; Liu, W. A Novel Solver for Simulation of Flows from Continuum Regime to Rarefied Regime at Moderate Knudsen Number. J. Comput. Phys. 2020, 415, 109548. [Google Scholar] [CrossRef]
- Polikarpov, A.; Graur, I.; Sharipov, F. Sublimation and Deposition in Gaseous Mixtures. Int. J. Heat Mass Transf. 2020, 160, 120213. [Google Scholar] [CrossRef]
- Voronich, I.V.; Titarev, V.A. Numerical Analysis of Rarefied Gas Flow through a System of Short Channels. Comput. Math. Math. Phys. 2023, 63, 2227–2243. [Google Scholar] [CrossRef]
- Basdanis, T.; Valougeorgis, D.; Sharipov, F. Viscous and Thermal Velocity Slip Coefficients via the Linearized Boltzmann Equation with Ab Initio Potential. Microfluid. Nanofluid. 2023, 27, 75. [Google Scholar] [CrossRef]
- Guo, Z.; Xu, K.; Wang, R. Discrete Unified Gas Kinetic Scheme for All Knudsen Number Flows: Low-Speed Isothermal Case. Phys. Rev. E 2013, 88, 033305. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Wang, R.; Xu, K. Discrete Unified Gas Kinetic Scheme for All Knudsen Number Flows. II. Thermal Compressible Case. Phys. Rev. E 2015, 91, 033313. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhu, L.; Wang, R.; Guo, Z. Discrete Unified Gas Kinetic Scheme for All Knudsen Number Flows. III. Binary Gas Mixtures of Maxwell Molecules. Phys. Rev. E 2018, 97, 053306. [Google Scholar] [CrossRef] [PubMed]
- SALOME PLATFORM-The Open-Source Platform for Numerical Simulation. Available online: https://www.salome-platform.org/ (accessed on 17 January 2024).
- Sharipov, F. Rarefied Gas Flow through a Long Tube at Arbitrary Pressure and Temperature Drops. J. Vac. Sci. Technol. A 1997, 15, 2434–2436. [Google Scholar] [CrossRef]
- Sharipov, F.; Bertoldo, G. Rarefied Gas Flow through a Long Tube of Variable Radius. J. Vac. Sci. Technol. A 2005, 23, 531–533. [Google Scholar] [CrossRef]
- Tantos, C.; Kritikos, E.; Varoutis, S.; Day, C. Kinetic Modeling of Polyatomic Heat and Mass Transfer in Rectangular Microchannels. Heat Mass Transf. 2023, 59, 167–184. [Google Scholar] [CrossRef]
- Pantazis, S.; Valougeorgis, D.; Sharipov, F. End Corrections for Rarefied Gas Flows through Capillaries of Finite Length. Vacuum 2013, 97, 26–29. [Google Scholar] [CrossRef]
- Graur, I.A.; Polikarpov, A.P.; Sharipov, F. Numerical Modelling of Rarefied Gas Flow through a Slit at Arbitrary Pressure Ratio Based on the Kinetic Equation. Z. Angew. Math. Phys. 2012, 63, 503–520. [Google Scholar] [CrossRef]
- Kestin, J.; Knierim, K.; Mason, E.A.; Najafi, B.; Ro, S.T.; Waldman, M. Equilibrium and Transport Properties of the Noble Gases and Their Mixtures at Low Density. J. Phys. Chem. Ref. Data 1984, 13, 229–303. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Y.; Zeng, J.; Wu, L. Further Acceleration of Multiscale Simulation of Rarefied Gas Flow via a Generalized Boundary Treatment. J. Comput. Phys. 2024, 503, 112830. [Google Scholar] [CrossRef]

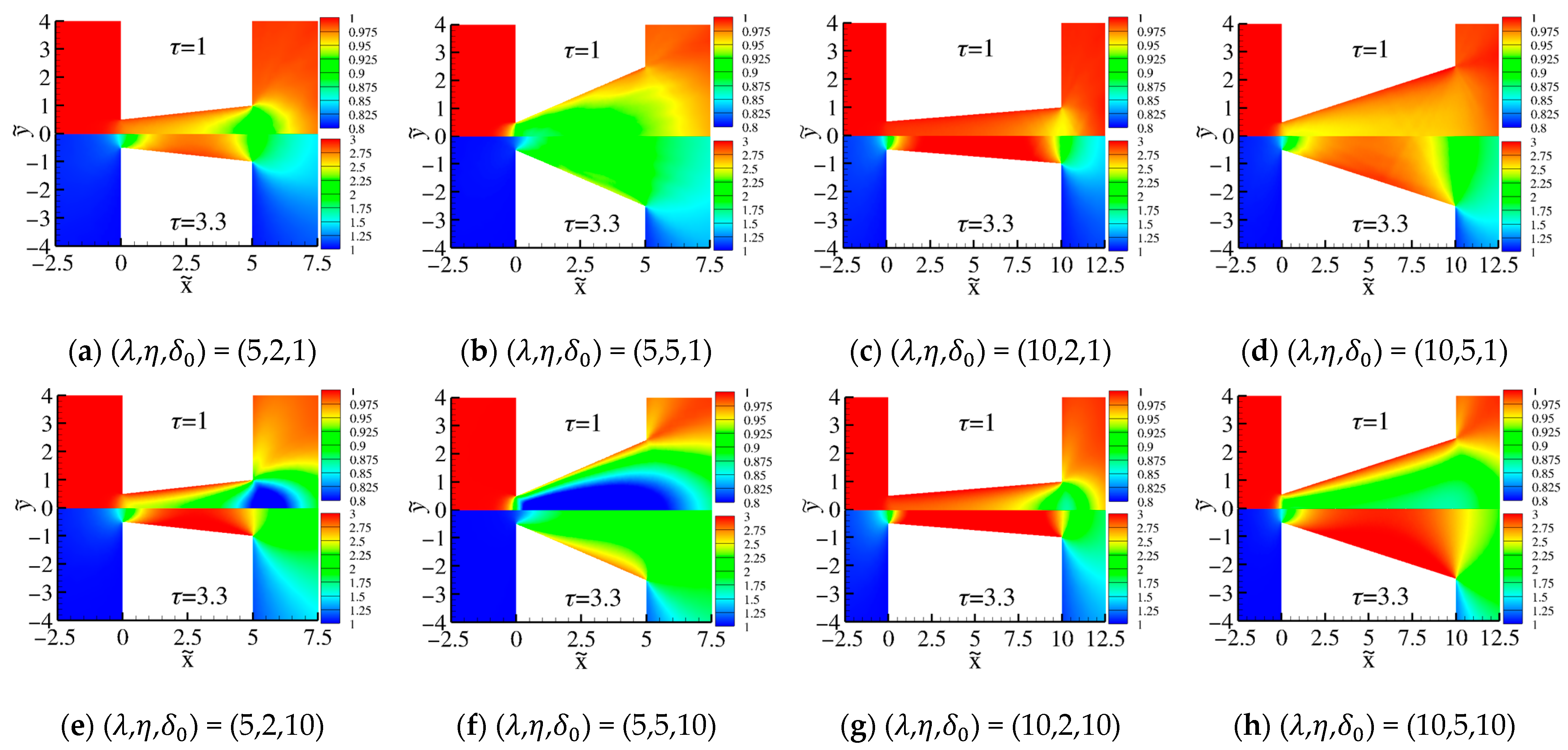
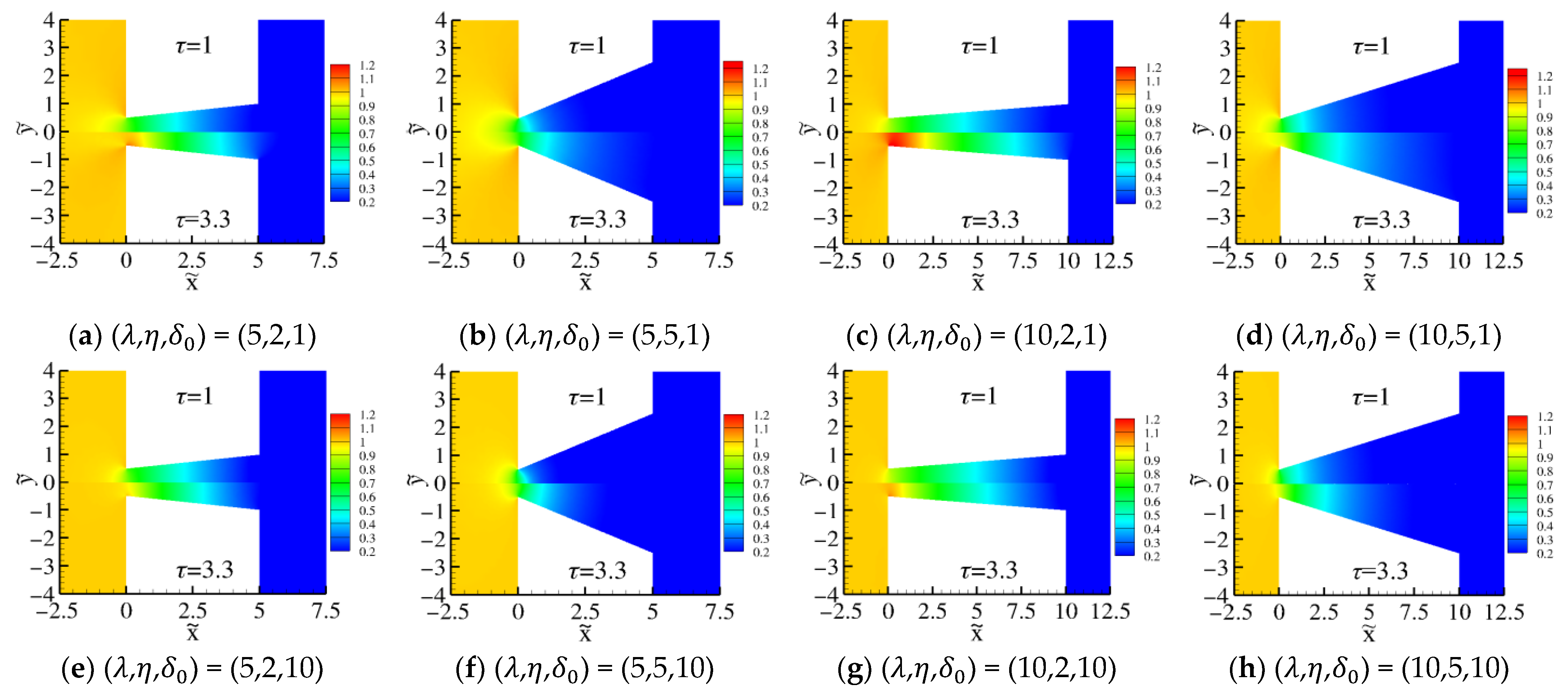

| ) | ) | ) | ||||
|---|---|---|---|---|---|---|
| [28] | Present Work | [28] | Present Work | [18] | Present Work | |
| 0.1 | 0.630 | 0.630 (0.0%) | 0.354 | 0.354 (0.0%) | 0.951 | 0.946 (0.53%) |
| 1 | 0.706 | 0.716 (1.4%) | 0.419 | 0.428 (2.1%) | 1.06 | 1.04 (0.94%) |
| 10 | 1.03 | 1.02 (0.97%) | 0.832 | 0.838 (0.72%) | 1.39 | 1.39 (0.0%) |
| [26] | Present Work | ||
|---|---|---|---|
| 0.1 | 0.1 | 18.3 | 18.4 (0.55%) |
| 1 | 13.9 | 14.0 (0.72%) | |
| 10 | 25.0 | 25.0 (0.0%) | |
| 0.5 | 0.1 | 9.45 | 9.52 (0.74%) |
| 1 | 7.95 | 7.98 (0.38%) | |
| 10 | 17.4 | 17.4 (0.0%) | |
| 0.9 | 0.1 | 1.82 | 1.84 (1.10%) |
| 1 | 1.66 | 1.66 (0.0%) | |
| 10 | 4.14 | 4.15 (0.24%) |
| 0.1 | 0.5 | 0.8 | |||
|---|---|---|---|---|---|
| 1 | 2 | 0 | 0.837 | 0.465 | 0.186 |
| 0.1 | 0.862 | 0.486 | 0.196 | ||
| 0.5 | 0.936 | 0.551 | 0.227 | ||
| 1 | 1.00 | 0.617 | 0.260 | ||
| 5 | 1.28 | 0.983 | 0.470 | ||
| 10 | 1.40 | 1.23 | 0.685 | ||
| 5 | 0 | 0.898 | 0.499 | 0.199 | |
| 0.1 | 0.927 | 0.523 | 0.211 | ||
| 0.5 | 1.01 | 0.595 | 0.246 | ||
| 1 | 1.08 | 0.668 | 0.282 | ||
| 5 | 1.36 | 1.06 | 0.519 | ||
| 10 | 1.47 | 1.28 | 0.748 | ||
| 5 | 2 | 0 | 0.517 | 0.287 | 0.115 |
| 0.1 | 0.525 | 0.293 | 0.118 | ||
| 0.5 | 0.548 | 0.313 | 0.127 | ||
| 1 | 0.571 | 0.335 | 0.138 | ||
| 5 | 0.733 | 0.497 | 0.220 | ||
| 10 | 0.893 | 0.680 | 0.322 | ||
| 5 | 0 | 0.780 | 0.433 | 0.174 | |
| 0.1 | 0.802 | 0.452 | 0.182 | ||
| 0.5 | 0.867 | 0.507 | 0.208 | ||
| 1 | 0.928 | 0.562 | 0.235 | ||
| 5 | 1.20 | 0.896 | 0.419 | ||
| 10 | 1.35 | 1.16 | 0.619 | ||
| 10 | 2 | 0 | 0.364 | 0.203 | 0.0812 |
| 0.1 | 0.363 | 0.201 | 0.0803 | ||
| 0.5 | 0.361 | 0.202 | 0.0812 | ||
| 1 | 0.366 | 0.209 | 0.0850 | ||
| 5 | 0.455 | 0.295 | 0.129 | ||
| 10 | 0.578 | 0.409 | 0.187 | ||
| 5 | 0 | 0.623 | 0.346 | 0.139 | |
| 0.1 | 0.636 | 0.356 | 0.143 | ||
| 0.5 | 0.670 | 0.383 | 0.156 | ||
| 1 | 0.705 | 0.415 | 0.172 | ||
| 5 | 0.932 | 0.650 | 0.294 | ||
| 10 | 1.13 | 0.894 | 0.439 | ||
| 0.1 | 0.5 | 0.8 | ||||||
|---|---|---|---|---|---|---|---|---|
| w/o | w/ | w/o | w/ | w/o | w/ | |||
| 1 | 2 | 0.5 | 484 | 6.08 | 419 | 32.1 | 395 | 34.5 |
| 1 | 407 | 20.7 | 347 | 44.1 | 325 | 43.4 | ||
| 5 | 351 | 67.9 | 262 | 59.4 | 227 | 48.1 | ||
| 10 | 433 | 124 | 302 | 90.2 | 223 | 52.9 | ||
| 5 | 0.5 | 1199 | 191 | 1079 | 241 | 1037 | 245 | |
| 1 | 1049 | 227 | 941 | 267 | 906 | 272 | ||
| 5 | 1027 | 366 | 839 | 329 | 746 | 286 | ||
| 10 | 1324 | 550 | 1023 | 432 | 776 | 315 | ||
| 5 | 2 | 0.5 | 100 | 5.04 | 82.9 | 15.3 | 77.4 | 15.4 |
| 1 | 78.3 | 8.73 | 64.6 | 15.9 | 60.5 | 15.2 | ||
| 5 | 57.1 | 17.5 | 43.1 | 14.2 | 39.6 | 12.4 | ||
| 10 | 66.8 | 30.6 | 44.9 | 18.5 | 37.3 | 12.3 | ||
| 5 | 0.5 | 202 | 78.5 | 177 | 85.5 | 169 | 84.1 | |
| 1 | 168 | 78.5 | 147 | 80.9 | 141 | 80.0 | ||
| 5 | 155 | 99.0 | 122 | 79.2 | 110 | 69.2 | ||
| 10 | 210 | 150 | 147 | 102 | 111 | 73.0 | ||
| 10 | 2 | 0.5 | 51.4 | 4.33 | 41.6 | 9.49 | 38.8 | 9.43 |
| 1 | 39.2 | 5.47 | 31.9 | 9.01 | 30.0 | 8.63 | ||
| 5 | 26.4 | 8.19 | 20.7 | 7.08 | 19.5 | 6.58 | ||
| 10 | 28.7 | 13.1 | 20.4 | 8.33 | 18.1 | 6.32 | ||
| 5 | 0.5 | 95.6 | 45.2 | 83.0 | 46.8 | 79.3 | 45.8 | |
| 1 | 76.6 | 41.1 | 67.4 | 41.5 | 65.2 | 41.1 | ||
| 5 | 64.9 | 44.4 | 52.9 | 36.6 | 49.2 | 33.3 | ||
| 10 | 85.5 | 65.8 | 60.9 | 44.8 | 49.1 | 34.2 | ||
| 0.1 | 0.5 | 0.8 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Inlet | Middle | Outlet | Inlet | Middle | Outlet | Inlet | Middle | Outlet | |||
| 1 | 2 | 0.1 | 0.45 | 0.51 | 0.53 | 0.19 | 0.16 | 0.13 | 0.065 | 0.047 | 0.036 |
| 1 | 0.50 | 0.60 | 0.63 | 0.24 | 0.20 | 0.16 | 0.086 | 0.063 | 0.048 | ||
| 10 | 0.66 | 0.91 | 1.1 | 0.51 | 0.47 | 0.38 | 0.23 | 0.17 | 0.13 | ||
| 5 | 0.1 | 0.54 | 0.40 | 0.31 | 0.21 | 0.091 | 0.059 | 0.070 | 0.026 | 0.016 | |
| 1 | 0.61 | 0.49 | 0.39 | 0.27 | 0.12 | 0.077 | 0.094 | 0.035 | 0.021 | ||
| 10 | 0.76 | 0.81 | 0.74 | 0.56 | 0.27 | 0.16 | 0.26 | 0.10 | 0.058 | ||
| 10 | 2 | 0.1 | 0.13 | 0.19 | 0.34 | 0.066 | 0.063 | 0.057 | 0.025 | 0.019 | 0.015 |
| 1 | 0.13 | 0.19 | 0.35 | 0.068 | 0.065 | 0.061 | 0.026 | 0.020 | 0.016 | ||
| 10 | 0.19 | 0.27 | 0.60 | 0.13 | 0.13 | 0.12 | 0.058 | 0.045 | 0.036 | ||
| 5 | 0.1 | 0.27 | 0.29 | 0.27 | 0.13 | 0.064 | 0.042 | 0.046 | 0.018 | 0.011 | |
| 1 | 0.28 | 0.31 | 0.31 | 0.15 | 0.076 | 0.050 | 0.055 | 0.021 | 0.013 | ||
| 10 | 0.45 | 0.54 | 0.60 | 0.32 | 0.17 | 0.11 | 0.14 | 0.056 | 0.034 | ||
| 1 | 3.3 | |||
|---|---|---|---|---|
| 5 | 2 | 0.1 | 0.525 | 0.517 |
| 1 | 0.571 | 0.500 | ||
| 10 | 0.894 | 0.484 | ||
| 5 | 0.1 | 0.802 | 0.799 | |
| 1 | 0.928 | 0.878 | ||
| 10 | 1.35 | 1.06 | ||
| 10 | 2 | 0.1 | 0.363 | 0.356 |
| 1 | 0.366 | 0.313 | ||
| 10 | 0.579 | 0.272 | ||
| 5 | 0.1 | 0.636 | 0.631 | |
| 1 | 0.705 | 0.635 | ||
| 10 | 1.13 | 0.660 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tantos, C.; Litovoli, F.; Teichmann, T.; Sarris, I.; Day, C. Numerical Study of Rarefied Gas Flow in Diverging Channels of Finite Length at Various Pressure Ratios. Fluids 2024, 9, 78. https://doi.org/10.3390/fluids9030078
Tantos C, Litovoli F, Teichmann T, Sarris I, Day C. Numerical Study of Rarefied Gas Flow in Diverging Channels of Finite Length at Various Pressure Ratios. Fluids. 2024; 9(3):78. https://doi.org/10.3390/fluids9030078
Chicago/Turabian StyleTantos, Christos, Foteini Litovoli, Tim Teichmann, Ioannis Sarris, and Christian Day. 2024. "Numerical Study of Rarefied Gas Flow in Diverging Channels of Finite Length at Various Pressure Ratios" Fluids 9, no. 3: 78. https://doi.org/10.3390/fluids9030078
APA StyleTantos, C., Litovoli, F., Teichmann, T., Sarris, I., & Day, C. (2024). Numerical Study of Rarefied Gas Flow in Diverging Channels of Finite Length at Various Pressure Ratios. Fluids, 9(3), 78. https://doi.org/10.3390/fluids9030078









