Passive Control of Vortices in the Wake of a Bluff Body
Abstract
1. Introduction
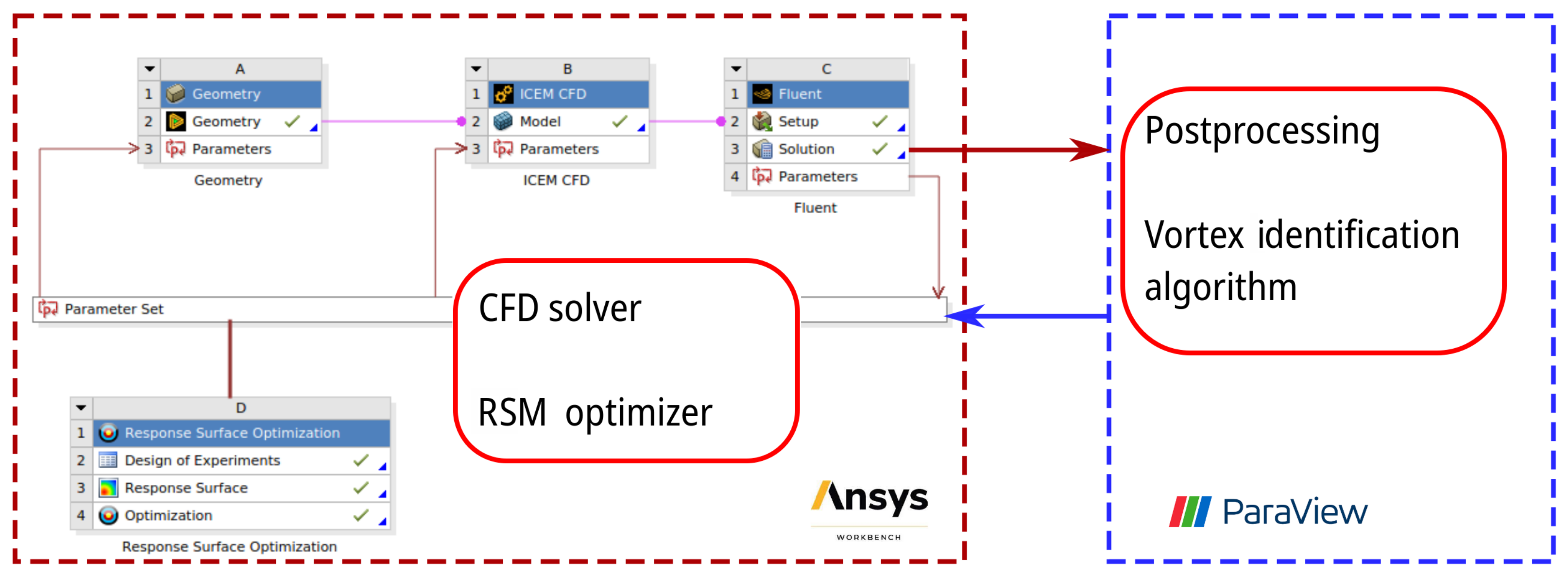
2. Methodology
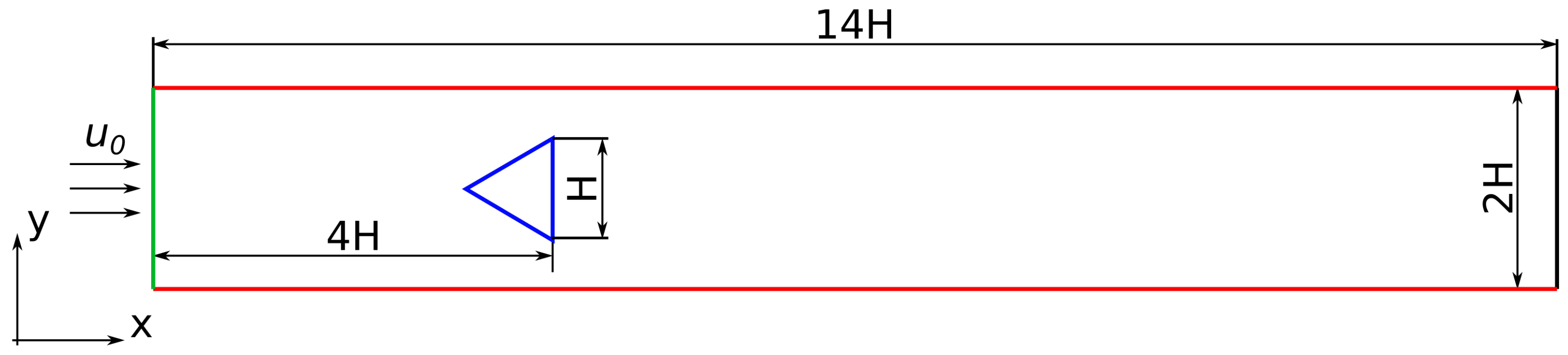
2.1. Computational Domain and Mesh
2.2. Flow Solution Method
2.3. Vortex Identification Method
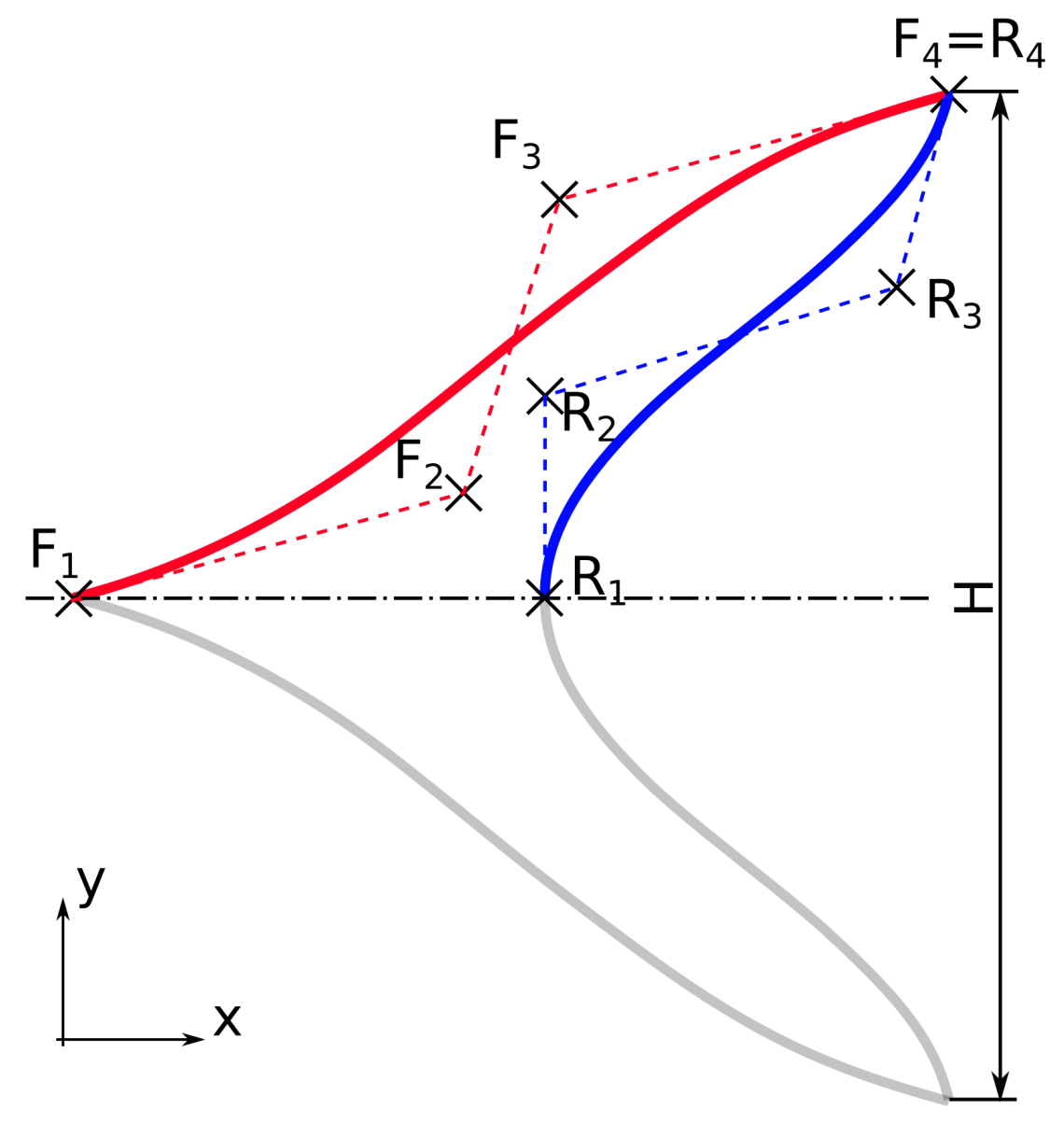
2.4. Parametrization and Optimization Method
3. Results and Discussion
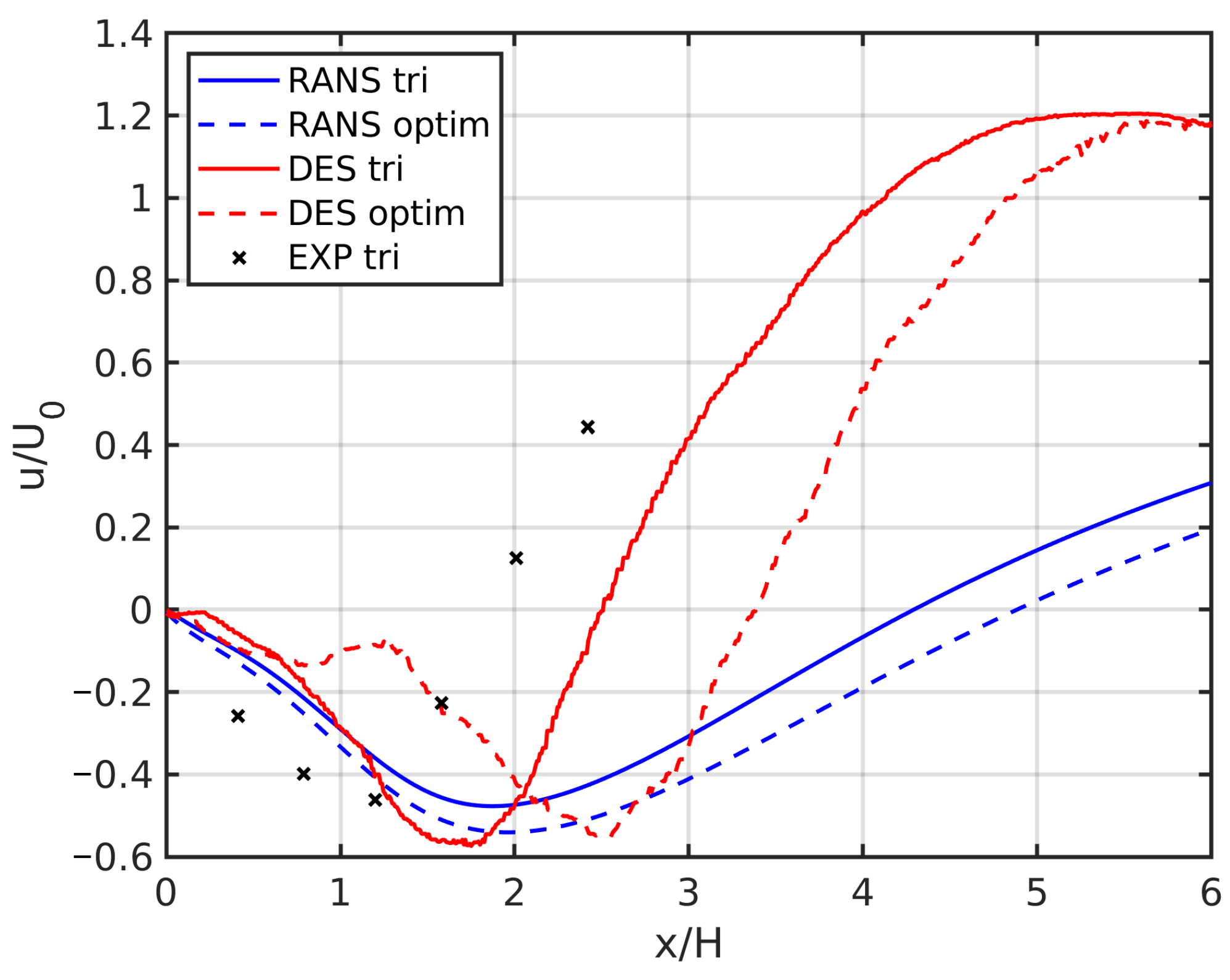
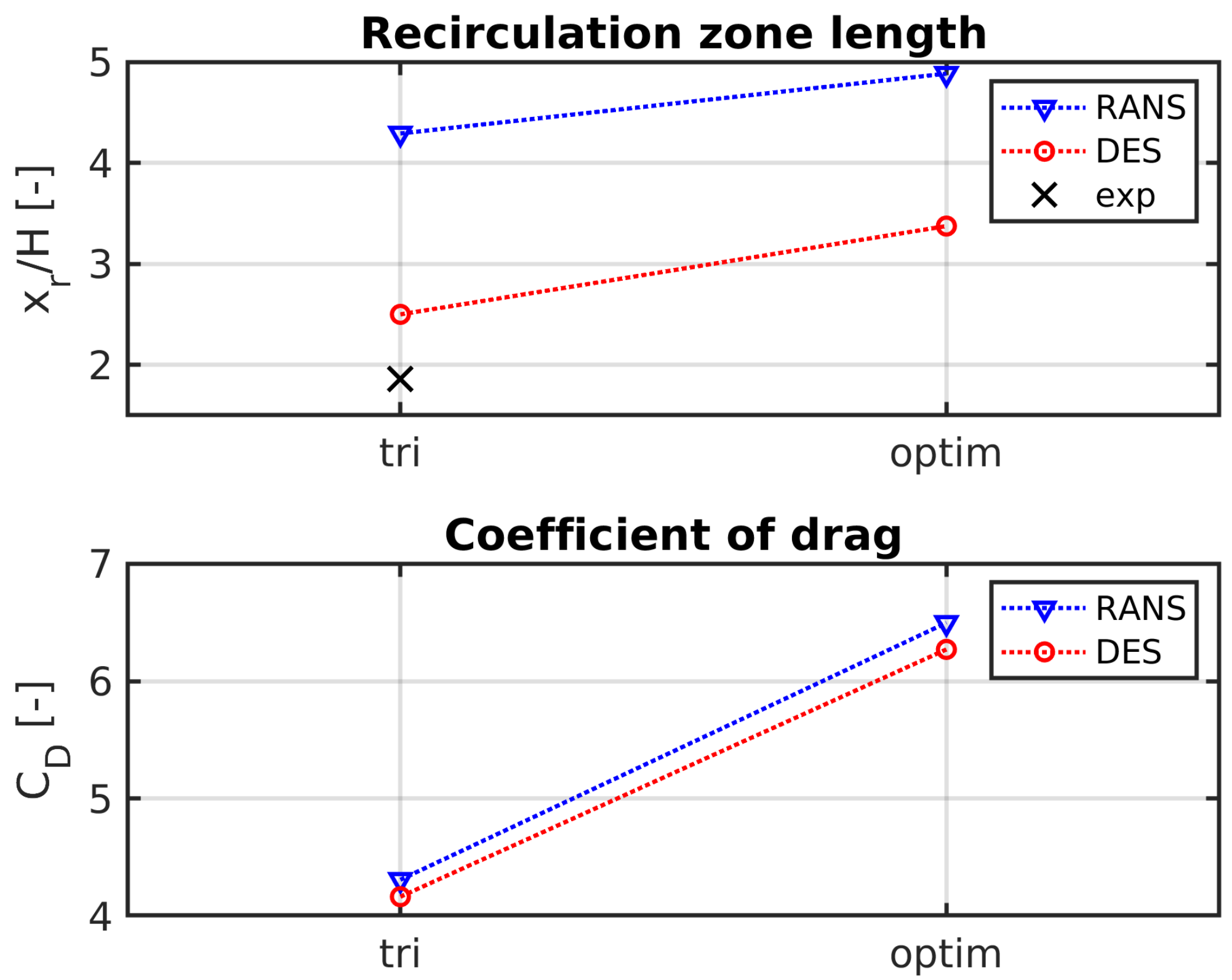
3.1. Validation of the Numerical Model
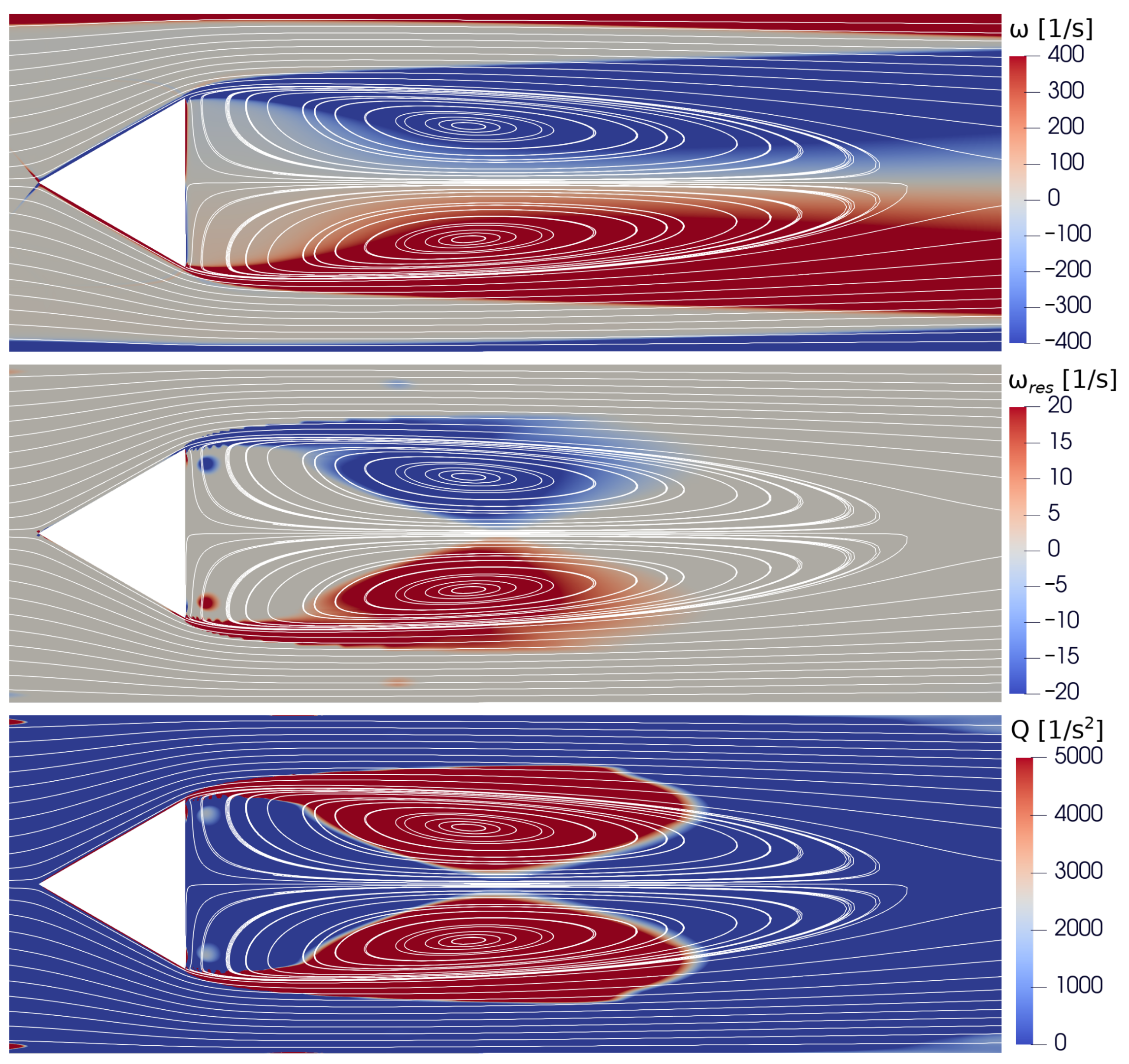
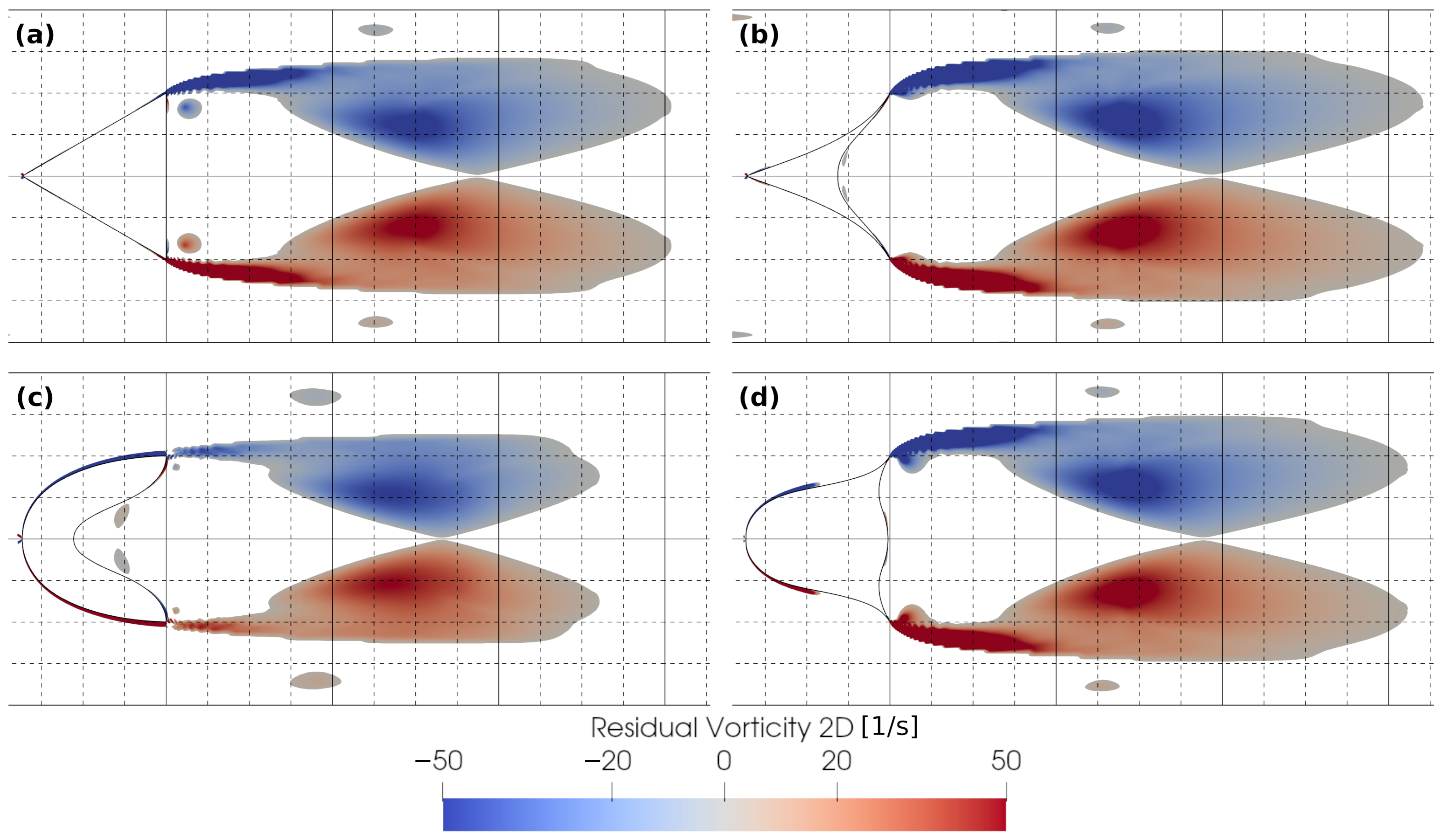
3.2. Vortex Detection
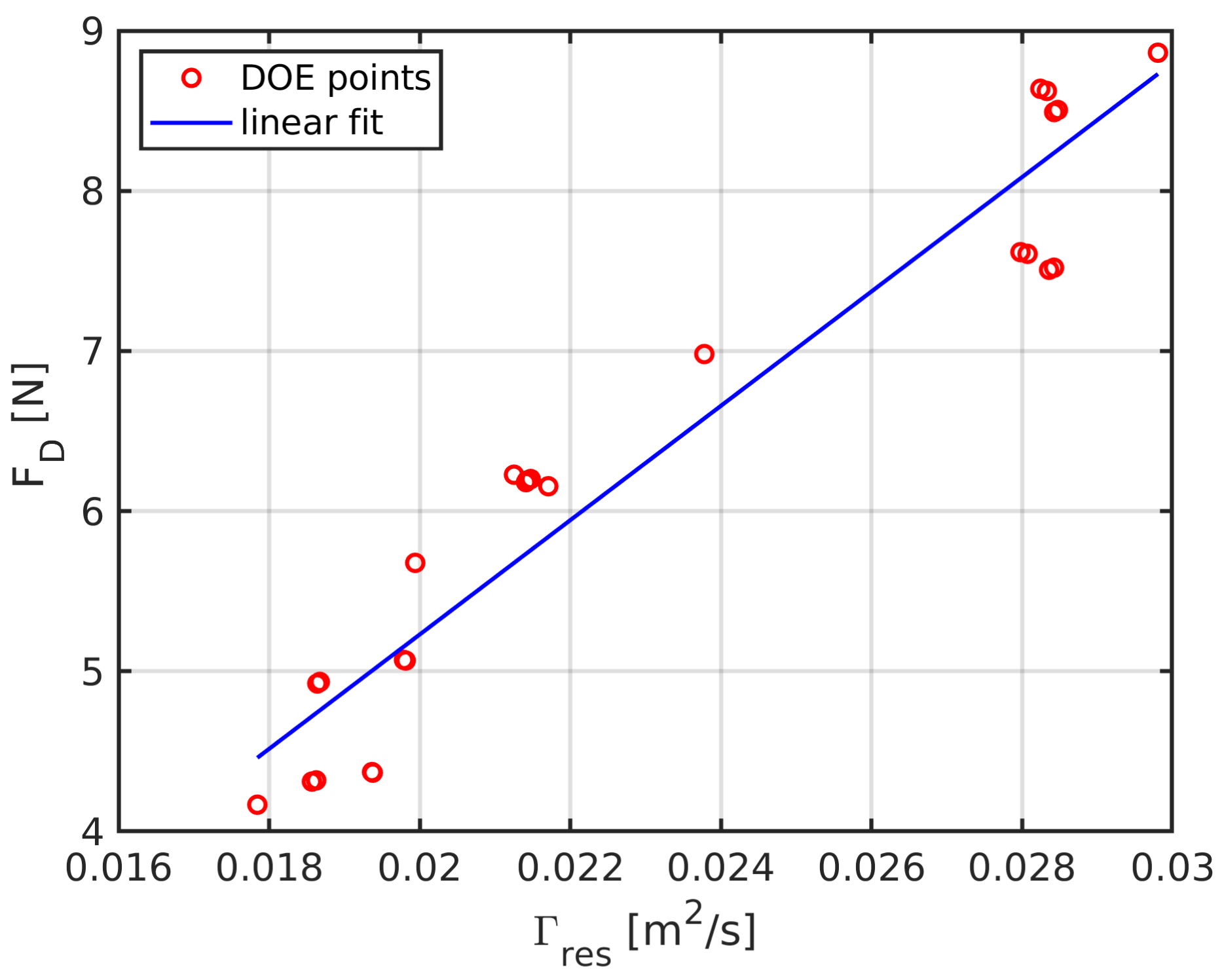
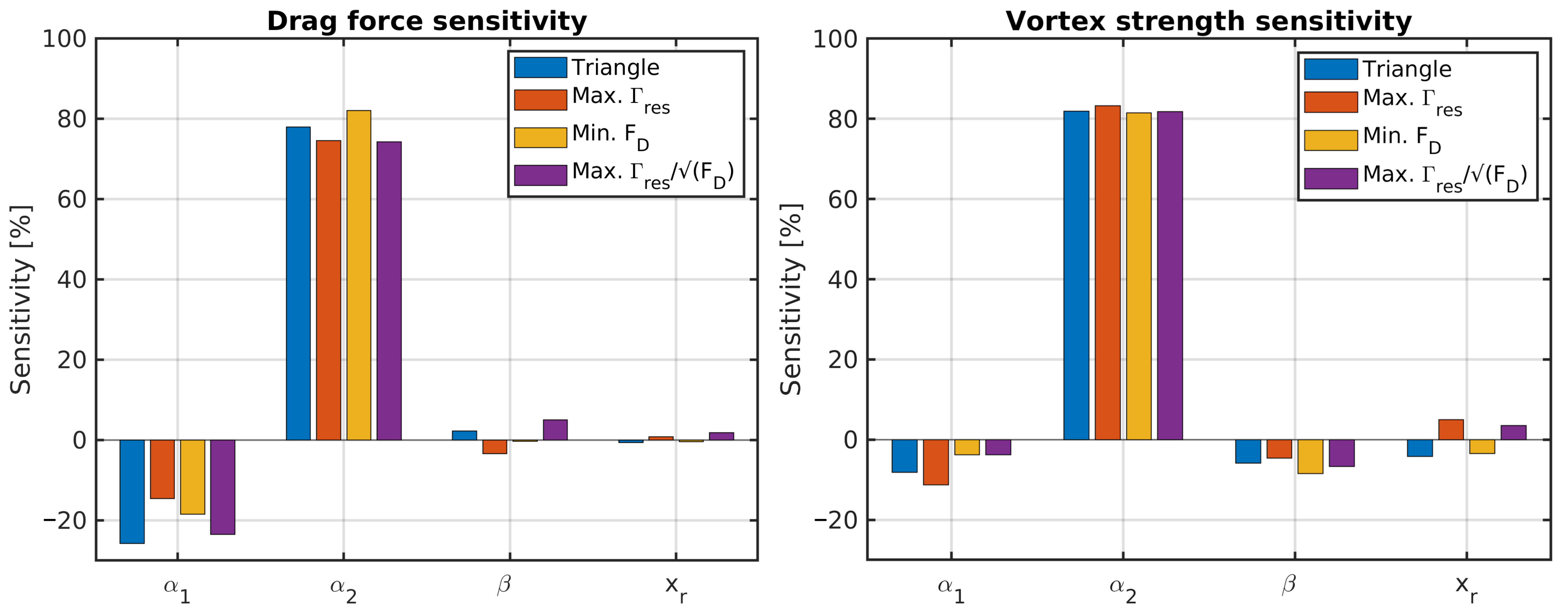
3.3. Optimization of the Bluff Body Geometry
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DES | Detached Eddy Simulation |
| DOE | Design of Experiments |
| LES | Large Eddy Simulationokes |
| SST | Shear Stress Transport |
| TDM | Triple Decomposition of Motion |
References
- Gao, D.; Deng, Z.; Yang, W.; Chen, W. Review of the excitation mechanism and aerodynamic flow control of vortex-induced vibration of the main girder for long-span bridges: A vortex-dynamics approach. J. Fluids Struct. 2021, 105, 103348. [Google Scholar] [CrossRef]
- Shtork, S.; Suslov, D.; Skripkin, S.; Litvinov, I.; Gorelikov, E. An Overview of Active Control Techniques for Vortex Rope Mitigation in Hydraulic Turbines. Energies 2023, 16, 5131. [Google Scholar] [CrossRef]
- Yang, B.; Newton, P.; Martinez-Botas, R. Understanding of Secondary Flows and Losses in Radial and Mixed Flow Turbines. J. Turbomach. 2020, 142, 081006. [Google Scholar] [CrossRef]
- De Tavernier, D.; Ferreira, C.; Viré, A.; LeBlanc, B.; Bernardy, S. Controlling dynamic stall using vortex generators on a wind turbine airfoil. Renew. Energy 2021, 172, 1194–1211. [Google Scholar] [CrossRef]
- Elcrat, A.; Ferlauto, M.; Zannetti, L. Point vortex model for asymmetric inviscid wakes past bluff bodies. Fluid Dyn. Res. 2014, 46, 031407. [Google Scholar] [CrossRef]
- Protas, B. Linear feedback stabilization of laminar vortex shedding based on a point vortex model. Phys. Fluids 2004, 16, 4473–4488. [Google Scholar] [CrossRef]
- Illingworth, S.J.; Naito, H.; Fukagata, K. Active control of vortex shedding: An explanation of the gain window. Phys. Rev. E 2014, 90, 043014. [Google Scholar] [CrossRef] [PubMed]
- Balsa, C.; Otero-Espinar, M.V.; Gama, S. Exploring Controlled Passive Particle Motion Driven by Point Vortices on a Sphere. Computation 2024, 12, 23. [Google Scholar] [CrossRef]
- Mitchell, A.M.; Délery, J. Research into vortex breakdown control. Prog. Aerosp. Sci. 2001, 37, 385–418. [Google Scholar] [CrossRef]
- Rashidi, S.; Hayatdavoodi, M.; Esfahani, J.A. Vortex shedding suppression and wake control: A review. Ocean Eng. 2016, 126, 57–80. [Google Scholar] [CrossRef]
- Gursul, I.; Wang, Z. Flow Control of Tip/Edge Vortices. AIAA J. 2018, 56, 1731–1749. [Google Scholar] [CrossRef]
- Miura, H.; Kida, S. Identification of Tubular Vortices in Turbulence. J. Phys. Soc. Jpn. 1997, 66, 1331–1334. [Google Scholar] [CrossRef]
- Ducci, A.; Yianneskis, M. Vortex Identification Methodology for Feed Insertion Guidance in Fluid Mixing Processes. Chem. Eng. Res. Des. 2007, 85, 543–550. [Google Scholar] [CrossRef]
- Hunt, J. Vorticity and Vortex Dynamics in Complex Turbulent Flows. Trans. Can. Soc. Mech. Eng. 1987, 11, 21–35. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian Coherent Structures. Annu. Rev. Fluid Mech. 2015, 47, 137–162. [Google Scholar] [CrossRef]
- Portela, L.M. Identification and Characterization of Vortices in the Turbulent Boundary Layer. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1998. [Google Scholar]
- Sujudi, D.; Haimes, R. Identification of swirling flow in 3-D vector fields. In Proceedings of the 12th Computational Fluid Dynamics Conference, San Diego, CA, USA, 19–22 June 1995. [Google Scholar] [CrossRef]
- Sadarjoen, I.A.; Post, F.H. Geometric Methods for Vortex Extraction. In Data Visualization ’99; Proceedings of the Joint EUROGRAPHICS and IEEE TCVG Symposium on Visualization, Vienna, Austria, 26–28 May 1999; Gröller, E., Löffelmann, H., Ribarsky, W., Eds.; Springer: Vienna, Austria, 1999; pp. 53–62. [Google Scholar]
- Haller, G.; Hadjighasem, A.; Farazmand, M.; Huhn, F. Defining coherent vortices objectively from the vorticity. J. Fluid Mech. 2016, 795, 136–173. [Google Scholar] [CrossRef]
- Banks, D.; Singer, B. Vortex tubes in turbulent flows: Identification, representation, reconstruction. In Proceedings of the Proceedings Visualization ’94, Washington, DC, USA, 21 October 1994; pp. 132–139. [Google Scholar] [CrossRef]
- Hadjighasem, A.; Farazmand, M.; Blazevski, D.; Froyland, G.; Haller, G. A critical comparison of Lagrangian methods for coherent structure detection. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 053104. [Google Scholar] [CrossRef]
- Epps, B. Review of Vortex Identification Methods. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Günther, T.; Theisel, H. The State of the Art in Vortex Extraction: The State of the Art in Vortex Extraction. Comput. Graph. Forum 2018, 37, 149–173. [Google Scholar] [CrossRef]
- KolÁř, V. Vortex Identification: New Requirements and Limitations. Int. J. Heat Fluid Flow 2007, 28, 638–652. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Chong, M.S.; Perry, A.E.; Cantwell, B.J. A general classification of three-dimensional flow fields. Phys. Fluids A Fluid Dyn. 1990, 2, 765–777. [Google Scholar] [CrossRef]
- Liu, C.; Gao, Y.; Tian, S.; Dong, X. Rortex—A new vortex vector definition and vorticity tensor and vector decompositions. Phys. Fluids 2018, 30, 035103. [Google Scholar] [CrossRef]
- Liu, C.; Gao, Y.s.; Dong, X.r.; Wang, Y.q.; Liu, J.m.; Zhang, Y.n.; Cai, X.s.; Gui, N. Third generation of vortex identification methods: Omega and Liutex/Rortex based systems. J. Hydrodyn. 2019, 31, 205–223. [Google Scholar] [CrossRef]
- Morajkar, R.R.; Klomparens, R.L.; Eagle, W.E.; Driscoll, J.F.; Gamba, M.; Benek, J.A. Relationship Between Intermittent Separation and Vortex Structure in a Three-Dimensional Shock/Boundary-Layer Interaction. AIAA J. 2016, 54, 1862–1880. [Google Scholar] [CrossRef]
- Morajkar, R.R.; Gamba, M. Turbulence Characteristics of Supersonic Corner Flows in a Low Aspect Ratio Rectangular Channel. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Wang, F.; Li, W.; Wang, S. Polar Cyclone Identification from 4D Climate Data in a Knowledge-Driven Visualization System. Climate 2016, 4, 43. [Google Scholar] [CrossRef]
- Pátý, M.; Resta, E.; Ferlauto, M.; Marsilio, R. On the Use of Vortex Identification for the Optimisation of Trapped Vortex Devices. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar] [CrossRef]
- Pátý’, M.; Lavagnoli, S. A Novel Vortex Identification Technique Applied to the 3D Flow Field of a High-Pressure Turbine. J. Turbomach. 2020, 142, 031004. [Google Scholar] [CrossRef]
- Nagata, R.; Watanabe, T.; Nagata, K.; da Silva, C.B. Triple decomposition of velocity gradient tensor in homogeneous isotropic turbulence. Comput. Fluids 2020, 198, 104389. [Google Scholar] [CrossRef]
- Fujii, S.; Gomi, M.; Eguchi, K. Cold Flow Tests of a Bluff-Body Flame Stabilizer. J. Fluids Eng. 1978, 100, 323–332. [Google Scholar] [CrossRef]
- Liou, M.S. A sequel to AUSM: AUSM+. J. Comput. Phys. 1996, 129, 364–382. [Google Scholar] [CrossRef]
- Poinsot, T.; Lele, S. Boundary conditions for direct simulations of compressible viscous reacting flows. J. Comput. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. Rech. Aerosp. 1994, 1, 5–21. [Google Scholar]
- Spalart, P.; Deck, S.; Shur, M.; Squires, K.; Strelets, M.; Travin, A. A New Version of Detached-eddy Simulation, Resistant to Ambiguous Grid Densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Kolář, V. A note on integral vortex strength. J. Hydrol. Hydromech. 2010, 58, 23–28. [Google Scholar] [CrossRef][Green Version]
- ANSYS, Inc. DesignXplorer User’s Guide, 2022. Release 2022 R2. Available online: https://ansyshelp.ansys.com/ (accessed on 1 May 2024).
- Kim, W.W.; Lienau, J.J.; Van Slooten, P.R.; Colket, M.B.; Malecki, R.E.; Syed, S. Towards Modeling Lean Blow Out in Gas Turbine Flameholder Applications. J. Eng. Gas Turbines Power 2006, 128, 40–48. [Google Scholar] [CrossRef]




Triangle | Max.  | Min.  | Max.  | |
| 1.0 | 1.44 | 0.58 | 1.22 | |
| 1.0 | 1.4 | 0.56 | 1.37 | |
| 1.0 | 1.17 | 0.73 | 1.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pátý, M.; Valášek, M.; Resta, E.; Marsilio, R.; Ferlauto, M. Passive Control of Vortices in the Wake of a Bluff Body. Fluids 2024, 9, 131. https://doi.org/10.3390/fluids9060131
Pátý M, Valášek M, Resta E, Marsilio R, Ferlauto M. Passive Control of Vortices in the Wake of a Bluff Body. Fluids. 2024; 9(6):131. https://doi.org/10.3390/fluids9060131
Chicago/Turabian StylePátý, Marek, Michael Valášek, Emanuele Resta, Roberto Marsilio, and Michele Ferlauto. 2024. "Passive Control of Vortices in the Wake of a Bluff Body" Fluids 9, no. 6: 131. https://doi.org/10.3390/fluids9060131
APA StylePátý, M., Valášek, M., Resta, E., Marsilio, R., & Ferlauto, M. (2024). Passive Control of Vortices in the Wake of a Bluff Body. Fluids, 9(6), 131. https://doi.org/10.3390/fluids9060131





