Comparison of Libration- and Precession-Driven Flows: From Linear Responses to Broadband Dynamics
Abstract
:1. Introduction
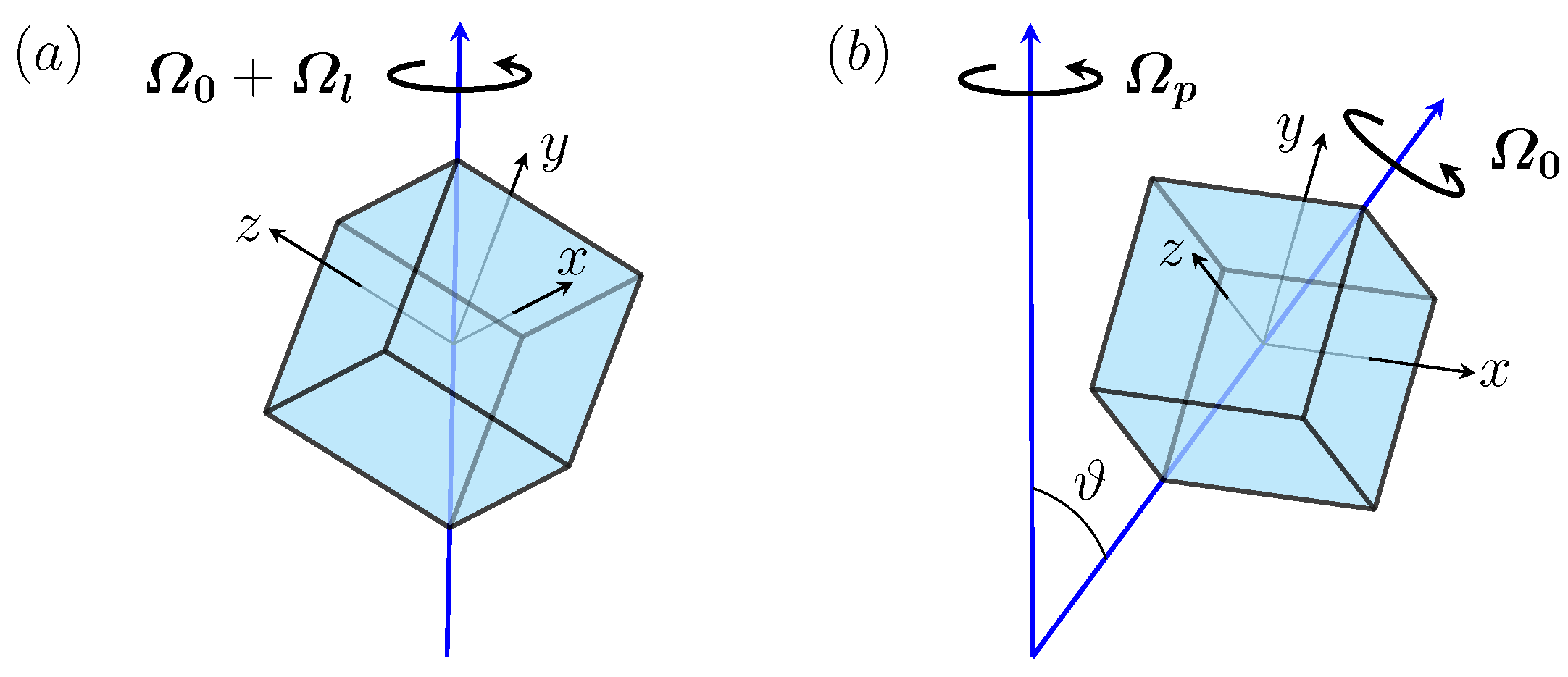
2. Governing Equations, the Numerics to Solve Them, and Their Symmetries
2.1. Governing Equations
2.2. Numerics
2.3. Symmetries
3. Linear Responses to Librational and Precessional Forcings
3.1. Linear Inviscid Ray Tracing
3.2. Viscous Linear Responses
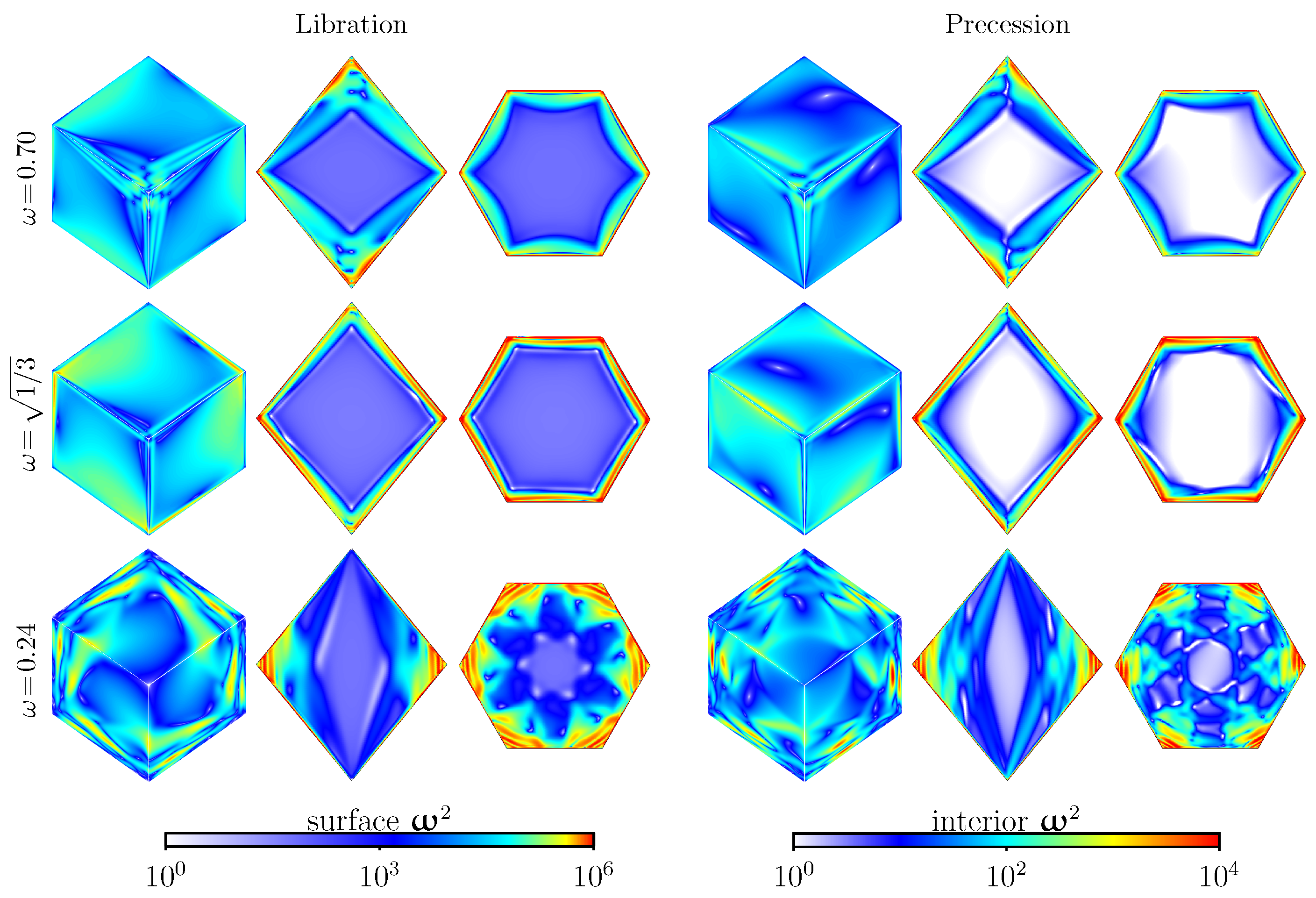
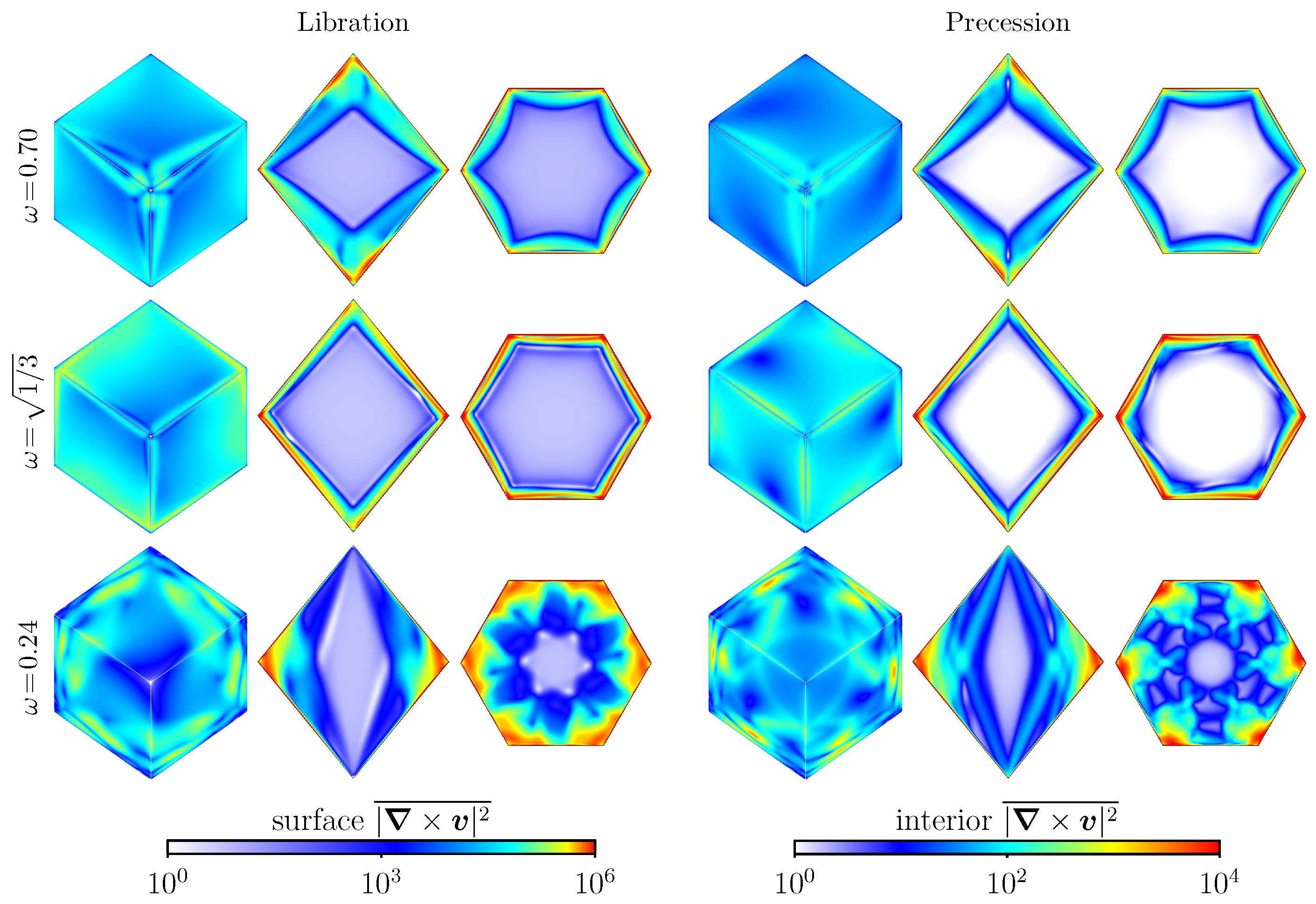
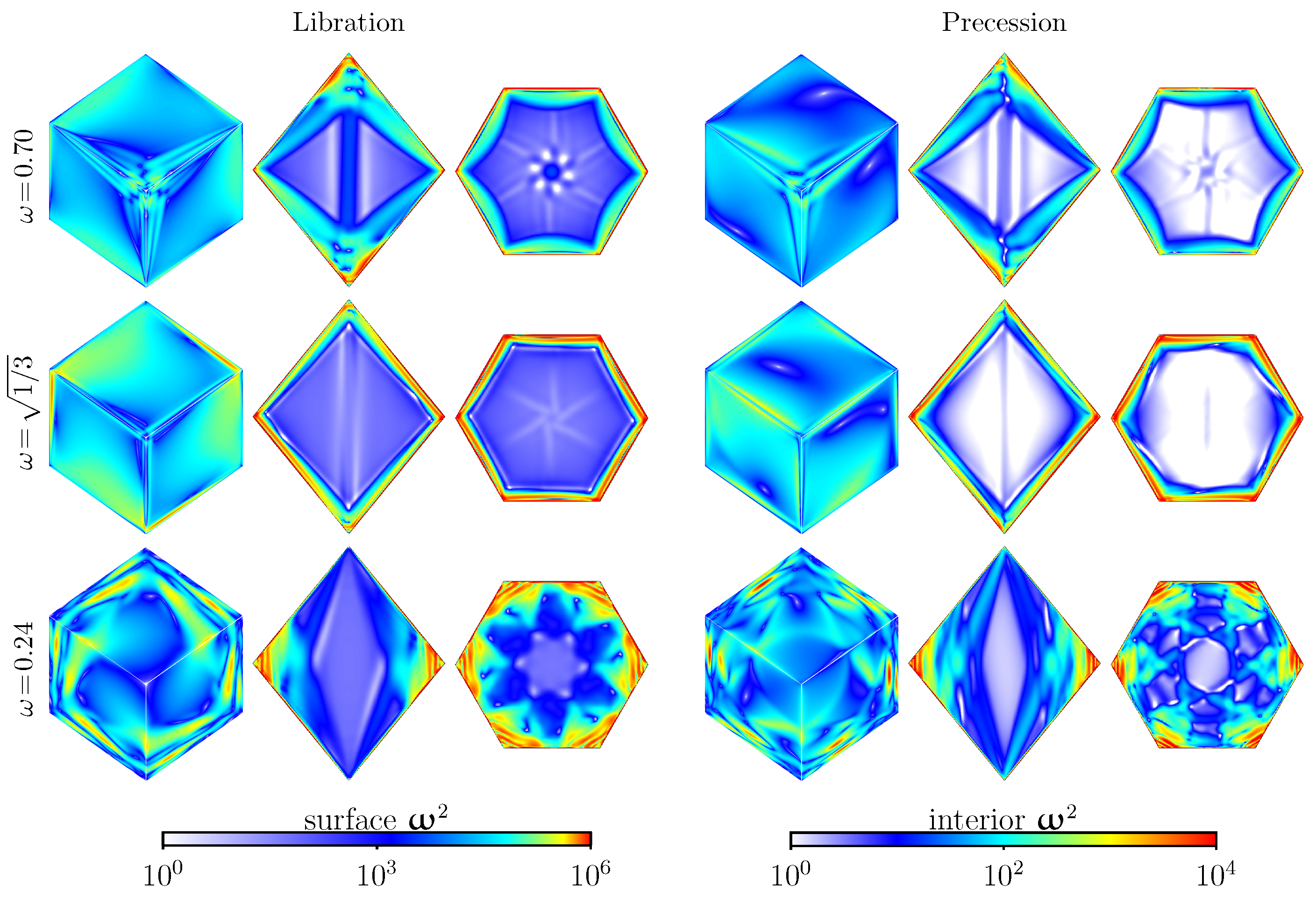
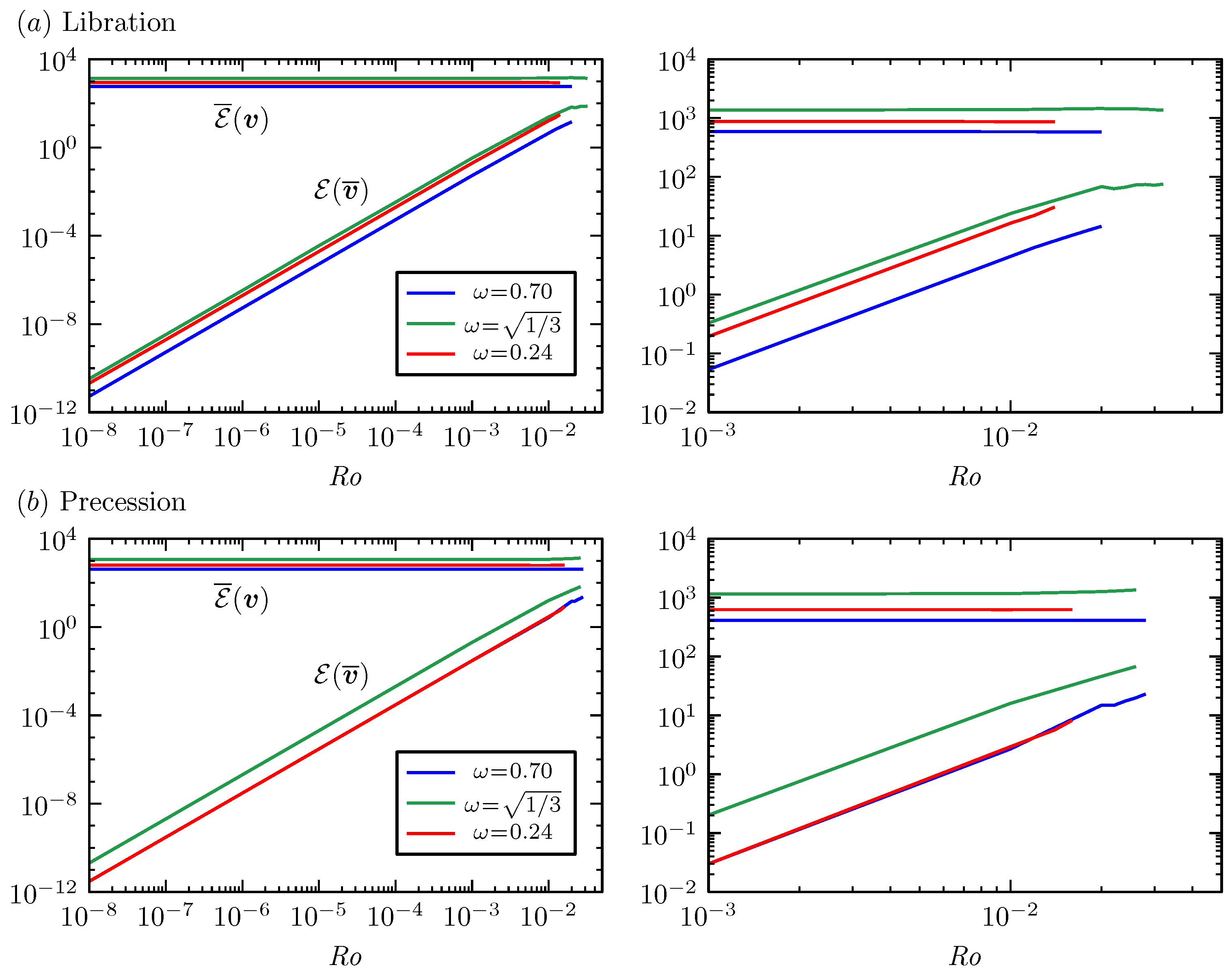
4. Primary Viscous Nonlinear Responses
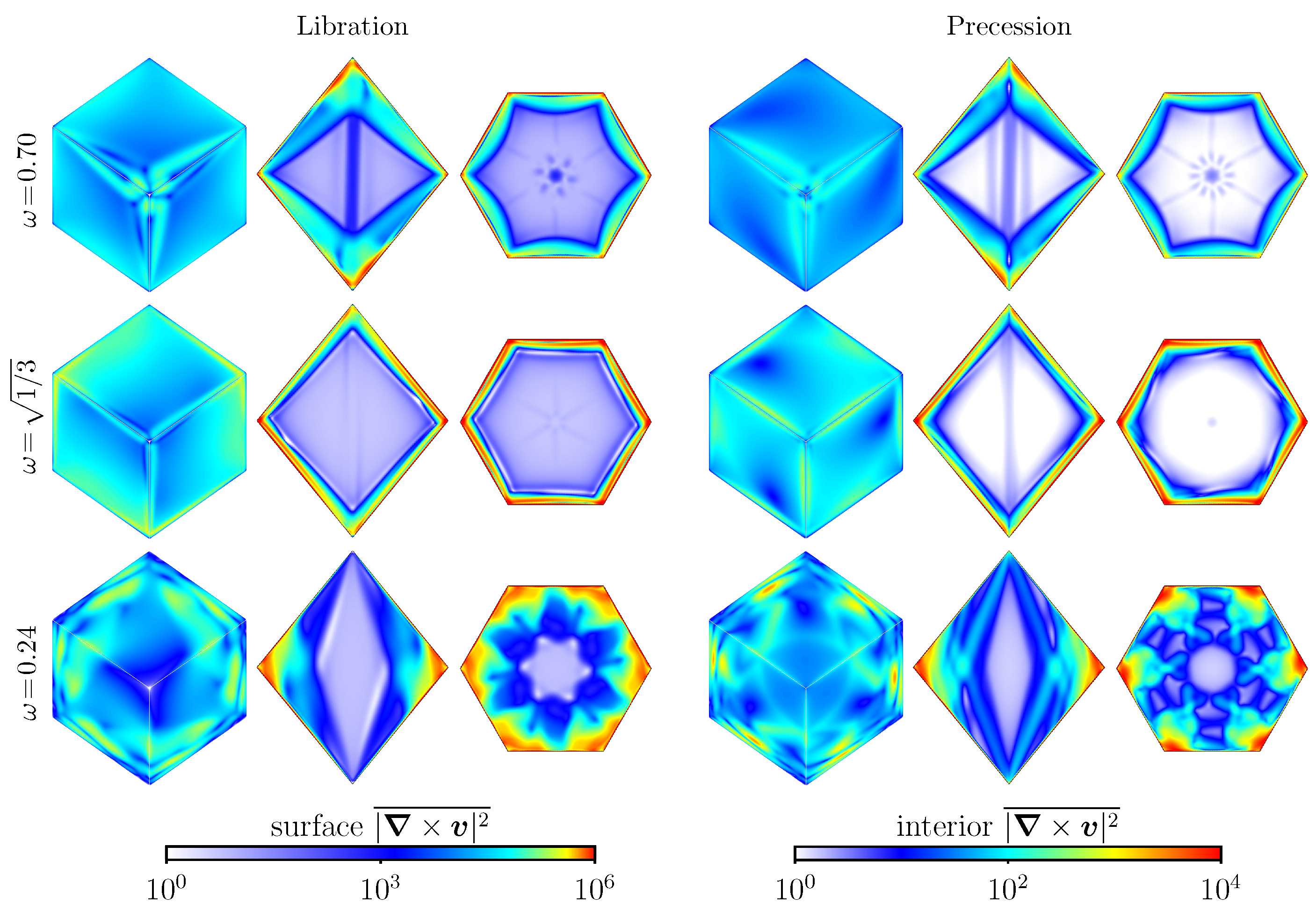
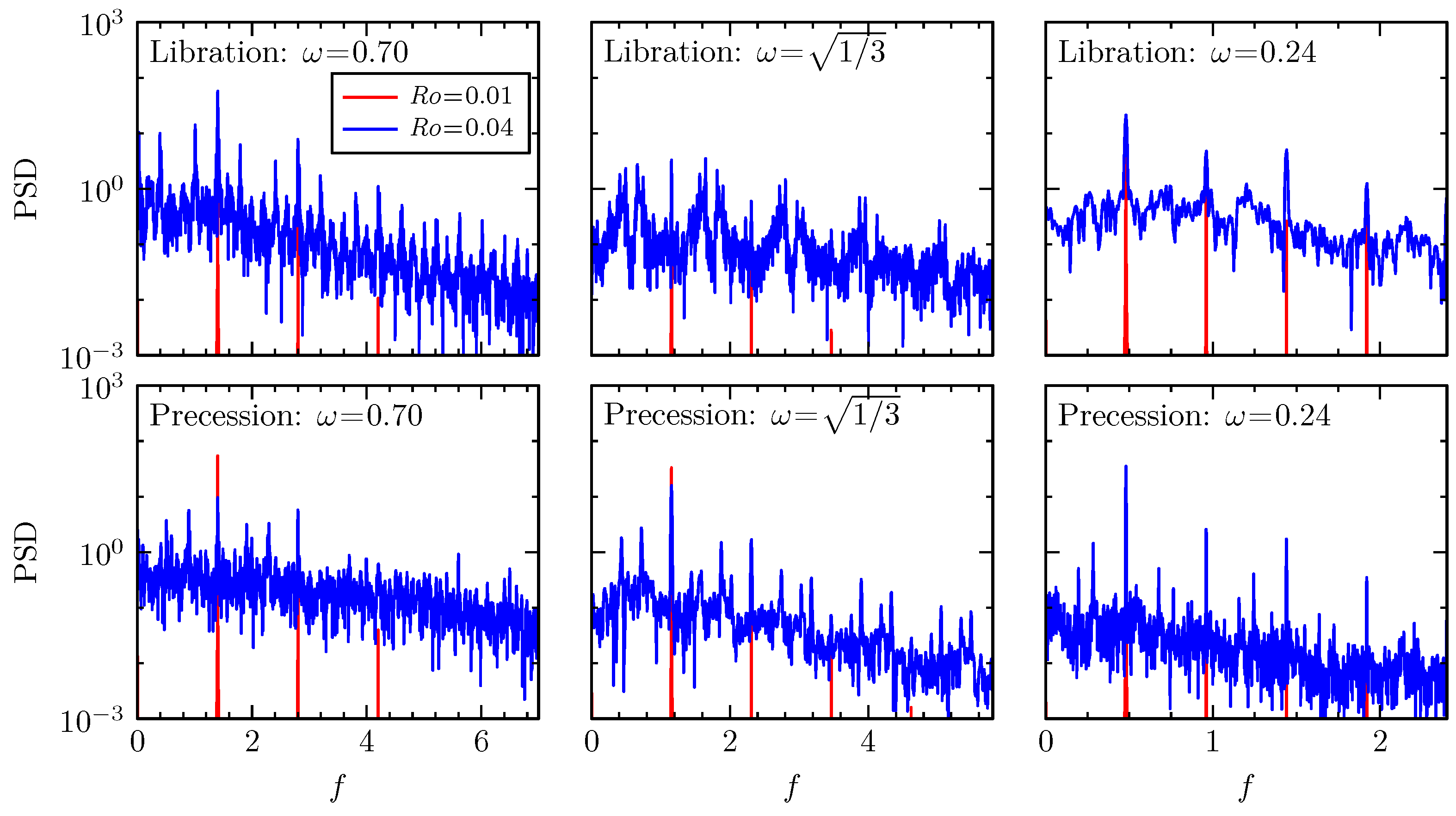
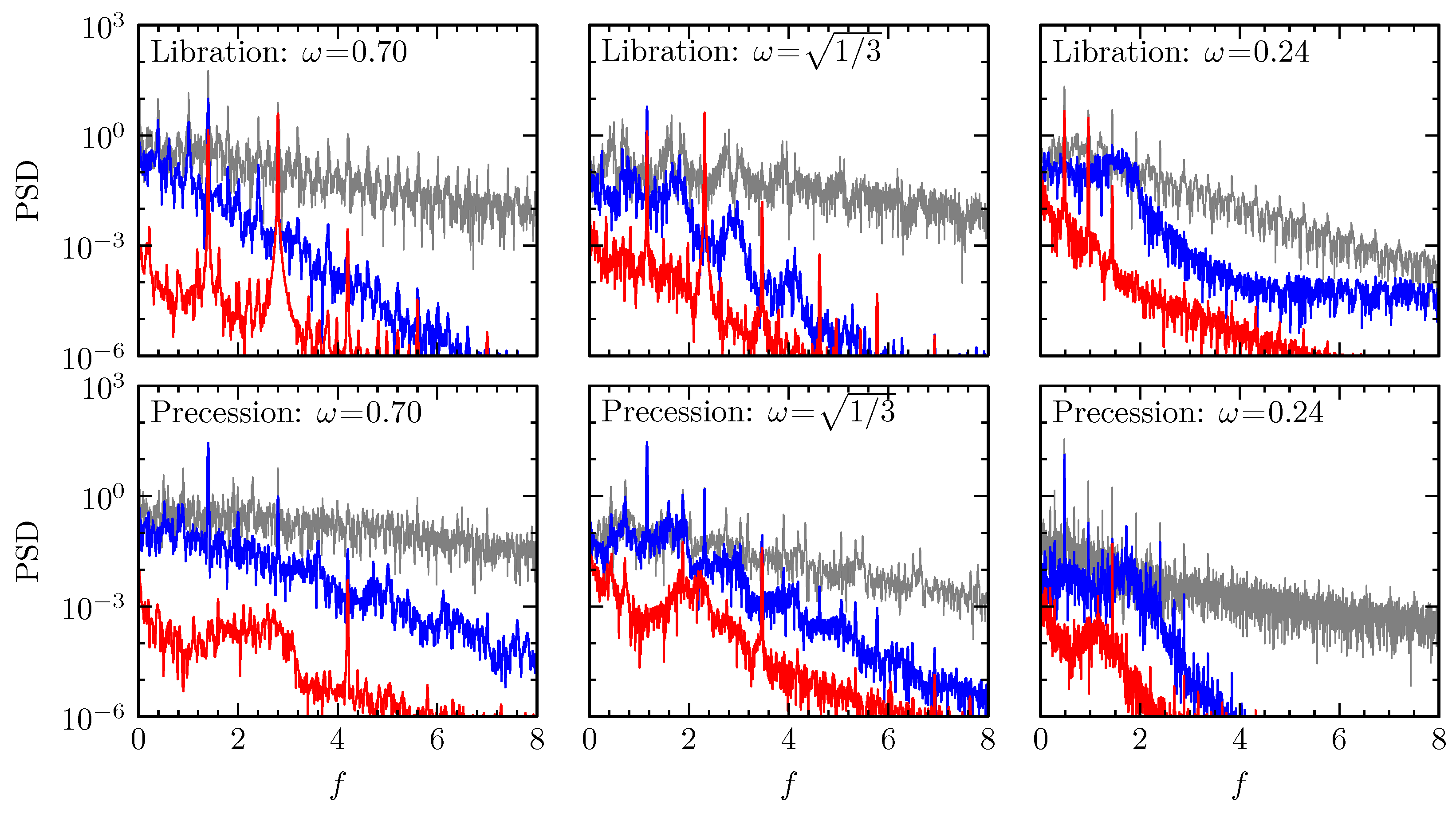
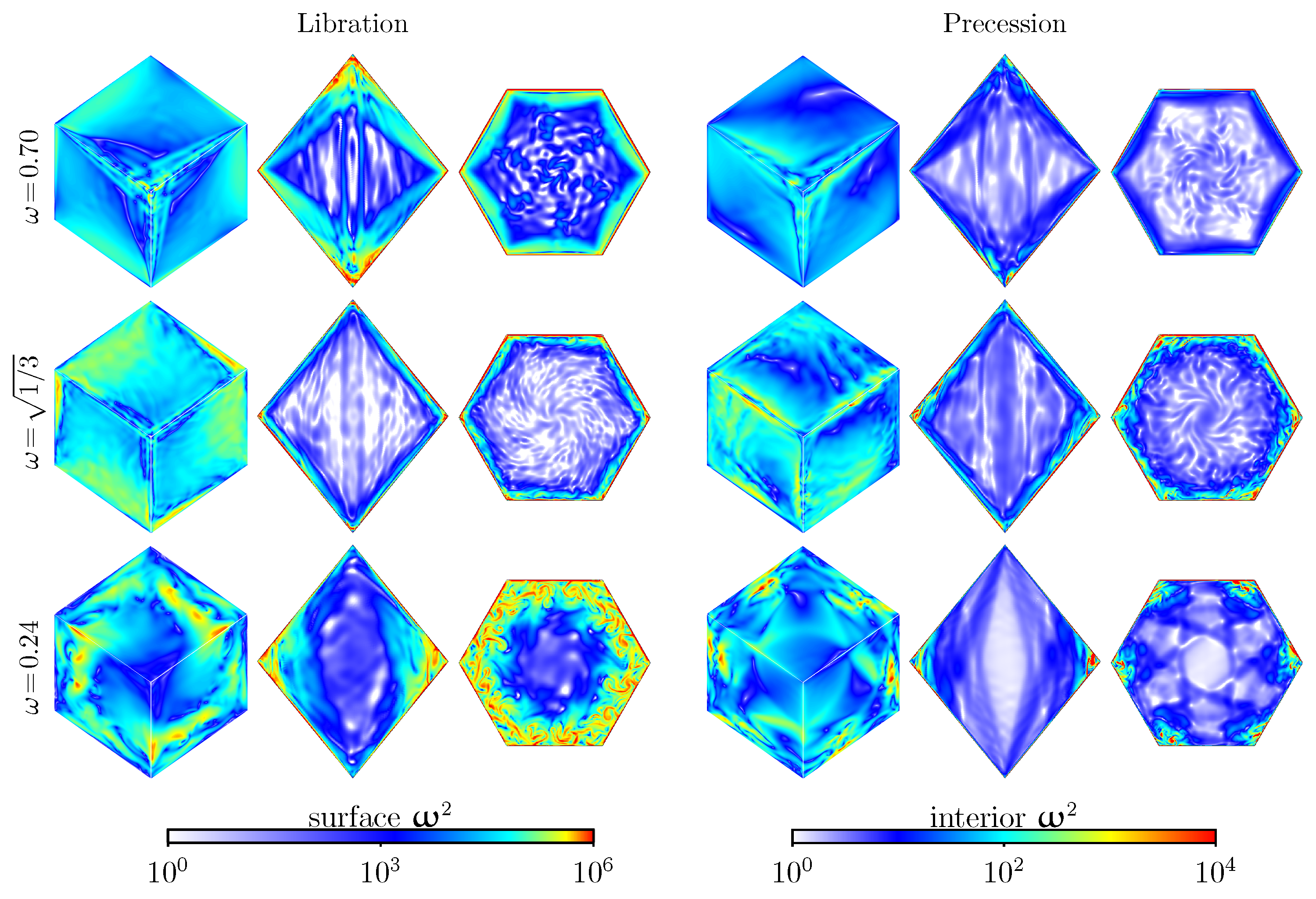
5. Instabilities to Broadband Dynamics
6. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Emission Direction of an Edgebeam
References
- Le Bars, M.; Cebron, D.; Le Gal, P. Flows driven by libration, precession, and tides. Annu. Rev. Fluid Mech. 2015, 47, 163–193. [Google Scholar] [CrossRef]
- Le Bars, M.; Barik, A.; Burmann, F.; Lathrop, D.P.; Noir, J.; Schaeffer, N.; Triana, S.A. Fluid Dynamics Experiments for Planetary Interiors. Surv. Geophys. 2022, 43, 229–261. [Google Scholar] [CrossRef]
- Wu, K.; Welfert, B.D.; Lopez, J.M. Librational forcing of a rapidly rotating fluid-filled cube. J. Fluid Mech. 2018, 842, 469–494. [Google Scholar] [CrossRef]
- Wu, K.; Welfert, B.D.; Lopez, J.M. Precessing cube: Resonant excitation of modes and triadic resonance. J. Fluid Mech. 2020, 887, A6. [Google Scholar] [CrossRef]
- Maas, L.R.M. On the amphidromic structure of inertial waves in a rectangular parallelepiped. Fluid Dynam. Res. 2003, 33, 373–401. [Google Scholar] [CrossRef]
- Boisson, J.; Lamriben, C.; Maas, L.R.M.; Cortet, P.P.; Moisy, F. Inertial waves and modes excited by the libration of a rotating cube. Phys. Fluids 2012, 24, 076602. [Google Scholar] [CrossRef]
- Welfert, B.D.; Lopez, J.M.; Wu, K. Inertial wave attractors in rapidly rotating tilted cuboids. Proc. R. Soc. A 2023, 479, 20220876. [Google Scholar] [CrossRef]
- Phillips, O.M. Energy transfer in rotating fluids by reflection of inertial waves. Phys. Fluids 1963, 6, 513–520. [Google Scholar] [CrossRef]
- Wu, K.; Welfert, B.D.; Lopez, J.M. Inertial wave attractors in librating cuboids. J. Fluid Mech. 2023, 973, A20. [Google Scholar] [CrossRef]
- Greenspan, H.P. On inviscid theory of rotating fluids. Stud. Appl. Math. 1969, 48, 19–28. [Google Scholar] [CrossRef]
- Beardsley, R.C. An experimental study of inertial waves in a closed cone. Stud. Appl. Math. 1970, 49, 187–196. [Google Scholar] [CrossRef]
- Greenspan, H.P. The Theory of Rotating Fluids; Cambridge University Press: Cambridge, UK, 1968. [Google Scholar]
- Wu, K.; Huang, F.K.; Shen, J. A new class of higher-order decoupled schemes for the incompressible Navier–Stokes equations and applications to rotating dynamics. J. Comput. Phys. 2022, 458, 111097. [Google Scholar] [CrossRef]
- Wu, K.; Welfert, B.D.; Lopez, J.M. Reflections and focusing of inertial waves in a librating cube with the rotation axis oblique to its faces. J. Fluid Mech. 2020, 896, A5. [Google Scholar] [CrossRef]
- Wu, K.; Welfert, B.D.; Lopez, J.M. Reflections and focusing of inertial waves in a tilted librating cube. J. Fluid Mech. 2022, 947, A10. [Google Scholar] [CrossRef]
- Lopez, J.M.; Shen, J.; Welfert, B.D.; Wu, K. Boundary-confined waves in a librating cube. J. Fluid Mech. 2022, 952, R2. [Google Scholar] [CrossRef]
- Wang, C.Y. Cylindrical tank of fluid oscillating about a state of steady rotation. J. Fluid Mech. 1970, 41, 581–592. [Google Scholar] [CrossRef]
- Lin, Y.; Noir, J. Libration-driven inertial waves and mean zonal flows in spherical shells. Geophys. Astrophys. Fluid Dyn. 2021, 115, 258–279. [Google Scholar] [CrossRef]
- Subbotin, S.; Shiryaeva, M. On the linear and non-linear fluid response to the circular forcing in a rotating spherical shell. Phys. Fluids 2021, 33, 066603. [Google Scholar] [CrossRef]
- Subbotin, S.; Shiryaeva, M. Steady vortex flow induced by inertial wave attractor in a librating cylinder with sloping ends. Microgravity Sci. Technol. 2022, 34, 89. [Google Scholar] [CrossRef]
- Subbotin, S.; Shmakova, N.; Kozlov, V.; Ermanyuk, E. Nonlinear regimes of inertial wave attractors generated by a precessing lid: Zonal flows and Rossby waves. Phys. Fluids 2023, 35, 074110. [Google Scholar] [CrossRef]
- Shiryaeva, M.; Subbotina, M.; Subbotin, S. Linear and non-Linear dynamics of inertial waves in a rotating cylinder with antiparallel inclined ends. Fluid Dyn. Mater. Process. 2024, 20, 787–802. [Google Scholar] [CrossRef]
- Rubio, A.; Lopez, J.M.; Marques, F. Interacting oscillatory boundary layers and wall modes in modulated rotating convection. J. Fluid Mech. 2009, 625, 75–96. [Google Scholar] [CrossRef]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Afrajmovich, V.S.; Shil’nikov, L.P. Invariant two-dimensional tori, their breakdown and stochasticity. Am. Math. Soc. Transl. 1991, 149, 201–212. [Google Scholar]
- Boury, S.; Sibgatullin, I.; Ermanyuk, E.; Shmakova, N.; Odier, P.; Joubaud, S.; Maas, L.R.M.; Dauxois, T. Vortex cluster arising from an axisymmetric inertial wave attractor. J. Fluid Mech. 2021, 926, A12. [Google Scholar] [CrossRef]
- Sibgatullin, I.N.; Ermanyuk, E.V. Internal and inertial wave attractors: A review. J. Appl. Mech. Tech. Phys. 2019, 60, 284–302. [Google Scholar] [CrossRef]
- Mora, D.O.; Monsalve, E.; Brunet, M.; Dauxois, T.; Cortet, P.P. Three-dimensionality of the triadic resonance instability of a plane inertial wave. Phys. Rev. Fluids 2021, 6, 074801. [Google Scholar] [CrossRef]
- Rieutord, M.; Georgeot, B.; Valdettaro, L. Wave attractors in rotating fluids: A paradigm for ill-posed Cauchy problems. Phys. Rev. Lett. 2000, 85, 4277–4280. [Google Scholar] [CrossRef]
- Maas, L.R.M. Wave focusing and ensuing mean flow due to symmetry breaking in rotating fluids. J. Fluid Mech. 2001, 437, 13–28. [Google Scholar] [CrossRef]
- Maas, L.R.M. Wave attractors: Linear yet nonlinear. Int. J. Bifurc. Chaos 2005, 15, 2757–2782. [Google Scholar] [CrossRef]
- Borcia, I.D.; Harlander, U. Inertial waves in a rotating annulus with inclined inner cylinder: Comparing the spectrum of wave attractor frequency bands and the eigenspectrum in the limit of zero inclination. Theor. Comput. Fluid Dyn. 2013, 27, 397–413. [Google Scholar] [CrossRef]
- Rieutord, M.; Georgeot, B.; Valdettaro, L. Inertial waves in a rotating spherical shell: Attractors and asymptotic spectrum. J. Fluid Mech. 2001, 435, 103–144. [Google Scholar] [CrossRef]
- Favier, B.; Le Dizès, S. Inertial wave super-attractor in a truncated elliptic cone. J. Fluid Mech. 2024, 980, A6. [Google Scholar] [CrossRef]
- Brunet, M.; Dauxois, T.; Cortet, P.P. Linear and nonlinear regimes of an inertial wave attractor. Phys. Rev. Fluids 2019, 4, 034801. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, K.; Welfert, B.D.; Lopez, J.M. Comparison of Libration- and Precession-Driven Flows: From Linear Responses to Broadband Dynamics. Fluids 2024, 9, 151. https://doi.org/10.3390/fluids9070151
Wu K, Welfert BD, Lopez JM. Comparison of Libration- and Precession-Driven Flows: From Linear Responses to Broadband Dynamics. Fluids. 2024; 9(7):151. https://doi.org/10.3390/fluids9070151
Chicago/Turabian StyleWu, Ke, Bruno D. Welfert, and Juan M. Lopez. 2024. "Comparison of Libration- and Precession-Driven Flows: From Linear Responses to Broadband Dynamics" Fluids 9, no. 7: 151. https://doi.org/10.3390/fluids9070151
APA StyleWu, K., Welfert, B. D., & Lopez, J. M. (2024). Comparison of Libration- and Precession-Driven Flows: From Linear Responses to Broadband Dynamics. Fluids, 9(7), 151. https://doi.org/10.3390/fluids9070151





