Experimental Investigation of the Performance of a Novel Ejector–Diffuser System with Different Supersonic Nozzle Arrays
Abstract
1. Introduction
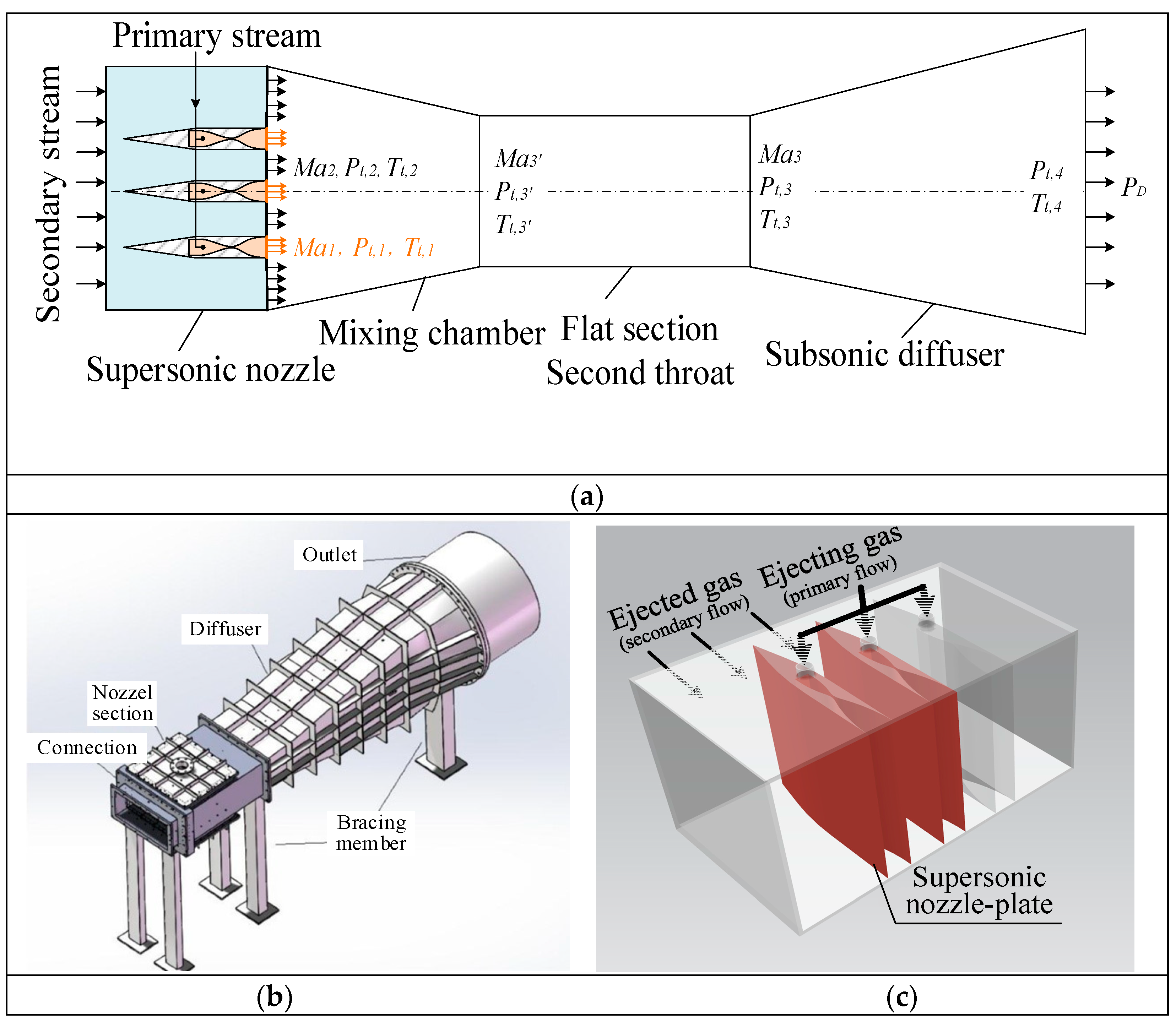
2. One-Dimensional Diffuser Model
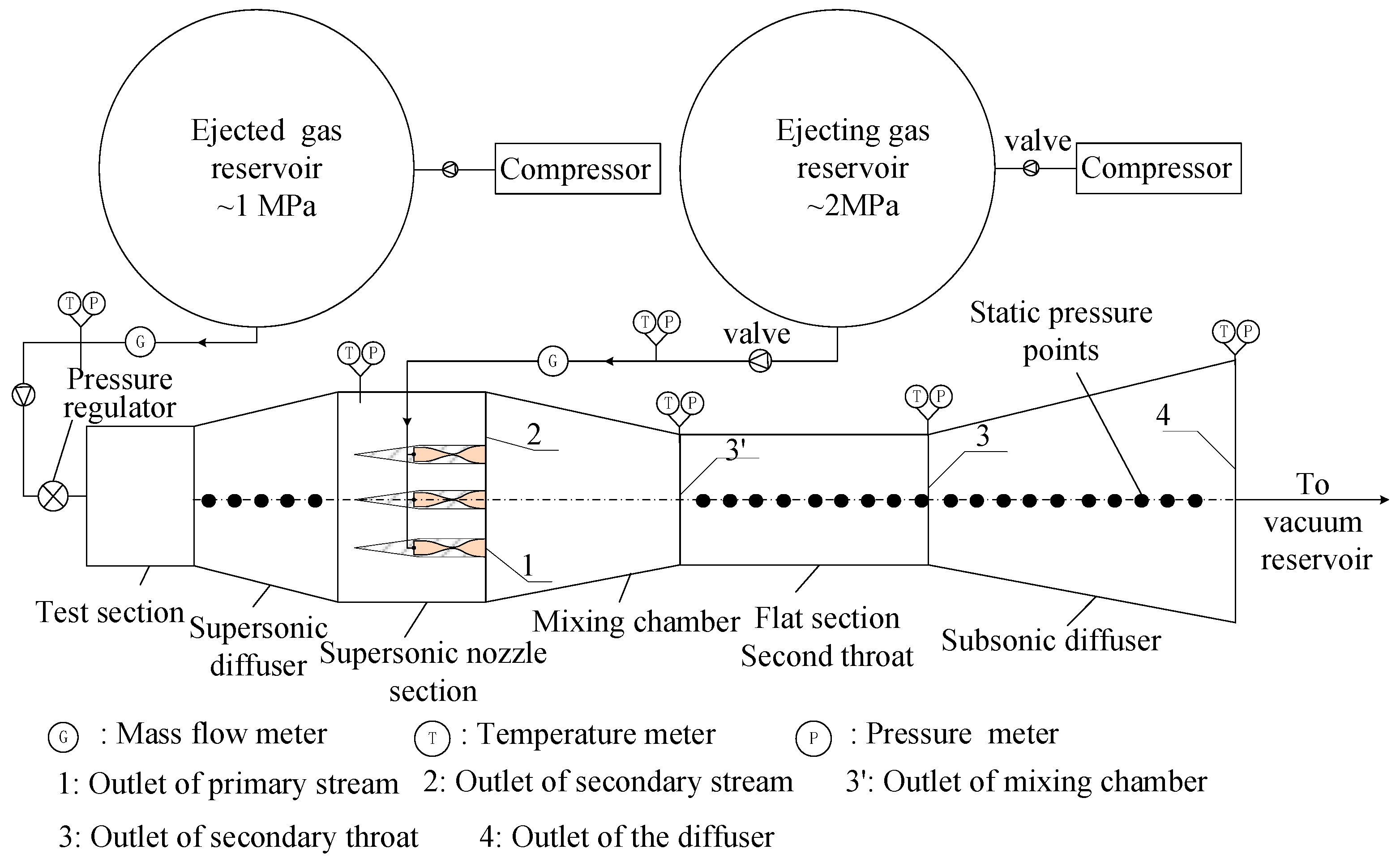
3. Experimental Setup
4. Results and Discussion
4.1. Design and Analysis of Ejector–Diffuser System
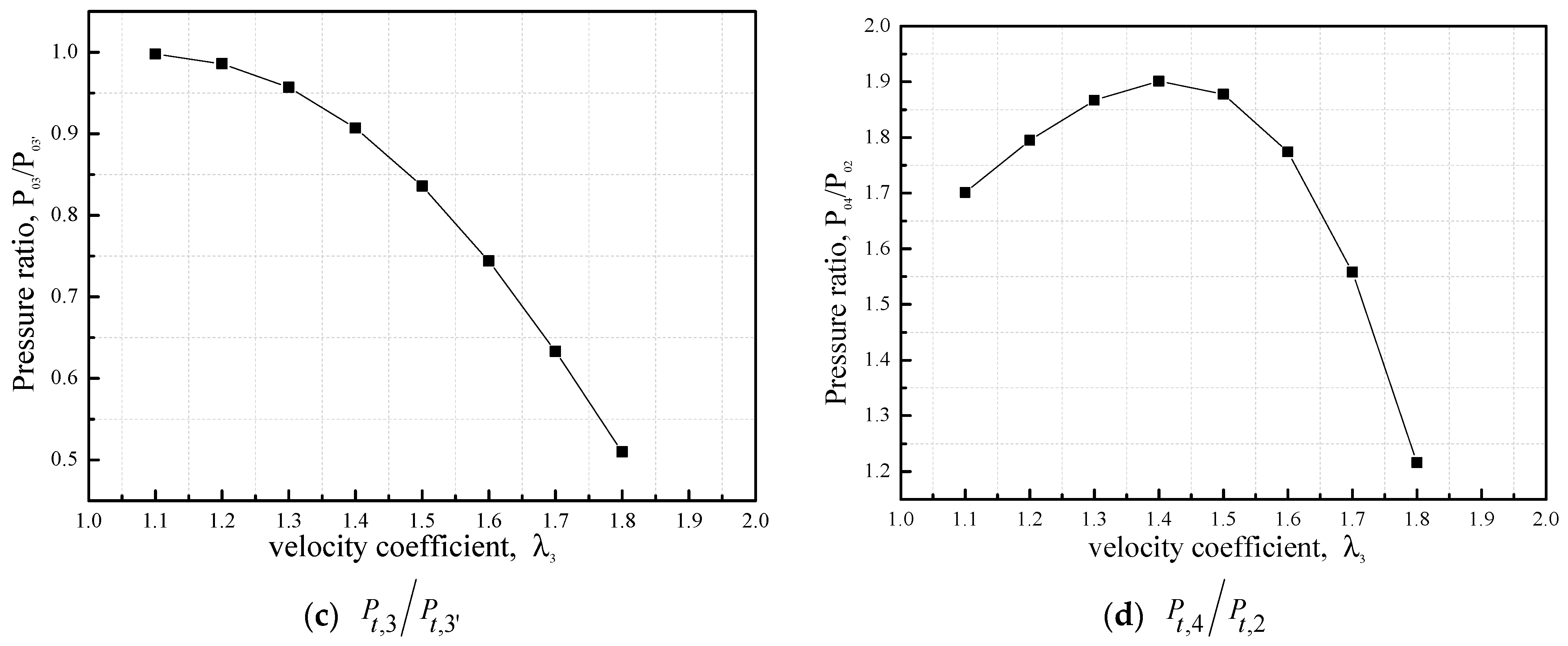
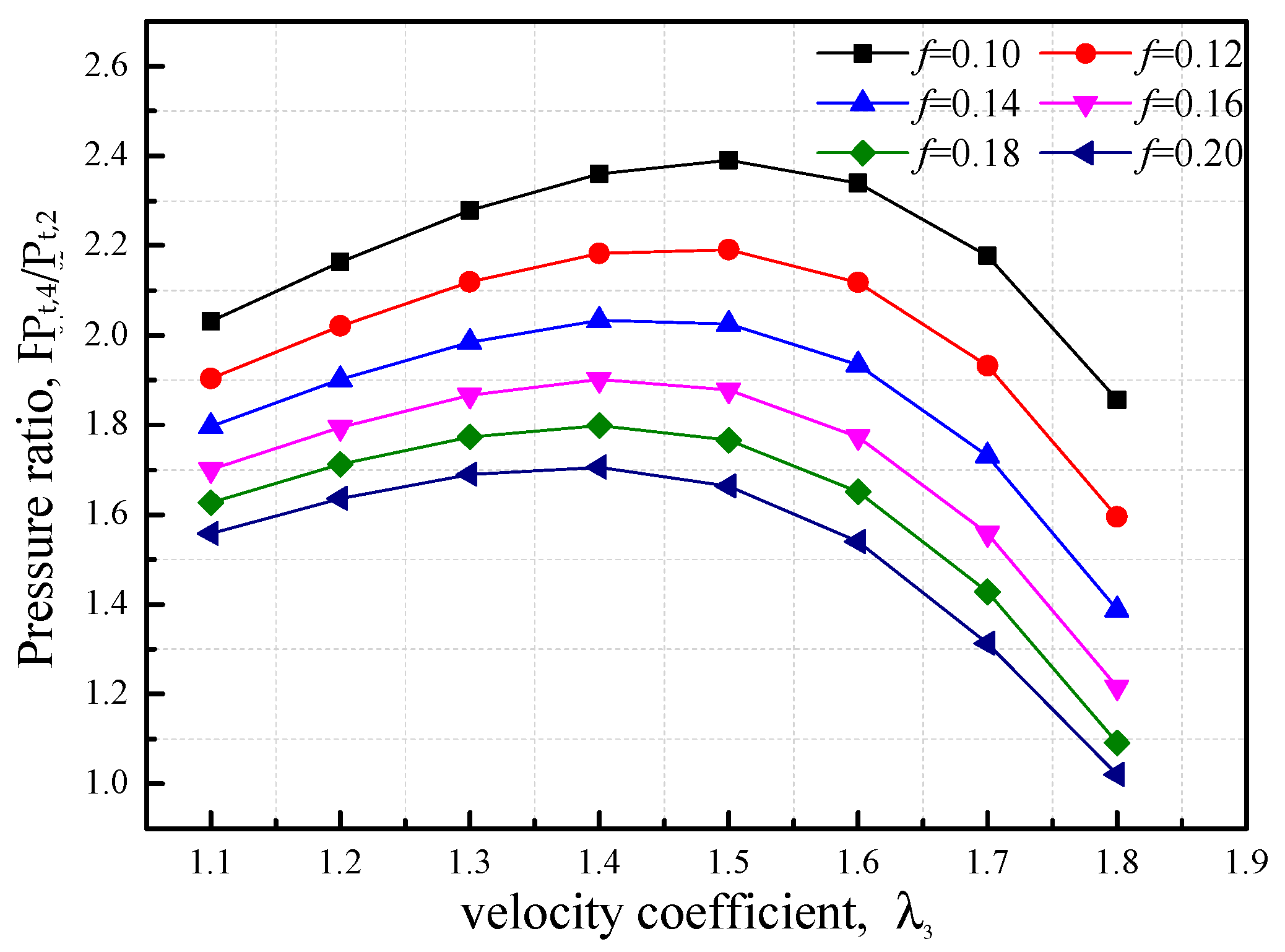
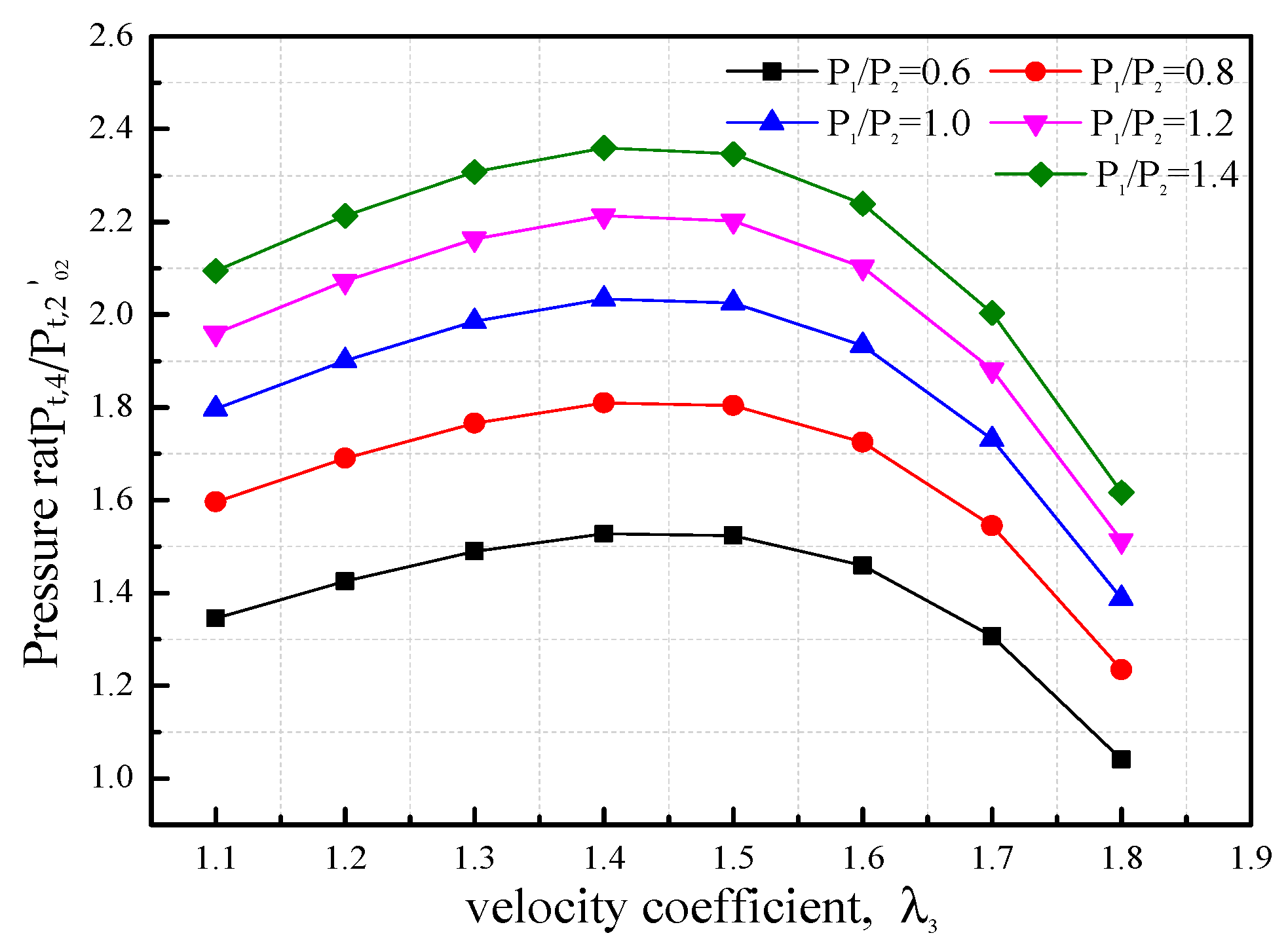
4.1.1. Performance Parameters vs. Velocity Coefficient
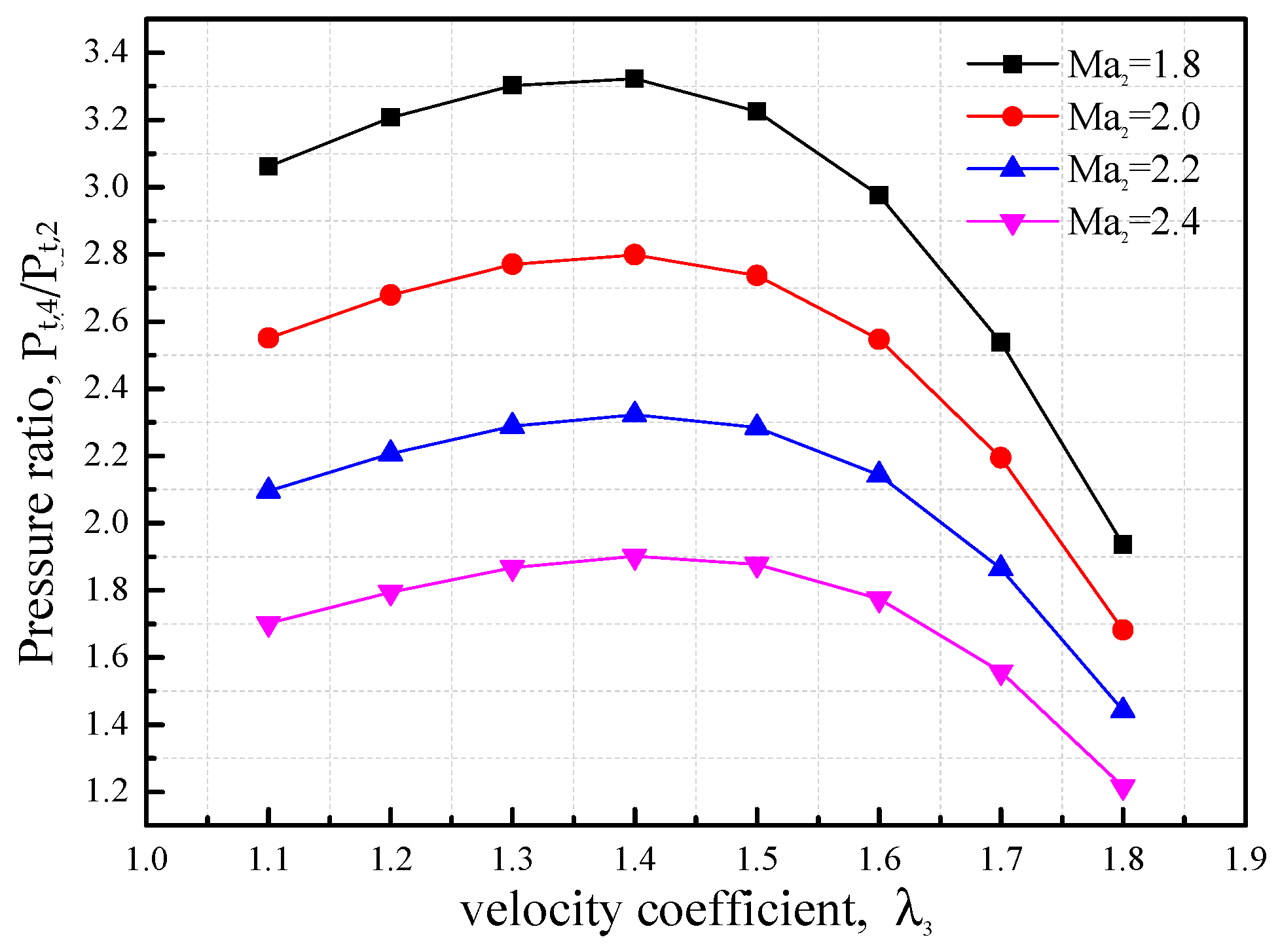
4.1.2. Effect of Mach Number
4.1.3. Effect of Mass Flow Rate
4.1.4. Effect of Static Pressure
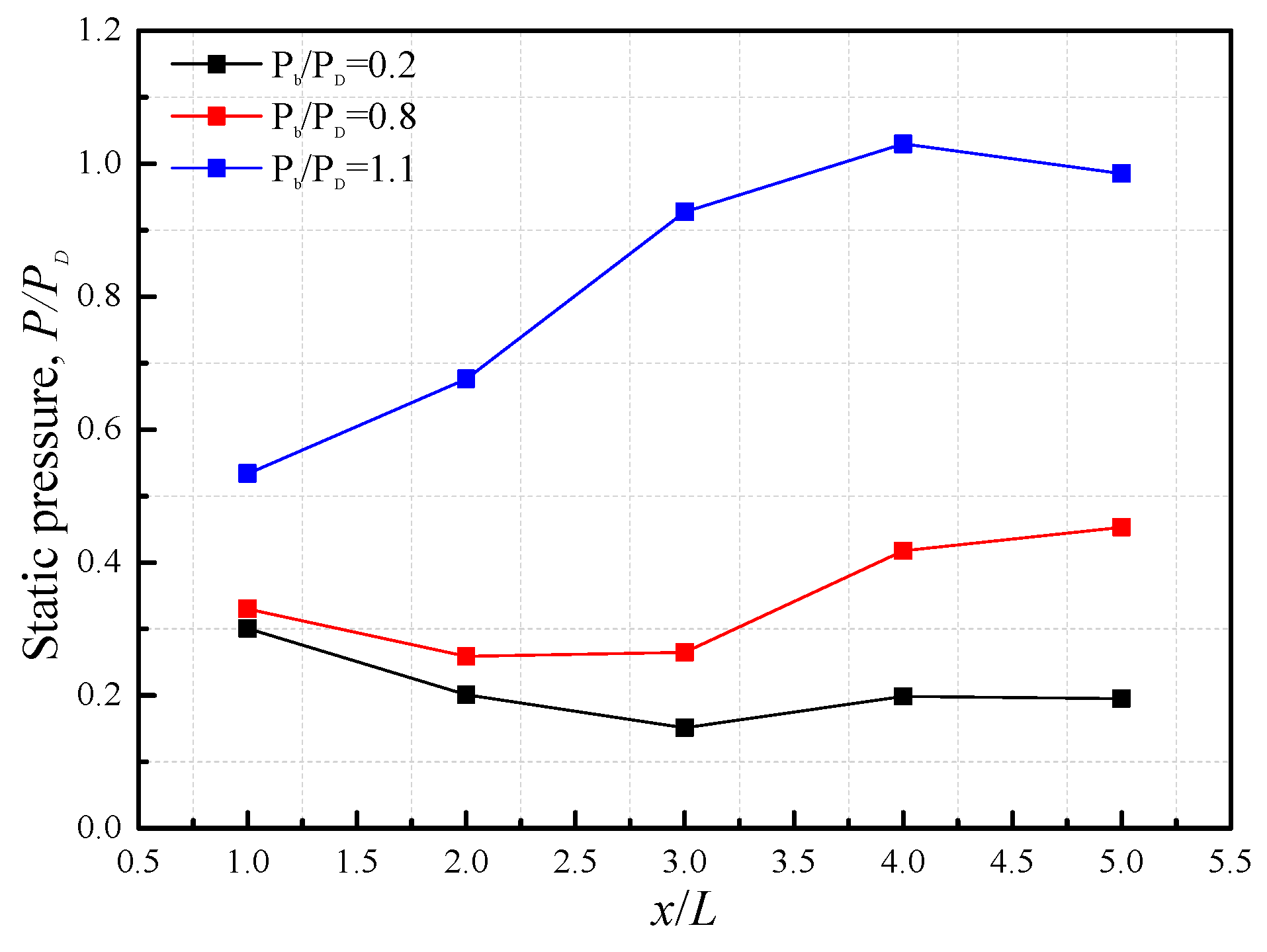
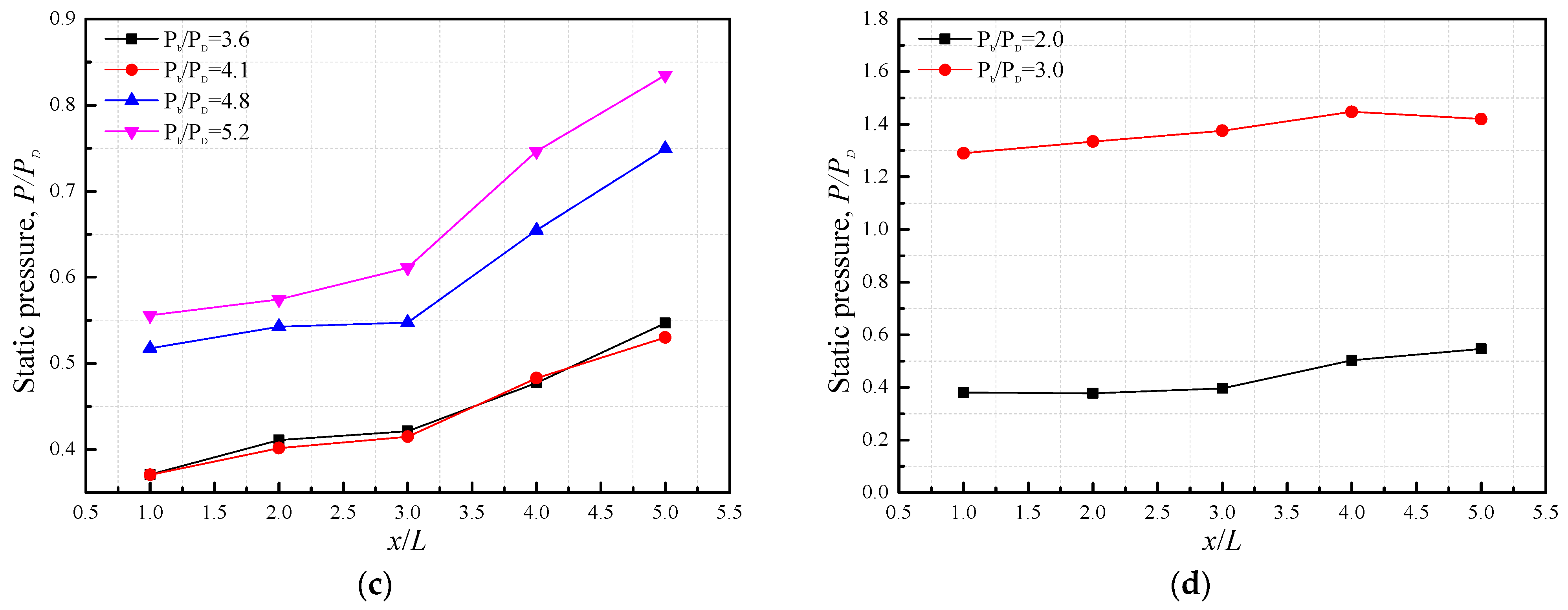
4.2. Static Wall Pressure of Supersonic Diffuser
4.3. Performance of Ejector–Diffuser
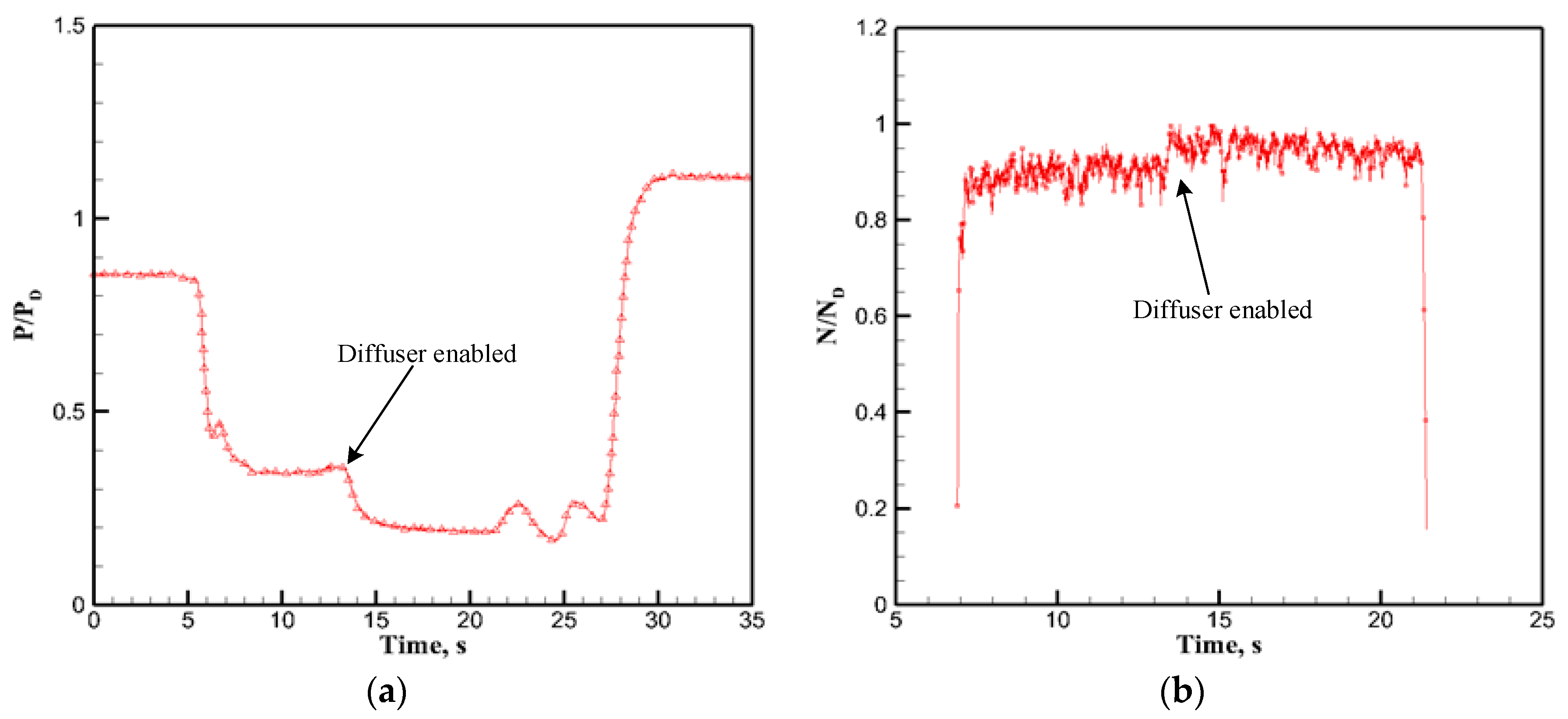
4.3.1. Pressure Controlling Performance in Wind Tunnel Test
4.3.2. Power Enhancement for COIL Laser
5. Conclusions
- (1)
- For given inlet gas parameters, the initial cross-section area of the supersonic–supersonic ejector–diffuser can be determined through 1D analysis. It was found that the optimal contraction ratio of the mixing chamber can be predicted by the designed pressure ratio and mass flow ratio.
- (2)
- The aerodynamic choking phenomenon occurs when the inlet pressure of the ejecting stream reaches a critical value, resulting in the high-frequency vibration of the ejector system. Therefore, the off-designed operating condition should be clarified and avoided.
- (3)
- The position, type and number of nozzle plates have a significant influence on the pressure-boosting ability. For an ejector–diffuser system with three long nozzle plates, the outlet pressure of the ejector can be boosted to a maximum value of 4.5 PD, while an ejector–diffuser system with three short nozzle plates has a better ability in terms of stabilizing pressure, and the outlet pressure can be improved to 4.1 ~5.2 .
- (4)
- The designed supersonic–supersonic ejector–diffuser system has a wide range of working conditions and is economically viable. Different operating conditions can be realized by changing the number and type of nozzle plates. The experimental results show that long nozzle plates exhibit better performance in terms of maintaining pressure stability in the test section while short nozzle plates have a better pressure-matching performance and entrainment ratio under high-backpressure conditions.
- (5)
- The boundary layer and the shock interaction can be easily controlled by adjusting the position of the nozzle plate in a supersonic–supersonic ejector with a rectangular section compared with a round ejector. The boundary layer can be destroyed by setting the supersonic nozzle plate near the wall region.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Sectional area, m2 | |
| Specific heat, J kg−1 K−1 | |
| Sound velocity, m s−1 | |
| Critical sound velocity, m s−1 | |
| Gas velocity, m s−1 | |
| Entrainment ratio, | |
| Mach number | |
| Pressure ratio, | |
| Mass flow rate, kg s−1 | |
| Static pressure, kPa | |
| Total pressure, kPa | |
| Global gas constant number | |
| Total temperature, K | |
| Static temperature, K | |
| Greek Symbols | |
| Ratio of area, | |
| Ratio of area, | |
| Velocity coefficient, | |
| Ratio of specific heat, | |
| Ratio of specific heat, | |
| Ratio of total temperature, | |
| Subscripts | |
| 0 | Stagnation parameter |
| 1 | Outlet of nozzle-plates |
| 2 | Outlet of nozzle section |
| 3′ | Outlet of mixing chamber |
| 3 | Outlet of flat section |
| 4 | Outlet of subsonic diffuser |
References
- Zhang, J.; Geng, J.; Yang, S.; Cheng, F.; Zhu, G.; Wang, C.; Yang, Z.; Lyu, Y. Influence of geometric parameters on the performance of ejector used in aeroengine air system. Therm. Sci. Eng. Prog. 2023, 37, 101571. [Google Scholar] [CrossRef]
- Zhang, J.-Y.; Wang, C.; Yang, S.; Cheng, F.-N.; Geng, J.X.; Yang, Z.X.; Lyu, Y.W.; Yu, L. Research on Performance of Multi-nozzle Ejector for Aero-engine Air System. Therm. Sci. Eng. Prog. 2023, 38, 101651. [Google Scholar] [CrossRef]
- Braimakis, K. Solar ejector cooling systems: A review. Renew. Energy 2021, 164, 566–602. [Google Scholar] [CrossRef]
- Braccio, S.; Guillou, N.; Le Pierrès, N.; Tauveron, N.; Phan, H.T. Mass-flowrate-maximization thermodynamic model and simulation of supersonic real-gas ejectors used in refrigeration systems. Therm. Sci. Eng. Prog. 2023, 37, 101615. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, Z.; Yang, Y.; Jiang, P.X. Flow Visualization of Supersonic Two-phase Transcritical Flow of CO2 in an Ejector of a Refrigeration System. Int. J. Refrig. 2017, 74, 354–361. [Google Scholar] [CrossRef]
- Ünal, S.; Cihan, E.; Erdinç, M.T.; Bilgili, M. Influence of mixing section inlet and diffuser outlet velocities on the performance of ejector-expansion refrigeration system using zeotropic mixture. Therm. Sci. Eng. Prog. 2022, 33, 101338. [Google Scholar] [CrossRef]
- Bharate, G.; Kumar, R.A. Starting transients in second throat vacuum ejectors for high altitude testing facilities. Aerosp. Sci. Technol. 2021, 113, 106687. [Google Scholar] [CrossRef]
- Lijo, V.; Kim, H.D.; Matsuo, S.; Setoguchi, T. A study of the supersonic ejector–diffuser system with an inlet orifice. Aerosp. Sci. Technol. 2012, 23, 321–329. [Google Scholar] [CrossRef]
- Karthick, S.K.; Rao, S.M.V.; Jagadeesh, G.; Reddy, K.P.J. Experimental parametric studies on the performance and mixing characteristics of a low area ratio rectangular supersonic gaseous ejector by varying the secondary flow rate. Energy 2018, 161, 832–845. [Google Scholar] [CrossRef]
- Kuo, J.K.; Wu, P.R.; Yang, T.F.; Yan, W.M. Optimal technical analysis of vacuum ejector for passive hydrogen recovery. Int. J. Hydrog. Energy 2023, 48, 8260–8272. [Google Scholar]
- Li, Y.; Shen, S.; Niu, C.; Mu, X.; Zhang, L. The effect of variable motive pressures on the performance and shock waves in a supersonic steam ejector with non-equilibrium condensing. Int. J. Therm. Sci. 2023, 185, 108034. [Google Scholar] [CrossRef]
- Śmierciew, K.; Butrymowicz, D.; Karwacki, J.; Bergander, M.J.; Gagan, J. Design, fabrication, and investigations of prototype supersonic micro-ejector for innovative cooling system of electronic components. Int. J. Refrig. 2023, 153, 323–336. [Google Scholar] [CrossRef]
- Barber, T.J.; Anderson, O.L. Computational Study of a Supersonic Mixer-ejector Exhaust System. J. Propuls. Power 1992, 8, 927–934. [Google Scholar] [CrossRef][Green Version]
- Tyagi, R.K.; Rajesh, R.; Singhal, G.; Mainuddin; Dawar, A.L.; Endo, M. Parametric studies of a supersonic COIL with angular jet singlet oxygen generator. Infrared Phys. Technol. 2003, 44, 271–279. [Google Scholar] [CrossRef]
- Tyagi, R.K.; Rajesh, R.; Singhal, G.; Mainuddin; Dawar, A.L.; Endo, M. Supersonic COIL with angular jet singlet oxygen generator. Opt. Laser Technol. 2003, 35, 395–399. [Google Scholar] [CrossRef]
- Singhal, G.; Mainuddin; Rajesh, R.; Tyagi, R.K.; Dawar, A.L. Supersonic diffuser for pressure recovery in SCOIL system. Opt. Laser Technol. 2010, 42, 219–224. [Google Scholar] [CrossRef]
- Opgenorth, M.J.; Sederstrom, D.; McDermott, W.; Lengsfeld, C.S. Maximizing pressure recovery using lobed nozzles in a supersonic ejector. Appl. Therm. Eng. 2012, 37, 396–402. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Z.; Wu, J.; Xu, W. Investigation on the pressure matching performance of the constant area supersonic-supersonic ejector. Therm. Sci. 2015, 19, 631–643. [Google Scholar] [CrossRef]
- Petrovic, A.; Jovanovic, M.Z.; Genic, S.; Bugaric, U.; Delibasic, B. Evaluating performances of 1-D models to predict variable area supersonic gas ejector performances. Energy 2018, 163, 270–289. [Google Scholar] [CrossRef]
- Hanafi, A.S.; Mostafa, G.M.; Waheed, A.; Fathy, A. 1-D Mathematical Modeling and CFD Investigation on Supersonic Steam Ejector in MED-TVC. Energy Procedia 2015, 75, 3239–3252. [Google Scholar] [CrossRef]
- Rao, S.M.V.; Jagadeesh, G. Novel Supersonic Nozzles for Mixing Enhancement in Supersonic Ejectors. Appl. Therm. Eng. 2014, 71, 62–71. [Google Scholar] [CrossRef]
- Eames, I.; Aphornratana, S.; Haider, H. A theoretical and experimental study of a small-scale steam jet refrigerator. Int. J. Refrig. 1995, 18, 378–386. [Google Scholar] [CrossRef]
- Yadav, S.K.; Pandey, K.M.; Kumar, V.; Gupta, R. Computational analysis of a supersonic two-stage ejector. Mater. Today Proc. 2021, 38, 2700–2705. [Google Scholar] [CrossRef]
- Kumar, V.; Singhal, G.; Subbarao, P.M.V. Study of supersonic flow in a constant rate of momentum change (CRMC) ejector with frictional effects. Appl. Therm. Eng. 2013, 60, 61–71. [Google Scholar] [CrossRef]
- Lamberts, O.; Chatelain, P.; Bartosiewicz, Y. Numerical and experimental evidence of the Fabri-choking in a supersonic ejector. Int. J. Heat Fluid Flow 2018, 69, 194–209. [Google Scholar] [CrossRef]
- Ye, W.; Zhang, J.; Xu, W.; Zhang, Z. Numerical investigation on the flow structures of the multi-strut mixing enhancement ejector. Appl. Therm. Eng. 2020, 179, 115653. [Google Scholar] [CrossRef]
- Chong, D.; Hu, M.; Chen, W.; Wang, J.; Liu, J.; Yan, J. Experimental and numerical analysis of supersonic air ejector. Appl. Energy 2014, 130, 679–684. [Google Scholar] [CrossRef]
- Rizzo, F.; D’Alessandro, V.; Montelpare, S.; Giammichele, L. Computational study of a bluff body aerodynamics: Impact of the laminar-to-turbulent transition modeling. Int. J. Mech. Sci. 2020, 178, 105620. [Google Scholar] [CrossRef]
- Chong, D.; Yan, J.; Wu, G.; Liu, J. Structural optimization and experimental investigation of supersonic ejectors for boosting low pressure natural gas. Appl. Therm. Eng. 2009, 29, 2799–2807. [Google Scholar] [CrossRef]
- Bouhanguel, A.; Desevaux, P.; Gavignet, E. Flow visualization in supersonic ejectors using laser tomography techniques. Int. J. Refrig. 2011, 34, 1633–1640. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Jia, L.; Zhao, H.; Wang, C. Influence investigation of friction on supersonic ejector performance. Int. J. Refrig. 2018, 85, 229–239. [Google Scholar] [CrossRef]
- El Zohbi, B.; Bukharin, N.; Assoum, H.H.; Abed-Meraim, K.; Sakout, A.; El Hassan, M. Investigation of the effects of the jet nozzle geometry and location on the performance of supersonic fluid ejectors. Energy Rep. 2022, 8, 228–233. [Google Scholar] [CrossRef]




| Parameters | Value | Unit |
|---|---|---|
| 4.5 | - | |
| 300 | K | |
| 0.5~2.0 | MPa | |
| 1.4 | - | |
| 287 | J kg−1 K−1 |
| Parameters | Value | Unit |
|---|---|---|
| 2.4 | - | |
| 600 | K | |
| 0.2~100 | kPa | |
| 1.5 | - | |
| 849 | J kg−1 K−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, D.; Gu, Y.; Li, W.; Chen, J. Experimental Investigation of the Performance of a Novel Ejector–Diffuser System with Different Supersonic Nozzle Arrays. Fluids 2024, 9, 155. https://doi.org/10.3390/fluids9070155
Xu D, Gu Y, Li W, Chen J. Experimental Investigation of the Performance of a Novel Ejector–Diffuser System with Different Supersonic Nozzle Arrays. Fluids. 2024; 9(7):155. https://doi.org/10.3390/fluids9070155
Chicago/Turabian StyleXu, Dachuan, Yunsong Gu, Wei Li, and Jingxiang Chen. 2024. "Experimental Investigation of the Performance of a Novel Ejector–Diffuser System with Different Supersonic Nozzle Arrays" Fluids 9, no. 7: 155. https://doi.org/10.3390/fluids9070155
APA StyleXu, D., Gu, Y., Li, W., & Chen, J. (2024). Experimental Investigation of the Performance of a Novel Ejector–Diffuser System with Different Supersonic Nozzle Arrays. Fluids, 9(7), 155. https://doi.org/10.3390/fluids9070155








