Two-Dimensional Carbon: A Review of Synthesis Methods, and Electronic, Optical, and Vibrational Properties of Single-Layer Graphene
Abstract
:1. Introduction
- Carbon-Based Nanomaterials
- Low-Dimensional Materials
- concerning materials whose nanometric scale implies a reduced dimensionality (that is the presence of at least one dimension which is much smaller to the other ones), which gives rise to some peculiar properties. Therefore, beyond a classic three-dimensional material, two-, one-, and zero-dimensional nanomaterials can be found [15,16].
2. Carbon
- sp hybridization
- which involves the 2s orbital and a single 2p orbital (Figure 3a). The resulting two hybrid orbitals are placed at intermediate energy (Figure 3b), are characterized by asymmetric lobes (due to the 2p contribution), and aligned on a single axis, thus assuming a linear geometry (Figure 3c). In the formation of molecular bonds, the sp orbitals contribute to the formation of a triple bond together with two remaining 2p orbitals, as in ethyne molecule. In this case, two carbon atoms share the electron of one sp orbital to form one σ bond and the electrons of both the remaining 2p orbitals to form a π bonds (Figure 3d).
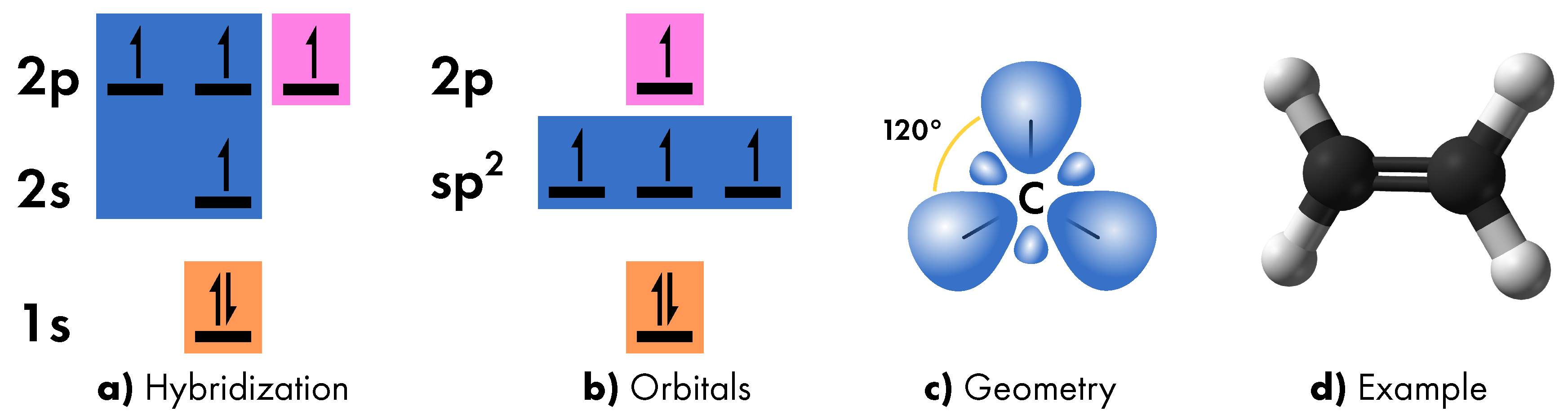
- sp2 hybridization
- which involves the 2s orbital and two 2p orbitals (Figure 4a). As in the previous case, the three hybrid orbitals are placed at intermediate energy (Figure 4b), are characterized by asymmetric lobes (due to the 2p contribution), but are now arranged along three different axes, thus assuming a planar triangular geometry (Figure 4c). In the formation of molecular bonds, the sp2 orbitals contribute to the formation of a double bond together with the only remaining 2p orbital, as in ethene molecule. In this case, the two carbon atoms share one electron of one sp2 orbital so as to form a σ bond and the electron of the remaining 2p orbital for the formation of a π bond (Figure 4d). A notable case is benzene molecule whereby three π bonds give rise to a delocalized orbital all around the carbon hexagon. Such a feature is relevant for electron transport in carbon systems.
- sp3 hybridization
- which involves the 2s orbital and all the 2p orbitals (Figure 5a). As in the previous case, the three hybrid orbitals are placed at intermediate energy (Figure 5b), are characterized by asymmetric lobes (due to the 2p contribution), but are now arranged along four different axes, thus assuming a tetrahedral geometry (Figure 5c). In the formation of molecular bonds, the sp3 orbitals contribute to the formation of single bonds, as in ethane molecule. In this case, the two carbon atoms share only the electron of one sp3 orbital to form a σ bond (Figure 5d).
Allotropes of Carbon
3. Electronic Structure
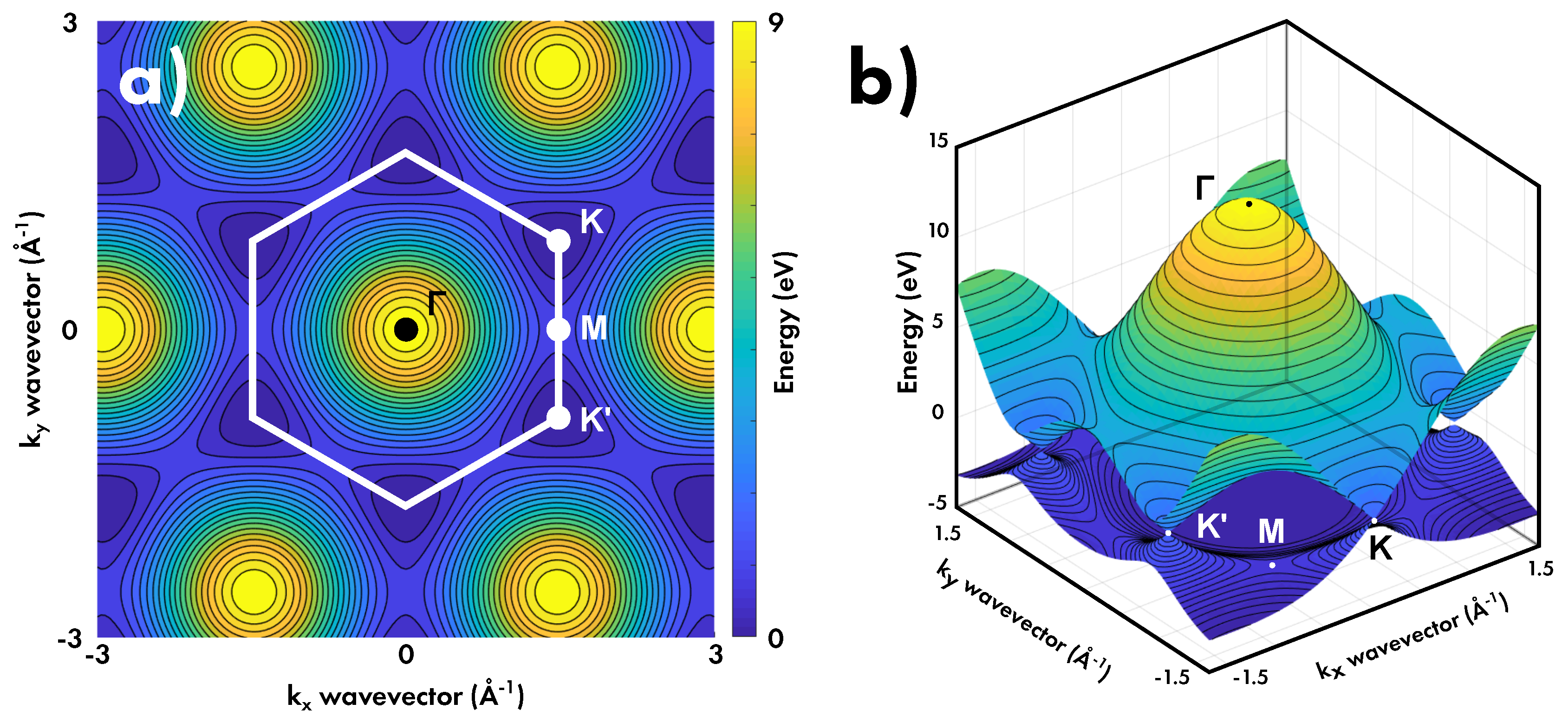
3.1. Energy Bands
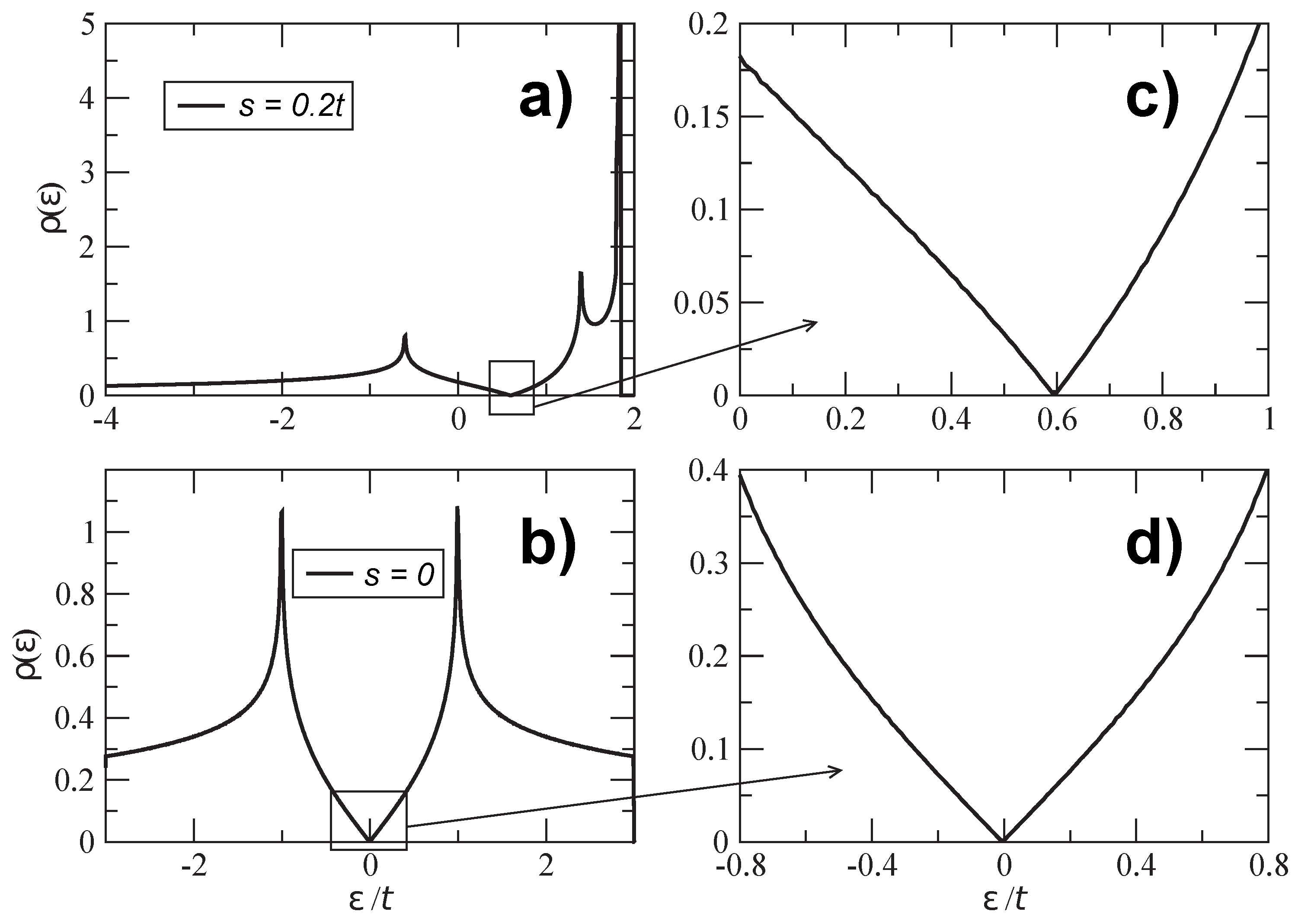
3.2. Charge Carrier Density
4. Optical Properties
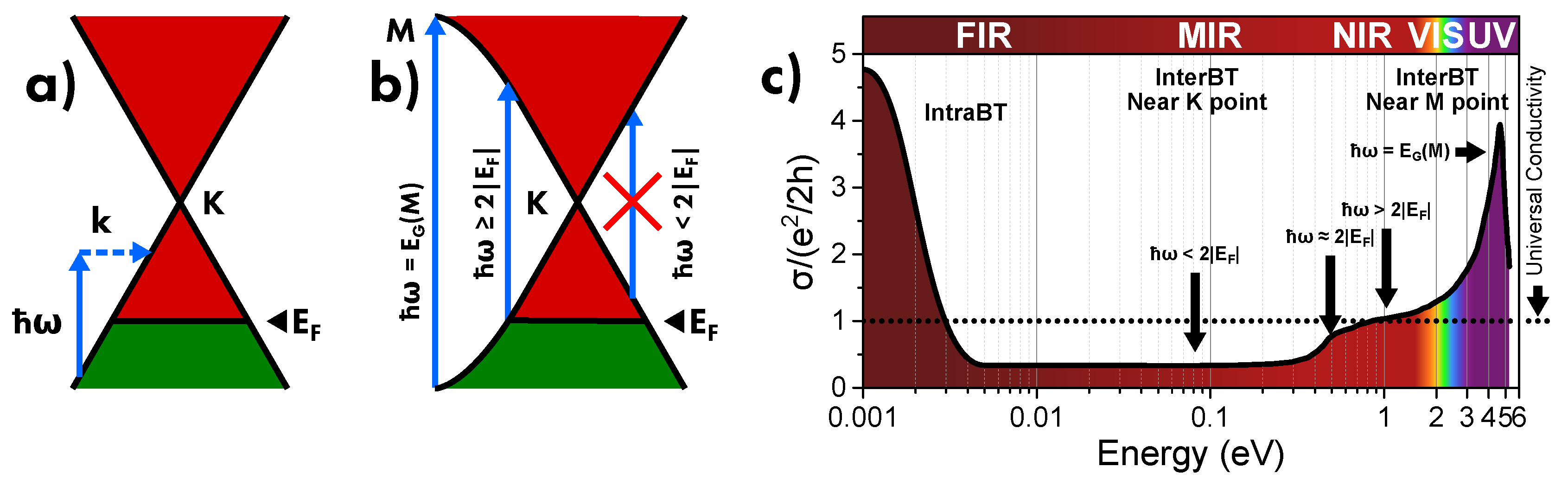
4.1. Light Absorption
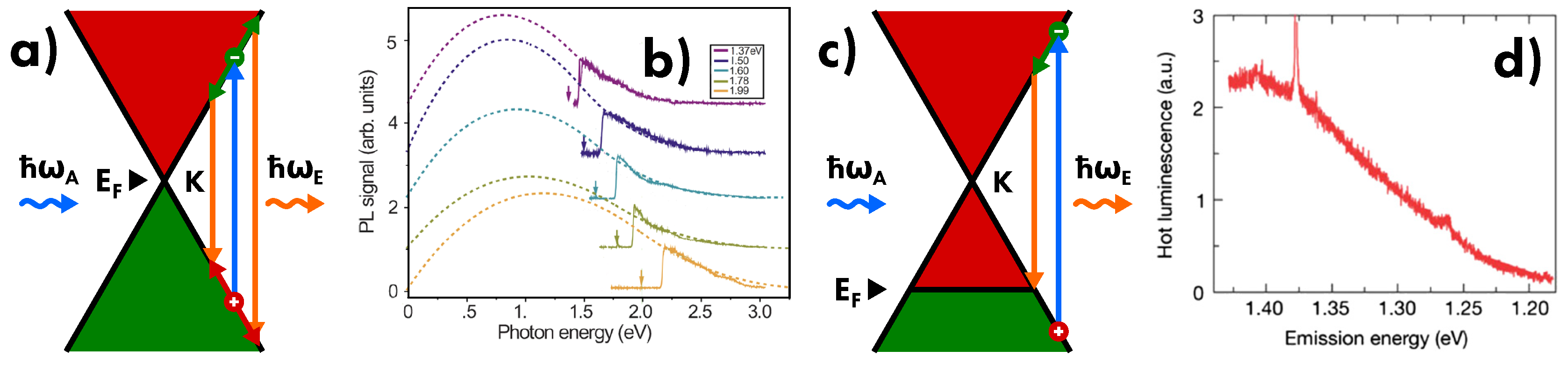
4.2. Light Emission
5. Vibrational Properties
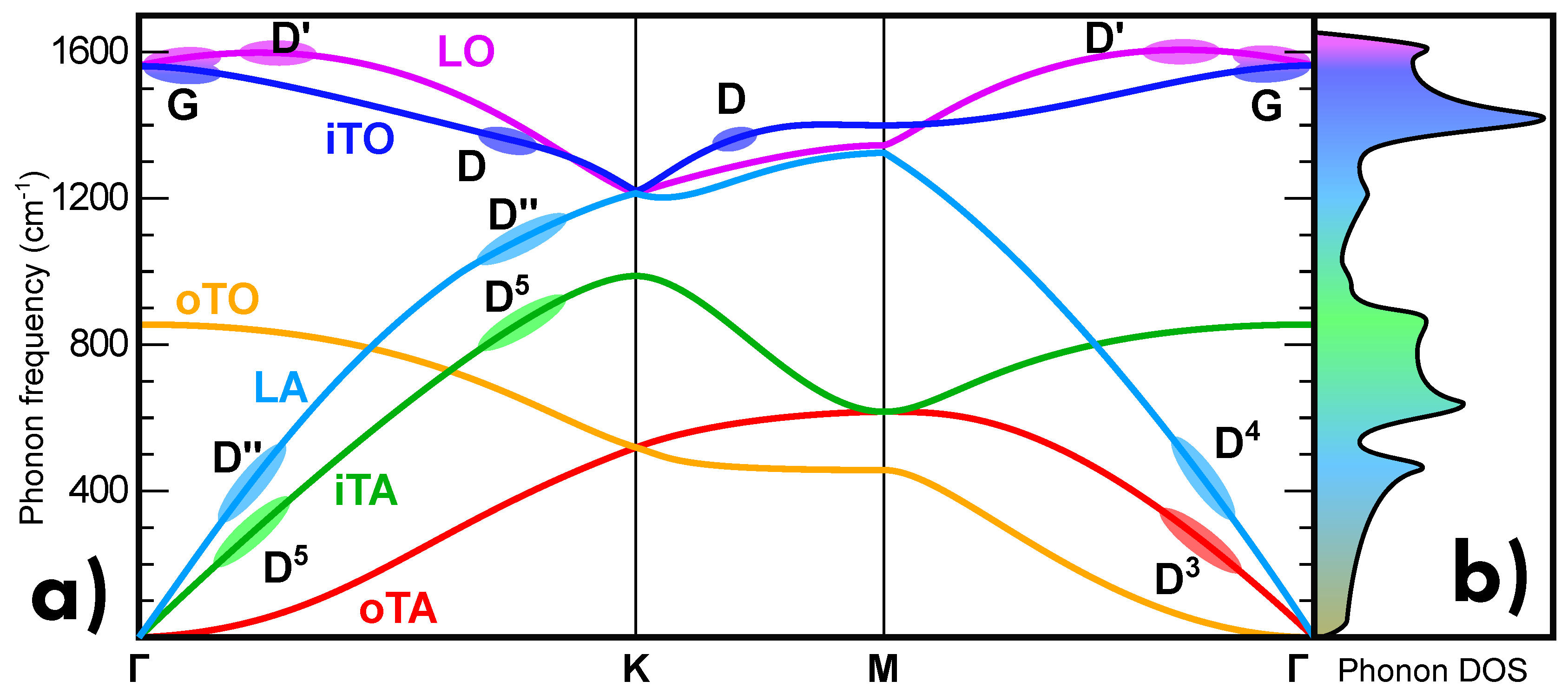
5.1. Normal Modes and Phonon Dispersion
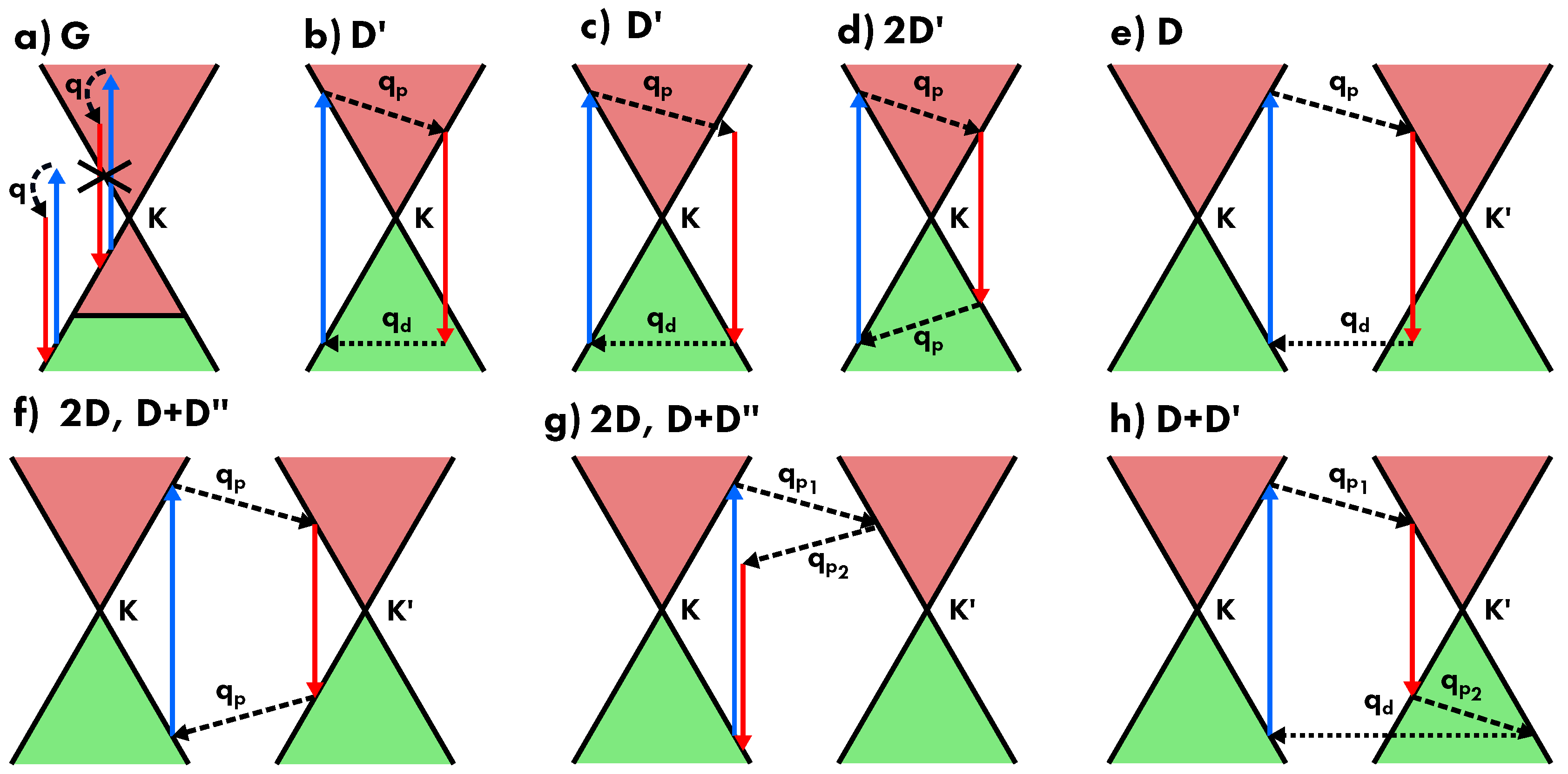
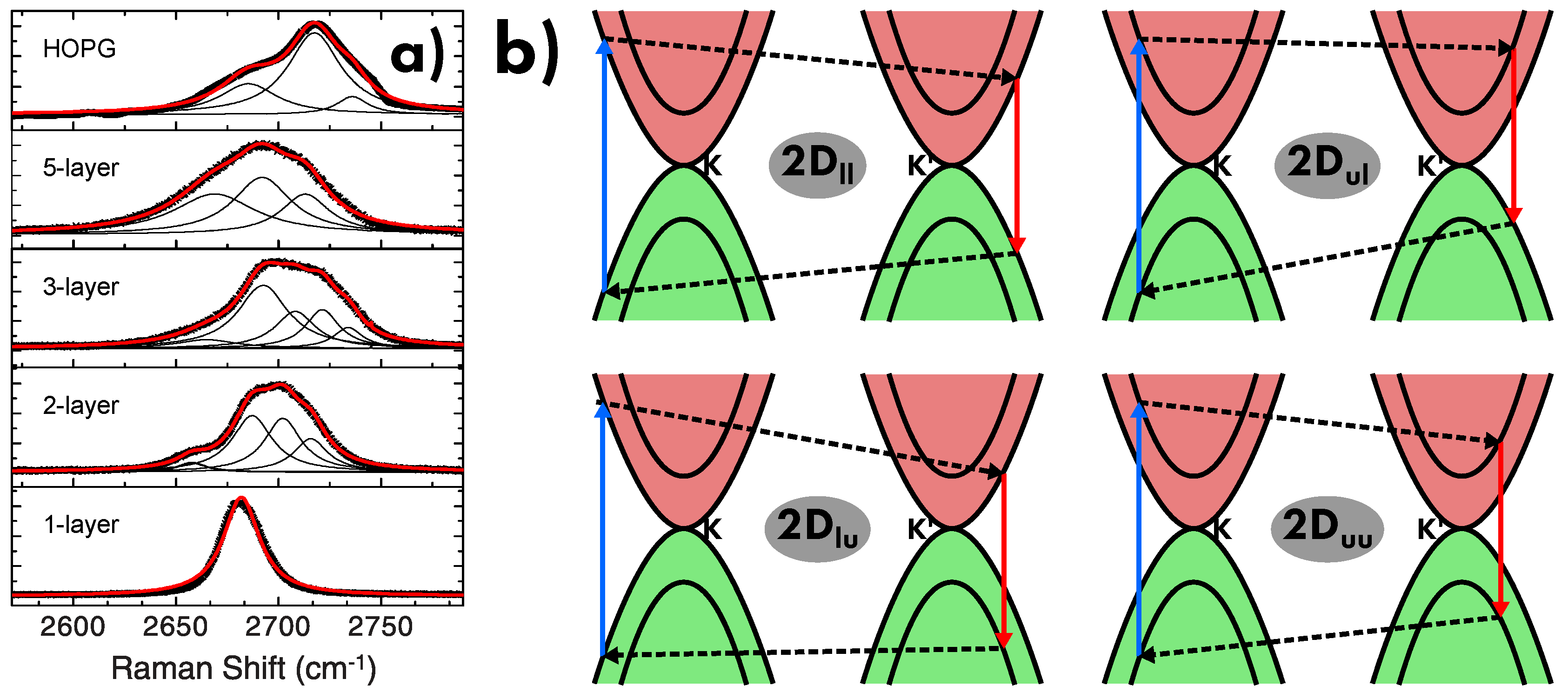
5.2. Raman Scattering Processes
- G band:
- belongs to a single-phonon process, in which a non-resonant electron-hole pair is scattered by a low-wavevector phonon in iTO branch corresponding to the two E2g vibrational modes (Figure 16a).
- D’ band:
- belongs to an intravalley defect-assisted single-phonon process, in which a resonant electron-hole pair is scattered by a low-q phonon in LO branch corresponding to the two E’ vibrational modes and by a defect (Figure 16b,c).
- 2D’ band:
- intravalley two-phonon process, in which a resonant electron-hole pair is scattered by two equal low-q phonons in LO branch corresponding to the two E’ vibrational modes (Figure 16d).
- D band:
- intervalley defect-assisted one-phonon process, in which a resonant electron-hole pair is scattered by a high-q phonon in iTO branch corresponding to the A’1 vibrational mode and by a defect (Figure 16e).
- 2D band:
- intervalley two-phonon process, in which a resonant electron-hole pair is scattered by two equal high-q phonons in iTO branch corresponding to the A’1 vibrational mode (Figure 16f,g).
- D+D’ band:
- intervalley defect-assisted two-phonon process, in which a resonant electron-hole pair is scattered by two different wavevector phonons, the one at low-q in iTO branch corresponding to the two E’ vibrational modes and the other at high-q in LO branch corresponding to the A’1 vibrational mode, and by a defect (Figure 16h).
- D+D’’ band:
- intervalley defect-assisted two-phonon process, in which a resonant electron-hole pair is scattered by two different wavevector phonons both at high-q value, the one in iTO corresponding to the two E’ vibrational modes and the other in LA branch corresponding to the E’ vibrational mode (Figure 16f,g).
6. Influencing Factors on Raman Scattering
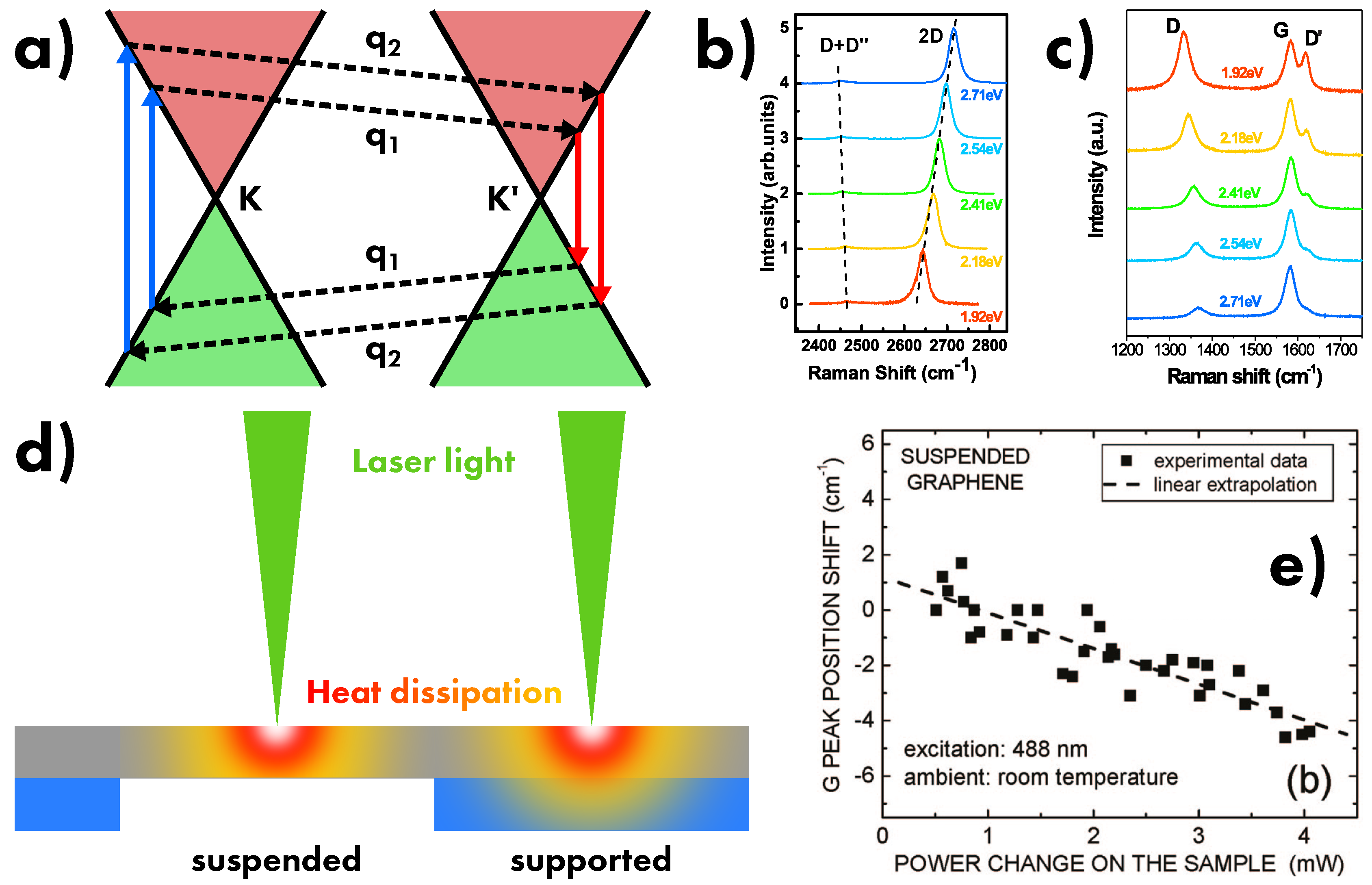
6.1. Laser Energy and Power
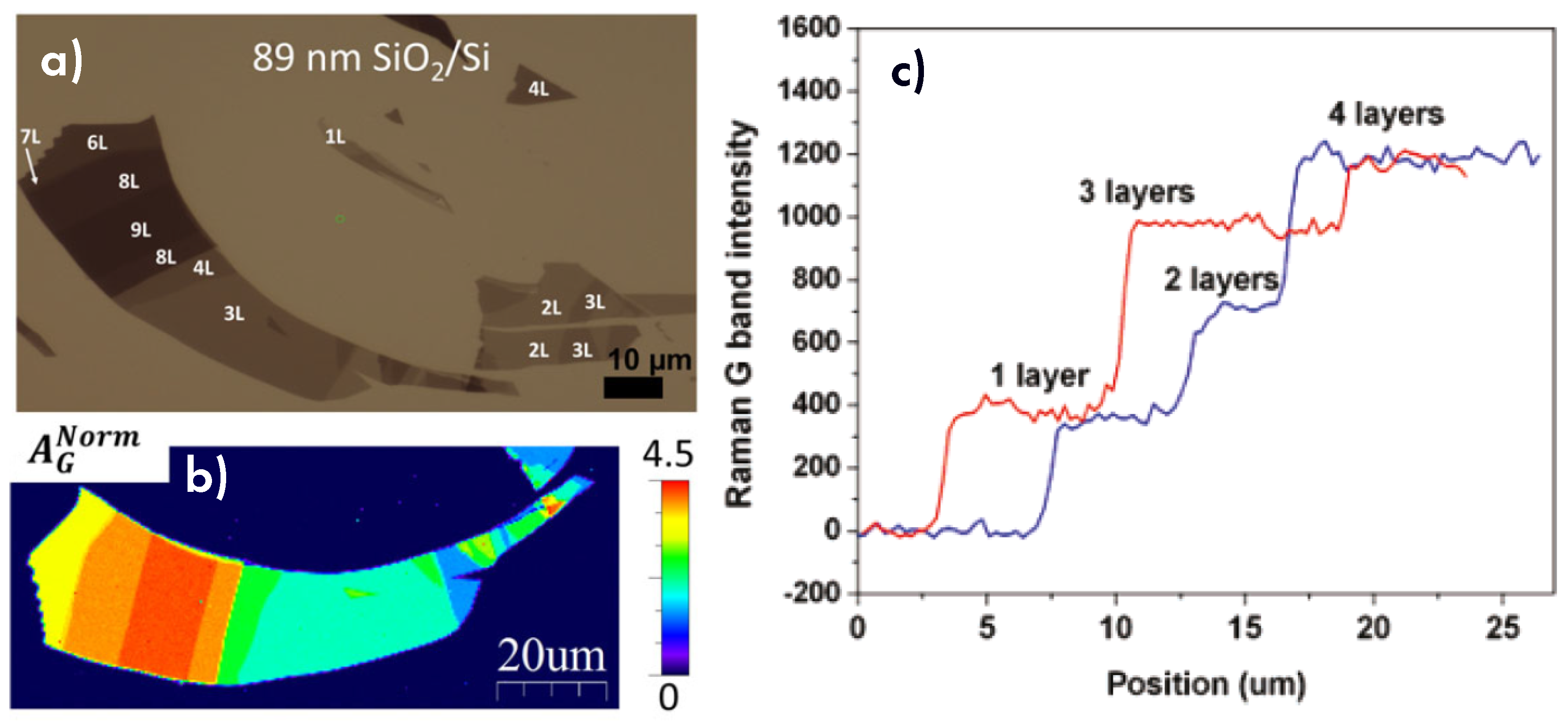
6.2. Number of Layers
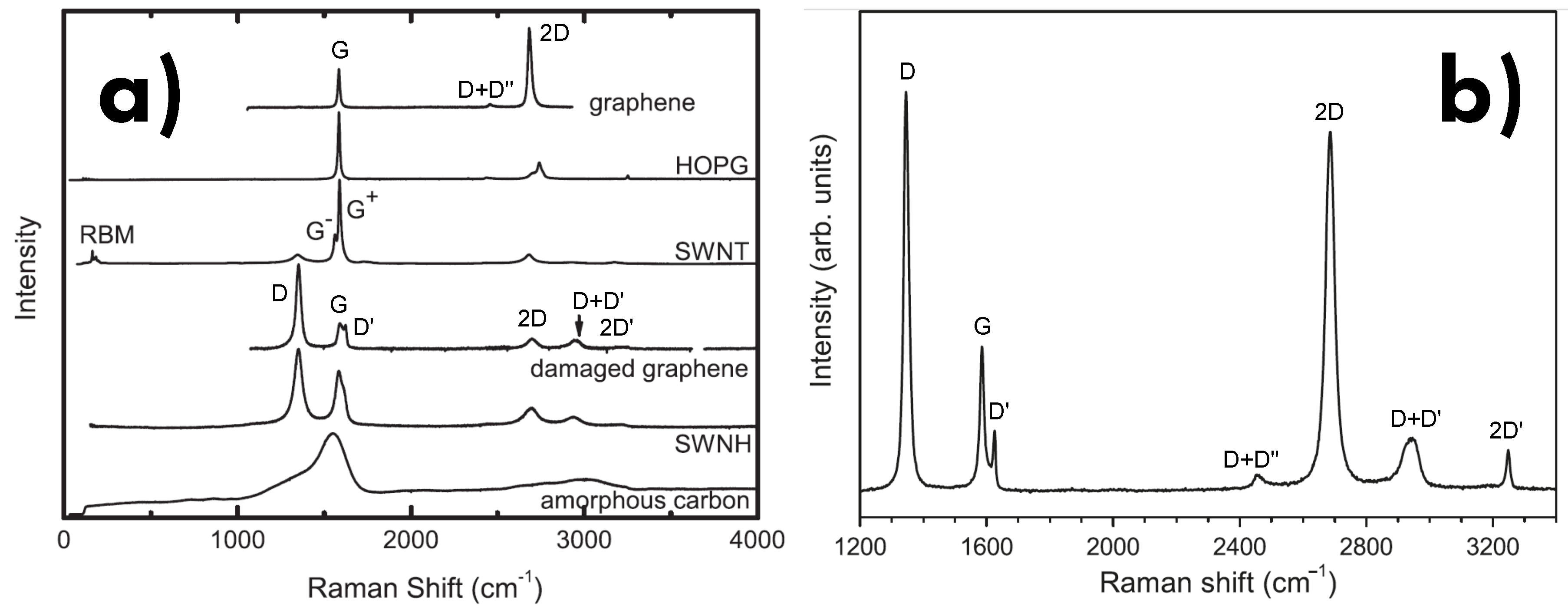
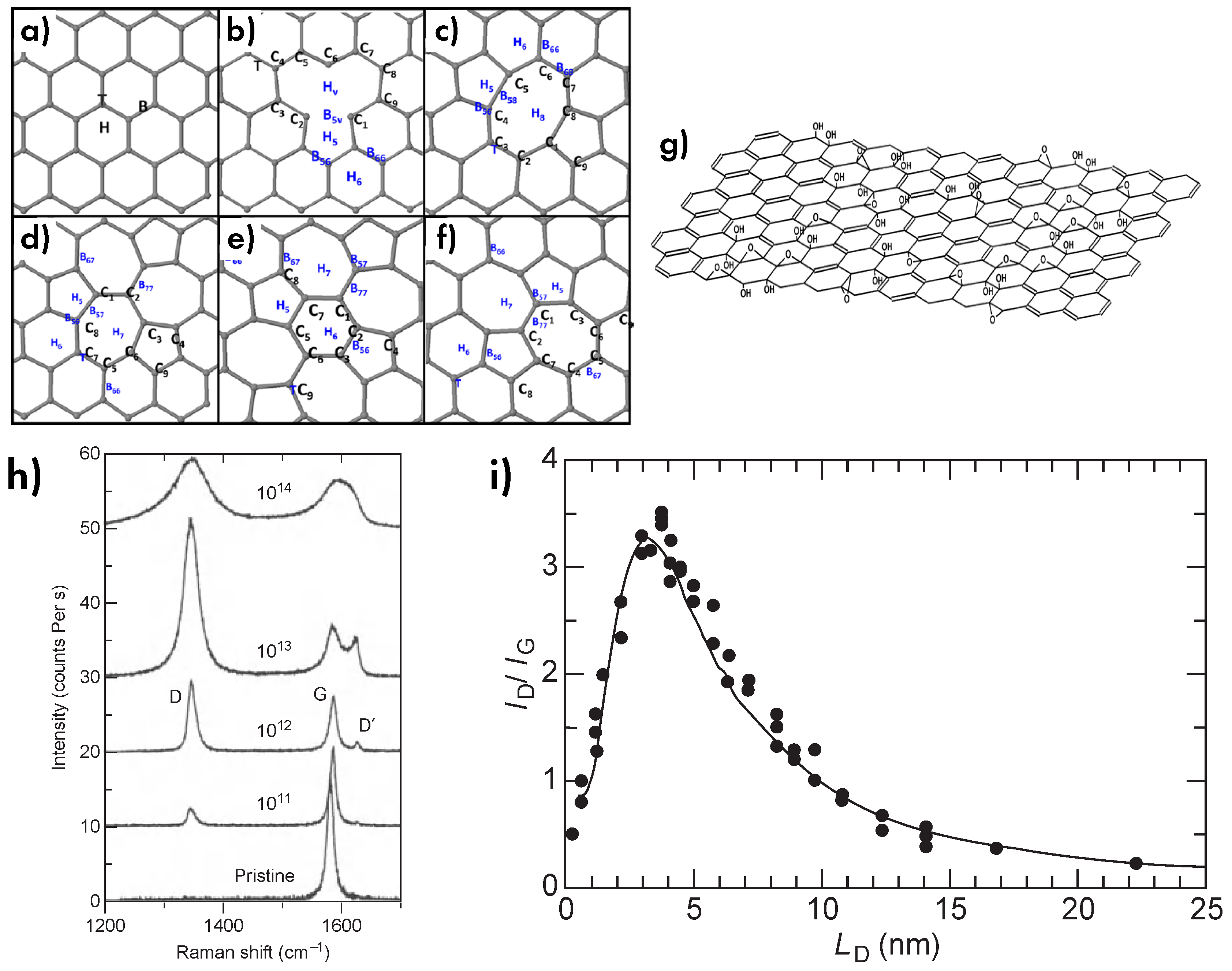
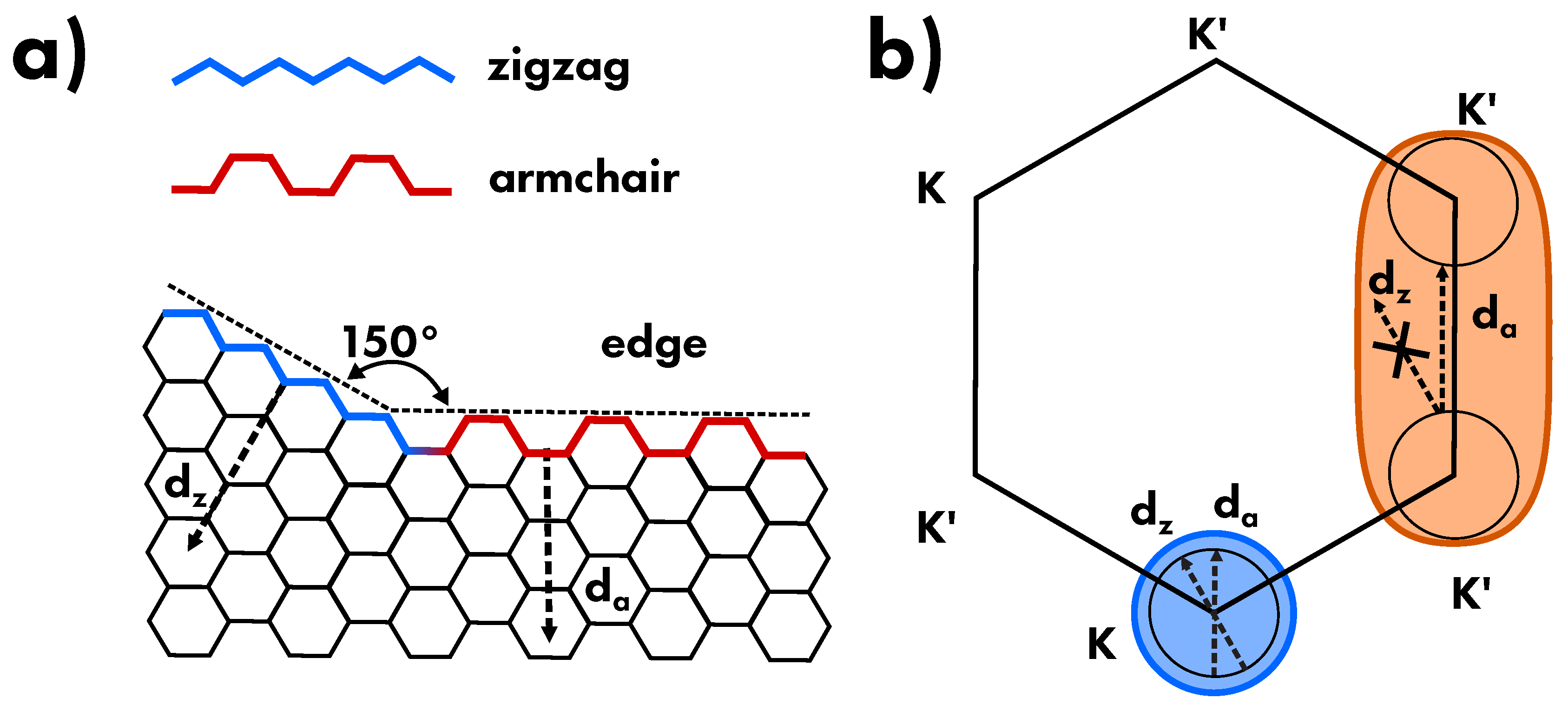
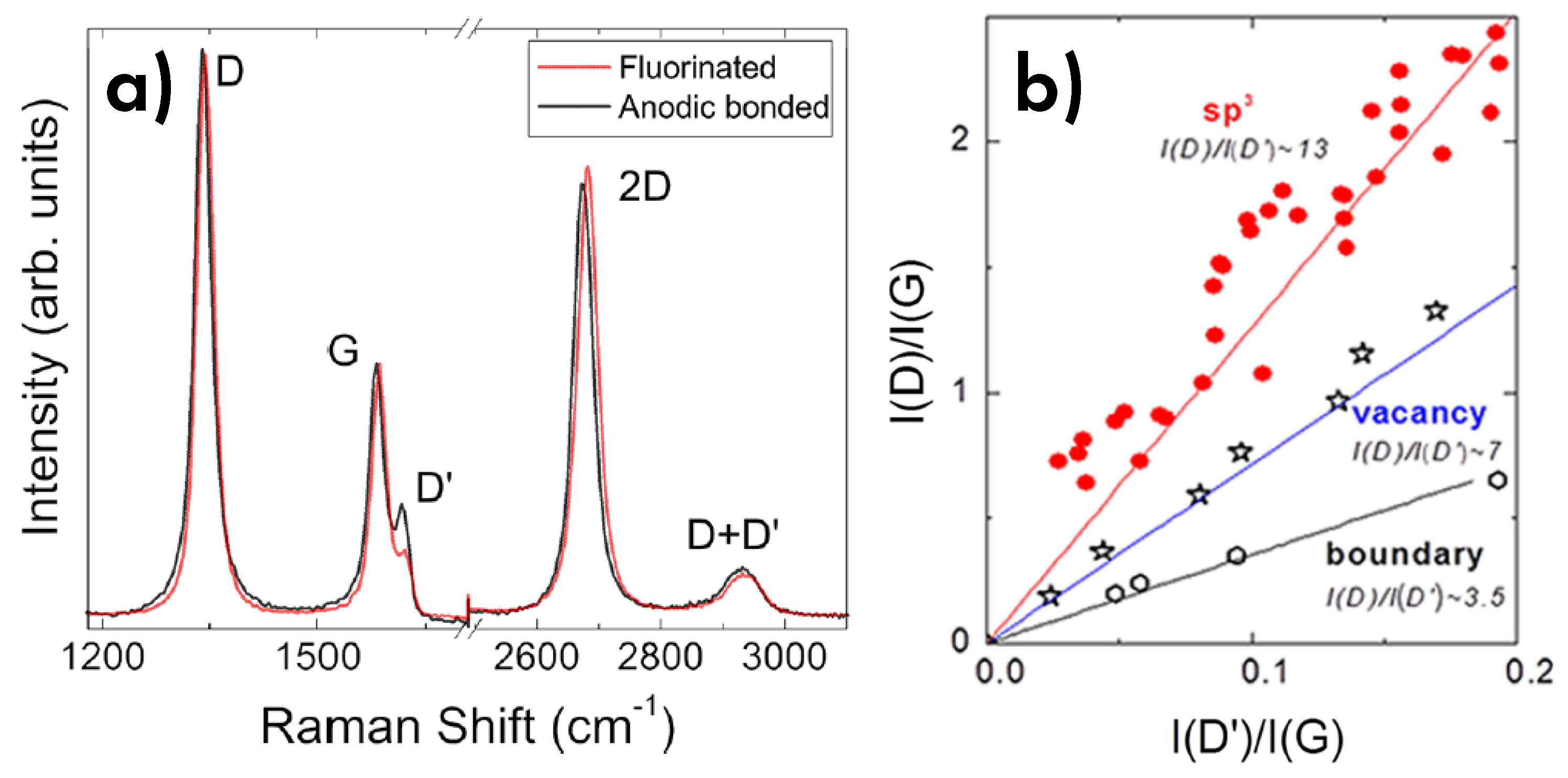
6.3. Defects and disorder
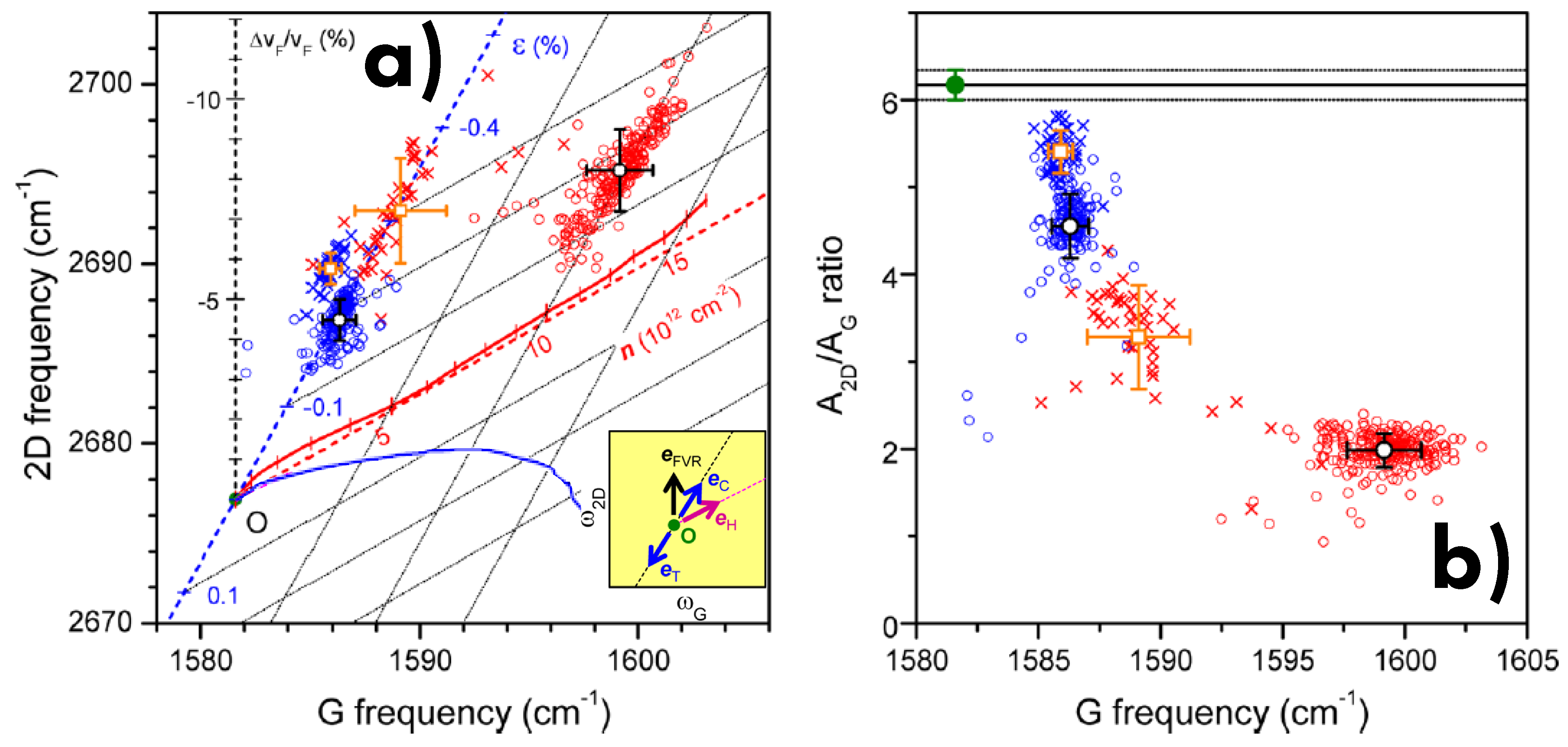
6.4. Strain
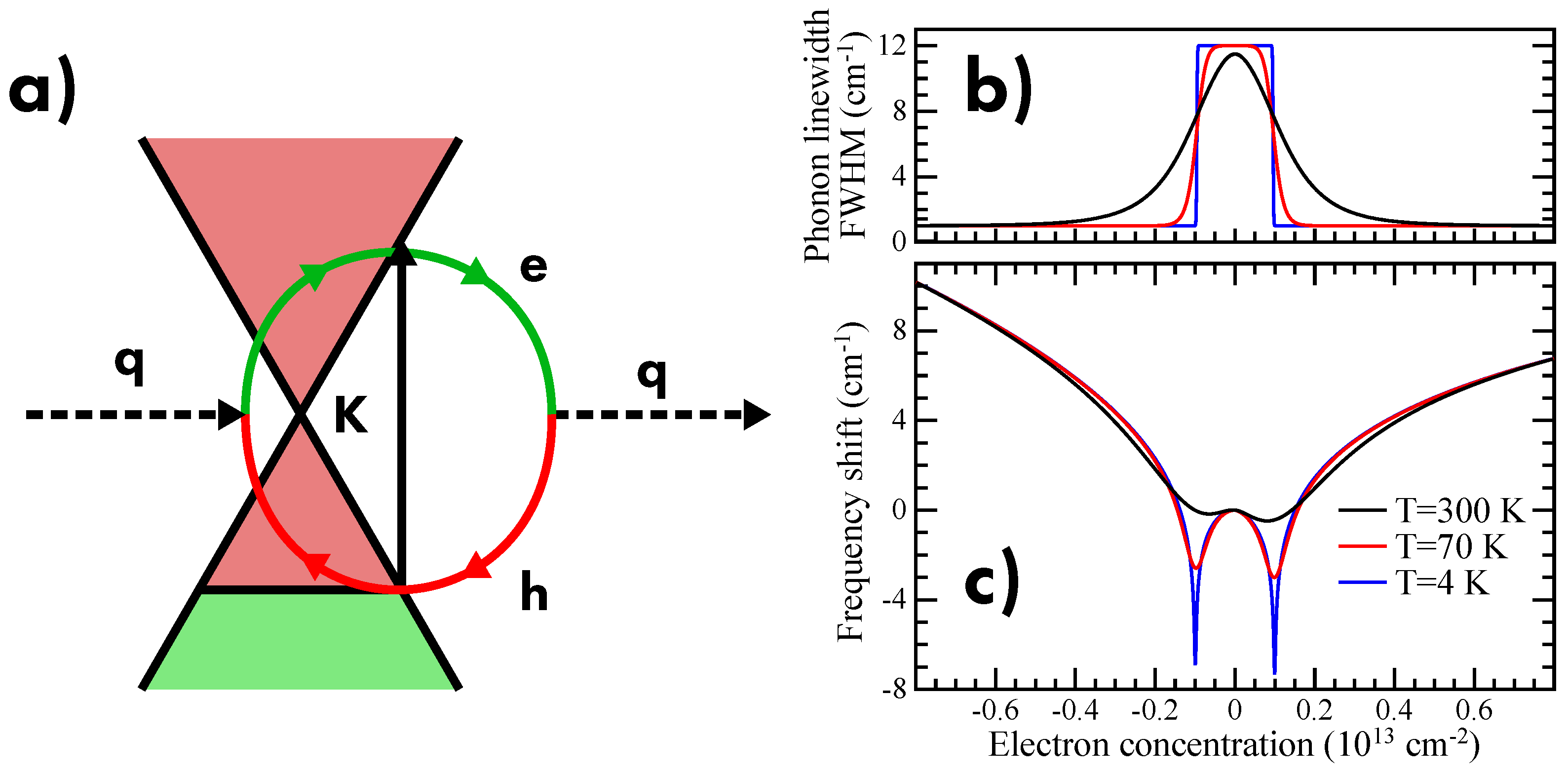
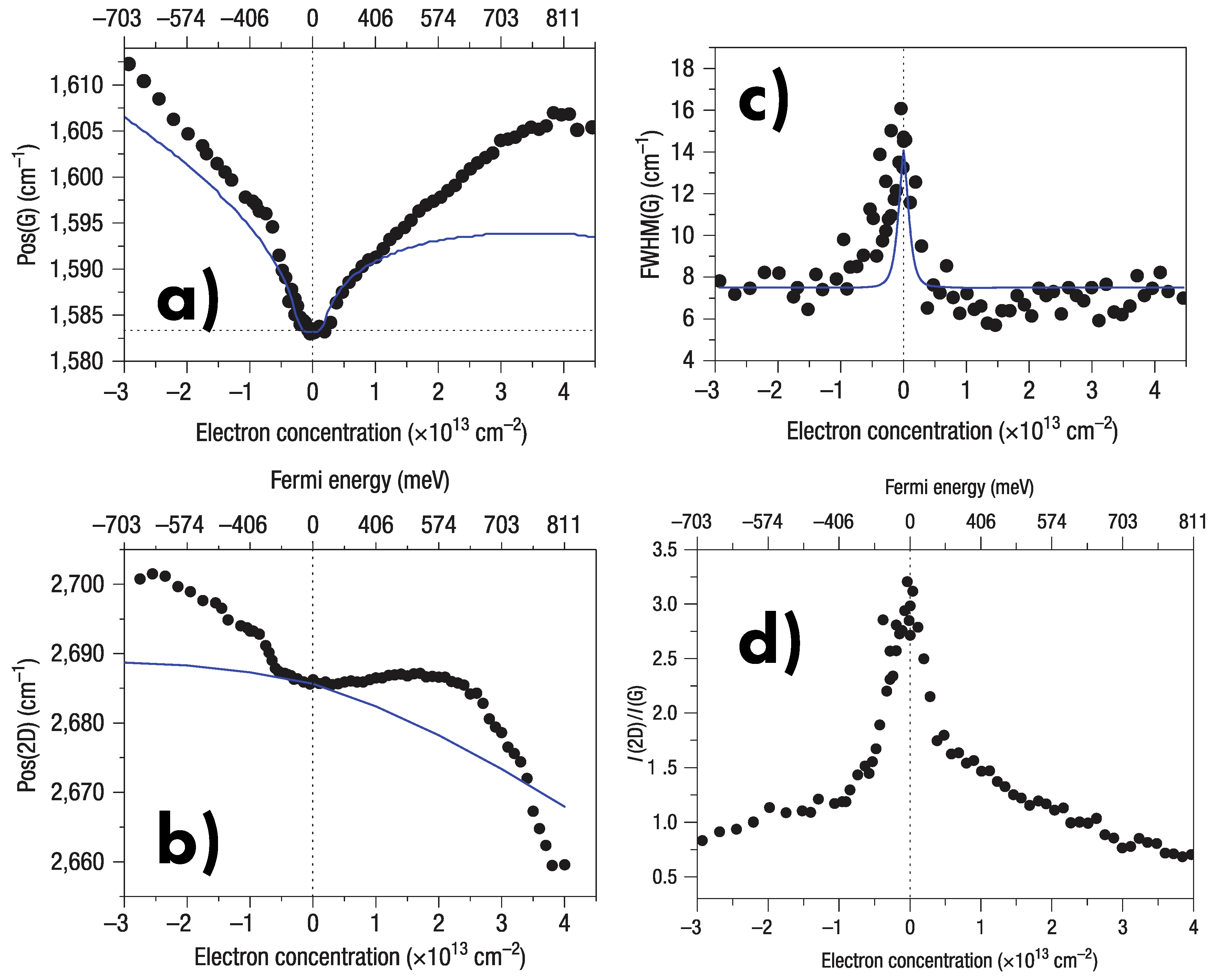
6.5. Doping
7. Synthesis Methods
7.1. Top Down
- Mechanical Exfoliation
- based on the separation of the single graphene sheets which constitute graphite (Figure 28a), and thanks to its simplicity this method was used for the first isolation of graphene [1]. On its favor, it produces the highest quality of graphene because of the high purity of graphite, and moreover it is a relatively easy procedure since the vertical stacking of graphene sheets is assured only by weak van der Waals interactions. For this reason this technique can be extended to other van der Waals heterostructures, such as transition metal dichalcogenide (, , , ). However, this method is limited by two main factors: the small amount of product and in the exiguous extension of graphene flakes, the latter factor bypassable by using of HOPG as raw material [42]. In detail, the direct manipulation of top graphene sheet on graphite can be performed both by scotch tape and by tips originally produced for scanning probe microscopy [24,42].
- Liquid-phase Exfoliation
- in this case the exfoliation procedure is performed in liquid-phase, and the separation of graphene sheets is obtained by sonication (Figure 28b) [24,25,42]. This procedure is preferable to the mechanical exfoliation since in comparison it produces a large quantity of graphene flakes with larger lateral size. By contrast, the most critical issue consists of the damaging of the internal structure of graphene flakes in which some defects can be induced. However, some investigations have shown that this undesired effect can be avoided by putting in solution some specific chemicals, such as surfactants [113] or intercalating molecules [114], which facilitate the exfoliation, thus requiring weaker sonication [25,42].
- Electrochemical exfoliation
- performed in liquid-phase as the previous method, but based on the use of a graphite source (usually HOPG) as electrodes in an electrolyte solution (Figure 28c). In this casethe produced graphene features low defect concentration because the sheets separation is induced by the electrochemical reaction rather than by mechanical waves, thus assuring the production of a high-quality graphene [25].
- Graphene Oxide Reduction
- uses graphene oxide (GO) as main precursor. GO is usually obtained by many methods, such as from the exfoliation of graphite oxide (Hummer’s method) which follows a top down strategy [115], or by using glucose as source (Tang-Lau method) according to a bottom up strategy [116]. Concerning the first case, the exfoliation of graphite oxide is easier than that of native graphite, thus featuring notable advantages with its respect [25]. Both chemical or thermal approaches can be exploited for the reduction of GO (Figure 28d) and the quality of graphene is determined by the degree of reduction actually reached, usually never complete [117,118]. Some authors usually name this material graphene but it should be referred as reduced graphene oxide (rGO) because of its peculiar properties. In fact, rGO significantly differs from actual graphene, and it is thereby preferred for applications which take profit from the presence of functional groups onto graphene (optical and liquid application), rather than in those in which a high purity level is mandatory (solid state microelectronic) [85,89].
7.2. Bottom Up
- Chemical Vapor Deposition (CVD)
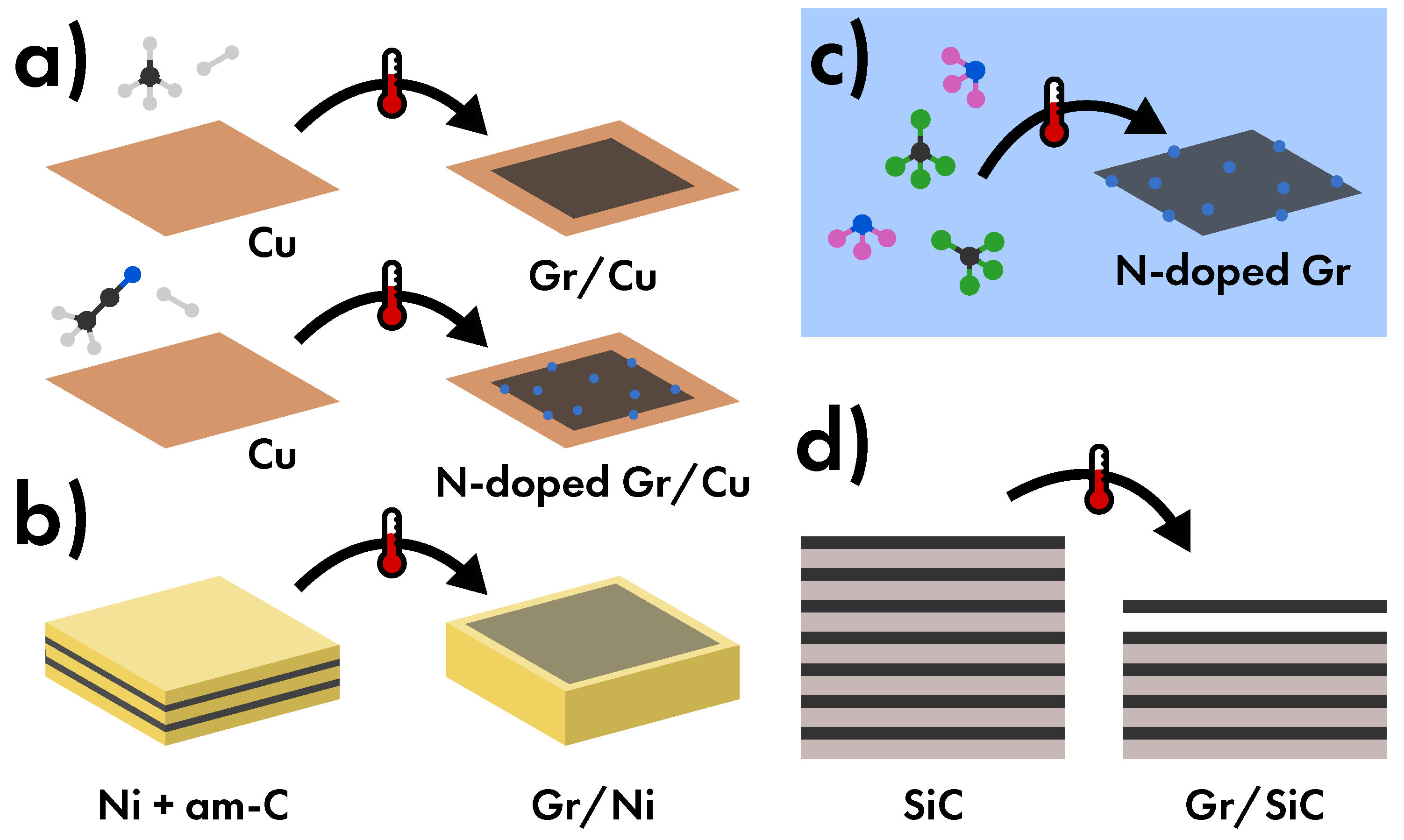
- is one of the most common methods for the production of graphene for microelectronic application both because the excellent features of the produced graphene and because it makes use of technologies well established in microelectronics industry. In particular, a mixture of molecular hydrogen and small hydrocarbon as carbon source (methane, ethane) are used to grow layer by layer the largest high-quality graphene flakes onto various substrates made by transition metals (, , , ) [8]. Moreover, by varying the precursors, it is possible to include specific dopant elements in graphene such as boron, nitrogen or oxygen in order to obtain B-doped, N-doped, or O-doped graphene (Figure 29a). Thereafter, graphene is covered by a protective layer usually made by polymers such as poly(methyl methacrylate) and then transferred onto the other substrates by using thermal release tape. Unfortunately, precisely this step constitutes the weakness of CVD methods, since some residues of the protective layer keep onto graphene even after dedicated cleaning bath [24,42,119,120]. Finally, plasma-enhanced CVD has proved an excellent method to grow vertical graphene nanosheets, i.e., a special graphene morphology which features peculiar transport properties of interest for microelectronics [121,122,123].
- Thermal Annealing
- basing on CVD method, produces graphene by using a couple or a multiple stack of an amorphous carbon layer deposited onto a metal layer (, and are the most common choices). The annealing dissolves the amorphous carbon into the metal layer, and thus obtaining the segregation of a thin carbon layer, i.e., graphene, onto the surface of the metal (Figure 29b) [24,124,125]
- Solvothermal
- in its turn similar to CVD method, produces graphene by means of the reaction between some chemicals in liquid phase (Figure 29c). Some reaction is based on the pyrolysis or the thermal decomposition of carbon-based precursors [24,126,127]. Moreover, other methods use also precursor species containing nitrogen, such as in the case of the reaction between and , thus inducing the formation of N-doped graphene flakes [124,128].
- Epitaxial Growth
- based on the synthesis of graphene by the thermal decomposition of the surface of (Figure 29d). In addition to the very high-quality structure of graphene obtained by this technique, the real advantage is the growth of graphene directly on a semiconductor. In this way it is possible to obtain the same quality of CVD, but avoiding the transfer step and the problem related to the transfer stage [25,129,130,131,132].
8. Conclusions
Funding
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Bonaccorso, F.; Sun, Z.; Hasan, T.; Ferrari, A.C. Graphene photonics and optoelectronics. Nat. Photonics 2010, 4, 611. [Google Scholar] [CrossRef]
- Allen, M.J.; Tung, V.C.; Kaner, R.B. Honeycomb carbon: A review of graphene. Chem. Rev. 2009, 110, 132–145. [Google Scholar] [CrossRef]
- Randviir, E.P.; Brownson, D.A.C.; Banks, C.E. A decade of graphene research: Production, applications and outlook. Mater. Today 2014, 17, 426–432. [Google Scholar] [CrossRef]
- Kim, S.B.; Park, J.Y.; Kim, C.S.; Okuyama, K.; Lee, S.E.; Jang, H.D.; Kim, T.O. Effects of graphene in dye-sensitized solar cells based on nitrogen-doped TiO2 composite. J. Phys. Chem. C 2015, 119, 16552–16559. [Google Scholar] [CrossRef]
- Schwierz, F. Graphene transistors. Nat. Nanotechnol. 2010, 5, 487–496. [Google Scholar] [CrossRef]
- Bae, S.; Kim, H.; Lee, Y.; Xu, X.; Park, J.S.; Zheng, Y.; Balakrishnan, J.; Lei, T.; Kim, H.R.; Song, Y.I.; et al. Roll-to-roll production of 30-inch graphene films for transparent electrodes. Nat. Nanotechnol. 2010, 5, 574. [Google Scholar] [CrossRef]
- Patel, K.; Tyagi, P.K. P-type multilayer graphene as a highly efficient transparent conducting electrode in silicon heterojunction solar cells. Carbon 2017, 116, 744–752. [Google Scholar] [CrossRef]
- Giannazzo, F.; Greco, G.; Roccaforte, F.; Sonde, S. Vertical transistors based on 2D materials: Status and prospects. Crystals 2018, 8, 70. [Google Scholar] [CrossRef]
- Giannazzo, F.; Fisichella, G.; Greco, G.; La Magna, A.; Roccaforte, F.; Pécz, B.; Yakimova, R.; Dagher, R.; Michon, A.; Cordier, Y. Graphene integration with nitride semiconductors for high power and high frequency electronics. Phys. Status Solidi (A) 2017, 214, 1600460. [Google Scholar] [CrossRef]
- Zubair, A.; Nourbakhsh, A.; Hong, J.Y.; Qi, M.; Song, Y.; Jena, D.; Kong, J.; Dresselhaus, M.; Palacios, T. Hot Electron Transistor with van der Waals Base-Collector Heterojunction and High-Performance GaN Emitter. Nano Lett. 2017, 17, 3089–3096. [Google Scholar] [CrossRef] [PubMed]
- Mannequin, C.; Delamoreanu, A.; Latu-Romain, L.; Jousseaume, V.; Grampeix, H.; David, S.; Rabot, C.; Zenasni, A.; Vallee, C.; Gonon, P. Graphene-HfO2-based resistive RAM memories. Microelectron. Eng. 2016, 161, 82–86. [Google Scholar] [CrossRef]
- Fitzer, E.; Kochling, K.H.; Boehm, H.; Marsh, H. Recommended terminology for the description of carbon as a solid (IUPAC Recommendations 1995). Pure Appl. Chem. 1995, 67, 473–506. [Google Scholar] [CrossRef]
- Jeevanandam, J.; Barhoum, A.; Chan, Y.S.; Dufresne, A.; Danquah, M.K. Review on nanoparticles and nanostructured materials: History, sources, toxicity and regulations. Beilstein J. Nanotechnol. 2018, 9, 1050–1074. [Google Scholar] [CrossRef]
- Pokropivny, V.; Skorokhod, V. Classification of nanostructures by dimensionality and concept of surface forms engineering in nanomaterial science. Materi. Sci. Eng. C 2007, 27, 990–993. [Google Scholar] [CrossRef]
- Kumar, N.; Kumbhat, S. Carbon-Based Nanomaterials, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Nasir, S.; Hussein, M.; Zainal, Z.; Yusof, N. Carbon-based nanomaterials/allotropes: A glimpse of their synthesis, properties and some applications. Materials 2018, 11, 295. [Google Scholar] [CrossRef]
- Roduner, E. Size matters: Why nanomaterials are different. Chem. Soc. Rev. 2006, 35, 583–592. [Google Scholar] [CrossRef]
- Dresselhaus, M.; Jorio, A.; Saito, R. Characterizing graphene, graphite, and carbon nanotubes by Raman spectroscopy. Annu. Rev. Condens. Matter Phys. 2010, 1, 89–108. [Google Scholar] [CrossRef]
- Malard, L.M.; Pimenta, M.A.A.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectroscopy in graphene. Phys. Rep. 2009, 473, 51–87. [Google Scholar] [CrossRef]
- Mak, K.F.; Ju, L.; Wang, F.; Heinz, T.F. Optical spectroscopy of graphene: from the far infrared to the ultraviolet. Sol. Stat. Commun. 2012, 152, 1341–1349. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene, 2009 Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Lee, H.C.; Liu, W.W.; Chai, S.P.; Mohamed, A.R.; Aziz, A.; Khe, C.S.; Hidayah, N.M.; Hashim, U. Review of the synthesis, transfer, characterization and growth mechanisms of single and multilayer graphene. RSC Adv. 2017, 7, 15644–15693. [Google Scholar] [CrossRef]
- Coroş, M.; Pogăcean, F.; Măgeruşan, L.; Socaci, C.; Pruneanu, S. A brief overview on synthesis and applications of graphene and graphene-based nanomaterials. Front. Mater. Sci. 2019, 13, 23–32. [Google Scholar] [CrossRef]
- Saito, R.; Dresselhaus, G.; Dresselhaus, M. Physical Properties of Carbon Nanotubes; World Scientific: Singapore, 1998. [Google Scholar]
- Pace, N.R. The universal nature of biochemistry. Proc. Natl. Acad. Sci. USA 2001, 98, 805–808. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Belenkov, E.A.; Greshnyakov, V.A. Classification schemes for carbon phases and nanostructures. New Carbon Mater. 2013, 28, 273–282. [Google Scholar] [CrossRef]
- Heimann, R.; Evsyukov, S.; Koga, Y. Carbon allotropes: A suggested classification scheme based on valence orbital hybridization. Carbon 1997, 35, 1654–1658. [Google Scholar] [CrossRef]
- Grundmann, M. Physics of Semiconductors, 1st ed.; Springer International Publishing: Basel, Switzerland, 2006. [Google Scholar]
- Solomons, T.W.G.; Fryhle, C.B. Organic Chemistry, 10th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Bransden, B.H.; Joachain, C.J. Physics of Atoms and Molecules, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 1983. [Google Scholar]
- Poater, J.; Duran, M.; Sola, M. Analysis of electronic delocalization in buckminsterfullerene (C60). Int. J. Quantum Chem. 2004, 98, 361–366. [Google Scholar] [CrossRef]
- Popov, I.A.; Bozhenko, K.V.; Boldyrev, A.I. Is graphene aromatic? Nano Res. 2012, 5, 117–123. [Google Scholar] [CrossRef]
- Kroes, J.M.H.; Fasolino, A.; Katsnelson, M.I. Density functional based simulations of proton permeation of graphene and hexagonal boron nitride. Phys. Chem. Chem. Phys. 2017, 19, 5813–5817. [Google Scholar] [CrossRef] [Green Version]
- Bhushan, B. Springer Handbook of Nanotechnology; Springer: Berlin, Germany, 2017; Chapter 3. [Google Scholar]
- Kogan, E.; Nazarov, V. Symmetry classification of energy bands in graphene. Phys. Rev. B 2012, 85, 115418. [Google Scholar] [CrossRef] [Green Version]
- van Haeringen, W.; Junginger, H.G. Symmetry classification of energy bands in graphene. Sol. Stat. Commun. 1696, 7, 1723–1725. [Google Scholar] [CrossRef]
- Wallace, P.R. The band theory of graphite. Phys. Rev. 1947, 71, 622. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Yu, Y.J.; Zhao, Y.; Ryu, S.; Brus, L.E.; Kim, K.S.; Kim, P. Tuning the graphene work function by electric field effect. Nano Lett. 2009, 9, 3430–3434. [Google Scholar] [CrossRef] [PubMed]
- Rao, C.N.R.; Sood, A.K. Graphene: Synthesis, Properties, and Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197. [Google Scholar] [CrossRef] [PubMed]
- Blundell, S.J.; Blundell, K.M. Concepts in Thermal Physics; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Bena, C.; Kivelson, S.A. Quasiparticle scattering and local density of states in graphite. Phys. Rev. B 2005, 72, 125432. [Google Scholar] [CrossRef] [Green Version]
- Ando, T.; Zheng, Y.; Suzuura, H. Dynamical conductivity and zero-mode anomaly in honeycomb lattices. J. Phys. Soc. Jpn. 2002, 71, 1318–1324. [Google Scholar] [CrossRef]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine structure constant defines visual transparency of graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef]
- Horng, J.; Chen, C.F.; Geng, B.; Girit, C.; Zhang, Y.; Hao, Z.; Bechtel, H.A.; Martin, M.; Zettl, A.; Crommie, M.F.; et al. Drude conductivity of Dirac fermions in graphene. Phys. Rev. B 2011, 83, 165113. [Google Scholar] [CrossRef]
- Ju, L.; Geng, B.; Horng, J.; Girit, C.; Martin, M.; Hao, Z.; Bechtel, H.A.; Liang, X.; Zettl, A.; Shen, Y.R.; et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 2011, 6, 630. [Google Scholar] [CrossRef]
- Yang, Y.; Kolesov, G.; Kocia, L.; Heller, E.J. Reassessing graphene absorption and emission spectroscopy. Nano Lett. 2017, 17, 6077–6082. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, S.; Perello, D.J.; Biswas, C.; Ghosh, A.; Van Luan, N.; Park, J.; Yao, F.; Rotkin, S.V.; Lee, Y.H. Determining the Fermi level by absorption quenching of monolayer graphene by charge transfer doping. Nanoscale 2016, 8, 18710–18717. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lim, S.C.; Chae, S.J.; Maeng, I.; Choi, Y.; Cha, S.; Lee, Y.H.; Choi, H. Ultrafast zero balance of the oscillator-strength sum rule in graphene. Sci. Rep. 2013, 3, 2663. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jorio, A.; Dresselhaus, M.; Saito, R.; Dresselhaus, G.F. Raman Spectroscopy in Graphene Related Systems; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Avouris, P.; Heinz, T.F.; Low, T. 2D Materials: Properties and Devices; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Dresselhaus, M.S.; Jorio, A.; Hofmann, M.; Dresselhaus, G.; Saito, R. Perspectives on carbon nanotubes and graphene Raman spectroscopy. Nano Lett. 2010, 10, 751–758. [Google Scholar] [CrossRef]
- Venezuela, P.; Lazzeri, M.; Mauri, F. Theory of double-resonant Raman spectra in graphene: Intensity and line shape of defect-induced and two-phonon bands. Phys. Rev. B 2011, 84, 035433. [Google Scholar] [CrossRef]
- Diery, W.A.; Moujaes, E.A.; Nunes, R.W. Nature of localized phonon modes of tilt grain boundaries in graphene. Carbon 2018, 140, 250–258. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Basko, D.M. Raman spectroscopy as a versatile tool for studying the properties of graphene. Nat. Nanotechnol. 2013, 8, 235. [Google Scholar] [CrossRef]
- Mafra, D.; Samsonidze, G.; Malard, L.; Elias, D.; Brant, J.; Plentz, F.; Alves, E.; Pimenta, M. Determination of LA and TO phonon dispersion relations of graphene near the Dirac point by double resonance Raman scattering. Phys. Rev. B 2007, 76, 233407. [Google Scholar] [CrossRef]
- Costa, S.D.; Righi, A.; Fantini, C.; Hao, Y.; Magnuson, C.; Colombo, L.; Ruoff, R.S.; Pimenta, M.A. Resonant Raman spectroscopy of graphene grown on copper substrates. Sol. Stat. Commun. 2012, 152, 1317–1320. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Malekpour, H.; Balandin, A.A. Raman-based technique for measuring thermal conductivity of graphene and related materials. J. Raman Spectrosc. 2018, 49, 106–120. [Google Scholar] [CrossRef]
- Judek, J.; Gertych, A.P.; Świniarski, M.; apińska, A.; Dużyńska, A.; Zdrojek, M. High accuracy determination of the thermal properties of supported 2D materials. Sci. Rep. 2015, 5, 12422. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Moore, A.L.; Zhu, Y.; Li, X.; Chen, S.; Shi, L.; Ruoff, R.S. Thermal transport in suspended and supported monolayer graphene grown by chemical vapor deposition. Nano Lett. 2010, 10, 1645–1651. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Moore, A.L.; Cai, W.; Suk, J.W.; An, J.; Mishra, C.; Amos, C.; Magnuson, C.W.; Kang, J.; Shi, L.; et al. Raman measurements of thermal transport in suspended monolayer graphene of variable sizes in vacuum and gaseous environments. ACS Nano 2010, 5, 321–328. [Google Scholar] [CrossRef]
- Seol, J.H.; Jo, I.; Moore, A.L.; Lindsay, L.; Aitken, Z.H.; Pettes, M.T.; Li, X.; Yao, Z.; Huang, R.; Broido, D.; et al. Two-dimensional phonon transport in supported graphene. Science 2010, 328, 213–216. [Google Scholar] [CrossRef]
- Ni, Z.H.; Wang, H.M.; Kasim, J.; Fan, H.M.; Yu, T.; Wu, Y.H.; Feng, Y.P.; Shen, Z.X. Graphene thickness determination using reflection and contrast spectroscopy. Nano Lett. 2007, 7, 2758–2763. [Google Scholar] [CrossRef]
- Bayle, M.; Reckinger, N.; Felten, A.; Landois, P.; Lancry, O.; Dutertre, B.; Colomer, J.F.; Zahab, A.A.; Henrard, L.; Sauvajol, J.L.; et al. Determining the number of layers in few-layer graphene by combining Raman spectroscopy and optical contrast. J. Raman Spectrosc. 2018, 49, 36–45. [Google Scholar] [CrossRef]
- Malard, L.M.; Guimaraes, M.H.D.; Mafra, D.L.; Jorio, A. Group-theory analysis of electrons and phonons in N-layer graphene systems. Phys. Rev. B 2009, 79, 125426. [Google Scholar] [CrossRef]
- Begliarbekov, M.; Sul, O.; Kalliakos, S.; Yang, E.H.; Strauf, S. Determination of edge purity in bilayer graphene using micro-Raman spectroscopy. Appl. Phys. Lett. 2010, 97, 031908. [Google Scholar] [CrossRef]
- Ni, Z.; Wang, Y.; Yu, T.; You, Y.; Shen, Z. Reduction of Fermi velocity in folded graphene observed by resonance Raman spectroscopy. Phys. Rev. B 2008, 77, 235403. [Google Scholar] [CrossRef] [Green Version]
- Mehmood, F.; Pachter, R.; Lu, W.; Boeckl, J.J. Adsorption and diffusion of oxygen on single-layer graphene with topological defects. J. Phys. Chem. C 2013, 117, 10366–10374. [Google Scholar] [CrossRef]
- Yu, Q.; Jauregui, L.A.; Wu, W.; Colby, R.; Tian, J.; Su, Z.; Cao, H.; Liu, Z.; Pandey, D.; Wei, D.; et al. Control and characterization of individual grains and grain boundaries in graphene grown by chemical vapour deposition. Nat. Mater. 2011, 10, 443. [Google Scholar] [CrossRef] [PubMed]
- Bissett, M.A.; Izumida, W.; Saito, R.; Ago, H. Effect of domain boundaries on the Raman spectra of mechanically strained graphene. ACS Nano 2012, 6, 10229–10238. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Xia, Z. Mechanisms of oxygen reduction reaction on nitrogen-doped graphene for fuel cells. J. Phys. Chem. C 2011, 115, 11170–11176. [Google Scholar] [CrossRef]
- Qu, L.; Liu, Y.; Baek, J.B.; Dai, L. Nitrogen-doped graphene as efficient metal-free electrocatalyst for oxygen reduction in fuel cells. ACS Nano 2010, 4, 1321–1326. [Google Scholar] [CrossRef] [PubMed]
- Robinson, J.T.; Burgess, J.S.; Junkermeier, C.E.; Badescu, S.C.; Reinecke, T.L.; Perkins, F.K.; Zalalutdniov, M.K.; Baldwin, J.W.; Culbertson, J.C.; Sheehan, P.E.; et al. Properties of fluorinated graphene films. Nano Lett. 2010, 10, 3001–3005. [Google Scholar] [CrossRef]
- Liu, H.; Hou, Z.; Hu, C.; Yang, Y.; Zhu, Z. Electronic and magnetic properties of fluorinated graphene with different coverage of fluorine. J. Phys. Chem. C 2012, 116, 18193–18201. [Google Scholar] [CrossRef]
- Banhart, F.; Kotakoski, J.; Krasheninnikov, A.V. Structural defects in graphene. ACS Nano 2010, 5, 26–41. [Google Scholar] [CrossRef]
- Kramm, U.I.; Herrmann-Geppert, I.; Behrends, J.; Lips, K.; Fiechter, S.; Bogdanoff, P. On an easy way to prepare metal–nitrogen doped carbon with exclusive presence of MeN4-type sites active for the ORR. J. Am. Chem. Soc. 2016, 138, 635–640. [Google Scholar] [CrossRef]
- Bhatt, M.D.; Lee, G.; Lee, J.S. Density Functional Theory (DFT) Calculations for Oxygen Reduction Reaction Mechanisms on Metal-, Nitrogen-co-doped Graphene (M-N2-G (M = Ti, Cu, Mo, Nb and Ru)) Electrocatalysts. Electrochim. Acta. 2017, 228, 619–627. [Google Scholar] [CrossRef]
- Esrafili, M.D.; Saeidi, N.; Dinparast, L. Epoxidation of ethylene over Pt-, Pd-and Ni-doped graphene in the presence of N2O as an oxidant: A comparative DFT study. New J. Chem. 2017, 41, 9815–9825. [Google Scholar] [CrossRef]
- Yu, L.; Pan, X.; Cao, X.; Hu, P.; Bao, X. Oxygen reduction reaction mechanism on nitrogen-doped graphene: A density functional theory study. J. Catal. 2011, 282, 183–190. [Google Scholar] [CrossRef]
- Kaukonen, M.; Krasheninnikov, A.V.; Kauppinen, E.; Nieminen, R.M. Doped graphene as a material for oxygen reduction reaction in hydrogen fuel cells: A computational study. ACS Catal. 2013, 3, 159–165. [Google Scholar] [CrossRef]
- Chen, D.; Feng, H.; Li, J. Graphene oxide: Preparation, functionalization, and electrochemical applications. Chem. Rev. 2012, 112, 6027–6053. [Google Scholar] [CrossRef] [PubMed]
- Cançado, L.G.; Jorio, A.; Ferreira, E.M.; Stavale, F.; Achete, C.A.; Capaz, R.B.; Moutinho, M.V.d.O.; Lombardo, A.; Kulmala, T.; Ferrari, A.C. Quantifying defects in graphene via Raman spectroscopy at different excitation energies. Nano Lett. 2011, 11, 3190–3196. [Google Scholar] [CrossRef] [PubMed]
- Lucchese, M.M.; Stavale, F.; Ferreira, E.M.; Vilani, C.; Moutinho, M.; Capaz, R.B.; Achete, C.; Jorio, A. Quantifying ion-induced defects and Raman relaxation length in graphene. Carbon 2010, 48, 1592–1597. [Google Scholar] [CrossRef]
- Froehlicher, G.; Berciaud, S. Raman spectroscopy of electrochemically gated graphene transistors: Geometrical capacitance, electron-phonon, electron-electron, and electron-defect scattering. Phys. Rev. B 2015, 91, 205413. [Google Scholar] [CrossRef]
- He, H.; Klinowski, J.; Forster, M.; Lerf, A. A new structural model for graphite oxide. Chem. Phys. Lett. 1998, 287, 53–56. [Google Scholar] [CrossRef]
- You, Y.; Ni, Z.; Yu, T.; Shen, Z. Edge chirality determination of graphene by Raman spectroscopy. Appl. Phys. Lett. 2008, 93, 163112. [Google Scholar] [CrossRef] [Green Version]
- Casiraghi, C.; Hartschuh, A.; Qian, H.; Piscanec, S.; Georgi, C.; Fasoli, A.; Novoselov, K.; Basko, D.; Ferrari, A. Raman spectroscopy of graphene edges. Nano Lett. 2009, 9, 1433–1441. [Google Scholar] [CrossRef]
- Eckmann, A.; Felten, A.; Mishchenko, A.; Britnell, L.; Krupke, R.; Novoselov, K.S.; Casiraghi, C. Probing the nature of defects in graphene by Raman spectroscopy. Nano Lett. 2012, 12, 3925–3930. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Pachter, R.; Mehmood, F.; Islam, A.E.; Maruyama, B.; Boeckl, J.J. A Raman spectroscopy signature for characterizing defective single-layer graphene: Defect-induced I (D)/I(D’) intensity ratio by theoretical analysis. Carbon 2015, 90, 53–62. [Google Scholar] [CrossRef]
- Bunch, J.S.; Verbridge, S.S.; Alden, J.S.; Van Der Zande, A.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Impermeable atomic membranes from graphene sheets. Nano Lett. 2008, 8, 2458–2462. [Google Scholar] [CrossRef] [PubMed]
- Tiefenauer, R.F.; Dalgaty, T.; Keplinger, T.; Tian, T.; Shih, C.J.; Vörös, J.; Aramesh, M. Monolayer Graphene Coupled to a Flexible Plasmonic Nanograting for Ultrasensitive Strain Monitoring. Small 2018, 14, 1801187. [Google Scholar] [CrossRef] [PubMed]
- Bae, S.H.; Lee, Y.; Sharma, B.K.; Lee, H.J.; Kim, J.H.; Ahn, J.H. Graphene-based transparent strain sensor. Carbon 2013, 51, 236–242. [Google Scholar] [CrossRef]
- Dong, J.; Liu, S.; Fu, Y.; Wang, Q. Investigation of strain-induced modulation on electronic properties of graphene field effect transistor. Phys. Lett. A 2017, 381, 292–297. [Google Scholar] [CrossRef]
- Mohiuddin, T.; Lombardo, A.; Nair, R.; Bonetti, A.; Savini, G.; Jalil, R.; Bonini, N.; Basko, D.; Galiotis, C.; Marzari, N.; et al. Uniaxial strain in graphene by Raman spectroscopy: G peak splitting, Grüneisen parameters, and sample orientation. Phys. Rev. B 2009, 79, 205433. [Google Scholar] [CrossRef]
- Frank, O.; Tsoukleri, G.; Riaz, I.; Papagelis, K.; Parthenios, J.; Ferrari, A.C.; Geim, A.K.; Novoselov, K.S.; Galiotis, C. Development of a universal stress sensor for graphene and carbon fibres. Nat. Commun. 2011, 2, 255. [Google Scholar] [CrossRef] [Green Version]
- Androulidakis, C.; Tsoukleri, G.; Koutroumanis, N.; Gkikas, G.; Pappas, P.; Parthenios, J.; Papagelis, K.; Galiotis, C. Experimentally derived axial stress–strain relations for two-dimensional materials such as monolayer graphene. Carbon 2015, 81, 322–328. [Google Scholar] [CrossRef]
- Lazzeri, M.; Mauri, F. Nonadiabatic Kohn anomaly in a doped graphene monolayer. Phys. Rev. Lett. 2006, 97, 266407. [Google Scholar] [CrossRef]
- Das, A.; Pisana, S.; Chakraborty, B.; Piscanec, S.; Saha, S.K.; Waghmare, U.V.; Novoselov, K.S.; Krishnamurthy, H.R.; Geim, A.K.; Ferrari, A.C.; et al. Monitoring dopants by Raman scattering in an electrochemically top-gated graphene transistor. Nat. Nanotechnol. 2008, 3, 210. [Google Scholar] [CrossRef] [PubMed]
- Yoon, D.; Moon, H.; Son, Y.W.; Choi, J.S.; Park, B.H.; Cha, Y.H.; Kim, Y.D.; Cheong, H. Interference effect on Raman spectrum of graphene on SiO 2/Si. Phys. Rev. B 2009, 80, 125422. [Google Scholar] [CrossRef]
- Wu, J.B.; Lin, M.L.; Cong, X.; Liu, H.N.; Tan, P.H. Raman spectroscopy of graphene-based materials and its applications in related devices. Chem. Soc. Rev. 2018, 47, 1822–1873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miwa, R.; Schmidt, T.M.; Scopel, W.; Fazzio, A. Doping of graphene adsorbed on the a-SiO2 surface. Appl. Phys. Lett. 2011, 99, 163108. [Google Scholar] [CrossRef]
- Fan, X.; Zheng, W.; Chihaia, V.; Shen, Z.; Kuo, J.L. Interaction between graphene and the surface of SiO2. J. Phys. Condens. Matter. 2012, 24, 305004. [Google Scholar] [CrossRef]
- Gao, W.; Xiao, P.; Henkelman, G.; Liechti, K.M.; Huang, R. Interfacial adhesion between graphene and silicon dioxide by density functional theory with van der Waals corrections. J. Phys. D: Appl. Phys. 2014, 47, 255301. [Google Scholar] [CrossRef]
- Lee, J.E.; Ahn, G.; Shim, J.; Lee, Y.S.; Ryu, S. Optical separation of mechanical strain from charge doping in graphene. Nat. Commun. 2012, 3, 1024. [Google Scholar] [CrossRef] [Green Version]
- Ahn, G.; Kim, H.R.; Ko, T.Y.; Choi, K.; Watanabe, K.; Taniguchi, T.; Hong, B.H.; Ryu, S. Optical probing of the electronic interaction between graphene and hexagonal boron nitride. ACS Nano. 2013, 7, 1533–1541. [Google Scholar] [CrossRef]
- Liang, F.; Xu, H.; Wu, X.; Wang, C.; Luo, C.; Zhang, J. Raman spectroscopy characterization of two-dimensional materials. Chin. Phys. B 2018, 27, 037802. [Google Scholar] [CrossRef]
- Armano, A.; Buscarino, G.; Cannas, M.; Gelardi, F.M.; Giannazzo, F.; Schilirò, E.; Nigro, R.L.; Agnello, S. Influence of oxide substrates on monolayer graphene doping process by thermal treatments in oxygen. Carbon 2019, 149, 546–555. [Google Scholar] [CrossRef]
- Armano, A.; Buscarino, G.; Cannas, M.; Gelardi, F.M.; Giannazzo, F.; Schilirò, E.; Agnello, S. Monolayer graphene doping and strain dynamics induced by thermal treatments in controlled atmosphere. Carbon 2018, 127, 270–279. [Google Scholar] [CrossRef]
- Nicolosi, V.; Chhowalla, M.; Kanatzidis, M.G.; Strano, M.S.; Coleman, J.N. Liquid exfoliation of layered materials. Science 2013, 340, 1226419. [Google Scholar] [CrossRef]
- Hadi, A.; Zahirifar, J.; Karimi-Sabet, J.; Dastbaz, A. Graphene nanosheets preparation using magnetic nanoparticle assisted liquid phase exfoliation of graphite: The coupled effect of ultrasound and wedging nanoparticles. Ultrason. Sonochem. 2018, 44, 204–214. [Google Scholar] [CrossRef] [PubMed]
- Hummers, W.S., Jr.; Offeman, R.E. Preparation of graphitic oxide. J. Am. Chem. Soc. 1958, 80, 1339. [Google Scholar] [CrossRef]
- Tang, L.; Li, X.; Ji, R.; Teng, K.S.; Tai, G.; Ye, J.; Wei, C.; Lau, S.P. Bottom-up synthesis of large-scale graphene oxide nanosheets. J. Mater. Chem. 2012, 22, 5676–5683. [Google Scholar] [CrossRef]
- Yao, Z.; Nie, H.; Yang, Z.; Zhou, X.; Liu, Z.; Huang, S. Catalyst-free synthesis of iodine-doped graphene via a facile thermal annealing process and its use for electrocatalytic oxygen reduction in an alkaline medium. Chem. Commun. 2012, 48, 1027–1029. [Google Scholar] [CrossRef]
- Wang, S.J.; Geng, Y.; Zheng, Q.; Kim, J.K. Fabrication of highly conducting and transparent graphene films. Carbon 2010, 48, 1815–1823. [Google Scholar] [CrossRef]
- Mattevi, C.; Kim, H.; Chhowalla, M. A review of chemical vapour deposition of graphene on copper. J. Mater. Chem. 2011, 21, 3324–3334. [Google Scholar] [CrossRef]
- Ito, Y.; Christodoulou, C.; Nardi, M.V.; Koch, N.; Sachdev, H.; Müllen, K. Chemical vapor deposition of N-doped graphene and carbon films: The role of precursors and gas phase. ACS Nano 2014, 8, 3337–3346. [Google Scholar] [CrossRef]
- Zhao, J.; Shaygan, M.; Eckert, J.; Meyyappan, M.; Rümmeli, M.H. A growth mechanism for free-standing vertical graphene. Nano Lett. 2014, 14, 3064–3071. [Google Scholar] [CrossRef]
- Sahoo, G.; Ghosh, S.; Polaki, S.; Mathews, T.; Kamruddin, M. Scalable transfer of vertical graphene nanosheets for flexible supercapacitor applications. Nanotechnology 2017, 28, 415702. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Gao, E.; Liu, P.; Zhou, D.; Geng, D.; Xue, X.; Wang, L.; Jiang, K.; Xu, Z.; Yu, G. Facile growth of vertically-aligned graphene nanosheets via thermal CVD: The experimental and theoretical investigations. Carbon 2017, 121, 1–9. [Google Scholar] [CrossRef]
- Wang, H.; Maiyalagan, T.; Wang, X. Review on recent progress in nitrogen-doped graphene: Synthesis, characterization, and its potential applications. ACS Catal. 2012, 2, 781–794. [Google Scholar] [CrossRef]
- Prekodravac, J.; Marković, Z.; Jovanović, S.; Budimir, M.; Peruško, D.; Holclajtner-Antunović, I.; Pavlović, V.; Syrgiannis, Z.; Bonasera, A.; Todorović-Marković, B. The effect of annealing temperature and time on synthesis of graphene thin films by rapid thermal annealing. Synth. Met. 2015, 209, 461–467. [Google Scholar] [CrossRef]
- Singh, D.K.; Iyer, P.; Giri, P. Improved chemical synthesis of graphene using a safer solvothermal route. Int. J. Nanosci. 2011, 10, 39–42. [Google Scholar] [CrossRef]
- Choucair, M.; Thordarson, P.; Stride, J.A. Gram-scale production of graphene based on solvothermal synthesis and sonication. Nat. Nanotechnol. 2009, 4, 30. [Google Scholar] [CrossRef]
- Deng, D.; Pan, X.; Yu, L.; Cui, Y.; Jiang, Y.; Qi, J.; Li, W.X.; Fu, Q.; Ma, X.; Xue, Q.; et al. Toward N-doped graphene via solvothermal synthesis. Chem. Mater. 2011, 23, 1188–1193. [Google Scholar] [CrossRef]
- Mishra, N.; Boeckl, J.; Motta, N.; Iacopi, F. Graphene growth on silicon carbide: A review. Phys. Status Solidi (A) 2016, 213, 2277–2289. [Google Scholar] [CrossRef]
- Berger, C.; Song, Z.; Li, X.; Wu, X.; Brown, N.; Naud, C.; Mayou, D.; Li, T.; Hass, J.; Marchenkov, A.N.; et al. Electronic confinement and coherence in patterned epitaxial graphene. Science 2006, 312, 1191–1196. [Google Scholar] [CrossRef]
- Virojanadara, C.; Syväjarvi, M.; Yakimova, R.; Johansson, L.; Zakharov, A.; Balasubramanian, T. Homogeneous large-area graphene layer growth on 6 H-SiC (0001). Phys. Rev. B 2008, 78, 245403. [Google Scholar] [CrossRef]
- Emtsev, K.V.; Bostwick, A.; Horn, K.; Jobst, J.; Kellogg, G.L.; Ley, L.; McChesney, J.L.; Ohta, T.; Reshanov, S.A.; Röhrl, J.; et al. Towards wafer-size graphene layers by atmospheric pressure graphitization of silicon carbide. Nat. Mater. 2009, 8, 203. [Google Scholar] [CrossRef] [PubMed]

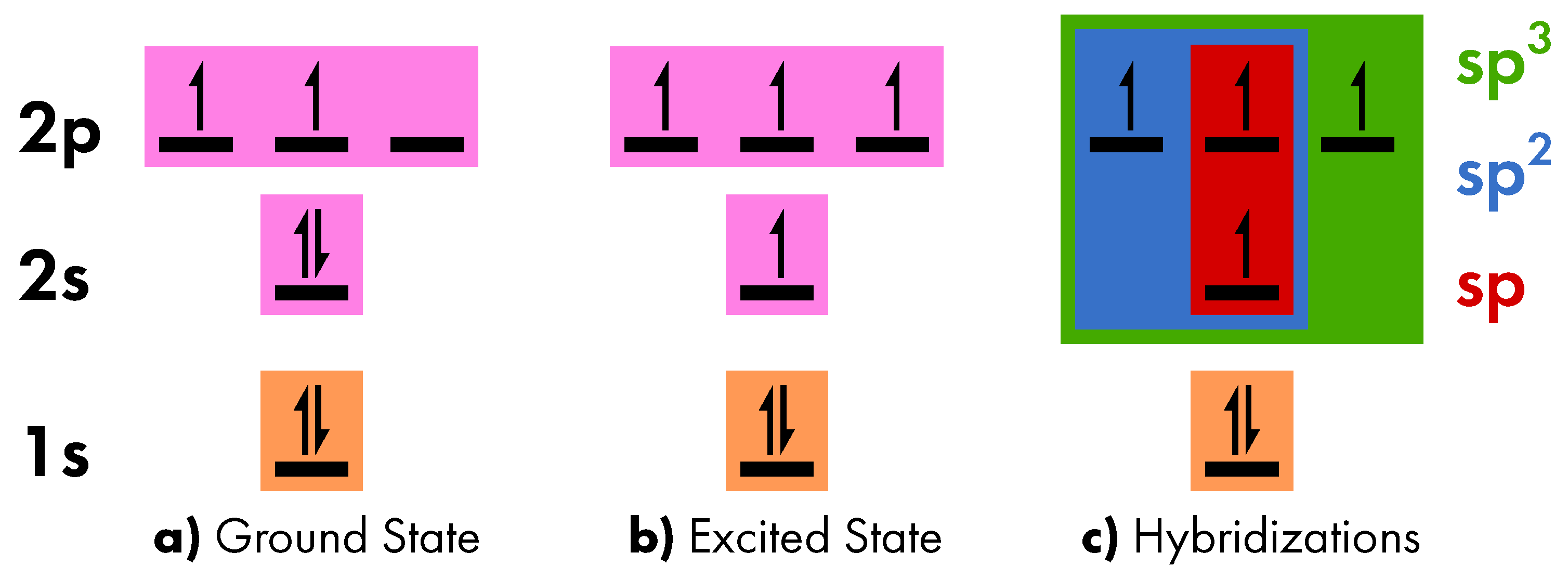







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Armano, A.; Agnello, S. Two-Dimensional Carbon: A Review of Synthesis Methods, and Electronic, Optical, and Vibrational Properties of Single-Layer Graphene. C 2019, 5, 67. https://doi.org/10.3390/c5040067
Armano A, Agnello S. Two-Dimensional Carbon: A Review of Synthesis Methods, and Electronic, Optical, and Vibrational Properties of Single-Layer Graphene. C. 2019; 5(4):67. https://doi.org/10.3390/c5040067
Chicago/Turabian StyleArmano, Angelo, and Simonpietro Agnello. 2019. "Two-Dimensional Carbon: A Review of Synthesis Methods, and Electronic, Optical, and Vibrational Properties of Single-Layer Graphene" C 5, no. 4: 67. https://doi.org/10.3390/c5040067
APA StyleArmano, A., & Agnello, S. (2019). Two-Dimensional Carbon: A Review of Synthesis Methods, and Electronic, Optical, and Vibrational Properties of Single-Layer Graphene. C, 5(4), 67. https://doi.org/10.3390/c5040067






