Mechanisms of Carbon Nanotubes and Graphene Growth: Kinetics versus Thermodynamics

Abstract

Thermodynamics must be favorable for the growth of carbon nanotubes (CNTs) and graphene to take place, but a kinetic study is required to find the operating mechanism. In fact, thermodynamics indicates whether a reaction is possible; however, the route prevailing is not necessarily the most thermodynamically favorable, but the fastest one. Detailed kinetic studies state that there are three alternative routes operating under different temperature and pressure rates. The modes and rates of diffusion of carbon (C) atoms and noble metals have been known since the 1930s, but proof of C bulk diffusion operating in CNT growth came from detailed kinetic studies performed in the early 1970s, when reversible versus irreversible C formation was discussed with examples. The reason for interstitial C bulk diffusion in transition metals is evidenced based on the values of covalent radius. The reason for operating under steady-state conditions (linearity of the weight versus time) when searching for the operating mechanism is discussed herein. The steady-state C formation process operates sometimes with two different solid phases at each side of the catalyst particle (e.g., Ni and Ni₃C), with thicknesses proportional to 1/D of the respective C bulk diffusivities when the carbon bulk diffusion step is the rate-determining one.

1. Introduction

It is vital to understand the role of thermodynamics versus kinetics in a given reaction. Thermodynamics is important for understanding the ranges in which a given reaction can occur, and it must be favorable. However, thermodynamics provides no information on the reaction mechanism, as the prevailing route is the fastest one. Therefore, detailed kinetics is an essential approach for understanding the mechanism operating in given conditions. Changes in kinetic behavior are sometimes erroneously interpreted as being a change of mechanism in cases where the same mechanism is still operating, but with an alternative rate-determining step. Density functional theory (DFT) is also used to predict the dominant formation modes in CNT growth. This information is of interest, but it can be misleading if used to find the prevailing mechanism.

Recently, Jourdain and Bichara included thermodynamic data in their comprehensive review on the growth of carbon nanotubes [1]. The mechanisms of CNT and graphene layer formation are better understood when solid-state reaction kinetics is studied in detail (

Table 1. Evidence of C bulk diffusion operating, not surface diffusion, based on the kinetic behavior.

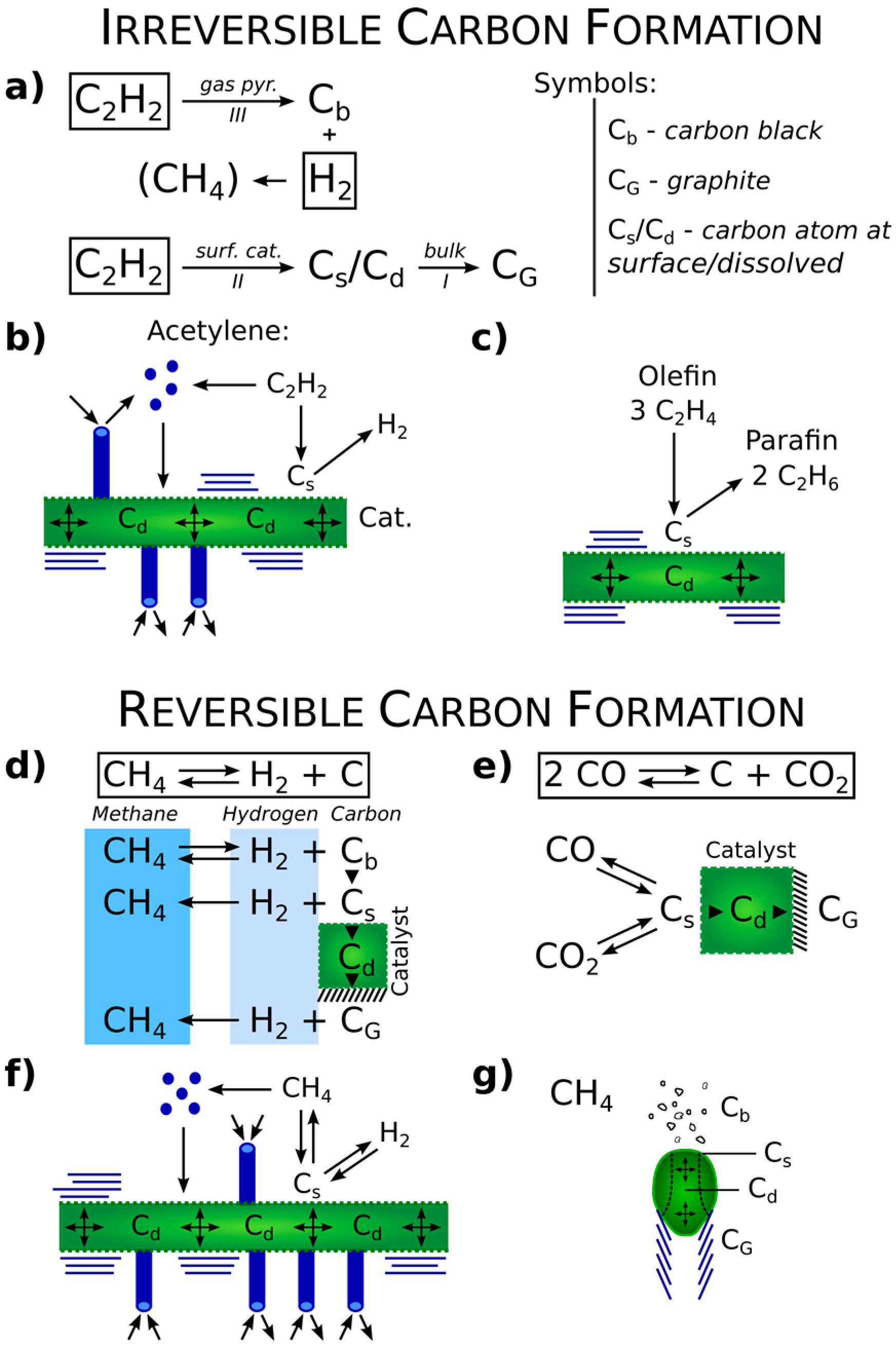
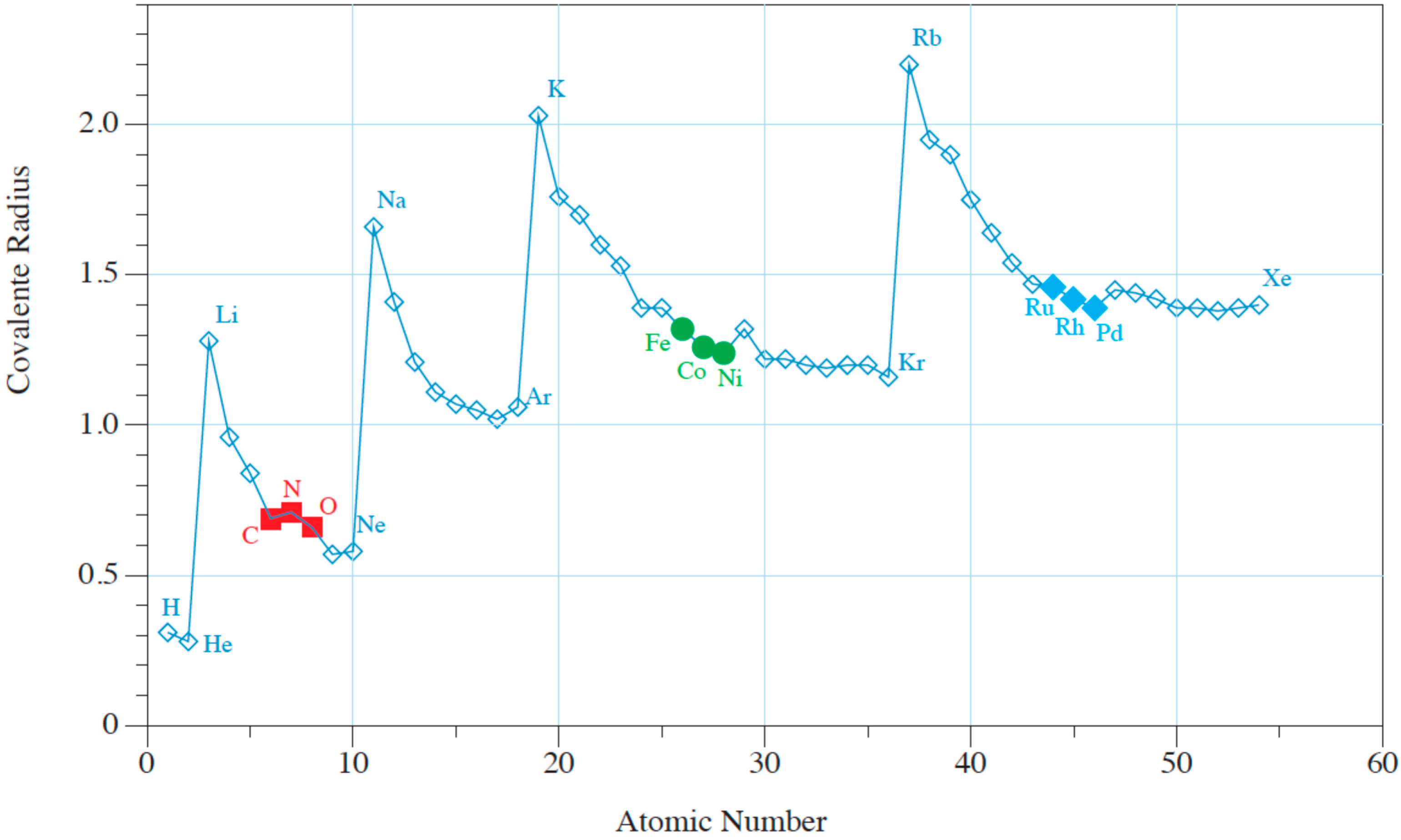
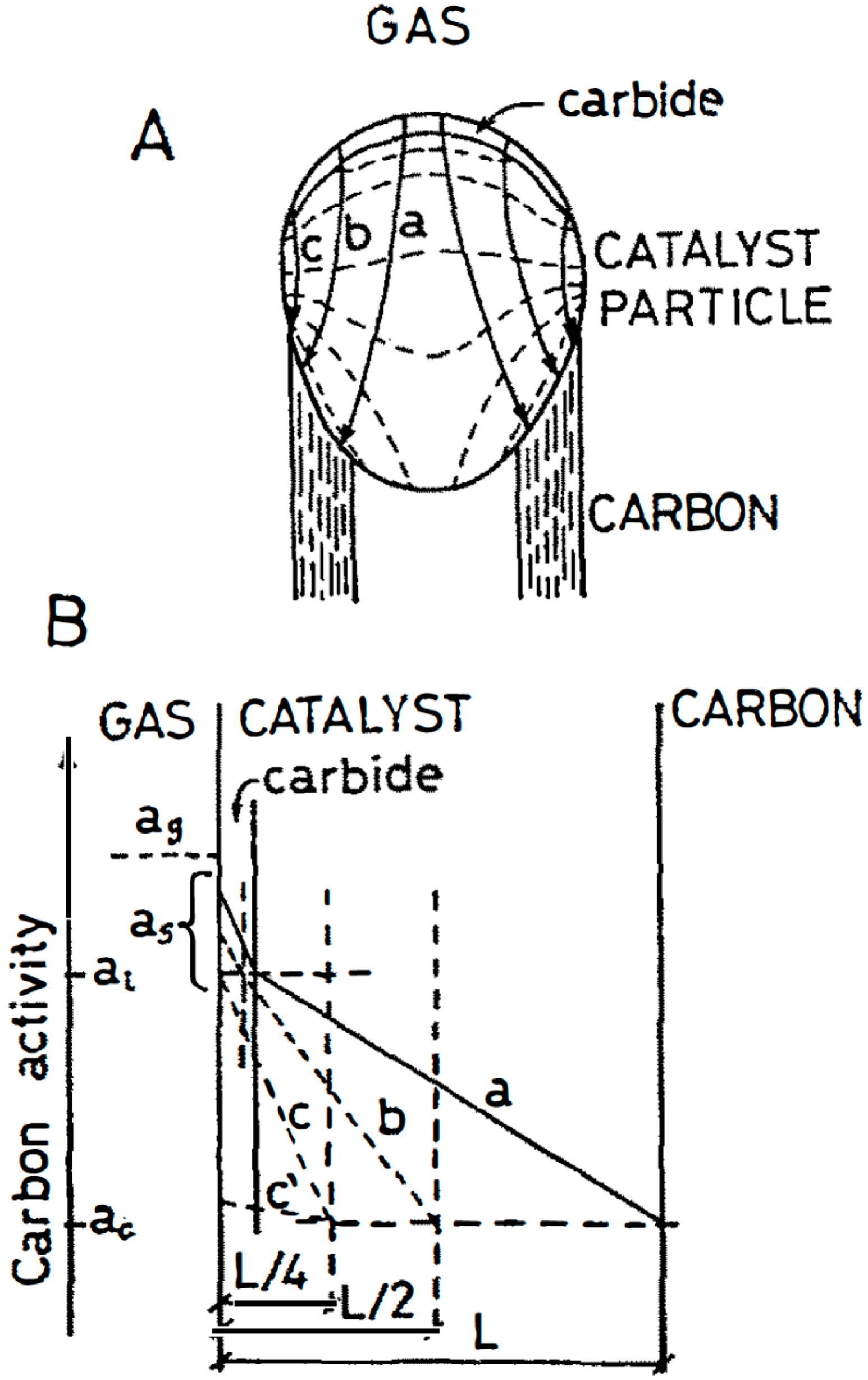
Observed Behavior	Bulk Diffusion	Surface Diffusion
Zero order reaction kinetics	Yes	No
Temperature dependence, Ea~Cdif.	Yes	No
Various gases, same rates (route I, low T)	Yes	Yes
Ni3C recession	Yes	No
Nucleation inhibits further nucleation	Yes	No
Kinetic linearity	Yes	Yes
Smaller particles, faster growth	Yes	Yes
C bulk diffusion: covalent radius ratio	Yes	No

), and C and H bulk diffusion in transition and noble metals are considered [2,3]. Detailed kinetic studies performed 50 years ago clearly evidenced the mechanism of catalytic carbon formation from olefins and acetylene using Fe, Co, Ni [4]. A more detailed description of the C flux and solid-state phase geometry was included in a study of C formation on steel [5].

2. Thermodynamics versus Kinetics. Reversible versus Irreversible Carbon Formation

Thermodynamics may be used to indicate which reaction conditions are favorable for carbon formation. However, kinetics is the appropriate approach for mapping the active reaction conditions prevailing, in order to understand the operating mechanism and to maximize production. It is frequently asserted that diamond does not turn to graphite despite thermodynamics. Again, the prevailing reaction route is the fastest one, not necessarily the one with the most favorable thermodynamics.

Another important point is the reversibility of a reaction. A prevailing route may not operate in the reverse mode just by changing the thermodynamic conditions. Examples are shown in Figure 1 of reversible and irreversible carbon formation. Bromley and Strickland-Constable, using CO/CO₂ [6], and Bernardo and Trimm, covering three gas systems (CO₂/CO; H₂/CH₄; H₂O/CO₂–H₂), made detailed kinetic studies of carbon formation versus gasification [7]. When a mechanism is well understood, thermodynamic control is useful to optimize production and structure.

In the comprehensive review by Jourdain and Bichara, the dissociation energies of C–H bonds, Gibbs free energy as a function of temperature and Ellingham diagram for carbide formation were included; a very useful reference for knowing the possible regions of temperature and pressure at which C formation may occur [1]. However, only kinetics can reveal the active reaction conditions prevailing and to understand the operating mechanism.

Thermodynamics must be favorable, but the prevailing reaction route must be determined by studying kinetics and discovering the mechanism (as the prevailing reaction route is the fastest one, not the one with the most favorable thermodynamics, as already stated). Aiming at understanding CNT nucleation and growth, numerous Monte Carlo/molecular dynamics studies, as well as fullerene-like cap formation studies, have been performed in recent years. Several groups have used the Molecular Dynamics (MD) and Monte Carlo (MC) methods of computer simulation and DFT calculations. All those studies are of interest, but do not predict the prevailing operating mechanism—just like thermodynamics. Kinetics is the key to understanding operating mechanisms.

3. Interstitial Carbon Bulk Diffusion Operation

Interstitial bulk diffusion operates when small moving atoms are present in a solid. Barrer indicated that interstitial diffusion prevails when the covalent radius of the solute versus the solvent is less than 0.59 [8]. Covalent radiuses of the elements up to an atomic number of 55 are graphically represented in Figure 2. The list of covalent radiuses shown in

Table 2. Melting points, Tammann temperatures and interstitial C diffusion data for seven metals frequently used as catalysts for carbon formation. Ratios of atomic radiuses (AR) of solute (C atoms) and solvent (metal catalysts) are between 0.50–0.54. As a rule, when the ratio is below 0.59, interstitial diffusion operates [8]. That ratio condition is fulfilled by carbon atoms bulk diffusion in all metals included.

Metal	Melting (°C)	TTa (°C)	ARsolv (pm)	ARsolu/ARsolv
Fe	1538	632	140	0.50
Co	1495	611	135	0.52
Ni	1455	590	135	0.52
Cu	1083	405	135	0.52
Ru	2334	1030	130	0.54
Rh	1964	845	135	0.52
Pd	1555	641	140	0.50

indicates that interstitial diffusion operates with C atoms dissolved in transition and noble metals. Barrer’s book is an excellent basis on which to review bulk diffusion in solids, which was a very active research area in the period 1910–1950. Some researchers relate high solubility with high diffusivity in solids, but Barrer remarked that in most cases, an increase of solubility (e.g., with temperature change) corresponds to lower solubility.

4. Recent Graphene Nucleation Studies

Geometry of the catalyst nanoparticle has a key role in the rate and shape of C growth. Geometry is essentially a consequence of the initial mode of catalyst nanoparticle formation. One region of the particle surface will nucleate more easily. This corresponds to lower C interstitial diffusion. Therefore, further graphene nucleation in adjoining areas is not possible. The shape of the nanoparticles can change progressively above the Tammann temperature, due to interaction of the graphene growth process with the particle external surface. Bamboo-like growth has recently been discussed [9]. It is well known today that CNT chirality is influenced by geometry due to graphene nucleation, surface bending and growth mode adjustments.

Several studies by Lund et al. confirmed the C bulk diffusion mechanism and evidenced the gas phase carbon activity (a_c) as a driving force for C dissolution and diffusion [10,11]. The driving force for diffusion is the difference in carbon activity in the two sides of the catalyst particle. The carbon activity on the external catalyst surface depends on the gas temperature driven C diffusion model. Our kinetic study provided evidence against that proposal (see Figure 2); the rate of carbon formation from C2, C3 olefins (exothermic) was exactly the same using butenes (endothermic). The model of Lund et al. used a simple geometry. However, CNT nucleation and growth locations should be taken in account. Lund et al. reminded the readers of the Darkens experiment, using Fick’s law based on concentration versus activity. The flow was correctly predicted using the thermodynamic activity: J = D (da_c/dx).

Several authors have recently studied the initial formation of graphene monolayer islands on certain crystal faces of metal nanoparticles (2012–2016) [12,13]. The islands usually become hexagonal and sometimes triangular, after a few minutes at 500 °C. Picher et al. [12] used environmental transmission electron microscopy (TEM) to study nucleation of single-walled carbon nanotubes (SWCNTs) formed from C₂H₂ on cobalt nanoparticles. They studied the stability of the graphene islands on Ni(111) with zigzag edges with different energies, depending on the carbon atoms interaction to hollow or on-top Ni sites.

The formation of graphene sheets (being lifted to convert into nanotubes) was observed (with time resolved observations). Cabrero-Vilatella et al. [13] proposed a model for graphene growth on transition metals (SLG-single layer versus FLG-few layer).

Gao et al. studied graphene nucleation from C₂H₄ on Cu(111) at 1000 °C [14]. Monolayer islands with two domain orientations were observed. Eres et al. studied “single crystal graphene growth” on Cu foils [15].

These studies showed that a layer of graphene is formed on suitable catalysts (Fe, Co Ni) at low temperatures (reactant gas surface catalytic dissociation) and in many transition and noble metals at higher temperatures. In this case, pyrolysis forms C₂/C₃ particles in the gas phase that impinge on the catalyst particle surface, dissolve and diffuse randomly. A graphene layer nucleates and grows on (111) facets, in the case of Ni. When the graphene layer bends 90° at a nanoparticle (111) facet edge, graphene growth occurs. The preferential geometry of the growing graphene nanoislands and the way growth evolves when the nanoislands touch the borders of the crystal facet may be of interest for understanding chirality options.

Inside the catalyst nanoparticle and near the nanotube growth region, the C concentration is always low, due to its local constant consumption. Therefore, the driving force for carbon diffusion inside the metal nanoparticle is maintained (Figure 3). Kinetics data help to clarify the details of the mechanism prevailing under a given temperature and pressure conditions, as well as the role of nanoparticle geometry, crystal structure and preliminary pretreatment procedures. It is clear that, in catalytic and hybrid growth, a new graphene layer is always formed below the previous one. However, in pyrolytic growth, a new graphene layer is formed above the previous one, as previously remarked.

5. Comprehensive Kinetics, Activation Energies and Reaction Orders

As already mentioned, kinetics is the key to understanding the prevailing reaction routes. Optimizing rates and shape is easier when the reaction mechanism is known. Nucleation and growth take place at different regions of the catalyst particle, with different crystal orientation.

Different sizes and shapes of nanoparticles facilitate different forms of growth. When using catalyst nanoparticles, CNT growth involves solid-state diffusion both during initial solid-state changes at nano level and then as an essential sustained step supplying carbon to the growth process. The time found for 2 mm “penetration” of C in a Fe metal block at 1000 °C was 61 h [16]. Therefore, we can estimate that the time required to “penetrate” into a Fe nanoparticle with a diameter of 20 nm is 2 s. Therefore, nanoscale facilitates the diffusion process.

Kinetic linearity is observed in some reactions involving solids, as discussed by Budnikov and Ginstling, and attributed to the rate of the process, being limited by internal diffusion (see Figure 4) [17]. However, linearity just means that a reaction is operating in the steady state.

The studies summarized above confirm that isothermal kinetic studies are a reliable approach for understanding a reaction mechanism in this case. There have now been several recent kinetic studies of catalytic carbon formation based on carbon growth using nanoparticles [18,19,20,21,22,23,24,25].

The alternative Arrhenius plots observed were recently revised [2]. Figure 3 illustrates the kinetic behavior observed in some of those studies—including the occurrence of kinetic linearity. In the studies by Chesnokov et al. [18,19], the kinetics of C formation from butadiene Ni/Al₂O₃ gave experimental results very similar to those of Lobo [5,26] (see Figure 4A,B). The Arrhenius plot was not drawn here, but the rates were constant and the weight versus time plots were linear. The values of the rates can be fitted into Figure 3, with the same drop between 500 °C and 600 °C and an activation energy “which is consistent with the activation energy of carbon diffusion through Ni” [21].

Lobo studied the kinetics of C formation on Fe, Co and Ni 50 years ago [4]. The experiments lasted around 3–4 h each, to include a sufficiently long period of steady-state rate (linearity of the weight versus time record). A total of 160 experiments were performed, 60 with just the hydrocarbon and 100 with a combination of H₂ and a C₂ to C₄ olefin or C₂H₂. Alternative gas pressures and temperatures were used, so that reaction orders and activation energies were evaluated. These studies confirmed that isothermal kinetic studies are a reliable approach to understand a reaction mechanism in this case, and the operating rate determining step as well. Three kinetic routes were clearly observed, as summarized in

Table 3. Kinetic routes observed in CNT/graphene formation based on several detailed kinetic studies. A remark on how to change routes is included.

Kinetic Routes	I—Catalytic Route	II—Hybrid Route	III—Pyrolytic Route (CVD)
Temperature Range and Growth Mode	300–550 °C Surface catalysis, C diffuse & grows	550–700 °C C black atoms dissolve & grow	600–900 °C C black forming graphene layers
Carbon Formation Type	Geometry selective surface catalysis + growth	Selective nucleation and growth catalysis	Impingement, non-selective C2, C3… Cn
Surface Catalysis: C Atoms Formed?	Yes. Selective Ex: Ni(100)	No	No
Carbon Atoms Bulk Diffusion?	Yes	Yes	No
CNTs/CNFs Growth: Shape Catalysis	CNTs growth CNFs growth Selective Ex: Ni(111)	CNTs growth CNFs growth Selective	External surface layers on CNTs, other forms at very high T
How to Change Routes? Remarks	Higher T	Higher P	Carbon fouling on the walls
Active Catalysts	Ni, Co, Fe	Pt, Ru, Mo, Ni…	No catalysts, just shape interaction
Temperature Range and Growth Mode	300–550 °C Surface catalysis, C diffuse and grows	550–700 °C C black atoms dissolve and grow	600–900 °C C black forming graphene layers

[6].

6. Recent Kinetic Studies

Fick’s laws “rule” solid-state chemistry inside the catalyst nanoparticles, both during initial solid-state changes (Fick’s 2nd law) and during steady-state carbon growth (constant C atoms flux, Fick’s 1st law).

In fact, linearity is scientific evidence that a steady-state carbon deposition is taking place and no further solid-state changes are occurring. This means that the meta-stable solid-state phases formed initially under reaction conditions are stable or metastable. Rotation of solid-state phases was proposed in 1970 by McKee as the basic mechanism for catalytic carbon gasification [27] and adopted by several authors since then. In our opinion, this is not correct. There are no “molecules” in the solid state, just atoms and ions. Fick’s laws “rule”, kinetically speaking. The occurrence of carbon bulk diffusion through the catalyst in catalytic carbon formation has, in fact, been proved in 1971, based on detailed kinetics [26]. Bulk diffusion of C atoms through the Ni thin crystal was proved, as well as inhibition of further graphene nucleation on catalyst surface areas at short distances. This is most probably due to the lowering of C atoms concentration inside the metal particle.

Searching for a mechanism to explain catalytic C formation reactions just by using thermodynamics or first principles density theory and ignoring kinetics is not correct. C surface diffusion prevailing over C bulk diffusion through the catalyst is very unlikely, as remarked in several solid-state chemistry studies, due to the pre-exponential factor required in the kinetic equation [8]. Additionally, interstitial C atoms dissolved in bulk move randomly but cannot react to form a product. C atoms react easily on the surface.

Monzon et al. studied the kinetics of carbon formation from C₂H₄/H₂ on Fe and of CH₄ on Ni and Ni-Co supported on Mg-Al [20,22] (check Figure 4C,D). Sustained linearity was observed in many cases. Rate decrease with time (30 to 60 min) was observed at higher temperatures and attributed to progressive encapsulation. We may say that route III is progressively prevailing over route II, due to the covering of the catalyst surface with gas phase formed carbon (probably C₂, C₃ flakes). Carbon deposition continues with successive layers of graphene being formed around the original catalytic/hybrid CNTs.

Puretzky et al. observed, at 600 °C, a progressive decrease of the rate but, at higher temperatures, they found a progressive increase [23,24,25]. Carbon growth was not evaluated by weight/mass changes, but by CNT growth (length). The progressive decrease in reaction rate may be due to: (a) Reduction of the C flux through the catalyst particles; (b) more difficult access of the reactant gas to the nanoparticles surface; or (c) progressive solid-state changes (in geometry, in size or in composition). The changes in shape are facilitated above the Tammann temperature, as discussed below for the case of bamboo-like growth. An estimation of the activation energy in the 500–700 °C range, using their data, gives ~35 Kcal/mole. This suggests that C bulk diffusion is the rate-determining step. The reaction order should be zero.

Linearity does not mean that a single solid phase is present as catalyst—just that the geometry and thickness of the solid phase or phases assumed by the catalyst particles are stable or meta-stable. This has been discussed in detail for the case of catalytic carbon gasification, following a similar reverse mechanism: carbon atoms from coke dissolve and diffuse through the catalyst nanoparticle and react with a gas (O₂, CO₂, H₂O, H₂, etc.) at the external surface [28,29]. The relevance of the Tammann temperature to the effectiveness of the catalyst–carbon contact was proposed.

Using Ni, initial formation of Ni₃C was found to be unstable, once graphite nucleates. DeJong and Geus evidenced this, on the basis of a study using magnetism change measurements [30]. The recession of Ni₃C was demonstrated using saturation magnetization. In 15 min, Ni seems to be totally converted to Ni₃C, but then it recedes in a few minutes—certainly due to instability of Ni₃C, in the presence of the just formed graphene. However, Ni₃C (persistent) is the phase in equilibrium with the reactant gas (CH₄, at 570 °C). The constant C flux during carbon growth ensures that both equilibria are operating, each at different sides of the Ni nanoparticle. In fact, the return of Ni magnetization was not 100%.

The knowledge of the solid-state phases prevailing during reaction must be known to find the details of the operating mechanism. Nowadays, many authors use Raman shift [31]. However, this information is usually obtained at ca. 80 °C. The dependence of Raman shift signal with temperature has been studied in some detail [32,33]. However, information about the solid-state phases that are active under steady-state reaction conditions is required. These phases are frequently different.

Thus, in order to identify the phases prevailing and operating during reaction, we need in situ observations like TEM, X-ray diffraction (XRD), etc., and this is usually not available using commercial Raman shift. Another difficulty that occurs, particularly using nanoparticles, is the detection of thin phases: invisible, but kinetically essential (see Figure 3). It is sometimes possible to identify a very thin phase to use a non-active gas phase composition. If no reaction is taking place an enlargement of the thin phase takes place.

Scanning temperatures are a useful initial method for finding the active experimental conditions, but without steady state experiments exhibiting linearity, a true kinetic study cannot be performed.

The rate drops when route II changes to route III (see Table 3). There is no increase in CNTs length growth, just thickness growth by new graphene layers formation. In vertically aligned carbon nanotube (VACNT) arrays, the interstitial diffusion of the reactant gas to the bottom of the arrays may become the rate-determining step. The rates may decrease progressively, as the diffusion distance gets longer and longer.

Bedewy et al. also studied the kinetics of aligned CNTs grown from C₂H₄/H₂, at 750 °C, catalyzed by Fe/Al₂O₃, measuring the length change [34]. Linearity was observed. As remarked above, linearity means that a constant carbon flux is operating through the catalyst nanoparticles and initial solid-state changes have ceased. In this case, the rate must depend on the impingement on the catalyst nanoparticles of pyrolytically formed C₂/C₃ species, followed by C diffusion through the nanoparticle (Fick’s Law). C atoms join the growth process at the base of the CNT. A full kinetic study would require pressure versus rate measurements (evaluating reaction order) and activation energy determination, by plotting rates at various temperatures. These authors found diameter dependence in CNTs growth kinetics: smaller diameter CNTs growth “activates more slowly” but has “longer catalytic lifetimes”.

Geohegan et al. studied kinetics by in situ growth rate measurements and length control of vertically aligned arrays of multi-walled carbon nanotubes (VA-MWCNT) grown from C₂H₂ on Mo-Fe-Al films. Linearity of growth over time was observed at 600 °C and above. The highest growth rates were observed at 730 °C. They used interference fringes and laser beam to measure the nanotubes length [24].

Salipira et al. studied C formation from CH₄ on Ni as a function of catalyst preparation modes [35]. In the range of 600−700 °C, the hybrid route (II) prevailed. Deactivation of the catalyst was observed at 700 °C and above. They noticed that “nickel particles were encapsulated by graphene layers when methane conversion was performed at 700 and 900 °C”. This was certainly due to the prevalence of the pyrolytic route (III). A relation between catalyst particle diameter versus CNT diameter was found.

7. Conclusions

In this review paper, we intended to correct the approach frequently used: that the operating mechanism in carbon formation can be found-based in thermodynamic information. We consider that:

1. To understand a reaction mechanism and optimize production “kinetics is more important than thermodynamics”.

2. The carbon formation mechanism involving C bulk diffusion, through transition and noble metals used as catalysts, has been proved in the past by isothermal detailed kinetic studies of weight gain, using microbalances.

3. A kinetic linearity record of weight gain is evidence that a steady-state growth regime is operating.

4. Thermodynamics is important for indicating the regions of temperature and gas pressure where a reaction may operate, but it does not indicate the prevailing route and which mechanism is taking place.

5. It is important to understand the stable solid-state phases of the metal catalyst or alloy operating under reaction conditions, at each side of the catalyst metal particle, and explain the geometry of the solid-state phases observed—usually at the nano-scale.

In conclusion, detailed kinetics is the key to obtaining evidence of the operating mechanism.